0.   引言

桩基础在近海结构设施中起着重要的作用，桩基础经常受到水平动荷载的作用，如波浪荷载、风荷载和水平地震荷载等。因此，分析动力荷载作用下桩的动力响应具有重要的意义^[1-2]。由于桩体的振动直接受周围土体的影响，因此桩–土动力相互作用一直是研究的热点问题^[3-4]。此外，不同于陆地上的结构，海上结构物如高桩码头、海上风机、石油平台等还需要考虑水–桩–土之间的耦合作用。因此，考虑到海上构筑物的安全，有必要研究在水平动力荷载作用下考虑水–桩–土耦合作用的桩体动力响应。

近年来，水平动力荷载作用下桩–土耦合振动问题受到了学者们的广泛关注。在早期，许多学者将桩周土体视为Winkler模型^[5-7]。Winkler模型用弹簧和阻尼器代替土体介质，将多维边值问题转化为简单的垂直方向一维波传播的杆问题，该模型简单易用，促进了桩基水平振动响应的理论研究。然而，大多数模型参数的确定都是根据经验而非理论推导，不能真实反映桩–土耦合振动效应。Novak等^[8]、Nogami等^[9]提出了平面应变模型，得到了在桩体顶部动荷载作用下桩体动力刚度和阻尼的表达式。平面应变模型优于Winker模型，需要注意的是，在平面应变模型中，垂直方向的应变为零，波只在水平方向传播，忽略了周围土体的三维波效应；郑长杰等^[10]建立了黏弹性土层中大直径管桩水平动力响应的解析解；栾鲁宝等^[11]研究了黏弹性土层中桩–土横向耦合振动问题，同时考虑了竖向应力梯度变化和轴向荷载二阶效应的影响。

近海结构物动力分析时应考虑结构与水的相互作用，因为结构与水的相互作用对结构动力响应有重要影响。假设土体地基为刚性，各学者对水–结构动力相互作用进行了一系列的研究。此外，在不考虑水体表面波和压缩性的情况下，水体对结构的动水压力可以用附加质量代替。Chwang等^[12]基于二维势流理论，提出了斜面刚性坝上动水压力的精确解；Williams^[13]采用边界积分法研究了水中圆柱体的动力响应；刘振宇等^[14]给出了内外水作用下圆形空心桥墩动水压力的表达式，在一定程度上对由Li等提出的动水压力表达式进行了修正和简化；Wang等^[15]提出了一种可以用于任意截面形状结构地震反应分析的子结构方法，结果表明该方法的精度足以满足工程应用。

对于近海结构而言，大量研究表明水体和土体介质对结构动力响应都有一定的影响^[16-20]。目前，虽然大部分数值方法都可以方便、高效地解决水–桩–土相互作用问题。然而对于某些参数的研究，解析方法有时比数值分析方法更加方便。因此，本文建立了水体和土体阻抗下水平振动桩的解析解。此外，还对桩的振动特性进行了参数化研究。

1.   计算模型及基本假定

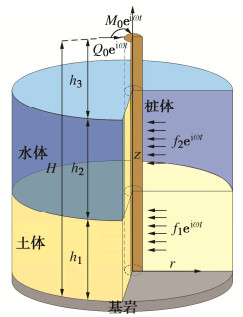
水–桩–土相互作用系统模型如图 1所示。桩体顶部受到动力荷载${Q_0}{{\text{e}}^{{\text{i}}\omega t}}$和${M_0}{{\text{e}}^{{\text{i}}\omega t}}$的作用（其中$\omega$，$t$分别为圆频率和时间），(r, z)表示桩体柱坐标系，桩体半径、土体厚度、水深、桩体出水面高度和桩体总高度分别为r₀，h₁，h₂，h₃，H。

图  1  水–桩–土相互作用系统模型

Figure  1.  Model for water-pile-soil interaction system

下载: 全尺寸图片 幻灯片

本文在建立方程时采用如下假定条件：①水体在水平方向是无限的，且是无旋、无黏性，在动力荷载作用之前不发生扰动；②桩体采用线黏弹性Euler梁模拟，桩体截面为圆形，桩体与水体、土体和刚性地基接触良好，接触面不发生滑移；③土体为黏弹性、均质、各向同性介质，土体材料阻尼采用与频率无关的滞回阻尼；④在水平动荷载作用下水–土相互作用影响较小，因此未考虑水–土相互作用；⑤忽略与水平振动相关的土体竖向位移^[9-10]。

1.1   水体控制方程

根据线性波浪理论，水体动水压力在柱坐标下可以表示为$p(r,\theta ,z){{\text{e}}^{{\text{i}}\omega t}}$，以水体动水压力表示的控制方程为

式中，$k = \omega /{c_{\text{w}}}$，${c_{\text{w}}}$为水中波传播的速度。当水体波速${c_{\text{w}}} \to \infty$时，$k \to 0$，此时水体表示不可压缩。当水体为不可压缩介质时，水体对桩体的作用可以用附加质量表示，且此时水体没有考虑辐射阻尼的影响^[21]。

1.2   土体控制方程

在土体介质中，土体径向位移和环向位移可以分别表示为$u_r^{}(r,\theta ,z){{\text{e}}^{{\text{i}}\omega t}}$，$u_\theta ^{}(r,\theta ,z){{\text{e}}^{{\text{i}}\omega t}}$。

土体径向位移表示的耦合动力控制方程为

土体环向位移表示的耦合动力控制方程为

式中，$\lambda _{\text{s}}^{\text{*}}{\text{ = }}2G_{\text{s}}^{\text{*}}{\nu _{\text{s}}}/(1 - 2{\nu _{\text{s}}})$为土体复Lame常数，${\nu _{\text{s}}}$为土体泊松比，$G_{\text{s}}^{\text{*}} = {G_{\text{s}}}{\text{(}}1 + 2{\text{i}}{\beta _{\text{s}}}{\text{)}}$为土体复剪切模量，${G_{\text{s}}}$为土体剪切模量，${\beta _{\text{s}}}$为土体滞后阻尼，${\rho _{\text{s}}}$为土体质量密度。

1.3   桩体控制方程

根据动力平衡条件，容易建立桩体动力控制方程。则以桩体在土体、水体和空气中的水平位移${w_{{{\text{p}}_i}}}{{\text{e}}^{{\text{i}}\omega t}}(i =$ $1,2,3)$表示的动力控制方程为

式中，${E_{\text{p}}}$，${I_{\text{p}}}$和${m_{\text{p}}}{\text{ = }}{\rho _{\text{p}}}{\text{π }}r_0^2$分别为桩体弹性模量、截面惯性矩和单位长度的质量，$E_{\text{p}}^ * = {E_{\text{p}}}(1 + 2i{\beta _{\text{p}}})$，${\beta _{\text{p}}}$为桩体滞后阻尼，${f_i}(i = 1,2,3)$分别为土体、水体和空气$({f_3} = 0)$对桩体的阻抗力。

1.4   边界条件

水–桩–土相互作用系统需要满足以下边界条件：

桩体顶部边界条件

水体表面边界条件

当忽略自由表面波时，边界条件（8）就变换为${\left. {p(r,\theta ,z)} \right|_{z = {h_1} + {h_2}}} = 0$。

水–土交界面边界条件

基岩表面边界条件

桩段连接面边界条件

桩–土交界面边界条件

桩–水交界面边界条件

水体动水压力无穷远处边界条件

土体位移无穷远处边界条件

2.   方程的求解

2.1   桩–土相互作用

根据亥姆霍兹分解、分离变量法和边界条件（10）~（12），（23），（24），（27）和（28）可以得到土体径向位移和环向位移为^[9]

式中${g_i} = \frac{{(2i - 1)\pi }}{{2{h_1}}},i = 1,2,3, \cdots$；$q_i^2 = \frac{{G_{\text{s}}^{\text{*}}g_i^2 - {\rho _{\text{s}}}{\omega ^2}}}{{\lambda _{\text{s}}^{\text{*}} + 2G_{\text{s}}^{\text{*}}}}$；$s_i^2 = \frac{{G_{\text{s}}^{\text{*}}g_i^2 - {\rho _{\text{s}}}{\omega ^2}}}{{G_{\text{s}}^{\text{*}}}}$；${A_i}$，${B_i}$是未知系数。

根据桩–土位移连续边界条件可得

式中，

再根据力和位移的关系，可以得到土体阻抗力${f_1}$为

式中，${b_{{\text{h}}i}}$为第i阶水平阻抗因子，${b_{{\text{h}}i}} = - {\text{π }}{r_0}\{ (\lambda _{\text{s}}^ * + 2G_{\text{s}}^{\text{*}}) \cdot$ $q_i^2{K_1}({q_i}{r_{\text{0}}}) + G_{\text{s}}^ * {T_{1i}}s_i^2{K_1}({s_i}{r_{\text{0}}})\}$。

当$i = 1$时，将式（33）代入式（5）可以得到用桩体在土中的位移表示的控制方程为

式（34）的解由两部分组成，齐次方程的通解${w_{{{\text{h}}_1}}}({z_1})$和非齐次方程的特解${w_{{{\text{t}}_{\text{1}}}}}({z_1})$可以表示为

其中非齐次方程的特解${w_{{{\text{t}}_{\text{1}}}}}({z_1})$可以表示为

式中，${b_i}$为常数。

将式（36）代入式（34），可以得到常数${b_i}$为

齐次方程的通解可以表示为

式中，${Q_1}$，${Q_2}$，${Q_3}$，${Q_4}$为未知常数。

将式（36）~（38）代入式（35）可得

桩与土体接触良好，因此结合式（29），（40）进一步利用三角函数正交性，${A_i}$的表示式为

式中，

将式（41）代入式（40）可得

式中，

2.2   桩–水相互作用

根据分离变量法，再进一步利用边界条件（8），（9），（25）和（26），可以得到水体水平方向对桩体的阻抗力${f_2}$^[21]：

式中${h_1} \leqslant {z_2} \leqslant {h_1} + {h_2}$，${r_1} = - {\text{i}}r{\lambda _j}\sqrt {{\text{1}} - {{{\text{(}}\omega /{\lambda _j}c{\text{)}}}^2}}$；${\lambda }_{j}=\left\{\begin{array}{c}{\overline{\lambda }}_{j}\mathrm{tanh}({\overline{\lambda }}_{j}{h}_{2})=\frac{{\omega }^{2}}{g}(j=0)\\ {\lambda }_{j}\mathrm{tan}({\lambda }_{j}{h}_{2})=\frac{-{\omega }^{2}}{g}(j\ge 0）\end{array}\right.$，${\bar \lambda _j}$为${\lambda _j}$的虚部；${a_{hj}} = \frac{{\rho {\text{π }}r_0^2{\omega ^2}H_1^{\left( 2 \right)}({r_1})}}{{{r_1}H_1^{\left( 2 \right)'}({r_1})}}$是第j阶水平阻抗因子；${C_j}$是未知系数。

当$i = 2$时，将式（45）代入式（5）可以得到用桩体在水中的位移表示的控制方程：

与桩–土相互作用求解类似，式（48）解可以表示为

式中，${Q_5}$，${Q_6}$，${Q_7}$，${Q_8}$为未知常数。

桩与水体也接触良好，因此结合式（46），（49），进一步利用三角函数正交性得到${U_{1j}}$的表示式为

式中，

将式（50）代入式（49）可得

式中，

2.3   空气中桩

当$i = 3$时，用桩体在空气中的位移表示的控制方程为

式中，${h_2} \leqslant {z_3} \leqslant {h_2} + {h_3}$。

式（54）的通解可以表示为

式中，${Q_9}$，${Q_{10}}$，${Q_{11}}$，${Q_{12}}$为由未知常数。

2.4   桩体位移求解

将式（43），（52），（55）代入边界条件（13）~（15），（17），（19），（21）和式（16），（18），（20），（22）和式（6），（7），经过一些转化可得

将式（57），（58）代入式（56）并结合式（59），可得

未知系数${\boldsymbol{Q}_{{w_1}}}$，${\boldsymbol{Q}_{{w_2}}}$和${\boldsymbol{Q}_{{w_3}}}$分别可以通过式（57），（58），（60）得到。基于这些系数，桩体位移可以确定。

3.   模型验证

为了评价桩–土、桩–水相互作用对桩体顶部位移的影响，采用表 1列出的土体、水体和桩体的参数。本文中假设桩体顶部施加的剪力和弯矩分别为1 ${\text{MN}}$和1${\text{kN}} \cdot {\text{m}}$，输入振动频率$f$的区间范围为0∶0.05∶20。

表  1  桩体、土体和水体参数

Table  1.  Parameters of pile, soil and water

桩长H/m	桩出水面长度h3/m	直径2r0/m	杨氏模量Ep/GPa	密度${\rho _{\text{p}}}$/(kg·m-3)	滞后阻尼${\beta _{\text{p}}}$	土体厚度h1/m	杨氏模量Es/MPa	密度${\rho _{\text{s}}}$/(kg·m-3)	泊松比${\nu _{\text{s}}}$	滞后阻尼${\beta _{\text{s}}}$	水深h2/m	密度$\rho$/(kg·m-3)	波速${c_{\text{w}}}$/(m·s-1)
60	0	4	30	2500	0.02	30	5	1800	0.3	0.02	30	1000	1438

下载: 导出CSV 

| 显示表格

本文中土体位移和水体速度势的表达式是一个无穷级数。因此，有必要将无穷级数转化为有限级数。从图 2中可以看出，在无水和有水情况下将无穷级数截断为5~10项，结果趋于收敛。因此，i和j可以分别取为6，7。

图  2  桩体位移收敛性分析

Figure  2.  Convergence tests on displacement of pile

下载: 全尺寸图片 幻灯片

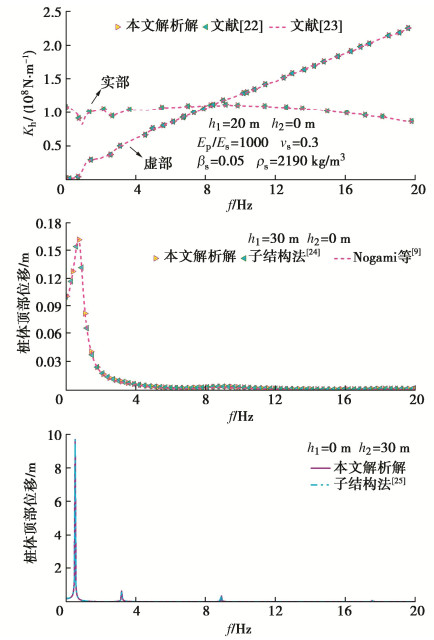
为了验证本文方法的合理性，在频域下将本文解析解分别退化为两种情况：①第一种为无水有土情况的解析解与付鹏等^[22]、郑长杰等^[23]、子结构法（王丕光等^[24]）和Novak法^[9]的解进行对比。②第二种为无土有水情况的解析解与子结构分析方法的解（王丕光等^[25]）进行对比，结果见图 3。最后，在时域下将本文水–桩–土系统模型的解析解与子结构法和有限元ABAQUS法进行对比，结果见图 4，其中水平动荷载采用的是狄拉克脉冲，幅值为${10^6}$，脉冲激励时间0.2 s，如图 5所示。从图 3，4中可看出，本解析解与子结构法、Novak法和有限元ABAQUS法吻合较好。

图  3  解析法与其他几种方法的对比

Figure  3.  Comparison between analytical method and other methods

下载: 全尺寸图片 幻灯片

图  4  解析法与子结构法和Abaqus的位移时程对比

Figure  4.  Comparison of time history of displacement among analytical method, substructure and Abaqus methods

下载: 全尺寸图片 幻灯片

图  5  狄拉克脉冲

Figure  5.  Dirac impulse

下载: 全尺寸图片 幻灯片

4.   数值算例

4.1   自由表面波的影响

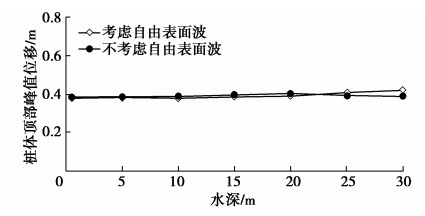
图 6表示有水有土情况时，考虑与不考虑自由表面波情况下桩体顶部位移峰值随着水深的变化。从图 6中可以看出，水体自由表面波对桩体位移响应的影响很小，几乎可以忽略。因此，后面的算例基于无自由表面波分析。

图  6  考虑与不考虑自由表面波情况下桩体位移峰值随着水深的变化

Figure  6.  Variation of displacement at pile top with water depth considering or not considering free surface waves

下载: 全尺寸图片 幻灯片

4.2   频域下水深的影响

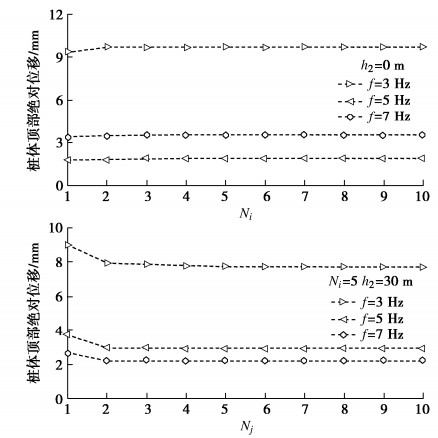
图 7表示有土情况时，不同水深下桩体顶部位移绝对值随着频率的变化关系。

图  7  不同水深情况下桩体顶部位移随频率的变化

Figure  7.  Variation of displacement with frequency under different thicknesses of water layer at pile head

下载: 全尺寸图片 幻灯片

从图 7中可以看出，水深对桩体顶部位移有一定影响，且位移峰值对应的频率随着水深的增加而减小。

为了方便分析在不同土体和桩体参数情况下，水体对混凝土桩和钢管桩顶部位移响应的影响。定义R₁，R₂为有水时桩体顶部最大位移绝对值与无水时桩体顶部最大位移绝对值的比值，R₂为有水时桩体顶部最大位移绝对值对应频率与无水时桩体最大位移绝对值对应频率的比值（桩体总长度不变），其中钢管桩的弹性模量、密度、半径和泊松比分别取210 GPa，7850 kg/m³，4 m和0.2，薄壁厚度取为6 cm。

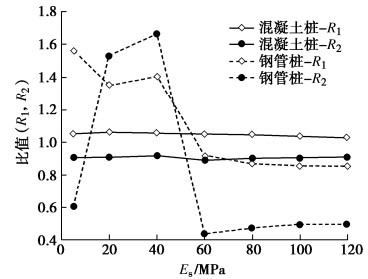
图 8~10表示混凝土桩和钢管桩R₁和R₂随着桩体半径、土体弹性模量和土体阻尼的变化。

图  8  R₁和R₂随桩体半径的变化

Figure  8.  Variation of R₁ and R₂ with pile radius

下载: 全尺寸图片 幻灯片

图  9  R₁和R₂随土体弹性模量的变化

Figure  9.  Variation of R₁ and R₂ with soil modulus

下载: 全尺寸图片 幻灯片

图  10  R₁和R₂随土体阻尼的变化

Figure  10.  Variation of R₁ and R₂ with soil damping

下载: 全尺寸图片 幻灯片

从图 8可以看出，随着桩体半径的增大，水体对混凝土桩和钢管桩顶部位移响应有一定影响；还可以看到，在半径为2 m时，水体对桩体顶部位移响应的影响不大，因此，图 9，10中定义r₀=4 m。从图 9，10可以看出，随着土体弹性模量和桩体弹性模量的增大，水体对混凝土桩顶部位移响应的影响范围为3%~10%，而对钢管桩顶部位移响应的影响范围为15%~60%；且从图中可以看出，随着土体和桩体参数的改变，水体对混凝土桩的自振频率影响范围为9%~15%，而对钢管桩的自振频率影响范围为40%~70%。

通过结果来看水体对钢管桩的影响较大，虽然钢管桩的弹性模量和密度较大，但是由于是空心桩体，所以单位截面质量远小于混凝土实心桩体，从而造成水体对钢管桩的影响更加显著。

4.3   时域下水深的影响

图 11表示不同水深情况下桩体顶部位移随时间的变化，其中水平动荷载采用的是狄拉克脉冲，幅值为${10^6}$，脉冲激励时间0.2 s，如图 5所示，且桩体总长度不变，柱形图是不同水深情况下与无水情况下桩顶位移峰值的比值误差。从图 11中可以看出，在桩长不变的情况下，相比于无水，水深小于20 m时对桩体位移响应的影响可以忽略不计。

图  11  不同水深情况下桩体顶部位移随时间的变化

Figure  11.  Variation of displacement with time under different thicknesses of water layer at pile head

下载: 全尺寸图片 幻灯片

图 12表示满水情况（桩长随着水深的变化而变化）以及不同半径和土体弹性模量时，其中Error（%）定义为不同水深情况下与无水情况下桩顶位移峰值的比值。从图 12中可以看出，在一定土体厚度情况下，水深15 m以下对桩体位移响应的影响在7%左右，从工程角度来说一般可以忽略不计。

图  12  不同桩体半径和土体弹性模量以及水深情况下有水与无水桩顶位移峰值的比值误差

Figure  12.  Ratio errors of peak displacement at pile top with and without water under different pile radiis, soil elastic modulis and water depths

下载: 全尺寸图片 幻灯片

5.   结论

本文建立了考虑水–桩–土相互作用的端承桩在桩顶水平动力荷载作用下动力响应的解析解。为了探讨水平动荷载作用下桩体的振动特性，进行了一些参数化研究。主要得出3点结论。

（1）水体自由表面波对桩体位移响应的影响很小，几乎可以忽略。

（2）水体深度的变化对桩体顶部位移有一定的影响，且峰值位移对应的频率随着水深的增加而减小。

（3）随着桩体和土体参数变化，水体对混凝土桩和钢管桩位移响应都有一定影响，且从工程角度来说，水深小于15 m时对桩位移响应影响可以忽略不计。