考虑颗粒破碎的钙质砂边界面循环本构模型

王兆南; 王刚; 叶沁果; 查京京

doi:10.11779/CJGE202105012

考虑颗粒破碎的钙质砂边界面循环本构模型 English Version

王兆南^{1, 2,},
王刚^{1, 2, ,},
叶沁果^{1, 2},
查京京^{1, 2}

1.
山地城镇建设与新技术教育部重点实验室,重庆　400045
2.
重庆大学土木工程学院,重庆　400045

基金项目:

国家自然科学基金项目 51679016

重庆市研究生科研创新项目 CYB20032

详细信息

作者简介:
王兆南(1994—),男,博士研究生,主要从事岩土工程数值计算方面的研究工作。E-mail: znwang@cqu.edu.cn

通讯作者:
王刚, E-mail: cewanggang@163.com

中图分类号: TU43
计量
- 文章访问数: 343
- HTML全文浏览量: 57
- PDF下载量: 192
出版历程
- 收稿日期: 2020-07-12
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-04-30

Cyclic bounding surface model for carbonate sand incorporating particle breakage

WANG Zhao-nan^{1, 2,},
WANG Gang^{1, 2, ,},
YE Qin-guo^{1, 2},
ZHA Jing-jing^{1, 2}

1.
Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400045, China
2.
School of Civil Engineering, Chongqing University, Chongqing 400045, China

摘要

摘要: 钙质砂作为一种海洋生物成因的易破碎材料,由其构成的地基在海洋环境下长期受到动荷载的作用,故模拟钙质砂在循环荷载作用下的颗粒破碎及其对应力应变行为的影响具有重要意义。将引起塑性应变和颗粒破碎的机制分解为两种：有效球应力增加引起的压缩机制和剪应力比变化引起的剪切机制。压缩机制引起的颗粒破碎可由Hardin公式模拟,为适应复杂应力路径,在Hardin公式的基础上建立了增量型的压缩破碎模型。剪切机制引起的颗粒破碎满足两个“递减率”：①在每一个单向剪切过程中,颗粒破碎的累积速率总是在单向剪切起始处最大,并随着单向剪应变的增加而减小；②在总的剪切过程中,颗粒破碎的累积速率随颗粒破碎量的增大而逐渐减小。在边界面本构模型框架中引入所建立的压缩和剪切破碎模型,通过随颗粒破碎量移动的临界状态线反映颗粒破碎对模量、强度和剪胀等应力应变行为的影响,建立了一个考虑颗粒破碎的循环本构模型。通过对钙质砂的单调和循环三轴试验结果的模拟初步验证了所提出本构模型的合理性。
- 钙质砂 /
- 颗粒破碎 /
- 循环荷载 /
- 边界面 /
- 本构模型
Abstract: The carbonate sand is a crushable granular material formed by the marine organisms, and its foundation is subjected to long-term dynamic loading under the ocean environment. Hence, it is of great significance to simulate the particle breakage of the carbonate sand under cyclic loading and its influences on the stress-strain behavior. The mechanism of particle breakage is decomposed of two parts: the compression mechanism with the increase in the mean effective stress, and the shear mechanism with the change of shear stress ratio. The particle breakage caused by the compression mechanism can be simulated by the Hardin’s formula. In order to adapt to the complex stress path, an incremental compression breakage model is established on the basis of the Hardin’s formula. The shear-induced breakage model includes two "declining rules" under the cyclic loading: (1) The accumulate rate of the particle breakage has a maximum value at the initial phase of the monotonic shear process, but decreases with the increasing shear strain. (2) It continuously descends during the whole shear process with the increasing amount of the particle breakage. The compression and shear breakage models are introduced to the framework of the bounding surface constitutive model, and a novel constitutive model considering the particle breakage is established by reflecting the effects of the particle breakage on the stress-strain behaviors such as modulus, strength and dilatancy through the critical state line moving with the amount of the particle breakage. The simulation capability of the proposed constitutive model is verified by comparing with the experimental results of the carbonate sand which is under the monotonic and cyclic drained triaxial compression tests.
- carbonate sand /
- particle breakage /
- cyclic loading /
- bounding surface /
- constitutive model

HTML全文

0. 引言

钙质砂是珊瑚和其他海洋生物的残骸破碎沉积的产物,广泛分布于热带和亚热带的珊瑚礁海域。钙质砂作为中国南海填海造陆的主要材料,因其特殊的力学特性而受到了广泛地关注和研究。已有研究表明,钙质砂颗粒内部存在大量孔隙,加之外形多棱角、不规则的几何特点,使得钙质砂颗粒在较低的围压下即会出现折断、磨损、破碎等现象,进而表现出了与陆源硅质不同的特殊力学特性^[1-3]。探究钙质砂力学特性的核心则在于揭示其颗粒破碎规律及其对于力学行为和变形特性的影响。

近年来,对于钙质砂颗粒破碎和力学行为的研究主要集中在单调荷载作用下的室内试验与本构模型方面。单调荷载下的压缩试验^[3]、环剪试验^[4-5]、单剪试验^[6]以及不同应力路径下的三轴试验^{[2, 7-9]}都表明钙质砂的颗粒破碎是一个受颗粒级配、颗粒大小、应力水平、加载路径等因素影响的过程。破碎的过程又作用于其剪胀、强度、临界状态等力学性质,故在建立本构模型时,在剪胀方程^[10]、硬化参数^[11-13]、临界状态^[14-15]等模型元素中都需考虑颗粒破碎的影响。

海洋环境下的钙质砂地基除了受到上部结构的静荷载以外,还受到波浪、交通、地震等一系列循环动荷载的作用。然而,目前关于循环荷载作用下钙质砂颗粒破碎和力学特性的研究却较少^{[6-7, 16-17]}。少量试验表明^{[6, 16, 18]},即使在很小的压力水平下,循环荷载的反复作用也会使得钙质砂颗粒产生颗粒破碎,并且破碎随着循环振次的增加而逐渐增大。现有的考虑颗粒破碎的循环本构模型大多是针对高堆石坝填筑料^[19-22]或重载铁路道砟^[23]提出的,它们的颗粒强度较高、粒径较大,其颗粒破碎主要是因为工作环境的高压力而产生的。钙质砂的粒径较小、颗粒强度较低,并且钙质砂地基一般所处的压力水平都较低,故在本构模拟时应同时考虑压力和循环剪切作用引起的颗粒破碎。

本文基于等向压缩试验与环向剪切试验所揭示的基本规律,将颗粒破碎分解为压缩破碎和剪切破碎两部分,分别建立相应的破碎模型,然后借鉴已有的颗粒破碎本构模型的做法,引入破碎临界状态面,建立了考虑颗粒破碎的边界面循环本构模型。

1. 模型描述

1.1 加载机制及屈服面

将引起塑性应变和颗粒破碎的机制分解为压缩和剪切两部分,应力增量采用如下分解方式^[24]：

$d σ = d s + d p I = p d r + d p \frac{σ}{p}$ ,

(1)

式中,加粗的变量表示张量, $σ$ , $s$ 分别为应力张量和偏应力张量,I为Kronecker符号, $I = δ i j$ , $r = s / p$ 为偏应力比张量。pdr代表剪切作用, $d p σ / p$ 代表压缩作用。本构模型描述中用到的其它应力应变量为

$\begin{array}{l} q = \sqrt{3 s : s / 2}, \\ γ = \sqrt{3 e : e / 2}, \\ η = q / p = \sqrt{3 r : r / 2}, \\ ε_{v} = tr (ε), \end{array}}$

(2)

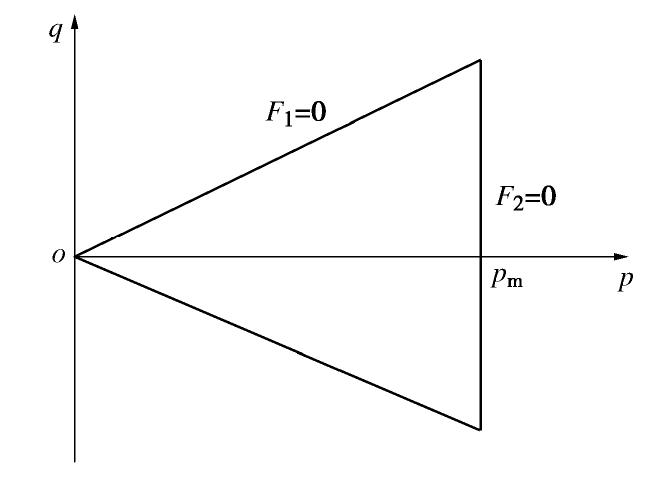
式中,q, $η$ 分别为广义剪应力和广义剪应力比, $γ$ , $ε_{v}$ 为广义剪应变和体变,e为偏应变张量。

上述压缩和剪切机制在p–q平面内对应的屈服面如图1所示,可表示为

图 1 p–q平面内的屈服面F₁和F₂

Figure 1. Yielding surfaces F₁ and F₂ on p–q plane

下载: 全尺寸图片幻灯片

$\begin{array}{l} F_{1} = η / g (θ) - η_{m,c}, \\ F_{2} = p - p_{m}, \end{array}}$

(3)

式中, $η_{m,c}$ 为三轴压缩条件下的历史最大剪应力比,p_m为历史最大平均有效应力,分别决定了屈服面F₁,F₂的大小。插值函数 $g (θ)$ 采用杨雪强等^[25]提出的表述形式：

$g (θ) = \frac{1}{\sin (\frac{π}{3} + \frac{1}{3} \sin^{- 1} (B \sin 3 θ))} (θ \in [- π/6, π/ 6])$ ,

(4)

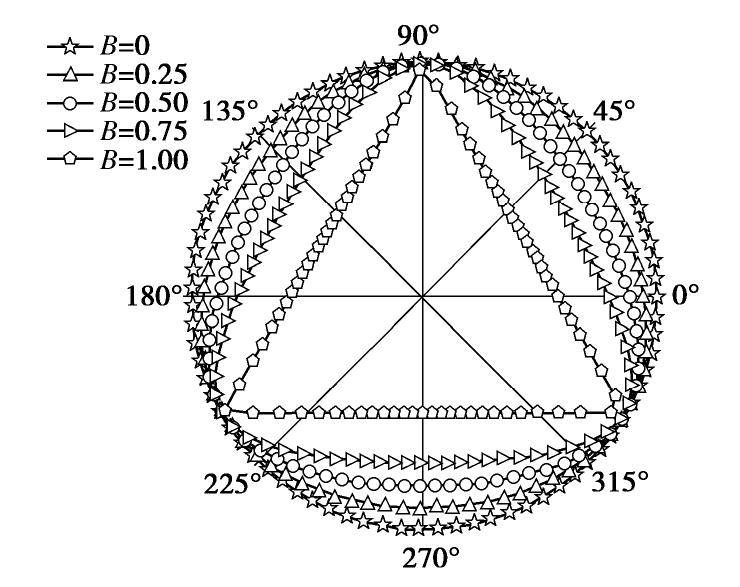
式中, $θ$ 为罗德角,B为决定 $π$ 平面上屈服面F₁破坏迹线形状的变量（图2）,其表达式为

图 2 变量B对屈服面形状的影响

Figure 2. Effects of B on yielding shape

下载: 全尺寸图片幻灯片

$B = 2.5 (1 - 3 / (3 + η_{m,c}))$ 。

(5)

1.2 应变计算

基于弹塑性理论框架,将应变增量分为弹性和塑性两部分：

$d ε = d ε^{e} + d ε^{p}$ 。

(6)

弹性应变采用广义胡克定律计算：

$d ε^{e} = \frac{d s}{2 G} + \frac{d p}{3 K} I = \frac{1}{2 G} p d r + (\frac{1}{2 G} r + \frac{1}{3 K} I) d p$ 。

(7)

弹性剪切模量G和体积模量K可分别表示为^[26]

$\begin{array}{l} G = G_{0} \frac{{(2.973 - e)}^{2}}{(1 + e)} p_{a} \sqrt{\frac{p}{p_{a}}}, \\ K = \frac{1 + e}{κ} p_{a} \sqrt{\frac{p}{p_{a}}}, \end{array}}$

(8)

式中,G₀为初始剪切模量, $κ$ 为回弹曲线的斜率。

塑性应变分别由剪切机制和压缩机制计算。剪切机制的塑性加载指数L为

$L = d γ^{p} = 〈 p d r : n 〉 / H_{r}$ ,

(9)

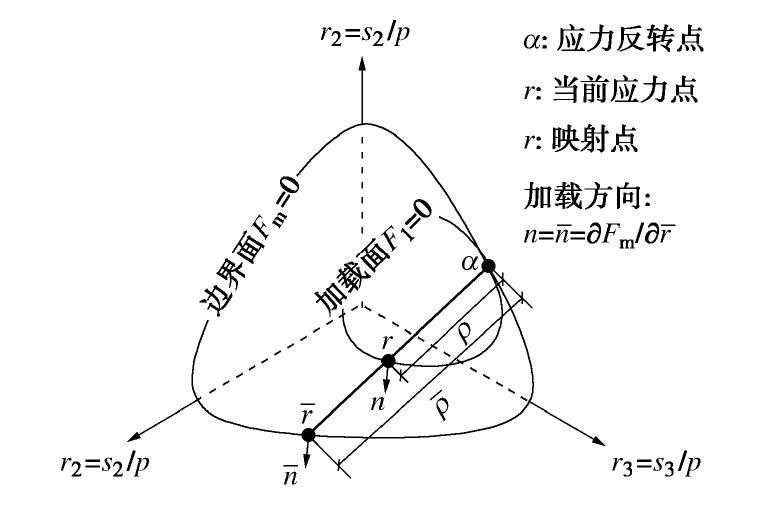
式中, $γ^{p}$ 为广义塑性剪应变, $〈 x 〉$ 为Macauley算符,当x>0 $〈 x 〉 = x$ ,当x≤0h(x)=0,n为加载方向（如图3所示）,H_r为剪切塑性模量^[27]

$H_{r} = h g (θ) G [\frac{M_{p}}{η_{m,c}} (\frac{\bar{ρ}}{ρ}) - 1]$ ,

(10)

其中,h为模型参数。 $\bar{ρ}$ , $ρ$ 分别为映射中心到边界面和当前应力点的距离（图3）。

图 3 映射法则及加载方向

Figure 3. Mapping rules and loading directions

下载: 全尺寸图片幻灯片

剪切机制产生的塑性偏应变 $d e^{p}$ 和塑性体变 $d ε_{v,r}^{p}$ 可分别表示为

$\begin{array}{l} d e^{p} = L m = \frac{〈 p d r : n 〉}{H_{r}} m, \\ d ε_{v,r}^{p} = L D = \frac{〈 p d r : n 〉}{H_{r}} D, \end{array}}$

(11)

式中,D为剪胀因子,m为塑性偏应变 $d e^{p} 。$ 的流动方向,规定流动方向m与加载方向n都与边界面上映射点处的法线方向 $\bar{n}$ 相一致（图3）,即 $m = n = \bar{n} = \partial F_{m} /$ $\partial \bar{r}$ 。边界面模型的映射法则以及加卸载的判断可参考文献[24,27]。

若忽略与屈服面F₂相关的塑性偏应变,则压缩机制产生的塑性体变 $d ε_{v,p}^{p}$ 可表示为

$d ε_{v,p}^{p} = h (p - p_{m}) 〈 d p 〉 / H_{p}$ ,

(12)

式中,h(x)为heaveside函数（若x>0,则h(x)=1,若x≤0,则h(x)=0）,H_p为压缩塑性模量^[24],

$H_{p} = \frac{1 + e}{λ - κ} [\frac{M_{p}}{M_{p} - η / g (θ)}] p_{a} \sqrt{\frac{p}{p_{a}}}$ ,

(13)

其中, $λ$ 为压缩曲线的斜率。

1.3 颗粒破碎

采用Hardin^[28]所提出的相对破碎B_r来定量描述颗粒破碎的程度。与塑性应变一样,颗粒破碎也可分解为压缩和剪切两部分^[29]：

$d B_{r} = d B_{r,c} + d B_{r,s}$ ,

(14)

式中,B_r,c为压缩破碎,B_r,s为剪切破碎。

（1）压缩破碎

Lee等^[30]在极高的围压下针对堆石料进行了一系列常剪应力比 $η$ 的压缩试验。试验结果表明,在恒定的剪应力比下,颗粒破碎随着平均有效应力的增大而增大,直到接近一个恒定值。基于该试验结果,Hardin提出了一个可以描述等剪应力比下,颗粒破碎随平均有效应力变化的破碎模型^{[9, 29]}。但是该模型为全量形式,不能用于压缩和剪切耦合的复杂应力路径的计算。为此,本文采用以下增量形式的模型^[29]：

$d B_{r,c} = k_{0} (1 + η^{3}) {(1 - \frac{B_{r}}{\bar{\bar{B_{r}}}})}^{2} 〈 d p 〉$ ,

(15)

式中,k₀为材料参数, $B_{r}$ 为已经累计的颗粒破碎量, $\bar{\bar{B_{r}}}$ 为终极颗粒破碎量。终极颗粒破碎是指在颗粒破碎所能达到的终极值。Hardin假设粒状土最终都会破碎为粒径小于0.075 mm的粉粒,因此 $\bar{\bar{B r}} = 1$ ；然而Einav^[31]认为最终的颗粒级配为分形级配,因此 $\bar{\bar{B_{r}}} = B_{r,f}$ ,B_r,f为分形级配所对应的相对破碎值。

（2）剪切破碎

基于环向剪切试验^[4-5]和循环三轴试验^[16]结果,循环剪切条件下颗粒破碎的累积过程满足两个“递减率”：①在总的循环加载过程中,颗粒破碎的累积速率随自身累积值的增加而减小；②在每一个单向剪切的过程中,颗粒破碎的累积速率总是在单向剪切起始处最大,然后随单向剪应变的增加而不断减小。

为了反映“递减率①”,设颗粒破碎在循环剪切机制下的增量为

$d B_{r,s} = d B_{r,eff} \exp (- α B_{r})$ ,

(16)

式中, $α$ 为材料常数。B_r为当前颗粒破碎的累积值,B_r,eff为“有效相对破碎”。有效相对破碎可以理解为单调加载条件下颗粒破碎随广义塑性剪应变 $γ^{p}$ 的累积值,它的引入是为了反映“递减率②”。

对于单调加载条件下颗粒破碎的“递减率②”,可以采用Wang等^[9]提出的双曲线形式的破碎法则进行描述：

$B_{r,eff} = \frac{γ}{1 / R_{B0} + γ / \bar{B_{r}}}$ ,

(17)

式中, $γ$ 为剪应变,R_B0为初始剪切破碎率,代表了双曲线起始处的斜率, $\bar{B_{r}}$ 为做极限破碎,代表了在某一恒定围压下,B_r所能达到的最大值。

$\begin{array}{l} R_{B0} = c_{1} {(\frac{p}{p_{a}})}^{c_{2}}, \\ \bar{B_{r}} = \frac{p}{A p_{a} + p} \bar{\bar{B_{r}}}, \end{array}}$

(18)

式中,c₁,c₂为材料常数, $p_{a}$ 为大气压强（ $p_{a}$ =101 kPa）,A为无量纲参数。

将式（17）对剪应变 $γ$ 求导可得

$d B_{r,eff} = \frac{R_{B0}}{{(1 + {γ_{mono} R_{B0} / \bar{B}}_{r})}^{2}} d γ^{p}$ ,

(19)

式中, $γ_{mono}$ 为每一次单调加载时剪应变的长度,在每一次应力反转时都被置零,且始终为正。

1.4 颗粒破碎临界状态

颗粒破碎导致颗粒级配拓宽,而Wood等^[32]通过数值试验证明了临界状态线随着颗粒级配的拓宽而下降,因此采用下式来拟合临界状态线^[32-33]：

$e_{cs} = e_{Γ} (B_{r}) - λ_{p} \ln (p / p_{a})$ 。

(20)

式中 $λ_{p}$ 为临界状态线在 $e - \ln p$ 平面内的斜率； $e_{Γ} (B_{r})$ 为 $p = p_{a}$ 时所对应的孔隙比,随着相对破碎值的增大而减小,

$e_{Γ} (B_{r}) = e_{Γ0} - λ_{b} B_{r}$ ,

(21)

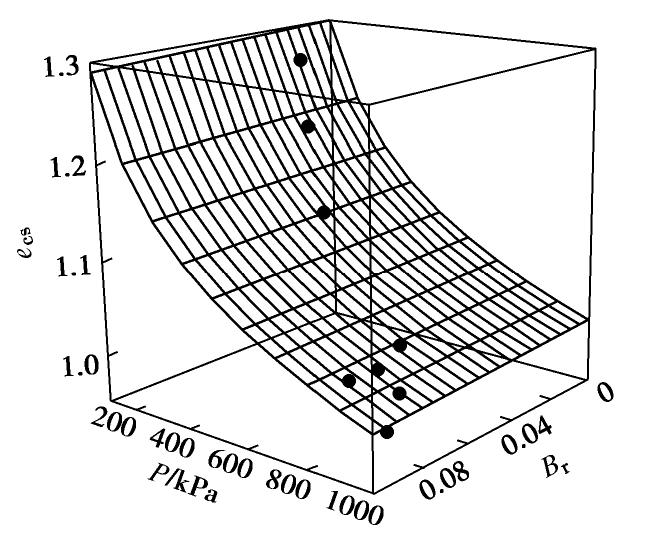
其中, $e_{Γ0}$ 为没有发生颗粒破碎时（B_r = 0）的 $e_{Γ}$ 值,λ_b为材料参数。式（20）在 $p - q - B_{r}$ 空间中表述为一个曲面（图4）,称为破碎临界状态面。

图 4 破碎临界状态面

Figure 4. Critical state surface of breakage

下载: 全尺寸图片幻灯片

由于颗粒破碎的影响,粒状材料的临界状态应力比M_cs也不再只是一个恒定的常数,而是随着颗粒破碎的累积,逐渐呈现减小的趋势（图5）。本文采用Wang等^[9]对临界状态应力比M_cs的描述：

图 5 临界状态应力比随颗粒破碎的变化

Figure 5. Variation of critical stress ratio with particle breakage

下载: 全尺寸图片幻灯片

$M_{cs} = M_{cs0} \exp (- n_{b} B_{r})$ ,

(22)

式中,M_cs0为相对破碎B_r = 0时所对应的临界状态应力比,n_b为材料常数。

采用Been等^[34]所提出的状态相关参数将当前应力比e与临界应力比e_cs相关联：

$ψ = e - e_{cs}$ 。

(23)

并将式（22）代入与状态相关的峰值应力比M_p和剪胀应力比M_d中,即可引入颗粒破碎对于强度和剪胀的影响^[9]：

$\begin{array}{l} M_{p} = M_{cs} exp(- n_{p} ψ) = M_{cs0} exp(- n_{p} ψ - n_{b} B_{r}), \\ M_{d} = M_{cs} exp(n_{d} ψ) = M_{cs0} exp(n_{d} ψ - n_{b} B_{r}), \end{array}}$

(24)

式中,n_p,n_d为材料常数。由式（24）中可知,M_p,M_d除了与状态参数 $ψ$ 相关以外,还与颗粒破碎的累积量B_r有关,且峰值应力比M_p和相态转换应力比M_d都随着颗粒破碎的增加而逐渐降低。

剪切机制下的剪胀因子D为^{[24, 27]}：

$D = d_{0} \exp (- β ε_{v,r}^{p}) (M_{d} - η / g (θ))$ ,

(25)

式中,d₀, $β$ 为模型参数。

2. 模型参数

本模型共有18个参数（表1）：①颗粒破碎参数c₁,c₂,A,k₀, $α$ ；②临界状态参数 $e_{Γ 0}$ , $λ_{b}$ , $λ_{p}$ ,M_cs0和n_b；③剪胀参数d₀,β；④弹性参数G₀,κ；⑤塑性参数n_p,n_d, $λ$ ,h。其中,参数G₀,κ,n_p,n_d, $λ$ ,h,d₀的确定方法可参考文献[24,27],破碎参数k₀可通过拟合不同压力下的等向固结试验点获得。c₁,c₂,A的确定方法：首先采用式（17）拟合三轴排水条件下不同围压的颗粒破碎点,从而得到不同围压下曲线的R_B0, $\bar{B_{r}}$ 。然后,采用式（18）在 $R_{B0} - p_{0}$ 平面内（p₀为初始有效应力）平面内拟合数据点即可得到c₁,c₂,在 $\bar{B_{r}} - p_{cs}$ 平面内（p_cs为临界有效应力）拟合数据点可得到参数A。c₁,c₂,A需根据实际的拟合情况进行调整。

表 1 本构模型参数

Table 1. Parameters of constitutive model

颗粒破碎	临界状态	剪胀	弹性	塑性
c₁=0.07	e_Γ0=1.302	d₀=0.9	G₀=225	n_p=1.0
c₂=1.2	λ_b=0.1	β=1000	κ=0.007	n_d=2.2
A=55.0	λ_p=0.128			h=0.3
α=400	M_cs0=1.838			λ=0.012
k₀=2.5×10⁶	n_b=1.393

下载: 导出CSV

| 显示表格

临界状态线在 $e - \ln (p / p_{a})$ 平面内的斜率和截距即为参数 $λ_{p}$ , $e_{Γ}$ 。若 $e_{Γ}$ 已知,则可以通过式（21）在 $e_{Γ} - B_{r}$ 平面内拟合得到 $λ_{b}$ 。通过在 $M_{cs} - B_{r}$ 平面内拟合式（22）,可获得参数M_cs0,n_b。

剪胀参数β通过拟合剪胀因子D与剪应力比 $η$ 之间的关系确定。

3. 模型验证

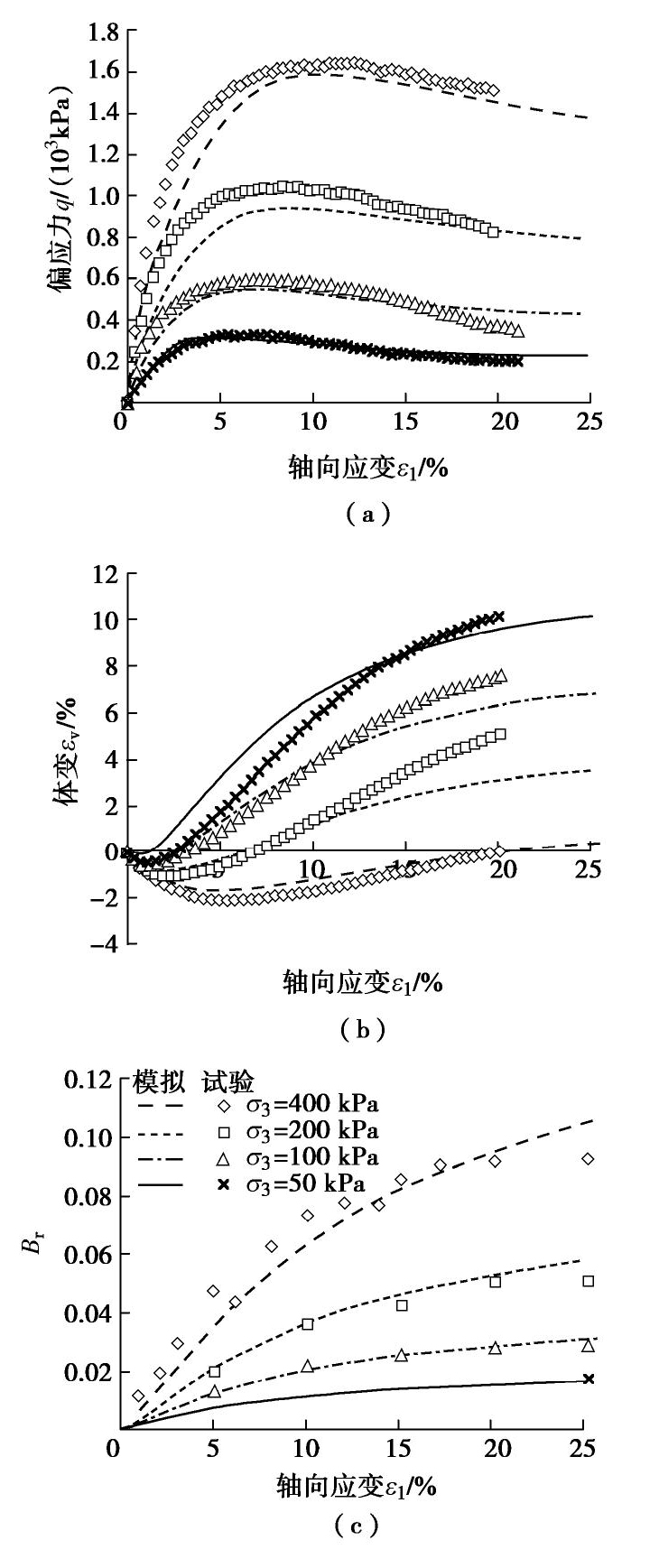
首先验证模型在单调加载条件下的表现。Wang等^[9]针对中国南海珊瑚砂进行了一系列的较低围压下的单调三轴排水试验。钙质砂的粒径为0.6～0.8 mm。三轴试样的直径39.1 mm、高80 mm,初始相对密度为75%,围压为400,200,100,50 kPa。图6给出模型的模拟结果与试验结果的对比。可以看出,模型能够较好地模拟出珊瑚砂在单调排水三轴条件下的应力应变和体变行为,并准确地反映了珊瑚砂的应变软化以及剪胀。图6（c）给出了模型对于颗粒破碎随轴向应变的演化过程的模拟结果,表明了单调加载条件下的“递减率②”的正确性。

图 6 单调三轴排水试验的模拟结果

Figure 6. Simulated results of monotonic drained triaxial compression tests

下载: 全尺寸图片幻灯片

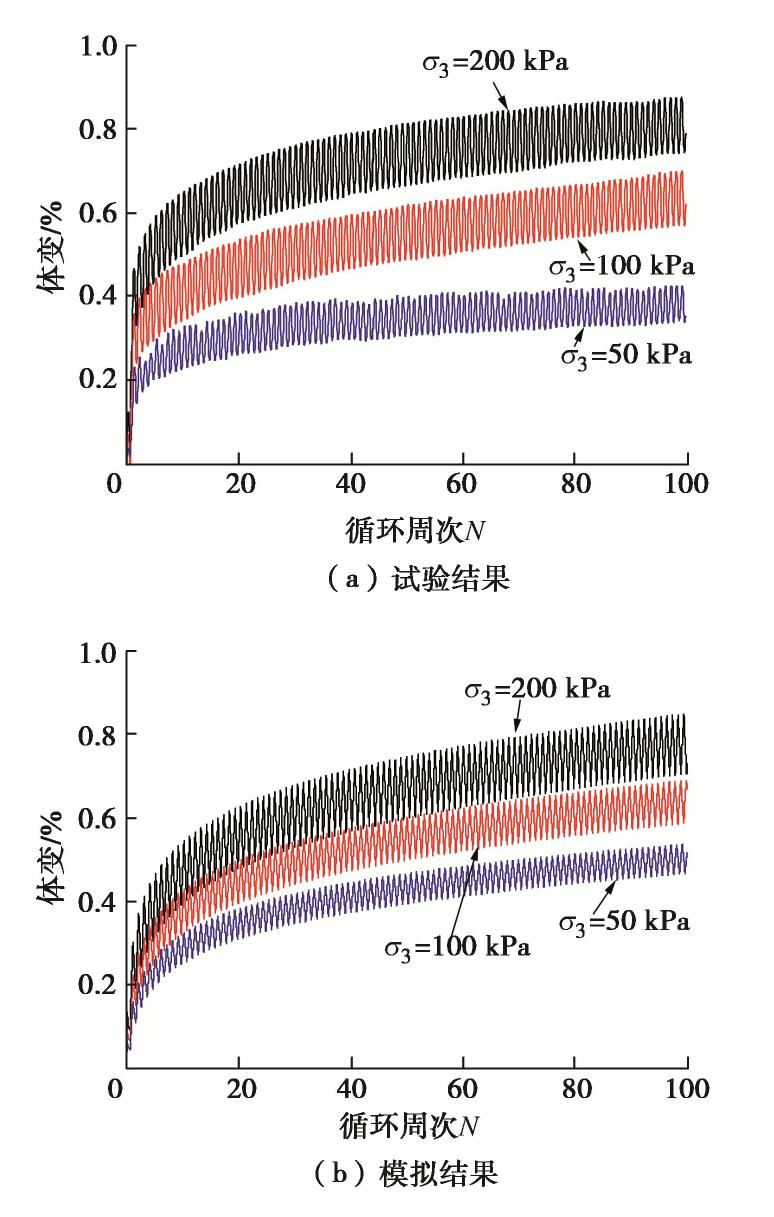
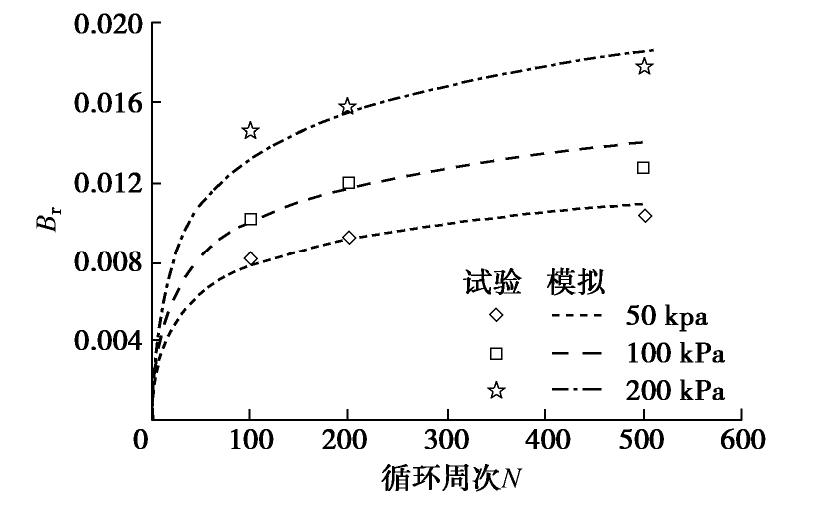
王刚等^[16]选择了与上述静三轴试验相同初始状态的多组试样,并对其在排水条件下进行了不同循环周次的动三轴试验。图7给出了在CSR=0.3时采用该模型对200,100,50 kPa围压下的试样循环体变的累积过程的模拟结果。从图7可以看出,该模型可以较好地反映循环荷载下体变的累积过程^[5]。图8给出了颗粒破碎随循环周次增加的演化过程。可以看出,模型基本上可以反映颗粒破碎随循环周数N不断增加的发展趋势,证明了本文所提出的颗粒破碎模型的合理性。

图 7 循环三轴排水试验的模拟结果

Figure 7. Simulated results of cyclic drained triaxial compression tests

下载: 全尺寸图片幻灯片

图 8 相对破碎随循环周次演化过程的模拟结果

Figure 8. Simulated results of development of relative breakage with cyclic number

下载: 全尺寸图片幻灯片

4. 结论

基于已有的试验结果,将引起颗粒破碎的机制分解为了压缩和剪切两部分,并分别建立了与之相对应的破碎模型,在边界面本构模型的框架内,引入颗粒破碎临界状态面,发展出了一个可以模拟钙质砂在循环加载条件下颗粒破碎行为的本构模型,并通过对单调和循环三轴试验结果的模拟验证了模型的合理性。模型的主要特征如下：

（1）将引起塑性变形以及颗粒破碎的机制分解为压缩机制和剪切机制,它们分别对应平均有效应力的增加和剪应力比的变化。

（2）在恒定的剪应力比下,压缩破碎法则下的累积速率随着平均有效应力的增加而增加,随着已累积的颗粒破碎量的增加而减小。因此,在Hardin公式的基础上,提出了一个增量型的压缩破碎模型,以模拟压缩和剪切耦合应力路径下压缩机制引起的颗粒破碎的发展过程。

（3）提出了两个“递减率”来描述循环剪切作用引起的颗粒破碎：①在每一个单向剪切过程中,颗粒破碎的累积速率总是在单向剪切起始处最大,并随着单向剪应变的增加而减小；②在总的剪切过程中,颗粒破碎的累积速率随颗粒破碎量的增大而逐渐减小。

图 1 p–q平面内的屈服面F₁和F₂

Figure 1. Yielding surfaces F₁ and F₂ on p–q plane

下载: 全尺寸图片幻灯片

图 2 变量B对屈服面形状的影响

Figure 2. Effects of B on yielding shape

下载: 全尺寸图片幻灯片

图 3 映射法则及加载方向

Figure 3. Mapping rules and loading directions

下载: 全尺寸图片幻灯片

图 4 破碎临界状态面

Figure 4. Critical state surface of breakage

下载: 全尺寸图片幻灯片

图 5 临界状态应力比随颗粒破碎的变化

Figure 5. Variation of critical stress ratio with particle breakage

下载: 全尺寸图片幻灯片

图 6 单调三轴排水试验的模拟结果

Figure 6. Simulated results of monotonic drained triaxial compression tests

下载: 全尺寸图片幻灯片

图 7 循环三轴排水试验的模拟结果

Figure 7. Simulated results of cyclic drained triaxial compression tests

下载: 全尺寸图片幻灯片

图 8 相对破碎随循环周次演化过程的模拟结果

Figure 8. Simulated results of development of relative breakage with cyclic number

下载: 全尺寸图片幻灯片

表 1 本构模型参数

Table 1 Parameters of constitutive model

颗粒破碎临界状态剪胀弹性塑性

c₁=0.07 e_Γ0=1.302 d₀=0.9 G₀=225 n_p=1.0
c₂=1.2 λ_b=0.1 β=1000 κ=0.007 n_d=2.2
A=55.0 λ_p=0.128 h=0.3
α=400 M_cs0=1.838 λ=0.012
k₀=2.5×10⁶ n_b=1.393

下载: 导出CSV

参考文献(34)

[1]	张家铭, 蒋国盛, 汪稔. 颗粒破碎及剪胀对钙质砂抗剪强度影响研究[J]. 岩土力学, 2009, 30(7): 2043-2048. doi: 10.3969/j.issn.1000-7598.2009.07.029 ZHANG Jia-ming, JIANG Guo-sheng, WANG Ren. Research on influences of particle breakage and dilatancy on shear strength of calcareous sands[J]. Rock and Soil Mechanics, 2009, 30(7): 2043-2048. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.07.029
[2]	张家铭, 张凌, 蒋国盛, 等. 剪切作用下钙质砂颗粒破碎试验研究[J]. 岩土力学, 2008(10): 195-199. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200810039.htm ZHANG Jia-ming, ZHANG Ling, JIANG Guo-sheng, et al. Research on particle crushing of calcareous sands under triaxial shear[J]. Rock and Soil Mechanics, 2008(10): 195-199. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200810039.htm
[3]	王刚, 叶沁果, 查京京. 珊瑚礁砂砾料力学行为与颗粒破碎的试验研究[J]. 岩土工程学报, 2018, 40(5): 802-810. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805006.htm WANG Gang, YE Qin-guo, ZHA Jing-jing. Experimental study on mechanical behavior and particle crushing of coral sand-gravel fills[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 802-810. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805006.htm
[4]	WEI H, ZHAO T, HE J, et al. Evolution of particle breakage for calcareous sands during ring shear tests[J]. International Journal of Geomechanics, 2018, 18(2): 04017153. doi: 10.1061/(ASCE)GM.1943-5622.0001073
[5]	COOP M R, SORENSEN K K, FREITAS T B, et al. Particle breakage during shearing of a carbonate sand[J]. Géotechnique, 2004, 54(3): 157-163. doi: 10.1680/geot.2004.54.3.157
[6]	纪文栋, 张宇亭, 王洋, 等. 循环单剪下珊瑚钙质砂和普通硅质砂剪切特性对比研究[J]. 岩土力学, 2018, 39(增刊1): 291-297. doi: 10.16285/j.rsm.2018.0580 JI Wen-dong, ZHANG Yu-ting, WANG Yang, et al. Comparative study on shear characteristics of coral calcareous sand and ordinary siliceous sand under cyclic single shear[J]. Rock and Soil Mechanics, 2018, 39(S1): 291-297. (in Chinese) doi: 10.16285/j.rsm.2018.0580
[7]	NANDA S, SIVAKUMAR V, DONOHUE S, et al. Small strain behavior and crushability of Ballyconnelly carbonate sand under monotonic and cyclic loading[J]. Canadian Geotechnical Journal, 2017, 55(4).
[8]	YU F. Particle breakage in triaxial shear of a coral sand[J]. Soils and Foundations, 2018, 58(4): 866-880. doi: 10.1016/j.sandf.2018.04.001
[9]	WANG G, WANG Z, YE Q, et al. Particle breakage and deformation behavior of carbonate sand under drained and undrained triaxial compression[J]. International Journal of Geomechanics, 2020, 20(3): 04020012. doi: 10.1061/(ASCE)GM.1943-5622.0001601
[10]	JIA Y, CHI S, LIN G. Constitutive model for coarse granular aggregates incorporating particle breakage[J]. Rock and Soil Mechanics, 2009, 30(11): 3261-3260. doi: 10.3969/j.issn.1000-7598.2009.11.007
[11]	YAO Y, YAMAMOTO H, WANG N. Constitutive model considering sand crushing[J]. Soils and Foundations, 2011, 48(2): 12-15.
[12]	YAO Y P, LIU L, LUO T, et al. Unified hardening (UH) model for clays and sands[J]. Computers and Geotechnics, 2019, 110: 326-343. doi: 10.1016/j.compgeo.2019.02.024
[13]	姚仰平, 刘林, 罗汀. 砂土的UH模型[J]. 岩土工程学报, 2016, 38(12): 2147-2153. doi: 10.11779/CJGE201612002 YAO Yang-ping, LIU Lin, LUO Ting. UH model for sands[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2147-2153 (in Chinese) doi: 10.11779/CJGE201612002
[14]	RUSSELL A R, KHALILI N. A bounding surface plasticity model for sands exhibiting particle crushing[J]. Canadian Geotechnical Journal, 2004, 41(6): 1179-1192. doi: 10.1139/t04-065
[15]	蔡正银, 侯贺营, 张晋勋, 等. 考虑颗粒破碎影响的珊瑚砂临界状态与本构模型研究[J]. 岩土工程学报, 2019, 41(6): 989-995. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201906002.htm CAI Zheng-yin, HOU He-ying, ZHANG Jin-xun, et al. Critical state and constitutive model for coral sand considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(6): 989-995. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201906002.htm
[16]	王刚, 查京京, 魏星. 循环三轴应力路径下钙质砂颗粒破碎演化规律[J]. 岩土工程学报, 2019, 41(4): 755-760. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904025.htm WANG Gang, ZHA Jing-jing, WEI Xing. Evolution of particle crushing of coral sand under cyclic triaxial stress path[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 755-760. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904025.htm
[17]	刘汉龙, 肖鹏, 肖杨, 等. MICP胶结钙质砂动力特性试验研究[J]. 岩土工程学报, 2018, 40(1): 44-51. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm LIU Han-long, XIAO Peng, XIAO Yang, et al. Dynamic behaviors of MICP-treated calcareous sand in cyclic tests[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(1): 44-51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm
[18]	WANG G, ZHA J, Particle breakage evolution during cyclic triaxial shearing of a carbonate sand[J]. Soil Dynamics and Earthquake Engineering, 2020, 138: 106326.
[19]	CHEN Q, INDRARATNA B, CARTER J P, et al. Isotropic-kinematic hardening model for coarse granular soils capturing particle breakage and cyclic loading under triaxial stress space[J]. Canadian Geotechnical Journal, 2016, 53(4): 646-658.
[20]	LIU H, ZOU D, LIU J. Constitutive modeling of dense gravelly soils subjected to cyclic loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(14): 1503-1518.
[21]	张凌凯, 王睿, 张建民, 等. 考虑颗粒破碎效应的堆石料静动力本构模型[J]. 岩土力学, 2019, 40(7): 2547-2554, 2562. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907008.htm ZHANG Ling-kai, WANG Rui, ZHANG Jian-min, et al. A static and dynamic constitutive model of rockfill material considering particle breakage[J]. Rock and Soil Mechanics, 2019, 40(7): 2547-2554, 2562. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907008.htm
[22]	刘恩龙, 陈生水, 李国英, 等. 循环荷载作用下考虑颗粒破碎的堆石体本构模型[J]. 岩土力学, 2012, 33(7): 1972-1978. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201207010.htm LIU En-long, CHEN Shen-shui, LI Guo-ying, et al. A constitutive model for rockfill materials incorporating grain crushing under cyclic loading[J]. Rock and Soil Mechanics, 2012, 33(7): 1972-1978. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201207010.htm
[23]	SUN Y, XIAO Y, WEN J. Bounding surface model for ballast with additional attention on the evolution of particle size distribution[J]. Science China Technological Sciences, 2014, 57(7): 1352-1360.
[24]	WANG Z L, DAFALIAS Y F, SHEN C K. Bounding surface hypoplasticity model for sand[J]. J Eng Mech-ASCE, 1990, 116(5): 983-1001.
[25]	杨雪强, 朱志政, 何世秀, 等. 对Lade-Duncan, Matsuoka-Nakai和Ottosen等破坏准则的认识[J]. 岩土工程学报, 2006, 28(3): 337-342. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200603013.htm YANG Xue-qiang, ZHU Zhi-zheng, HE Shi-xiu, et al. Researches on failure criteria of Lade-Duncan, Matsuoka-Nakai and Ottosen[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 337-342. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200603013.htm
[26]	RICHART F E, HALL J R, WOODS R D. Vibrations of soils and foundations[M]. Englewood Cliffs, NJ: Prentice-Hall, 1970.
[27]	LI X S. A sand model with state-dependent dilatancy[J]. Géotechnique, 2002, 52(3): 173-186.
[28]	HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177-1192.
[29]	WANG Z, WANG G, YE Q. A constitutive model for crushable sands involving compression and shear induced particle breakage[J]. Computers and Geotechnics, 2020, 126: 103757.
[30]	LEE K L, FARHOOMAND I. Compressibility and crushing of granular soil in anisotropic triaxial compression[J]. Canadian Geotechnical Journal, 1967, 4(1): 68-86.
[31]	EINAV I. Breakage mechanics-Part I: Theory[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(6): 1274-1297.
[32]	WOOD D M, MAEDA K. Changing grading of soil: Effect on critical states[J]. Acta Geotechnica, 2008, 3(1): 3-14.
[33]	CIANTIA M O, ARROYO M, O'SULLIVAN C, et al. Grading evolution and critical state in a discrete numerical model of Fontainebleau sand[J]. Géotechnique, 2019, 69(1): 1-15.
[34]	BEEN K, JEFFERIES M G. A state parameter for sands[J]. Géotechnique, 1985, 35(2): 99-112.

施引文献(5)

期刊类型引用(3)

1.	王涛，孙婷婷，占鑫杰，吕冲，陈浩. 氯离子在典型黏土地基中的迁移特性研究. 河南科学. 2023(08): 1134-1141 . 百度学术
2.	尹康，刘霖，白瑞刚. 隔离材料对复合污染物的运移阻滞效应研究. 内蒙古工业大学学报(自然科学版). 2023(06): 561-565 . 百度学术
3.	杨婷，杨成艳，郑举功，查文化，梁海安，冯岩岩. Ca~(2+)盐溶液在高庙子膨润土中的扩散研究. 辐射防护. 2022(02): 146-154 . 百度学术

其他类型引用(2)

资源附件(0)

图(8) / 表(1)

计量

文章访问数: 343
HTML全文浏览量: 57
PDF下载量: 192
被引次数: 5

0. 引言
1. 模型描述
1.1 加载机制及屈服面
1.2 应变计算
1.3 颗粒破碎
1.4 颗粒破碎临界状态
2. 模型参数
3. 模型验证
4. 结论

考虑颗粒破碎的钙质砂边界面循环本构模型 English Version

作者简介: 王兆南(1994—),男,博士研究生,主要从事岩土工程数值计算方面的研究工作。E-mail: znwang@cqu.edu.cn

通讯作者: 王刚, E-mail: cewanggang@163.com

计量

出版历程