0.   引言

钙质砂是一种CaCO₃含量大于50%且海洋生物成因的特殊土类,具有形状不规则、内部孔隙较多、颗粒强度低等特点^[1],在常应力状态下就能产生颗粒破碎,从而导致钙质砂的粒径分布发生变化,致使其力学性质发生改变。颗粒破碎与力学性质的关系,在土力学中已经成为一个新课题^[2]。因此,有必要深入研究应力条件下钙质砂的颗粒破碎特性,以及对力学性质的影响机制。

为了研究钙质砂的颗粒破碎对力学性质的影响,国内外一些学者采用侧限压缩试验^[3-6]、环剪试验^[7-10]、循环单剪试验^[11]等来研究钙质砂的颗粒破碎特性。究其原因,在于上述几种试验方法中,侧限压缩试验容易对钙质砂产生高的压缩应力,而环剪试验、循环单剪试验可对钙质砂产生高的剪切应变。这些试验通过产生的高应力或高应变,旨在能最大限度地促进钙质砂的颗粒破碎,以便从中能探索到颗粒破碎的演化特性和对力学性质的影响规律。然而,在侧限压缩试验中,土样的应力状态往往与实际情况不太相符,试样无法产生剪切破坏；而环剪试验、循环单剪试验中的土样,虽然能产生剪应力,但是存在着试样剪切面固定和人为确定的缺陷。

近年来,许多学者利用常规的动、静三轴试验^[12-17]来研究颗粒破碎对钙质砂力学性质的影响。然而,受应力水平较低的限制,常规三轴试验所能促成的颗粒破碎程度往往比较有限。仅有少数学者采用高围压的三轴试验来研究钙质砂的颗粒破碎特性^[18],但研究的广度和深度还十分有限,需要进一步认识钙质砂在高围压下的三轴剪切破碎特性。此外,近期有研究成果显示^[19-20],钙质砂在各粒组中的含量对其力学特性有重要影响,因此有必要深入认识钙质砂在剪切过程中粒径分布的变化规律,尤其是粒组含量的变化规律。

本文利用高压三轴试验系统,对不同初始分布的钙质砂进行高围压下的三轴固结排水剪切试验,旨在研究钙质砂在剪切过程中的颗粒粒径分布、粒组颗粒含量、颗粒破碎率等的演化规律,通过调查钙质砂的应力和应变特征,探索颗粒破碎率与应力–应变的关系,研究颗粒破碎对钙质砂抗剪强度的影响机制。

1.   材料与方法

1.1   试验土样

供试土料取自中国南海岛礁,利用相对密度仪测得其相对密度为2.75,利用X射线荧光光谱仪测得其等效CaCO₃含量为96.39%。钙质砂经清洗、风干后备用。为研究初始粒径分布对钙质砂颗粒破碎的影响,并考虑到在相同应力水平下,均匀分布的钙质砂比非均匀分布时的颗粒破碎量更高,采用筛析法制备了编号为SCS和DCS的两种土样。其中均匀分布的SCS样,由粒径范围2～1 mm的单个粒组土粒构成；非均匀分布的DCS样,由粒径范围2～1 mm和1～0.5 mm的两个粒组的土粒构成,质量百分比各占50%。

在自然界中,具有统计意义上的自相似对称特征的土壤,具有一定的分形特性^[21]。天然土体的粒径分布具有分形特征,已是普遍存在的自然规律。土体粒径分布的分形关系,可采用土粒累计质量与粒径的关系来定义^[22],即

式中 d为土粒粒径；d_i为第i级筛孔径（i = 1, 2, …, n）；d_max为土粒最大粒径；M（d<d_i）为粒径小于d_i的土粒累积质量；M_t为土粒总质量；D为分形维数。

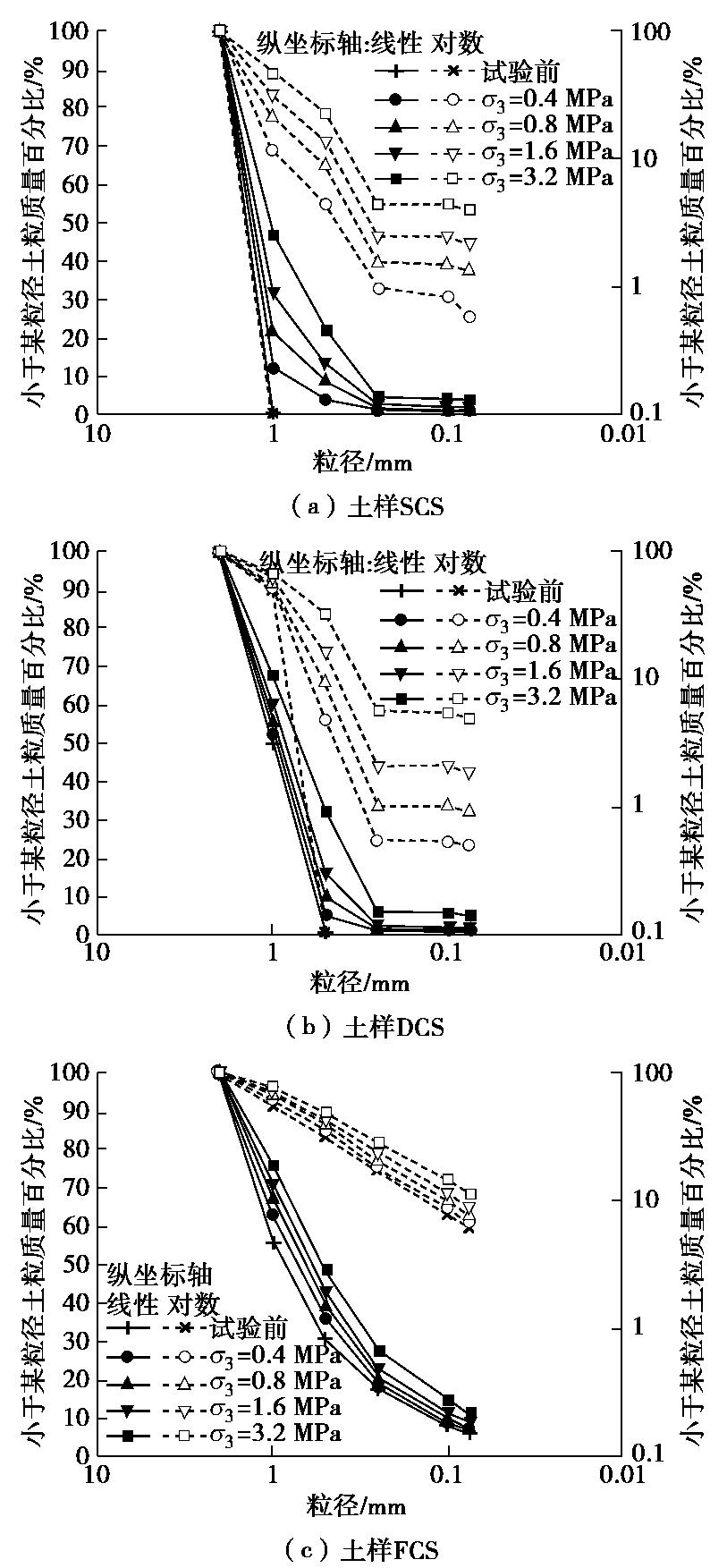
为了让制备的土样与天然土体可资比较,并考虑自相似粒径分布数据的分形维数值约为2.2^[23]。在粒径d≤2 mm的范围内,设定D=2.15并按照式（1）计算各粒组含量,利用筛析法制备编号为FCS的土样,使其初始粒径分布具有分形特性,以表征天然土体的自然级配状况。3种土样的初始粒径分布曲线如图1所示,在线性和对数的二种纵坐标轴上分别表示。

图  1  初始粒径分布曲线

Figure  1.  Initial particle-size distribution curves

下载: 全尺寸图片 幻灯片

式（1）等号左侧表示粒径小于d_i的土粒质量百分比,等号右侧表示粒径d_i,分别与粒径分布曲线图中的纵、横坐标轴相对应。因此利用粒径分布曲线图,就可以初步考察粒径分布的分形特性。从图1可以发现,土样FCS的粒径分布曲线,在纵坐标为对数的双对数坐标轴上,是一条直线（虚线所示）。由式（1）可知,若直线斜率为k,则分形维数D=3-k。图1还显示,由初始单一粒组（SCS）和双粒组（DCS）构成的土样,粒径分布曲线在双对数坐标轴上显示是非线性的,因而不具有分形特性。

1.2   试验装置

试验采用英国GDS公司生产的高压三轴试验系统（HTPAS）,为应变控制式。试样直径50 mm,高100 mm。轴向加载由伺服电机控制,最大轴向力100 kN,最大轴向位移50 mm,加载速率在0.0001～10 mm/min之间任意可调。三轴压力室由金属制成,可耐压20 MPa。围压的加压介质采用非导电的变压器油,试样用特殊材料制成的薄膜包裹,与变压器油隔开。围压和反压均由电机控制的压力体积控制器施加,围压变化范围0～16 MPa,反压变化范围0～4 MPa。

试验由计算机全过程自动控制。首先从菜单中选择试验类型,输入围压,剪切速率等试验参数和试验终止条件。试验开始后,计算机直接控制围压、反压和剪切速率等,并自动记录上述参数及轴向位移、轴向荷载、孔隙水压力、体积变化等参数。

1.3   试验方案

为方便比较,3种试样均按照初始相对密实度D_r=0.5的中密状态制备。采用砂雨技术分层装样,即利用砂漏斗保持相等的落距向下灌砂。试样的物理参数见表1,可见因初始粒径分布不同,各试样的最大和最小孔隙比差异较大。由于钙质砂质脆、易碎,形状不规则,分层装样不易控制,使得制成试样的相对密实度与预设值略有偏差,但均为中密状态。

表  1  试样的物理参数

Table  1.  Physical parameters of samples

试样编号	初始干密度ρd0/(g·cm-3)	初始孔隙比e0	最大孔隙比emax	最小孔隙比emin	相对密实度Dr
SCS	1.24	1.21	1.41	0.94	0.43
DCS	1.35	1.03	1.28	0.79	0.51
FCS	1.45	0.90	1.20	0.62	0.52

下载: 导出CSV 

| 显示表格

试样在三轴仪中利用反压饱和,在0.4,0.8,1.6,3.2 MPa的4种围压作用下,对试样进行固结排水剪切试验。控制轴向应变20%作为试验终止标准,目的是尽可能地增大钙质砂的颗粒破碎率。为了研究4种围压下的钙质砂在三轴排水剪切过程中的颗粒破碎演化规律,对土样FCS还增设5%,10%,15%的3种轴向应变,作为钙质砂在剪切过程中的中间阶段,当到达预设的轴向应变时终止试验,3种土样共进行了24组试验。试验完毕后,取出试样作粒度分析,按照土工试验方法标准,细筛孔径依次为2,1,0.5,0.25,0.075 mm,筛析法获得试样的粒径分布数据,绘得粒径分布曲线。

本文采用Hardin^[24]建议的相对破碎率B_r来量化钙质砂的颗粒破碎程度,即在粒径分布曲线图上,将粒径分布曲线与0.075 mm粒径截断线所围成的面积定义为破碎势,将试验前和试验后的破碎势之差定义为破碎量,则相对破碎率为破碎量与试验前的破碎势的比值。

2.   结果与分析

2.1   粒径分布的演化

图2为不同围压下各试样的粒径分布曲线,在半对数和双对数的坐标轴上分别表示。图2显示,初始均匀分布的土样SCS比初始非均匀分布的土样DCS和分形分布的土样FCS,颗粒破碎程度更高,而且随着围压的增加,这种差别愈加显著。

图  2  粒径分布曲线

Figure  2.  Particle-size distribution curves

下载: 全尺寸图片 幻灯片

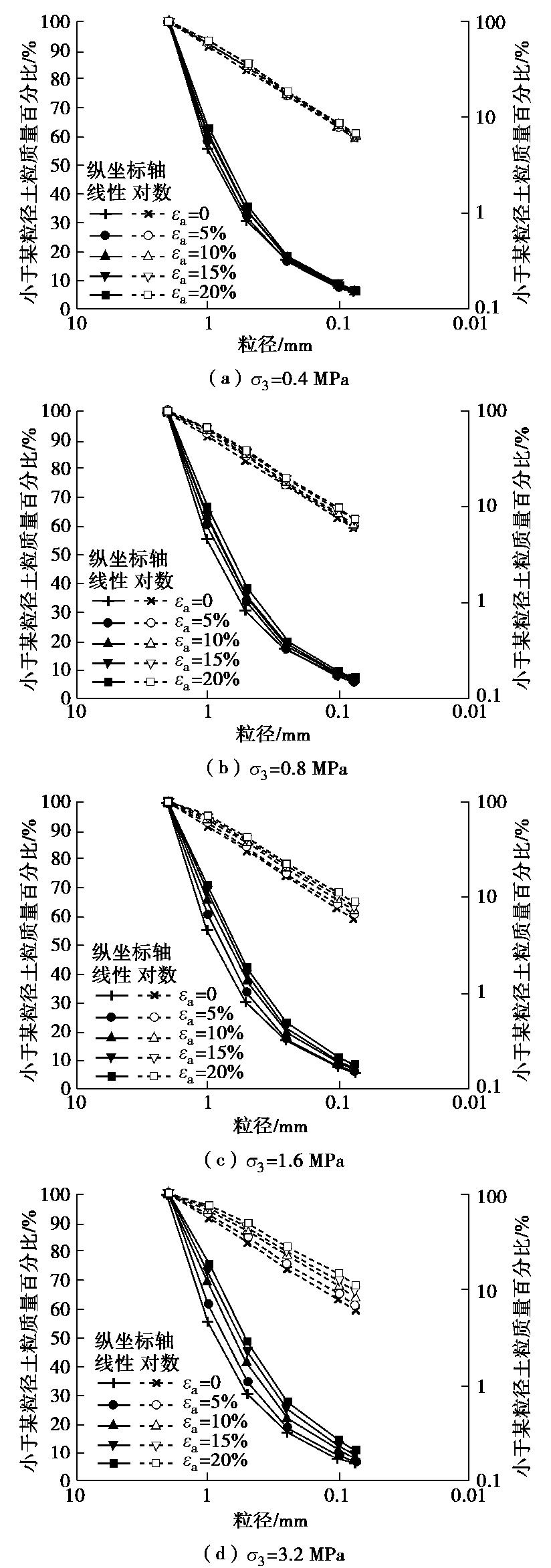
Turcotte^[25]认为,任何初始分布的土粒都将随着颗粒破碎的增加而趋向一种自相似的分形分布,该论断已得到实验验证。考察粒径分布曲线在双对数坐标轴上的形状,从图2（a）,（b）可知,在${\sigma }_3$=3.2 MPa的高围压下,土样SCS和DCS的粒径分布曲线仍是非线性的,二者均不具有分形特性。原因在于不同初始分布的土粒趋向于分形分布,是一个渐进性的变化过程^[23],而土样SCS和DCS当前的颗粒破碎程度,尚不足以促成向分形分布转变。而图2（c）显示,初始分形分布的土样FCS在任何围压下的颗粒破碎,粒径分布曲线与初始分布一样,均具有分形特征。

图3为不同围压下土样FCS在不同轴向应变时的粒径分布曲线,可从中考察三轴剪切过程中初始分形土体的粒径分布是如何演化的。图3显示,无论围压是大是小,随着轴向应变的发展,在双对数坐标轴上的粒径分布曲线为一簇直线,分形特征非常明显。

图  3  粒径分布曲线的演化

Figure  3.  Evolution of particle-size distribution curves

下载: 全尺寸图片 幻灯片

通过检验粒径分布数据自相似性的显著性程度,可以进一步明确三轴剪切过程中分形粒径分布的演化规律。式（1）表示的是一个严格的自相似分形分布,利用式（1）和粒径分布数据作线性回归分析,将获得的分形维数D和拟合相关系数R²列于表2,从中可以发现,无论围压和轴向应变是多少,粒径分布数据自相似性的显著性水平都非常高,R²值的变化范围在0.992～0.999之间,说明初始分形的粒径分布曲线在三轴剪切过程中始终保持着较为严格的分形特性。分形维数随围压及轴向应变的增长而增大,也即分形维数随着颗粒破碎的增长而增大。

表  2  分形维数和拟合相关系数

Table  2.  Values of fractal dimension and correlation coefficient

围压${\sigma }_3$/MPa	轴向应变εa/%	分形维数D	相关系数R2
0	0	2.150	1.000
0.4	5	2.158	0.999
	10	2.168	0.999
	15	2.177	0.998
	20	2.185	0.997
0.8	5	2.163	0.996
	10	2.171	0.997
	15	2.206	0.998
	20	2.223	0.998
1.6	5	2.181	0.994
	10	2.217	0.992
	15	2.247	0.996
	20	2.275	0.998
3.2	5	2.196	0.998
	10	2.257	0.993
	15	2.307	0.993
	20	2.347	0.992

下载: 导出CSV 

| 显示表格

2.2   粒组含量的演化

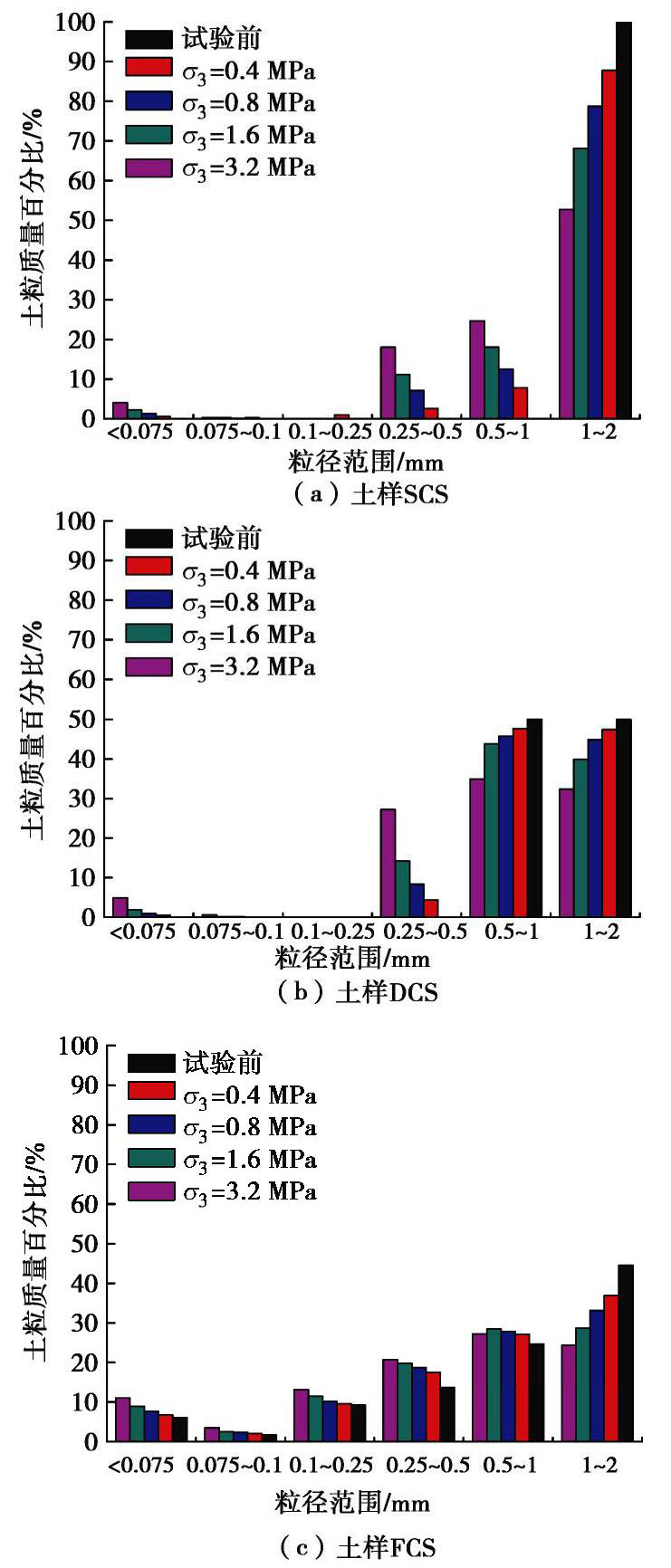
图4给出了3种土样在不同围压下各粒组的颗粒含量。图4（a）,（b）显示,随着围压的增加,颗粒破碎致使土样SCS的颗粒,在粒径范围2～1 mm的含量大幅减少,在粒径范围1～0.5 mm和0.5～0.25 mm的含量大增；土样DCS在粒径范围2～1 mm和1～0.5 mm的颗粒含量减少,在粒径范围0.5～0.25 mm的颗粒含量增加。而在粒径小于0.25 mm的各个粒组,两种土样的颗粒含量极少,说明破碎后的颗粒主要向相邻的下一级小粒径粒组中迁移,因而显示出依次逐级破碎现象。土样FCS因初始分布就包含有各个粒组的土粒,依照颗粒破碎的迁移机制,各粒组中的破碎颗粒依次向下一级小粒径区间迁移,因此,除了粒径范围2～1 mm粒组外,其它各粒组的含量均有所增加,见图4（c）。

图  4  不同粒组含量的演化

Figure  4.  Evolution of different particle fraction contents

下载: 全尺寸图片 幻灯片

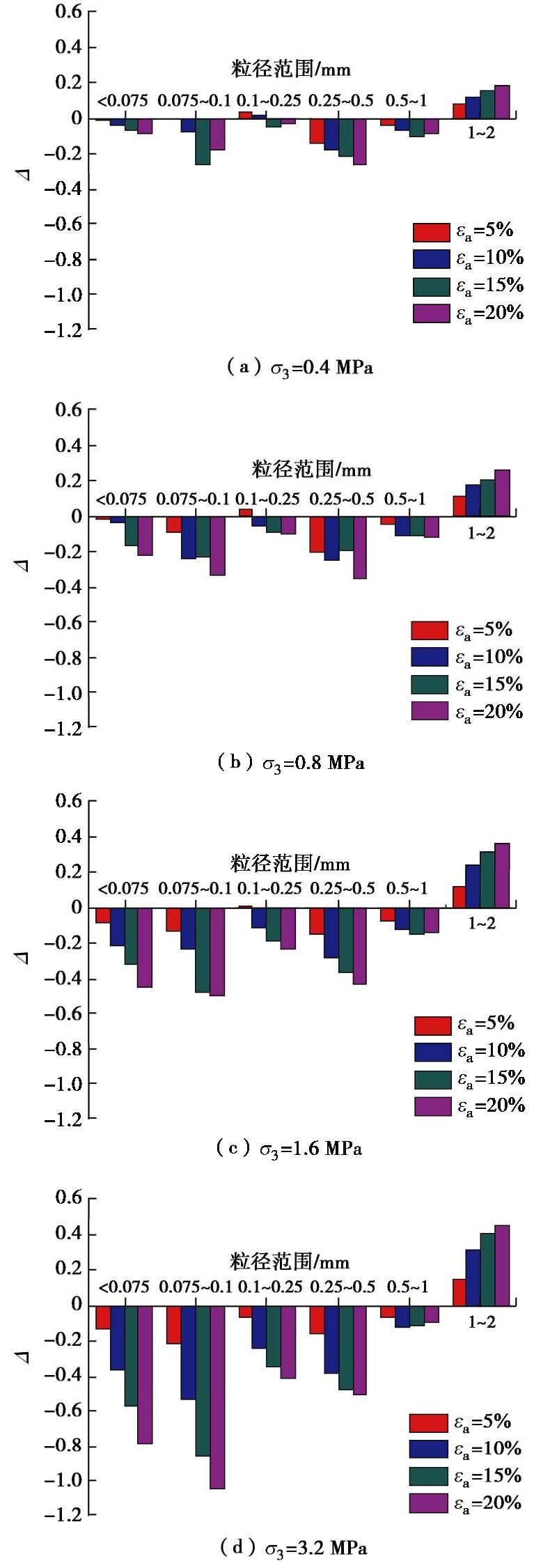
为了进一步弄清不同粒组的颗粒破碎及迁移状况,本文用各粒组破碎前与破碎后的颗粒含量之差,与破碎前的颗粒含量之比值Δ,来表征不同粒组颗粒含量相对于初始含量的变化,即

式中,M₀为破碎前粒组的颗粒含量,M为破碎后粒组的颗粒含量,除了遗留在该粒组的颗粒含量外,还包括其它粒组颗粒破碎补充进来的颗粒含量。因此,式（2）描述的是破碎后各粒组的相对含量而非绝对含量的变化。

由式（2）可知,当M=0时,Δ=1,表示本粒组颗粒完全破碎,存留下来的颗粒消失殆尽,且没有其它粒组给予补充；当M<M₀时,0<Δ<1,表示本粒组颗粒破碎量高于其它粒组的补充；当M=M₀时,Δ=0,表示本粒组的颗粒破碎与其它粒组的补充相抵,相对含量不变；当M>M₀时,Δ为负值,表示其它粒组补充进来的颗粒含量,大于本粒组因破碎而减少的颗粒含量。实际上,纪文栋等^[26]曾利用破碎后与破碎前各粒组含量之差与破碎前粒组含量的比值,来表示不同粒组的相对含量变化,显然,这个比值与Δ的概念基本一致,但互为相反数。

图5为土样FCS在剪切过程中各粒组相对含量的变化。可以发现,在不同围压下的三轴剪切过程中,不同粒组颗粒含量的变化有如下几个特点：

图  5  土样FCS的粒组相对含量的演化

Figure  5.  Evolution of relative fraction content of particles of FCS samples

下载: 全尺寸图片 幻灯片

（1）粒径范围在2～1 mm的粒组,其Δ值始终是一个小于1的正数。因不可能有来自于其它粒组破碎颗粒的补充,该粒组含量的减少全部归咎于本粒组的颗粒破碎。显然仍有大部分的初始大颗粒被保留,并未因全部剪破而荡然无存。

（2）粒径范围在0.1～0.25 mm的粒组,在低围压（${\sigma }_3$=0.4 MPa）及剪切初始阶段（ε_a=5%）,Δ是一个小于1的正数,表明本粒组的颗粒破碎要大于其它粒组颗粒的补充。但随着围压的增加及剪切进程的发展,Δ值由正转负,表明其它粒组补充进来的颗粒含量,大于本粒组因破碎减少的颗粒含量。

（3）粒径小于1 mm的其它各个粒组,Δ基本上呈现为负值,说明从相邻粒组破碎补充进来的颗粒含量,要大于本粒组破碎而减少的颗粒含量,这种差距随围压的增加及剪切进程的发展而逐渐扩大。

图5还显示,随着轴向应变的增加,总体上,各粒组Δ值的增减比例渐趋稳定,表明不同粒组的颗粒含量相对于初始含量的变化,趋于一个稳定的比例。这意味着破碎颗粒优先向相邻的下一级粒组迁移的机制,使得初始分形的粒径分布在颗粒破碎过程中,自相似分形特性能得以保持。

2.3   应力–应变–体应变特征

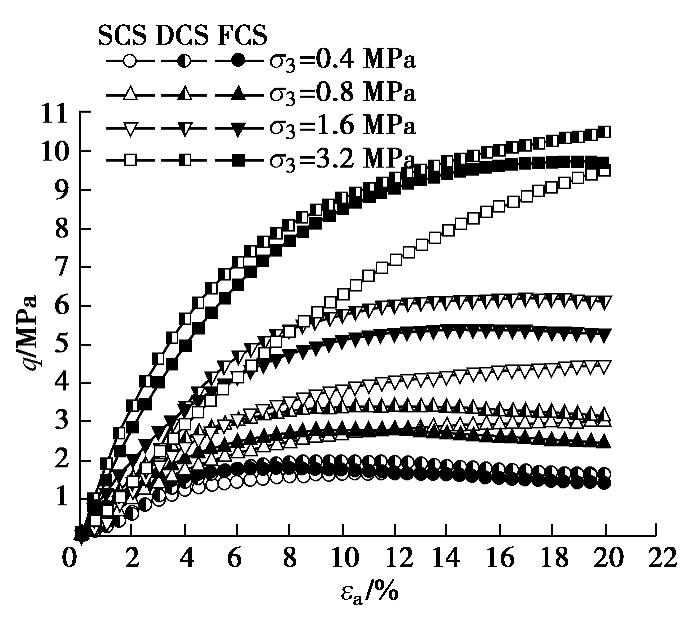
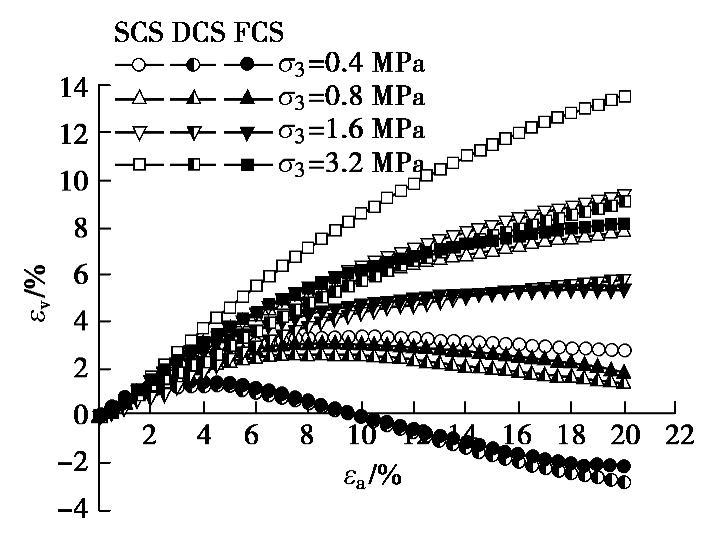
图6～8给出了3种试样在4种围压下的三轴排水剪切试验结果。图6为偏应力q=${\sigma }_1-{\sigma }_3$与轴向应变ε_a的关系曲线,从中可以发现,3种试样在低围压（${\sigma }_3$=0.4～0.8 MPa）下的应力–应变曲线表现为应变软化,随着轴向应变的增大,偏应力增至峰值后逐渐降低；围压增至1.6 MPa时的应力–应变曲线则表现为应变硬化,随着轴向应变的增加,不出现峰值剪应力,大应变下的偏应力趋于不变；在${\sigma }_3$=3.2 MPa的高围压下,即使到达试验终止时的轴向应变,偏应力仍未趋于稳定。

图  6  偏应力与轴向应变的关系

Figure  6.  Relationship between deviator stress and axial strain

下载: 全尺寸图片 幻灯片

图  7  体应变与轴向应变的关系

Figure  7.  Relationship between volumetric strain and axial strain

下载: 全尺寸图片 幻灯片

图  8  主应力比与轴向应变的关系

Figure  8.  Relationship between principal stress ratio and axial strain

下载: 全尺寸图片 幻灯片

图7为体应变ε_v与轴向应变的关系曲线,可以发现,3种试样在低围压下均表现出剪胀特性,随着轴向应变的增加,体应变先缩小后膨胀。初始均匀分布的土样SCS,剪胀现象不显著。而初始非均匀分布的土样DCS和FCS,剪胀现象十分明显,剪胀变化幅度大,轴向应变增加到一定量时,体应变甚至转为负值。随着围压的增大,各试样的剪胀倾向减少,由剪胀过渡到剪缩状态,在高围压下各试样的体应变均表现为剪缩,需要相当大的轴向应变,才会趋于不胀不缩。

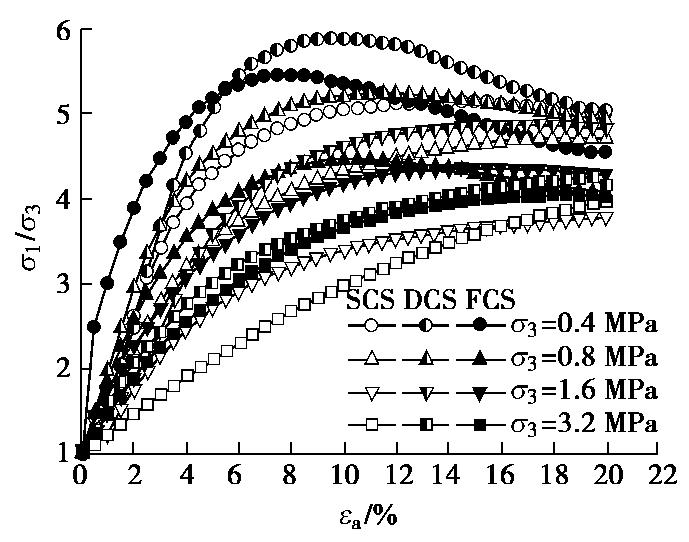
图8为主应力比${\sigma }_1$/${\sigma }_3$与轴向应变的关系曲线,可看出低围压下各试样的应变软化和剪胀程度。图8显示,在低围压下,随着轴向应变的增加,主应力比持续增加,达到峰值后又不断减小,降低幅度与体应变曲线中的剪胀变化趋势相一致。在同样围压下,试样的初始粒径分布愈不均匀,应变软化和剪胀效应愈明显。高围压下,随着轴向应变的增加,主应力比不出现峰值,各试验最后的主应力比趋于大致的定值。

2.4   破碎率的演化

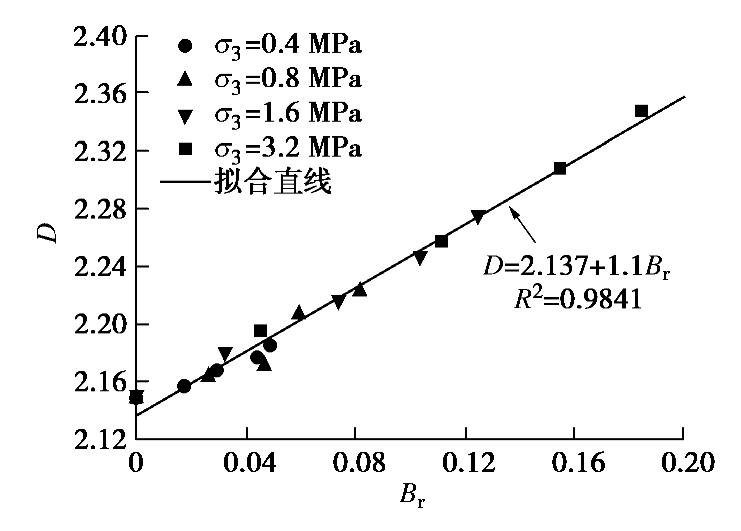
图9显示了土样FCS在剪切过程中的分形维数与破碎率的关系。可以发现,分形维数与破碎率之间存在较为显著的线性回归关系,与围压大小无关。这一规律与石英砂在侧限压缩下颗粒破碎的分形维数与破碎率的关系相一致^[27],说明分形维数的大小反映的是颗粒的破碎程度,与土粒性质、破碎方式等因素无关。

图  9  破碎率对分形维数的影响

Figure  9.  Influences of breakage index on fractal dimension

下载: 全尺寸图片 幻灯片

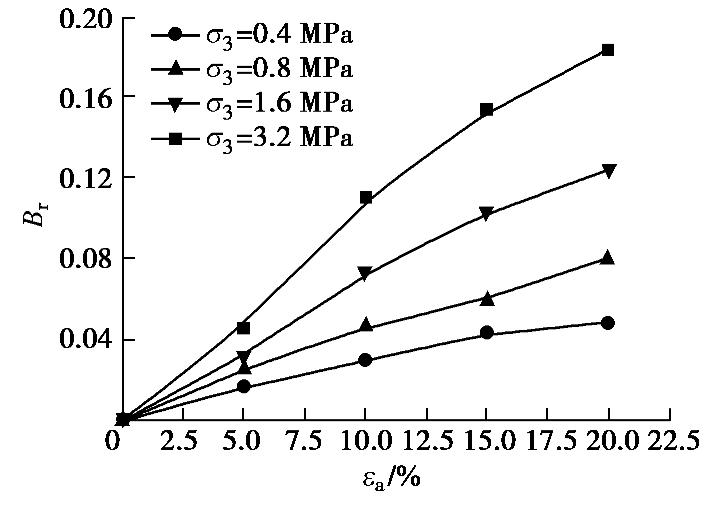
图10为土样FCS在不同围压下的轴向应变对破碎率的影响,从中可知,随着轴向应变的增加,破碎率持续增大。各个围压下的破碎率与轴向应变近似呈线性增加的关系。相同轴向应变下,围压越大,破碎率越大。

图  10  轴向应变对破碎率的影响

Figure  10.  Influences of axial strain on breakage index

下载: 全尺寸图片 幻灯片

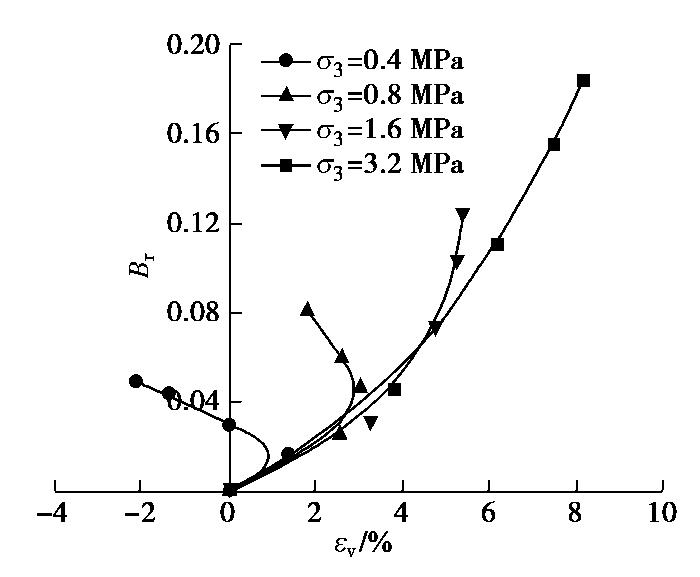
图11为土样FCS在不同围压下的体应变对破碎率的影响,从中发现,在较低围压下（${\sigma }_3$≤0.8 MPa）,体应变开始有少量的剪缩,然后转为剪胀,试验终止时的破碎率较小。随着围压增大,体应变增大,破碎率也增大,颗粒破碎部分抵消了剪胀作用,剪胀效应消失。在高围压下（${\sigma }_3$=3.2 MPa）,体应变表现为剪缩作用,试验终止时的体应变和破碎率较大。

图  11  体应变对破碎率的影响

Figure  11.  Influences of volumetric strain on breakage index

下载: 全尺寸图片 幻灯片

图12为FCS样在不同围压下的偏应力对破碎率的影响,从中看到在低围压下,应变软化作用使偏应力在峰值后略有降低,破碎率较小。不同围压下,当偏应力增至趋于稳定,对应的偏应力定值和破碎率各不相同。围压越大,偏应力定值越大,破碎率也越大。

图  12  偏应力对破碎率的影响

Figure  12.  Influences of deviator stress on breakage index

下载: 全尺寸图片 幻灯片

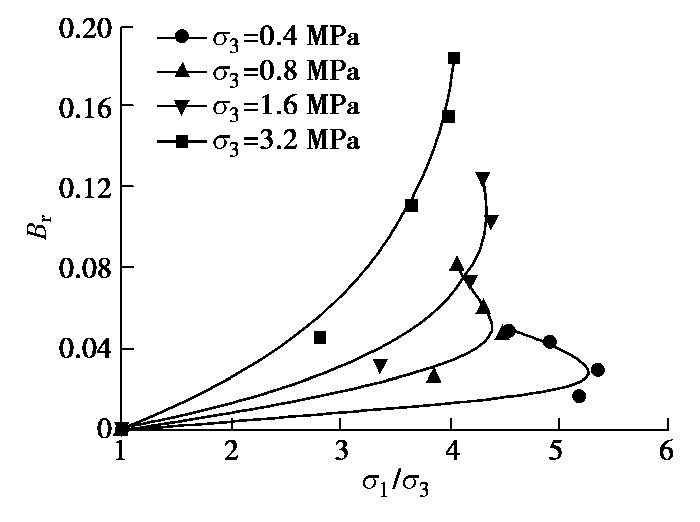
图13为FCS样在不同围压下的主应力比对破碎率的影响,从中可发现,无论是低围压下的应变软化导致主应力比达到峰值后再降低的剪胀作用,还是高围压下的应变硬化致使主应力比无峰值平缓变化的剪缩作用,殊途同归,不同围压下的主应力比将趋于大致的定值。围压越大,试验终止时的破碎率越大。

图  13  主应力比对破碎率的影响

Figure  13.  Influences of principal stress ratio on breakage index

下载: 全尺寸图片 幻灯片

2.5   颗粒破碎对强度的影响

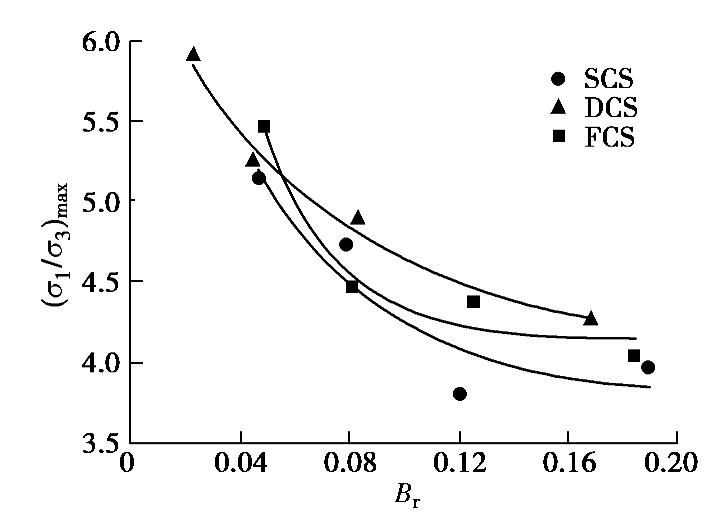
根据应力–应变曲线的剪应力峰值确定的摩擦角,可定义为峰值内摩擦角${\varphi }_{\text{p}}$。在大应变下,剪应力保持常数,体积不再变化,此条件下的摩擦角可定义为最终内摩擦角。如图6,7所示,钙质砂在三轴排水剪下的应力–应变曲线显示了应变软化和硬化二种不同的性质,当轴向应变到达20%时,低围压时的偏应力和体应变基本趋于稳定,但高围压下的试样体积,胀缩还未停止,因此无法直接测定最终内摩擦角。

图14为各试样的峰值主应力比（${\sigma }_1$/${\sigma }_3$）_max与破碎率的关系,从中可以发现,峰值主应力比随着破碎率的增加而逐渐降低,当破碎率较小时,（${\sigma }_1$/${\sigma }_3$）_max降幅较快,当破碎率较大时,（${\sigma }_1$/${\sigma }_3$）_max降幅变小。按照莫尔–库仑强度理论,无黏性土在三轴排水剪中的内摩擦角$\varphi$与主应力比${\sigma }_1$/${\sigma }_3$的关系为

图  14  峰值主应力比与破碎率的关系

Figure  14.  Relationship between peak principal stress ratio and breakage index

下载: 全尺寸图片 幻灯片

由式（3）可知,主应力比的降低,意味着降低了砂土的内摩擦角。根据三轴排水试验结果中的峰值主应力比,可计算峰值内摩擦角为

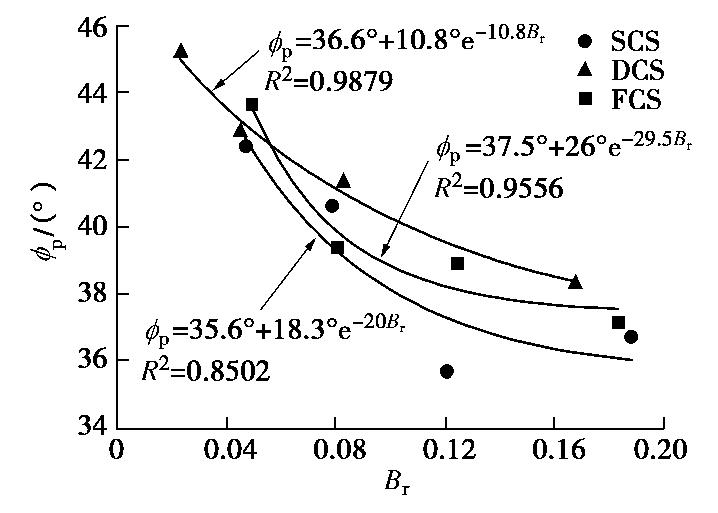
图15为峰值内摩擦角与破碎率的关系,从中可发现,同峰值主应力比与破碎率的关系基本相似,峰值内摩擦角随着破碎率的增加而逐渐降低。对该现象可用颗粒的咬合作用来解释：在低围压下的三轴排水剪切,颗粒破碎量尚小,剪胀作用增大了颗粒的咬合摩擦,需要做更多的功能来克服,因而就具有了较高的峰值内摩擦角。随着围压的增大,偏应力增加,破碎率也增大,颗粒破碎部分抵消剪胀作用,剪胀性逐渐消失,咬合作用渐渐消除,仅剩下滑动摩擦,内摩擦角接近于滑动摩擦角。因此,峰值内摩擦角不仅因颗粒初始分布的不同而有所差异,而且还随围压而变。

图  15  峰值内摩擦角与破碎率的关系

Figure  15.  Relationship between peak angle of internal friction and breakage index

下载: 全尺寸图片 幻灯片

对各试样的峰值内摩擦角与破碎率的试验数据进行拟合分析,发现采用指数函数来描述峰值内摩擦角与破碎率之间的非线性关系,拟合程度的显著性水平较高,见图15。因此,峰值内摩擦角可表示为

式中,${\varphi }_0$,${\varphi }_1$,A均为试验常数,与钙质砂的性质和初始粒径分布有关。

式（5）显示,随着破碎率的增大,峰值内摩擦角逐渐降低,一直降到趋近于${\varphi }_0$的常数。这一规律可从Vesic等^[28]对砂土进行的高围压下排水三轴试验的结果中得到解释。Vesic等发现,当围压增至更高时,无论砂土的初始状态如何,颗粒破碎机理将起主导作用,试样破坏时的体应变速率渐趋于零,从而变成了一个理想的塑性体,其内摩擦角也趋于定值。由此可见,式（5）较好地反映了粒状土的颗粒破碎对强度参数的影响规律。其中,${\varphi }_0$有明确的物理意义,即为最终的内摩擦角。可以预见,峰值内摩擦角随着破碎率的增大而持续降低,最后与最终的内摩擦角趋于一致,从而不随试验条件而变。

3.   结论

本文对3种不同初始分布的钙质砂进行了4种围压下的三轴排水剪切试验,研究剪切过程中钙质砂的颗粒破碎特性及对应力应变和抗剪强度的影响,主要结论如下：

（1）初始分形的粒径分布曲线在三轴排水剪切过程中,始终保持着较为严格的分形特性。分形维数随围压及应变的增长而增大,与破碎率之间存在着较为显著的线性回归关系。

（2）钙质砂的颗粒破碎机制为,各粒组破碎后的颗粒主要向相邻的下一级小粒径粒组迁移,使得初始分形的粒径分布,在颗粒破碎过程中的分形特性能得以保持。

（3）钙质砂的应力应变特性与围压大小和初始分布有关,围压越低,初始分布越不均匀,剪胀效应越显著。随着围压的增大,剪胀倾向减少,逐渐过渡到剪缩状态。

（4）钙质砂的破碎率随剪切过程中的应变和剪应力的增长而增大。当偏应力和主应力比增至稳定不变时,围压越大,破碎率越大。

（5）钙质砂的峰值内摩擦角随着破碎率的增大而降低,最终趋于定值。用非线性的指数函数来描述二者之间的关系,揭示了颗粒破碎对钙质砂抗剪强度的影响规律。