分数阶黏弹性地基中洞周超孔隙水压力消散特性分析

黄明华; 胡可馨; 赵明华

doi:10.11779/CJGE202008009

分数阶黏弹性地基中洞周超孔隙水压力消散特性分析 English Version

黄明华^{1, 2,},
胡可馨^{1, 2},
赵明华^{1, 2}

1.
湖南大学建筑安全与节能教育部重点实验室,湖南　长沙　410082
2.
湖南大学土木工程学院,湖南　长沙　410082

基金项目:

国家重点研发计划项目 2019YFC1511100

国家重点研发计划项目 2016YFC0800200

湖南省自然科学基金项目 2019JJ50055

详细信息

作者简介:
黄明华(1983—),男,博士,副教授,主要从事岩土工程方面的教学和科研工作。E-mail：hmh666@163.com

中图分类号: TU43
计量
- 文章访问数: 274
- HTML全文浏览量: 39
- PDF下载量: 142
出版历程
- 收稿日期: 2019-09-01
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-07-31

Dissipation characteristics of excess pore-water pressure around tunnels in viscoelastic foundation using a fractional-derivative model

HUANG Ming-hua^{1, 2,},
HU Ke-xin^{1, 2},
ZHAO Ming-hua^{1, 2}

1.
MOE Key Laboratory of Building Safety and Energy Efficiency, Hunan University, Changsha 410082, China
2.
College of Civil Engineering, Hunan University, Changsha 410082, China

摘要

摘要: 针对黏弹性地基中洞周超孔隙水压力消散问题,首先,采用分数阶Merchant模型来描述洞周饱和软黏土的流变特性,并借助拉普拉斯变换及逆变换方法,推导该模型柔度函数；其次,基于饱和软黏土二维固结状态下超孔隙水压力消散的偏微分方程,采用保角变换和分离变量方法,推导超孔隙水压力关于时间和空间变量的两个独立方程及其在拉普拉斯域内的解析表达式；再次,基于Crump方法,建立时域内超孔隙水压力的数值计算方法,并将超孔隙水压力解答退化为弹性和整数阶黏弹性地基的情况,与已有解答进行对比,验证其可靠性；最后,基于建立的解答,对洞周超孔隙水压力的消散特性进行研究,分析分数阶阶次、模量比、黏滞系数和边界条件的影响。结果表明：分数阶阶次和黏滞系数对超孔隙水压力消散的影响均呈现为两个不同的阶段。在消散初期,分数阶阶次和黏滞系数越大,超孔隙水压力消散越快；而在消散后期,分数阶阶次和黏滞系数越大,超孔隙水压力则消散越慢。模量比越大所对应的饱和软黏土层越软,超孔隙水压力消散越慢,且模量比的影响在超孔隙水压力消散中后期更为明显。洞周排水边界条件对超孔隙水压力消散的影响,消散初期主要体现在靠近洞周一侧,之后,逐渐向远离洞周一侧延伸和传递。
- 岩土工程 /
- 黏弹性地基 /
- 超孔隙水压力 /
- 消散特性 /
- 分数阶导数
Abstract: The dissipation characteristics of the excess pore-water pressure around tunnels in viscoelastic foundation are investigated by using a fractional-derivative model. Firstly, the fractional-derivative Merchant model is introduced to describe the rheological behavior of the saturated soft foundation around tunnels, and its compliance function is deduced by means of the Laplace transform and its inverse transform. Secondly, using the methods of conformal mapping and variable separating, two independent equations only including the variable of time and only including the variable of space are derived from the partial differential equation governing the dissipation of the excess pore-water pressure during two-dimensional consolidation process, and the analytical solution of the excess pore-water pressure is also formulated in the Laplace domain. Thirdly, the numerical method for the excess pore-water pressure in the time domain is presented based on the Crump method. The developed solution is simplified into two special cases for the elastic foundation and viscoelastic foundation of integer order, and its correctness is validated against the existing solutions of these two special cases. Finally, using the developed solution, the dissipation characteristics of the excess pore-water pressure around tunnels are investigated, and the influences of fractional order, modulus ratio, viscosity coefficient and boundary condition are discussed. The results show that the influences of the fractional order and viscosity coefficient on the dissipation of the excess pore-water pressure have two distinct stages. In the early stage, larger fractional order and larger viscosity coefficient bring about faster dissipation of the excess pore-water pressure; while at the later stage, they lead to slower dissipation of the excess pore-water pressure. Larger modulus ratio means softer foundation, and it also results in slower dissipation of the excess pore-water pressure. In addition, at the middle stage, the modulus ratio has a much greater influence. In the early stage, the effect of the inner boundary condition on the excess pore-water pressure mainly emerges on the regions close to the tunnels, and then this effect is spread far away.
- geotechnical engineering /
- viscoelastic foundation /
- excess pore-water pressure /
- dissipation characteristic /
- fractional-derivative model

HTML全文

0. 引言

合理开发和利用地下空间已成为解决城市人口激增、空间拥挤、交通阻塞及环境污染等问题的重要途径。在城市相对集中的沿江和滨海等饱和软黏土区域,地下空间开发所引起的长期沉降相当显著,通常为总沉降的30%〜90%^[1-3]。长期沉降不仅影响地下空间自身安全,如隧道衬砌开裂和渗漏水等,还会对周围环境和邻近建/构筑物等产生危害,如地下管线变形过大和地面建筑倾斜等。从长期沉降的发展机理来看^[3],地下空间开发对周围土体产生扰动后,所引起的超孔隙水压力消散及土体的流变特性是产生长期沉降的两个重要因素。因此,研究黏弹性地基中隧道施工等地下空间开发活动所引起的洞周超孔隙水压力消散问题具有重要的理论意义和工程应用价值。

针对洞周超孔隙水压力消散问题,国内外学者展开了较为广泛的研究。Carter等^[4-5]以Biot固结理论为框架,推导了弹性地基中洞周超孔隙水压力以及土体应力场和位移场的解析计算方法,洞周边界分为完全透水和完全不透水两种情况。在此基础上,Li等^[6-7]通过引入半渗透边界条件,将上述解答拓展至弹性半空间体内具有有限渗透性边界的洞周超孔隙水压力消散问题。基于Terzaghi-Rendulic二维固结理论,王志良等^[8]及申林方等^[9]推导了洞周不透水条件下饱和弹性地基中超孔隙水压力的解析解,分析了渗透系数、土体弹性模量以及隧洞埋深等参数对超孔隙水压力消散的影响。上述研究均将土体视为弹性介质,没有考虑其流变特性。为考虑土体流变特性对洞周超孔隙水压力消散的影响,詹美礼等^[10]以Terzaghi-Rendulic二维固结理论为基础,采用三元件Merchant模型描述土体的流变特性,推导了洞周超孔隙水压力的解析解,洞周边界为完全透水和完全不透水两种情况。童磊^[3]将三元件Merchant模型推广至四元件Burgers模型,建立了相应的解析解,研究了土体特性对超孔隙水压力消散的影响。针对泥炭质土层盾构施工引起的长期沉降问题,王志良等^[11]采用五元件模型来描述泥炭质土的流变特性,耦合Terzaghi-Rendulic二维固结理论,建立了完全不透水边界条件下洞周超孔隙水压力的解析解。综合考虑洞周土体流变和衬砌半渗透特性,李翔宇等^[12]建立了半透水边界条件下黏弹性地基中洞周超孔隙水压力的解析解,分析了不同衬砌透水程度对超孔隙水压力消散和分布的影响。刘干斌等^[13]基于Biot固结理论,运用推广的李氏比拟法,建立了半透水边界条件下黏弹性地基中深埋洞周的超孔隙水解答,研究了深埋条件下洞周超孔隙水压力以及土体应力和位移场的变化规律。上述研究虽考虑了土体流变特性对洞周超孔隙水压力消散特性的影响,但均采用经典流变模型（即整数阶流变模型）来描述土体的流变特性。然而,试验研究表明^[14-15],经典流变模型有时难以很好地描述材料的流变特性,特别是在初始流变阶段,通常需要较多的元件组合才能获得较好的模拟精度。

分数阶流变模型是经典流变模型的进一步拓展和延伸,采用分数阶导数代替整数阶导数来描述元件的本构关系。众多学者发现,分数阶流变模型可以采用相对较少的模型参数来更好地模拟材料的流变特性^[16-17]。自Gemant^[18]首次建立分数阶流变模型描述材料的流变特性以来,分数阶流变模型已逐渐成为岩土工程等领域的研究热点之一。Bagley等^[19]从能量耗散角度对分数阶流变模型的本构方程进行讨论和验证。Koller^[20]建立了多个分数阶流变模型,并对其流变特性进行了研究。赵永玲等^[21]和孙雅珍等^[22]采用分数阶流变模型分别研究了橡胶材料和沥青路面的流变特性。在岩土工程领域,Yin等^[17]、刘林超等^[23]、孙海忠等^[24]、Zhu等^[25]、何利军等^[26]、李锐铎等^[27]采用分数阶Kelvin模型、分数阶Merchant模型、分数阶Burger模型以及分数阶五元件模型等来拟合不同地区或不同类型软黏土的流变试验数据,得到很好的拟合结果,证明了分数阶流变模型描述软黏土流变特性的有效性和适用性。在此基础上,Wang等^[28]、解益等^[29]、刘忠玉等^[15,30]将分数阶流变模型应用到饱和软黏土一维流变固结分析中,研究了一维固结条件下分数阶黏弹性地基中孔隙水压力消散及土体变形发展规律。汪磊等^[31]、李林忠等^[32]、田乙等^[33]进一步建立了单面半透水、双面半透水以及连续排水边界条件下分数阶黏弹性地基的一维固结问题,分析了复杂边界条件对超孔隙水压力消散的影响。基于分数阶流变模型,Huang等^[34-35]研究了一维降水以及砂井固结条件下黏弹性地基中的超孔隙水压力消散问题,分析了分数阶流变模型参数对超孔隙水压力消散的影响。但是,目前尚未见分数阶流变模型应用于洞周超孔隙水压力消散问题的相关研究。

在以上学者的研究基础上,本文引入分数阶流变模型对黏弹性地基中洞周超孔隙水压力消散问题进行研究和探讨。首先,基于分数阶Merchant模型和Terzaghi-Rendulic二维固结理论,建立分数阶黏弹性地基中超孔隙水压力消散的控制方程；其次,借助保角变换、分离变量、Laplace变换及逆变换等方法,建立洞周超孔隙水压力的解答及其计算方法,并与文献已有解答进行对比；最后,探讨分数阶流变模型参数和边界条件对洞周超孔隙水压力消散特性的影响。

1. 解析问题的描述

1.1 分数阶Merchant模型

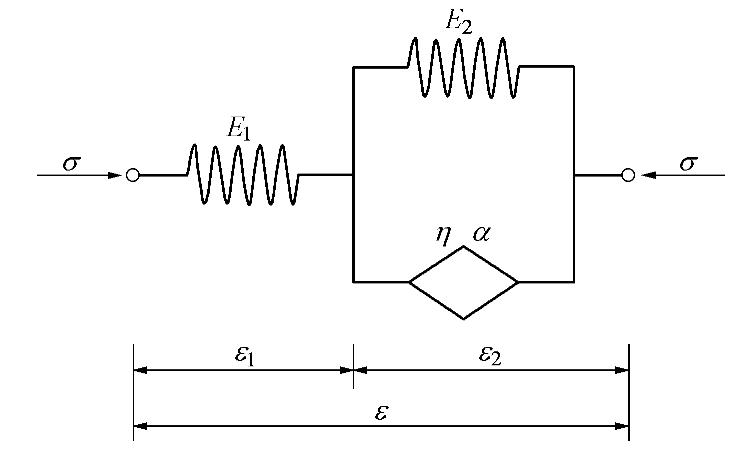
如图1所示,分数阶Merchant模型为三元件模型,由一个弹簧元件和一个Kelvin体所组成。基于分数阶微积分理论,分数阶流变模型采用分数阶导数关系来描述传统整数阶流变模型中的Abel黏壶。基于此,分数阶Merchant模型的总应力和总应变可以表示为^[25]

。

${\begin{array}{l} ε = ε_{1} + ε_{2}, \\ σ = E_{1} ε_{1} = E_{2} ε_{2} + E_{2} λ^{α}^{RL} D_{t}^{^{α}} ε_{2} 。 \end{array}$

(1)

图 1 分数阶Merchant模型

Figure 1. Fractional-derivative Merchant model

下载: 全尺寸图片幻灯片

式中 $σ$ 为总应力； $ε$ 为总应变； $ε_{1}$ 和 $ε_{2}$ 分别为弹簧元件和Kelvin体所产生的应变； $E_{1}$ 和 $E_{2}$ 为弹簧元件和Kelvin体的弹性模量； $λ = η / E_{2}$ 为Kelvin体的黏滞时间, $η$ 为其Abel黏壶的黏滞系数, $t$ 为时间, $^{RL} D_{t}^{^{α}}$ 为Riemann-Liouville型分数阶导数,其定义为^[16]

$^{RL} D_{t}^{α} ε (t) = \frac{1}{Γ (n - α)} \frac{d}{d t} \int_{0}^{t} {(t - τ)}^{n - α - 1} ε (τ) d τ$ ,

(2)

式中, $Γ (\cdot)$ 为Gamma函数, $α \in [n - 1, n)$ 为分数阶阶次, $n \geq 1$ 为自然数, $τ$ 为积分变量。对于分数阶流变模型,通常取 $0 \leq α \leq 1$ 。

对式（1）进行拉普拉斯变换,整理得到

$L (ε) = \frac{1}{E_{1}} (1 + \frac{κ}{λ^{α} s^{α} + 1}) L (σ)$ 。

(3)

式中, $κ = E_{1} / E_{2}$ , $L (\cdot)$ 表示拉普拉斯变换, $s$ 为一个复变量。

令 $σ = H (t)$ ,其中 $H (t)$ 为Heaviside函数,则利用卷积定理和拉普拉斯逆变换,由式（3）可以得到分数阶Merchant模型的柔度函数 $J (t)$ 为

$J (t) = \frac{1}{E_{1}} L^{- 1} (\frac{1}{s} + \frac{1}{s} \cdot \frac{κ}{λ^{α} s^{α} + 1})$ ,

(4)

式中, $L^{- 1} (\cdot)$ 表示拉普拉斯逆变换。当 $α = 1$ 时,式（4）可简化为

$J (t) = \frac{1}{E_{1}} [1 + κ (1 - e^{- \frac{t}{λ}})]$ 。

(5)

式（5）为整数阶Merchant模型的柔度函数^[9]。当 $α = 0$ 时,式（4）可简化为

$J (t) = \frac{κ + 2}{2 E_{1}}$ 。

(6)

式（6）为线弹性模型的柔度函数^[10]。可见,线弹性模型和整数阶Merchant模型均可视为分数阶Merchant模型的两个特例。

1.2 计算模型与控制方程

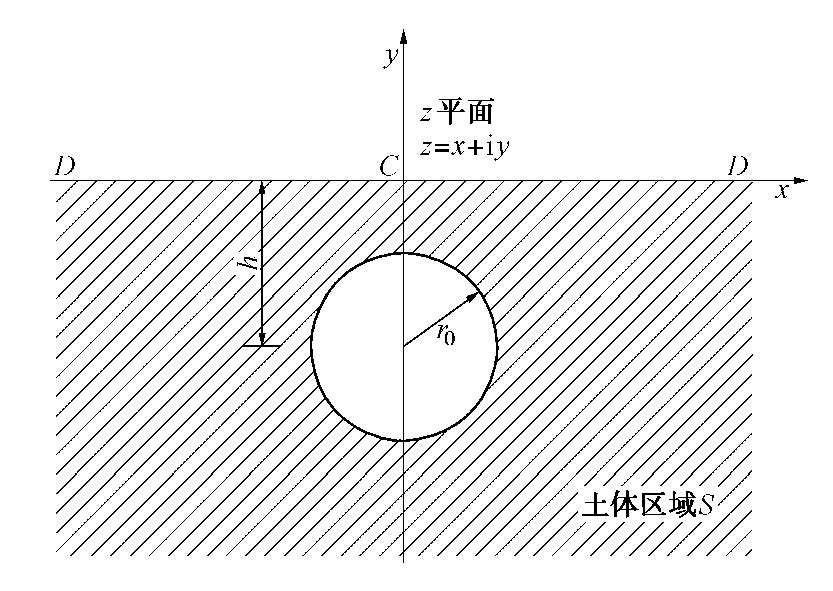
分析时,将洞周饱和软黏土层视为带圆孔的半无限平面,如图2所示。图2中,h为洞周埋深,r₀为洞周外径,C为平面坐标原点,D为无限远处的点,S区域为洞周饱和软黏土层。为了便于理论推导,本文采用如下假设^[10-12]：①饱和软黏土为各向同性介质,其应力应变关系服从分数阶Merchant模型,且所有黏弹性参数均为常数；②孔隙水和土颗粒的压缩可忽略不计,孔隙水流动服从达西定律,且饱和软黏土的渗透系数为常数；③土体变形十分微小,可忽略其对坐标的影响；④采用Terzaghi-Rendulic固结理论,土体中各点变形完全自由,且其所承受的总应力不随时间变化。基于上述假设,饱和软黏土二维固结状态下超孔隙水压力消散的偏微分方程可以表示为^[10-12]

$u_{x x} + u_{y y} = \frac{γ_{w}}{k m_{v}} (u_{t} + E_{1} \int_{0}^{t} u_{τ} J_{t - τ} d τ)$ 。

(7)

图 2 半无限空间中洞周土体计算模型图

Figure 2. Model for soft soil around tunnel in half space

下载: 全尺寸图片幻灯片

式中 $u$ 为超孔隙水压力； $u_{x x}$ 和 $u_{y y}$ 分别为 $u$ 关于x和y的二阶导数； $u_{t}$ 为 $u$ 关于t的一阶导数； $m_{v}$ 为土体压缩系数； $k$ 为渗透系数； $γ_{w}$ 为水的重度。

饱和软黏土所占区域为一个带圆孔的半无限平面,拥有地表和洞周内壁两个边界。在地表处,可以认为其完全透水,即超孔隙水压力为零；在洞周内壁处,通常按两种情况进行考虑：①施工期间,衬砌尚未完成,洞周内壁允许排水；②竣工后,洞周衬砌不允许排水。因此,两种情况下的边界条件（分别记为第一类边界、第二类边界条件）可以表示为

$\begin{matrix} {\begin{cases} {u |}_{y = 0} = 0 \\ {u |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} & , & {\begin{cases} {u |}_{y = 0} = 0 \\ {u_{r} |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} \end{matrix}$ 。

(8)

另外,在初始时刻 $t = 0$ 时,饱和软黏土层中的超孔隙水压力可表示为

${u |}_{t = 0} = u_{0} (x, y)$ 。

(9)

将式（4）代入式（7）中,并进行拉普拉斯变换,得到

$\frac{\partial^{2} \tilde{u}}{\partial x^{2}} + \frac{\partial^{2} \tilde{u}}{\partial y^{2}} = \frac{γ_{w}}{k m_{v}} (1 + \frac{κ}{λ^{α} s^{α} + 1}) (s \tilde{u} - u_{0})$ ,

(10)

式中, $\tilde{u} = L (u)$ 。式（10）为拉普拉斯域内基于分数阶Merchant模型的饱和软黏土中超孔隙水压力消散控制方程。在拉普拉斯域内,第一、二类边界条件式（8）可表示为

$\begin{matrix} {\begin{cases} {\tilde{u} |}_{y = 0} = 0 \\ {\tilde{u} |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} & , & {\begin{cases} {\tilde{u} |}_{y = 0} = 0 \\ {{\tilde{u}}_{r} |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} \end{matrix}$ 。

(11)

2. 超孔隙水压力解答推导与验证

2.1 保角变换

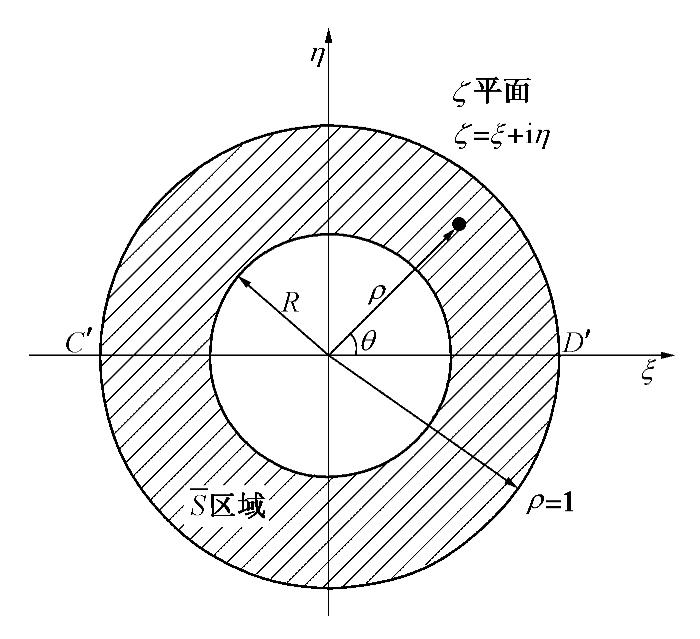
为研究图2中所示z平面内半无限空间中的单一孔洞问题,需采用保角变换,将其可转换为 $ζ$ 平面中的圆环域问题,如图3所示。映射函数为^[9-10]

$z = - i a \frac{1 + ζ}{1 - ζ}$ ,

(12)

图 3 保角变换映射计算模型图

Figure 3. Model after conformal mapping

下载: 全尺寸图片幻灯片

式中, $z = x + i y$ , $ζ = ξ + i η = ρ (\cos θ + i \sin θ)$ , $a = \sqrt{h^{2} - r_{0}^{2}}$ , $i = \sqrt{- 1}$ 为虚数单位。根据映射函数GOTOBUTTON ZEqnNum973390 \* MERGEFORMAT (12),图2中z平面上点C和D点分别映射成为图3中 $ζ$ 平面上点 $C^{'}$ 和 $D^{'}$ 点；洞周线 $| z + h i | = r_{0}$ 映射为圆环 $| ζ | = R$ ,水平线 $z = \bar{z}$ 映射为圆环 $| ζ | = 1$ ,求解域S区域映射为两个圆环间的 $\bar{S}$ 区域。

利用映射函数式（12）,方程（10）可以变换为

$\begin{matrix} \frac{\partial^{2} \tilde{u}}{\partial ρ^{2}} + \frac{1}{ρ} \frac{\partial \tilde{u}}{\partial ρ} + \frac{1}{ρ^{2}} \frac{\partial^{2} \tilde{u}}{\partial θ^{2}} = \frac{γ_{w}}{k m_{v}} \frac{4 a^{2}}{{(1 + ρ^{2} - 2 ρ \cos θ)}^{2}} \cdot \\ (1 + \frac{κ}{λ^{α} s^{α} + 1}) (s \tilde{u} - u_{0}) \end{matrix}$ 。

(13)

式中, $ρ$ 为径向坐标, $θ$ 为环向坐标。相应地,第一、二类边界条件式（11）变换为

$\begin{matrix} {\begin{cases} {\tilde{u} |}_{ρ = 1} = 0 \\ {\tilde{u} |}_{ρ = R} = 0 \end{cases} & , & {\begin{cases} {\tilde{u} |}_{ρ = 1} = 0 \\ {{\tilde{u}}_{ρ} |}_{ρ = R} = 0 \end{cases} \end{matrix}$ ,

(14)

式中, $R = (h - \sqrt{h^{2} - r_{0}^{2}}) / r_{0}$ 。

2.2 超孔隙水压力解答推导

方程（13）可采用分离变量法进行求解,令

$u (ρ, θ, t) = W (ρ, θ) T (t)$ ,

(15)

上述解答形式的拉普拉斯变换为

$\tilde{u} (ρ, θ, s) = W (ρ, θ) \tilde{T} (s)$ 。

(16)

将式（16）代入方程（13）中,得到如下两个方程：

$W_{, χ χ} + χ^{- 1} W_{, χ} + ϑ^{2} W = 0$ ,

(17)

$(1 + \frac{κ}{λ^{α} s^{α} + 1}) (s \tilde{T} - T_{0}) + \frac{k m_{v}}{4 a^{2} γ_{w}} ϑ^{2} \tilde{T} = 0$ 。

(18)

式中 $χ = {(1 + ρ^{2} - 2 ρ \cos θ)}^{- 1 / 2}$ ； $T_{0}$ 为时间项函数 $T (t)$ 的初始值,取 $T_{0} = 1$ ； $ϑ$ 为特征值。根据式（14）,方程（17）的第一、二类边界条件可表示为

$\begin{matrix} {\begin{cases} {W |}_{χ = χ_{1}} = 0 \\ {W |}_{χ = χ_{0}} = 0 \end{cases} & , & {\begin{cases} {W |}_{χ = χ_{1}} = 0 \\ {W_{χ} |}_{χ = χ_{0}} = 0 \end{cases} \end{matrix}$ ,

(19)

式中, $χ_{0} = {(1 + R^{2} - 2 R \cos θ)}^{- 1 / 2}$ , $χ_{1} = {(2 - 2 \cos θ)}^{- 1 / 2}$ 。

方程（17）为零阶Bessel方程,其通解为

$W (χ) = A J_{0} (ϑ χ) + B N_{0} (ϑ χ)$ ,

(20)

式中, $J_{0}$ 和 $N_{0}$ 分别为零阶Bessel函数和Neumann函数,A和B为待定系数。

将边界条件式（19）代入式（20）中,并确保式（20）为非零解,即系数A和B不同时为零,则可得到第一、二类边界条件下,关于 $ϑ$ 的特征方程分别为

$J_{0} (ϑ χ_{1}) N_{0} (ϑ χ_{0}) - N_{0} (ϑ χ_{1}) J_{0} (ϑ χ_{0}) = 0$ ,

(21)

$J_{0} (ϑ χ_{1}) N_{1} (ϑ χ_{0}) - N_{0} (ϑ χ_{1}) J_{1} (ϑ χ_{0}) = 0$ 。

(22)

式中, $J_{1}$ 和 $N_{1}$ 分别为一阶Bessel函数和Neumann函数。特征方程（21）和（22）中均含有变量 $ϑ$ 。对于每个确定的 $ϑ$ 值,均可从式（21）和（22）中分别求出n个特征值 $ϑ_{n}$ ,求解方法同文献[7]和[8]。第一类边界条件下的特征值 $ϑ_{n}$ 由式（21）求得,记为 $ϑ_{n 1}$ ；第二类边界条件下的特征值 $ϑ_{n}$ 由式（22）求得,记为 $ϑ_{n 2}$ 。对应于每个特征值 $ϑ_{n}$ ,方程（17）式的通解可表示为

$W_{n} (χ) = A_{n} J_{0} (ϑ_{n} χ) + B_{n} N_{0} (ϑ_{n} χ)$ ,

(23)

式中, $A_{n}$ 和 $B_{n}$ 为待定系数。由式（19）中 $χ = χ_{1}$ 处的边界,可得

$B_{n} = - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} A_{n}$ 。

(24)

将式（24）代入式（23）中,得到

$W_{n} (χ) = A_{n} [J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)]$ 。

(25)

另外,对于每个特征值 $ϑ_{n}$ ,式（18）可改写为

$(1 + \frac{κ}{λ^{α} s^{α} + 1}) (s {\tilde{T}}_{n} - T_{n, 0}) + β_{n} {\tilde{T}}_{n} = 0$ ,

(26)

式中, $β_{n} = k m_{v} ϑ_{n}^{2} / (4 a^{2} γ_{w})$ , $T_{n, 0}$ 为函数 $T_{n} (t)$ 的初始值,不失一般性,取 $T_{n, 0} = 1$ 。求解方程（26）,得到

${\tilde{T}}_{n} = \frac{λ^{α} s^{α} + κ + 1}{(λ^{α} s^{α} + κ + 1) s + (λ^{α} s^{α} + 1) β_{n}}$ 。

(27)

对式（27）两端做拉普拉斯逆变换,得到

$T_{n} = \frac{1}{2 πi} \int_{c - i \infty}^{c + i \infty} \frac{(λ^{α} s^{α} + κ + 1) e^{s t}}{(λ^{α} s^{α} + κ + 1) s + (λ^{α} s^{α} + 1) β_{n}} d s$ ,

(28)

式中, $c$ 为大于 ${\tilde{T}}_{n}$ 所有奇点实部的实数。通常,在 $0 < α < 1$ 的情况下,式（28）无解析表达式,其可采用Crump方法^[36]进行计算：

$T_{n} = \frac{e^{c t}}{T_{c}} [\frac{1}{2} {\tilde{T}}_{n} (c) + \sum_{l = 1}^{\infty} {\tilde{T}}_{n} (c + \frac{i l π}{T_{c}}) \cdot e^{\frac{i l π t}{T_{c}}}]$ ,

(29)

式中, $T_{c}$ 拉普拉斯逆变换的计算时间周期,通常可取为最大计算时间的两倍。

对应于n个特征值 $ϑ_{n}$ ,式（25）,（28）均可分别给出n个线性独立的解答 $W_{n}$ 和 $T_{n}$ 。将其进行线性叠加,并代入式（15）中,可得到超孔隙水压力的解答为

$\begin{matrix} u (ρ, θ, t) = \sum_{n}^{\infty} W_{n} (χ) T_{n} (t) \\ = \sum_{n}^{\infty} A_{n} [J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)] T_{n} (t) \end{matrix}$ 。

(30)

式中,系数 $A_{n}$ 由初始条件确定,即

$\sum_{n}^{\infty} W_{n} (χ) = u_{0}$ 。

(31)

将式（31）两端同时乘以 $W_{m}$ ,并将其沿 $χ$ 从 $χ_{0}$ 至 $χ_{1}$ 积分,则根据解答 $W_{n}$ 的正交性^[3,10],可得

$A_{n} = \frac{\int_{χ_{0}}^{χ_{1}} [J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)] u_{0} d χ}{\int_{χ_{0}}^{χ_{1}} {[J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)]}^{2} d χ}$ 。

(32)

2.3 超孔隙水压力解答验证

为了验证分数阶黏弹性地基中洞周超孔隙水压力解答（30）的正确性,将其与已有的线弹性和黏弹性地基中的洞周超孔隙水压力解答进行对比。当 $α = 0$ 时,分数阶Merchant模型退化为线弹性模型。此时,式（28）可表示为

$T_{n} = \frac{1}{2 πi} \int_{c - i \infty}^{c + i \infty} \frac{(κ + 2) e^{s t}}{(κ + 2) s + 2 β_{n}} d s = e^{- {β^{'}}_{n} t}$ ,

(33)

式中, ${β^{'}}_{n} = 2 β_{n} / (κ + 2)$ 。对应的,超孔隙水压力解答（30）可表示为

$u = \sum_{n}^{\infty} W_{n} e^{- {β^{'}}_{n} t}$ 。

(34)

当 $α = 1$ 时,分数阶Merchant模型退化为整数阶Merchant模型。此时,式（28）可表示为

$\begin{array}{l} T_{n} = \frac{1}{2 πi} \int_{c - i \infty}^{c + i \infty} \frac{(λ s + κ + 1) e^{s t}}{(λ s + κ + 1) s + (λ s + 1) β_{n}} d s \\ = \frac{1}{ω_{n, 1} - ω_{n, 2}} \sum_{l = 1}^{2} {(- 1)}^{l + 1} (ω_{n, l} - \frac{1 + κ}{λ}) e^{- ω_{n, l} t} \end{array}$ 。

(35)

其中,

$\begin{matrix} ω_{n, 1} \\ ω_{n, 2} \end{matrix} = \frac{1}{2} [\frac{1 + κ + λ β_{n}}{λ} \pm \sqrt{{(\frac{1 + κ}{λ} + β_{n})}^{2} - \frac{4 β_{n}}{λ}}]$ 。

(36)

对应超孔隙水压力解答（30）可表示为

$u = \sum_{n}^{\infty} \sum_{l = 1}^{2} \frac{{(- 1)}^{l + 1} W_{n}}{ω_{n, 1} - ω_{n, 2}} (ω_{n, l} - \frac{1 + κ}{λ}) e^{- ω_{n, l} t}$ 。

(37)

解答（34）与申林方等^[9]所建立的线弹性地基中洞周超孔隙水压力解答一致；解答（37）与詹美礼等^[10]所建立的整数阶Merchant黏弹性地基中洞周超孔隙水压力解答一致。可见,本文解答是正确的,且线弹性和整数阶Merchant黏弹性地基中洞周超孔隙水压力解答为本文解答的两个特例。

3. 超孔隙水压力消散特性分析

为分析分数阶黏弹性地基中洞周超孔隙水压力的消散特性,选取某隧道工程参数为^[10]：半径 $r_{_{0}} = 5 m$ ,埋深 $h = 15 m$ ,地面堆载 $q = 200 kPa$ ,饱和软黏土的渗透系数 $k = 1.99 mm/d$ ,弹性模量 $E_{1} = 6 MPa$ ,泊松比 $μ = 0.3$ ,黏滞系数 $η = 4.92 \times 10^{5} MPa \cdot d$ 。为简化分析,假设地面堆载为大面积均布堆载,其在洞周饱和软黏土中所引起的初始超孔隙水压力近似于均匀分布且等于堆载集度q,即 $u_{0} = q$ 。根据上述参数,利用式（30）即可计算获得分数阶黏弹性地基中洞周的超孔隙水压力值。

3.1 不同分数阶阶次下超孔隙水压力消散特性

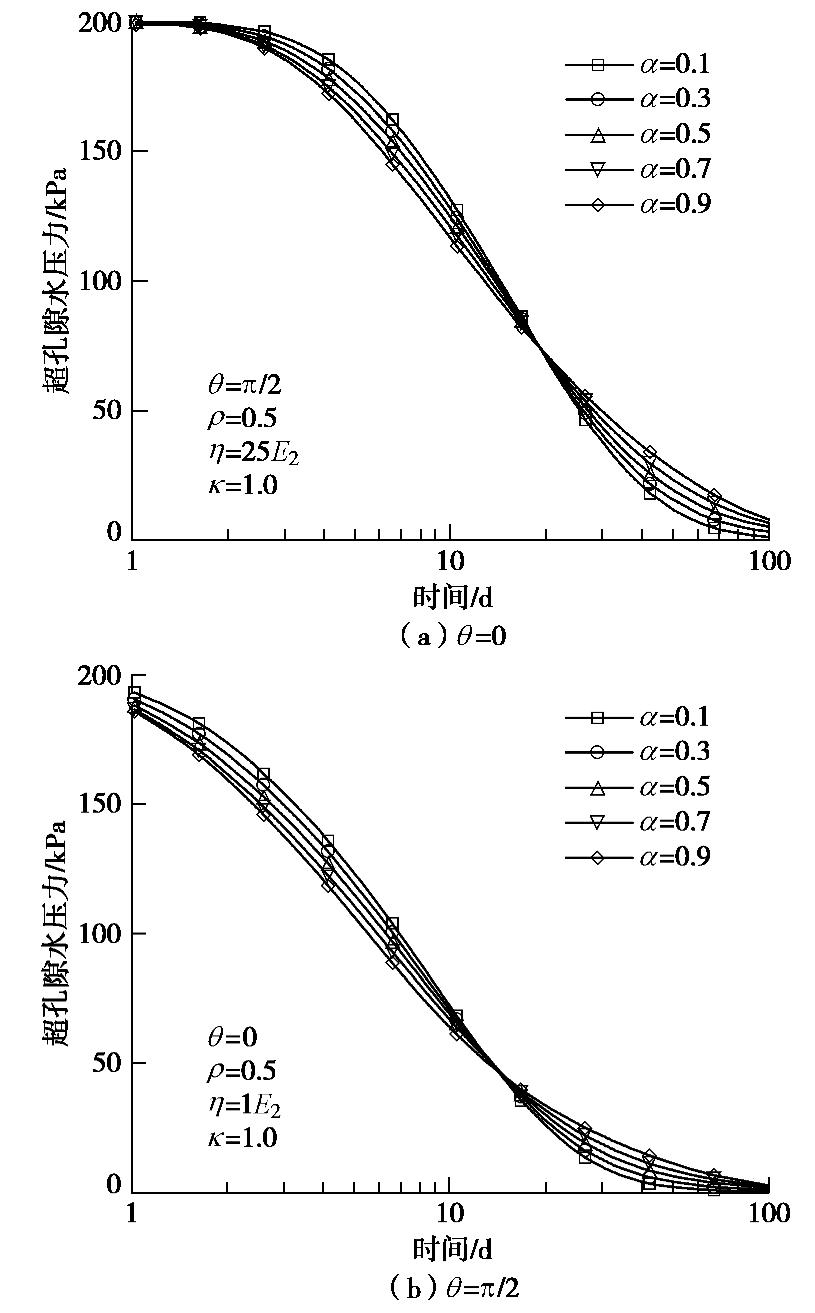
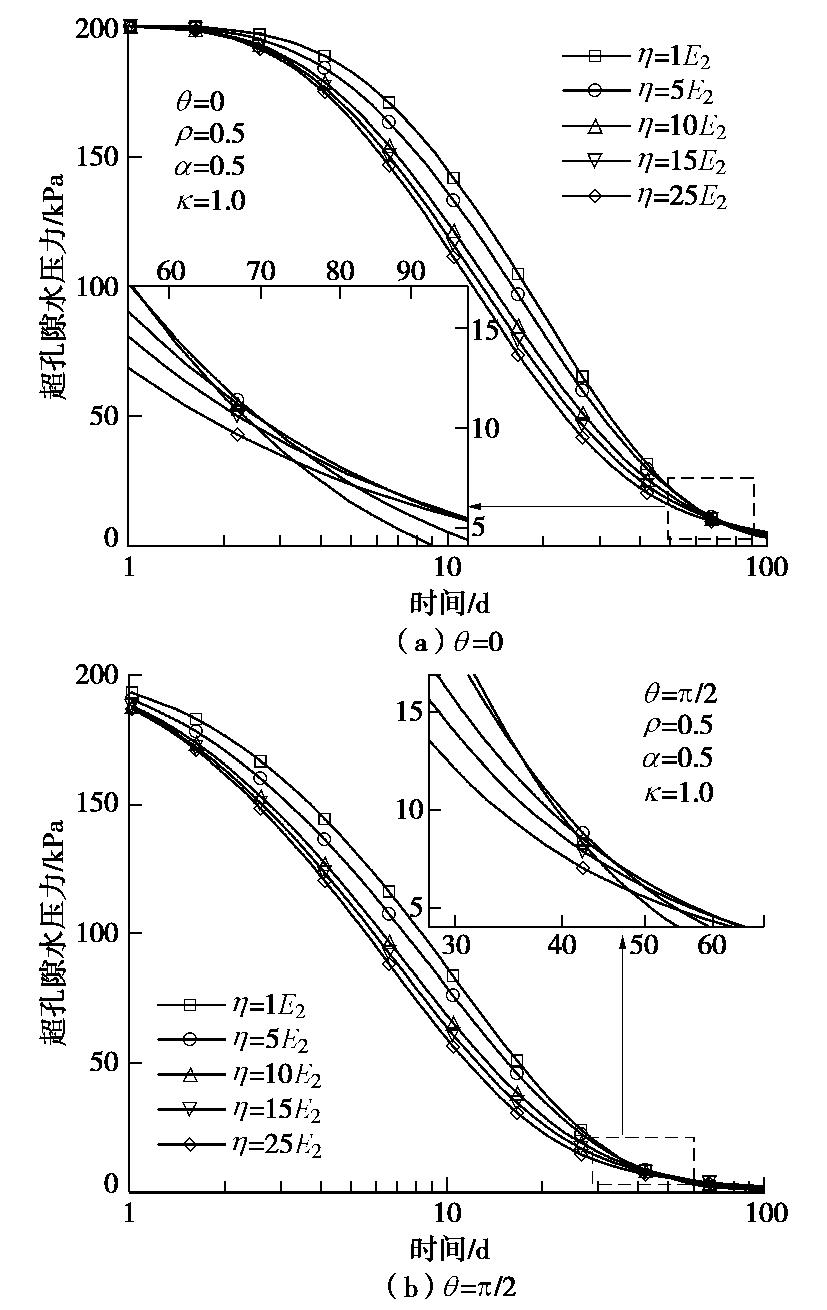
分数阶阶次 $α$ 为分数阶Merchant模型描述饱和软黏土变形特性的一个量纲为“1”参数。当其在0和1之间变化时,Abel黏壶（也称为分数阶元件）的受力特性将介于理想固体和理想流体之间。分数阶阶次 $α$ 较小时,其受力特性与理想固体（即弹簧单元）相似,力的大小受变形和刚度控制；而分数阶阶次 $α$ 较大时,其受力特性与理想流体（即黏壶单元）相似,力的大小由变形率和黏滞系数控制。图4给出了不同分数阶阶次下洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处超孔隙水压力的消散规律。限于篇幅,这里只给出洞周内壁允许排水（即第一类边界）条件下的计算结果,洞周内壁不允许排水（即第二类边界）条件下的计算结果与之类似,不再列出。从图4可以看出,随着消散时间的增大,洞周超孔隙水压力消散曲线出现相互交叉的现象,即在不同的消散阶段,分数阶阶次 $α$ 对超孔隙水压力消散特性的影响是不同的。在消散初期,分数阶阶次 $α$ 越大,超孔隙水压力消散越快,即在同一时刻,超孔隙水压力越小；而在消散后期,分数阶阶次 $α$ 越大,超孔隙水压力则消散越慢,即在同一时刻,超孔隙水压力越大。上述现象是由分数阶元件的力学特性所引起的。在消散初期,饱和软黏土层的变形尚未得到充分发展,变形很小,其对土层有效应力的影响很小。此时,土体有效应力主要由变形率所主导。分数阶阶次 $α$ 越大,分数阶元件的受力特性越接近理想流体,其力的大小受到变形率的影响越大,从而使得在相同变形率的条件下,所引起的土体有效应力越大,即土体中的超孔隙水压力消散越快。而在消散后期,饱和软黏土层的变形得到了充分的发展,其对土体有效应力起到了主导作用。在此阶段,分数阶阶次 $α$ 越小,则分数阶元件的受力特性则越接近理想固体,其力的大小受变形的影响则更为明显,从而使得相同变形的条件下,所引起的土体有效应力越大,即土体中的超孔隙水压力消散越快；反之,分数阶阶次 $α$ 越大,土体中的超孔隙水压力消散则越慢。

图 4 不同分数阶阶次下超孔隙水压力的消散规律

Figure 4. Dissipation of excess pore-water pressure under different fractional orders

下载: 全尺寸图片幻灯片

3.2 不同模量比下超孔隙水压力消散特性

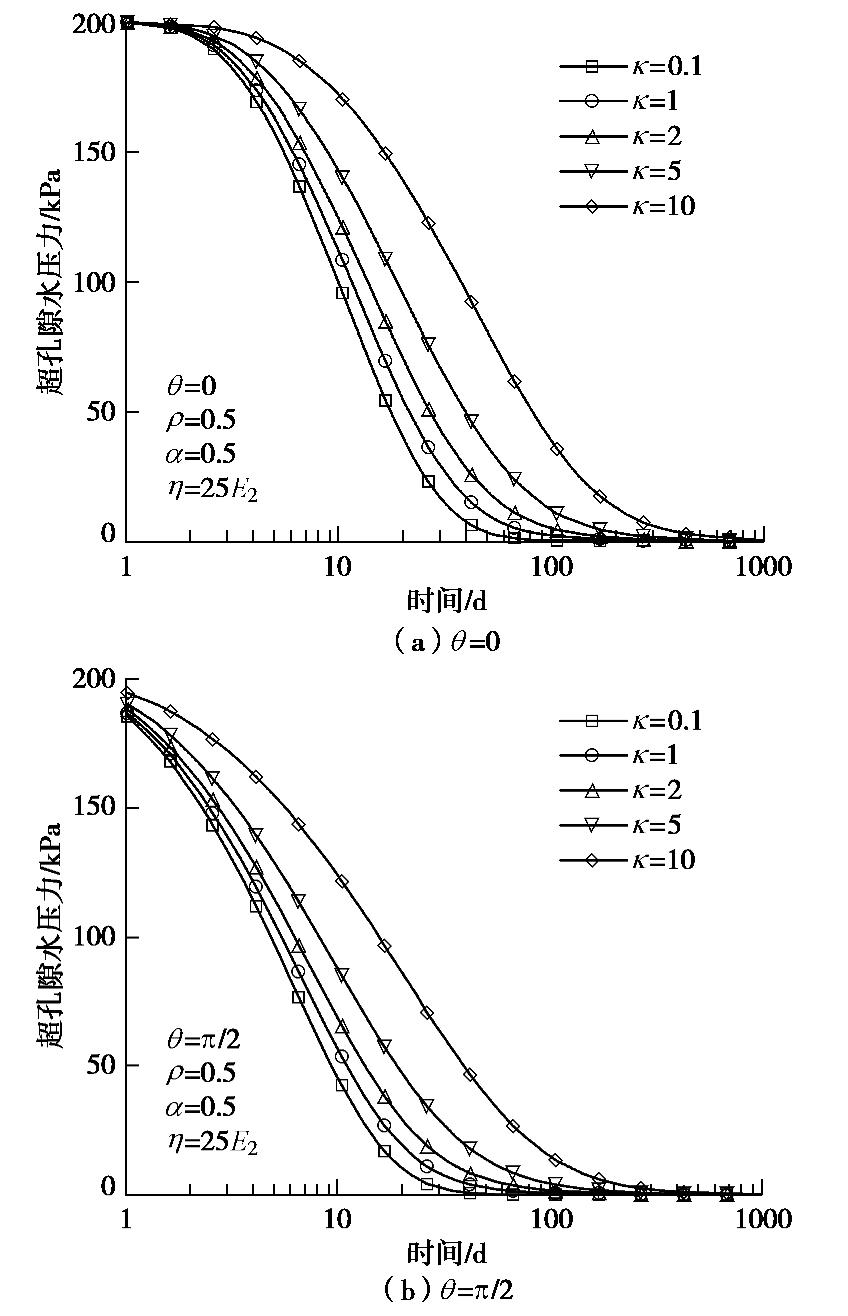
模量比 $κ$ 为分数阶Merchant模型中独立弹簧单元的弹性模量 $E_{1}$ 与Kelvin体中弹簧单元的弹性模量 $E_{2}$ 之比。计算时, $E_{1}$ 取为6 MPa, $E_{2} = E_{1} / κ$ 随着模量比 $κ$ 发生变化。针对洞周内壁允许排水的情况,图5给出了不同模量比下洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处超孔隙水压力的消散规律。可以看出,随着模量比的增大,洞周超孔隙水压力消散越慢,即在同一时刻,超孔隙水压力越大。这是因为,在给定 $E_{1}$ 的情况下,模量比 $κ$ 越大,所对应的 $E_{2}$ 则越小,即土层越软。在超孔隙水压力消散即土体变形过程中,土层越软,土中有效应力发展得越慢,从而使得超孔隙水压力消散得越慢。在超孔隙水压力消散前期即土体变形相对较小时,模量比 $κ$ 所产生的影响较小；而在超孔隙水压力消散中后期即土体变形得到较为充分的发展时,模量比 $κ$ 所产生的影响则变得较为明显。

图 5 不同模量比下超孔隙水压力的消散规律

Figure 5. Dissipation of excess pore-water pressure under different modulus ratios

下载: 全尺寸图片幻灯片

3.3 不同黏滞系数下超孔隙水压力消散特性

黏滞系数是表征饱和软黏土流变特性的重要指标之一。土体的黏滞系数越大,土体的流变特性越显著,其沉降发展越缓慢,沉降完成所需的时间也越长^[37]。针对洞周内壁允许排水的情况,图6给出了不同黏滞系数下洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处超孔隙水压力的消散规律。可以看出,不同黏滞系数下,洞周超孔隙水压力的消散曲线出现相互交叉的现象,其与不同分数阶阶次下超孔隙水压力的消散现象类似,如图4所示。在消散前期,黏滞系数越大,超孔隙水压力消散得越快,即同一时刻,超孔隙水压力值越小；而在消散后期,黏滞系数越大,超孔隙水压力消散得越慢,即同一时刻,超孔隙水压力值越大。这种现象与黏弹性饱和软黏土一维固结中的超孔隙水压力消散现象相同^[38],其可采用分数阶Merchant模型的力学特性来解释。如图1所示,分数阶Merchant流变模型由一个独立弹簧和一个Kelvin体串联组成,二者承受的应力值相等,均为饱和软黏土所承受的有效应力。在消散前期,特别是初始阶段,饱和软黏土层所产生变形还非常小,其对土体有效应力的贡献和影响都很小。在这一阶段,土体有效应力主要由Kelvin体中Abel黏壶承担。因此,较大的黏滞系数会诱发较大的土体有效应力,从而加速了超孔隙水压力的消散。在消散后期,饱和软黏土中的变形已得到了较为充分的发展,其对土体有效应力的贡献和影响变得更为明显,甚至起主导作用。土体的黏滞系数越大,其沉降发展就越缓慢,即同一时刻,沉降值越小。因此,在该阶段,黏滞系数越大,其沉降和有效应力发展越缓慢,从而使得超孔隙水压力消散得越慢。

图 6 不同黏滞系数下超孔隙水压力的消散规律

Figure 6. Dissipation of excess pore-water pressure under different viscosity coefficients

下载: 全尺寸图片幻灯片

3.4 不同边界条件下超孔隙水压力分布和消散特性

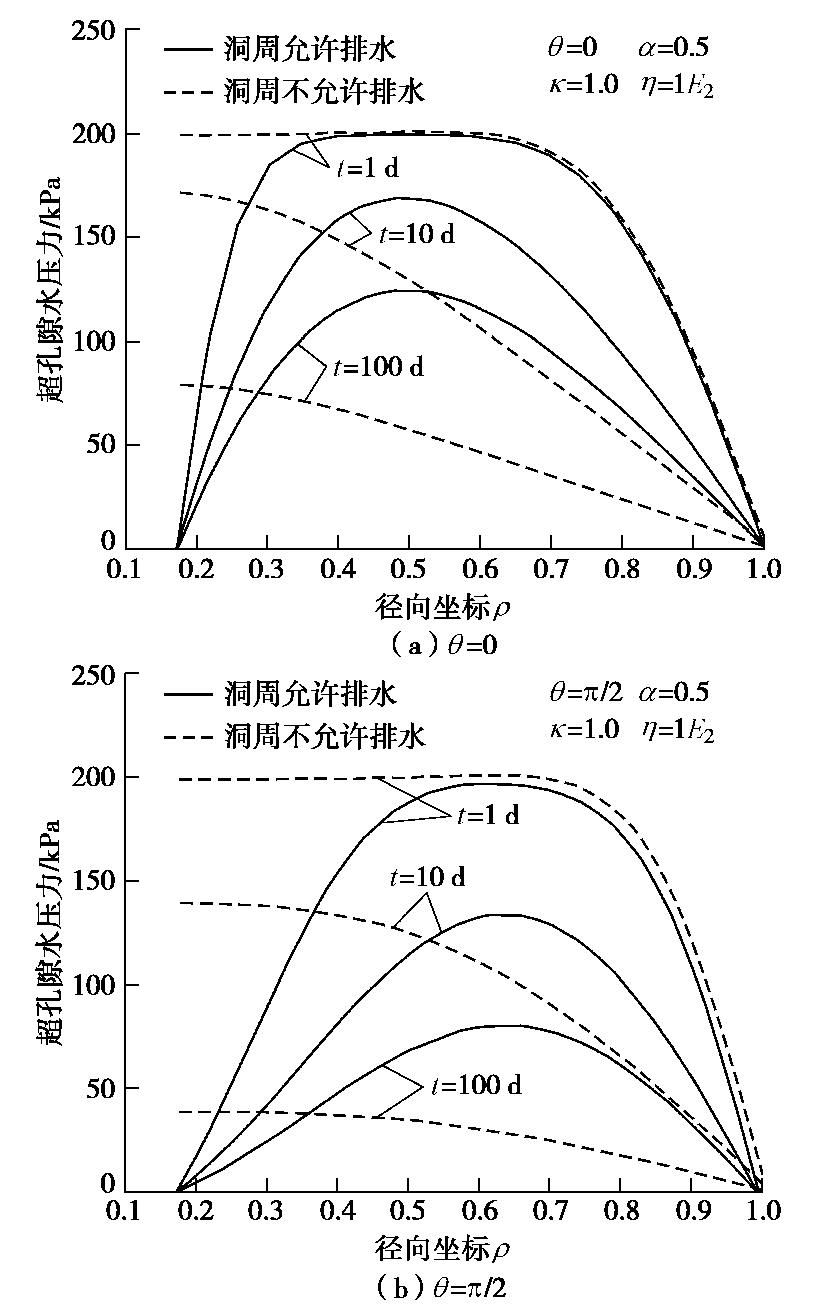
针对施工期间衬砌未完成和竣工后衬砌已完成的两种情况,本文建立了洞周允许排水和不允许排水两种边界条件下的超孔隙水压力解答。针对上述两种边界条件,图7给出了洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处在不同时刻的超孔隙水压力分布规律。可以看出,洞周允许排水时,超孔隙水压力在径向坐标 $ρ$ 的两端为零,其沿径向坐标 $ρ$ 呈现先增加而后减小的分布规律；洞周不允许排水时,超孔隙水压力在靠近洞周一侧为最大值,在远离洞周一侧为零,其沿径向坐标 $ρ$ 呈现逐渐减小的分布规律。在超孔隙水压力消散初期,边界条件所产生的影响主要体现在靠近洞周一侧；之后,其影响逐渐向远离洞周一侧延伸。此外,图7（a）和（b）的对比表明,与洞侧壁 $θ = 0$ 处超孔隙水压力的消散相比,洞顶 $θ = π / 2$ 处超孔隙水压力的消散更快,且超孔隙水压力消散前期,边界条件在洞顶 $θ = π / 2$ 处所产生的影响也更为明显。

图 7 不同边界条件下超孔隙水压力分布和消散规律

Figure 7. Distribution and dissipation of excess pore-water pressure under different boundary conditions

下载: 全尺寸图片幻灯片

4. 结论

本文基于分数阶导数理论,借助保角变换、拉普拉斯变换及逆变换方法,推导了分数阶Merchant模型的柔度函数,建立了分数阶黏弹性地基中洞周超孔隙水压力的解答及其计算方法,分析了分数阶阶次、模量比、黏滞系数以及边界条件对超孔隙水压力消散特性的影响,取得以下4点结论。

（1）分数阶阶次和黏滞系数对超孔隙水压力消散特性的影响均呈现两个不同的阶段：消散初期,分数阶阶次和黏滞系数越大,超孔隙水压力消散越快；消散后期,分数阶阶次和黏滞系数越大,超孔隙水压力则消散越慢。

（2）模量比越大即饱和软黏土层越软,超孔隙水压力消散越慢,且模量比的影响在超孔隙水压力消散中后期更为明显。

（3）洞周允许排水时,超孔隙水压力沿径向呈先增加后减小的分布规律；洞周不允许排水时,其沿径向呈逐渐减小的分布规律。消散初期,边界条件对超孔隙水压力消散的影响主要体现在靠近洞周一侧,之后,其影响逐渐向远离洞周一侧延伸。

（4）将本文解答退化为线弹性和整数阶黏弹性地基的情况,并与已有解答进行对比,验证了本文解答的可靠性。同时,本文解答将洞周超孔隙水压力消散问题延伸至分数阶导数层次,更具一般性,可为相应的工程实例分析提供理论支撑。

图 1 分数阶Merchant模型

Figure 1. Fractional-derivative Merchant model

下载: 全尺寸图片幻灯片

图 2 半无限空间中洞周土体计算模型图

Figure 2. Model for soft soil around tunnel in half space

下载: 全尺寸图片幻灯片

图 3 保角变换映射计算模型图

Figure 3. Model after conformal mapping

下载: 全尺寸图片幻灯片

图 4 不同分数阶阶次下超孔隙水压力的消散规律

Figure 4. Dissipation of excess pore-water pressure under different fractional orders

下载: 全尺寸图片幻灯片

图 5 不同模量比下超孔隙水压力的消散规律

Figure 5. Dissipation of excess pore-water pressure under different modulus ratios

下载: 全尺寸图片幻灯片

图 6 不同黏滞系数下超孔隙水压力的消散规律

Figure 6. Dissipation of excess pore-water pressure under different viscosity coefficients

下载: 全尺寸图片幻灯片

图 7 不同边界条件下超孔隙水压力分布和消散规律

Figure 7. Distribution and dissipation of excess pore-water pressure under different boundary conditions

下载: 全尺寸图片幻灯片

参考文献(38)

[1]	YI X, ROWE, R K, LEE K M. Observed and calculated pore pressures and deformations induced by an earth balance shield[J]. Canadian Geotechnical Journal, 1993, 30(3): 476-490. doi: 10.1139/t93-041
[2]	SHIRLAW J N. Observed and calculated pore pressures and deformations induced by an earth balance shield: discussion[J]. Canadian Geotechnical Journal, 1995, 32(1): 181-189. doi: 10.1139/t95-017
[3]	童磊. 软土浅埋隧道变形、渗流及固结性状研究[D]. 杭州: 浙江大学, 2010. TONG Lei. Studies on Land Subsidence, Seepage Field and Consolidation Behavior of Soft Soil Around a Shallow Circular Tunnel[D]. Hangzhou: Zhejiang University, 2010. (in Chinese)
[4]	CATER J P, SMALL J C, BOOKER J R. A theory of finite elastic consolidation[J]. International Journal of Solids and Structures, 1977, 13(5): 467-478. doi: 10.1016/0020-7683(77)90041-5
[5]	CATER J P, BOOKER J R. Elastic consolidation around a deep circular tunnel[J]. International Journal of Solids and Structures, 1982, 18(12): 1059-1074. doi: 10.1016/0020-7683(82)90093-2
[6]	LI X. Stress and displacement field around a deep circular tunnel with partial sealing[J]. Computers and Geotechnics, 1999, 24(2): 125-140. doi: 10.1016/S0266-352X(98)00035-4
[7]	LI X, BERRONES R F. Time-dependent behavior of partially sealed circular tunnels[J]. Computers and Geotechnics, 2002, 29(6): 433-449. doi: 10.1016/S0266-352X(02)00005-8
[8]	王志良, 刘铭, 谢建斌, 等. 盾构施工引起地表固结沉降问题的研究[J]. 岩土力学, 2013, 34(增刊1): 127-133. doi: 10.16285/j.rsm.2013.s1.045 WANG Zhi-liang, LIU Ming, XIE Jian-bin, et al. Research on consolidation settlement of ground surface caused by shield tunneling[J]. Rock and Soil Mechanics, 2013, 34(S1): 127-133. (in Chinese) doi: 10.16285/j.rsm.2013.s1.045
[9]	申林方, 王志良, 魏纲, 等. 盾构施工引起土体超孔隙水压力消散问题的研究[J]. 铁道学报, 2015, 37(6): 112-118. doi: 10.3969/j.issn.1001-8360.2015.06.016 SHEN Lin-fang, WANG Zhi-liang, WEI Gang, et al. Research on dissipation of excess pore water pressure caused by shield tunneling[J]. Journal of the China Railway Society, 2015, 37(6): 112-118. (in Chinese) doi: 10.3969/j.issn.1001-8360.2015.06.016
[10]	詹美礼, 钱家欢, 陈绪禄. 黏弹性地基中洞周土体固结问题的解析解[J]. 河海大学学报, 1993, 21(2): 54-60. ZHAN Mei-li, QIAN Jia-huan, CHEN Xu-lu. Theoretical analysis for consolidation of viscoelastic clay about circular tunnels in foundations[J]. Journal of Hohai University, 1993, 21(2): 54-60. (in Chinese)
[11]	王志良, 瞿嘉安, 申林方, 等. 泥炭质土层盾构施工扰动引起隧道长期沉降的研究[J]. 岩土工程学报, 2017, 39(8): 1416-1424. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201708011.htm WANG Zhi-liang, QU Jia-an, SHEN Lin-fang, et al. Long-term settlement of tunnel caused by shield tunneling in peaty soil[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(8): 1416-1424. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201708011.htm
[12]	李翔宇, 刘国彬, 刘铭, 等. 考虑半渗透边界的隧道周围超孔隙水压力消散解[J]. 岩土工程学报, 2014, 36(1): 75-82. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201401008.htm LI Xiang-yu, LIU Guo-bin, LIU Ming, et al. Analytical study on dissipation of excess pore water pressures around tunnels with semi-permeable boundary condition[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 75-82. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201401008.htm
[13]	刘干斌, 谢康和, 施祖元. 黏弹性土体中深埋圆形隧道的应力和位移分析[J]. 工程力学, 2004, 21(5): 132-138. doi: 10.3969/j.issn.1000-4750.2004.05.028 LIU Gan-bin, XIE Kang-he, SHI Zu-yuan, et al. Analysis of stress and displacement around a deep circular tunnel in viscoelastic soil[J]. Engineering Mechanics, 2004, 21(5): 132-138. (in Chinese) doi: 10.3969/j.issn.1000-4750.2004.05.028
[14]	ZHANG C Y. Viscoelastic Fracture Mechanics[M]. Beijing: Science Press, 2006.
[15]	刘忠玉, 杨强. 基于分数阶Kelvin模型的饱和黏土一维流变固结分析[J]. 岩土力学, 2017, 38(12): 3680-3697. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201712037.htm LIU Zhong-yu, YANG Qiang. One-dimensional rheological consolidation analysis of saturated clay using fractional order Kelvin's model[J]. Rock and Soil Mechanics, 2017, 38(12): 3680-3697. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201712037.htm
[16]	PODLUBNY I. Fractional Differential Equations[M]. California: Academic Press, 1999.
[17]	YIN D S, WU H, CHENG C, et al. Fractional order constitutive model of geomaterials under the condition of triaxial test[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(8): 961-972. doi: 10.1002/nag.2139
[18]	GEMANT A. A method of analyzing experimental results obtained from elasto-viscous bodies[J]. Journal of Applied Physics, 1936, 7(1): 311-317.
[19]	BAGLEY R L, TORVIK P J. On the fractional calculus model of viscoelasticity behavior[J]. Journal of Rheology, 1986, 30(1): 133-155. doi: 10.1122/1.549887
[20]	KOELLER R C. Application of fractional calculus to the theory of viscoelasticity[J]. Journal of Applied Mechanics, 1984, 51(2): 299-307. doi: 10.1115/1.3167616
[21]	赵永玲, 侯之超. 基于分数导数的橡胶材料两种黏弹性本构模型[J]. 清华大学学报(自然科学版), 2013, 53(3): 378-383. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB201303017.htm ZHAO Yong-ling, HOU Zhi-chao. Two viscoelastic constitutive models of rubber materials using fractional derivations[J]. Journal of Tsinghua University (Science and Technology), 2013, 53(3): 378-383. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB201303017.htm
[22]	孙雅珍, 朱传江, 王立保. 基于分数阶导数沥青路面松弛应力强度因子分析[J]. 中外公路, 2015, 25(2): 65-68. https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201502016.htm SUN Ya-zhen, ZHU Chuan-jiang, WANG Li-bao. Analysis based on fractional derivative asphalt pavement relaxed stress intensity factor[J]. Journal of China and Foreign Highway, 2015, 25(2): 65-68. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201502016.htm
[23]	刘林超, 闫启方, 孙海忠. 软土流变特性的模型研究[J]. 岩土力学, 2006, 27(增刊1): 214-217. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2006S1048.htm LIU Lin-chao, YAN Qi-fang, SUN Hai-zhong. Study on model of rheological property of soft clay[J]. Rock and Soil Mechanics, 2006, 27(S1): 214-217. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2006S1048.htm
[24]	孙海忠, 张卫. 一种分析软土黏弹性的分数导数开尔文模型[J]. 岩土力学, 2007, 28(9): 1983-1986. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200709040.htm SUN Hai-zhong, ZHANG Wei. Analysis of soft soil with viscoelastic fractional derivative Kelvin model[J]. Rock and Soil Mechanics, 2007, 28(9): 1983-1986. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200709040.htm
[25]	ZHU H H, ZHANG C C, MEI G X, et al. Prediction of one-dimensional compression behavior of Nansha clay using fractional derivatives[J]. Marine Georesources & Geotechnology, 2016, 35(5): 688-697.
[26]	何利军, 孔令伟, 吴文军, 等. 采用分数阶导数描述软黏土蠕变的模型[J]. 岩土力学, 2011, 32(增刊1): 239-249. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S2039.htm HE Li-jun, KONG Ling-wei, WU Wen-jun, et al. A description of creep model for soft soil with fractional derivative[J]. Rock and Soil Mechanics, 2011, 32(S1): 239-249. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S2039.htm
[27]	李锐铎, 乐金朝. 基于分数阶导数的软土非线性流变本构模型[J]. 应用基础与工程科学学报, 2014, 22(5): 856-863. https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201405002.htm LI Rui-duo, YUE Jin-chao. Nonlinear rheological constitute of soft soil based on fractional order derivative theory[J]. Journal of Basis Science and Engineering, 2014, 22(5): 856-863. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201405002.htm
[28]	WANG L, SUN D A, LI P C, et al. Semi-analytical solution for one-dimensional consolidation of fractional derivative viscoelastic saturated soils[J]. Computers and Geotechnics, 2017, 83: 30-39.
[29]	解益, 李培超, 汪磊, 等. 分数阶导数黏弹性饱和土体一维固结半解析解[J]. 岩土力学, 2017, 38(11): 3240-3246. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711021.htm XIE Yi, LI Pei-chao, WANG Lei, et al. Semi-analytical solution for one-dimensional consolidation of viscoelastic saturated soil with fractional order derivative[J]. Rock and Soil Mechanics, 2017, 38(11): 3240-3246. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711021.htm
[30]	刘忠玉, 崔鹏陆, 郑占垒. 基于非牛顿指数渗流和分数阶Merchant模型的一维流变固结分析[J]. 岩土力学, 2019, 40(6): 2029-2038. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906002.htm LIU Zhong-yu, CUI Peng-lu, ZHENG Zhan-lei, et al. Analysis of one-dimensional rheological consolidation with flow described by non-Newtonian index and fractional-order Merchant's model[J]. Rock and Soil Mechanics, 2019, 40(6): 2029-2038. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906002.htm
[31]	汪磊, 李林忠, 徐永福, 等. 半透水边界下分数阶黏弹性饱和土一维固结特性分析[J]. 岩土力学, 2018, 39(11): 4142-4148. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201811029.htm WANG Lei, LI Lin-zhong, XU Yong-fu, et al. Analysis of one-dimensional consolidation of fractional viscoelastic saturated soils with semi-permeable boundary[J]. Rock and Soil Mechanics, 2018, 39(11): 4142-4148. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201811029.htm
[32]	李林忠, 汪磊, 李培超, 等. 任意荷载下双面半透水边界分数阶导数黏弹性饱和土层一维固结[J]. 工程地质学报, 2018, 26(6): 1480-1489. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201806010.htm LI Lin-zhong, WANG Lei, LI Pei-chao, et al. One-dimensional consolidation of fractional derivative viscoelastic saturated soil layer with symmetric semi-permeable boundaries under arbitrary loading[J]. Journal of Engineering Geology, 2018, 26(6): 1480-1489. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201806010.htm
[33]	田乙, 吴文兵, 蒋国盛, 等. 连续排水边界下分数阶黏弹性饱和土体一维固结分析[J]. 岩土力学, 2019, 40(8): 3054-3061. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201908022.htm TIAN Yi, WU Wen-bing, JIANG Guo-sheng, et al. One-dimensional consolidation of viscoelastic saturated soils with fractional order derivative based on continuous drainage boundary[J]. Rock and Soil Mechanics, 2019, 40(8): 3054-3061. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201908022.htm
[34]	HUANG M H, LI J C. Consolidation of viscoelastic soil by vertical drains incorporating fractional-derivative model and time-dependent loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(1): 239-256.
[35]	HUANG M H, LI D. A One-dimensional fractional- derivative viscoelastic model for the aquitard consolidation of an aquifer system[J]. Geofluids, 2019(2): 1-11.
[36]	CRUMP K S. Numerical inversion of Laplace transforms using a Fourier series approximation[J]. Journal of the Association for Computing Machinery, 1976, 23(1): 89-96.
[37]	张先伟, 王常明. 结构性软土的黏滞系数[J]. 岩土力学, 2011, 32(11): 3276-3282. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201111015.htm ZHANG Xian-wei, WANG Chang-ming. Viscosity coefficient of structural soft clay[J]. Rock and Soil Mechanics, 2011, 32(11): 3276-3282. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201111015.htm
[38]	XIE K H, XIE X Y, LI B H. Analytical theory for one-dimensional consolidation of clayey soils exhibiting rheological characteristics under time-dependent loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(14): 1833-1855.

施引文献(13)

期刊类型引用(8)

1.	龚昭祺，林廷松，李文乾，胡安峰. 考虑渗透各向异性的隧道周围饱和软土固结特性分析. 地基处理. 2024(01): 16-22 . 百度学术
2.	谢森林，胡安峰，肖志荣，汪美慧，胡训健，陈俞超. 基于广义Voigt模型的半渗透边界隧道周围饱和软土固结分析. 岩土力学. 2024(07): 2024-2036 . 百度学术
3.	谢森林，胡安峰，肖志荣，陈缘，汪美慧. 渗漏病害加剧影响下隧道周围土体流变固结分析. 岩石力学与工程学报. 2024(10): 2570-2580 . 百度学术
4.	仉文岗，唐学成，刘汉龙，杨文钰，刘智成，王鲁琦，李红蕊. 静-动荷载作用下欠固结软土盾构隧道长期沉降与最优埋深计算方法. 隧道建设(中英文). 2024(09): 1829-1840 . 百度学术
5.	丁峰，程扬，钱春宇，宋春雨，陈龙珠. 双洞隧道地铁运行引起的软土地基振动及孔压研究. 土木工程与管理学报. 2024(05): 71-77 . 百度学术
6.	胡安峰，姜浩，肖志荣，谢森林，龚昭祺，李文乾. 基于分数阶模型的隧道周围土体非线性流变固结分析. 浙江大学学报(工学版). 2023(11): 2227-2234 . 百度学术
7.	张思峰，任子夤，郑帅，张驰. 黄河冲积平原区静压管桩超静孔隙水压力时空效应试验研究. 路基工程. 2022(01): 53-57 . 百度学术
8.	杨光，顾昊，刘尚蔚，包腾飞，孙锦，栾博文. 基于分数阶模式的高拱坝变形安全监控研究构想. 水利水电科技进展. 2022(05): 85-93+120 . 百度学术