土石堤坝渗漏病险试验装置的研制及初步应用

马朝阳; 任杰; 南胜豪; 徐松

doi:10.11779/CJGE20220902

土石堤坝渗漏病险试验装置的研制及初步应用 English Version

西安理工大学省部共建西北旱区生态水利国家重点实验室, 陕西西安 710048

基金项目:

国家自然科学基金项目 52379134

陕西省科技创新团队项目 2022TD-01

水利部水库大坝安全重点实验室开放基金项目 YK323001

详细信息

作者简介:
马朝阳(1995—)，男，硕士研究生，主要从事土石堤坝健康诊断与风险评估方面的研究。E-mail: mzyang1129@163.com

通讯作者:
任杰, E-mail: renjie@xaut.edu.cn

中图分类号: TV641
计量
- 文章访问数: 345
- HTML全文浏览量: 44
- PDF下载量: 105
出版历程
- 收稿日期: 2022-07-19
- 网络出版日期: 2023-05-10
- 刊出日期: 2023-10-31

Development and initial application of test devices for leakage of earth-rockfill dams

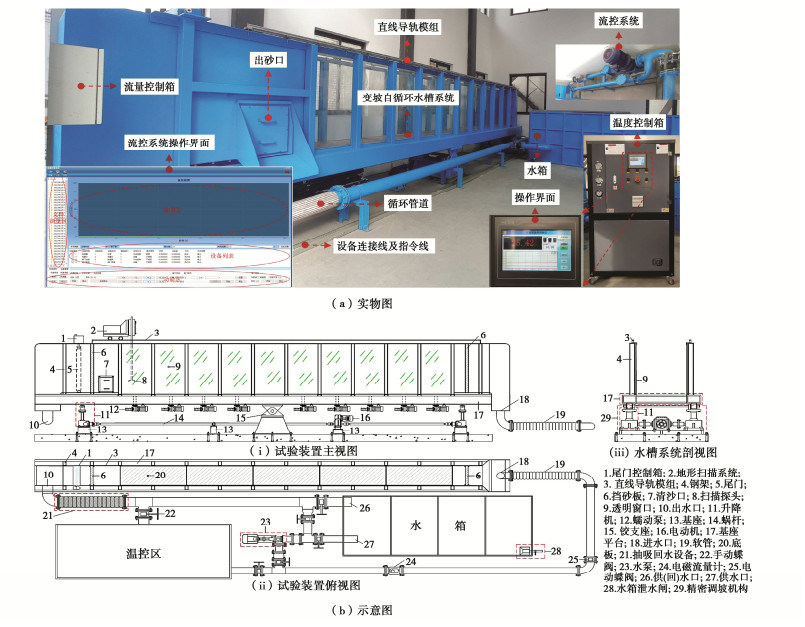
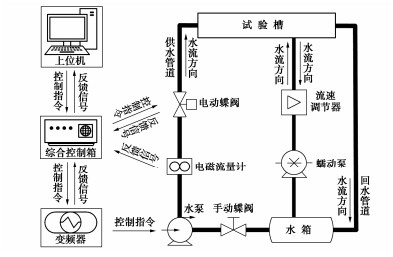
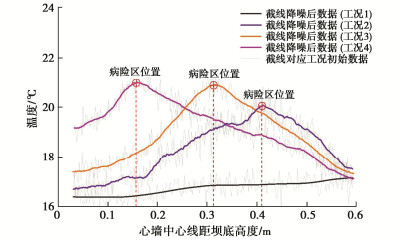
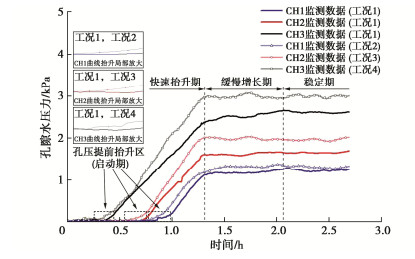
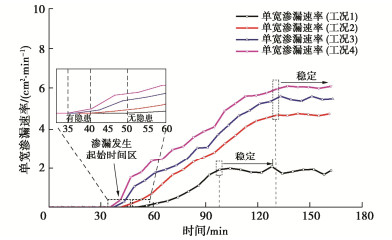
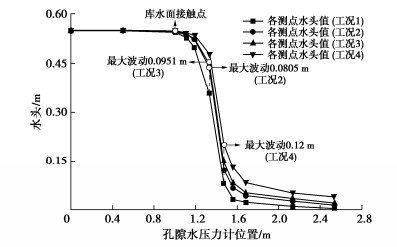
State Key Laboratory of Eco-hydraulics in Northwest Arid Region, Xi′an University of Technology, Xi′an 710048, China

摘要

摘要: 为准确模拟渗漏病险发生条件下土石堤坝渗流特性，研制一种土石堤坝渗漏病险试验装置。该装置能够精准控制试验槽坡度、输水流量、库水温度等试验变量，可实现边壁及底板平整度的自动校核、流控系统与温控系统的自动化控制、多种供吸水组合方式的水循环、库水的分级与线性升温和降温、坝体温度场和体积变形以及孔隙水压力的动态监测等功能。选用黏土心墙堆石坝为研究对象，初步开展了土石堤坝渗漏病险试验研究。研究表明：渗漏病险区将改变坝体的流热双场，其周围的温度变幅大于孔压变幅；随着渗漏病险区逐步下移，所在位置处的温度值显著增大，浸润线的波动情况与坝体渗流速率也随之增大，影响坝体渗流稳定性的不利情况逐渐增强。该装置能够准确模拟各工况真实情况以及多场耦合效应对土石堤坝渗漏病险发生发展过程的影响，能够实时监测渗漏病险发展过程中各物理场演变情况，为深入研究土石堤坝渗流特性提供一种有效的技术工具。
- 土石堤坝 /
- 渗漏 /
- 试验装置 /
- 试验方法 /
- 温度场 /
- 渗流场
Abstract: To accurately simulate the seepage characteristics of earth-rockfill dams during leakage, a test device is developed. The device can precisely control the test variables such as platform slope, water supply discharge, water temperature, etc. The device can realize the automatic check of the flatness of the side wall and the bottom plate, the automatic control of the flow control system and the temperature control system, the water circulation of various water supply and suction combinations, and piecewise or linear temperature rise and drop control of the upstream reservoir water, dynamic monitoring of dam body temperature field, volume deformation and pore water pressure. A clay core wall rockfill dam is selected as the research object, and the leakage tests on earth-rockfill dams are conducted. The results show that the leakage will change the seepage field and temperature field of the dam body, causing the surrounding temperature value to change significantly. With the gradual downward movement of the leakage area, the temperature value at the location increases significantly, the fluctuation of the saturation line and the seepage rate of the dam also increase, and the adverse conditions affecting the seepage stability of the dam body gradually increase. The test device can accurately simulate the real situation of various working conditions and the influences of multiphysics coupling effects on the leakage occurrence and development process of earth-rockfill dams, and it can monitor the evolution of various physical fields in the leakage development process in real time, providing an effective technical tool for the in-depth study on the seepage characteristics of earth-rockfill dams.
- earth-rockfill dam /
- leakage /
- test device /
- test method /
- temperature field /
- seepage field

HTML全文

0. 引言

无论是寒区工程^[1-2],还是人工冻结技术应用中^[3-7],都会遇到冻土的融化。冻土在融化过程中,会产生显著沉降变形或者累积超静孔隙水压力,这些均会造成附近建筑物及土层的变形破坏。与土体冻结过程中的冻胀破坏^[8-10]类似,冻土融化过程也严重威胁冻土相关工程的安全。

许多学者进行了冻土融化过程相关的研究,除了试验和测试外^[11-14],也有一些模型方面的成果。Morgenstern等^[15-16],Nixon等^[17]基于相变热传导纽曼解答以及太沙基一维固结理论建立了冻土的一维融化固结模型（以下简称MN模型）,并给出了模型解析解答；试验对比表明,模型对低含冰量冻土预测结果较好,而对高含冰量冻土则偏差较大。Zhou等^[18]在MN模型基础上,考虑了冻土中未冻水对传热的影响以及外部变荷载条件,建立了改进的融化固结模型,并给出了模型的解析解答。对于高含冰量冻土,小变形固结理论体系下的MN模型及其改进并不适用。Foriero等^[19]在Gibson大变形固结理论^[20]的基础上建立了一维大变形融化固结理论,考虑的相界面位置是时间的幂函数。实际上,相界面位置变化是与传热过程相关联的,基于此,Yao等^[21-22]建立了三维大变形融化固结理论；Qi等^[23],Wang等^[24],Wang等^[25]对Yao等的大变形融化固结理论进行了改进,并计算了寒区工程中的冻土融化过程。Yao等的模型并未考虑大变形对传热控制方程的影响,Dumais等^[26]做出了改进,给出了大变形坐标系下的传热方程,并建立了新的一维大变形融化固结模型。

在人工冻结技术应用中,冻结壁在完成临时使命后会逐渐融化,而自然融化过程往往较长,长时间沉降及孔压消散会带来许多不确定因素。因而常采用人工强制解冻的方式,即利用高温热水强制融化冻土（70℃或更高）^[27-28]；在天然冻土区,为了方便施工,有时也采用高温热水强制融化冻土。人工强制融化过程与天然融化过程有所不同,前者由于高温作用,融区内土颗粒、水的热膨胀不可忽视,融区内发生的不是普通固结,而是热固结^[29-32]。因此,冻土在高温融化过程中,超静孔压、沉降等的演变与普通融化过程是不同的,上述的模型均不适用。本文考虑饱和冻土在高温下的一维融化热固结过程,推导建立过程的理论模型,并给出模型的解析解答。

1. 模型基本方程

图1为饱和冻土在高温下一维融化过程的示意图。冻土初始温度为均匀T₀,低于冻结温度T_f；开始融化时,上表面z = 0迅速升温到某一高温T_w。冻土融化过程中,融化锋面S(t)逐渐向下移动,热固结发生在上表面与融化界面之间,而上表面荷载一次施加,作用在单位面积上的大小为P_ob。

图 1 高温下饱和冻土一维融化过程示意图

Figure 1. Schematic diagram of 1-D thawing process of saturated frozen soil under high temperature

下载: 全尺寸图片幻灯片

MN模型的基本假设也在本文模型中采用：①冻土含冰量较少,过程是小变形过程；②冻土融化过程中,融土处于饱和状态,即不考虑空气相的影响；③不考虑固结水流对流作用对传热的影响,传热部分近似为半无限大物体相变热传导；④忽略冰水相变体积变化对传热、热固结过程的影响,而只在最后计算沉降时加以讨论。

传热部分的控制方程为

$C_{v} \frac{\partial T}{\partial t} = \frac{\partial}{\partial z} (k_{h} \frac{\partial T}{\partial z}) - L ρ_{w} \frac{\partial θ_{u}}{\partial t} (0 < z < \infty)$ ,

(1)

$T (z, 0) = T_{0}$ ,

(2)

$T (0, t) = T_{w}$ ,

(3)

式中,T为温度,z为位置坐标,t为时间,C_v为土体体积热容,k_h为土体导热系数,L为冰相变的潜热,θ_u为体积未冻水含量, $ρ_{w}$ 为水的密度。

式（1）中C_v,k_h均随土体成分变化而变化,一般可用各成分的算术或几何平均表示^[18]；冻土中未冻水与负温的关系即为冻结特性,可以用下式描述（不考虑滞后效应^[33]）：

$\begin{matrix} θ_{u} = \frac{ρ_{d}}{100 ρ_{w}} \exp (0.2618 + 0.5519 \ln S_{a} - \\ 1.4495 S_{a}^{- 0.2640} \ln | T |) \end{matrix}$ ,

(4)

式中,ρ_d为土的干密度,S_a为土的比表面积。

热固结发生在融化区0< z <S(t)内,在建立热固结方程时,主要考虑土颗粒、水的热膨胀性,而不考虑它们的压缩性。土颗粒部分体积变化率为

$\frac{1}{V} \frac{\partial V_{s}}{\partial t} = (1 - n) a_{s} \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(5)

式中,V为总体积,V_s为土颗粒体积,n为孔隙率,a_s为土颗粒的热膨胀系数。

孔隙的变形主要包括水流的净流入和水的热膨胀两部分,可以描述为

$\frac{1}{V} \frac{\partial V_{e}}{\partial t} = - \frac{\partial q_{w}}{\partial z} + n a_{w} \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(6)

式中,V_e为孔隙体积,q_w为固结水流速度,a_w为水的热膨胀系数。

结合式（5）,（6）得到^[29]：

$\begin{matrix} \frac{\partial ε_{v}}{\partial t} = \frac{1}{V} \frac{\partial V_{s}}{\partial t} + \frac{1}{V} \frac{\partial V_{e}}{\partial t} \\ = - \frac{\partial q_{w}}{\partial z} + [n a_{w} + (1 - n) a_{s}] \frac{\partial T}{\partial t} (0 < z < S (t)) \end{matrix}$ ,

(7)

式中, $ε_{v}$ 为体应变。

融化区中固结水流满足达西定律

$q_{w} = - \frac{k_{g}}{γ_{w}} \frac{\partial P}{\partial z}$ ,

(8)

式中,P为超静孔压,k_g为渗透系数, $γ_{w}$ 为水的重度。

将式（8）代入式（7）得到

$\frac{\partial ε_{v}}{\partial t} = \frac{k_{g}}{γ_{w}} \frac{\partial^{2} P}{\partial z^{2}} + \bar{a} \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(9)

式中, $\bar{a} = n a_{w} + (1 - n) a_{s}$ 。

考虑热应力作用时,土体有效应力形式表达的一维本构方程为^[29]

${σ^{'}}_{z z} = E_{s} ε_{z z} - β (T - T_{f})$ ,

(10)

式中, ${σ^{'}}_{z z}$ 为z方向土体有效应力, $ε_{z z}$ 为z方向土体应变,均以拉为正（而孔压则以压为正）,E_s为土体压缩模量,β为土体热应力系数,都可以表示为土体的变形模量E和泊松比 $ν$ 的关系式^{[29, 31]}

$\begin{array}{l} E_{s} = \frac{1 - ν}{1 + ν} \frac{E}{1 - 2 ν} ， \\ β = \frac{E}{1 - 2 ν} a_{sm} ， \end{array}}$

(11)

其中, $a_{sm}$ 为土体的热膨胀系数,一般可取 $a_{sm} = \bar{a}$ 。

在深度z处,由太沙基有效应力原理得到

${σ^{'}}_{z z} = - P_{ob} - γ^{'} z + P$ ,

(12)

式中, $γ^{'} = γ - γ_{w}$ , $γ$ 为土的重度。

由式（10）,（12）可以得到：

$\begin{array}{l} \frac{\partial P}{\partial t} = E_{s} \frac{\partial ε_{z z}}{\partial t} - β \frac{\partial T}{\partial t} & (0 < z < S (t)) \end{array}$ 。

(13)

在一维问题中 $ε_{v} = ε_{z z}$ ,利用式（9）,（13）可以得到融化区热固结方程：

$C_{g} \frac{\partial^{2} P}{\partial z^{2}} = \frac{\partial P}{\partial t} + A \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(14)

式中, $A = β - E_{s} \bar{a}$ , $C_{g}$ 为固结系数, $C_{g} = k_{g} E_{s} / γ_{w}$ 。

如图1所示,考虑融化界面上的单元 $V =$ $Δ S (t) \times A_{c}$ , $A_{c}$ 为横截面积。Δt时间间隔内该单元体积变化量为ΔV,ΔV由水流净流入及温度膨胀两部分组成；融化界面下方为冻土,无水流,所以有

$Δ V = - \frac{k_{g}}{γ_{w}} {\frac{\partial P}{\partial z} |}_{S (t)} A_{c} Δ t + \bar{a} Δ T V$ 。

(15)

根据式（10）界面单元应变为

$ε_{z z} = \frac{Δ {σ^{'}}_{z z} + β Δ T}{E_{s}}$ 。

(16)

在融化界面z = S(t)上,土体有效应力为

${σ^{'}}_{z z} = - P_{ob} - γ^{'} S (t) + P (S (t), t)$ 。

(17a)

式（16）中增量对应的初始状态为冻土融化但未发生体积变化时的状态,此时外荷载尚未传递给土骨架,有效应力一般取为0^[15]。

因此式（16）中有效应力增量为

$Δ {σ^{'}}_{z z} = {σ^{'}}_{z z} = - P_{ob} - γ^{'} S (t) + P (S (t), t)$ 。

(17b)

由式（15）,（16）得到的应变应相等,同时相界面温度恒定即增量 $Δ T$ 为0,从而有

$- \frac{k_{g}}{γ_{w}} {\frac{\partial P}{\partial z} |}_{S (t)} \frac{Δ t}{Δ S (t)} = \frac{- P_{ob} - γ^{'} S (t) + P (S (t), t)}{E_{s}}$ 。

(18)

式（18）经整理后得到

$[P_{ob} + γ^{'} S (t) - P (S (t), t)] \frac{d S (t)}{d t} = C_{g} {\frac{\partial P}{\partial z} |}_{S (t)}$ 。

(19)

土体上边界为完全透水边界,因此有

$P (0, t) = 0$ 。

(20)

式（14）,（19）,（20）构成融化区热固结作用的基本方程。

2. 模型解析求解

2.1 融化界面及温度场部分解答

MN模型传热部分应用了纽曼相变热传导的解答,且由于不考虑热膨胀,模型仅需要确定融化界面的位置；文献[18]进一步考虑了冻土融化与普通相变热传导的不同,采用式（1）～（4）为基本方程,给出了融化界面及温度场的解析解答,下面介绍并直接应用该解答。

在融化区内,温度场解答为

$T (z, t) = a_{1} + b_{1} erfc (\frac{z}{2 \sqrt{α_{1} t}}) (0 < z < S (t))$ ,

(21)

$S (t) = α_{thaw} \sqrt{t}$ ,

(22)

式中, $α_{1}$ 为融化区中土的热扩散系数,参数a₁,b₁, $α_{thaw}$ 均可以表示为常数 $λ_{1}$ 的表达式,

$\begin{array}{l} a_{1} = \frac{T_{f} - T_{w} erfc (λ_{1})}{erf (λ_{1})} ， \\ b_{1} = \frac{T_{w} - T_{f}}{erf (λ_{1})} ， \\ α_{thaw} = 2 λ_{1} \sqrt{α_{1}} ， \end{array}}$

(23)

其中,erf(•),erfc(•)分别为误差函数和误差补函数,而 $λ_{1}$ 的求解过程详见文献[18]。

2.2 热固结部分解答

对于融化区域0 < z < S(t) 内的热固结问题,引入如下变量：

$u (z, t) = P (z, t) - P_{ob} - C z$ ,

(24)

式中, $C = 2 R^{2} γ^{'} / (1 + 2 R^{2})$ ,R为融化固结比, $R = α_{thaw} /$ $2 \sqrt{C_{g}}$ ^[15]。

由式（14）,（19）,（20）,变量u(z, t)的控制方程为

$\begin{array}{l} C_{g} \frac{\partial^{2} u}{\partial z^{2}} = \frac{\partial u}{\partial t} + A \frac{\partial T}{\partial t} & (0 < z < S (t) = α_{thaw} \sqrt{t}) \end{array}$ ,

(25)

$u (0, t) = - P_{ob}$ ,

(26)

$C_{g} \frac{\partial u}{\partial z} [S (t), t] = - u [S (t), t] \frac{d S (t)}{d t}$ 。

(27)

融区内热物性均为常数,温度场满足如下方程：

$\frac{\partial T}{\partial t} = α_{1} \frac{\partial^{2} T}{\partial z^{2}} (0 < z < S (t) = α_{thaw} \sqrt{t})$ 。

(28)

定义如下变量

$Ω = u + \frac{A α_{1}}{α_{1} - C_{g}} T$ 。

(29)

由式（25）,（28）可知,变量 $Ω$ 满足如下控制方程：

$C_{g} \frac{\partial^{2} Ω}{\partial z^{2}} = \frac{\partial Ω}{\partial t} (0 < z < S (t) = α_{thaw} \sqrt{t})$ 。

(30)

在融化界面S(t)上,变量 $Ω$ 满足

$\begin{matrix} - [Ω (S (t), t) - \frac{A α_{1}}{α_{1} - C_{g}} T_{f}] \frac{d S (t)}{d t} \\ = C_{g} {[\frac{\partial Ω}{\partial z} - \frac{A α_{1}}{α_{1} - C_{g}} \frac{\partial T}{\partial z}] |}_{S (t)} \end{matrix}$ 。

(31)

引入相似变量 $η = z / 2 \sqrt{C_{g} t}$ ,可将关于 $Ω$ 的偏微分方程变为如下常微分方程^[34-35]：

$\frac{d^{2} Ω}{d η^{2}} + 2 η \frac{d^{2} Ω}{d η} = 0 (0 < η < R) ，$

(32a)

$Ω (0) = - P_{ob} + \frac{A α_{1}}{α_{1} - C_{g}} (a_{1} + b_{1})$ ,

(32b)

${(2 R Ω + \frac{d Ω}{d η}) |}_{η = R} = \frac{A α_{1}}{α_{1} - C_{g}} [2 R T_{f} - \frac{2 b_{1}}{\sqrt{π} F} \exp (- λ_{1}^{2})] ，$

(32c)

式中,F为导温固结比, $F = \sqrt{α_{1} / C_{g}}$ 。

式（32a）的通解为^[34-35]

$Ω = a + b erfc (η)$ ,

(33)

式中,系数a,b由边界条件式（32b）,（32c）确定。

根据式（32b）,（32c）可以得到：

$a = \frac{A α_{1}}{α_{1} - C_{g}} (a_{1} + b_{1}) - P_{ob} - b$ ,

(34)

$\begin{matrix} b = - \frac{\sqrt{π} R P_{ob}}{\exp (- R^{2}) + \sqrt{π} R erf (R)} + \\ \frac{A α_{1}}{α_{1} - C_{g}} b_{1} \frac{\exp (- λ_{1}^{2}) + \sqrt{π} F R \erf (λ_{1})}{F \exp (- R^{2}) + \sqrt{π} F R \erf (R)} \end{matrix}$ 。

(35)

将a,b代入式（33）,利用式（21）,（24）,（29）可以得到超静孔隙压力的解析解答,将解答整理成无量纲形式为

$\begin{array}{l} \bar{P} = ε \frac{F^{2}}{F^{2} - 1} \frac{\erf (λ_{1} \bar{z})}{\erf (λ_{1})} - ε \frac{F^{2}}{F^{2} - 1} \frac{\erf (R \bar{z})}{\erf (λ_{1})} \cdot \\ \frac{\sqrt{π} F R \erf (λ_{1}) + \exp (- λ_{1}^{2})}{\sqrt{π} F R \erf (R) + F \exp (- R^{2})} + \frac{\sqrt{π} R \erf (R \bar{z})}{\sqrt{π} R \erf (R) + \exp (- R^{2})} + \\ W_{r} \bar{z} \frac{2 R^{2}}{2 R^{2} + 1} (0 < \bar{z} < 1) \end{array}$ ,

(36)

式中

$\begin{array}{l} \bar{P} = \frac{P (z, t)}{P_{ob}} ， \\ \bar{z} = \frac{z}{S (t)} ， \\ ε = \frac{A (T_{w} - T_{f})}{P_{ob}} ， \\ W_{r} = \frac{γ^{'} S (t)}{P_{ob}} 。 \end{array}}$

(37)

式（36）表明无量纲超静孔压 $\bar{P}$ 是无量纲变量 $\bar{z}$ ,W_r, $ε$ ,R,F的函数,式中虽然包含 $λ_{1}$ ,但 $λ_{1}$ =R/F并不是独立变量。W_r是融土浮自重与外荷载之比,也正比于t^0.5,称之为自重时间因子； $ε$ 为热固结强度与外荷载之比,称之为热固结强度因子。

获得超静孔压后,沉降变形可以由下式计算^[31]：

$\begin{matrix} S_{t} = - \int_{0}^{S (t)} ε_{z z} d z = - \int_{0}^{S (t)} [{σ^{'}}_{z z} + β (T - T_{f})] / E_{s} d z \\ = \int_{0}^{S (t)} [P_{ob} + γ^{'} z - P - β (T - T_{f})] / E_{s} d z \end{matrix}$ ,

(38)

式中,S_t为融化热固结沉降。

将超静孔压代入式（38）,积分后可以整理成如下的无量纲形式：

${\bar{S}}_{t} = {\bar{S}}_{t 1} + {\bar{S}}_{t 2} - {\bar{S}}_{t 3}$ ,

(39)

式中, ${\bar{S}}_{t} = S_{t} / S (t)$ ,右侧各项为

$\begin{matrix} {\bar{S}}_{t 1} = δ (1 + \frac{W_{r}}{2}) - \frac{\sqrt{π} δ [ierfc (R) + R - ierfc (0)]}{\exp (- R^{2}) + \sqrt{π} R \erf (R)} - \\ \frac{δ W_{r} R^{2}}{2 R^{2} + 1} \end{matrix}$ ,

(40)

$\begin{array}{l} {\bar{S}}_{t 2} = δ ε \frac{F^{2}}{F^{2} - 1} [\frac{ierfc (R) + R - ierfc (0)}{R \erf (λ_{1})} \cdot \\ \frac{\exp (- λ_{1}^{2}) + \sqrt{π} F R \erf (λ_{1})}{F \exp (- R^{2}) + \sqrt{π} F R \erf (R)} - \frac{ierfc (λ_{1}) + λ_{1} - ierfc (0)}{λ_{1} \erf (λ_{1})}] ， \end{array}$

(41)

${\bar{S}}_{t 3} = δ ζ \frac{- λ_{1} erfc (λ_{1}) - ierfc (λ_{1}) + ierfc (0)}{λ_{1} \erf (λ_{1})}$ ,

(42)

其中, $ierfc (ε) = \int_{ε}^{+ \infty} erfc (z) d z$ 。

式（40）～（42）中无量纲量 $ζ$ , $δ$ 为

$\begin{array}{l} ζ = \frac{β (T_{w} - T_{f})}{P_{ob}} ， \\ δ = \frac{P_{ob}}{E_{s}} ， \end{array}}$

(43)

式中, $ζ$ 为热应力强度与荷载之比,称为热应力因子, $δ$ 为荷载压缩变形。

式（39）中 ${\bar{S}}_{t 1}$ 为普通固结引起的沉降, ${\bar{S}}_{t 2}$ 为由热固结引起的孔压变化导致的沉降（称为热压作用）,而 ${\bar{S}}_{t 3}$ 是热膨胀作用引起的膨胀变形。对于冻土中冰融化体积变化造成的直接沉降则为0.1n,而本文主要讨论式（39）给出的融化热固结变形。

3. 算例及分析

3.1 与相关模型及解答的一致性

可以用于热固结模型及解答对比的完整试验结果较少,这也是文献[29～32]热固结计算未进行试验对比的原因；而冻土在高温下融化热固结过程则更为特殊,因此本文主要通过与已有模型及解答的一致性来阐述本文结果的正确性。

MN模型是冻土一维融化过程的经典模型,常被用于对比参照,如文献[26]中融化大变形固结理论、文献[18]中考虑未冻水及变荷载的融化固结理论均是通过与MN模型的对比来说明结果的正确性的。

在不考虑温度对融化区的作用时,热应力系数β = 0,参数 $\bar{a} = 0$ ,从而式（14）中温度变化率项系数A = 0,式（36）直接退化为

$\bar{P} = \frac{\sqrt{π} R \erf (R \bar{z})}{\sqrt{π} R \erf (R) + \exp (- R^{2})} + W_{r} \bar{z} \frac{2 R^{2}}{2 R^{2} + 1} (0 < \bar{z} < 1)$ 。

(44)

容易看出,退化后的模型与MN模型是一致的,且式（44）与MN模型的解答一致^[15]。

另一方面,在融化区0 < z < S(t)内,热固结控制方程与文献[31]中的热固结方程相同,文献[32]中热固结方程在忽略对流换热并考虑瞬时荷载后也与本文一致。

3.2 孔压计算结果

式（36）中温度对超静孔压的影响主要在前两项,而前两项正比于如下函数：

$\begin{array}{l} g (\bar{z}, F, R) = \frac{F^{2}}{F^{2} - 1} \frac{\erf (λ_{1} \bar{z})}{\erf (λ_{1})} - \\ \frac{F^{2}}{F^{2} - 1} \frac{\erf (R \bar{z})}{\erf (λ_{1})} \frac{\sqrt{π} F R \erf (λ_{1}) + \exp (- λ_{1}^{2})}{\sqrt{π} F R \erf (R) + F \exp (- R^{2})} \end{array}$ 。

(45)

图2给出了不同条件下g函数随F的变化。从图2中可以看出,g函数始终为负值,且在F=1处的间断点是可去间断点。由式（36）,温度的作用会增加还是减小超静孔压主要取决于A的正负,下面就A的取值作一些讨论。

图 2 超静孔压解答中g函数的变化

Figure 2. g function in analytical solution of excessive pore water pressure

下载: 全尺寸图片幻灯片

表1给出了文献[29]中两种材料的相关参数及由这些参数计算得到的A值,两种材料的A均为负值。从式（36）可知,A为负值时,高温作用会增加超静孔压,文献[29]中热固结的计算结果确实如此。

表 1 文献[29]中材料参数及A的计算值

Table 1. Material parameters and computed values of A in Ref.[29]

材料	a_w/(10^-4℃^-1)	a_s/(10^-6℃^-1)	a_sm/(10^-6℃^-1)	n	E/MPa	v	A/(10^-4MPa℃^-1)
A	3	3	3	0.25	5.0	0.2	-4.2083
B	3	3	3	0.375	2.880	0.2	-3.6120

下载: 导出CSV

| 显示表格

文献[29]中土体的热膨胀系数a_sm并未取 $\bar{a}$ ,一般情况下若a_sm取为 $\bar{a}$ ,则可以根据式（11）得到

$A = \frac{2 ν v}{1 + ν} \frac{E}{1 - 2 ν} \bar{a}$ 。

(46)

通常材料泊松比小于0.5,因而A为正值,根据式（36）可知此时高温作用会降低超静孔压,文献[31]中的计算A取为正值,确实也出现了超静孔压降低到负值的结果。

参数A的取值不影响解答的应用,本文在下面的算例中A取为正值,此时ε也为正值。根据相关文献中的数据^[36],导温固结比F一般小于10,而其他的无量纲参数则没有明显范围限制。

图3分别给出了R为20,5,2时不同 $ε$ 下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。从图中可以看出,A为正值时高温作用造成了超静孔压的下降,并且形成了一定的负压区,这与前述分析是一致的；该特征也可以通过控制方程式（14）解释,由于融区内温度的上升,抵消了部分本应造成的超静孔压的上升,从而导致实际超静孔压与忽略高温作用时相比有所降低。随着热固结强度因子 $ε$ 的增加,热压作用引起的孔压下降愈加显著,但热压作用影响的相对范围（ $\bar{z}$ 的范围）没有明显改变。

图 3 ε对

$\bar{P}$ 影响

Figure 3. Effects of ε on

$\bar{P}$

下载: 全尺寸图片幻灯片

对比图3可知,随着R的减小,热压作用的相对影响范围增大,即减小融化界面速度或增加土的固结系数会导致热压作用影响到相对深处（ $\bar{z}$ 较大的位置）。

图4给出了不同R下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。在R=20时,热压作用影响集中在 $\bar{z} < 0.1$ 的范围；在R=10时,热压作用的影响扩大到 $\bar{z} < 0.3$ ；在R = 5时,该影响范围增大到 $\bar{z} < 0.6$ ；而在R进一步减小到2,1时,热压作用的影响范围已扩大到整个融区。随着R减小,另一个变化特征是热压作用影响的峰值强度逐渐减弱；当R减小为1时,负压区已经消失。这表明减小融化界面速度或增加土的固结系数会使得热压作用的影响在融区内变得更均匀。

图 4 R对

$\bar{P}$ 影响

Figure 4. Effects of R on

$\bar{P}$

下载: 全尺寸图片幻灯片

图5给出了不同F下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。导温固结因子F表示热扩散与固结的相对强弱,F增大代表热扩散相对变强,融区的温度更高且温度影响扩散更远,这也导致热压作用变强且逐渐影响到相对深处,这与图5中的结果是一致的。

图 5 F对

$\bar{P}$ 影响

Figure 5. Effects of F on

$\bar{P}$

下载: 全尺寸图片幻灯片

图6给出了不同W_r下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。W_r代表了时间和自重的作用,W_r增加表示融化区域增加,自重作用增强,因此 $\bar{P}$ 也增加；图中结果还表明W_r增加对热压作用强度影响不大,同时也基本不改变热压作用的相对影响范围。

图 6 W_r对

$\bar{P}$ 影响

Figure 6. Effects of W_r on

$\bar{P}$

下载: 全尺寸图片幻灯片

3.3 沉降量计算结果

因为P_ob可以很小,沉降量计算时两个无量纲变量ζ, ε是没有上限的,但是δζ与δε却有一定的限制,根据定义有

$\begin{array}{l} δ ζ = \frac{β (T_{w} - T_{f})}{E_{s}} ， \\ δ ε = \frac{A (T_{w} - T_{f})}{E_{s}} 。 \end{array}}$

(47)

若冻土在高温T_w=T_f+80℃下融化,采用文献[32]中的参数,土体E=3 MPa, $ν$ = 0.45,土颗粒热膨胀系数为2.5×10^-5℃^-1,水的热膨胀系数2×10^-4℃^-1,则计算得到的δζ大约为10^-2；材料泊松比一般小于0.5,此时δε与δζ的比值小于2/3,该比值在泊松比为0.45时约为0.62。下面算例中考虑δ = 0.03, $ζ$ = 1/3,ε = 0.62ζ。

图7给出了各部分无量纲沉降随W_r的变化,热压作用部分和热膨胀作用部分基本不随W_r变化,而普通固结和总沉降部分随着W_r增加而线性增加,该变化规律也可以直接从式（39）得出；从图中还可以看出,热膨胀作用强于热压作用,因此温度的净效果是膨胀变形,该膨胀变形会抵消部分普通固结沉降,因而总沉降较普通固结沉降略有降低。

图 7 各部分无量纲沉降随W_r的变化

Figure 7. Variation of different dimensionless settlements with W_r

下载: 全尺寸图片幻灯片

图8给出了各部分无量纲沉降随F变化的曲线,普通固结部分不随F变化,而热膨胀作用、热压作用均随F增加而近似线性增长,且热膨胀作用始终强于热压作用；在F变化范围内,普通固结部分强于温度引起的净膨胀变形,因而总沉降为正值,它随F增大而减小。随着F增大,热扩散相对增强,融区内温度整体提高,这是热膨胀作用、热压作用均增强的原因。

图 8 各部分无量纲沉降随F的变化

Figure 8. Variation of different dimensionless settlements with F

下载: 全尺寸图片幻灯片

图9给出了各部分无量纲沉降随R变化的曲线,随着R增加,热压作用早期增加后又逐渐减小,热膨胀作用则一直减小,后者始终强于前者；普通固结沉降也逐渐减小,且它始终强于温度引起的净膨胀变形,因而逐渐减小的总沉降始终为正值。R的增加代表融化界面推进速度相对于固结速度的增加,即融区迅速扩大,而固结及热扩散则相对缓慢,因此各部分无量纲沉降基本随R的增加而逐渐减小。

图 9 各部分无量纲沉降随R的变化

Figure 9. Variation of different dimensionless settlements with R

下载: 全尺寸图片幻灯片

上述结果表明,温度的净效果是膨胀变形,该效果弱于普通固结沉降,因此总的效果是沉降。实际上,如果δ增大,普通固结沉降会增加,而温度净效果由于δζ值的限制仍然弱于普通固结作用；另一方面,冰相变体积变化会造成无量纲沉降0.1n,因此一般不会出现温度引起的净膨胀变形占优势的情形。

4. 结论与展望

人工冻土融化过程中,常采用高温热水强制加速解冻,该方法在寒区工程施工中也有应用。本文针对饱和冻土在高温下的一维融化过程,开展了理论建模及解析计算研究,得到5点结论。

（1）建立了饱和冻土在高温作用下一维融化过程的理论模型,该模型包含传热部分与热固结部分。前者为全区域考虑冻土中未冻水的相变热传导过程,而后者为融化区土体在高温、荷载及自重作用下产生的热固结过程。模型在忽略了温度引起的土颗粒、水热膨胀作用后退化为Morgenstern和Nixon的经典一维融化固结模型。

（2）考虑初始温度T₀和表面融化温度T_w,对上述冻土一维融化热固结模型进行了解析求解,其中传热部分解答为已有结果,而热固结部分解答则为本文推导获得。该解析解在忽略高温热膨胀作用后退化为Morgenstern和Nixon模型的解答。

（3）利用解析解对融区内的超静孔压进行了计算。温度对 $\bar{P}$ 的影响即热压作用取决于热固结强度因子ε,本文ε为正值,因此热压作用为负值,且随着ε增加热压作用增强；随着R的减小,热压作用逐渐影响到 $\bar{z}$ 较大的位置,且热压作用强度在融化区内趋于均匀；随着F的增大,热压作用同样逐渐影响到 $\bar{z}$ 较大的位置,而热压作用在融区内会整体增强（该点与R的影响不同）；W_r的增加会增加 $\bar{P}$ ,但基本不改变热压作用强度及相对影响范围。

（4）利用解析解答对融化区内的沉降进行了计算。热压作用会增加沉降,但热膨胀作用会减小沉降,温度的净效果为膨胀变形；温度作用的净效果小于普通固结沉降,因而融化热固结总体表现为沉降；考虑到冰相变体积缩小引起的沉降,冻土在高温下融化时温度引起的净膨胀变形不会占主导。

（5）对于工程实际中复杂条件下的融化热固结问题,需要对本文模型进行数值求解,而本文建立的解析解答为发展模型高精度数值方法提供了对比基准。

图 1 试验装置示意图和原理图

Figure 1. Schematic diagram and physical diagram of test devices

下载: 全尺寸图片幻灯片

图 2 流控系统示意图

Figure 2. Schematic diagram of flow control system

下载: 全尺寸图片幻灯片

图 3 坝体模型剖面图

Figure 3. Section view of dam model

下载: 全尺寸图片幻灯片

图 4 坝体模型土料级配曲线图

Figure 4. Grain-size distribution curves of soils of dam model

下载: 全尺寸图片幻灯片

图 5 仪器布设图

Figure 5. Layout of instruments

下载: 全尺寸图片幻灯片

图 6 坝体填筑模型图

Figure 6. Dam body model

下载: 全尺寸图片幻灯片

图 7 光纤光栅温度计与光纤测温结果对比图

Figure 7. Comparison of results of fiber grating thermometer and fiber temperature measurement

下载: 全尺寸图片幻灯片

图 8 各工况坝体温度分布云图

Figure 8. Cloud map of temperature distribution of dam under various working conditions

下载: 全尺寸图片幻灯片

图 9 不同工况下温度监测结果

Figure 9. Monitoring results of temperature under different working conditions

下载: 全尺寸图片幻灯片

图 10 各工况心墙中心线监测结果

Figure 10. Monitoring results of center line of core wall under various working conditions

下载: 全尺寸图片幻灯片

图 11 不同工况下孔隙水压力监测结果

Figure 11. Monitoring results of pore water pressure under different working conditions

下载: 全尺寸图片幻灯片

图 12 不同工况下坝体单宽渗漏速率时序曲线

Figure 12. Variation of single-width leakage rate of dam body with time under different working conditions

下载: 全尺寸图片幻灯片

图 13 各工况浸润线监测结果

Figure 13. Monitoring results of infiltration line under various working conditions

下载: 全尺寸图片幻灯片

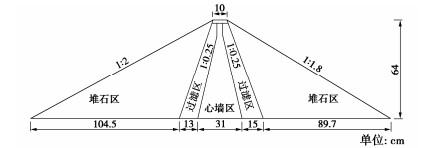
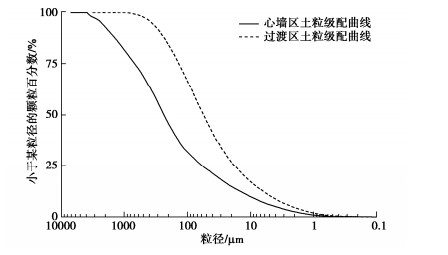
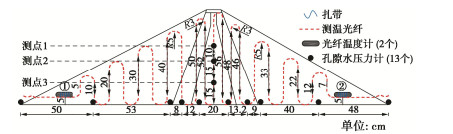
表 1 各分区土料参数

Table 1 Parameters of soils in each area of dam body

坝体分区	渗透系数Κ/(m·s^-1)	密度 ρ/(g·cm^-3)	含水率w/%
堆石区	4.71×10^-2	1.69	1.99
过滤区	2.83×10^-5	1.79	6.87
病险区	2.83×10^-5	1.79	6.87
心墙区	5.16×10^-7	2.03	8.81

下载: 导出CSV

表 2 各工况设置详情

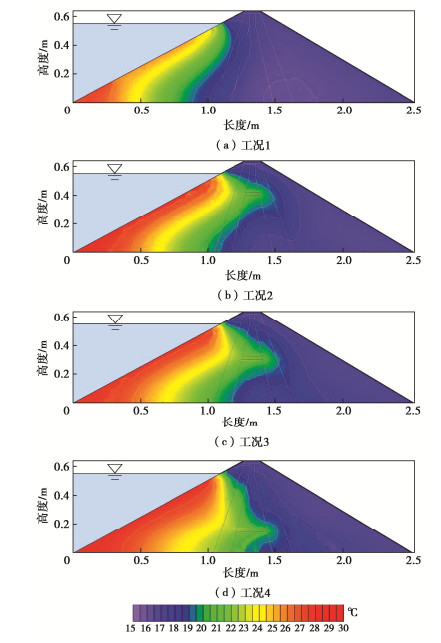
Table 2 Setting details of each working condition

工况	入渗水温/ ℃	入渗水头/ cm	距坝基高度/cm	备注
1	28	55	—	无病险
2	28	55	40	高位
3	28	55	30	中位
4	28	55	15	低位

下载: 导出CSV

参考文献(26)

[1]	SALMASI F, NOROUZI R, ABRAHAM J, et al. Effect of inclined clay core on embankment dam seepage and stability through LEM and FEM[J]. Geotechnical and Geological Engineering, 2020, 38(6): 6571-6586. doi: 10.1007/s10706-020-01455-7
[2]	苏怀智, 周仁练. 土石堤坝渗漏病险探测模式和方法研究进展[J]. 水利水电科技进展, 2022, 42(1): 1-10, 39. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD202201001.htm SU Huaizhi, ZHOU Renlian. Research progress and prospect of earth-rockfill dam leakage detection modes and method[J]. Advances in Science and Technology of Water Resources, 2022, 42(1): 1-10, 39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD202201001.htm
[3]	SCHMITZ V, ERPICUM S, EL KADI ABDERREZZAK K, et al. Overtopping-induced failure of non-cohesive homogeneous fluvial dikes: effect of dike geometry on breach discharge and widening[J]. Water Resources Research, 2021, 57(7): 029660.
[4]	钟登华, 时梦楠, 崔博, 等. 大坝智能建设研究进展[J]. 水利学报, 2019, 50(1): 38-52, 61. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201901006.htm ZHONG Denghua, SHI Mengnan, CUI Bo, et al. Research progress of the intelligent construction of dams[J]. Journal of Hydraulic Engineering, 2019, 50(1): 38-52, 61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201901006.htm
[5]	彭铭, 毕竞超, 朱艳, 等. 存在高渗透区的黏土心墙土石坝渗流稳定性分析[J]. 水利学报, 2020, 51(11): 1347-1359. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202011005.htm PENG Ming, BI Jingchao, ZHU Yan, et al. Seepage stability analysis of earth and rockfill dam with clay core by considering high permeability zones[J]. Journal of Hydraulic Engineering, 2020, 51(11): 1347-1359. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202011005.htm
[6]	DONG H Z, CHEN J S, LI X Y. Delineation of leakage pathways in an earth and rockfill dam using multi-tracer tests[J]. Engineering Geology, 2016, 212: 136-145. doi: 10.1016/j.enggeo.2016.08.003
[7]	RATIAT A, KHETTAL T, MEDDI M. The piezometric and isotopic analysis of leaks in earth dams: the case of the fountain of Gazelle Dam, Biskra, Algeria[J]. Environmental Earth Sciences, 2020, 79(6): 138. doi: 10.1007/s12665-020-8886-8
[8]	LUO Y L, NIE M, XIAO M. Flume-scale experiments on suffusion at bottom of cutoff wall in sandy gravel alluvium[J]. Canadian Geotechnical Journal, 2017, 54(12): 1716-1727. doi: 10.1139/cgj-2016-0248
[9]	ROCHIM A, MAROT D, SIBILLE L, et al. Effects of hydraulic loading history on suffusion susceptibility of cohesionless soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(7): 04017025. doi: 10.1061/(ASCE)GT.1943-5606.0001673
[10]	NGUYEN C D, BENAHMED N, ANDÒ E, et al. Experimental investigation of microstructural changes in soils eroded by suffusion using X-ray tomography[J]. Acta Geotechnica, 2019, 14(3): 749-765. doi: 10.1007/s11440-019-00787-w
[11]	孔纲强, 孙学谨, 刘汉龙, 等. 孔隙液体对透明土渗透特性影响对比试验[J]. 水利学报, 2017, 48(11): 1303-1310. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201711005.htm KONG Gangqiang, SUN Xuejin, LIU Hanlong, et al. Contrast experiments on permeability of transparent soil influenced by pore fluids[J]. Journal of Hydraulic Engineering, 2017, 48(11): 1303-1310. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201711005.htm
[12]	梁越, 陈鹏飞, 林加定, 等. 基于透明土技术的多孔介质孔隙流动特性研究[J]. 岩土工程学报, 2019, 41(7): 1361-1366. doi: 10.11779/CJGE201907022 LIANG Yue, CHEN Pengfei, LIN Jiading, et al. Pore flow characteristics of porous media based on transparent soil technology[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1361-1366. (in Chinese) doi: 10.11779/CJGE201907022
[13]	谷敬云, 罗玉龙, 张兴杰, 等. 基于平面激光诱导荧光的潜蚀可视化试验装置及其初步应用[J]. 岩石力学与工程学报, 2021, 40(6): 1287-1296. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106019.htm GU Jingyun, LUO Yulong, ZHANG Xingjie, et al. A suffusion visualization apparatus based on planar laser induced fluorescence and the preliminary application[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(6): 1287-1296. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106019.htm
[14]	HUNTER R P, BOWMAN E T. Visualisation of seepage-induced suffusion and suffosion within internally erodible granular media[J]. Géotechnique, 2018, 68(10): 918-930.
[15]	NAN S H, REN J, NI F, et al. Heat tracing of embankment dam leakage: laboratory experiments and 2D numerical modelling[J]. Journal of Hydrology, 2022, 608: 127663.
[16]	王新建, 潘纪顺. 堤坝多集中渗漏通道位置温度探测研究[J]. 岩土工程学报, 2010, 32(11): 1800-1805. http://www.cgejournal.com/cn/article/id/8471 WANG Xinjian, PAN Jishun. Location detection of concentrated-leakage passages in dam by groundwater temperature[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1800-1805. (in Chinese) http://www.cgejournal.com/cn/article/id/8471
[17]	谷艳昌, 王士军, 庞琼, 等. 土坝温度场反馈渗流场可行性研究[J]. 岩土工程学报, 2014, 36(9): 1721-1726. doi: 10.11779/CJGE201409020 GU Yanchang, WANG Shijun, PANG Qiong, et al. Feasibility of temperature field feeding back seepage field for earth dams[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1721-1726. (in Chinese) doi: 10.11779/CJGE201409020
[18]	CUONG B Q, ZHOU Y H, ZHAO C J. Seepage evaluation in embankment dam based on short-term temperature observation and heat injection[J]. Electronic Journal of Geotechnical Engineering, 2016, 21(26): 10493-10506.
[19]	GHAFOORI Y, MAČEK M, VIDMAR A, et al. Analysis of seepage in a laboratory scaled model using passive optical fiber distributed temperature sensor[J]. Water, 2020, 12(2): 367.
[20]	王家琛, 朱鸿鹄, 王静, 等. 基于主动加热光纤法的毛细阻滞入渗模型试验研究[J]. 岩土工程学报, 2021, 43(1): 147-155. doi: 10.11779/CJGE202101017 WANG Jiachen, ZHU Honghu, WANG Jing, et al. Laboratory model tests on capillary barrier infiltration using actively heated fiber optic method[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(1): 147-155. (in Chinese) doi: 10.11779/CJGE202101017
[21]	SMITH M, KONRAD J M. Analysis of the annual thermal response of an earth dam for the assessment of the hydraulic conductivity of its compacted till core[J]. Canadian Geotechnical Journal, 2008, 45(2): 185-195.
[22]	GHAFOORI Y, VIDMAR A, ŘÍHA J, et al. A review of measurement calibration and interpretation for seepage monitoring by optical fiber distributed temperature sensors[J]. Sensors, 2020, 20(19): 5696.
[23]	何斌, 徐剑飞, 何宁, 等. 分布式光纤传感技术在高面板堆石坝内部变形监测中的应用[J]. 岩土工程学报, 2023, 45(3): 627-633. doi: 10.11779/CJGE20220089 HE Bin, XU Jianfei, HE Ning, et al. Application of distributed optical fiber sensing technology in internal deformation monitoring of high face rockfill dam[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(3): 627-633. (in Chinese) doi: 10.11779/CJGE20220089
[24]	SU H Z, TIAN S G, CUI S S, et al. Distributed optical fiber-based theoretical and empirical methods monitoring hydraulic engineering subjected to seepage velocity[J]. Optical Fiber Technology, 2016, 31: 111-125.
[25]	SU H Z, CUI S S, WEN Z P, et al. Experimental study on distributed optical fiber heated-based seepage behavior identification in hydraulic engineering[J]. Heat and Mass Transfer, 2019, 55(2): 421-432.
[26]	CHEN J A, CHENG F, XIONG F, et al. An experimental study: Fiber Bragg grating–hydrothermal cycling integration system for seepage monitoring of rockfill dams[J]. Structural Health Monitoring, 2017, 16(1): 50-61.