随机地震作用下隧道动力响应的概率密度演化分析

张冬梅; 郭力; 申轶尧; 黄忠凯

doi:10.11779/CJGE2024S20033

随机地震作用下隧道动力响应的概率密度演化分析 English Version

张冬梅^{1, 2,},
郭力¹,
申轶尧^1, ,,
黄忠凯¹

1.
同济大学土木工程学院, 上海 200092
2.
青海大学土木水利学院, 青海西宁 810016

基金项目:

国家重点研发计划课题 2022YFC3800905

国家自然科学基金项目 52238010

国家自然科学基金项目 52090082

国家自然科学基金项目 51408205

上海市“科技创新行动计划”优秀学术/技术带头人计划项目 22XD1430200

同济大学学科交叉联合攻关项目 2022-3-ZD-07

青海省科学技术厅基础研究计划项目 2023-ZJ-926M

详细信息

作者简介:
张冬梅(1975—)，女，博士，教授，主要从事盾构隧道安全评估方面的研究工作。E-mail: dmzhang@tongji.edu.cn

通讯作者:
申轶尧, E-mail: sshenyiyao@163.com

中图分类号: TU435;TU93
计量
- 文章访问数: 91
- HTML全文浏览量: 11
- PDF下载量: 21
出版历程
- 收稿日期: 2024-06-20
- 刊出日期: 2024-09-30

Probabilistic density evolution analysis of dynamic response of tunnels under stochastic earthquakes

1.
College of Civil Engineering, Tongji University, Shanghai 200092, China
2.
College of Civil Engineering and Water Resoures, Qinghai University, Xining 810016, China

摘要

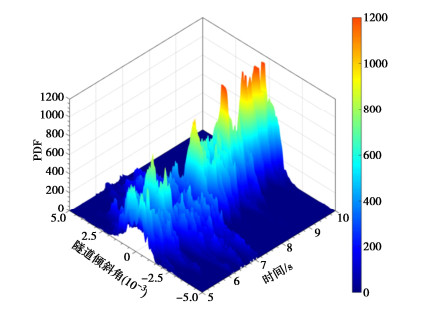
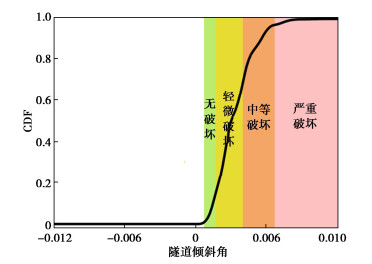
摘要: 由于地震动的随机性特征，确定性方法难以完全考虑地震动复杂随机性特点，采用随机分析方法研究隧道结构的地震响应对地下结构抗震设计具有重要的现实意义。以软土场地中圆形隧道结构为研究对象，建立典型工程场地下土体-隧道整体非线性动力相互作用分析模型，利用随机地震动模型生成符合抗震设计规范要求的非平稳地震动，将概率密度演化分析方法引入到隧道结构抗震分析中，初步探讨了隧道结构抗震性能概率密度演化特征，并以隧道倾斜角为抗震性能指标，利用概率密度演化方法求解隧道结构响应的概率密度函数，得到隧道在无破坏、轻微破坏、中等破坏和严重破坏时隧道倾斜角的超越概率。研究结果表明：隧道倾斜角在四种破坏状态下的超越概率分别为98.88%，86.10%，30.90%和3.70%；提出的概率密度演化方法可以准确获取隧道倾斜角瞬时概率信息，为研究隧道结构抗震性能的概率演化特征提供了新的思路和途径。
- 隧道结构 /
- 概率密度演化方法 /
- 随机地震 /
- 动力响应 /
- 超越概率
Abstract: Due to the stochastic characteristics of ground motion, it is difficult for the deterministic method to completely consider the complex stochastic characteristics of ground motion. It is of great practical significance to study the seismic response of tunnel structures by using the stochastic analysis method for the seismic design of underground structures. In this study, the research object is a typical circular tunnel structure in soft soils. First, a nonlinear interaction analysis model for the underground soil tunnel in a typical project site is established. Then, a random seismic model is used to generate a non-stationary seism that matches the requirements of the seismic design code. A probability density evolution analysis method is introduced into the seismic analysis of the tunnel structure, which initially explores the evolution characteristics of the probability density of its seismic performance. Using the tunnel inclination angle as the seismic performance index, the probability density function of the tunnel structural response is solved by using the probability density evolution method, and the exceedance probabilities of the tunnel inclination angle are obtained when the tunnel has no damage, slight damage, moderate damage and severe damage. The results show that the exceedance probabilities of the tunnel inclination angle in the four damage states are 98.88%, 86.10%, 30.90% and 3.70%, respectively. The proposed probability density evolution method can accurately obtain the instantaneous probability information of the tunnel inclination angle, and provide a new prospect for the study on the probability evolution characteristics of seismic performance of the tunnel structures.
- tunnel structure /
- probability density evolution method /
- stochastic earthquake /
- dynamic response /
- exceedance probability

HTML全文

0. 引言

随着城市化进程不断加速，城市地下空间的开发越来越受到人们的关注。大规模的新建地铁盾构隧道在掘进过程中，不可避免地出现穿越既有建筑桩基的工况^[1]。隧道开挖引起的地层应力释放，造成既有桩基周围地层的应力场发生改变，从而导致桩基产生附加变形和附加内力，并造成桩基承载力发生变化，而过度的承载力损失将危及上部结构安全^[2-3]。因此，准确评价隧道近接施工对既有摩擦桩基的影响是当前城市地下空间开发所面临的较为紧迫的问题。

当前，针对隧道施工引起的邻近桩基响应问题，学者们基于现场实测、模型试验^[4-5]、数值模拟和理论解析等方法已取得了较为丰硕的成果。如李雪等^[6]针对饱和砂土地区盾构隧道超近接高铁桥墩摩擦桩的工程问题，对既有高铁桥墩桩基变形进行了现场测试；Loganathan等^[7]和孙庆等^[8]采用离心机试验研究了隧道开挖对邻近桩基的瞬态和长期影响，指出隧道开挖影响下邻近桩基最大横向变形和附加弯矩均发生在隧道轴线附近。

隧道施工引起的邻近桩基响应问题，实质为隧道−土体−桩基之间相互作用。学者们已构建了十分丰富的解析计算模型。如ZHANG等^[9]基于Pasternak地基模型及桩侧土体影响，研究了被动桩在盾构掘进下水平向变形响应；程康等^[10]等进一步考虑桩基的横向剪切性能，将桩简化成Pasternak地基上的Timoshenko梁，进一步研究了盾构掘进引起的桩基水平变形；冯国辉等^[11-13]分别将既有桩基视为Winkler地基和Pasternak地基中的Euler-Bernoulli梁，分析了盾构掘进下邻近桩基的横向附加响应。

本文在既有研究的基础上，结合隧道开挖前后地层应力场的变化，建立盾构近接施工下邻近摩擦桩基承载力解析计算模型，分析了隧道施工对既有摩擦桩基承载特性的影响机制，并进一步基于三维有限元分析论证了隧道洞周地层加固对既有桩基变形控制的有效性。

1. 盾构近接施工扰动下摩擦桩基承载特性分析

1.1 基本思路

盾构施工对邻近摩擦桩基承载特性的影响，实质在于隧道施工会引起周围土体应力场重分布，而导致摩擦桩侧法向正应力和切向剪应力发生变化，继而影响桩侧摩阻力。因此对于盾构施工扰动下邻近摩擦桩基承载力分析的基本思路：

（1）隧道施工前，地层内任一点的应力状态由围岩自重生成竖向应力 ${\sigma _{{\text{v0}}}}$ 、水平向应力 ${\sigma _{{\text{h0}}}}$ ，将该值作为桩侧地层应力状态初始值，可求得初始桩侧阻力 ${Q_{{\text{s0}}}}$ 。

（2）计算隧道施工后地层内任一点的竖向应力 ${\sigma _{\text{v}}}$ 、水平应力 ${\sigma _{\text{h}}}$ 和剪应力 ${\tau _{xy}}$ ，根据此时的应力状态计算隧道施工后的桩侧阻力Q_s。

（3）结合步骤（1），（2），求得摩擦桩基承载力变化值 $\Delta {Q_{\text{s}}} = {Q_{{\text{s}}0}} - {Q_{\text{s}}}$ 。

1.2 解析模型的建立及基本假定

为获得盾构近接施工扰动下临近摩擦桩基的承载特性，建立如图 1所示的隧道-地层-桩基相互作用模型。图 1中x，y为弹性半空间任意一点的直角坐标，r，θ为相应的极坐标；h为隧道轴线埋深； ${\sigma _r}$ ， ${\sigma _\theta }$ ， ${\tau _{r\theta }}$ 分别为任意一点土体径向应力、环向应力和剪应力；l为桩基长度；x₀为桩基轴线与隧道轴线的水平间距；r₀为隧道开挖半径。

图 1 隧道-地层-桩基相互作用模型

Figure 1. Interaction model for tunnel-stratum-pile

下载: 全尺寸图片幻灯片

在理论计算时作如下基本假定：

（1）为避免地层应力场计算时的奇异，隧道覆径比大于1.5。

（2）忽略土体与衬砌之间的摩擦力，即接触面处的剪应力满足：

${\left. \tau \right|_{r = {r_0}}} = 0 。$

(1)

（3）采用间隙参数w表征盾构开挖引起的等效地层损失，计算方法为

$w = {V_{\text{l}}}\frac{{\pi {r_0}^2}}{{2\pi {r_0}}} = \frac{1}{2}{V_{\text{l}}}{r_0} 。$

(2)

式中：V_l为地层损失率。

1.3 初始桩侧阻力 ${Q_{{\text{s0}}}}$

任在原岩应力状态下，桩侧任意一点的应力状态为

$\left.\begin{array}{l}{\sigma }_{\text{v}0}=\gamma (h-y)\text{，}\\ {\sigma }_{\text{h}0}=k{\sigma }_{\text{v}0}\text{，}\\ {\tau }_{xy\text{0}}=0。\end{array} \right\}$

(3)

式中： $\gamma$ 为土体有效重度；k为侧压力系数。

根据摩擦桩基承载理论，此时桩基承载力为

${Q_{{\text{s}}0}} = {\text{π }}d\int_l^{} {{f_{{\text{s0}}}}(y){\text{d}}y} = {\text{π }}d\int_l^{} {({\tau _{xy{\text{0}}}} + {k_{\text{s}}}{\sigma _{{\text{h}}0}}){\text{d}}y} 。$

(4)

式中：d为桩基直径；f_s0为初始状态下的桩侧摩阻力分布函数； ${k_{\text{s}}}$ 为桩侧界面摩擦系数， ${k_{\text{s}}} = \tan {\delta _\varphi }$ ；δ_φ为界面摩擦角。

1.4 开挖扰动后桩侧阻力Q_s

以干砂地层为例，BOBET基于应力函数法给出了此类地层中隧道开挖后任意一点的应力，即

$\begin{array}{l} {\sigma _r} = \frac{{{a_0}}}{{{r^2}}} - \frac{1}{2}\gamma h(1 + k) + \left[ {\frac{1}{4}\gamma r(k + 3) - 2{{c'}_1}} \right.{r^{ - 3}} + \hfill \\ \quad \;\;\; \left. {\frac{1}{2}{c_1}{r^{ - 1}}} \right]\sin \theta + \left[ {\frac{1}{2}\gamma h(1 - k) - 6{{a'}_2}{r^{ - 4}} - 2{{b'}_2}{r^{ - 2}}} \right] \cdot \hfill \\ \;\; \cos 2\theta + \left[ { - \frac{1}{4}\gamma r(1 - k) - 12{{c'}_3}{r^{ - 5}} - 6{{d'}_3}{r^{ - 3}}} \right]\sin 3\theta \text{，} \end{array}$

(5a)

$\begin{array}{l} {\sigma _\theta } = - \frac{{{a_0}}}{{{r^2}}} - \frac{1}{2}\gamma h(1 + k) + \left[ {\frac{1}{4}\gamma r(3k + 1) + 2{{c'}_1}} \right.{r^{ - 3}} - \hfill \\ \quad \;\;\;\left. {\frac{1}{2}{c_1}{r^{ - 1}}} \right]\sin \theta + \left[ { - \frac{1}{2}\gamma h(1 - k) + 6{{a'}_2}{r^{ - 4}} + 2{{b'}_2}{r^{ - 2}}} \right] \cdot \hfill \\ \;\; \cos 2\theta + \left[ {\frac{1}{4}\gamma r(1 - k) + 12{{c'}_3}{r^{ - 5}} + 6{{d'}_3}{r^{ - 3}}} \right]\sin 3\theta \text{，} \end{array}$

(5b)

$\begin{align} {\tau _{r\theta }} = &\left[ {\frac{1}{4}\gamma r(1 - k) + 2{{c'}_1}{r^{ - 3}}} \right]\cos \theta - \left[ {\frac{1}{2}\gamma h(1 - k) + } \right. \hfill \\ &\left. {6{{a'}_2}{r^{ - 4}} + 2{{b'}_2}{r^{ - 2}}} \right]\sin 2\theta - \left[ {\frac{1}{4}\gamma r(1 - k) - } \right.12{{c'}_3}{r^{ - 5}} - \hfill \\ & \qquad \qquad \left. {6{{d'}_3}{r^{ - 3}}} \right]\cos 3\theta 。\end{align}$

(5c)

式中： ${a_0}$ ， ${a'_2}$ ， ${b'_2}$ ， ${c_1}$ ， ${c'_1}$ ， ${c'_3}$ ， ${d'_1}$ ， ${d'_3}$ 为常数，可根据问题的边界条件确定，其他符号意义同前。

进一步，可通过坐标变换将地层中一点应力状态（式（5））由极坐标系转换到直角坐标系，即

${\sigma _x} = \frac{{{\sigma _r} + {\sigma _\theta }}}{2} + \frac{{{\sigma _r} - {\sigma _\theta }}}{2}\cos 2\theta - {\tau _{r\theta }}\sin 2\theta \text{，}$

(6a)

${\tau _{xy}} = \frac{{{\sigma _r} - {\sigma _\theta }}}{2}\sin 2\theta + {\tau _{r\theta }}\cos 2\theta 。$

(6b)

将式（5）代入式（6），结合摩擦桩基承载理论，得到隧道开挖扰动后的桩基承载力，即

${Q_s} = \pi d\int_l {{f_s}(y)} dy = \pi d\int_l {{\text{(}}{\tau _{xy}} + {k_{\text{s}}}{\sigma _x}{\text{)}}} dy 。$

(7)

式中：f_s为隧道开挖后桩侧摩阻力分布函数； ${\sigma '_x}$ ， ${\tau '_{xy}}$ 分别表示直角坐标系下任意一点的有效水平应力和剪应力。

1.5 隧道开挖对摩擦桩基承载力的影响分析

以某地铁盾构隧道连续侧穿老旧建筑群施工为工程背景，基于上述隧道开挖前后摩擦桩基承载力理论分析，进行隧道开挖对邻近摩擦桩基承载特性的影响分析。选取典型工况：既有桩基及开挖隧道位于砂土地层中，地层重度约为18 k N/m³，侧压力系数约为0.32，根据地勘资料，计算时地层弹性模量和泊松比分别取30 MPa，0.3；盾构隧道开挖半径为3.14 m，轴线埋深为15 m，隧道衬砌采用C50钢筋混凝土管片，管片厚度为0.3 m，弹性模量和泊松比分别为34500 MPa，0.2；既有建筑物桩基直径为0.5 m。为反映隧道施工对摩擦桩基承载能力的影响，定义摩擦桩基承载力影响因子R_Q：

${R_Q} = \frac{{{Q_s}}}{{{Q_{s0}}}} 。$

(8)

R_Q>1表示承载力提高，R_Q<1表示承载力损失，当R_Q=1时表示承载力无变化。

如图 2所示为桩隧横向间距为1.5r₀，地层损失率为0.8%时，摩擦桩基承载力影响因子随桩长的变化曲线。由图可见：承载力影响因子变化曲线随桩长的增大而呈漏斗状分布，当l/h<1.0时，承载力影响因子随桩长的增大而迅速减小，而当l/h>1.0时，承载力影响因子随桩长的增大而又逐渐增大，并逐渐趋近于1.0；桩隧相对埋深越趋近1.0，承载力影响因子变化梯度越大，承载力损失越多；当桩基端部与隧道轴线相平时，即l/h=1.0时，其承载力损失最多，在本算例中此时承载力影响因子R_Q=0.17，桩基承载力损失82.9%。

图 2 桩基承载力影响因子随桩长的变化曲线

Figure 2. Relationship between impact factor on bearing capacity of pile and its length

下载: 全尺寸图片幻灯片

如图 3所示为当桩隧横向间距为3.0 r₀，桩隧相对埋深l/_h = 1.0时，摩擦桩基承载力影响因子随地层损失率的变化曲线。由图 3可见：摩擦桩基承载力损失因子与地层损失率呈线性相关关系，随着地层损失率的增大，摩擦桩基承载力影响因子随之线性减小；在本算例中，当地层损失率仅为0.4%时，承载力影响因子为0.98，而当地层损失率增大至1.8%时，摩擦桩基承载力影响因子减小至0.15，变化84.7%。

图 3 桩基承载力影响因子随地层损失率的变化曲线

Figure 3. Relationship between impact factor on bearing capacity of pile and ground loss ratio

下载: 全尺寸图片幻灯片

2. 盾构侧穿摩擦桩基建筑物控制技术

盾构隧道施工对周围岩土体造成扰动，应力平衡状态改变造成围岩应力释放，导致临近桩基产生沉降变形。综合前述计算分析，从地层加固措施入手减小盾构施工对邻近桩基的影响，通过注浆加固地层的方式减小盾构施工扰动在地层中的传播。

2.1 计算模型及计算参数

所建立的盾构-围岩-建筑物的三维数值模型如图 4所示，模型尺寸为长60 m (沿隧道开挖方向)，宽120 m (垂直隧道开挖方向)，高50 m (沿地层深度方向)。模型侧面约束水平位移，底部为固定边界，上表面为自由边界，共划分56972个单元，41673个节点。数值模型中盾构隧道管片外径6.0 m，内径5.4 m，厚度300 mm，宽度1.2 m，采用C50混凝土，考虑衬砌接头对管片刚度的削弱效应，管片刚度需折减15%。

图 4 三维数值模型

Figure 4. 3D numerical model

下载: 全尺寸图片幻灯片

模型中地层采用摩尔库仑模型，盾壳、隧道衬砌、同步注浆区（即后文所述的等代层）、袖阀管注浆加固区、建筑物梁板柱、桩基础均采用线弹性模型。地层、等代层、袖阀管注浆加固区采用实体单元模拟，盾壳、隧道衬砌、建筑楼板采用板单元模拟，建筑框架梁、立柱、建筑桩基采用梁单元模拟。参数取值见表 1。

表 1 结构参数取值

Table 1. Values of structural parameters

名称	密度 γ/(kN·m^-3)	弹性模量 E/GPa	泊松比
盾壳	78.5	210	0.30
隧道衬砌	25.0	29.3	0.20
建筑框架 (梁、板、柱)	25.0	20.4	0.20
桩基础	25.0	24.0	0.20
等代层	20.0	0.06	0.25
袖阀管注浆加固区	22.0	0.25	0.25

下载: 导出CSV

| 显示表格

2.2 盾构隧道施工过程模拟

（1）同步注浆

在盾构机施工过程中，在盾尾管片脱出后，由于盾构机刀盘的超挖间隙、装配管片所需的操作间隙、盾构机壳的厚度3个因素将会在盾构管片和土体间产生盾尾间隙。为了减小施工扰动，控制地层变形，在盾构掘进过程中将会采取同步注浆对盾尾间隙进行填充。但是实际工程中，由于地层向盾尾间隙道的移动程度、注浆体注浆后的分布情况、隧道围岩壁面受扰动的范围和程度等情况相对复杂，因此，在建模过程中通常将注浆体简化为均质的、弹性的、等厚的等代层处理，等代层的厚度δ可为

$\delta = \mu \varDelta 。$

(9)

式中：Δ为盾尾间隙的理论计算值；μ为折减系数，取值范围为0.7~2.0，对于极软土层取上限值，对于硬土层取下限值。

根据盾构穿越地层条件及施工扰动范围及程度取等代层厚度为100 mm，弹性模量为60 MPa，泊松比为0.25，采用线弹性体模拟，并根据实际施工情况取注浆压力为300 kPa。

（2）土仓压力

对于土压平衡盾构机而言，掌子面的稳定一般依靠于密封土仓的土仓压力平衡掌子面前方的水土压力，并且考虑到盾构刀盘切削土体使土体剥落而导致土仓压力不稳定的情况，为了防止掌子面坍塌，根据施工经验，一般会预留10~20 kPa的预备压力，所以土仓压力一般按下式确定：

${P_0} = {P_c} + {P_w} + p 。$

(10)

式中：P₀为土仓压力； ${P_c}$ 为土压力； ${P_w}$ 为水压力；P为预备压力。其中 ${P_c}$ =∑K₀ ${\gamma _i}{z_i}$ ， ${P_c} = {\gamma _{\text{w}}}h$ ，K₀为土体静止侧压力系数， ${\gamma _i}$ 为第i层土的重度， ${z_i}$ 为第i层土的厚度， ${\gamma _{\text{w}}}$ 为水的重度，h为地下水位都盾构刀盘的高度。

通过计算取土仓压力为200 kPa均布施加于开挖面土体上。

（3）盾壳与地层摩擦力

盾构掘进过程，盾构机和地层发生相对运动而产生摩擦力，会使得盾构机周围土体由于剪切作用而向前运动，沿伸到地表则表现为地表隆起或者沉降。盾壳和地层间的摩擦力计算公式为

$f = {\mu _s}\sum {{\gamma _i}{z_i}} 。$

(11)

式中：μ_s为盾构机与地层的摩擦系数，通过计算得到的摩擦力为153 kPa。

3. 计算结果分析

3.1 地层位移

在整个开挖过程中，注浆加固区附近的土体变形明显变小，当双线隧道开挖完成后，对于未进行注浆加固的工况来说，沉降发生区域在左线隧道和右线隧道间呈长条带状分布，而注浆加固后，沉降发生区域沿开挖方向呈现“两头大，中间小”分布，凸向隧道左线。选取隧道轴线纵向30 m处的横断面作为分析断面，对加固地层前后的地表沉降进行分析，计算结果如图 5所示。

图 5 距起始开挖面30 m处地表横向沉降

Figure 5. Lateral settlements of surface

下载: 全尺寸图片幻灯片

由图 5可知，地表沉降曲线呈“U”字形，符合“Peck”曲线分布，并与实测数据有较好的拟合度。当右线隧道开挖完成时，地表沉降最大值出现在右线隧道正上方，当左线隧道开挖完成后，地层受二次开挖扰动，沉降值变大，沉降槽宽度加宽，最低点往左移动。对于距起始开挖面30 m处的横断面而言，处于加固区，受右线隧道开挖影响减小，沉降最大值出现在左线隧道正上方附近，注浆加固前后沉降明显变小，最大值分别为14.8，10.7 mm，降低27.8%。

3.2 桩基变形

选取距离起始开挖面最近的一排3根桩进行分析，距离隧道由近到远分别为桩基P1，P2，P3。由图 6可知，双线隧道开挖完后，由于土体的卸荷作用，桩基发生挠曲变形，桩基顶部向隧道方向移动，桩基底部远离隧道移动。离隧道越远，桩基水平位移越小，由于上部结构的约束作用，各单桩桩顶位移基本相同。在注浆加固后，桩基水平位移明显减小，桩顶最大水平位移由2.6 mm减少至1.4 mm，降低46%。

图 6 加固地层前后桩基水平位移分布曲线

Figure 6. Distribution curves of horizontal displacement of pile foundation before and after reinforcement of strata

下载: 全尺寸图片幻灯片

如图 7所示为加固地层和未加固地层工况下左右线贯通后桩基竖向位移沿桩身埋深分布曲线。由图 7可见：桩身沉降沿桩身基本相同，离隧道越远，沉降越小，桩基P1，P2沉降受隧道开挖影响较大，在注浆加固后，桩基沉降由5.7 mm减少至2.6 mm，降低54%。

图 7 加固地层前后桩基竖向位移分布曲线

Figure 7. Distribution curves of vertical displacement of pile foundation before and after reinforcement of strata

下载: 全尺寸图片幻灯片

4. 结论

针对盾构近接施工对邻近摩擦桩基的影响问题，分别建立了隧道开挖扰动下摩擦桩基承载力解析计算模型和三维数值分析模型，探明了隧道开挖对既有摩擦桩基承载力的影响机制，并论证了地层加固对桩基变形控制的有效性，得到3点结论。

（1）基于摩擦桩基承载力理论和隧道开挖前后地层应力场的分析，建立了隧道开挖影响下摩擦桩基承载力计算方法，并定义摩擦桩基承载力影响因子分析了不同工况下隧道施工对桩基承载力的影响。

（2）隧道施工对不同长度的摩擦桩基影响不同，当桩端埋深与隧道轴线埋深一致时，桩基承载力损失最为严重，而当桩长远大于隧道埋深时其承载力损失较小；隧道施工时的地层损失率越大，桩基承载损失越严重，二者呈正相关。

（3）建立了盾构侧穿浅层摩擦桩基建筑物施工的三维有限元模型，分析了盾构侧穿桩基施工时的桩基沉降变形规律。计算结果表明在采取洞周地层加固措施后，隧道围岩注浆加固后土体变形明显变小，可有效减少临近桩基水平位移和桩身的沉降。

图 1 土层剪切模量与阻尼比曲线

Figure 1. Curves of shear modulus and damping ratio of soils

下载: 全尺寸图片幻灯片

图 2 土体非线性本构模型参数标定

Figure 2. Parameter correction for nonlinear constitutive model of soils

下载: 全尺寸图片幻灯片

图 3 典型时段内的隧道倾斜角概率密度曲面

Figure 3. Probability density surface of tunnel inclination angle in a typical time interval

下载: 全尺寸图片幻灯片

图 4 累计分布函数曲线

Figure 4. Curve of cumulative distribution function

下载: 全尺寸图片幻灯片

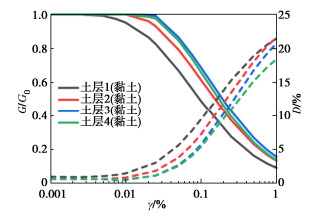
表 1 土层剖面参数表

Table 1 Parameters of soil strata

土层	埋深/m	剪切波速 ${v_{\text{s}}}$ /(m·s^-1)	剪切强度S_u/kPa	密度/(kg·m^-3)	泊松比
^#1	0~10	250	100	1800	0.30
^#2	10~25	300	280	1800	0.30
^#3	25~35	400	400	1900	0.30
^#4	35~70	600	500	1900	0.30

下载: 导出CSV

参考文献(19)

[1]	何川, 李林, 张景, 等. 隧道穿越断层破碎带震害机理研究[J]. 岩土工程学报, 2014, 36(3): 427-434. doi: 10.11779/CJGE201403004 HE Chuan, LI Lin, ZHANG Jing, et al. Seismic damage mechanism of tunnels through fault zones[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 427-434. (in Chinese) doi: 10.11779/CJGE201403004
[2]	高波, 王峥峥, 袁松, 等. 汶川地震公路隧道震害启示[J]. 西南交通大学学报, 2009, 44(3): 336-341, 374. doi: 10.3969/j.issn.0258-2724.2009.03.005 GAO Bo, WANG Zhengzheng, YUAN Song, et al. Lessons learnt from damage of highway tunnels in Wenchuan earthquake[J]. Journal of Southwest Jiaotong University, 2009, 44(3): 336-341, 374. (in Chinese) doi: 10.3969/j.issn.0258-2724.2009.03.005
[3]	HUANG Z K, PITILAKIS K, ARGYROUDIS S, et al. Selection of optimal intensity measures for fragility assessment of circular tunnels in soft soil deposits[J]. Soil Dynamics and Earthquake Engineering, 2021, 145: 106724. doi: 10.1016/j.soildyn.2021.106724
[4]	汪振. 跨活动断裂带岩体隧道抗错断措施及其减灾效果与机理研究[D]. 北京: 北京工业大学, 2022. WANG Zhen. Study on anti-fault measures and disaster reduction effect and mechanism of rock tunnel across active fault zone[D]. Beijing: Beijing University of Technology, 2022. (in Chinese)
[5]	LI J, CHEN J B. The principle of preservation of probability and the generalized density evolution equation[J]. Structural Safety, 2008, 30(1): 65-77. doi: 10.1016/j.strusafe.2006.08.001
[6]	LI J, CHEN J B. Stochastic Dynamics of Structures[M]. Newyork: Wiley, 2009.
[7]	孔宪京, 庞锐, 徐斌, 等. 考虑堆石料软化的坝坡随机地震动力稳定分析[J]. 岩土工程学报, 2019, 41(3): 414-421. doi: 10.11779/CJGE201903002 KONG Xianjing, PANG Rui, XU Bin, et al. Stochastic seismic stability analysis of dam slopes considering softening of rockfills[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(3): 414-421. (in Chinese) doi: 10.11779/CJGE201903002
[8]	HUANG Y, XIONG M. Dynamic reliability analysis of slopes based on the probability density evolution method[J]. Soil Dynamics and Earthquake Engineering, 2017, 94: 1-6. doi: 10.1016/j.soildyn.2016.11.011
[9]	徐斌, 陈柯好, 王星亮, 等. 液化土中管道随机地震响应分析与可靠度评价研究[J]. 岩土工程学报, 2024, 46(1): 81-89. doi: 10.11779/CJGE20221096 XU Bin, CHEN Kehao, WANG Xingliang, et al. Stochastic seismic response analysis and reliability evaluation of pipelines in liquefied soil[J]. Chinese Journal of Geotechnical Engineering, 2024, 46(1): 81-89. (in Chinese) doi: 10.11779/CJGE20221096
[10]	李杰, 艾晓秋. 基于物理的随机地震动模型研究[J]. 地震工程与工程振动, 2006, 26(5): 21-26. LI Jie, AI Xiaoqiu. Study on random model of earthquake ground motion based on physical process[J]. Earthquake Engineering and Engineering Dynamics, 2006, 26(5): 21-26. (in Chinese)
[11]	PENG Y B, MEI Z, LI J. Stochastic seismic response analysis and reliability assessment of passively damped structures[J]. Journal of Vibration and Control, 2014, 20(15): 2352-2365. doi: 10.1177/1077546313486910
[12]	CHEN J B, LI J. Stochastic seismic response analysis of structures exhibiting high nonlinearity[J]. Computers & Structures, 2010, 88(7/8): 395-412.
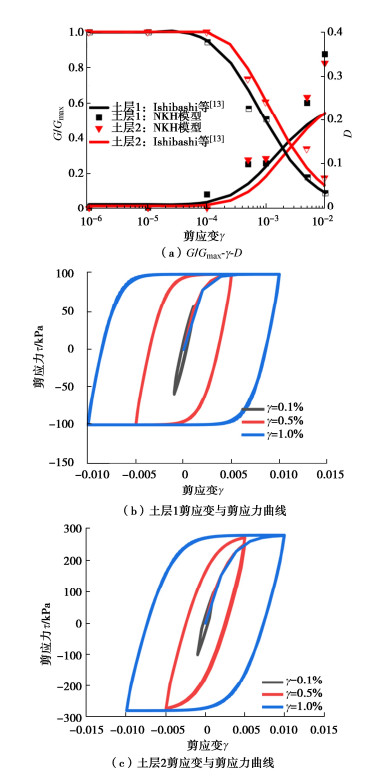
[13]	ISHIBASHI I, ZHANG X J. Unified dynamic shear moduli and damping ratios of sand and clay[J]. Soils and Foundations, 1993, 33(1): 182-191. doi: 10.3208/sandf1972.33.182
[14]	ANASTASOPOULOS I, GEORGARAKOS T, GEORGIANNOU V, et al. Seismic performance of bar-mat reinforced-soil retaining wall: Shaking table testing versus numerical analysis with modified kinematic hardening constitutive model[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 1089-1105. doi: 10.1016/j.soildyn.2010.04.020
[15]	ANASTASOPOULOS I, GELAGOTI F, KOURKOULIS R, et al. Simplified constitutive model for simulation of cyclic response of shallow foundations: validation against laboratory tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(12): 1154-1168.
[16]	HASHASH Y M A, HOOK J J, SCHMIDT B, et al. Seismic design and analysis of underground structures[J]. Tunnelling and Underground Space Technology, 2001, 16(4): 247-293.
[17]	LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media[J]. Journal of the Engineering Mechanics Division, 1969, 95(4): 859-877.
[18]	KOIZUMO A. Seismic Damages and Case Study for Shield Tunnel[M]. Beijing: China Architecture and Building Press, 2009.
[19]	王继栋. 基于pushover法地铁盾构隧道抗震弹塑性分析及性能指标研究[D]. 成都: 西南交通大学, 2016. WANG Jidong. Elasto-plastic Analysis and Performance Index Research of Subway Shield Tunnel Based on Pushover Method[D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese)