随机地震作用下隧道动力响应的概率密度演化分析

张冬梅; 郭力; 申轶尧; 黄忠凯

doi:10.11779/CJGE2024S20033

随机地震作用下隧道动力响应的概率密度演化分析 English Version

张冬梅^{1, 2,},
郭力¹,
申轶尧^1, ,,
黄忠凯¹

1.
同济大学土木工程学院, 上海 200092
2.
青海大学土木水利学院, 青海西宁 810016

基金项目:

国家重点研发计划课题 2022YFC3800905

国家自然科学基金项目 52238010

国家自然科学基金项目 52090082

国家自然科学基金项目 51408205

上海市“科技创新行动计划”优秀学术/技术带头人计划项目 22XD1430200

同济大学学科交叉联合攻关项目 2022-3-ZD-07

青海省科学技术厅基础研究计划项目 2023-ZJ-926M

详细信息

作者简介:
张冬梅(1975—)，女，博士，教授，主要从事盾构隧道安全评估方面的研究工作。E-mail: dmzhang@tongji.edu.cn

通讯作者:
申轶尧, E-mail: sshenyiyao@163.com

中图分类号: TU435;TU93
计量
- 文章访问数: 92
- HTML全文浏览量: 11
- PDF下载量: 21
出版历程
- 收稿日期: 2024-06-20
- 刊出日期: 2024-09-30

Probabilistic density evolution analysis of dynamic response of tunnels under stochastic earthquakes

1.
College of Civil Engineering, Tongji University, Shanghai 200092, China
2.
College of Civil Engineering and Water Resoures, Qinghai University, Xining 810016, China

摘要

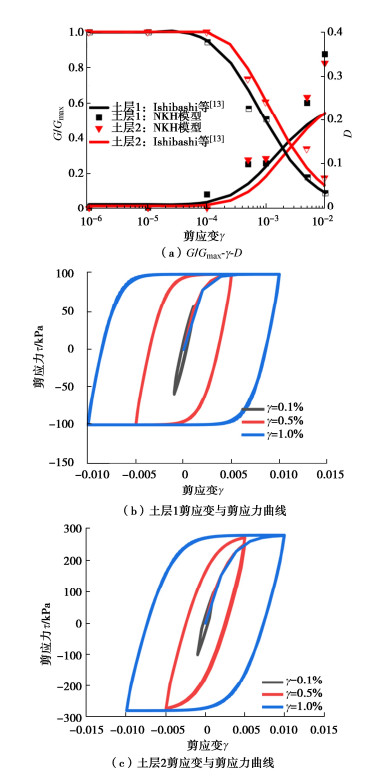
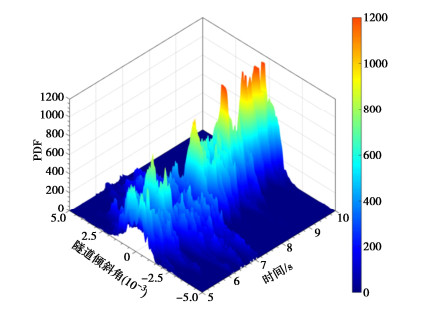
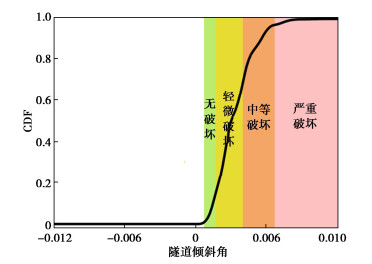
摘要: 由于地震动的随机性特征，确定性方法难以完全考虑地震动复杂随机性特点，采用随机分析方法研究隧道结构的地震响应对地下结构抗震设计具有重要的现实意义。以软土场地中圆形隧道结构为研究对象，建立典型工程场地下土体-隧道整体非线性动力相互作用分析模型，利用随机地震动模型生成符合抗震设计规范要求的非平稳地震动，将概率密度演化分析方法引入到隧道结构抗震分析中，初步探讨了隧道结构抗震性能概率密度演化特征，并以隧道倾斜角为抗震性能指标，利用概率密度演化方法求解隧道结构响应的概率密度函数，得到隧道在无破坏、轻微破坏、中等破坏和严重破坏时隧道倾斜角的超越概率。研究结果表明：隧道倾斜角在四种破坏状态下的超越概率分别为98.88%，86.10%，30.90%和3.70%；提出的概率密度演化方法可以准确获取隧道倾斜角瞬时概率信息，为研究隧道结构抗震性能的概率演化特征提供了新的思路和途径。
- 隧道结构 /
- 概率密度演化方法 /
- 随机地震 /
- 动力响应 /
- 超越概率
Abstract: Due to the stochastic characteristics of ground motion, it is difficult for the deterministic method to completely consider the complex stochastic characteristics of ground motion. It is of great practical significance to study the seismic response of tunnel structures by using the stochastic analysis method for the seismic design of underground structures. In this study, the research object is a typical circular tunnel structure in soft soils. First, a nonlinear interaction analysis model for the underground soil tunnel in a typical project site is established. Then, a random seismic model is used to generate a non-stationary seism that matches the requirements of the seismic design code. A probability density evolution analysis method is introduced into the seismic analysis of the tunnel structure, which initially explores the evolution characteristics of the probability density of its seismic performance. Using the tunnel inclination angle as the seismic performance index, the probability density function of the tunnel structural response is solved by using the probability density evolution method, and the exceedance probabilities of the tunnel inclination angle are obtained when the tunnel has no damage, slight damage, moderate damage and severe damage. The results show that the exceedance probabilities of the tunnel inclination angle in the four damage states are 98.88%, 86.10%, 30.90% and 3.70%, respectively. The proposed probability density evolution method can accurately obtain the instantaneous probability information of the tunnel inclination angle, and provide a new prospect for the study on the probability evolution characteristics of seismic performance of the tunnel structures.
- tunnel structure /
- probability density evolution method /
- stochastic earthquake /
- dynamic response /
- exceedance probability

HTML全文

0. 引言

随着中国软土地区城市地下空间工程的大规模建设，基坑工程朝着更大、更深、更复杂的趋势发展。基坑开挖卸荷作用会打破土体原有平衡状态，引起基坑周边土体应力重分布，进而导致地层产生位移和变形，最终对邻近既有建筑产生不利影响^[1-2]。而软土由于物理力学特性差和结构性强等特点，受扰动后极易发生性能劣化，产生较大应力变化和变形^[3]。因此，预测基坑开挖引起地表位移对确保既有建筑物的风险预警具有重要意义。

学者们对基坑开挖引起地表位移预测开展了深入研究，研究方法主要包括数值模拟^[4]、解析解法^[5]等。这些方法在一定程度上反映了土体本构关系和基坑开挖与土体之间的力学响应，但存在本构关系确定困难、计算成本高、推导过程复杂和效率较低等缺点。机器学习作为一种高效的代理模型，成为基坑开挖引起地表位移的一种高效方法^[6]。赵华菁等^[7]基于实测数据，对比反向传播算法BP和长短期记忆神经网络LSTM预测结果，得出LSTM模型具有较好的稳定性。张生杰等^[8]基于LSTM模型对地下连续墙的变形预测，并与传统神经网络模型相比，证明了该模型的稳定性和可靠性。徐长节等^[9]通过支持向量机SVM、多层感知器模型ANN、长短期记忆模型LSTM模型及门循环单元模型GRU模型对支护结构最大侧移预测，得出GRU模型总体预测效果最好。单一神经网络预测模型有较好的准确性和可靠性，但受限于数据特征提取能力，并不能很好的处理非线性和非平稳序列^[10]。

综上所述，本文结合CNN模型和单一时序神经网络LSTM模型、GRU模型，建立混合神经网络CNN-LSTM模型、CNN-GRU模型。基于基坑开挖引起邻近地表位移实测数据，对比单一时序神经网络LSTM模型、GRU模型和混合时序神经网络CNN-LSTM模型、CNN-GRU模型的预测精度，并将混合时序神经网络CNN-LSTM模型、CNN-GRU模型的优化效果进行比较，为基坑开挖引起邻近地表位移预测提供参考。

1. 时序预测模型建立

1.1 卷积神经网络CNN模型

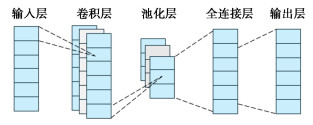
卷积神经网络CNN模型具有局部连接和权值共享特性，可高效实现输入特征的提取。其结构特征可分为输入层、卷积层、池化层、全连接层和输出层，如图 1所示。其中，卷积层通过卷积运算对数据特征提取，池化层通过去除数据进行特征降维，最后通过全连接层特征加权，提高数据特征质量。

图 1 CNN神经网络

Figure 1. CNN neural network

下载: 全尺寸图片幻灯片

1.2 长短期记忆神经网络LSTM模型

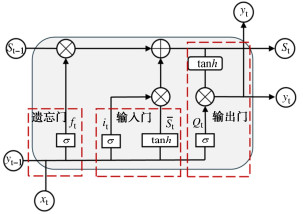
长短期记忆神经网络LSTM模型具有长效记忆能力和在必要时更新信息的特性，实现考虑时序性输入参数。其结构特征可分为遗忘门、输入门和传输门，如图 2所示。其中，输入门通过激活函数，决定输入信息，遗忘门选择信息保留，输出门控制信息输出，通过反向传播算法进行训练，以此适应数据特征。LSTM模型中参数计算公式为

${f_t} = \sigma \left( {{{\boldsymbol{W}}_{\mathrm{f}x}}{x_t} + {{\boldsymbol{W}}_{\mathrm{f}h}}{y_{t - 1}} + {b_\mathrm{f}}} \right) \text{，}$

(1)

${i_t} = \sigma \left( {{{\boldsymbol{W}}_{ix}}{x_t} + {{\boldsymbol{W}}_{ih}}{y_{t - 1}} + {b_i}} \right) \text{，}$

(2)

$\tilde{S}_t=\tanh \left(\boldsymbol{W}_{\mathrm{c}x} x_t+\boldsymbol{W}_{\mathrm{c}h} y_{t-1}+b_{\mathrm{c}}\right),$

(3)

${S_t} = {f_t} \otimes {S_{t - 1}} + {i_i} \otimes {S_t} \text{，}$

(4)

${O_t} = \sigma \left( {{{\boldsymbol{W}}_{\mathrm{o}x}}{x_t} + {{\boldsymbol{W}}_{\mathrm{o}h}}{h_{t - 1}} + {b_\mathrm{o}}} \right) \text{，}$

(5)

${h_t} = {O_t} \otimes \tanh {S_t} 。$

(6)

图 2 LSTM单元结构图

Figure 2. Structure of LSTM cell

下载: 全尺寸图片幻灯片

式中：x_t为输入特征；S_t，S_t-1为记忆单元中的状态向量；W为输出门的权重；b为输入门的偏置项；σ与tanh为激活函数； $\otimes$ 为矩阵元素相乘。

1.3 门控循环单元GRU模型

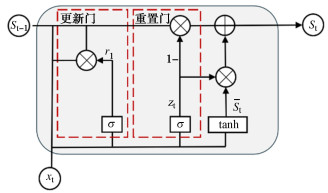
门控循环单元GRU模型是LSTM模型的改进模型，实现少于LSTM模型输入参数，取得与LSTM模型相同效果。其结构特征可分为更新门和重置门，如图 3所示。其中，更新门控制保留多少前一时刻状态信息到当前状态程度。重置门控制当前状态与先前信息结合程度。GRU模型中各参数的计算公式为

${z_t} = \sigma \left( {{{\boldsymbol{W}}_z} \cdot \left[ {{s_{t - 1}},{x_t}} \right]} \right) \text{，}$

(7)

${r_1} = \sigma \left( {{{\boldsymbol{W}}_r} \cdot \left[ {{s_{t - 1}},{x_t}} \right]} \right) \text{，}$

(8)

$\tilde{S}_t=\tanh \left(\boldsymbol{W} \cdot\left[s_{t-1} \cdot r_1, x_t\right]\right) \quad,$

(9)

$s_t=\left(1-z_t\right) s_{t-1}+z_t \tilde{S}_t 。$

(10)

图 3 GRU模型结构

Figure 3. Structure of GRU model

下载: 全尺寸图片幻灯片

1.4 混合时序神经网络CNN-LSTM模型和CNN- GRU模型

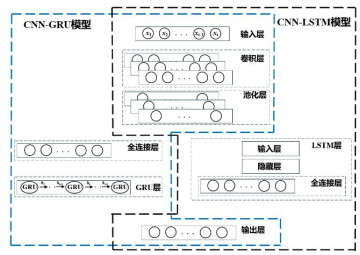
混合时序神经网络CNN-LSTM模型是基于CNN模型的空间特征提取能力，将数据进行多次重复卷积和池化后，有效提取强化后的特征信息，通过LSTM模型中门的控制机制，对CNN模型提取的特征值进行长短期记忆训练。混合时序神经网络模型CNN-GRU模型是在CNN模型提取特征信息基础上，引入GRU模型中重置门和更新门，捕捉数据中的时序关系，实现对未来数据的预测，其结构特征如图 4所示。

图 4 CNN-LSTM和CNN-GRU结构

Figure 4. Structure of CNN-LSTM and CNN-GRU

下载: 全尺寸图片幻灯片

2. 地表位移预测框架搭建

2.1 工程概况

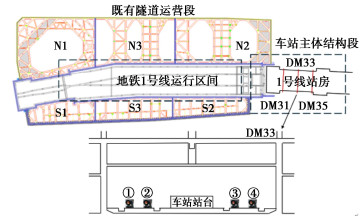
本文选取杭州某邻近既有车站基坑开挖工程为依托。基坑开挖工程平面尺寸约为210 m×85 m，深度约为15 m。南、北基坑工程的正中间是地铁1号线从打铁关站至西湖文化站隧道运营段，地铁1号线车站主体结构紧邻基坑东侧，在车站主体结构中设有多个监测断面，站台两侧各设置两组监测棱镜，如图 5所示。

图 5 杭州某邻近既有隧道基坑开挖工程概况

Figure 5. Overview of project adjacent to excavation of existing tunnel in Hangzhou

下载: 全尺寸图片幻灯片

2.2 数据集建立

通过棱镜采集DM33断面中车站主体结构段地表位移数据，共计186组。为提高模型收敛速度，对数据集进行如下归一化处理：

$x^*=\frac{x-x_{\min }}{x_{\max }-x_{\min }} 。$

(11)

式中： ${x^*}$ 为归一化后数据；x为归一化前数据；x_max为样本最大值；x_min为样本最小值。

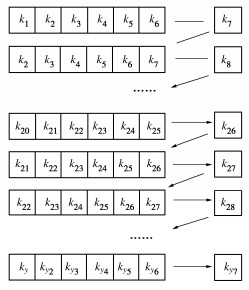
将归一化后的数据集采用滚动预测方法，得到180组数据，滚动预测方法具体步骤如下：

（1）设置滚动窗口为7，输入层神经元数量为6，输出层为神经元数量为1。

（2）进行地表位移滚动预测，将k_y-k_y+6时刻实测数据作为k_y+7时刻的数据的输入特征，k_y+7时刻数据为输出层。

（3）重复上述步骤，进行滚动迭代，最终建立所有时刻的地表位移数据集，如图 6所示。

图 6 滚动预测法

Figure 6. Rolling forecasting method

下载: 全尺寸图片幻灯片

2.3 预测模型结构设计

将数据集以8︰1︰1比例分为训练集、验证集和测试集，分别输入到单一时序神经网络预测模型LSTM模型、GRU模型和混合时序神经网络预测模型CNN-GRU模型、CNN-LSTM模型中进行预测。

单一神经网络主要取决于神经元数目与层数对预测模型结果的影响。GRU模型网络模块：初始参数设置为1层GRU，神经元数目为32，随机失活系数为0.01。LSTM网络模块：设置为1层LSTM，神经元数目为32，随机失活系数为0.01。

混合神经网络中主要设置CNN模型卷积层数和时序预测中神经元目数对预测模型结果的影响^[11]。混合时序神经网络预测模块初始设置如下：CNN模型特征提取模块为一层Conv1 D层，卷积核数为16，大小为2；LSTM模型模块：神经元目数为32，随机失活系数为0.01。GRU模型模块，神经元数目为32，随机失活系数为0.01。

2.4 模型预测精度

为检验模型预测精度，通过平均绝对误差MAE、平均相对误差MAPE和均方根误差RMSE对模型预测结果进行评价，计算公式为

$\text{RMSE} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} } \text{，}$

(12)

$\text{MAPE} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|} \text{，}$

(13)

$\text{MAE} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{{\hat y}_i} - {y_i}} \right|} 。$

(14)

式中：N为样本个数； ${\hat y_i}$ 为输出预测值； ${y_i}$ 为真实值。

3. 模型预测结果

3.1 模型预测结果分析

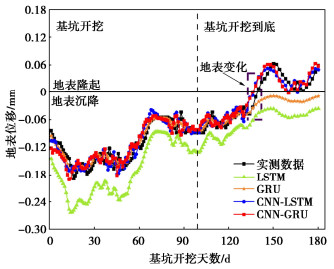
以180组实测地表位移数据为基础，分别通过LSTM模型、GRU模型、CNN-LSTM模型和CNN-GRU模型对数据集进行训练预测，4种模型预测结果如图 7所示。

图 7 地表位移预测值对比

Figure 7. Comparison of predicted surface displacements

下载: 全尺寸图片幻灯片

由图 7可知，4种模型预测结果均能捕捉到地表位移实测数据的变化趋势。对于单一神经网络模型，LSTM模型和GRU模型均未能预测到地表由沉降到隆起的变化，且LSTM模型整体拟合度较差，这可能是预测误差随着时间序列长度增加而累积，引起LSTM模型预测值明显偏离实测值^[12]。此外，地表由沉降到隆起的过程存在复杂的非线性关系，LSTM模型和GRU模型虽然能够处理非线性问题，但是在小样本数据情况下仍可能无法准确地捕捉到复杂的非线性变化，忽略了由沉降变为隆起的相关性特征。对于混合神经网络模型，CNN-LSTM模型和CNN-GRU模型预测效果均优于单一神经网络模型，且对于地表由沉降到隆起的变化也有较好的预测效果。这可能是在CNN模型数据空间特征提取作用下，LSTM模型^[13]和GRU模型能够更好地捕捉数据中的空间特征和序列依赖关系。

3.2 预测精度及优化效果

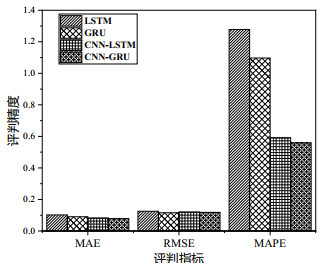
图 8是4种模型预测结果的平均绝对误差MAE、平均相对误差MAPE和均方根误差RMSE对比。从图 8中可以看出，对于平均绝对误差MAE，4种模型预测结果均在0.1以下，即4种模型预测偏差较小。对于均方根误差RMSE，4种模型预测结果均处于0.1左右，即4种模型均有较好的拟合能力。对于平均相对误差MAPE，CNN-GRU最小，其次是CNN-LSTM模型，然后是GRU模型，最后是LSTM模型，即CNN-GRU模型具有最优的预测准确性。表 1是单一时序神经网络预测模型和混合时序神经网络预测模型预测精度对比。由表 1可知，相较于单一时序神经网络预测模型LSTM模型和GRU模型，混合时序神经网络预测模型CNN-LSTM模型和CNN-GRU模型具有较好优化效果。对于平均绝对误差MAE、平均相对误差MAPE和均方根误差RMSE，CNN-LSTM模型较LSTM模型分别降低了24.4%，53.8%，4.1%，CNN-GRU模型较GRU模型分别降低了13.9%，49.1%，1%。由此可见，特征提取后的LSTM模型和GRU模型均表现出较好的预测效果。

图 8 地表位移预测精度对比

Figure 8. Comparison of prediction accuracies of surface displacement

下载: 全尺寸图片幻灯片

表 1 预测模型评价指标

Table 1. Evaluation indexes of prediction models

评判指标	LSTM	CNN-LSTM	优化效果/%	GRU	CNN-GRU	优化效果/%
MAE	0.1019	0.0819	24.4	0.0902	0.0782	13.9
MAPE	1.2779	0.5909	53.8	1.0970	0.5581	49.1
RMSE	0.1251	0.1199	4.1	0.1185	0.1174	1.0

下载: 导出CSV

| 显示表格

4. 结论

以杭州某邻近既有车站基坑开挖工程为研究对象，分别建立LSTM模型、GRU模型、、CNN-LSTM模型以及CNN-GRU模型预测邻近基坑开挖引起地表位移实测数据，分析模型预测效果和预测精度。得到2点结论。

（1）模型预测效果中CNN-GRU模型预测效果最优，CNN-LSTM模型次之，其次是GRU模型，最后是LSTM模型。在CNN模型的数据空间特征提取作用下，LSTM模型和GRU模型能够更好地捕捉数据中的空间特征和序列依赖关系。

（2）CNN-LSTM模型和CNN-GRU模型相较于LSTM模型和GRU模型有较好的优化效果，对于平均绝对误差MAE、平均相对误差MAPE和均方根误差RMSE，CNN-LSTM模型较LSTM模型分别降低了24.4%，53.8%，4.1%，CNN-GRU模型较GRU模型分别降低了13.9%，49.1%和1%。

图 1 土层剪切模量与阻尼比曲线

Figure 1. Curves of shear modulus and damping ratio of soils

下载: 全尺寸图片幻灯片

图 2 土体非线性本构模型参数标定

Figure 2. Parameter correction for nonlinear constitutive model of soils

下载: 全尺寸图片幻灯片

图 3 典型时段内的隧道倾斜角概率密度曲面

Figure 3. Probability density surface of tunnel inclination angle in a typical time interval

下载: 全尺寸图片幻灯片

图 4 累计分布函数曲线

Figure 4. Curve of cumulative distribution function

下载: 全尺寸图片幻灯片

表 1 土层剖面参数表

Table 1 Parameters of soil strata

土层	埋深/m	剪切波速 ${v_{\text{s}}}$ /(m·s^-1)	剪切强度S_u/kPa	密度/(kg·m^-3)	泊松比
^#1	0~10	250	100	1800	0.30
^#2	10~25	300	280	1800	0.30
^#3	25~35	400	400	1900	0.30
^#4	35~70	600	500	1900	0.30

下载: 导出CSV

参考文献(19)

[1]	何川, 李林, 张景, 等. 隧道穿越断层破碎带震害机理研究[J]. 岩土工程学报, 2014, 36(3): 427-434. doi: 10.11779/CJGE201403004 HE Chuan, LI Lin, ZHANG Jing, et al. Seismic damage mechanism of tunnels through fault zones[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 427-434. (in Chinese) doi: 10.11779/CJGE201403004
[2]	高波, 王峥峥, 袁松, 等. 汶川地震公路隧道震害启示[J]. 西南交通大学学报, 2009, 44(3): 336-341, 374. doi: 10.3969/j.issn.0258-2724.2009.03.005 GAO Bo, WANG Zhengzheng, YUAN Song, et al. Lessons learnt from damage of highway tunnels in Wenchuan earthquake[J]. Journal of Southwest Jiaotong University, 2009, 44(3): 336-341, 374. (in Chinese) doi: 10.3969/j.issn.0258-2724.2009.03.005
[3]	HUANG Z K, PITILAKIS K, ARGYROUDIS S, et al. Selection of optimal intensity measures for fragility assessment of circular tunnels in soft soil deposits[J]. Soil Dynamics and Earthquake Engineering, 2021, 145: 106724. doi: 10.1016/j.soildyn.2021.106724
[4]	汪振. 跨活动断裂带岩体隧道抗错断措施及其减灾效果与机理研究[D]. 北京: 北京工业大学, 2022. WANG Zhen. Study on anti-fault measures and disaster reduction effect and mechanism of rock tunnel across active fault zone[D]. Beijing: Beijing University of Technology, 2022. (in Chinese)
[5]	LI J, CHEN J B. The principle of preservation of probability and the generalized density evolution equation[J]. Structural Safety, 2008, 30(1): 65-77. doi: 10.1016/j.strusafe.2006.08.001
[6]	LI J, CHEN J B. Stochastic Dynamics of Structures[M]. Newyork: Wiley, 2009.
[7]	孔宪京, 庞锐, 徐斌, 等. 考虑堆石料软化的坝坡随机地震动力稳定分析[J]. 岩土工程学报, 2019, 41(3): 414-421. doi: 10.11779/CJGE201903002 KONG Xianjing, PANG Rui, XU Bin, et al. Stochastic seismic stability analysis of dam slopes considering softening of rockfills[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(3): 414-421. (in Chinese) doi: 10.11779/CJGE201903002
[8]	HUANG Y, XIONG M. Dynamic reliability analysis of slopes based on the probability density evolution method[J]. Soil Dynamics and Earthquake Engineering, 2017, 94: 1-6. doi: 10.1016/j.soildyn.2016.11.011
[9]	徐斌, 陈柯好, 王星亮, 等. 液化土中管道随机地震响应分析与可靠度评价研究[J]. 岩土工程学报, 2024, 46(1): 81-89. doi: 10.11779/CJGE20221096 XU Bin, CHEN Kehao, WANG Xingliang, et al. Stochastic seismic response analysis and reliability evaluation of pipelines in liquefied soil[J]. Chinese Journal of Geotechnical Engineering, 2024, 46(1): 81-89. (in Chinese) doi: 10.11779/CJGE20221096
[10]	李杰, 艾晓秋. 基于物理的随机地震动模型研究[J]. 地震工程与工程振动, 2006, 26(5): 21-26. LI Jie, AI Xiaoqiu. Study on random model of earthquake ground motion based on physical process[J]. Earthquake Engineering and Engineering Dynamics, 2006, 26(5): 21-26. (in Chinese)
[11]	PENG Y B, MEI Z, LI J. Stochastic seismic response analysis and reliability assessment of passively damped structures[J]. Journal of Vibration and Control, 2014, 20(15): 2352-2365. doi: 10.1177/1077546313486910
[12]	CHEN J B, LI J. Stochastic seismic response analysis of structures exhibiting high nonlinearity[J]. Computers & Structures, 2010, 88(7/8): 395-412.
[13]	ISHIBASHI I, ZHANG X J. Unified dynamic shear moduli and damping ratios of sand and clay[J]. Soils and Foundations, 1993, 33(1): 182-191. doi: 10.3208/sandf1972.33.182
[14]	ANASTASOPOULOS I, GEORGARAKOS T, GEORGIANNOU V, et al. Seismic performance of bar-mat reinforced-soil retaining wall: Shaking table testing versus numerical analysis with modified kinematic hardening constitutive model[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 1089-1105. doi: 10.1016/j.soildyn.2010.04.020
[15]	ANASTASOPOULOS I, GELAGOTI F, KOURKOULIS R, et al. Simplified constitutive model for simulation of cyclic response of shallow foundations: validation against laboratory tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(12): 1154-1168.
[16]	HASHASH Y M A, HOOK J J, SCHMIDT B, et al. Seismic design and analysis of underground structures[J]. Tunnelling and Underground Space Technology, 2001, 16(4): 247-293.
[17]	LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media[J]. Journal of the Engineering Mechanics Division, 1969, 95(4): 859-877.
[18]	KOIZUMO A. Seismic Damages and Case Study for Shield Tunnel[M]. Beijing: China Architecture and Building Press, 2009.
[19]	王继栋. 基于pushover法地铁盾构隧道抗震弹塑性分析及性能指标研究[D]. 成都: 西南交通大学, 2016. WANG Jidong. Elasto-plastic Analysis and Performance Index Research of Subway Shield Tunnel Based on Pushover Method[D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese)