Centrifugal model tests and numerical simulations of dragging motion state of Hall anchor
-
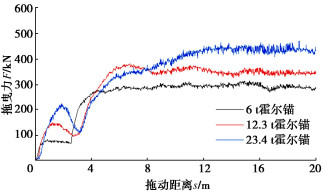
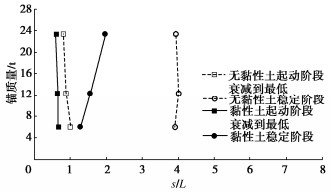
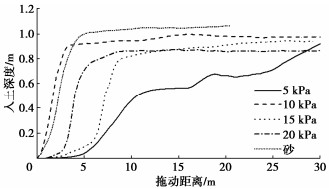
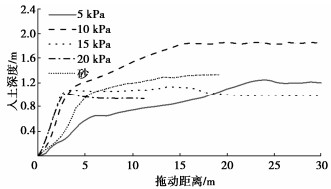
摘要: 对于平铺或浅埋在海床中的海底管道和电缆，意外的拖锚作业是影响其安全运营的重要因素之一。由于锚在土中的拖动过程中时刻发生着土的大变形和破坏，涉及材料非线性、几何非线性及接触非线性等诸多力学问题，通过解析的研究手段很难准确地分析拖锚过程。采用离心模型试验和数值分析相结合的手段展开拖锚研究，测试和计算了不同重量的船锚在不同类型海床上的运动趋势、拖曳力发展规律、入土深度等。结果表明，在低强度的黏性土海床上拖锚，极有可能会产生一种假抓底现象；在中高强度的黏性土海床上拖锚，锚的拖动过程可以分为土台形成阶段、锚爪楔入阶段和运动稳定阶段三个阶段；在无黏性土和黏性土海床上，达到稳定阶段时拖动的距离分别是锚长的4倍和1.27~1.96倍；对于质量大于6 t的霍尔锚，无论在黏性土海床还是非黏性土海床上，锚爪的入土深度均大于1 m，拖锚作业很有可能会对海管或海缆造成直接损坏，需要引起重视。Abstract: For the submarine pipelines and cables laid flat or shallowly buried in the seabed, the accidental anchor dragging operation is one of the important factors affecting their safe operation. Due to the large deformation and failure of soil during the dragging process of the anchor in the soil, it involves many mechanical problems such as material nonlinearity, geometric nonlinearity and contact nonlinearity. It is difficult to accurately analyze the dragging process through the analytical research methods. In this paper, the centrifugal model tests and numerical analysis are used to study the dragging anchor. The motion trend, the development law of drag force and the penetration depth of anchors with different weights on different types of seabed are tested and calculated. The results show that the dragging anchor in low-strength cohesive soil is likely to produce a false bottom grabbing phenomenon. For the anchors are dragged on the medium- and high-strength cohesive soil seabed, the dragging process of the anchors can be divided into three stages: soil platform formation, anchor claw wedge and motion stability. On the non-cohesive soil and cohesive soil seabeds, the drag distance at the stability stage is 4 and 1.27 ~ 1.96 times the anchor length, respectively. For the Hall anchor with the weight greater than 6 t, whether on the cohesive soil seabed or the non-cohesive soil seabed, the penetration depth of the anchor claw is greater than 1 m, and the dragging operation is likely to cause direct damage to the submarine pipelines or cables, which needs attention.
-
0. 引言
钙质砂是一种分布于热带海洋的特殊岩土介质，由于其成因和组构上的特殊性导致其工程力学性质与普通的陆源砂有明显区别。目前国内外针对钙质砂地基应力变化及破坏模式等研究很少，其工程特征及地基性能尚无明确统一的说法，这给基础设施的设计、施工建设带来很大的困难，因此需要研究钙质砂类岩土的应力特性和承载机理。
钙质砂的应力特性，国内外已作了一些研究。文哲等[1]采用中国南沙某岛礁吹填珊瑚钙质砂，在级配和组分分析的基础上，研究不同密实度、含水率条件下轴向荷载钙质砂的剪切力学特性。王刚等[2]进行钙质砂不破碎三轴剪切过程的数值试验，以确定临界状态与固定级配的对应关系。相盈盈[3]采用三轴固结不排水剪切试验，对南海海区岛礁饱和钙质砂进行剪切特性分析。张季如等[4]为了研究不同应力路径对钙质砂的颗粒破碎和力学性质的影响，对不同固结压力的钙质砂进行了5种应力路径下的排水三轴压缩试验。Lade等[5]针对珊瑚砂的时间变量开展了三轴压缩试验，提出了应力下降原因。Yamamuro等[6]开展了钙质砂三轴排水试验，考虑了不同的围压状态和相对密实度，抗剪强度与轴向应变的变化规律。其他学者[7-9]对钙质砂的工程承载特性进行了部分研究。
由以上研究可以发现，针对钙质珊瑚砂的力学工程特性性质已经已有一定基础，与其他砂类试验对比分析，结果显示钙质砂是一种天然特殊砂，钙质砂在高压条件下发生颗粒破碎，其破碎性质也会引起钙质砂的力学性质发生改变，其性质与普通砂存在很大差异，工程中不能使用普通砂的成果分析。目前有关三轴试验剪切速率的影响因素相关研究较少，本文在不同围压下采用不同剪切速率对高低围压下钙质砂进行三轴固结排水试验，分析围压、剪切速率对钙质砂应力影响分析。
1. 三轴排水剪切试验
1.1 试验材料
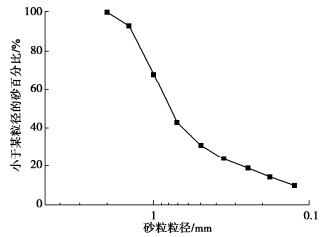
试验采用的试样取自中国海南省三沙市西沙群岛，试样中存在大块的砂砾和尖锐的贝壳，见图 1，为避免戳破橡胶膜影响试验，对原试样进行烘干、筛分、按一定比例进行配比后使用见图 2，试验筛除大于2 mm颗粒的钙质砂，将钙质砂分为9个粒径范围，不同粒径含量见表 1。颗粒级配见图 3，试验用钙质砂基本物理参数见表 2。
表 1 试样粒径范围Table 1. Grain-size ranges of sample粒径/mm 1.45~2 1~1.45 0.71~1 0.5~0.71 0.355~0.5 百分比/% 7 25 25 12 7 粒径/mm 0.25~0.355 0.18~0.25 0.125~0.18 0.075~0.125 百分比/% 5 4.5 4.5 10 表 2 试样基本物理参数Table 2. Basic physical parameters of sampleGS emax emin D60/mm D30/mm D10/mm 2.80 0.58 1.07 0.9 0.49 0.125 1.2 试验仪器
试验采用英国GDS公司生产的自动三轴试验系统GDSTAS完成（图 4）。应变控制速率从0.00001~9.99999 mm/min。压力室最大承受压力为3.5 MPa，2 MPa孔隙水压力传感器精度为全量程的0.15%，内置水下荷重传感器精度为全量程的0.1%。3 MPa/ 200 mm3标准围压/体积控制器（围压控制），具有自动压力和体积溢出保护，测量精度为量测值的0.25%，压力精度为全量程的0.1%，体积变化测量和显示分辨率为1 mm3。3 MPa/200 mm3标准反压/体积控制器（反压控制），具有自动压力和体积溢出保护，测量精度为量测值的0.25%，压力精度为全量程的0.1%，体积变化测量和显示分辨率为1 mm3。
1.3 试验方案
试验方案如表 3所示。试验为三轴固结排水试验，试样相对密实度为70%，有效围压为300，600 kPa。剪切应变速率分别为0.15%，0.035%，0.0045%/min，研究钙质砂在不同围压、不同剪切速率下的应力变化特性。试样直径为50 mm，高度100 mm。
表 3 试验方案Table 3. Test schemes相对密实度Dr 有效围压/kPa 剪切应变速率/(%·min-1) 0.70 300，600 0.0045，0.035，0.15 试验采用干法制样，将配比好的试样按一定质量分层装入模具，因钙质砂的特性导致内部空隙较多，试验中利用CO2、水头饱和、反压饱和相结合的方法对试样进行饱和，提高试样的饱和度。首先从试样底部缓慢通入CO2，从试样顶部排出，通气时间为2 h，此过程置换试样内部的空气。然后水头饱和，从试样底部缓慢进水，从试样顶部排水，控制水流速度，时间为2 h，此过程置换试样中的CO2。最后进行反压分级饱和，并监测试样饱和度，直到饱和度大于95%。接下来进行试样固结，实时监测孔隙水压力变化，直到孔隙水压力消散，有效围压达到预定值。按照设定的剪切速率进行三轴排水试验，轴向位移达到20%试验停止。
2. 结果分析
2.1 围压与剪切速率对偏应力影响
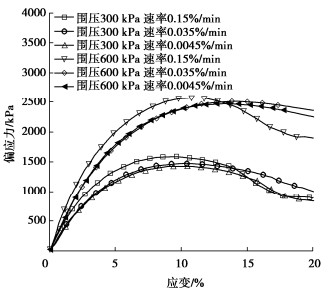
不同围压下各剪切速率的偏应力应变曲线，见图 5。偏应力曲线趋势相同，剪切初期偏应力上升较快，当应变超过5%时偏应力增长变缓，低围压下应变达到10%左右时偏应力出现峰值，高围压下应变达到12%左右时偏应力出现峰值，随后偏应力开始下降，高围压偏应力峰值出现的较晚。
不同围压下剪切速率对峰值的影响规律相同，偏应力峰值随剪切速率的增大而增大，剪切速率越快应力峰值越大，应力下降也越快应力下降比越大，可见剪切速率对应力的峰值大小及残余剪切强度有一定影响。低围压下不同剪切速率最大偏应力峰值差比为11%，且在低围压约束力下剪切速率减小时试样颗粒发生重组后再剪切，因此速率0.035%，0.0045%/min的偏应力峰值软化后又会出现硬化趋势；高围压下不同剪切速率最大偏应力峰值差比为4%，可见低围压下剪切速率对偏应力峰值影响更大。这与福建标准砂的性质不同，周杰[10]对不同应力下福建标准砂进行5种剪切速率试验，表明在低应力下砂的抗剪强度与剪切速率基本无关，高围压下，砂的抗剪强度随剪切速度增大而减小。
2.2 围压与剪切速率对偏应力比影响
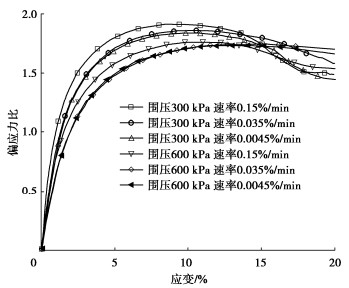
不同围压下各剪切速率的偏应力比曲线，见图 6。偏应力比曲线趋势相同先增大后减小趋于稳定。围压越小偏应力比上升越快、偏应力比越大，可见低围压下的剪切效果更明显，偏应力和峰值的变化情况相对于平均有效应力的变化更大，因为围压越低对颗粒束缚较小，钙质砂的越容易发生错动导致偏应力上升。应力应变分析中低围压下剪切速率越小时偏应力出现峰值然后减小有又硬化的趋势，因此在低围压下剪切速率越小偏应力比峰值后减小有又上升趋势。
相同围压下剪切速率越大，偏应力增长越快、偏应力比越大，剪切时砂粒之间重组排列，高剪切速度使得砂粒之间迅速咬合偏应力快速上升导致试样破坏，钙质砂的结构特征使得对剪切速率更加敏感。但是相对于0.15%/min的剪切速度，0.035%/min和0.0045%/min的速度偏应力比的变化几乎相同，可见当剪切速率低于一定速率时，偏应力比的变化并不受剪切速度的影响。
2.3 围压与剪切速率对应力路径影响
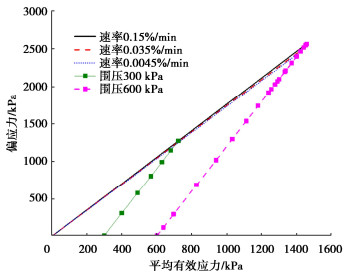
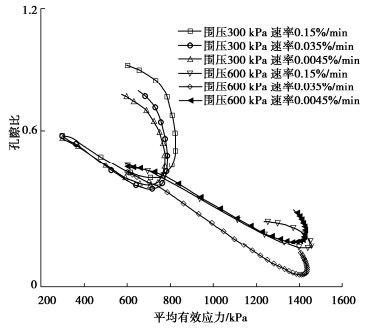
固结排水试验的偏应力-平均有效应力曲线，见图 7。不同围压条件下，偏应力-平均有效应力关系曲线都是斜率为3的直线，是因为剪切时排水条件使得孔压保持稳定值不变，且围压为一定值，根据平均有效应力为p′=[2(σ3−μ)+(σ1−μ)]/3，σ3为围压，σ1为轴向应力，μ为孔隙水压力，经计算相邻点有效应力变化为p′=（σ11−σ12）/3，即为轴向应力差除以3，相邻点偏应力为q′=σ11−σ12，即为轴向应力差，所以曲线斜率为q′/p′=3。
不同剪切速率下的破坏线q′=Mp′趋势相同，由应力应变分析可以看出偏应力峰值随剪切速率的增大而增大，破坏线是关系偏应力峰值与圆点的连线，可见剪切速率越大破坏线角度越大，三条线的M值近似为1.75，由公式φ=arcsin（3M/(6+M)）=42°，钙质砂的内摩擦角近似为42°。这由钙质砂的结构特性决定，钙质砂形状不规则且尖锐，颗粒之间咬合错动，剪切破坏角较大，内摩擦角较大。
2.4 围压与剪切速率对孔隙比影响
不同围压及剪切速率条件下，孔隙比-平均有效应力关系曲线，见图 8。偏应力峰值以前平均有效应力逐渐增大，偏应力峰值以后平均有效应力逐渐变小，且偏应力峰值以前不同围压下孔隙比相对于平均有效应力的下降速率相近呈线性变化，可见孔隙比与平均有效应力的变化趋势在剪切初始阶段不受剪切速率的变化影响。偏应力峰值以后孔隙比相对于平均有效应力变化呈曲线增大状态。
剪切过程中试样体积先减小后增大，孔隙比表现为先减小后增大，拐点发生在偏应力峰值的前后，剪切过程表现为密砂的特征。不同围压孔隙比下降速率相近，低围压剪缩阶段剪切速率对孔隙比的影响不明显，剪缩阶段颗粒之间位置调整砂粒发生相互错动重新排列压实，试样体积减小，孔隙比减小。剪胀阶段剪切速率对孔隙比的影响较大，剪切速率越大，孔隙比增大越快，随着剪切阶段颗粒间的作用力逐渐小于颗粒的抗剪强度试样破坏，尖利不规则的砂粒重新组合排列试样体积增大，孔隙比增大。
3. 结论
本文开展了钙质砂三轴排水剪切试验速率对应力特性影响研究，分析不同围压、不同剪切速率状态下钙质砂剪切过程中应力的变化规律，得出以下4点结论。
（1）偏应力应变曲线趋势相同，偏应力曲线均出现峰值，高围压偏应力峰值出现比低围压偏应力峰值出现的晚。剪切速率越快，偏应力峰值越大，偏应力下降越快，剪切速率对偏应力峰值大小及残余剪切强度有一定影响，低围压下剪切速率对偏应力峰值影响更大。
（2）偏应力比应变曲线趋势相同先增大后减小趋于稳定。围压越小偏应力比上升越快，偏应力比越大，相同围压下剪切速率越大，偏应力比增长越快偏应力比越大。当剪切速率低于一定速度时，偏应力比的变化并不受剪切速度的影响。
（3）不同围压下偏应力平均有效应力的关系是斜率为3的直线，不同速率下的破坏线趋势相同，偏应力峰值随剪切速率的增大而增大，破坏线是关系偏应力峰值与圆点的连线，因此剪切速率越大破坏线角度越大，破坏线的斜率近似为1.75，钙质砂内摩擦角近似为42°。
（4）偏应力峰值以前平均有效应力逐渐增大，偏应力峰值以后平均有效应力逐渐变小，且偏应力峰值以前不同围压下孔隙比相对于平均有效应力的下降速率相近。低围压剪缩阶段剪切速率对孔隙比下降速率的影响不明显，剪胀阶段剪切速率越大，孔隙比的增长越大。
-
![]()
图 3 无黏性土海床霍尔锚入土过程
Figure 3. Process of penetration of Hall anchor in cohesive soil seabed
![]()
图 4 不同霍尔锚在不同强度海床中的开挖照片
Figure 4. Excavation photos of different Hall anchors in seabed with different strength
![]()
图 5 船锚在低强度黏性土海床的入土过程
Figure 5. Penetration process of archor in low-strength cohesive soil seabed
![]()
图 8 不同阶段锚质量与s/L对应关系
Figure 8. Corresponding relationship between anchor weight and s/L at different stages
表 1 海床土体有限元模型参数
Table 1 Parameters of finite element model for seabed soil
材料 密度/
(kg·m-3)弹性模量E 泊松比ν 内摩擦角/(°) 黏聚力/
kPa黏土 1750 500Su 0.48 0 5/10/15/20 砂 1950 8 MPa 0.3 33 0 
下载: 导出CSV
表 2 入土深度统计表
Table 2 Statistical table of penetration depth of anchors
锚质量/
t10 kPa黏性土 20 kPa黏性土 无黏性土 试验值/m 计算值/
m试验
值/m计算值/
m试验值/
m计算值/
m6 1.53 1.30 — 0.87 ＞0.70 1.06 12.3 2.18 1.86 — 1.01 ＞1.40 1.33 23.4 — 2.91 — 1.31 ＞2.10 2.02
下载: 导出CSV
-
[1] 李海学, 朱青春, 魏颂珂. 船舶锚泊作业对海底管道安全风险分析[J]. 石油工程建设, 2023, 49(5): 47-50. https://www.cnki.com.cn/Article/CJFDTOTAL-SYGJ202305005.htm LI Haixue, ZHU Qingchun, WEI Songke. Analysis of safety risk of submarine pipelines in ship anchoring operations[J]. Petroleum Engineering Construction, 2023, 49(5): 47-50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SYGJ202305005.htm
[2] 任宇晓, 闫澍旺, 闫玥, 等. 基于CEL方法对拖锚过程的数值分析[J]. 地下空间与工程学报, 2017, 13(6): 1573-1578. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201706021.htm REN Yuxiao, YAN Shuwang, YAN Yue, et al. Numerical analysis on dragging anchors in soil based on CEL[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(6): 1573-1578. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201706021.htm
[3] 闫澍旺, 任宇晓, 孙立强, 等. 砂土中的拖锚模型试验及锚抓力计算方法研究[J]. 中国造船, 2016, 57(1): 103-115. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC201601012.htm YAN Shuwang, REN Yuxiao, SUN Liqiang, et al. Model test and calculation of holding capacity of hall anchor in dragging process in sand[J]. Shipbuilding of China, 2016, 57(1): 103-115 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC201601012.htm
[4] 孙倩, 周宏, 周沛林. 应急抛锚状态下拖锚对海管的撞击损伤[J]. 集美大学学报(自然科学版), 2018, 23(4): 279-286. https://www.cnki.com.cn/Article/CJFDTOTAL-JMXZ201804006.htm SUN Qian, ZHOU Hong, ZHOU Peilin. Study on the collision damage of submarine pipelines by towing anchor under emergency anchorage[J]. Journal of Jimei University(Natural Science), 2018, 23(4): 279-286. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JMXZ201804006.htm
[5] 池寅, 时豫川, 吴海洋, 等. 砂质海床中船锚运动全过程数值模拟[J]. 武汉大学学报(工学版), 2017, 50(6): 807-814. https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD201706002.htm CHI Yin, SHI Yuchuan, WU Haiyang, et al. Numerical simulation of whole movement process of an anchor in sandy seabed[J]. Engineering Journal of Wuhan University, 2017, 50(6): 807-814. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD201706002.htm
[6] 包承纲, 饶锡保. 土工离心模型的试验原理[J]. 长江科学院院报, 1998, 15(2): 1-3, 7. https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB802.000.htm BAO Chenggang, RAO Xibao. Principle of the geotechnical centrifuge model test[J]. Journal of Yangtze River Scientific Research Institute, 1998, 15(2): 1-3, 7. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB802.000.htm
[7] 中华人民共和国船舶行业标准. 霍尔锚: GB/T 546—2016)[S]. 2016. PRC Shipbuilding Industry Standard. Hall anchor: GB/T 546—2016[S]. 2016. (in Chinese)
[8] JÁKY J. The coefficient of earth pressure at rest[J]. Journal for the Society of Hungarian Architects and Engineers, 1944, 7: 355-358.
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
