A data-driven model for predicting shear strength indexes of normally consolidated soils
-
摘要: 抗剪强度指标的准确获取对工程设计具有决定性作用,目前试验方法确定的强度指标过于依靠工程经验,导致最终的取值具有不确定性。集成学习模型是机器学习的一个子类,在处理复杂的数据和任务时表现出强大的性能。为了能更准确地获得抗剪强度指标,以正常固结土为研究对象,利用不同的集成学习算法建立其抗剪强度指标的预测模型。通过均方根误差(RMSE)、可决系数(R2)、绝对值误差(MAE)评估不同模型的泛化能力,并采用Adaboost算法进行输入参数的敏感性分析。结果表明抗剪强度采用Adaboost、内摩擦角采用RF、黏聚力采用Adaboost算法具有最佳的泛化能力,其测试集R2可分别达到0.925,0.965,0.942。敏感性分析结果显示,对抗剪强度影响最大的参数为干密度、含水率和法向应力;对内摩擦角影响最大的参数为曲率系数、黏粒含量和含水率;对黏聚力影响最大的参数为含水率、干密度和液限。本文所建立的预测模型可为工程中抗剪强度指标的选取及运用机器学习方法研究土体强度参数提供参考。Abstract: The accurate determination of shear strength indexes is crucial for engineering soils. Currently, the strength indexes determined by the test method depend too much on engineering experience, which leads to the uncertainty of the final value. The ensemble learning is a subclass of machine learning that exhibits strong performance when dealing with complex data and tasks. To enhance the precision of the shear strength indexes, based on the normally consolidated soils, a model is established using the diverse ensemble learning algorithms for predicting the shear strength indexes of soils. Various models are assessed for their generalization capability using the root mean square error (RMSE), coefficient of determination (R2) and absolute value error (MAE). The Adaboost algorithm is employed for the sensitivity analysis of input parameters. The findings indicate that the Adaboost algorithm yields the best generalization for the shear strength the RF for the internal friction angle, and the Adaboost algorithm for the cohesion, achieving respective test-set R2 values of 0.925, 0.965 and 0.942. The sensitivity analyses reveal that the dry density, moisture content and normal stress exert the most significant influence on the shear strength, while the key factors for the internal friction angle are the coefficient of curvature, viscous grain content and water content. The water content, dry density and liquid limit are identified as the primary influencers on the cohesion. The data-driven model established herein offers guidance for selecting the shear strength indexes in engineering and investigating strength parameters of soils through the machine learning methods.
-
0. 引言
在岩土工程中,基础、挡土墙、边坡等土工结构的设计以及路堤稳定性、土压力和地基承载力的计算等均需用到土的抗剪强度指标。抗剪强度指标的选取关乎土工结构的设计与安全,不合理的取值会造成工程灾害发生、工程造价提高等不良影响[1],中国某些软土地基基坑坍塌就是由于强度指标选择不当而造成的。但土的抗剪强度指标受到多种因素的影响,首先取决于土本身的物理性质,即土的组成、土的状态和土的结构,其次还取决于它所受的应力状态[2],各因素之间相互作用及其影响机理较为复杂[3],难以解释,因此目前主要还是依靠室内试验和现场原位试验确定其取值。
胡海军等[4]比较了不同试验测试方法及其适用性,指出试验方法的选择对确定抗剪强度指标有很大的影响,且不同施工期需采用不同的抗剪强度指标;闫澎旺等[5]指出十字板剪切试验不能准确反映实际滑动面的强度,并通过大量的试验结果回归分析得到软黏土的抗剪强度指标,但其回归方程的某些参数也是依靠经验取值.由于试验手段获取的抗剪强度指标会受到试验条件的限制,具有精度难以保证以及过于依靠“经验”而导致的不确定性等缺点,越来越多的学者选择采用数值分析或机器学习等非试验方法获取抗剪强度指标[6-7]。其中,机器学习(machine learning)是人工智能领域的1个子领域[8],它可以通过让计算机系统自动识别数据中的模式、规律和趋势,从而使其能够对目标参数进行准确的预测和决策。随着近些年人工智能领域的发展,机器学习在工程领域中已经得到大量的应用并表现出惊人的能力[9]。
对于土体抗剪强度指标的预测,也有不少学者采用不同的机器学习算法展开了大量研究。Das等[10]采用人工神经网络ANN预测黏土的内摩擦角,其测试集的可决系数R2达到0.868;Pham等[11]采用自适应模糊推理系统ANFIS预测软土的抗剪强度,并用SVM,ANN两种算法做对比,得出结论粒子群优化的ANFIS的预测效果最好,其拟合度为0.601;刘晓燕等[12]采用回归树和模型树对黏土的不排水抗剪强度展开预测,其用模型树法预测的测试集可决系数R2达到0.95;Rabbani等[13]采用灰狼算法等6种启发式算法对ANN进行优化,训练土体抗剪强度预测模型,最终得到增强灰狼算法优化ANN的预测效果最好,其测试集的可决系数R2达到0.819;顾春生等[14]采用PAC优化BP神经网络的方法预测黏性土的抗剪强度,其抗剪强度拟合度达到0.85,内摩擦角拟合度达到0.72。
虽然学者们已经使用各种算法对抗剪强度指标的预测模型进行了研究,但是这些模型的预测精度并未达到理想水平。且以上研究尚未针对抗剪强度τf、内摩擦角φ和黏聚力c这3个指标进行统一的建模研究。集成学习模型是一种将多个算法模型集成在一起以提高模型性能的方法。它有几种不同的方法,包括Bagging,Boosting和堆叠法,在处理复杂数据和任务时表现出强大的能力,具有泛化能力高、鲁棒性好等优点。针对上述问题,采用两种集成学习算法(RF算法和Adaboost算法)对τf,φ,c3个指标的预测进行统一的建模研究。采用RMSE3,R2,MAE评估不同预测模型的泛化能力,使该预测模型具备泛化误差小、稳定性好、不易过拟合等特点。最后采用Adaboost算法对输入参数进行敏感性分析,找到对抗剪强度、内摩擦角、黏聚力影响最大的输入参数。
1. 数据集准备及预处理
1.1 特征筛选
从影响土体抗剪强度的因素出发,考虑土体的抗剪强度首先取决于其基本物理性质:即土的组成、土的状态和土的结构,其次还取决于它当前所受的应力状态,因此选择用土体的基本物理参数以及所受的应力状态来预测其抗剪强度及其强度指标。故将模型的输入参数确定为相对质量密度Gs、塑限wp、液限wl、黏粒含量d0.005、塑性指数Ip、不均匀系数Cu、曲率系数Cc、含水率w、干密度ρd以及所受的法向应力σ。输出参数为抗剪强度τf和抗剪强度指标为内摩擦角φ、黏聚力c。
1.2 数据集准备及统计值描述
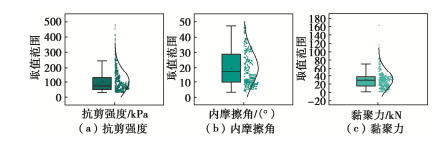
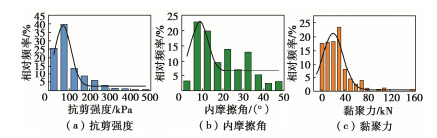
建立一个精确的抗剪强度指标预测模型,必须收集大量的试验数据,并通过机器学习算法对这些试验数据展开研究,找到输入变量和输出变量之间复杂的映射关系,数据集的质量对预测模型的精度起到决定性的作用。从文献[15~19]中共收集到695条有效的抗剪强度指标的试验数据,构成训练模型的数据集。绘制了τf,φ,c这3个输出参数的直方分布图,如图 1所示,以更清晰地观察其数据分布情况。并绘制了3个参数的箱型图进行异常值检测,如图 2所示。据图 2显示,抗剪强度和黏聚力均存在异常值的情况,且大部分异常值是超越了箱型图上限,因此在训练模型之前需将这些异常值剔除,内摩擦角则几乎不存在异常值的情况。将在拟合曲线上方的数据视为异常值,经筛选,抗剪强度存在11个异常值,黏聚力存在3个异常值,将异常值所在的数据列删除,最终用于训练模型的数据集为681条有效数据。
1.3 相关性分析
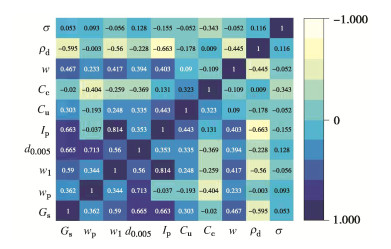
为了防止所建立的模型出现多重共线性,需要在训练模型之前进行输入变量之间的相关性分析。Spearman相关分析方法可用于衡量两个变量之间的非线性关系,且Spearman相关系数不要求数据满足正态分布或其他特定分布,对异常值相对较不敏感,具有较好的鲁棒性[20]。因此,采用Spearman相关系数法计算所有输入参数之间的相关系数。Spearman相关系数的计算公式为
rs=1−6∑d2in(n2−1)。 (1) 式中:di为xi与yi的等级差;n为样本组数。
图 3为各输入参数的Spearman等级相关系数矩阵热图。|rs|越接近于1,说明两个参数之间的相关性越强,正值代表两个参数之间具有正相关性,负值代表两个参数之间具有负相关性。可以看出,对角线上的相关系数为1,而其他大部分位置的相关系数都小于0.6,说明不同输入参数之间的相关性较低。因此,预测精度不受输入变量自相关性的影响。
2. 集成学习算法及训练策略
2.1 集成学习模型
集成学习是一种通过结合多个学习器来提高整体性能的机器学习方法。根据个体学习器的生存方式,集成学习大致可分为:①个体学习器间存在强依赖关系的序列化方法,如Adaboost算法;②个体学习器间不存在依赖关系的并行化方法,如随机森林算法。
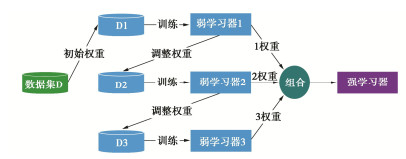
其中,Adaboost算法属于序列化集成学习算法,其核心思想是通过结合多个弱学习器(通常是简单且性能较差的学习器)来构建一个强学习器[21]。将该算法用于回归任务中的优点包括该算法对噪声数据具有鲁棒性、在处理复杂问题时的高准确性等,并且不需要特别复杂的弱学习器。然而,需要注意的是数据的离散化可能会导致信息损失,并且Adaboost在处理高维数据时效果不如其他算法,Adaboost算法的原理示意图见图 4。
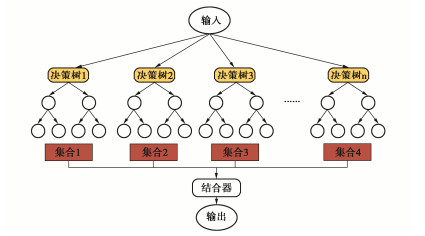
随机森林(RF)是Bagging的一个扩展变体,它是以决策树为基学习器构建Bagging集成的基础上,在决策树的训练过程中引入随机属性的选择。随机森林的训练效率常优于Bagging[22],因为在个体决策树的构建过程中,Bagging使用的是“确定型”决策树,在选择划分属性时要对节点的所有属性进行考察;而随机森林使用的是“随机型”决策树,只需考察一个属性子集。随机森林简单、容易实现、计算代价小,但在很多现实任务中展现出强大的性能,RF算法的原理示意图见图 5。
2.2 训练策略
将数据集按照8︰2的比例划分为训练集和测试集,训练集用于模型的训练,测试集用于评估模型的泛化能力。由于输入变量和输出变量的原始数据跨度范围相当大,为了避免奇异样本数据的出现,减少训练时间,使模型更快收敛,对原始数据基于以下线性映射函数进行归一化处理:
xn=x−xminxmax−xmin。 (2) 式中:xn为各参数的归一化数据;xmax为样本数据的最大值;xmin为数据样本中的最小值。
为了比较不同模型的泛化能力,使用评估回归模型最常用的RMSE,R2,MAE3个指标来评估各模型的预测性能:
RMSE =√1mm∑i=1(yi−^yi)2, (3) R2=1−m∑i=1(yi−˜y)2m∑i=1(yi−¯yi)2, (4) MAE=1mm∑i=1|yi−˜yi|。 (5) 式中:yi为真实的观测值,˜yi为预测值,¯yi为真实观测值的平均值。
3. 结果与讨论
3.1 泛化能力比较
在预测抗剪强度的任务中,RF算法和Adaboost算法在训练集和测试集上的3个评价指标统计于表 1。可决系数R2最接近于1的算法是Adaboost算法,训练集和测试集分别达到0.998,0.925。绝对值误差MAE最小的算法是Adaboost算法,训练集和测试集分别为0.942,13.272。均方根误差RMSE最小的算法是Adaboost算法,训练集和测试集的RMSE分别为3.809、22.244。综合3个评价指标,Adaboost算法预测土体抗剪强度的能力优于RF算法。
表 1 τf,φ,c预测模型各指标统计表Table 1. Indexes of prediction model for τf, φ and c模型 R2 MAE RMSE 训练 测试 训练 测试 训练 测试 τf RF 0.967 0.932 10.717 15.528 13.947 23.921 Adaboost 0.998 0.925 0.941 13.274 3.809 22.244 φ RF 0.997 0.965 0.901 1.469 1.167 1.536 Adaboost 0.991 0.964 0.192 0.579 0.413 2.189 c RF 0.952 0.910 2.860 3.978 4.087 5.623 Adaboost 0.978 0.942 0.734 1.251 2.777 4.377 在预测内摩擦角的任务中,RF算法和Adaboost算法在训练集和测试集上的3个评价指标统计于表 1。可决系数R2最接近于1的算法是RF算法,训练集和测试集分别达到0.997,0.965。绝对值误差MAE最小的算法是Adaboost,训练集和测试集分别为0.192,0.579。均方根误差RMSE最小的算法是RF,训练集和测试集的RMSE分别为1.167,1.536。但是Adaboost算法训练集和测试集的RMSE分别为0.413,2.189,测试集的误差远大于训练集的误差,可能出现了过拟合的现象。综合3个评价指标,RF算法预测内摩擦角的能力优于Adaboost算法,且Adaboost算法预测内摩擦角可能会出现过拟合。
在预测黏聚力的任务中,RF算法和Adaboost算法在训练集和测试集上的3个评价指标统计于表 1。R2最接近于1的算法是Adaboost算法,训练集和测试集分别达到0.978,0.942。MAE最小的算法是Adaboost,训练集和测试集分别为0.734,1.251。RMSE最小的算法是Adaboost,训练集和测试集的RMSE分别为2.777,4.377。综合3个评价指标,Adaboost算法预测黏聚力的能力优于RF算法。
3.2 不同模型综合能力比较结果
根据以上分析,综合考虑模型的泛化能力,预测抗剪强度、内摩擦角、黏聚力表现能力最好的算法分别是Adaboost,RF,Adaboost。3个算法在测试集中真实值和预测值的拟合参考图见图 6。
其中使用Adaboost算法预测内摩擦角时,训练结果显示测试集的误差远大于训练集的误差,可能出现了过拟合的现象。究其原因,可能为:①AdaBoost算法对异常值比较敏感,因为这些异常值可能在每一轮的训练过程中得到强调,从而影响模型的泛化能力。②Adaboost算法采用的弱学习器数量过多,虽然增加弱学习器的数量可以提高模型的复杂度,但也容易导致过拟合。
3.3 输入参数敏感性分析
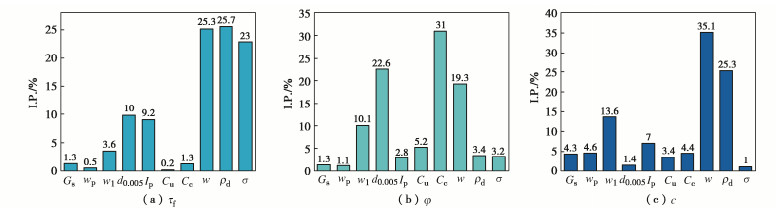
由于AdaBoost是一种迭代的学习方法,每一轮都在调整样本的权重以关注先前被错误分类的样本,因此对参数的敏感性较高。在Adaboost算法训练完成后会得到每个弱分类器的权重,每个弱分类器对应一个参数,这样就可以识别不同参数对模型性能的影响程度[23]。因此,为了评估模型的输入参数对抗剪强度指标的影响程度,采用Adaboost算法对参数做敏感性分析,分析结果见图 7。根据训练结果可以得到,对抗剪强度τf影响程度最大的3个参数为干密度、含水率和法向应力,分别占比25.7%,25.3%,23%;对内摩擦角影响程度最大的,个参数为曲率系数、黏粒含量和含水率,分别占比31%,22.6%,19.3%;对黏聚力影响程度最大的3个参数是含水率、干密度和液限,分别占比35.1%,25.3%,13.6%。在使用数据驱动模型预测相应指标时,若数据集缺失某些输入参数,可优先考虑将以上参数作为模型的输入参数。
4. 结论
提出了一种基于集成学习的正常固结土抗剪强度指标预测模型,利用土体常用的物理参数来预测土体的抗剪强度、内摩擦角和黏聚力,为工程中抗剪强度指标的选取提供参考。首先通过数据集的扩建及预处理,使用集成学习算法(RF,Adaboost)进行模型的构建,然后利用RMSE,R2,MAE3个评价指标评估模型的泛化能力,最后采用Adaboost算法进行输入参数的敏感性分析,得到2点结论。
(1)所建立的模型对τf,φ,c 3个参数的预测均取得了不错的效果。比较各模型的泛化能力,预测抗剪强度效果最好的算法是Adaboost算法,其测试集的R2可达0.925;预测内摩擦角效果最好的算法是RF,其测试集的R2可达0.965;预测粘聚力效果最好的算法是Adaboost,其测试集的R2可达0.942。
(2)敏感性分析结果表明:对抗剪强度影响最大的参数是干密度(25.7%)、含水率(25.3%)、法向应力(23%);对内摩擦角影响最大的3个参数是曲率系数(31%)、黏粒含量(22.6%)、含水率(19.3%);对粘聚力影响最大的3个参数是含水率(35.1%)、干密度(25.3%)、液限(13.6%)。
-
表 1 τf,φ,c预测模型各指标统计表
Table 1 Indexes of prediction model for τf, φ and c
模型 R2 MAE RMSE 训练 测试 训练 测试 训练 测试 τf RF 0.967 0.932 10.717 15.528 13.947 23.921 Adaboost 0.998 0.925 0.941 13.274 3.809 22.244 φ RF 0.997 0.965 0.901 1.469 1.167 1.536 Adaboost 0.991 0.964 0.192 0.579 0.413 2.189 c RF 0.952 0.910 2.860 3.978 4.087 5.623 Adaboost 0.978 0.942 0.734 1.251 2.777 4.377 -
[1] VANAPALLI S K, FREDLUND D G. Comparison of different procedures to predict unsaturated soil shear strength[C]// Advances in Unsaturated Geotechnics. Denver, 2000.
[2] 雷洁, 张国明, 刘连友, 等. 土壤抗剪强度测定与影响因素研究进展[J]. 北京师范大学学报(自然科学版), 2016, 52(4): 486-492. https://www.cnki.com.cn/Article/CJFDTOTAL-BSDZ201604014.htm LEI Jie, ZHANG Guoming, LIU Lianyou, et al. Measuring soil shear strength and impact factors[J]. Journal of Beijing Normal University (Natural Science), 2016, 52(4): 486-492. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BSDZ201604014.htm
[3] 雷国辉, 高翔, 徐可, 等. 饱和软黏土固结过程中的不排水抗剪强度特性[J]. 岩土工程学报, 2019, 41(1): 41-49. doi: 10.11779/CJGE201901004 LEI Guohui, GAO Xiang, XU Ke, et al. Behavior of undrained shear strength of saturated soft clay under consolidation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 41-49. (in Chinese) doi: 10.11779/CJGE201901004
[4] 胡海军, 魏丽敏, 冷伍明. 黏土强度指标的测定和选取[J]. 岩土力学, 2007, 28(12): 2698-2704. doi: 10.3969/j.issn.1000-7598.2007.12.042 HU Haijun, WEI Limin, LENG Wuming. Determination and choice of strength index of clay[J]. Rock and Soil Mechanics, 2007, 28(12): 2698-2704. (in Chinese) doi: 10.3969/j.issn.1000-7598.2007.12.042
[5] 闫澍旺, 封晓伟, 侯晋芳, 等. 用十字板强度推算软黏土抗剪强度指标的方法及应用[J]. 岩土工程学报, 2009, 31(12): 1805-1810. doi: 10.3321/j.issn:1000-4548.2009.12.001 YAN Shuwang, FENG Xiaowei, HOU Jinfang, et al. Deduction and application of strength parameters of soft clay by use of vane strength[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1805-1810. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.12.001
[6] ZHANG P, YIN Z Y, JIN Y F. Machine learning-based modelling of soil properties for geotechnical design: review, tool development and comparison[J]. Archives of Computational Methods in Engineering, 2022, 29(2): 1229-1245. doi: 10.1007/s11831-021-09615-5
[7] ZHANG W G, LI H R, LI Y Q, et al. Application of deep learning algorithms in geotechnical engineering: a short critical review[J]. Artificial Intelligence Review, 2021, 54(8): 5633-5673. doi: 10.1007/s10462-021-09967-1
[8] LI Y Y, RAHARDJO H, SATYANAGA A, et al. Soil database development with the application of machine learning methods in soil properties prediction[J]. Engineering Geology, 2022, 306: 106769. doi: 10.1016/j.enggeo.2022.106769
[9] ZHANG Q, BARRI K, JIAO P, et al. Genetic programming in civil engineering: advent, applications and future trends[J]. The Artificial intelligence review, 2021, 54(3): 1863-1885. doi: 10.1007/s10462-020-09894-7
[10] DAS S K, BASUDHAR P K. Prediction of residual friction angle of clays using artificial neural network[J]. Engineering Geology, 2008, 100(3/4): 142-145.
[11] PHAM B T, SON L H, HOANG T A, et al. Prediction of shear strength of soft soil using machine learning methods[J]. Catena, 2018, 166: 181-191. doi: 10.1016/j.catena.2018.04.004
[12] 刘晓燕, 蔡国军, 邹海峰, 等. 基于CPTU数据融合技术的黏性土应力历史与强度特性评价研究[J]. 岩土工程学报, 2019, 41(7): 1270-1278. doi: 10.11779/CJGE201907011 LIU Xiaoyan, CAI Guojun, ZOU Haifeng, et al. Prediction of stress history and strength of cohesive soils based on CPTU and data fusion techniques[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1270-1278. (in Chinese) doi: 10.11779/CJGE201907011
[13] RABBANI A, SAMUI P, KUMARI S. A novel hybrid model of augmented grey wolf optimizer and artificial neural network for predicting shear strength of soil[J]. Modeling Earth Systems and Environment, 2023, 9(2): 2327-2347. doi: 10.1007/s40808-022-01610-4
[14] 顾春生, 唐鑫, 朱常坤, 等. 基于主成分分析法优化神经网络的滆湖组黏性土抗剪强度预测[J]. 科学技术与工程, 2023, 23(28): 11980-11989. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS202328008.htm GU Chunsheng, TANG Xin, ZHU Changkun, et al. Prediction of shear strength of cohesive soil in Gehu formation based on back propagation neural network optimized by principal component analysis[J]. Science Technology and Engineering, 2023, 23(28): 11980-11989. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS202328008.htm
[15] 黄鑫中. 不同击实功下非饱和黄土强度特性研究[D]. 西安: 长安大学, 2021. HUANG Xinzhong. Study on Strength Characteristics of Unsaturated Loess Under Different Compaction Work[D]. Xi'an: Changan University, 2021. (in Chinese)
[16] 雷昊楠. 黄土剪切面特征及抗剪强度影响因素试验研究[D]. 西安: 长安大学, 2021. LEI Haonan. Research for Loess Shear Surface Characteristics and Influencing Factors of Shear Strength[D]. Xi'an: Changan University, 2021. (in Chinese)
[17] 朱志坤. 干密度和含水率对太原重塑黄土强度及强度参数影响的研究[D]. 太原: 太原理工大学, 2018. ZHU Zhikun. Effect of Dry Density and Water Content on the Stregth and Strength Parameters of Remolded Loess in Taiyuan[D]. Taiyuan: Taiyuan University of Technology, 2018. (in Chinese)
[18] 陈梦芸. 击实黏土抗拉强度研究[D]. 南京: 南京大学, 2014. CHEN Mengyun. Study on Tensile Strength of Compacted Clay[D]. Nanjing: Nanjing University, 2014. (in Chinese)
[19] 杨永亮. 不同击实因素对黄土状粉土击实特性及抗剪强度影响的试验研究[D]. 太原: 太原理工大学, 2019. YANG Yongliang. Effect of Different Compaction Factors on Compaction Characteristics and Shear Strength of Loess Silt[D]. Taiyuan: Taiyuan University of Technology, 2019. (in Chinese)
[20] DE WINTER J C F, GOSLING S D, POTTER J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: a tutorial using simulations and empirical data[J]. Psychological Methods, 2016, 21(3): 273-290. doi: 10.1037/met0000079
[21] SHRESTHA D L, SOLOMATINE D P. AdaBoost RT: a boosting algorithm for regression problems[J]. Proceedings of the IEEE International Joint Conference on Neural Networks, 2004, 2: 1163-1168.
[22] GONG H R, SUN Y R, SHU X, et al. Use of random forests regression for predicting IRI of asphalt pavements[J]. Construction and Building Materials, 2018, 189: 890-897. doi: 10.1016/j.conbuildmat.2018.09.017
[23] WEI P F, LU Z Z, SONG J W. Variable importance analysis: a comprehensive review[J]. Reliability Engineering & System Safety, 2015, 142: 399-432.



 下载:
下载: