Health status identification of modular-block-reinforced soil retaining walls after earthquakes
-
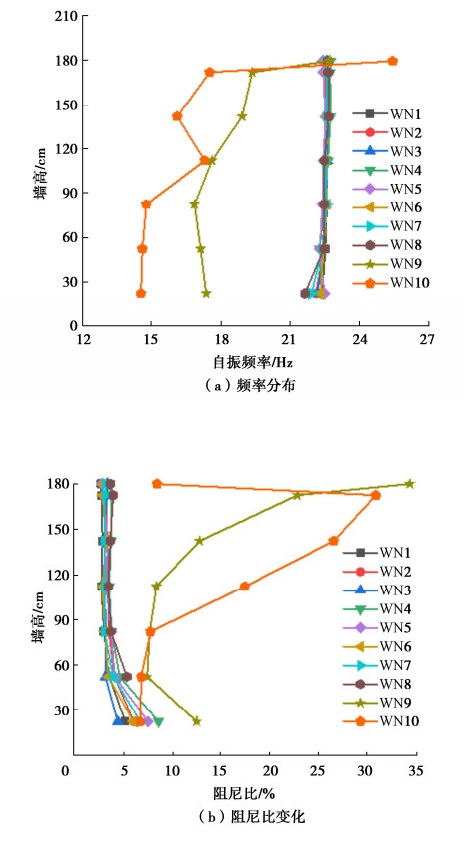
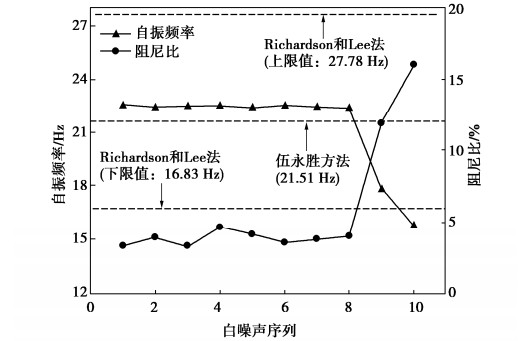
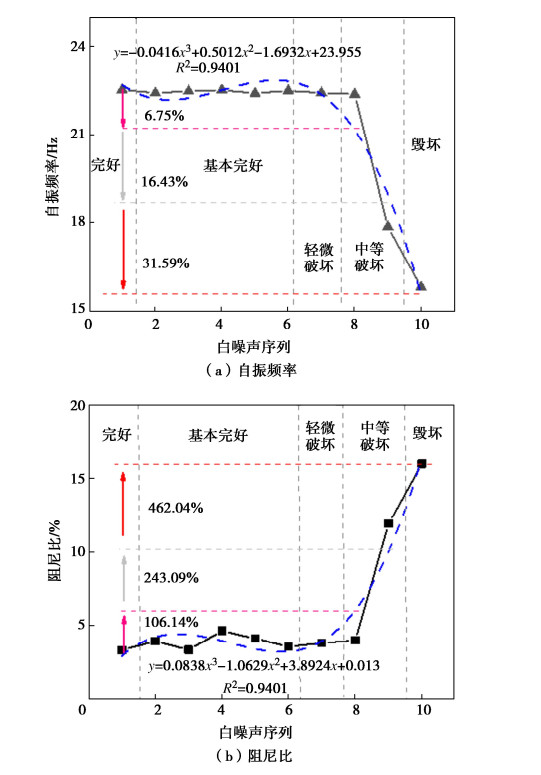
摘要: 采用时域识别方法分析了加筋土挡墙大型振动台模型试验在不同工况下动力特性(自振频率和阻尼比)分布规律，介绍了加筋土挡墙不同位置处动力特性的变化特征，阐述了不同损伤程度下加筋土挡墙动力特性分布规律，探究了动力特性变化幅值与加筋土挡墙损伤程度的定量关系。结果表明：加载阶段前期，加筋土挡墙各位置处的自振频率基本相同，阻尼比随着墙高的上升而减小；加载后期，挡墙自振频率明显下降、阻尼比大幅上升。采用数理方法获得了单级挡墙自振频率和阻尼比的分布曲线，得出了基本完好、轻微破坏、中等破坏和毁坏4个阶段自振频率和阻尼比变化幅度；当自振频率下降幅度为6.75%~16.43%，阻尼比上升幅度106.14%~243.09%时，可认为加筋土挡墙处于中等破坏阶段；当自振频率下降幅度为16.43%~31.59%、阻尼比上升幅度243.09%~462.04%时，可认为加筋土挡墙处于毁坏阶段。Abstract: Distribution of dynamic characteristics (natural frequency and damping ratio) of large-scale shaking table model tests on a reinforced soil retaining wall (RSRW) under different working conditions is analyzed by using the time-domain identification method. The variation characteristics of dynamic characteristics at different positions of the RSRW are introduced, and the distribution laws of its dynamic characteristics under different damage degrees are expounded. The quantitative relationship between the amplitude of dynamic characteristics and the damage degree of the RSRW is explored. The results show that at the early stage of loading stage, the natural frequencies are basically the same, and the damping ratio decreases with the increase of wall height. At the later stage of loading, the natural frequency of the RSRW decreases obviously, and the damping ratio increases greatly. The distribution curves of the natural frequency and damping ratio are obtained by the mathematical methods. The variation amplitudes of the natural frequency and damping ratio are obtained for the following four stages: basic intact, slight damage, moderate damage and destruction. When the decrease amplitude of the natural frequency is 6.75 % ~ 16.43 % and the increase amplitude of the damping ratio is 106.14 % ~ 243.09 %, it can be considered that the RSRW is at the middle failure stage. When the decreasing amplitude of the natural vibration frequency is 16.43 % ~ 31.59 % and the increasing amplitude of the damping ratio is 243.09 % ~ 462.04%, it can be considered that the RSRW is at the destruction stage.
-
0. 引言
海洋复合地基施工常存在定位难、制桩难、桩体质量差等缺点，始终制约着海洋基础设施工程的应用和发展[1-3]。本文借鉴在陆地上已成功应用于湿陷性黄土、盐渍土、膨胀土、红层风化土等特殊土的地基处理技术[4-6]——孔内深层强夯法（DDC），提出水下套管强夯碎石桩地基处理方法，施工工序为：先将钢套管打至设计深度并清理管内软泥；套管内分层填入碎石并使用夯锤夯实；上拔套筒一定高度并再次填料和夯实；直到形成串珠状的散体桩复合地基。该过程不仅能将碎石夯实压密，而且可以对海洋地基土体进行置换、挤密和排水，最终形成高强度的水下散体桩复合地基。该技术是将陆上孔内深层强夯桩复合地基技术进行改进，增加钢套筒隔断海水以实现海洋干作业施工，满足海洋软土地基处理的需求。然而在成桩过程中涉及夯锤-碎石-土体三者相互作用，目前还缺乏相应的研究。
孔内深层强夯法（DDC）的加固效果、承载性能、挤密影响范围、布桩形式等受到了广泛研究。孔洋等[7]对DDC法复合地基进行原位浸水载荷试验研究，发现DDC工法可以有效消除黄土的湿陷性。周小松等[8]得到DDC最优桩桩间距为2.0~3.0倍成孔直径。马军平[9]通过井探开挖发现DDC桩在宏观上形成葫芦状的桩体，这种不规则形状极大地提高了侧摩阻力，使复合地基承载力整体提高。冯志焱等[10]发现DDC处理后的复合地基可达到处理前土层承载力的2倍或更高。对于直接影响DDC后期承载特性的成桩过程的研究很少。
本文采用半模试验[11-12]针对水下套筒强夯技术开展研究，讨论了夯击能、单次填料量、土体强度等因素对水下套筒强夯碎石桩成桩过程的影响，分析了夯锤运动过程中的夯锤冲击力和夯沉量、桩体密度等的变化规律，为水下套管强夯碎石桩的工程应用提供参考。
1. 模型试验简介
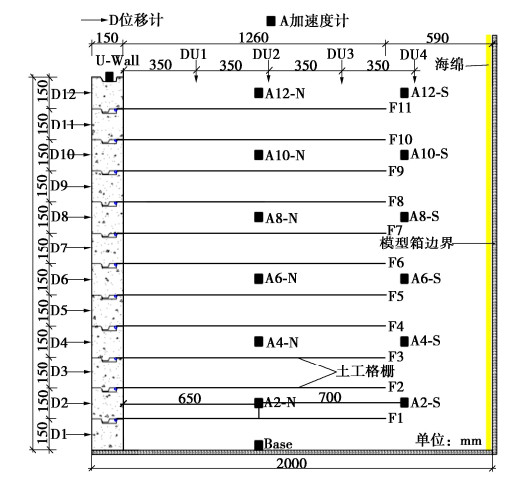
1.1 试验装置
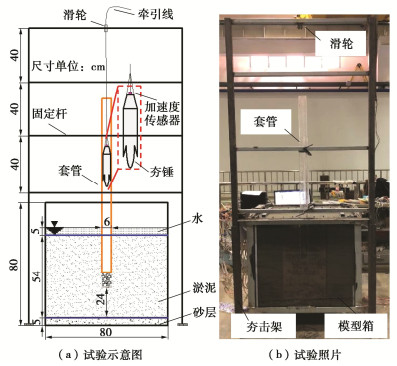
试验装置如图 1所示，由模型箱、套管、夯击架、夯锤组成。模型箱四周由透明钢化玻璃组成，尺寸为80 cm×80 cm×80 cm（长×宽×高）。半模试验套管为“D”字型，材质为透明有机玻璃，长度为130 cm，内径为5.4 cm，外径为6 cm。夯击架高度为220 cm，宽度为100 cm。定滑轮固定在可以平移的导杆上，牵引线穿过定滑轮，向下用力可将夯锤吊起。夯击过程中为保证套管位置固定，套管通过固定夹固定在固定杆上。夯锤上部固定通用压电式加速度传感器。为减小夯锤与套筒之间的阻力，每次夯击时在夯锤表面涂抹凡士林。夯击过程中通过动态数据采集仪持续监测夯锤加速度变化，动态数据采集仪型号为DH5922D，采样频率5 kHz。
砂垫层作为持力层和固结阶段排水层，厚度为5 cm。固结后软土层厚度为54 cm。为模拟水下环境，软土上部有5 cm的水。土体固结完成后，采用荷兰钻进行钻孔，孔深为30 cm，孔径为6 cm。随后放置套管、填料、进行夯击。夯击方式为每填料一次，夯击一次。填料时一旦填料高度到达套管底部就开始上拔套管，保证套管高于碎石。
1.2 夯锤模型
两种夯锤模型如图 2所示，质量均为1.5 kg。其中图 2（a）为传统平底夯锤，在陆地强夯[13-14]中经常使用。由于平底夯锤在水下套管强夯碎石桩中夯锤冲击会使碎石卡在夯锤与钢套筒之间，导致夯锤无法顺利拔出。因此对传统平底夯锤进行改进，设计了锥形夯锤，即图 2（b）所示的锥形夯锤，该夯锤底部椭球外层有一圈圆形护壁，可保证每次夯击时夯锤顺利拔出。
1.3 试验材料
本模型试验土样为淤泥质软土，取自天津市滨海吹填土区域。共采用3种不同强度的软土进行试验，首先配置含水率60%的淤泥将其充分搅拌，然后分层填入模型箱中。其中软土1在自重条件下固结，固结后的土体强度为1.5 kPa。软土2与软土3在堆载条件下固结，其中软土2的固结压力为18 kPa，固结后的土体强度为6.3 kPa；软土3的固结压力为50 kPa，固结后的土体强度为10 kPa。三种软土固结后通过渗透试验测得渗透系数分别为1.25×10-6 cm/s、1.54×10-7 cm/s、7.77×10-8 cm/s。土体详细物理参数如表 1所示。碎石粒径为6~8 mm，平均粒径为6.95 mm，颗粒相对质量密度为2.58，通过直剪试验测得内摩擦角为38.6°。
表 1 土体物理力学参数Table 1. Physical and mechanical parameters of soils参数 软土1 软土2 软土3 土粒相对质量密度 2.67 2.67 2.67 液限/% 43 43 43 塑限/% 22 22 22 塑性指数 21 21 21 含水率/% 55.90 45.40 41.00 密度/(g⋅cm−3) 1.60 1.75 1.88 不排水抗剪强度/kPa 1.5 6.3 10.0 渗透系数/(cm⋅s−1) 1.25×10-6 1.54×10-7 7.77×10-8 1.4 试验方案
共进行14组水下套筒强夯桩成桩模型试验，试验分组如表 2所示。其中T1作为对照组，其余13组试验分别研究了夯锤落距（H）、单次填料量（m）、土体强度（cu）等因素对水下套管强夯碎石桩夯锤运动的影响。夯锤落距分别为40，80，120 cm，代表 12，24，36 N·m三种夯击能（E）。单次填料量采用50，100，150 g三种质量。土体强度分别为1.5，6.3，10.0 kPa。
表 2 试验分组Table 2. Test groups编号 夯锤类型 H/
cmm/
gcu/
kPaE/
(N·m)夯击次数 T1 平底夯锤 80 100 6.3 24 19 T2 改进锥形夯锤 80 50 6.3 24 50 T3 80 100 6.3 24 18 T4 80 150 6.3 24 10 T5 40 50 6.3 12 35 T6 40 100 6.3 12 12 T7 40 150 6.3 12 7 T8 120 100 6.3 36 28 T9 40 100 1.5 12 30 T10 80 100 1.5 24 50 T11 120 100 1.5 36 66 T12 40 100 10 12 10 T13 80 100 10 24 13 T14 120 100 10 36 16 2. 试验结果和分析
2.1 夯锤运动过程分析
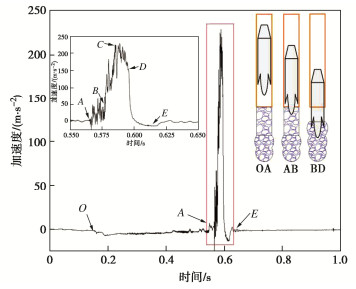
以T3中第10次夯击为例对锥形夯锤夯击过程进行分析，如图 3所示，加速度时程曲线呈单峰型，在夯击早期阶段，夯锤的加速度曲线出现明显的震荡，这反映了夯锤与碎石的压缩接触。夯击过程可分为以下4个阶段：
（1）夯锤下落阶段OA（0.13~0.565 s，持续时间435 ms）。由于夯锤与套筒之间存在摩擦，因此加速度值小于重力加速度，加速度均值为-6.01 m/s2（规定加速度、速度向上为正）。
（2）锤尖接触碎石阶段AB（0.565~0.576 s，持续时间11 ms）。夯锤尖部首先与碎石接触，插入碎石中，表现为加速度的小幅震荡。
（3）震荡阶段BD（0.576~0.596 s，持续时间20 ms）。此时夯锤尖部已没入碎石中，在此阶段夯锤与碎石群体发生多体碰撞，实测加速度发生高频震荡，并产生反力加速度峰值。夯锤的撞击力通过碎石传递给软土，造成软土密实。此阶段可分为震荡上行区和震荡下行区，震荡上行区BC加速度均值逐渐增加，在C点达到加速度峰值，震荡下行区CD加速度均值逐渐减小。
（4）快速下降阶段DE（0.596~0.618 s，持续时间22 ms）。此时碎石和软土都得到密实并伴随夯锤能量释放完毕，加速度曲线快速下降。
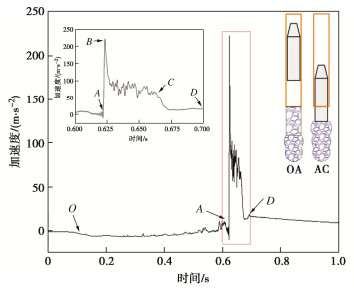
图 4为T1中第10次夯击的平底夯锤加速度-时程曲线，可以看出平底夯锤的加速度-时程曲线更加光滑平整，可分为三个阶段：夯锤下落阶段OA、冲击碎石阶段AC、快速下降阶段CD。由于夯锤是平底，因此冲击碎石阶段加速度震荡幅度没有锥形夯锤大，在夯击开始即产生反力加速度峰值，随后反力加速度逐渐减小并小幅震荡，而且BC段加速度存在近似平台区。图 4所示T1试验采用平底夯锤的反力峰值与图 3所示相同条件下的采用锥形夯锤得到的反力峰值接近，但反力的作用时间较长。
2.2 夯锤加速度峰值
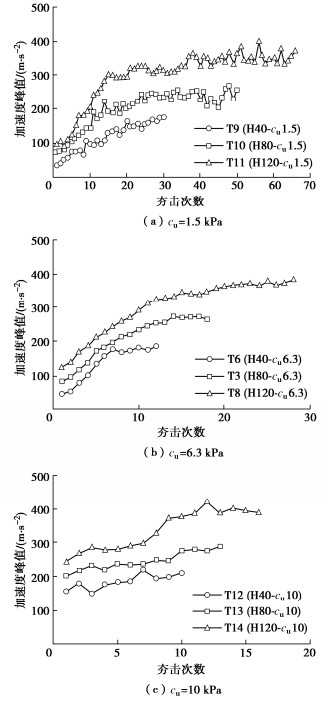
以夯锤每次下落到筒底碎石上时受到的反力加速度峰值作为衡量夯锤冲击力的指标。图 5统计了采用锥形夯锤，用不同落距、在不同土体强度中下落夯击时得到的反力加速度峰值。图 5可以看出，随着夯击次数的增加，反力加速度峰值逐渐增大，但是增长速度越来越慢，这主要是由于随着填料量和夯击次数的增加，碎石层厚度增大，密度和刚度增大，下部越来越密实，夯锤和碎石相互作用时间变短，因此加速度峰值逐渐增大。在相同强度的黏土地基中，夯锤的释放落距越大，加速度峰值越大。对比图 5中在不同强度土体中的加速度峰值可知，土体强度越大时，加速度峰值越大。土体强度越高时，限制了碎石的侧向膨胀，减小了碎石的沉降量，缩短了夯锤的能量释放时间，因此加速度峰值越高。
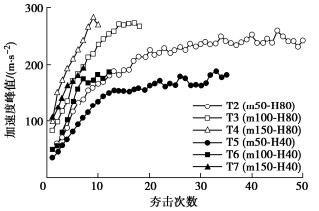
图 6对比了不同的单次填料量对夯锤的反力加速度峰值的影响，从图中可以看出，随着单次填料量的增加，夯锤加速度峰值增加，总的夯击次数减小。在T5中采用落距40 cm和单次填料量50 g时，从第14次夯击开始，加速度峰值不再增加，稳定在160 m/s2左右，在T2中采用落距80 cm和单次填料量50 g时，从第20次夯击开始，加速度峰值不再增加，稳定在220 m/s2左右。这主要是由于单次填料量过少，导致填入的碎石绝大部分被侧向挤压，碎石桩整体刚度没有增加。
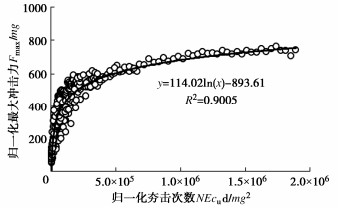
总结上述夯击次数（N）、夯击能（E）、土体强度（cu）、孔径（d）、单次填料质量（m）等参数对夯锤受到的反力加速度峰值（即夯锤冲击力）的影响，绘制了归一化的最大冲击力随归一化的夯击次数、夯击能、地基土体强度等的发展曲线，如图 7所示。纵坐标为归一化最大冲击力Fmax/mg，Fmax=mhamax，mh为夯锤质量，amax为前述图 3与图 4中的夯锤反力加速度峰值，g为重力加速度；横坐标为归一化夯击系数NEcud/(mg)2。可以看出两者之间具有良好的对数关系；归一化的最大冲击力随着归一化的夯击次数增长而逐渐增加，但增长速度逐渐变慢。根据图 7统计的归一化最大冲击力Fmax/mg与归一化夯击系数NEcud/(mg)2的结果，得到描述二者关系的拟合公式（1），其R2值为0.9005。利用式（1）可以对夯锤的最大冲击力进行预测。
Fmaxmg=114.02ln[NEcud(mg)2]−893.61。 (1) ![]()
图 7 归一化最大冲击应力与归一化夯击次数的关系Figure 7. Relationship between normalized maximum impact force and normalized drop number2.3 夯锤夯沉量
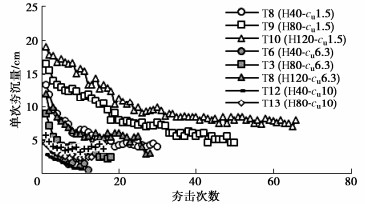
通过对夯锤的加速度进行二次积分，可得到每一次夯击时夯锤的夯沉量，采用不同落距在不同强度土体中的碎石沉降量如图 8所示，可以看出随着夯击次数的增加，碎石沉降量逐渐减小，前5次夯击的沉降量远大于后续夯击时的碎石沉降量，这主要是由于碎石桩底部有24 cm厚的软土层，在夯锤的作用下，碎石主要被挤入下部软土层中。夯击能量越大，碎石沉降量越大；土体强度越低，碎石沉降量越大。以T10为例，土体强度为1.5 kPa，落距为120 cm，碎石单次夯沉量均超过了10 cm，这说明在T10的较软的地基中采用过大的夯沉量，使得大部分碎石被挤入到周围软土中，不能形成有效的强夯碎石桩。因此在强度较低的土体中进行强夯碎石桩施工，应采用低落距强夯或者提高土体强度后再进行强夯碎石桩施工。
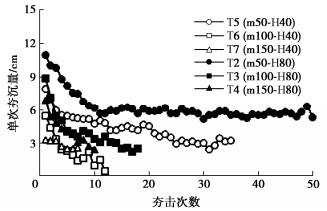
图 9为单次填料量对碎石沉降量的影响，从图 8可以看出，随着单次填料量的增加，碎石沉降量逐渐减小。当单次填充量过小时，碎石单次沉降量减小到某一值后保持稳定，在T2中，单次填料量为50 g，落距为80 cm，从第11次夯击后单次夯沉量约6 cm。在T5中，单次填料量为50 g，落距为40 cm，从第25次夯击后单次夯沉量约3 cm。
2.4 桩体密度
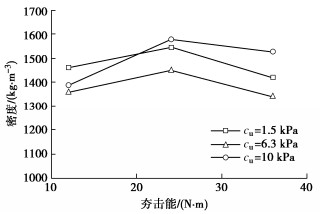
图 10给出了不同夯击能对碎石桩密度的影响，对于3种不同强度的软土，采用夯击能24 N⋅m（落距80 cm）时强夯碎石桩密度最大，过大或过小的夯击能都不能有效地增加强夯碎石桩密度。采用夯击能为24 N⋅m和36 N⋅m时在10 kPa的土体中强夯碎石桩密度最高，总填料量最少，因此在高强度软土中进行套管强夯碎石桩安装更经济有效。
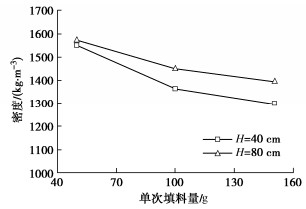
单次填料量对碎石桩密度的影响如图 11所示，从图 11可以看出，单次填料量也对强夯碎石桩密度产生重要影响，随着单次填料量的增加，碎石桩密度逐渐减小。但是当单次填料量过小时，增大夯锤落距，碎石桩密度并无明显提高，在T5中，填料量为50 g，落距为40 cm，强夯碎石桩密度为1553 kg/m3，当落距增加到80 cm时，在T2中强夯碎石桩密度为1570 kg/m3，并无明显的增加，因此当单次填料量过小时，夯锤采用低落距更为经济合适。
![]()
图 11 单次填料量对碎石桩密度的影响Figure 11. Effects of single filling mass on density of stone column3. 结论
本文针对水下套筒强夯技术开展了模型试验研究，对比分析了传统平底夯锤和新型锥形夯锤的夯击规律，研究了夯击能、单次填料量、土体强度等因素对成桩过程的影响，得出以下结论：
（1）采用新型锥形夯锤夯击到碎石后，得到的反力加速度呈现出震荡增大到峰值后迅速减小、反力作用时间短等特点；采用传统平底夯锤夯击到碎石后，得到的反力加速度表现为迅速增大到峰值再震荡减小、反力作用时间长等特点。相同条件下二者的反力加速度峰值较为接近。
（2）建立了夯锤夯击时的归一化最大冲击力关于夯击次数、夯击能、土体强度、单次填料质量等参数的拟合公式，可用于估算不同地基强度中夯击成桩时的峰值夯击力。随着夯击次数增大，夯锤的反力加速度峰值逐渐增大，但是增长速度放缓。
（3）夯击能量、单次填料量、地基强度等都对成桩质量有影响：夯击能过大将使碎石填料被挤到周围软土中降低碎石桩密度和强度、夯击能过小则无法起到理想的夯击密实效果；随着单次填料量增大，碎石桩密度逐渐减小。
-
![]()
图 4 动力特性与破坏程度间的对应关系
Figure 4. Corresponding relationship between dynamic characteristics and damage degree
表 1 试验工况
Table 1 Loading conditions
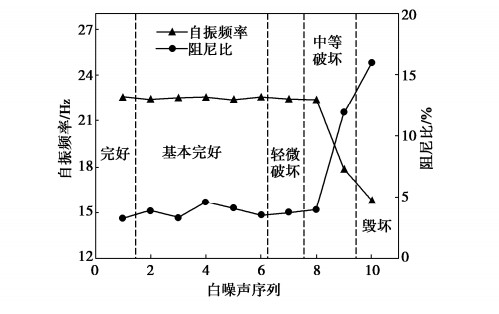
序号 输入波 加速度/g 相似比 工况代号 1 WN 0.05 1 WN1 WL, EL 0.1 4, 2 / 2 WN 0.05 1 WN2 WL, EL 0.2 4, 2 / 3 WN 0.05 1 WN3 WL, EL 0.4 4, 2 / 4 WN 0.05 1 WN4 WL, EL 0.6 4, 2 / 5 WN 0.05 1 WN5 WL, EL 0.8 4, 2 / 6 WN 0.05 1 WN6 WL, EL 1.0 4, 2 / 7 WN 0.05 1 WN7 WL, EL 1.2 4, 2 / 8 WN 0.05 1 WN8 WL 1.6 4, 2 / 9 WN 0.05 1 WN9 WL 2.0 4, 2 / 10 WN 0.05 1 WN10 
下载: 导出CSV
表 2 工况与损伤程度对应情况
Table 2 Conditions corresponding to damage degree
工况 WN1 WN2 WN3 WN4 WN5 WN6 WN7 WN8 WN9 WN10 位移指数/% 0 0.07 0.10 0.32 0.73 1.05 1.59 2.38 3.34 ＞3.8 损伤程度 完好 基本完好 轻微破坏 中等破坏 毁坏 注：位移指数为累计水平永久位移与总墙高的比值。
下载: 导出CSV
-
[1] HAN J, JIANG Y, XU C. Recent advances in geosynthetic-reinforced retaining walls for highway applications[J]. Frontiers of Structural and Civil Engineering, 2018, 12(2): 239-247. doi: 10.1007/s11709-017-0424-8
[2] ZHU Y M, ZHANG F, JIA S L. Embodied energy and carbon emissions analysis of geosynthetic reinforced soil structures[J]. Journal of Cleaner Production, 2022, 370: 133510. doi: 10.1016/j.jclepro.2022.133510
[3] KUWANO J, MIYATA Y, KOSEKI J. Performance of reinforced soil walls during the 2011 Tohoku earthquake[J]. Geosynthetics International, 2014, 21(3): 179-196. doi: 10.1680/gein.14.00008
[4] KOERNER R M, KOERNER G R. An extended data base and recommendations regarding 320 failed geosynthetic reinforced mechanically stabilized earth (MSE) walls[J]. Geotextiles and Geomembranes, 2018, 46(6): 904-912. doi: 10.1016/j.geotexmem.2018.07.013
[5] LI S H, CAI X G, JING L P, et al. Lateral displacement control of modular-block reinforced soil retaining walls under horizontal seismic loading[J]. Soil Dynamics and Earthquake Engineering, 2021, 141: 106485. doi: 10.1016/j.soildyn.2020.106485
[6] LING H I, LESHCHINSKY D, CHOU N N S. Post-earthquake investigation on several geosynthetic-reinforced soil retaining walls and slopes during the Ji-Ji earthquake of [J]. Soil Dynamics and Earthquake Engineering, 2001, 21(4): 297-313. doi: 10.1016/S0267-7261(01)00011-2
[7] CAWLEY P. Structural health monitoring: closing the gap between research and industrial deployment[J]. Structural Health Monitoring, 2018, 17(5): 1225-1244. doi: 10.1177/1475921717750047
[8] 朱宏伟, 姚令侃, 张旭海. 两种加筋土挡墙的动力特性比较及抗震设计建议[J]. 岩土工程学报, 2012, 34(11): 2072-2080. http://cge.nhri.cn/cn/article/id/14907 ZHU Hongwei, YAO Lingkan, ZHANG Xuhai. Comparison of dynamic characteristics between netted and packaged reinforced soil retaining walls and recommendations for seismic design[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2072-2080. (in Chinese) http://cge.nhri.cn/cn/article/id/14907
[9] HUANG C C. Seismic responses of vertical-faced wrap-around reinforced soil walls[J]. Geosynthetics International, 2019, 26(2): 146-163. doi: 10.1680/jgein.18.00044
[10] 徐鹏, 蒋关鲁, 胡耀芳, 等. 整体刚性面板加筋土挡墙基频影响因素计算分析[J]. 岩土力学, 2018, 39(12): 4475-4481. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812022.htm XU Peng, JIANG Guanlu, HU Yaofang, et al. Calculation of fundamental frequencies of reinforced retaining walls with full-height rigid facing[J]. Rock and Soil Mechanics, 2018, 39(12): 4475-4481. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812022.htm
[11] ABBASI O, GHANBARI A, HOSSEINI S A A. An analytical method for calculating the natural frequency of reinforced retaining walls with soil–structure interaction effect[J]. Geosynthetics International, 2014, 21(1): 53-61. doi: 10.1680/gein.13.00034
[12] SARBISHEI S, FAKHER A. Energy-based horizontal slice method for pseudo-static analysis of reinforced walls[J]. Geosynthetics International, 2012, 19(5): 370-384. doi: 10.1680/gein.12.00023
[13] RAMEZANI M S, GHANBARI A, HOSSEINI S A A. Analytical method for calculating natural frequencies of geosynthetic-reinforced wall with full-height concrete facing[J]. Geosynthetics International, 2017, 24(1): 1-13. doi: 10.1680/jgein.16.00011
[14] 伍永胜. 加筋土挡墙动力特性及抗震设计方法研究[D]. 长沙: 湖南大学, 2006. WU Yongsheng. Study on Dynamic Characteristics and Seismic Design Method of Reinforced Earth Retaining Wall[D]. Changsha: Hunan University, 2006. (in Chinese)
[15] HATAMI K, BATHURST R J. Effect of structural design on fundamental frequency of reinforced-soil retaining walls[J]. Soil Dynamics and Earthquake Engineering, 2000, 19(3): 137-157. doi: 10.1016/S0267-7261(00)00010-5
[16] 李思汉. 模块式加筋土挡墙动力反应试验研究及数值分析[D]. 廊坊: 防灾科技学院, 2018. LI Sihan. Experimental Study and Numerical Analysis of Dynamic Response of Modular Reinforced Earth Retaining Wall[D]. Langfang: Institute of Disaster Prevention, 2018. (in Chinese)
[17] LI S H, CAI X G, JING L P, et al. Reinforcement strain and potential failure surface of geogrid reinforced soil-retaining wall under horizontal seismic loading[J]. Shock and Vibration, 2020, 2020: 8864256.
[18] CAI X G, LI S H, XU H L, et al. Shaking table study on the seismic performance of geogrid reinforced soil retaining walls[J]. Advances in Civil Engineering, 2021, 2021: 6668713.
[19] 李思汉, 蔡晓光, 景立平, 等. 基于位移的模块式加筋土挡墙抗震设计方法研究[J]. 地震工程学报, 2023, 45(5): 1066-1074. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ202305008.htm LI Sihan, CAI Xiaoguang, JING Liping, et al. Displacement-based seismic design methods of a modular reinforced soil retaining wall[J]. China Earthquake Engineering Journal, 2023, 45(5): 1066-1074. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ202305008.htm
[20] 魏明, 罗强, 蒋良潍, 等. 悬臂式加筋土复合支挡结构振动台模型试验研究[J]. 岩石力学与工程学报, 2021, 40(3): 607-618. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103014.htm WEI Ming, LUO Qiang, JIANG Liangwei, et al. Shaking table tests of cantilevered reinforced soil retaining walls[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 607-618. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103014.htm
[21] YAZDANDOUST M. Investigation on the seismic performance of steel-strip reinforced-soil retaining walls using shaking table test[J]. Soil Dynamics and Earthquake Engineering, 2017, 97: 216-232. doi: 10.1016/j.soildyn.2017.03.011
[22] 徐琨鹏. 地下结构拟静力抗震分析方法及推覆试验研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2019. XU Kunpeng. Quasi-static Seismic Analysis Method and Pushover Test of Underground Structures[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2019. (in Chinese)
[23] HUANG C C, WU S H, WU H J. Seismic displacement criterion for soil retaining walls based on soil strength mobilization[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(1): 74-83. doi: 10.1061/(ASCE)1090-0241(2009)135:1(74)
[24] 张建经, 韩鹏飞. 重力式挡墙基于位移的抗震设计方法研究: 大型振动台模型试验研究[J]. 岩土工程学报, 2012, 34(3): 416-423. http://cge.nhri.cn/cn/article/id/14513 ZHANG Jianjing, HAN Pengfei. Displacement based seismic design method for gravity retaining walls-Large scale shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(3): 416-423. (in Chinese) http://cge.nhri.cn/cn/article/id/14513
计量
- 文章访问数: 92
- HTML全文浏览量: 20
- PDF下载量: 13
