Health status identification of modular-block-reinforced soil retaining walls after earthquakes
-
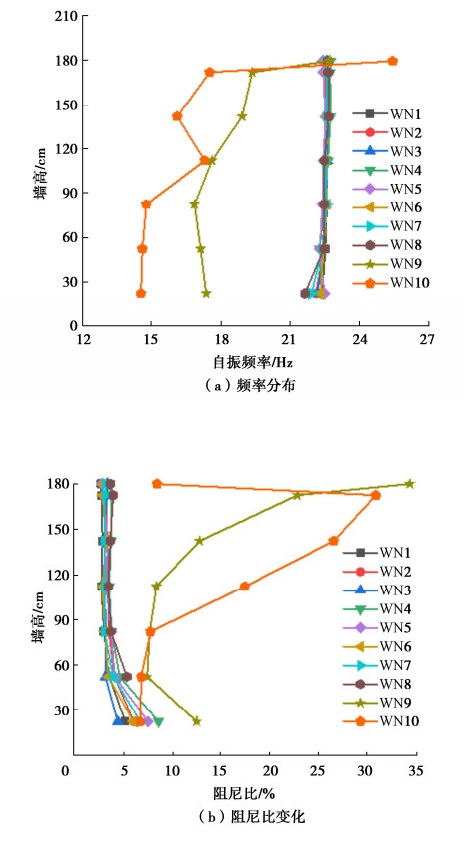
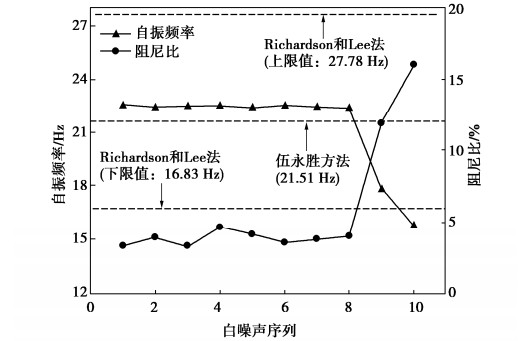
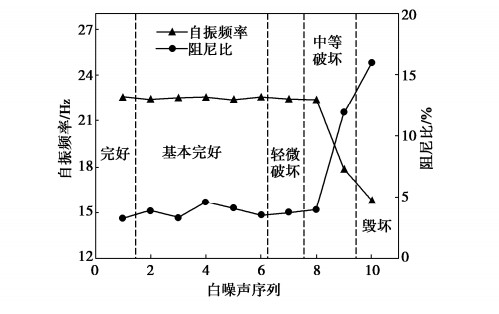
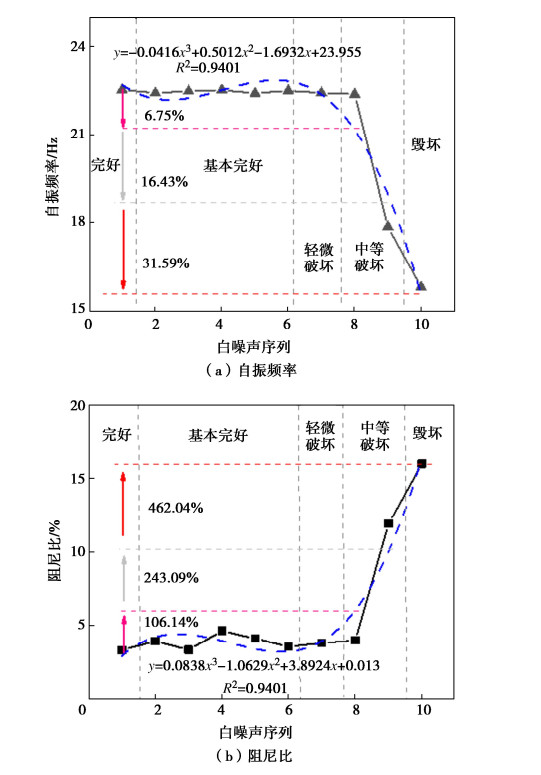
摘要: 采用时域识别方法分析了加筋土挡墙大型振动台模型试验在不同工况下动力特性(自振频率和阻尼比)分布规律,介绍了加筋土挡墙不同位置处动力特性的变化特征,阐述了不同损伤程度下加筋土挡墙动力特性分布规律,探究了动力特性变化幅值与加筋土挡墙损伤程度的定量关系。结果表明:加载阶段前期,加筋土挡墙各位置处的自振频率基本相同,阻尼比随着墙高的上升而减小;加载后期,挡墙自振频率明显下降、阻尼比大幅上升。采用数理方法获得了单级挡墙自振频率和阻尼比的分布曲线,得出了基本完好、轻微破坏、中等破坏和毁坏4个阶段自振频率和阻尼比变化幅度;当自振频率下降幅度为6.75%~16.43%,阻尼比上升幅度106.14%~243.09%时,可认为加筋土挡墙处于中等破坏阶段;当自振频率下降幅度为16.43%~31.59%、阻尼比上升幅度243.09%~462.04%时,可认为加筋土挡墙处于毁坏阶段。Abstract: Distribution of dynamic characteristics (natural frequency and damping ratio) of large-scale shaking table model tests on a reinforced soil retaining wall (RSRW) under different working conditions is analyzed by using the time-domain identification method. The variation characteristics of dynamic characteristics at different positions of the RSRW are introduced, and the distribution laws of its dynamic characteristics under different damage degrees are expounded. The quantitative relationship between the amplitude of dynamic characteristics and the damage degree of the RSRW is explored. The results show that at the early stage of loading stage, the natural frequencies are basically the same, and the damping ratio decreases with the increase of wall height. At the later stage of loading, the natural frequency of the RSRW decreases obviously, and the damping ratio increases greatly. The distribution curves of the natural frequency and damping ratio are obtained by the mathematical methods. The variation amplitudes of the natural frequency and damping ratio are obtained for the following four stages: basic intact, slight damage, moderate damage and destruction. When the decrease amplitude of the natural frequency is 6.75 % ~ 16.43 % and the increase amplitude of the damping ratio is 106.14 % ~ 243.09 %, it can be considered that the RSRW is at the middle failure stage. When the decreasing amplitude of the natural vibration frequency is 16.43 % ~ 31.59 % and the increasing amplitude of the damping ratio is 243.09 % ~ 462.04%, it can be considered that the RSRW is at the destruction stage.
-
0. 引言
非饱和状态是影响土体力学特性的重要因素。基质吸力的增加直接降低了土体的含水率,提高了土体的抗剪强度和模量,进而对岩土工程的稳定性产生显著影响。因此,土水特征研究一直是非饱和土研究的热点。
过去,人们对细粒土(如黏土、粉质黏土、砂土等)的土水特征进行了大量研究,但对大颗粒粗粒堆积土的土水特征研究较少,主要是受限于现有测试设备的尺寸,它们只能对小尺寸的土样进行测试。然而,粗粒堆积土含较多10~60 mm的颗粒,因此小尺寸试验设备不能满足大颗粒土体试验的基本要求(试样土样的直径需大于或等于土样最大粒径的5倍)。因此,目前鲜有报道粗粒堆积土土-水特征的研究成果。
而且,人们普遍认为,粗粒堆积土的持水能力较弱,对土体的变形和强度几乎没有影响,然而,目前的研究结果表明,土体的SWCC受许多因素的影响,如密度、干湿循环、应力历史、细粒土含量等[1-2]。其中,细粒土的含量对土体SWCC有更显著的影响。粗粒堆积土中不仅含有大颗粒,而且含有大量细粒土。随着细粒土含量的增加,土体的SWCC不可避免地会发生变化,土体的力学特性将逐渐受到影响。因此,在细粒土含量增加的条件下,对粗粒堆积土土水特性的研究具有重要的理论意义和实际应用价值。
土水特性试验是一种耗时的试验,因为在每个阶段的气体压力下,土体中的气液平衡时间较长。因此,一般来说,研究土体SWCC的快速方法是建立SWCC的经验公式[3],例如Van Genuishen公式和Fredlund公式属于这种预测方法。这些模型只需要使用少量的试验数据来拟合经验公式中的关键参数,就可以得到完整的SWCC。然而,使用经验公式获得SWCC也是基于一些试验数据。为了进一步简化SWC的应用,一些学者在总结了大量土体的SWCC后,建立了与土颗粒分布相关的SWCC预测模型。例如,Arya等[4]、Tyler等[5]、Sweijen等[6]都建立了许多基于土颗粒级配的SWCC预测模型。这些模型基于细粒土的SWCC预测,其对粗粒堆积土的适用性仍需进一步研究。
针对粗粒堆积土SWCC研究的不足,本文首先介绍了一种新开发的非饱和粗粒堆积土三轴试验系统,该系统可以对粗粒堆积土进行大尺寸SWCC试验。在此基础上,总结了粗粒堆积土的SWCC试验方法和吸力平衡标准,研究了细粒土含量增加条件下粗粒堆积土SWCC的变化规律。最后,利用经典的AP模型,分析并得出了适用于粗粒堆积土SWCC的预测方法。
1. 非饱和粗粒堆积土三轴仪
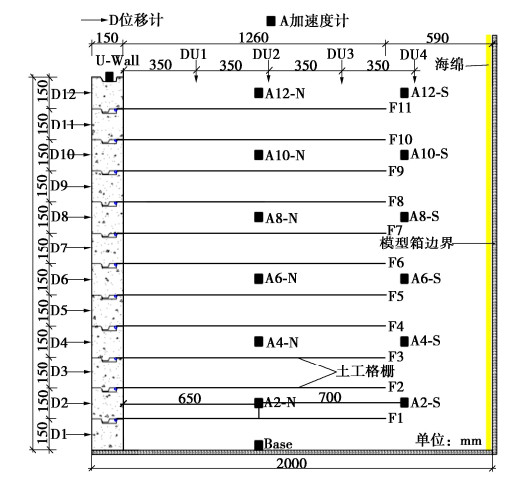
大型非饱和粗粒堆积土动静态三轴试验系统由压力控制系统、轴压加载系统、数据采集系统以及软件控制与分析系统组成。其中,涉及粗粒堆积土SWCC试验的主要系统和部件包括:陶土板底座、气压控制装置和排水测量系统,见图 1。大型非饱和三轴仪试样尺寸为150 mm×300 mm,该试验系统允许的最大颗粒粒径最大可达30 mm,这就大大消除了试验时替代大颗粒土所带来的偏差,试得试验结果更加符合实际。陶土板底座由3个具有高进气值的小陶土板构成,在有效隔绝土样气体排放的同时,避免了装样过程中陶土板受冲击破裂。
2. 非饱和粗粒堆积土SWCC试验方案
2.1 非饱和粗粒堆积土试样制备
试验土样取自某高铁站粗粒堆积土高填方边坡。为了研究不同细粒料含量(颗粒粒径小于0.075 mm)对粗粒堆积土土水特征曲线的影响,设计了3组细粒料含量不同的试样,细粒料质量含量分别为4.525%,9.05%,13.575%,试样的土颗粒级配见图 2。3组试样在粒径为5~30 mm的占比几乎相同,颗粒级配差异主要体现在5 mm粒径以下部分,并重点关注0.075 mm以下部分的含量。3组试样的干密度均控制为1.8 g/cm3。将配置好的试样搅拌均匀,分5次平均加入制样桶中。每次加样后应压实试样,控制单次加样高度为60 mm。
2.2 试验步骤与吸力平衡标准
粗粒土SWCC试验步骤参考细粒土试验步骤,不同的是,由于粗粒堆积土样品尺寸大、饱和含水率高,试验期间的气液平衡标准不同于细粒土试验。
小颗粒土壤水分特征试验的基质吸力平衡准则大致可分为两类:第一类是根据排水量与样本量的比例进行控制。例如,在褚进晶等[7]对黏土水的特性试验中,平衡标准是每2 h排水量小于样品体积的0.05%。第二类是控制排水量。例如,Pham[8]采用的平衡标准是,24 h内土壤样品的排水质量小于0.1 g。
由于粗粒堆积土样本的含水率相对较高,第二类控制标准对于大样本粗粒堆积土来说过于严格,因此根据第一类平衡标准来判断粗粒堆积土吸力平衡更合适。经过多次试验,发现以1 mL/h的出水速率作为吸力平衡的控制标准更为合理,即每1 h的排量小于样品体积的0.04%。
3. 细颗粒含量对粗粒堆积土SWCC影响
3.1 不同细颗粒含量试样试验结果
图 3给出了不同细颗粒含量试样的SWCC试验结果。由于试验数据点略少,采用经典VG模型对测得的试验数据进行拟合,以研究土壤水分特征参数,实测数据及拟合曲线见图 3(a)~(c)。
从图 3可以看出,与粉质黏土等细粒土相比,粗粒堆积土的持水能力相对较弱,土体中的水可以在较小的气压下排出,土体中的基质吸力相对较小。然而,随着细粒土含量的增加,粗粒堆积土的持水能力不断增加,土壤的进气值也相应增加,即Sa3 > Sa2 > Sa1,Sa1趋于0,未在图中展出。此外,随着细土含量的增加,土体的残余基质吸力也在增加,即ψ3 > ψ2 > ψ1,这也表明土壤的持水能力在增加,土体持水能力的提高必然会影响土体的变形和强度特性。
3.2 试验设备及方法可靠性验证
目前,关于粗粒堆积土土水特征的研究很少,仅通过前人极其有限的研究结果[9]作为对比数据,验证本文试验数据的合理性。对比试验数据见图 4。
通过对比可以发现,尽管土颗粒的分布不同,但粗粒堆积土的土水分布特征曲线具有明显的相似性,基质吸力范围基本相同。随着粗粒堆积土不均匀系数的增加,相同基质吸力下的饱和度逐渐升高,表明土体持水能力不断提高。上述对比结果说明了实验数据的合理性,证明了利用该三轴仪器进行试验的可靠性。
4. 基于AP模型的粗粒堆积土SWCC曲线预测方法
4.1 Arya-Paris模型
Arya-Paris模型[4]从土样土水特征曲线与颗分曲线的相似性出发,将土样视为由圆球状颗粒以及圆柱状孔隙组成的多孔介质,按照试样颗粒组成划定不同的粒组。将不同的颗粒分组视为若干等效粒径为Ri的相互独立的独立体,假设各独立体孔隙比与试样整体的孔隙比相同。各个独立体内的孔隙均为开口孔隙,并简化为毛细管通道。经此划分和简化后,结合一定合理化假设,即可求解土水特征曲线。具体过程可归纳为两条关键步骤:①通过求各组孔隙体积Vvi与总孔隙体积Vp的比值,推算各组孔隙充满水后的体积含水率θvi;②通过各组独立体颗粒个数ni和独立体孔隙半径ri,推算各级孔隙充满水后的基质吸力ψi。
综上所述,根据AP理论,在确定好试样颗粒级配后,就可以预测试样的土水特征曲线进行。具体过程可参见文献[17]。
4.2 Arya-Paris模型关键参数与预测效果分析
基于AP模型预测SWCC的过程中,考虑到土样理想孔隙和实际孔隙结构之间的差异,引入了一个经验参数,将每个独立体中的理想球形颗粒数ni转化为更真实的。这一参数是决定AP模型预测土样土水特征曲线实际效果的关键,现对其进行探讨。
关于值,Arya[4]进行了大量测试后得出结论,值在1.31~1.43,并建议取值为1.38,适用于大多数土体。随着对AP模型越来越深入的研究发现,取恒定值并不合理。一些研究人员认为,的值应符合土颗粒粒径越大,值越大的规则。为了更加准确地预测土-水分布特征曲线,研究者提出了3种确定经验参数值的方法[10-11],即线性拟合方法、非线性拟合方法及函数法。
图 5比较了基于非线性拟合方法、线性拟合方法以及函数法所确定的试样的SWCC曲线,对比结果总结如下:①通过函数法确定经验参数的方式,最终预测得到的试样土-水特征曲线与实测值偏差最大。②对于常数,当细粒土含量较低时,预测效果相对较好,但当细粒土含量增加时,常数取值的预测曲线与试验数据偏差较大,细粒土含量越高,偏差越大。③对于线性拟合方法得到的,当细粒土含量较低时,预测效果并不理想。但当细粒土含量增加时,预测效果相对理想,细土含量越高,预测曲线越好。④对于非线性拟合方法得到的,无论细粒土含量多少,预测曲线的方法都与试验数据吻合良好。因此,建议使用该方法预测粗粒堆积土的SWCC。
5. 结论
针对目前粗粒堆积土SWCC测试设备的缺乏和SWCC研究的不足,本文首先介绍了新开发的大型非饱和粗粒堆积土力学特性测试系统,并总结了粗粒堆积土SWCC的测试方法。然后分析了不同细粒土含量的粗粒堆积土SWCC的变化规律。最后,分析了不同α测定方法的AP模型对粗粒堆积土SWCC预测的影响,得到以下3点结论。
(1)对于粗粒堆积土,建议以1 mL/h的出水速率作为更合理的吸力平衡控制标准,即每1 h排水量小于样品体积的0.04%。
(2)对于粗粒堆积土,细粒土含量越高,迫使试样排水所需的空气压力越高(进气值越高),土体的残余基质吸力越高。这一规律意味着细粒土含量越高,粗粒堆积土的保水性能越好。
(3)AP模型中关键参数的确定方法,由非线性值得到的粗粒堆积土的SWCC曲线与试验数据最为吻合。建议使用该方法,预测粗粒堆积土的SWCC曲线。
-
表 1 试验工况
Table 1 Loading conditions
序号 输入波 加速度/g 相似比 工况代号 1 WN 0.05 1 WN1 WL, EL 0.1 4, 2 / 2 WN 0.05 1 WN2 WL, EL 0.2 4, 2 / 3 WN 0.05 1 WN3 WL, EL 0.4 4, 2 / 4 WN 0.05 1 WN4 WL, EL 0.6 4, 2 / 5 WN 0.05 1 WN5 WL, EL 0.8 4, 2 / 6 WN 0.05 1 WN6 WL, EL 1.0 4, 2 / 7 WN 0.05 1 WN7 WL, EL 1.2 4, 2 / 8 WN 0.05 1 WN8 WL 1.6 4, 2 / 9 WN 0.05 1 WN9 WL 2.0 4, 2 / 10 WN 0.05 1 WN10 表 2 工况与损伤程度对应情况
Table 2 Conditions corresponding to damage degree
工况 WN1 WN2 WN3 WN4 WN5 WN6 WN7 WN8 WN9 WN10 位移指数/% 0 0.07 0.10 0.32 0.73 1.05 1.59 2.38 3.34 >3.8 损伤程度 完好 基本完好 轻微破坏 中等破坏 毁坏 注:位移指数为累计水平永久位移与总墙高的比值。 -
[1] HAN J, JIANG Y, XU C. Recent advances in geosynthetic-reinforced retaining walls for highway applications[J]. Frontiers of Structural and Civil Engineering, 2018, 12(2): 239-247. doi: 10.1007/s11709-017-0424-8
[2] ZHU Y M, ZHANG F, JIA S L. Embodied energy and carbon emissions analysis of geosynthetic reinforced soil structures[J]. Journal of Cleaner Production, 2022, 370: 133510. doi: 10.1016/j.jclepro.2022.133510
[3] KUWANO J, MIYATA Y, KOSEKI J. Performance of reinforced soil walls during the 2011 Tohoku earthquake[J]. Geosynthetics International, 2014, 21(3): 179-196. doi: 10.1680/gein.14.00008
[4] KOERNER R M, KOERNER G R. An extended data base and recommendations regarding 320 failed geosynthetic reinforced mechanically stabilized earth (MSE) walls[J]. Geotextiles and Geomembranes, 2018, 46(6): 904-912. doi: 10.1016/j.geotexmem.2018.07.013
[5] LI S H, CAI X G, JING L P, et al. Lateral displacement control of modular-block reinforced soil retaining walls under horizontal seismic loading[J]. Soil Dynamics and Earthquake Engineering, 2021, 141: 106485. doi: 10.1016/j.soildyn.2020.106485
[6] LING H I, LESHCHINSKY D, CHOU N N S. Post-earthquake investigation on several geosynthetic-reinforced soil retaining walls and slopes during the Ji-Ji earthquake of [J]. Soil Dynamics and Earthquake Engineering, 2001, 21(4): 297-313. doi: 10.1016/S0267-7261(01)00011-2
[7] CAWLEY P. Structural health monitoring: closing the gap between research and industrial deployment[J]. Structural Health Monitoring, 2018, 17(5): 1225-1244. doi: 10.1177/1475921717750047
[8] 朱宏伟, 姚令侃, 张旭海. 两种加筋土挡墙的动力特性比较及抗震设计建议[J]. 岩土工程学报, 2012, 34(11): 2072-2080. http://cge.nhri.cn/cn/article/id/14907 ZHU Hongwei, YAO Lingkan, ZHANG Xuhai. Comparison of dynamic characteristics between netted and packaged reinforced soil retaining walls and recommendations for seismic design[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2072-2080. (in Chinese) http://cge.nhri.cn/cn/article/id/14907
[9] HUANG C C. Seismic responses of vertical-faced wrap-around reinforced soil walls[J]. Geosynthetics International, 2019, 26(2): 146-163. doi: 10.1680/jgein.18.00044
[10] 徐鹏, 蒋关鲁, 胡耀芳, 等. 整体刚性面板加筋土挡墙基频影响因素计算分析[J]. 岩土力学, 2018, 39(12): 4475-4481. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812022.htm XU Peng, JIANG Guanlu, HU Yaofang, et al. Calculation of fundamental frequencies of reinforced retaining walls with full-height rigid facing[J]. Rock and Soil Mechanics, 2018, 39(12): 4475-4481. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812022.htm
[11] ABBASI O, GHANBARI A, HOSSEINI S A A. An analytical method for calculating the natural frequency of reinforced retaining walls with soil–structure interaction effect[J]. Geosynthetics International, 2014, 21(1): 53-61. doi: 10.1680/gein.13.00034
[12] SARBISHEI S, FAKHER A. Energy-based horizontal slice method for pseudo-static analysis of reinforced walls[J]. Geosynthetics International, 2012, 19(5): 370-384. doi: 10.1680/gein.12.00023
[13] RAMEZANI M S, GHANBARI A, HOSSEINI S A A. Analytical method for calculating natural frequencies of geosynthetic-reinforced wall with full-height concrete facing[J]. Geosynthetics International, 2017, 24(1): 1-13. doi: 10.1680/jgein.16.00011
[14] 伍永胜. 加筋土挡墙动力特性及抗震设计方法研究[D]. 长沙: 湖南大学, 2006. WU Yongsheng. Study on Dynamic Characteristics and Seismic Design Method of Reinforced Earth Retaining Wall[D]. Changsha: Hunan University, 2006. (in Chinese)
[15] HATAMI K, BATHURST R J. Effect of structural design on fundamental frequency of reinforced-soil retaining walls[J]. Soil Dynamics and Earthquake Engineering, 2000, 19(3): 137-157. doi: 10.1016/S0267-7261(00)00010-5
[16] 李思汉. 模块式加筋土挡墙动力反应试验研究及数值分析[D]. 廊坊: 防灾科技学院, 2018. LI Sihan. Experimental Study and Numerical Analysis of Dynamic Response of Modular Reinforced Earth Retaining Wall[D]. Langfang: Institute of Disaster Prevention, 2018. (in Chinese)
[17] LI S H, CAI X G, JING L P, et al. Reinforcement strain and potential failure surface of geogrid reinforced soil-retaining wall under horizontal seismic loading[J]. Shock and Vibration, 2020, 2020: 8864256.
[18] CAI X G, LI S H, XU H L, et al. Shaking table study on the seismic performance of geogrid reinforced soil retaining walls[J]. Advances in Civil Engineering, 2021, 2021: 6668713.
[19] 李思汉, 蔡晓光, 景立平, 等. 基于位移的模块式加筋土挡墙抗震设计方法研究[J]. 地震工程学报, 2023, 45(5): 1066-1074. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ202305008.htm LI Sihan, CAI Xiaoguang, JING Liping, et al. Displacement-based seismic design methods of a modular reinforced soil retaining wall[J]. China Earthquake Engineering Journal, 2023, 45(5): 1066-1074. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ202305008.htm
[20] 魏明, 罗强, 蒋良潍, 等. 悬臂式加筋土复合支挡结构振动台模型试验研究[J]. 岩石力学与工程学报, 2021, 40(3): 607-618. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103014.htm WEI Ming, LUO Qiang, JIANG Liangwei, et al. Shaking table tests of cantilevered reinforced soil retaining walls[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 607-618. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103014.htm
[21] YAZDANDOUST M. Investigation on the seismic performance of steel-strip reinforced-soil retaining walls using shaking table test[J]. Soil Dynamics and Earthquake Engineering, 2017, 97: 216-232. doi: 10.1016/j.soildyn.2017.03.011
[22] 徐琨鹏. 地下结构拟静力抗震分析方法及推覆试验研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2019. XU Kunpeng. Quasi-static Seismic Analysis Method and Pushover Test of Underground Structures[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2019. (in Chinese)
[23] HUANG C C, WU S H, WU H J. Seismic displacement criterion for soil retaining walls based on soil strength mobilization[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(1): 74-83. doi: 10.1061/(ASCE)1090-0241(2009)135:1(74)
[24] 张建经, 韩鹏飞. 重力式挡墙基于位移的抗震设计方法研究: 大型振动台模型试验研究[J]. 岩土工程学报, 2012, 34(3): 416-423. http://cge.nhri.cn/cn/article/id/14513 ZHANG Jianjing, HAN Pengfei. Displacement based seismic design method for gravity retaining walls-Large scale shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(3): 416-423. (in Chinese) http://cge.nhri.cn/cn/article/id/14513




 下载:
下载: