软黏土基坑开挖诱发坑外地表沉降的时效解

应宏伟; 熊一帆; 李冰河; 吕唯; 程康; 张金红

doi:10.11779/CJGE20230727

软黏土基坑开挖诱发坑外地表沉降的时效解 English Version

应宏伟^{1, 2,},
熊一帆^1, ,,
李冰河³,
吕唯¹,
程康⁴,
张金红³

1.
河海大学岩土力学与堤坝工程教育部重点实验室, 江苏南京 210024
2.
浙江大学滨海和城市岩土工程研究中心, 浙江杭州 310058
3.
浙江省建筑设计研究院, 浙江杭州 310006
4.
中铁十一局集团有限公司, 湖北武汉 430061

基金项目:

国家自然科学基金项目 51678523

浙江省建设科研项目 2020K108

中央高校基本科研业务费资助项目 B200201012

详细信息

作者简介:
应宏伟(1971—)，男，博士，教授，主要从事地下工程、软黏土力学与地基处理方面的教学与科研工作。E-mail: ice898@zju.edu.cn

通讯作者:
熊一帆, E-mail: cxxyf0831@163.com

中图分类号: TU478
计量
- 文章访问数: 515
- HTML全文浏览量: 78
- PDF下载量: 156
出版历程
- 收稿日期: 2023-07-29
- 网络出版日期: 2024-04-18
- 刊出日期: 2024-09-30

Time-dependent solution for ground settlement induced by excavation in soft clay

1.
Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210024, China
2.
Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China
3.
Zhejiang Province Institute of Architectural Design and Research, Hangzhou 310006, China
4.
China Railway 11th Bureau Group Co., Ltd., Wuhan 430061, China

摘要

摘要: 对比理论和实测研究成果，发现既有坑外地表沉降计算方法不适用于蠕变效应显著的软土基坑。借助Lame方程和三参量黏弹性地基模型，推导得到柔性挡墙任意变位诱发坑外地表沉降的时效半解析解；将理论计算方法应用于杭州软土地区的两个深基坑工程实例，分析了从基坑开挖到地下室回筑的施工全过程中坑外地表沉降的发展规律。结果表明：①软土蠕变诱发不依赖于挡墙附加侧移的地表沉降，不仅导致软土基坑开挖期间的地表最大沉降与挡墙最大侧移之比远大于非软土基坑，而且引起坑外土体在地下室回筑期的持续沉降；②软土蠕变诱发的地表沉降随挡墙侧移的增大而增大，表现为凹槽沉降模式；③深厚软土深基坑的地表最大沉降与挡墙最大侧移之比主要受软土蠕变性和施工时间等因素的影响，与挡墙侧移量的关系不明显。
- 基坑开挖 /
- 地表沉降 /
- 软黏土蠕变 /
- 时效解
Abstract: By comparing the theoretical and measured results, it is observed that the current methods need to be revised in predicting the ground settlements induced by excavations in soft clay with a significant creep effect. Using the Lame equation and three-parameter viscoelastic foundation model, a time-dependent semi-analytical solution is derived for the ground settlements induced by arbitrary wall deflections. The solution is implemented in two excavations in Hangzhou soft clay, in which the development rules of the ground settlements from the soil excavation to basement construction are analyzed. The results indicate that: (1) The soft soil creep induces the ground settlements independently of the extra wall deflections, leading to a higher ratio of the maximum ground settlement to the maximum wall deflection during soil excavation compared to an excavation in non-soft clay. Furthermore, it results in continuous ground settlements during basement construction. (2) The ground settlements induced by the soft soil creep increase with wall deflections, showing the concave settlement mode. (3) The ratio of the maximum ground settlement to the maximum wall deflection of deep excavations in soft clay is primarily influenced by the creep characteristics of soft soil and construction duration, which appear unaffected by the wall deflections.
- excavation /
- ground settlement /
- soft soil creep /
- time-dependent solution

HTML全文

0. 引言

在建、构筑物密集的地区开挖基坑将不可避免地对邻近既有结构产生扰动，如房屋的沉降和不均匀沉降、隧道和地下管线的位移，严重时甚至会造成结构的破坏^[1]。因此，准确预测基坑开挖诱发的地表沉降具有重要的现实意义。

目前，研究基坑开挖诱发坑外地表沉降的方法主要有：①现场实测法。王卫东等^[2]整理统计了35个工程的实测数据，给出了上海软土地区深基坑地表最大沉降δ_vm与挡墙最大侧移δ_hm比值的平均值为0.84，该数值与江晓峰等^[3]归纳总结的平均值0.83极为接近；Tan等^[4]和Cheng等^[5]发现，及时浇筑混凝土底板能够有效抑制软土地区深基坑围护结构侧移和坑外土体位移的发展。②数值模拟法。Mu等^[6]利用实测数据对某基坑进行反分析建模，总结数值模型中土体位移的衰减规律，提出了考虑小应变特性的土体三维位移场经验公式；Ying等^[7]利用既有工程资料建立了杭州地铁基坑的标准化模型，基于标准化模型进行三维数值模拟，提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法。③理论解析法。Sagaseta^[8]利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发的土体位移解析公式；Xu等^[9]利用Sagaseta^[8]所提公式和面积等效原理，进一步推导了挡墙变形诱发土体位移的公式。钱建固等^[10]基于平面应变下的位移-位移弹性边值问题，从理论上推导了刚性挡墙在水平变位、绕墙趾转动模式下诱发的坑外地表沉降；以此为基础，许多学者进一步推导了柔性挡墙变位下坑外地表沉降的理论解答^[11-13]；当挡墙为抛物线模式时，所有理论解答给出δ_vm和δ_hm的关系为δ_vm/δ_hm≈0.4。

比较实测值^[2-3]与理论值^[11-13]可知，软土基坑的δ_vm/δ_hm实测值要远大于理论值，这是因为坑外软土的变形和强度会随时间发生明显变化，而既有理论解没有考虑软土的蠕变效应。针对既有研究的不足，本文借助Lame方程和三参量黏弹性地基模型，推导得到刚性挡墙平移变位和柔性挡墙任意变位诱发坑外地表沉降的时效半解析解；将理论计算方法应用于杭州软土地区的两个深基坑工程实例，分析了从基坑开挖到地下室回筑的施工全过程中坑外地表沉降的发展规律。

1. 理论计算方法

1.1 Flamant时效解

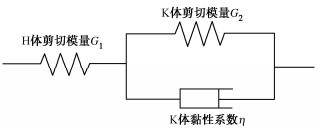
已有理论研究表明^[14-15]，三参量黏弹性地基模型能够较好地反映土体的瞬时变形以及随时间变化的蠕变。如图 1所示，三参量黏弹性地基模型由一个弹性元件（Hooke体）和黏性元件（Kelvin体）串联而成。

图 1 三参量黏弹性地基模型

Figure 1. Three-parameter viscoelastic foundation model

下载: 全尺寸图片幻灯片

祝彦知^[16]将一维三参量黏弹性地基模型推广至三维，并利用对应性原理得到Laplace变换域内弹性模量E和泊松比 $\nu$ 的表达式：

， 。

$\begin{array}{l}E(s)=\frac{9K({G}_{1}{G}_{2}+{G}_{1}\eta s)}{3K({G}_{1}+{G}_{2}+\eta s)+{G}_{1}{G}_{2}+{G}_{1}\eta s}\text{ }\text{，}\\ \nu (s)=\frac{3K({G}_{1}+{G}_{2}+\eta s)-2{G}_{1}{G}_{2}-2{G}_{1}\eta s}{6K({G}_{1}+{G}_{2}+\eta s)+2{G}_{1}{G}_{2}+2{G}_{1}\eta s}\text{ }。\end{array}\}$

(1)

式中：s为Laplace变换算子；K为整体的体积模量；G₁，G₂分别为H体和K体的剪切模量；η为K体黏性系数。

平面应变条件下，竖向集中力F作用于M(ξ, 0)诱发半平面地表任一点N(x, 0)的竖向位移为^[17]

。

${\delta _{\text{v}}} = \frac{{2(1 - {\nu ^2})F}}{{{\text{π }}E}}\ln \frac{L}{\rho } 。$

(2)

式中：L为M至Q(x_ref, 0)的距离，x=x_ref处地表沉降为零；ρ为M至N的距离。

假定竖向集中力F(t)=F₀H(t)，对F(t)进行Laplace变换，于是有

。

$F(s) = \frac{{{F_0}}}{s} 。$

(3)

将式（1），（3）代入式（2），并求Laplace逆变换可得Flamant时效解：

， 。

$\begin{array}{l}{\delta }_{\text{v}}=\frac{2J{F}_{0}}{\text{π}}\mathrm{ln}\frac{L}{\rho }\text{ }\text{，}\\ J=\frac{({G}_{1}+{G}_{2})(3K{G}_{1}+3K{G}_{2}+4{G}_{1}{G}_{2})}{4{G}_{1}{G}_{2}(3K{G}_{1}+3K{G}_{2}+{G}_{1}{G}_{2})}-\frac{1}{4{G}_{2}}{\text{e}}^{-\frac{{G}_{2}}{\eta }t}-\\ \frac{3{G}_{1}{}^{2}}{2(3K+{G}_{1})(6K{G}_{1}+6K{G}_{2}+{G}_{1}{G}_{2})}{\text{e}}^{-\frac{3K{G}_{1}+3K{G}_{2}+{G}_{1}{G}_{2}}{\left(3K+{G}_{1}\right)\eta }t}\text{ }。\end{array}\}$

(4)

1.2 刚性挡墙平移变位

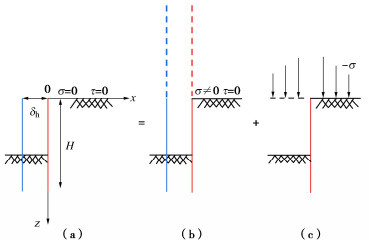
将刚性挡墙平移变位诱发坑外地表沉降简化为平面应变问题，图 2为力学模型。模型假定挡墙竖直，墙背光滑，深度为H，侧移为δ_h且瞬时施加；地基为均质、各向同性的黏弹性体，坑外地表水平且无超载。

图 2 力学模型

Figure 2. Mechanical model

下载: 全尺寸图片幻灯片

在不考虑体力的前提下，平面应变条件下的Lame方程可以表示为

， 。

$\begin{array}{l}({\lambda }_{1}+2{G}_{1})\frac{{\partial }^{2}u}{\partial {x}^{2}}+{G}_{1}\frac{{\partial }^{2}u}{\partial {z}^{2}}+({\lambda }_{1}+{G}_{1})\frac{{\partial }^{2}w}{\partial x\partial z}=0\text{ }\text{，}\hfill \\ ({\lambda }_{1}+2{G}_{1})\frac{{\partial }^{2}w}{\partial {z}^{2}}+{G}_{1}\frac{{\partial }^{2}w}{\partial {x}^{2}}+({\lambda }_{1}+{G}_{1})\frac{{\partial }^{2}u}{\partial x\partial z}=0\text{ }。\hfill \end{array}\}$

(5)

式中：u和w分别为土体的水平和竖向位移； ${\lambda _1}$ ，G₁为Lame系数， ${\lambda _1}$ =E₁ ${\nu _1}$ /[(1+ ${\nu _1}$ )(1–2 ${\nu _1}$ )]，G₁=E₁/[2(1+ ${\nu _1}$ )]，E₁和 ${\nu _1}$ 分别为H体的弹性模量和泊松比。

参考钱建固等^[10]的方法得到土体位移的通解：

， 。

$\begin{array}{l}\begin{array}{l}u={\displaystyle {\int }_{0}^{+\infty }\frac{1}{\alpha }\left[{K}_{1}\mathrm{cos}(\alpha z)+{K}_{2}\mathrm{sin}(\alpha z)\right]\cdot }\\ \text{ }(A+\alpha x){\text{e}}^{-\alpha x}\text{d}\alpha \text{ }\text{，}\end{array}\hfill \\ \begin{array}{l}w={\displaystyle {\int }_{0}^{+\infty }\frac{1}{\alpha }\left[-{K}_{2}\mathrm{cos}\left(\alpha z\right)+{K}_{1}\mathrm{sin}(\alpha z)\right]\cdot }\\ \text{ }\left(A-\frac{{\lambda }_{1}+3{G}_{1}}{{\lambda }_{1}+{G}_{1}}+\alpha x\right){\text{e}}^{-\alpha x}\text{d}\alpha \text{ }。\end{array}\hfill \end{array}\}$

(6)

式中：K₁，K₂和A为待定系数，可利用边界条件确定。由τ_xz|z=0=0得K₂=0；令K₃=K₁A，考虑墙背光滑条件下τ_xz|x=0=0，可得

。

${K_3} = \frac{{{\lambda _1} + 2{G_1}}}{{{\lambda _1} + {G_1}}}{K_1} 。$

(7)

将K₂和K₃代入式（6），则有

， 。

$\begin{array}{l}\begin{array}{l}u={\displaystyle {\int }_{0}^{+\infty }\frac{1}{\alpha }\mathrm{cos}\left(\alpha z\right)\left(1+\frac{{\lambda }_{1}+{G}_{1}}{{\lambda }_{1}+2{G}_{1}}\alpha x\right){K}_{3}{\text{e}}^{-\alpha x}\text{d}\alpha \text{ }\text{，}}\\ w={\displaystyle {\int }_{0}^{+\infty }\frac{1}{\alpha }\mathrm{sin}(\alpha z)\left(-\frac{{G}_{1}}{{\lambda }_{1}+2{G}_{1}}+\frac{{\lambda }_{1}+{G}_{1}}{{\lambda }_{1}+2{G}_{1}}\alpha x\right)\cdot }\end{array}\hfill \\ \text{ }{K}_{3}{\text{e}}^{-\alpha x}\text{d}\alpha \text{ }。\hfill \end{array}\}$

(8)

刚性挡墙平移变位的边界条件为侧移δ_h，于是有

。

$u = \int_0^{ + \infty } {\frac{1}{\alpha }{K_3}\cos (\alpha z){\text{d}}\alpha } = - {\delta _{\text{h}}} 。$

(9)

对δ_h采用Fourier余弦变换可得

。

$- {\delta _{\text{h}}} = - \frac{{2{\delta _{\text{h}}}}}{{\text{π }}}\int_0^{ + \infty } {\frac{{\sin (H\alpha )}}{\alpha }\cos {\text{(}}\alpha z{\text{)d}}\alpha } 。$

(10)

对比式（9），（10），则有

。

${K_3} = - \frac{{2{\delta _{\text{h}}}}}{{\text{π }}}\sin (H\alpha ) 。$

(11)

将式（11）代入式（8），于是有

， 。

$\begin{array}{l}u=-\frac{2{\delta }_{\text{h}}}{\text{π}}{\displaystyle {\int }_{0}^{+\infty }\frac{1}{\alpha }\mathrm{cos}\left(\alpha z\right)\left(1+\frac{{\lambda }_{1}+{G}_{1}}{{\lambda }_{1}+2{G}_{1}}\alpha x\right)\cdot }\\ \text{ }\mathrm{sin}(H\alpha ){\text{e}}^{-\alpha x}\text{d}\alpha \text{ }\text{，}\\ w=-\frac{2{\delta }_{\text{h}}}{\text{π}}{\displaystyle {\int }_{0}^{+\infty }\frac{1}{\alpha }\mathrm{sin}\left(\alpha z\right)\left(-\frac{{G}_{1}}{{\lambda }_{1}+2{G}_{1}}+\frac{{\lambda }_{1}+{G}_{1}}{{\lambda }_{1}+2{G}_{1}}\alpha x\right)\cdot }\\ \text{ }\mathrm{sin}(H\alpha ){\text{e}}^{-\alpha x}\text{d}\alpha \text{ }。\end{array}\}$

(12)

观察式（12）不难发现，w_|z=0=0，表明图 2（b）的挡墙侧移并不诱发地表沉降。

由式（6）可求得坑外土体应力场，进而推导得到所需施加的地表竖向正应力：

。

$\sigma = \frac{1}{{2\beta }}\int_0^{ + \infty } {\left( {1 - \alpha x} \right){K_3}{{\text{e}}^{ - \alpha x}}} {\text{d}}\alpha 。$

(13)

式中：β=(1– $\nu _1^2$ )/E₁。

将式（11）代入式（13），积分计算后可得

。

$\sigma = \frac{{{\delta _{\text{h}}}H({H^2} - {x^2})}}{{\beta {\text{π }}{{({x^2} + {H^2})}^2}}} 。$

(14)

将式（14）代入式（4），并对隐含于L，ρ的ξ积分可求得刚性挡墙平移变位诱发坑外地表沉降的时效显式解：

${\delta _{\text{v}}} = \frac{J}{\beta }\frac{{2{\delta _{\text{h}}}{H^2}}}{{\text{π }}}\left( {\frac{1}{{{x^2} + {H^2}}} - \frac{1}{{x_{{\text{ref}}}^2 + {H^2}}}} \right) 。$

(15)

值得说明的是，δ_v为z=0时的w；当t=0时，J=β。

令式（15）中的t=0可得到刚性挡墙平移变位诱发坑外地表沉降的弹性解，式（15）与弹性解的差值为土体蠕变诱发的地表沉降：

${\delta _{{\text{vc}}}} = \frac{{J - \beta }}{\beta }\frac{{2{\delta _{\text{h}}}{H^2}}}{{\text{π }}}\left( {\frac{1}{{{x^2} + {H^2}}} - \frac{1}{{x_{{\text{ref}}}^2 + {H^2}}}} \right) 。$

(16)

不难发现，蠕变沉降并不依赖于边界条件的改变，即蠕变会诱发坑外土体产生不依赖于挡墙附加侧移的沉降；挡墙侧移越大，相同时间内蠕变诱发的地表沉降也就越大。

1.3 柔性挡墙任意变位

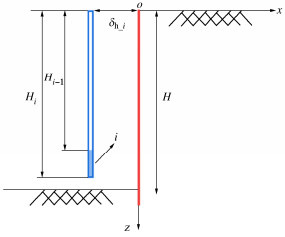
参考胡之锋等^[12]的做法，将柔性挡墙的侧移曲线划分为n个微段，每个微段的变位都视为刚性挡墙平移变位，通过求和所有微段变位诱发的地表沉降得到柔性挡墙任意变位诱发的坑外地表沉降，见图 3。

图 3 挡墙微段侧移诱发地表沉降计算示意图

Figure 3. Calculation diagram of ground settlements induced by wall deflection of a micro-segment

下载: 全尺寸图片幻灯片

当i=1，x_{1_ref}取无限大时，墙顶微段变位诱发的地表沉降可以表示为

$\Delta {\delta _{{\text{v}}\_}}_1 = \frac{J}{\beta }\frac{{2{\delta _{\text{h}}}{{_\_}_1}H_1^2}}{{{\text{π }}({x^2} + H_1^2)}} 。$

(17)

当i≥2时，深度为H_i和H_i–1的挡墙变位诱发的地表沉降分别为

$\begin{array}{l}{\delta }_{\text{v}\_}{}_{i}=\frac{J}{\beta }\frac{2{\delta }_{\text{h}}{{}_{\_}}_{i}{H}_{i}^{2}}{\text{π}}\left(\frac{1}{{x}^{2}+{H}_{i}^{2}}-\frac{1}{{x}_{i\_\text{ref}}^{2}+{H}_{i}^{2}}\right)\text{ }\text{，}\\ {\delta }_{\text{v}\_}{}_{i-1}=\frac{J}{\beta }\frac{2{\delta }_{\text{h}}{{}_{\_}}_{i}{H}_{i-1}^{2}}{\text{π}}\left(\frac{1}{{x}^{2}+{H}_{i-1}^{2}}-\frac{1}{{x}_{i-1\_\text{ref}}^{2}+{H}_{i-1}^{2}}\right)。\end{array}\}$

(18)

将x_{i_ref}=mH_i，x_{i–1_ref}=mH_i–1代入式（18），上下作差后则有

$\Delta {\delta _{{\text{v}}\_}}_i = \frac{J}{\beta }\frac{{2{\delta _{\text{h}}}{{_\_}_i}}}{{\text{π }}}\frac{{{x^2}(H_i^2 - H_{i - 1}^2)}}{{({x^2} + H_{i - 1}^2)({x^2} + H_i^2)}} 。$

(19)

运用叠加原理，柔性挡墙任意变位诱发坑外地表沉降的时效解可以表示为

${\delta _{\text{v}}} = \Delta {\delta _{{\text{v}}\_}}_1 + \sum\limits_{i = 2}^n {\Delta {\delta _{{\text{v}}\_}}_i} 。$

(20)

1.4 软土基坑分步施工工况下的计算思路

设置多道内撑的深基坑一般采用逐层开挖、设置支撑和逐层拆换撑的分步施工法，为考虑实际工程中的复杂分步施工工况，利用考虑应力加载历史的“陈氏加载法”^[18]思路计算多工况下考虑土体蠕变的基坑支护墙侧向变形诱发的坑外地表沉降。工况k的地表沉降可由下式求得

$\delta _{\text{v}}^k = \delta _{{\text{ve}}}^k + \sum\limits_{j = 1}^k {\delta _{{\text{vc}}}^j} 。$

(21)

式中： $\delta _{{\text{ve}}}^k$ 为工况k下的弹性沉降，将工况k的挡墙侧移作为式（20）的边界条件并令t=0可以计算得到； $\delta _{{\text{vc}}}^j$ 为工况j（1≤j≤k）的蠕变沉降，可由下式求得

$\delta _{{\text{vc}}}^j = \sum\limits_{p = 1}^j {\delta _{{\text{vc}}}^{pj}} 。$

(22)

式中： $\delta _{{\text{vc}}}^{pj}$ 体现了上文所述的考虑应力加载历史，含义为工况p（1≤p≤j）引起工况j时间段内的蠕变沉降，将工况p相较于工况p–1的挡墙侧移增量作为式（20）的边界条件，计算t=t_j+1–t_p和t=t_j–t_p的沉降差值可以得到。有关基坑施工工况及时间节点的定义可参考后文的表 1和表 3。

表 1 基坑施工时间表

Table 1. Construction schedule of excavation

工况	施工内容	t/d
1	开挖至–8.3 m，第2道支撑形成强度	t₁~t₂: 0~30
2	开挖至–13.8 m，第3道支撑形成强度	t₂~t₃: 30~67
3	开挖至–17.9 m，第4道支撑形成强度	t₃~t₄: 67~110
4	开挖至–22.1 m，第5道支撑形成强度	t₄~t₅: 110~142
5	开挖至–26.3 m，第6道支撑形成强度	t₅~t₆: 142~173
6	开挖至–30.2 m，底板形成强度	t₆~t₇: 173~230
7	地下室回筑施工	t₇~t₈: 230~680

下载: 导出CSV

| 显示表格

2. 工程应用实例一

2.1 工程概况

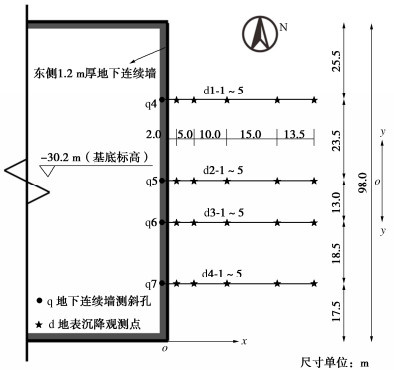
杭州中心项目超深顺作基坑采用分坑施工方法，Cheng等^[5]分析了B2分坑开挖的变形性状，但受限于当时项目施工进度，未报道地下室回筑期坑外土体的显著蠕变行为。地连墙深度范围内，自上而下的主要地层分别为①填土、②软土、③粉质黏土、④圆砾、⑤强风化和⑥中风化砂岩；基坑开挖深度为30.2 m，平面尺寸约98 m×92 m；围护结构采用厚1.2 m、深50 m的地连墙结合6道混凝土支撑和被动区加固；基坑外侧未降水，且围护墙进入不透水层隔绝了坑内外的水力联系，开挖和回筑过程中坑外水位基本稳定，故地下水对地表沉降的影响可忽略不计；基坑监测工作自2019年4月1日第1道支撑形成开始（见图 4），至2021年2月7日地下室施工完成结束，可分为如表 1所示的7个工况。

图 4 基坑监测点位示意图

Figure 4. Schematic diagram of excavation monitoring

下载: 全尺寸图片幻灯片

2.2 实测分析

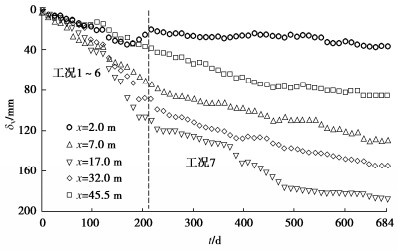
图 5给出了监测断面d2的地表沉降随时间的发展规律。由图 5可见，在整个基坑开挖过程中，地表沉降的速率较大，没有明显的平台期，这说明坑外土体没有因为支撑、底板强度形成期间开挖的暂停而放缓沉降。由于2.5 m厚的基础底板侧向刚度大、6道临时支撑和各层地下室楼板的拆换撑措施合理，地下室回筑期的挡墙侧移增量并不大。然而，坑外土体仍然产生了明显的沉降增量，可以认为工况7地表持续沉降的主要原因是深厚软土的蠕变。进一步观察可以发现，工况7中软土蠕变诱发的坑外地表沉降随距基坑侧壁距离的增大先增大后减小，表现为凹槽沉降模式^[19]。

图 5 地表沉降随时间的发展

Figure 5. Development of ground settlements versus time

下载: 全尺寸图片幻灯片

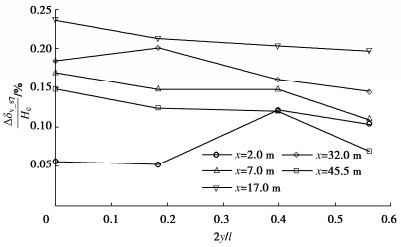
图 6给出了在工况7下，d1~d4监测断面的地表沉降增量与距基坑中心线距离的关系，其中Δδ_{v_s7}为工况7的地表沉降增量，y为平行于墙体轴线方向、距基坑中心线的距离，l为基坑的边长。可见，随着与基坑中心线纵向距离的增大，地表沉降增量总体呈下降趋势。考虑到基坑角部的侧移明显小于中部，可以认为挡墙侧移越大，相同时间内蠕变诱发的地表沉降也越大，这与时效解的结论是吻合的。

图 6 地下室施工期间纵向地表沉降增量

Figure 6. Increments of longitudinal ground settlements during basement construction

下载: 全尺寸图片幻灯片

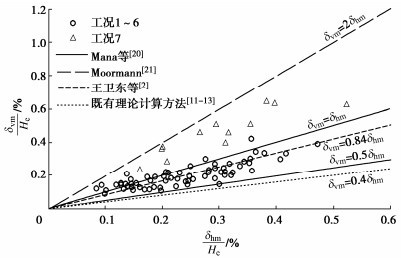
图 7给出了不同工况下地表最大沉降与挡墙最大侧移的关系，其中H_e为基坑开挖深度。可以看出，开挖工况的实测数据点大多落在Mana等^[20]提出的δ_vm/δ_hm=0.5~1.0的范围内，且与王卫东等^[2]得出的软土地区δ_vm/δ_hm平均值为0.84的结论较为吻合。地下室回筑工况的δ_vm/δ_hm相较于开挖工况明显提高，这主要是因为深厚软土的蠕变引发与挡墙附加侧移无关的土体沉降。显而易见，无论是开挖还是回筑工况，既有理论计算方法均不适用于软土地区，说明深开挖引起坑外地表沉降预测时考虑软土蠕变的必要性。

图 7 地表最大沉降与挡墙最大侧移的关系

Figure 7. Relationships between maximum ground settlements and.maximum wall deflections

下载: 全尺寸图片幻灯片

2.3 参数确定

有关杭州软土蠕变试验的研究中，邓会元等^[22]利用杭州软土进行三轴蠕变试验，得到了三参量黏弹性地基模型的拟合参数，然而不同 ${\sigma _3}$ 和 ${\sigma _1}$ – ${\sigma _3}$ 下K体参数的差异极大；还有一些试验研究表明^[23-24]，不同应力路径下软土的蠕变性状亦有区别，卸荷条件下的蠕变相较于轴向加载更为显著，得到的K体参数存在明显差异；不仅如此，本文时效解更需要将地基作为整体的计算参数，单一软土层的参数似乎很难体现坑外地基的性状。因此，本文通过对地下室回筑期地表沉降的发展规律反分析以获得所需的K体参数，H体参数则根据土层厚度求加权平均值（实例二同）。

对于土体黏弹性问题，一般假设体积模量与时间无关^[25]，此时K=E₁/[3(1–2 ${\nu _1}$ )]；H体剪切模量的计算公式则为G₁=E₁/[2(1+ ${\nu _1}$ )]。杨敏等^[26]认为土体弹性模量可近似取2.5~3.5倍的压缩模量；本文取E₁=3E_s1，E_s1为H体的压缩模量。根据土层厚度对不同土体参数求加权平均值可得到非时效计算参数。

基于得到的非时效计算参数和地表沉降实测值反分析K体计算参数。具体的，利用地下室回筑期d2-3的地表沉降收敛规律以及沉降增量分别确定η和G₂，反分析时扣除了拆换撑引起的挡墙侧移对地表沉降的影响。

表 2 土体参数

Table 2. Soil parameters

计算参数	数值	计算参数	数值
${\nu _1}$	0.37	G₁/MPa	4.8
E_s1/MPa	4.4	G₂/MPa	1.4
E₁/MPa	13.2	η/(MPa·d)	200
K/MPa	17.2

下载: 导出CSV

| 显示表格

2.4 与实测数据的对比分析

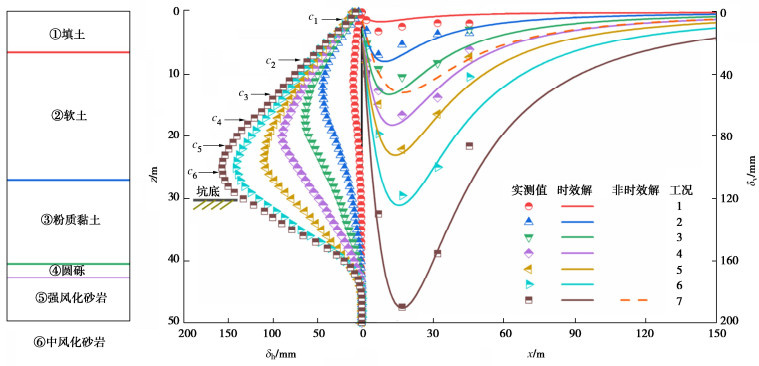
图 8给出了不同工况下基坑中心线横剖面地表沉降计算值与实测值的对比，以及相应工况下的实测墙体水平位移沿深度的分布曲线，其中c₁~c₆为6道混凝土支撑。结果表明，非时效解^[11-13]严重低估了地表沉降，不适用于蠕变效应显著的软土基坑。时效解虽然无法考虑土体的小应变特性，导致坑外远端的地表沉降收敛较为缓慢，表明理论计算方法的局限性；但其能够较好地模拟地表沉降的分布和随基坑施工各工况的发展变化规律，与实测值吻合较好。与实测分析的结论类似，蠕变不仅在开挖阶段引发了较大的地表沉降，还导致土体在地下室回填施工期间发生持续沉降。分析其机理，作者认为对于挡墙侧移较大的基坑，侧向应力大幅减小，而竖向应力基本不变，此种水平卸荷应力路径的蠕变竖向变形相较于轴向加载路径更为明显^[23]。

图 8 地表沉降计算值与实测值对比

Figure 8. Comparison of ground settlements between this study and measured results

下载: 全尺寸图片幻灯片

3. 工程应用实例二

3.1 工程概况

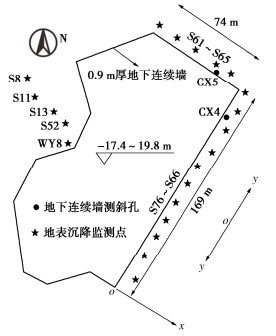
杭州天城广场深基坑采用顺作法施工，应宏伟等^[27]分析了土体蠕变对基坑变形的影响。地连墙深度范围内，自上而下的主要地层分别为①粉质黏土、②砂质粉土、③淤泥质粉质黏土、④粉质黏土；基坑开挖深度为17.4~19.8 m，坑底附近为深厚淤泥质土，平面形状不规则，周长约560 m；围护结构采用厚0.9 m、深40 m的地连墙结合3道混凝土支撑和被动区加固；基坑外侧未降水，且围护墙隔绝了坑内外的水力联系，故地下水对地表沉降的影响可忽略不计；基坑监测工作自第1道支撑形成开始（见图 9），至地下室施工完成结束，可分为如表 3所示的4个工况。

图 9 基坑监测点位示意图

Figure 9. Schematic diagram of excavation monitoring

下载: 全尺寸图片幻灯片

表 3 基坑施工时间表

Table 3. Construction schedule of excavation

工况	施工内容	t/d
1	开挖至–8.2 m，第2道支撑形成强度	t₁~t₂: 0~49
2	开挖至–13.6 m，第3道支撑形成强度	t₂~t₃: 49~106
3	开挖至坑底，底板形成强度	t₃~t₄: 106~240
4	地下室回筑施工	t₄~t₅: 240~441

下载: 导出CSV

| 显示表格

3.2 实测分析

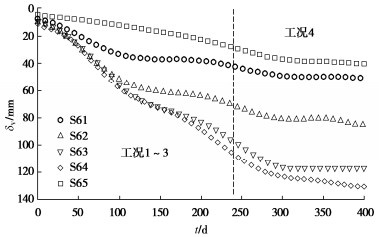
图 10给出了S61~S65的地表沉降随时间的发展规律，同样可认为工况4地下室回筑期地表持续沉降的主要诱因是深厚软土的蠕变。

图 10 地表沉降随时间的发展

Figure 10. Development of ground settlements versus time

下载: 全尺寸图片幻灯片

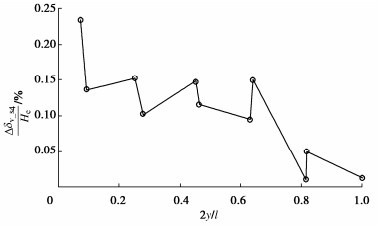
图 11给出了在工况4下，S66~S76的地表沉降增量与距基坑中心线距离的关系，其中Δδ_{v_s4}为工况4的地表沉降增量。可见，随着与基坑中心线纵向距离的增大，地表沉降增量总体呈下降趋势。同样的，认为实测数据验证了时效解的结论。

图 11 地下室施工期间纵向地表沉降增量

Figure 11. Increments of longitudinal ground settlements during basement construction

下载: 全尺寸图片幻灯片

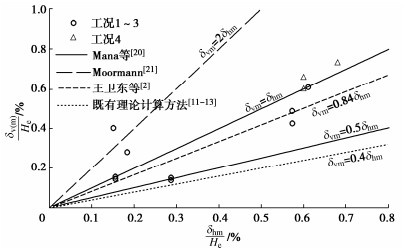
图 12给出了不同工况下地表沉降与挡墙最大侧移的关系。可以看出，不同工况的δ_v/δ_hm远大于既有理论计算方法的δ_vm/δ_hm，再次说明了提出考虑软土蠕变的坑外地表沉降计算方法的必要性。

图 12 地表沉降与挡墙最大侧移的关系

Figure 12. Relationships between ground settlements and maximum wall deflections

下载: 全尺寸图片幻灯片

应宏伟等^[27]给出了在工况4下，WY8~S8的地表沉降增量。同样的，发现工况4中软土蠕变诱发的坑外地表沉降随距基坑侧壁距离的增大先增大后减小，表现为凹槽沉降模式^[19]。限于篇幅，相关图表从略。

3.3 参数确定

实例二中，①粉质黏土、②砂质粉土厚度共约13 m，③淤泥质粉质黏土厚约18 m，④粉质黏土厚约19 m。从表 4中可以看出，反分析得到的G₂相较于实例一偏大，即地基蠕变性不如实例一，这符合实例二地基土上硬中软下硬的客观事实。

表 4 土体参数

Table 4. Soil parameters

计算参数	数值	计算参数	数值
${\nu _1}$	0.37	G₁/MPa	5.2
E_s1/MPa	4.7	G₂/MPa	2.5
E₁/MPa	14.1	η/(MPa·d)	200
K/MPa	17.9

下载: 导出CSV

| 显示表格

3.4 与实测数据的对比分析

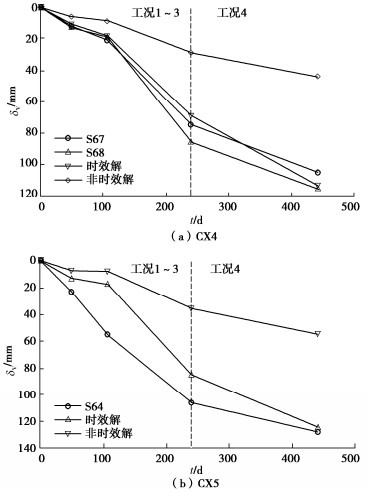
基于测点CX4、CX5的实测地表沉降和表 4的土体参数，图 13给出了地表沉降计算值与实测值随时间发展的对比。可以看出，非时效解^[11-13]严重低估了坑外地表沉降，不适用于蠕变效应显著的软土基坑；本文时效解则较好地模拟了坑外地表沉降随时间的发展变化规律，与实测值吻合较好。

图 13 地表沉降计算值与实测值对比

Figure 13. Comparison of ground settlements between this study and measured results

下载: 全尺寸图片幻灯片

4. 参数分析

以实例一为基础，探讨不同因素对软土基坑坑外地表沉降的影响。

4.1 K体剪切模量

图 14给出了K体剪切模量G₂对地表沉降、地表蠕变沉降的影响。从图 14中可以看出，G₂越小，蠕变引起的地表沉降越大，地表蠕变沉降在总沉降中所占比例越大，同时收敛过程中的变形增量也越大。地表蠕变沉降随距基坑侧壁距离的增大先增大后减小，表现为凹槽沉降模式^[19]，这与实测分析中的结论是一致的。

图 14 K体剪切模量的影响

Figure 14. Influences of shear modulus of K-body

下载: 全尺寸图片幻灯片

4.2 K体黏性系数

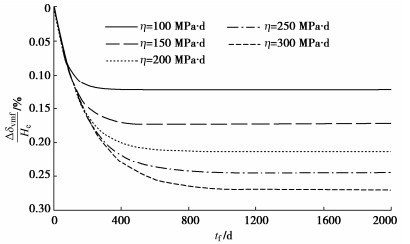
图 15给出了K体黏性系数η对基坑开挖结束后坑外地表最大沉降的影响，其中t_f以底板形成强度为时间起点，Δδ_vmf为相应的地表沉降增量。观察结果可知，随着η的增大，地表沉降增量和收敛时间都相对增加。对于软土基坑而言，土方开挖结束并不意味着地表沉降的收敛，因此需要密切关注地表沉降的进一步发展。

图 15 黏性系数对开挖结束后地表最大沉降的影响

Figure 15. Influence of viscosity coefficient on maximum ground settlement after soil excavation

下载: 全尺寸图片幻灯片

4.3 挡墙侧移

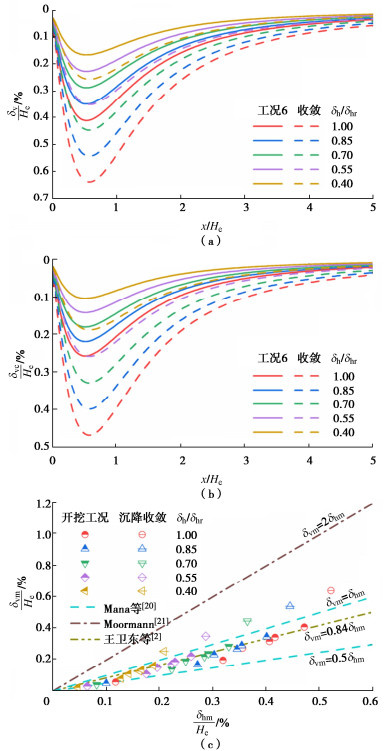
图 16给出了挡墙侧移对地表沉降、地表蠕变沉降和δ_vm/δ_hm的影响，其中δ_hr为实例一中的挡墙侧移。从图 16（a），（b）可以看出，挡墙侧移越大，地表沉降和蠕变诱发的地表沉降也就越大。观察图 16（c）不难发现，基坑开挖工况和地表沉降收敛时的δ_vm/δ_hm分别始终落在0.84，1.23附近，说明δ_vm/δ_hm与挡墙侧移量的关系不显著，可以认为δ_vm/δ_hm主要受软土蠕变性强弱、施工时间等因素的影响。

图 16 挡墙侧移的影响

Figure 16. Influences of wall deflections

下载: 全尺寸图片幻灯片

5. 结论

（1）对比理论和实测研究成果，发现既有坑外地表沉降计算方法不适用于蠕变效应显著的软土基坑。借助Lame方程和三参量黏弹性地基模型，推导得到刚性挡墙平移变位和柔性挡墙任意变位诱发坑外地表沉降的时效半解析解。

（2）将理论计算方法应用于杭州软土地区的两个深基坑工程实例，验证了本文时效解的合理性和适用性。进一步分析了从基坑开挖到地下室回筑的施工全过程中坑外地表沉降的发展规律，发现软土蠕变诱发不依赖于挡墙附加侧移的地表沉降，不仅导致软土基坑开挖期间的地表最大沉降与挡墙最大侧移之比远大于非软土基坑，而且引起土体在地下室回筑期的持续沉降。

（3）参数分析表明，软土蠕变诱发的地表沉降随挡墙侧移的增大而增大，表现为凹槽沉降模式；地表最大沉降与挡墙最大侧移之比主要受软土蠕变性强弱、施工时间等因素的影响，与挡墙侧移量的关系不明显。

图 1 三参量黏弹性地基模型

Figure 1. Three-parameter viscoelastic foundation model

下载: 全尺寸图片幻灯片

图 2 力学模型

Figure 2. Mechanical model

下载: 全尺寸图片幻灯片

图 3 挡墙微段侧移诱发地表沉降计算示意图

Figure 3. Calculation diagram of ground settlements induced by wall deflection of a micro-segment

下载: 全尺寸图片幻灯片

图 4 基坑监测点位示意图

Figure 4. Schematic diagram of excavation monitoring

下载: 全尺寸图片幻灯片

图 5 地表沉降随时间的发展

Figure 5. Development of ground settlements versus time

下载: 全尺寸图片幻灯片

图 6 地下室施工期间纵向地表沉降增量

Figure 6. Increments of longitudinal ground settlements during basement construction

下载: 全尺寸图片幻灯片

图 7 地表最大沉降与挡墙最大侧移的关系

Figure 7. Relationships between maximum ground settlements and.maximum wall deflections

下载: 全尺寸图片幻灯片

图 8 地表沉降计算值与实测值对比

Figure 8. Comparison of ground settlements between this study and measured results

下载: 全尺寸图片幻灯片

图 9 基坑监测点位示意图

Figure 9. Schematic diagram of excavation monitoring

下载: 全尺寸图片幻灯片

图 10 地表沉降随时间的发展

Figure 10. Development of ground settlements versus time

下载: 全尺寸图片幻灯片

图 11 地下室施工期间纵向地表沉降增量

Figure 11. Increments of longitudinal ground settlements during basement construction

下载: 全尺寸图片幻灯片

图 12 地表沉降与挡墙最大侧移的关系

Figure 12. Relationships between ground settlements and maximum wall deflections

下载: 全尺寸图片幻灯片

图 13 地表沉降计算值与实测值对比

Figure 13. Comparison of ground settlements between this study and measured results

下载: 全尺寸图片幻灯片

图 14 K体剪切模量的影响

Figure 14. Influences of shear modulus of K-body

下载: 全尺寸图片幻灯片

图 15 黏性系数对开挖结束后地表最大沉降的影响

Figure 15. Influence of viscosity coefficient on maximum ground settlement after soil excavation

下载: 全尺寸图片幻灯片

图 16 挡墙侧移的影响

Figure 16. Influences of wall deflections

下载: 全尺寸图片幻灯片

表 1 基坑施工时间表

Table 1 Construction schedule of excavation

工况	施工内容	t/d
1	开挖至–8.3 m，第2道支撑形成强度	t₁~t₂: 0~30
2	开挖至–13.8 m，第3道支撑形成强度	t₂~t₃: 30~67
3	开挖至–17.9 m，第4道支撑形成强度	t₃~t₄: 67~110
4	开挖至–22.1 m，第5道支撑形成强度	t₄~t₅: 110~142
5	开挖至–26.3 m，第6道支撑形成强度	t₅~t₆: 142~173
6	开挖至–30.2 m，底板形成强度	t₆~t₇: 173~230
7	地下室回筑施工	t₇~t₈: 230~680

下载: 导出CSV

表 2 土体参数

Table 2 Soil parameters

计算参数	数值	计算参数	数值
${\nu _1}$	0.37	G₁/MPa	4.8
E_s1/MPa	4.4	G₂/MPa	1.4
E₁/MPa	13.2	η/(MPa·d)	200
K/MPa	17.2

下载: 导出CSV

表 3 基坑施工时间表

Table 3 Construction schedule of excavation

工况	施工内容	t/d
1	开挖至–8.2 m，第2道支撑形成强度	t₁~t₂: 0~49
2	开挖至–13.6 m，第3道支撑形成强度	t₂~t₃: 49~106
3	开挖至坑底，底板形成强度	t₃~t₄: 106~240
4	地下室回筑施工	t₄~t₅: 240~441

下载: 导出CSV

表 4 土体参数

Table 4 Soil parameters

计算参数	数值	计算参数	数值
${\nu _1}$	0.37	G₁/MPa	5.2
E_s1/MPa	4.7	G₂/MPa	2.5
E₁/MPa	14.1	η/(MPa·d)	200
K/MPa	17.9

下载: 导出CSV

参考文献(27)

[1]	郑刚. 软土地区基坑工程变形控制方法及工程应用[J]. 岩土工程学报, 2022, 44(1): 1-36. ZHENG Gang. Method and application of deformation control of excavations in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(1): 1-36. (in Chinese)
[2]	王卫东, 徐中华, 王建华. 上海地区深基坑周边地表变形性状实测统计分析[J]. 岩土工程学报, 2011, 33(11): 1659-1666. WANG Weidong, XU Zhonghua, WANG Jianhua. Statistical analysis of characteristics of ground surface settlement caused by deep excavations in Shanghai soft soils[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1659-1666. (in Chinese)
[3]	江晓峰, 刘国彬, 张伟立, 等. 基于实测数据的上海地区超深基坑变形特性研究[J]. 岩土工程学报, 2010 32(增刊2): 570-573. JIANG Xiaofeng, LIU Guobin, ZHANG Weili, et al. Deformation characteristics of ultra-deep foundation pit in Shanghai based on measured data[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S2): 570-573. (in Chinese)
[4]	TAN Y, WEI B, ZHOU X, et al. Lessons learned from construction of Shanghai metro stations: importance of quick excavation, prompt propping, timely casting, and segmented construction[J]. Journal of Performance of Constructed Facilities, 2015, 29(4): 04014096. doi: 10.1061/(ASCE)CF.1943-5509.0000599
[5]	CHENG K, XU R Q, YING H W, et al. Observed performance of a 30.2 m deep-large basement excavation in Hangzhou soft clay[J]. Tunnelling and Underground Space Technology, 2021, 111: 103872. doi: 10.1016/j.tust.2021.103872
[6]	MU L L, HUANG M S. Small strain based method for predicting three-dimensional soil displacements induced by braced excavation[J]. Tunnelling and Underground Space Technology, 2016, 52: 12-22. doi: 10.1016/j.tust.2015.11.001
[7]	YING H W, CHENG K, LIU S J, et al. An efficient method for evaluating the ground surface settlement of Hangzhou metro deep basement considering the excavation process[J]. Acta Geotechnica, 2022, 17(12): 5759-5771. doi: 10.1007/s11440-022-01549-x
[8]	SAGASETA C. Analysis of undrained soil deformation due to ground loss[J]. Géotechnique, 1987, 37(3): 301–320. doi: 10.1680/geot.1987.37.3.301
[9]	XU K J, POULOS H G. Theoretical study of pile behaviour induced by a soil cut[C]//ISRM International Symposium. ISRM, 2000: ISRM-IS-2000-377.
[10]	钱建固, 王伟奇. 刚性挡墙变位诱发墙后地表沉降的理论解析[J]. 岩石力学与工程学报, 2013, 32(增刊1): 2698-2703. QIAN Jiangu, WANG Weiqi. Analytical solutions to ground settlement induced by movement of rigid retaining wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2698-2703. (in Chinese)
[11]	沈路遥, 钱建固, 张戎泽. 挡墙水平变位诱发地表沉降的简化解析解[J]. 岩土力学, 2016, 37(8): 2293-2298. SHEN Luyao, QIAN Jiangu, ZHANG Rongze. A simplified analytical solution for ground settlement induced by horizontal movement of retailing wall[J]. Rock and Soil Mechanics, 2016, 37(8): 2293-2298. (in Chinese)
[12]	胡之锋, 陈健, 邱岳峰, 等. 挡墙水平变位诱发地表沉降的显式解析解[J]. 岩土力学, 2018, 39(11): 4165-4175. HU Zhifeng, CHEN Jian, QIU Yuefeng, et al. Analytical formula for ground settlement induced by horizontal movement of retaining wall[J]. Rock and Soil Mechanics, 2018, 39(11): 4165-4175. (in Chinese)
[13]	FAN X Z, PHOON K K, XU C J, et al. Closed-form solution for excavation-induced ground settlement profile in clay[J]. Computers and Geotechnics, 2021, 137: 104266. doi: 10.1016/j.compgeo.2021.104266
[14]	MESQUITA A D, CODA H B. An alternative time integration procedure for Boltzmann viscoelasticity: a BEM approach[J]. Computers & Structures, 2001, 79(16): 1487-1496.
[15]	MESQUITA A D, CODA H B. A simple Kelvin and Boltzmann viscoelastic analysis of three-dimensional solids by the boundary element method[J]. Engineering Analysis with Boundary Elements, 2003, 27(9): 885-895. doi: 10.1016/S0955-7997(03)00060-2
[16]	祝彦知. 桩基础长期沉降与变形的黏弹性分析理论及应用[D]. 上海: 同济大学, 2006. ZHU Yanzhi. Viscoelastic Analysis Theory and Application of Long Term Settlement and Deformation of Pile Foundation[D]. Shanghai: Tongji University, 2006. (in Chinese)
[17]	FLAMANT A. Sur la répartition des pressions dans un solide rectangulaire chargé transversalement[J]. CR Acad Sci Paris, 1892, 114: 1465-1468.
[18]	陈宗基, 康文法. 岩石的封闭应力、蠕变和扩容及本构方程[J]. 岩石力学与工程学报, 1991, 10(4): 299-312. CHEN Zongji, KANG Wenfa. On the locked in stress, creep and dilatation of rocks, and the constitutive equations[J]. Chinese Journal of Rock Mechanics and Engineering, 1991, 10(4): 299-312. (in Chinese)
[19]	OU C Y, HSIEH P G, CHIOU D C. Characteristics of ground surface settlement during excavation[J]. Canadian Geotechnical Journal, 1993, 30(5): 758-767. doi: 10.1139/t93-068
[20]	MANA A I, CLOUGH G W. Prediction of movements for braced cuts in clay[J]. Journal of the Geotechnical Engineering Division, 1981, 107(6): 759-777. doi: 10.1061/AJGEB6.0001150
[21]	MOORMANN C. Analysis of wall and ground movements due to deep excavations in soft soil based on a new worldwide database[J]. Soils and Foundations, 2004, 44(1): 87-98. doi: 10.3208/sandf.44.87
[22]	邓会元, 戴国亮, 邱国阳, 等. 杭州湾淤泥质粉质黏土排水蠕变试验及元件蠕变模型[J]. 东南大学学报(自然科学版), 2021, 51(2): 318-324. DENG Huiyuan, DAI Guoliang, QIU Guoyang, et al. Drained creep test and component creep model of soft silty clay in Hangzhou Bay[J]. Journal of Southeast University (Natural Science Edition), 2021, 51(2): 318-324. (in Chinese)
[23]	周秋娟, 陈晓平. 侧向卸荷条件下软土典型力学特性试验研究[J]. 岩石力学与工程学报, 2009, 28(11): 2215-2221. doi: 10.3321/j.issn:1000-6915.2009.11.008 ZHOU Qiujuan, CHEN Xiaoping. Test research on typical mechanical characteristics of soft clay under lateral unloading condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(11): 2215-2221. (in Chinese) doi: 10.3321/j.issn:1000-6915.2009.11.008
[24]	贾敏才, 赵舜, 张震. 侧向卸荷条件下结构性软黏土蠕变特性试验研究[J]. 西南交通大学学报, 2020, 55(6): 1257-1263. JIA Mincai, ZHAO Shun, ZHANG Zhen. Experimental study on creep characteristics of structural soft clay under lateral unloading condition[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1257-1263. (in Chinese)
[25]	ZHANG Z G, HUANG M S, ZHANG C P, et al. Time-domain analyses for pile deformation induced by adjacent excavation considering influences of viscoelastic mechanism[J]. Tunnelling and Underground Space Technology, 2019, 85: 392-405. doi: 10.1016/j.tust.2018.12.020
[26]	杨敏, 赵锡宏. 分层土中的单桩分析法[J]. 同济大学学报(自然科学版), 1992, 20(4): 421-428. YANG Min, ZHAO Xihong. An approach for a single pile in layered soil[J]. Journal of Tongji University (Natural Science), 1992, 20(4): 421-428. (in Chinese)
[27]	应宏伟, 孙威, 吕蒙军, 等. 复杂环境下某深厚软土基坑的实测性状研究[J]. 岩土工程学报, 2014, 36(增刊2): 424-430. YING Hongwei, SUN Wei, LÜ Mengjun, et al. Measured characteristics of a deep soft soil excavation in complex environment[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(S2): 424-430. (in Chinese)