Dynamic compressive strength model for rock-steel fiber-reinforced concrete composite layer
-
摘要: 为了研究冲击荷载下岩石-钢纤维混凝土（R-SFRC）复合层的抗压强度模型，利用分离式霍普金森压杆对花岗岩、混凝土和R-SFRC复合层进行动态冲击压缩试验，并通过回归试验结果得到R-SFRC复合层的对数型、幂函数型和强度-应变率依赖机制型3种强度模型，同时考虑R-SFRC复合层界面相互作用，基于Mohr-Coulomb强度准则建立复合层动态抗压强度计算模型。结果表明，R-SFRC复合层动态抗压强度随应变率及钢纤维掺量增大而增大；3种回归模型拟合复合层动态抗压强度试验结果的相关系数范围为0.918~0.999，其中依赖机制型模型与试验结果的相关性最大；基于Mohr-Coulomb强度准则的3种模型得到的复合层抗压强度计算值相对试验值的误差范围为-9.23%~3.16%，对数型模型的误差最大值较小。R-SFRC复合层动态抗压强度计算模型可为混凝土支护隧道围岩设计提供理论基础。Abstract: In order to study the compressive strength model for rock-steel fiber-reinforced concrete (R-SFRC) composite layer under impact loading, the dynamic impact compression tests on the granite, concrete and R-SFRC composite layer are carried out by using the separated Hopkinson pressure bar to obtain the dynamic compressive strengths of different materials. With the regression fitting of the test results, three types of strength models for the R-SFRC composite layer called logarithmic, power function and strength-strain rate dependent mechanism are obtained, and the dynamic compressive strength models for the R-SFRC composite layer are established based on the Mohr-Coulomb strength criterion considering the interface interaction of the R-SFRC composite layer. The results show that the dynamic compressive strength of the R-SFRC composite layer increases with the increase of the strain rate and steel fiber content, and the range of the correlation coefficient of three regression models is 0.918~0.999, and the R2 of the dependent mechanism model is the largest. The error range of the theoretical value of the dynamic compressive strength calculated based on the Mohr-Coulomb strength criterion relative to the test value is -9.23%~3.16%, and the maximum error value of the logarithmic model is the smallest. The computational model for the dynamic compressive strength of the R-SFRC composite layer can provide a theoretical basis for the design of the surrounding rock of concrete-supported tunnels.
-
0. 引言
隧道及巷道的围岩因遭受岩爆、爆破以及地震等冲击荷载作用而产生破坏，影响工程施工人员和设备的安全[1]。钢纤维喷射混凝土能与围岩紧密结合，形成柔性支护结构提供支护抗力，因此，岩石-钢纤维混凝土（R-SFRC）复合层的力学性能影响支护结构的稳定性。
国内外学者对岩石-混凝土复合试件的剪切、劈裂抗拉和抗压等性能进行了研究。Jiang等[2]研究发现当法向应力由0.5 MPa增至4 MPa时，复合试件的抗剪强度提高了3~5倍，同时，混凝土强度为75 MPa复合试件的抗剪强度比10 MPa的增大1.5倍左右。Mouzannar等[3]认为界面处较大的粗糙度使复合试件界面黏结更加紧密，增大界面的抗剪强度。Chang等[4]研究表明复合试件的劈裂抗拉强度随加载方向与界面之间夹角的增大而增大，当加载方向与界面夹角呈90°时，混凝土强度对复合试件劈裂抗拉强度的影响最大，二者呈线性关系。Zhu等[5]发现较高强度混凝土内部的水化反应更加充分，减少了界面处的缺陷，增强了界面黏结性能。Zhao等[6]研究表明界面有黏结的复合试件静态抗压强度比无黏结的提高了24%。陈猛等[7]指出R-SFRC复合层的动态强度增长因子（dynamic increase factor, DIF）与应变率的对数呈线性关系；当应变率从35 s-1增至135 s-1，混凝土中掺入80 kg/m3钢纤维的复合层抗压强度与未掺入钢纤维相比增长了15.9%~30.1%。复合层的力学性能受单层及界面相互作用影响较大，建立复合层强度的理论计算模型需要以单层和界面力学性能为基础。
在岩石、混凝土和岩石-混凝土复合试件的强度计算模型研究方面，赵坚等[8]、宫凤强等[9]发现当应变率范围为10-4~100 s-1时，Mohr-Coulomb强度准则适用于计算围压小于100 MPa的岩石强度；Hoek-Brown强度准则能合理预测0~170 MPa围压的岩石强度。宫凤强等[10]研究表明，在0~30 MPa围压条件下，Mohr-Coulomb强度准则能有效预测应变率范围为10-6~102 s-1的岩石强度；Hoek-Brown强度准则能合理评估应变率范围为10-6~10-1 s-1的岩石强度；Griffith强度准则仅能用于判别应变率范围为101~102 s-1的岩石单轴抗压与抗拉强度之间的关系。钱七虎等[11]提出热活化与黏性机制并存竞争的材料强度-应变率依赖模型，能计算全应变率范围内的岩石强度。Gong等[12]、Si等[13]研究表明在0~15 MPa围压条件下，应变率范围为40~160 s-1时砂岩的动态抗压强度与应变率对数之间存在明显的线性关系，基于Mohr- Coulomb和Hoek-Brown强度准则建立的计算模型可有效预测岩石动态抗压强度。Fu等[14]发现当应变率范围为30~150 s-1时，Hoek-Brown比Mohr-Coulomb和Drucker-Prager强度准则更适用于计算围压低于12 MPa的混凝土强度。Lu等[15]根据强度-应变率关系建立了混凝土非线性动态强度准则，能利用低应变率下的混凝土强度计算出高应变率下的混凝土强度。Zhao等[16]发现与Coulomb和两参数Hoek-Brown强度准则相比，三参数广义Hoek-Brown强度准则更适用于计算岩石-混凝土复合试件的静态抗压强度。陈猛等[17]基于Mohr-Coulomb强度准则建立了R-SFRC复合层的静态抗压强度预测模型。目前，缺少针对R-SFRC复合层动态抗压强度计算模型的研究。
为探究R-SFRC复合层中岩石与混凝土的相互作用及R-SFRC复合层整体力学性能，本文对花岗岩、混凝土和R-SFRC复合层进行了动态抗压试验，分别通过试验结果回归和Mohr-Coulomb强度准则建立冲击荷载作用下R-SFRC复合层的抗压强度预测模型，可为冲击荷载作用下钢纤维喷射混凝土支护围岩设计提供理论依据。
1. 试验概况
1.1 原材料
花岗岩的物理和力学性能见表 1，岩石经钻芯、切割和磨平等工序后加工成直径100 mm，高度50 mm的圆柱体试件。保证试件两端面不平行度小于直径的0.1%，两端面与轴线垂直且偏差不大于0.25°。
表 1 花岗岩的物理及力学性能Table 1. Physical and mechanical properties of granite密度/
(kg·m-3)弹性模量/
GPa单轴抗压强度/MPa 泊松比 内摩擦角/(°) 3000 67.41 187.1 0.207 53 混凝土的胶凝材料采用P·O 42.5硅酸盐水泥；细骨料为细度模数2.56的河砂；粗骨料采用粒径为5~10 mm级配良好的碎石；采用38%减水率的聚羧酸减水剂；钢纤维为贝卡尔特端钩型钢纤维，物理及力学性能参数见表 2，不同类型混凝土配合比见表 3。
表 2 钢纤维的物理及力学性能Table 2. Physical and mechanical properties of steel fiber长度/
mm直径/
mm密度/
(kg·m-3)抗拉强度/
MPa弹性模量/
GPa35 0.3 7850 1150 220 表 3 混凝土配合比Table 3. Mixture proportions of concrete单位: kg/m3 材料类型 水泥 水 细骨料 粗骨料 减水剂 钢纤维 FC0 418 182 611 1239 4.18 0 FC4 418 182 611 1239 4.18 40 FC6 418 182 611 1239 4.18 60 FC8 418 182 611 1239 4.18 80 注：FC4，FC6和FC8分别表示钢纤维掺量为40，60，80 kg/m3的钢纤维混凝土。 1.2 试件制备
制备混凝土试件时，先将水泥和骨料置于搅拌机中干拌，再加入水和减水剂进行湿拌，搅拌时间不小于2 min，最后放入钢纤维，搅拌至纤维分散均匀。将拌合物筑入直径100 mm，高度50 mm的圆柱体模具中，振捣密实后盖上保鲜膜，24 h后脱模并放入标准养护室（温度为20℃±2℃，相对湿度不低于95%）中养护至28 d。
制备R-SFRC复合层试件时，先将混凝土拌合物筑入直径100 mm，高度50 mm的圆柱体模具中，再将表面浸湿的岩石试件置于振捣密实后的混凝土上部，混凝土上部砂浆与岩石表面贴合使二者黏结密实，24 h后脱去混凝土模具并放入标准养护室中养护至28 d。花岗岩与不同类型混凝土黏结形成复合层试件，分别为R-FC0，R-FC4，R-FC6，R-FC8。R-FC0表示由花岗岩与FC0组成的复合层试件。
1.3 试验方法
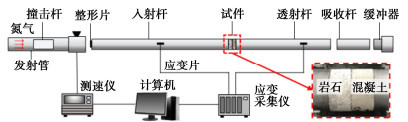
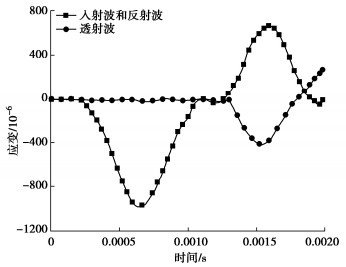
动态冲击压缩试验采用直径100 mm的分离式霍普金森压杆。撞击杆、入射杆、透射杆和吸收杆均为高强合金钢，长度分别为600，5000，3500，1200 mm，试验装置示意图如图 1所示。采用直径50 mm，厚度2 mm的橡胶片作为波形整形片贴于入射杆端部中央，入射波、反射波和透射波曲线如图 2所示。
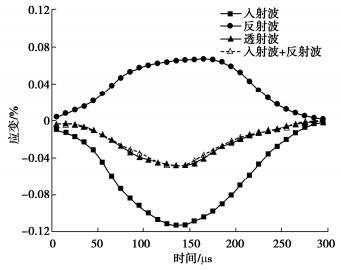
试验时，将复合层试件的两端面均匀涂抹凡士林（避免摩擦效应）夹在入射杆和透射杆之间，岩石层置于入射杆一侧。对R-SFRC复合层试件的SHPB试验进行应力平衡检验，见图 3，表明入射波与反射波之和约等于透射波，满足应力平衡要求[12]。试验设置5个目标应变率，分别为35，55，75，95，115 s-1。根据一维弹性应力波理论，通过“三波法”计算出应力、应变和应变率。针对每组应变率均重复3次测试，对试验结果取平均值。
2. 试验结果与分析
2.1 破坏形态
R-SFRC复合层试件在不同应变率下的破坏形态如图 4所示，在不同应变率下，岩石-钢纤维混凝土复合层试件比岩石-素混凝土复合层试件破坏程度小。由于混凝土弹性模量小于岩石弹性模量且二者泊松比值比较接近，导致轴向冲击作用下混凝土层的径向变形大于岩石层，在相互约束作用下，混凝土层和岩石层在界面分别受到径向压缩和拉伸作用。当应变率约为35 s-1时，混凝土层仅在外侧出现张应变破坏，岩石层不发生破坏，见图 4（a），（d）。当应变率增至75 s-1附近，混凝土层中的裂纹沿冲击方向扩展至黏结界面，混凝土层对岩石层界面的张拉作用增强，出现贯通岩石层和混凝土层的轴向裂缝，岩石层表现为劈裂拉伸破坏，混凝土层则表现为留芯破坏，见图 4（b），（e）。当应变率增至115 s-1附近，岩石层和混凝土层碎块尺寸减小、数量增多，岩石层仍呈现劈裂拉伸破坏模式，混凝土层则表现为压碎破坏，见图 4（c），（f）。
![]()
图 4 不同应变率下复合层试件的破坏形态Figure 4. Failure modes of composite layer specimens at different strain rates2.2 动态抗压强度
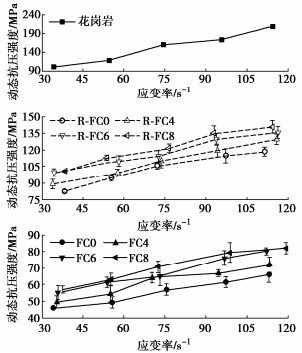
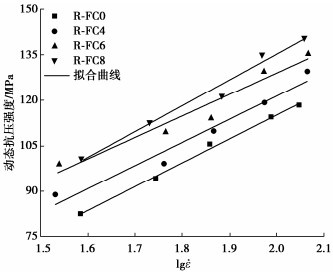
图 5为花岗岩、混凝土和R-SFRC复合层的动态抗压强度随应变率变化曲线图。不同类型试件的动态抗压强度随应变率增大而增大，均具有显著的应变率效应。当应变率从34.3 s-1增大到114.5 s-1时，岩石的动态抗压强度提高了107.9%；当应变率从34.2 s-1增大到119.3 s-1时，FC0，FC4，FC6，FC8的动态抗压强度分别提高了44.2%，45.5%，45.6%，43.7%。原因是在冲击荷载作用下，惯性效应和泊松效应使试件处于被动围压状态，裂缝的萌生和扩展受到限制，增大了试件破坏时达到的极限强度[18-19]。同时，随着应变率增大，试件内部裂纹增多，需要更多能量来驱动裂纹扩展，但能量在冲击荷载下没有足够时间累积，只能通过增大应力来抵消外部能量[20]。此外，应力波在试件内部快速传播，裂纹没有足够时间在试件中薄弱部分形成和发展，因此裂纹产生和扩展需要更大的荷载[18-19]。
![]()
图 5 动态抗压强度随应变率变化曲线Figure 5. Variation of dynamic compressive strength with strain rate当应变率从33.9 s-1增大到116.3 s-1时，R-FC0，R-FC4，R-FC6，R-FC8的动态抗压强度分别提高了43.5%，46.0%，36.7%，39.7%。由2.1节分析可知，黏结面处混凝土层和岩石层在径向分别产生受压和受拉作用，随着应变率增大，黏结面的环箍约束作用及惯性效应增强，混凝土层受到的围压作用增强[7, 17]。R-SFRC复合层的动态抗压强度介于岩石和混凝土之间，强度随应变率的变化规律更接近混凝土。
混凝土和R-SFRC复合层的动态抗压强度均随钢纤维掺量增多而增大。当应变率从34.2 s-1增大到119.3 s-1时，与FC0相比，FC8的动态抗压强度分别提高了24.6%，28.7%，24.2%，29.4%，24.2%；当应变率从33.9 s-1增大到116.3 s-1时，与R-FC0相比，R-FC8的动态抗压强度分别提高了22.1%，19.6%，15.1%，18.0%，18.8%。钢纤维在混凝土基体产生裂缝时发挥桥接作用，能有效抑制混凝土横向变形，使复合层黏结界面充分发挥对混凝土的约束作用，同时纤维的桥接作用消耗冲击荷载的能量[7, 17]，降低混凝土破坏程度，增大其动态抗压强度。综上，混凝土层达到极限强度时导致复合层发生整体破坏。
3. R-SFRC复合层动态抗压强度模型
3.1 R-SFRC复合层试验结果回归模型
（1）对数型模型
DIF定义为动态抗压强度（fd）与静态抗压强度（fs）的比值。Zhang等[18]研究表明，DIF与应变率的对数存在线性关系：
DIF=k1⋅lg˙ε+b1， (1) 即
fd=fs⋅(k1⋅lg˙ε+b1)。 (2) 式中：k1，b1为待定参数；˙ε为应变率（s-1）。
利用式（2）对R-SFRC复合层试验结果进行拟合，式中复合层静态抗压强度由文献[17]得到，拟合曲线如图 6所示，拟合结果见表 4。在R-SFRC复合层的动态抗压强度对数型模型中，参数k1反映复合层动态抗压强度增长因子对应变率对数的敏感程度。不同类型复合层的k1平均值为1.06，表明当应变率范围为35~115 s-1时，在复合层的动态抗压强度与应变率对数的线性关系曲线中，斜率接近于静态抗压强度值。
![]()
图 6 R-SFRC复合层的对数型模型拟合曲线Figure 6. Fitting curves of logarithmic model for R-SFRC composite layer表 4 回归模型中R-SFRC复合层的参数拟合值Table 4. Fitting values of parameters of R-SFRC composite layer using regression models复合层类型 对数型 幂函数型 依赖机制型 k1 b1 R2 k2 R2 k4 ˙εs n R2 R-FC0 1.132 -0.608 0.996 0.356 0.991 0.833 61.348 2.731 0.999 R-FC4 0.998 -0.207 0.963 0.362 0.980 3.873 364.699 1.198 0.998 R-FC6 1.001 -0.172 0.942 0.382 0.918 3.623 298.722 1.196 0.971 R-FC8 1.100 -0.456 0.979 0.378 0.977 1.584 108.280 1.392 0.993 （2）幂函数型模型
郭东明等[1]研究发现材料的动态抗压强度与应变率之间存在幂函数关系，即fd∝˙εn。宫凤强等[10]提出材料动态抗压强度与应变率的1/3次方成正比。对R-SFRC复合层试验结果进行幂函数拟合，发现拟合参数n值集中于1/3附近。考虑静态抗压强度的影响，对R-SFRC复合层动态抗压强度与应变率的幂函数关系式进行无量纲化处理，假设R-SFRC复合层动态抗压强度与应变率存在以下关系：
fd=fs⋅k2⋅˙ε13。 (3) 式中：k2为待定参数。
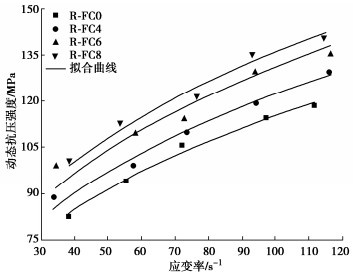
利用式（3）拟合R-SFRC复合层试验结果，式中复合层静态抗压强度由文献[17]得到，拟合曲线见图 7，拟合结果见表 4。在R-SFRC复合层的动态抗压强度幂函数型模型中，参数k2反映动态抗压强度增长因子随应变率变化的快慢程度。钢纤维混凝土制备的复合层的k2均比素混凝土的大，表明当应变率范围为35~115 s-1时，钢纤维混凝土制备的复合层动态抗压强度的应变率效应比素混凝土的强，原因是动态压缩过程中钢纤维拔出或桥连混凝土基体，可以耗散冲击能量，提高复合层的动态抗压强度。
![]()
图 7 R-SFRC复合层的幂函数型模型拟合曲线Figure 7. Fitting curves of power functional model for R-SFRC composite layer（3）强度-应变率依赖机制型模型
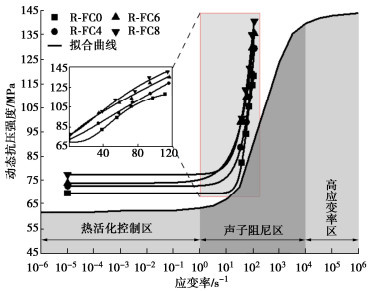
钱七虎等[11]提出了热活化与黏性机制并存竞争的材料强度模型，即不同机制在各应变率范围内分别占据主导地位，如图 8所示。在较高应变率范围内，材料强度-应变率依赖模型公式为[11, 21]
![]()
图 8 R-SFRC复合层的强度-应变率依赖机制型模型拟合曲线Figure 8. Fitting curves of strength-strain rate dependent mechanism model for R-SFRC composite layerfd=fs+k3(˙ε/˙εs)n(˙ε/˙εs)n+1。 (4) 式中：k3为宏观黏性对参数提高的最大幅值；˙εs为材料应变率曲线的拐点值，温度升高的贡献被隐性地包含在这一项中；n为控制应变率曲线陡峭程度的常数。
对式（4）进行无量纲化处理，得到
fd=fs⋅(1+k4(˙ε/˙εs)n(˙ε/˙εs)n+1)。 (5) 式中：k4为k3与材料静态抗压强度的比值。
用式（5）对R-SFRC复合层试验结果进行拟合，式中复合层静态抗压强度由文献[17]得到，拟合曲线见图 8，拟合结果见表 4。
对数型、幂函数型和强度-应变率依赖机制型模型拟合R-SFRC复合层试验数据的相关系数（R2）分别为0.942~0.996，0.918~0.991和0.971~0.999，对比3种强度模型的R2可知，依赖机制型模型与复合层动态抗压强度试验结果的相关性最大。3种模型均可对素混凝土和钢纤维混凝土制备的复合层动态抗压强度进行有效预测。
3.2 基于Mohr-Coulomb强度准则的计算模型
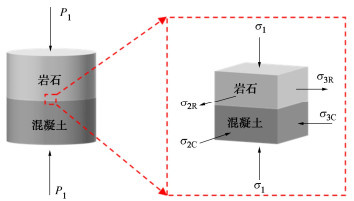
在脆性材料动态强度计算方面，Mohr-Coulomb强度准则应用较为广泛[11]。由第2节可知，复合层破坏是混凝土层先达到破坏强度导致的，因此，复合层中混凝土的动态抗压强度近似等于复合层动态抗压强度。文献[17]讨论了R-SFRC复合层中岩石层和混凝土层的界面相互作用，基于Mohr-Coulomb强度准则推导了复合层静态抗压强度计算公式。此外，当应变率范围为33.9~119.3 s-1时，岩石和混凝土的弹性模量、泊松比和内摩擦角随加载速率变化较小[22-23]，可认为此应变率范围内岩石和混凝土的动态弹性模量、泊松比和内摩擦角值近似等于静态值。综上，R-SFRC复合层静态抗压强度计算公式适用于应变率范围为33.9~119.3 s-1时的动态抗压强度计算，公式如下：
σ2C=−σ2R=σ3C=−σ3R=a⋅σ1， (6) a=(ERμC−ECμR)[EC(1−μR)+ER(1−μC)]， (7) σ1=fRC=fRC - C=fCd1−A⋅a， (8) A=1+sinφ1−sinφ。 (9) 式中：σ2R，σ2C，σ3R，σ3C分别为岩石和混凝土在2，3方向上的应力（MPa），见图 9；σ1为复合层的压缩应力（MPa）；ER，EC分别为岩石和混凝土的弹性模量（GPa）；μR，μC分别为岩石和混凝土的泊松比；fRC，fRC - C分别为复合层和复合层中混凝土的动态抗压强度（MPa）；fCd为混凝土的动态抗压强度（MPa）；φ为混凝土的内摩擦角（°）。
![]()
图 9 R-SFRC复合层界面处单元体应力分析图Figure 9. Stress analysis of element at interface of R-SFRC composite layer将对数型、幂函数型和强度-应变率依赖机制型模型分别代入式（8），得到3种基于Mohr-Coulomb强度准则的复合层动态抗压强度计算模型：
fRC=fCs1−A⋅a⋅(k1C⋅lg˙ε+b1C)， (10) fRC=fCs1−A⋅a⋅k2C⋅˙ε13， (11) fRC=fCs1−A⋅a⋅(1+k4C(˙ε/˙εsC)nC(˙ε/˙εsC)nC+1)。 (12) 式中：fCs为混凝土的静态抗压强度（MPa）。k1C，b1C，k2C，k4C，˙εsC和nC为混凝土动态试验结果的待定参数。
利用对数型、幂函数型和依赖机制型模型对混凝土试验结果进行拟合，式中混凝土静态抗压强度由文献[17]得到，拟合结果见表 5；将拟合结果代入公式（10）~（12）进行计算，式中岩石和混凝土的弹性模量、泊松比和内摩擦角值由文献[17]得到，复合层强度理论计算值见表 6。
表 5 回归模型中混凝土的参数拟合值Table 5. Fitting values of parameters of concrete using regression models材料类型 对数型 幂函数型 依赖机制型 k1C b1C R2 k2C R2 k4C ˙εsC nC R2 FC0 0.842 -0.357 0.941 0.287 0.961 0.476 81.603 4.923 0.988 FC4 0.940 -0.448 0.957 0.309 0.961 0.494 64.627 5.211 0.980 FC6 1.031 -0.516 0.947 0.334 0.966 0.725 68.548 3.012 0.972 FC8 1.038 -0.530 0.987 0.333 0.989 0.784 71.679 2.734 0.998 表 6 R-SFRC复合层的动态抗压强度计算值与试验值对比Table 6. Comparison of calculated and tested values of dynamic compressive strength of R-SFRC composite layer复合层类型 应变率/s-1 fe/MPa fRC1/MPa fRC2/MPa fRC3/MPa x1/% x2/% x3/% R-FC0 38.3 82.5±1.1 75.1 75.0 81.0 -8.93 -9.09 -1.87 55.4 94.2±3.0 89.5 88.2 85.5 -5.02 -6.33 -9.23 72.1 105.6±2.5 98.5 97.7 96.0 -6.77 -7.48 -9.08 97.2 114.6±6.4 105.9 106.3 107.4 -7.62 -7.27 -6.31 111.5 118.4±4.0 110.3 111.7 112.3 -6.87 -5.65 -5.17 R-FC4 33.9 88.8±4.3 82.8 83.4 83.9 -6.76 -6.03 -5.50 57.6 99.2±3.0 97.6 96.7 94.4 -1.59 -2.54 -4.83 73.5 109.9±5.8 105.9 104.9 106.9 -3.66 -4.52 -2.76 94.1 119.3±5.9 115.9 115.9 118.0 -2.86 -2.85 -1.13 115.9 129.6±4.6 121.9 123.1 120.8 -5.91 -5.03 -6.80 R-FC6 34.5 99.2±3.5 91.0 92.1 91.3 -8.28 -7.20 -8.01 58.1 109.7±4.9 106.3 105.4 103.5 -3.13 -3.88 -5.67 72.6 114.2±4.9 117.8 116.8 117.1 3.16 2.31 2.51 93.8 129.8±5.3 128.3 128.2 128.6 -1.16 -1.19 -0.95 116.3 135.6±5.4 133.8 134.7 133.2 -1.33 -0.68 -1.78 R-FC8 38.5 100.7±0.6 94.4 95.3 95.2 -6.26 -5.38 -5.51 53.7 112.7±2.7 109.2 108.3 113.3 -3.12 -3.92 0.56 76.5 121.5±4.0 119.7 118.6 119.3 -1.50 -2.40 -1.78 93.0 135.2±6.4 131.6 131.5 132.6 -2.67 -2.75 -1.91 114.4 140.7±5.7 138.9 140.0 139.0 -1.31 -0.49 -1.24 注：fe为R-SFRC复合层的动态抗压强度试验值；fRC1，fRC2和fRC3分别为基于Mohr-Coulomb强度准则建立的对数型、幂函数型和强度-应变率依赖机制型模型的R-SFRC复合层动态抗压强度计算值。xi为fRCi的误差，xi=(fRCi−fe)×100%/fe，i=1，2，3。 采用对数型、幂函数型和依赖机制型模型计算的复合层动态抗压强度值相对试验值的误差范围分别为-8.93%~3.16%，-9.09%~2.31%，-9.23%~2.51%，对数型模型的误差绝对值最大不超过8.93%。结合文献[7]中C30混凝土及其制备的复合层动态抗压强度试验数据，采用对数型、幂函数型和依赖机制型模型计算得到的复合层动态抗压强度值相对试验值的误差范围分别为-9.55%~5.89%，-8.18%~5.48%，-8.99%~7.03%，表明计算模型可用于不同强度混凝土制备的复合层动态抗压强度计算。与试验结果回归模型相比，基于Mohr-Coulomb强度准则的计算模型的优势在于，计算R-SFRC复合层的动态抗压强度只需要单层的力学性能参数。
4. 结论
本文对花岗岩、混凝土和R-SFRC复合层进行了应变率范围为33.9~119.3 s-1的动态抗压试验，并建立了R-SFRC复合层动态抗压强度计算模型，主要得到以下3点结论。
（1）岩石、混凝土和R-SFRC复合层的动态抗压强度均具有显著的应变率效应。混凝土和R-SFRC复合层的动态抗压强度均随钢纤维掺量增多而增大，纤维桥接作用可以有效提高混凝土动态抗压强度。复合层中混凝土层达到极限强度时导致复合层发生破坏。
（2）对数型、幂函数型和强度-应变率依赖机制型回归模型拟合R-SFRC复合层试验结果的R2范围为0.918~0.999，3种回归模型与复合层试验结果的相关性均较大，其中依赖机制型模型的R2最大。
（3）基于Mohr-Coulomb强度准则建立的3种强度计算模型通过单层力学性能参数计算R-SFRC复合层动态抗压强度，3种模型强度计算值相对试验值的误差范围为-9.23%~3.16%，其中对数型模型的误差最大值相对于其他两种模型最小。
-
![]()
图 4 不同应变率下复合层试件的破坏形态
Figure 4. Failure modes of composite layer specimens at different strain rates
![]()
图 5 动态抗压强度随应变率变化曲线
Figure 5. Variation of dynamic compressive strength with strain rate
![]()
图 6 R-SFRC复合层的对数型模型拟合曲线
Figure 6. Fitting curves of logarithmic model for R-SFRC composite layer
![]()
图 7 R-SFRC复合层的幂函数型模型拟合曲线
Figure 7. Fitting curves of power functional model for R-SFRC composite layer
![]()
图 8 R-SFRC复合层的强度-应变率依赖机制型模型拟合曲线
Figure 8. Fitting curves of strength-strain rate dependent mechanism model for R-SFRC composite layer
![]()
图 9 R-SFRC复合层界面处单元体应力分析图
Figure 9. Stress analysis of element at interface of R-SFRC composite layer
表 1 花岗岩的物理及力学性能
Table 1 Physical and mechanical properties of granite
密度/
(kg·m-3)弹性模量/
GPa单轴抗压强度/MPa 泊松比 内摩擦角/(°) 3000 67.41 187.1 0.207 53 
下载: 导出CSV
表 2 钢纤维的物理及力学性能
Table 2 Physical and mechanical properties of steel fiber
长度/
mm直径/
mm密度/
(kg·m-3)抗拉强度/
MPa弹性模量/
GPa35 0.3 7850 1150 220
下载: 导出CSV
表 3 混凝土配合比
Table 3 Mixture proportions of concrete
单位: kg/m3 材料类型 水泥 水 细骨料 粗骨料 减水剂 钢纤维 FC0 418 182 611 1239 4.18 0 FC4 418 182 611 1239 4.18 40 FC6 418 182 611 1239 4.18 60 FC8 418 182 611 1239 4.18 80 注：FC4，FC6和FC8分别表示钢纤维掺量为40，60，80 kg/m3的钢纤维混凝土。
下载: 导出CSV
表 4 回归模型中R-SFRC复合层的参数拟合值
Table 4 Fitting values of parameters of R-SFRC composite layer using regression models
复合层类型 对数型 幂函数型 依赖机制型 k1 k2 k4 R-FC0 1.132 -0.608 0.996 0.356 0.991 0.833 61.348 2.731 0.999 R-FC4 0.998 -0.207 0.963 0.362 0.980 3.873 364.699 1.198 0.998 R-FC6 1.001 -0.172 0.942 0.382 0.918 3.623 298.722 1.196 0.971 R-FC8 1.100 -0.456 0.979 0.378 0.977 1.584 108.280 1.392 0.993
下载: 导出CSV
表 5 回归模型中混凝土的参数拟合值
Table 5 Fitting values of parameters of concrete using regression models
材料类型 对数型 幂函数型 依赖机制型 FC0 0.842 -0.357 0.941 0.287 0.961 0.476 81.603 4.923 0.988 FC4 0.940 -0.448 0.957 0.309 0.961 0.494 64.627 5.211 0.980 FC6 1.031 -0.516 0.947 0.334 0.966 0.725 68.548 3.012 0.972 FC8 1.038 -0.530 0.987 0.333 0.989 0.784 71.679 2.734 0.998
下载: 导出CSV
表 6 R-SFRC复合层的动态抗压强度计算值与试验值对比
Table 6 Comparison of calculated and tested values of dynamic compressive strength of R-SFRC composite layer
复合层类型 应变率/s-1 /MPa /MPa /MPa /MPa /% /% /% R-FC0 38.3 82.5±1.1 75.1 75.0 81.0 -8.93 -9.09 -1.87 55.4 94.2±3.0 89.5 88.2 85.5 -5.02 -6.33 -9.23 72.1 105.6±2.5 98.5 97.7 96.0 -6.77 -7.48 -9.08 97.2 114.6±6.4 105.9 106.3 107.4 -7.62 -7.27 -6.31 111.5 118.4±4.0 110.3 111.7 112.3 -6.87 -5.65 -5.17 R-FC4 33.9 88.8±4.3 82.8 83.4 83.9 -6.76 -6.03 -5.50 57.6 99.2±3.0 97.6 96.7 94.4 -1.59 -2.54 -4.83 73.5 109.9±5.8 105.9 104.9 106.9 -3.66 -4.52 -2.76 94.1 119.3±5.9 115.9 115.9 118.0 -2.86 -2.85 -1.13 115.9 129.6±4.6 121.9 123.1 120.8 -5.91 -5.03 -6.80 R-FC6 34.5 99.2±3.5 91.0 92.1 91.3 -8.28 -7.20 -8.01 58.1 109.7±4.9 106.3 105.4 103.5 -3.13 -3.88 -5.67 72.6 114.2±4.9 117.8 116.8 117.1 3.16 2.31 2.51 93.8 129.8±5.3 128.3 128.2 128.6 -1.16 -1.19 -0.95 116.3 135.6±5.4 133.8 134.7 133.2 -1.33 -0.68 -1.78 R-FC8 38.5 100.7±0.6 94.4 95.3 95.2 -6.26 -5.38 -5.51 53.7 112.7±2.7 109.2 108.3 113.3 -3.12 -3.92 0.56 76.5 121.5±4.0 119.7 118.6 119.3 -1.50 -2.40 -1.78 93.0 135.2±6.4 131.6 131.5 132.6 -2.67 -2.75 -1.91 114.4 140.7±5.7 138.9 140.0 139.0 -1.31 -0.49 -1.24 注：为R-SFRC复合层的动态抗压强度试验值；，和分别为基于Mohr-Coulomb强度准则建立的对数型、幂函数型和强度-应变率依赖机制型模型的R-SFRC复合层动态抗压强度计算值。为的误差，，=1，2，3。
下载: 导出CSV
-
[1] 郭东明, 闫鹏洋, 凡龙飞, 等. 喷层混凝土-围岩组合体波动特性及动力特性研究[J]. 振动与冲击, 2018, 37(24): 85-91, 136. GUO Dongming, YAN Pengyang, FAN Longfei, et al. A study on the stress wave characteristics and dynamic mechanical property of the sprayed concrete-surrounding rock combined body[J]. Journal of Vibration and Shock, 2018, 37(24): 85-91, 136. (in Chinese)
[2] JIANG Q, YANG Y, YAN F, et al. Deformation and failure behaviours of rock-concrete interfaces with natural morphology under shear testing[J]. Construction and Building Materials, 2021, 293: 123468. doi: 10.1016/j.conbuildmat.2021.123468
[3] MOUZANNAR H, BOST M, LEROUX M, et al. Experimental study of the shear strength of bonded concrete–rock interfaces: surface morphology and scale effect[J]. Rock Mechanics and Rock Engineering, 2017, 50(10): 2601-2625. doi: 10.1007/s00603-017-1259-2
[4] CHANG X, LU J Y, WANG S Y, et al. Mechanical performances of rock-concrete bi-material disks under diametrical compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 104: 71-77. doi: 10.1016/j.ijrmms.2018.02.008
[5] ZHU J B, BAO W Y, PENG Q, et al. Influence of substrate properties and interfacial roughness on static and dynamic tensile behaviour of rock-shotcrete interface from macro and micro views[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 132: 104350. doi: 10.1016/j.ijrmms.2020.104350
[6] ZHAO B Y, LIU Y, LIU D Y, et al. Research on the influence of contact surface constraint on mechanical properties of rock-concrete composite specimens under compressive loads[J]. Frontiers of Structural and Civil Engineering, 2020, 14(2): 322-330. doi: 10.1007/s11709-019-0594-7
[7] 陈猛, 王浩, 齐迈, 等. 岩石–钢纤维混凝土复合层动态压缩性能试验研究[J]. 岩石力学与工程学报, 2020, 39(6): 1222-1230. CHEN Meng, WANG Hao, QI Mai, et al. Experimental study on dynamic compressive properties of composite layers of rock and steel fiber reinforced concrete[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(06): 1222-1230. (in Chinese)
[8] 赵坚, 李海波. 莫尔-库仑和霍克-布朗强度准则用于评估脆性岩石动态强度的适用性[J]. 岩石力学与工程学报, 2003, 22(2): 171-176. doi: 10.3321/j.issn:1000-6915.2003.02.001 ZHAO Jian, LI Haibo. Estimating the dynamic strength of rock using Mohr-coulomb and hoek-brown criteria[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 171-176. (in Chinese) doi: 10.3321/j.issn:1000-6915.2003.02.001
[9] 宫凤强, 司雪峰, 李夕兵, 等. 基于应变率效应的岩石动态Mohr-Coulomb准则和Hoek-Brown准则研究[J]. 中国有色金属学报, 2016, 26(8): 1763-1773. GONG Fengqiang, SI Xuefeng, LI Xibing, et al. Rock dynamic Mohr-Coulomb and Hock-Brown criteria based on strain rate effect[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(8): 1763-1773. (in Chinese)
[10] 宫凤强, 陆道辉, 李夕兵, 等. 不同应变率下砂岩动态强度准则的试验研究[J]. 岩土力学, 2013, 34(9): 2433-2441. GONG Fengqiang, LU Daohui, LI Xibing, et al. Experimental research of sandstone dynamic strength criterion under different strain rates[J]. Rock and Soil Mechanics, 2013, 34(9): 2433-2441. (in Chinese)
[11] 钱七虎, 戚承志. 岩石、岩体的动力强度与动力破坏准则[J]. 同济大学学报(自然科学版), 2008, 36(12): 1599-1605. doi: 10.3321/j.issn:0253-374X.2008.12.001 QIAN Qihu, QI Chengzhi. Dynamic strength and dynamic fracture criteria of rock and rock mass[J]. Journal of Tongji University (Natural Science), 2008, 36(12): 1599-1605. (in Chinese) doi: 10.3321/j.issn:0253-374X.2008.12.001
[12] GONG F Q, SI X F, LI X B, et al. Dynamic triaxial compression tests on sandstone at high strain rates and low confining pressures with split Hopkinson pressure bar[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 113: 211-219. doi: 10.1016/j.ijrmms.2018.12.005
[13] SI X F, GONG F Q, LI X B, et al. Dynamic Mohr–Coulomb and Hoek–Brown strength criteria of sandstone at high strain rates[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 115: 48-59. doi: 10.1016/j.ijrmms.2018.12.013
[14] FU Q, XU W R, HE J Q, et al. Dynamic strength criteria for basalt fibre-reinforced coral aggregate concrete[J]. Composites Communications, 2021, 28: 100983. doi: 10.1016/j.coco.2021.100983
[15] LU D C, WANG G S, DU X L, et al. A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete[J]. International Journal of Impact Engineering, 2017, 103: 124-137. doi: 10.1016/j.ijimpeng.2017.01.011
[16] ZHAO B Y, LIU Y, HUANG T Z, et al. Experimental study on strength and deformation characteristics of rock–concrete composite specimens under compressive condition[J]. Geotechnical and Geological Engineering, 2019, 37(4): 2693-2706. doi: 10.1007/s10706-018-00787-9
[17] 陈猛, 崔秀文, 颜鑫, 等. 岩石-钢纤维混凝土复合层抗压强度预测模型[J]. 岩土力学, 2021, 42(3): 638-646. CHEN Meng, CUI Xiuwen, YAN Xin, et al. Prediction model for compressive strength of rock-steel fiber reinforced concrete composite layer[J]. Rock and Soil Mechanics, 2021, 42(3): 638-646. (in Chinese)
[18] ZHANG X H, CHIU Y W, HAO H, et al. Dynamic compressive properties of Kalgoorlie basalt rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 135: 104512. doi: 10.1016/j.ijrmms.2020.104512
[19] 袁良柱, 苗春贺, 单俊芳, 等. 冲击下混凝土试样应变率效应和惯性效应探讨[J]. 爆炸与冲击, 2022, 42(1): 1-13. YUAN Liangzhu, MIAO Chunhe, SHAN Junfang, et al. On strain-rate and inertia effects of concrete samples under impact[J]. Explosion and shock waves, 2022, 42(1): 1-13. (in Chinese)
[20] FENG S W, ZHOU Y, WANG Y, et al. Experimental research on the dynamic mechanical properties and damage characteristics of lightweight foamed concrete under impact loading[J]. International Journal of Impact Engineering, 2020, 140: 103558. doi: 10.1016/j.ijimpeng.2020.103558
[21] 王健, 李二兵, 谭跃虎, 等. 层状盐岩及泥岩夹层动态力学特性对比试验研究[J]. 岩石力学与工程学报, 2017, 36(12): 3002-3011. WANG Jian, LI Erbing, TAN Yuehu, et al. Comparative experimental study on dynamic mechanical properties of bedded salt rock and mudstone interbed[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 3002-3011. (in Chinese)
[22] LI X Z, QI C Z. A micro-macro dynamic compressive-shear fracture model under static confining pressure in brittle rocks[J]. International Journal of Impact Engineering, 2018, 122: 109-118. doi: 10.1016/j.ijimpeng.2018.07.010
[23] ZHAO J, LI H B, WU M B, et al. Dynamic uniaxial compression tests on a granite[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(2): 273-277. doi: 10.1016/S0148-9062(99)00008-X
-
期刊类型引用(4)
1. 马殷军，杜腾飞，栾恩铭，张寿红，董江龙. 环境温度对青海湖地区含盐土水热变化规律试验研究. 水利与建筑工程学报. 2025(01): 55-60+79 . 
百度学术
2. 孔纲强，常洪林，王天赐，杨庆. 区域尺度地埋管地源热泵与能源地下结构开采浅层地热能评价综述. 岩土力学. 2024(05): 1265-1283 . 百度学术
3. 唐少容，殷磊，杨强，柯德秀. 微胶囊相变材料改良粉砂土的导热系数及预测模型. 中国粉体技术. 2024(03): 112-123 . 百度学术
4. 褚召祥，王一鸣，李晓昭，董凯军，顾晓滨，贾国圣. 岩土热导率预测正三棱柱-准内切球单元结构模型. 岩土工程学报. 2024(12): 2580-2590 . 本站查看
其他类型引用(3)
-
其他相关附件
计量
- 文章访问数: 354
- HTML全文浏览量: 80
- PDF下载量: 53
- 被引次数: 7
