A CPTU-based earth pressure model for deep excavations under complex environment and its practical application
-
摘要: 土压力计算是深基坑围护结构设计的重要组成部分，但现有土压力模型难以合理地考虑开挖扰动诱发土体工程性质演化影响。孔压静力触探（piezocone penetration test, CPTU）能够有效避免取样扰动，并快速提供连续的原位土测试参数（锥尖阻力、侧壁摩阻力、孔隙水压力）。基于CPTU原位测试和位移相关土压力模型，结合库仑土压力框架，综合考虑开挖诱发土体工程性质演化、邻近地下结构（受限空间）、土拱效应、地基土强度参数和土-结构界面摩擦角等影响因素，构建了复杂环境下深基坑土压力统一计算模型（主动状态至被动状态）。分别通过与室内1g模型试验和离心机试验结果对比，验证了所构建模型的准确性与合理性。进一步将所构建模型应用至太湖冲湖积相软土地区某邻近地铁车站的深基坑工程。现场分别在基坑开挖前后对围护结构的两侧（基坑内外）开展了CPTU原位测试，并监测得到了围护结构侧向变形与土压力变化。原位测试解译结果表明，基坑开挖显著地改变了周边土体状态参数，但对于有效内摩擦角的影响甚微。与现场所测土压力对比指出，基于CPTU的土压力模型能够较好地反映复杂环境下基坑土压力变化，成功实现了工程应用。
-
关键词:
- 孔压静力触探(CPTU) /
- 原位土力学 /
- 开挖扰动 /
- 受限空间 /
- 位移相关土压力
Abstract: The determination of earth pressure is a key element for the design of retaining structures of deep excavations. However, the existing earth pressure models can not reasonably consider the change of soil properties induced by excavation activities. The piezocone penetration test (CPTU) is capable of effectively avoiding the sampling disturbance and quickly providing the continuous in-situ testing parameters of soils (cone resistance, sleeve friction, pore water pressure). Combining the CPTU tests and the displacement-based earth pressure model, the change of soil properties induced by excavations, surrounding buried structures (confined soil), soil arching effects, soil strength parameters and friction angle of the soil-structure interface are comprehensively taken into account to develop a unified earth pressure model (from active- to passive-state) under the Coulomb's earth pressure framework. The comparisons of earth pressures obtained between 1g-/ng- model tests and the developed model are made for the validation. Subsequently, the developed model is employed in a deep excavation adjacent to a metro station in soft soils deposited in the Taihu Lake. The CPTU tests are then performed in the soils around both sides of retaining structures, of which the earth pressure and lateral deformation are also measured. The interpretation of in-situ testing results indicates that state parameters of soils significantly change due to excavations, but the effective friction angle almost remains unchanged. The further comparisons of earth pressures obtained between the measurement and the developed model indicate that the CPTU-based earth pressure model works well for a deep excavation under a complex environment, thus successfully reaching a practical application. -
0. 引言
准确计算土压力是深基坑围护结构（如板桩、地下连续墙或钻孔灌注桩等）设计与施工的重要内容之一[1-2]。基于极限平衡理论的朗肯/库仑解被广泛用于计算地下结构主动和被动土压力。然而，城市基坑开挖需要尽可能地降低围护结构的侧向变形，导致基坑周边土体大多处于小应变状态，土体变形小于或远小于设计标准，土体侧向应力无法接近或达到极限状态。此时，朗肯/库仑解显然偏于保守。因此，有必要寻求一种有效且实用的深基坑土压力计算模型。
已有大量试验[3-6]证明了支护结构土压力的发挥与土体侧向位移密切相关，为位移相关（非极限）土压力模型的提出奠定了基础。现有关于位移相关土压力计算方法主要可分为3类：①假设理想的土体应力-应变关系或土体位移-抗剪强度发挥比关系，结合莫尔应力圆和边界条件，建立平衡方程，推导得到任意应变条件下土体侧向应力[7-8]；②弹性地基梁或地基反力法[9-10]；③基于试验数据，选取合适的显式函数，考虑边界条件，构造位移相关土压力模型[11-15]。第①类方法假设合理，但需提前定义土体本构关系，模型参数不易获取。第②类方法将连续土体介质离散成一系列非连续弹簧，即便假定土体位移和反力关系为非线性，也无法正确反映连续介质相互作用，难以得到正确的土压力分布。此外，地基梁模型数学表达式较为复杂，不易求解。第③类方法虽缺乏严格的数学推导，但基于大量试验数据和合理的边界条件，计算参数简洁明了，具有较强的工程适用性。Potts等[16]指出，挡墙非线性土压力分布形成的本质是土-结构非线性行为的体现。因此，笔者认为，若能够正确认识挡墙位移/变形过程中土体工程性质的演化规律，获取足够准确的土体力学参数，基于更为简洁和直接的第③类方法，建立挡土墙从主动状态到被动状态的统一土压力模型是可实现的。
第③类方法的关键是选择合适的数学函数拟合土压力-位移曲线（ps-s曲线）。现有位移相关土压力模型中，主要采用指数函数（Mei模型[11]）、幂函数（英国规范[17]）、双曲线函数（Duncan模型[18]）、分段线性函数（AASHTO标准[19]）等。但上述模型均未考虑开挖引起土体工程性质变化对ps-s曲线的影响。除上述局限性外，笔者认为，建立复杂环境下深基坑土压力模型还需进一步考虑以下4个因素：①如何考虑基坑开挖扰动引起周边土体物理-力学-状态参数的变化？②如何考虑基坑开挖诱发墙体侧向变形模式以及基坑设计参数的影响？③如何考虑基坑周边邻近建（构）筑物的影响？④如何考虑墙后土拱效应等荷载传递机理的影响？本文重点探索如何基于现有位移相关土压力模型解决上述4个问题。
对比钻孔取样和室内单元试验，原位测试在岩土工程场地表征的重要性不断增加[20-21]。原位测试已成为岩土工程勘察的重要方法之一，尤其对于采用常规方法难以取样或难以完成室内测试的岩土材料（如砂土、粉土等）。通过与室内单元试验相比，Mayne等[22]总结了原位测试的主要优势：①扰动小，无需取样；②可迅速获得测试及解译结果；③可获得大量连续数据；④可评估整个场地的垂直和横向变异性。Li等[23]将静力触探（CPT/CPTU）应用于基坑开挖引起的桩基侧向承载力损失评价。李赞等[24]和Lu等[25]在基坑开挖不同阶段进行了CPTU原位测试工作，评估了基坑开挖扰动对土体工程性质的影响。上述研究表明，原位测试是评价深基坑开挖引起土体工程性质演化的有效方法之一。
综上所述，本文将原位测试方法与位移相关土压力模型结合，评价基坑开挖引起土压力模型参数的变化，拟解决所述深基坑土压力模型的第一个问题。进一步对深基坑围护结构变形进行监测，可获取墙体侧向变形发展过程；并将围护结构离散成多段平动模式下不同位移大小的墙体单元，拟解决第二个问题。在第二个问题的基础上，引入Lai等[26]和Li等[27]提出的库仑主动、被动土压力修正解，可考虑基坑邻近地铁车站或地铁隧道导致的受限空间问题和土拱效应问题，拟解决第三与第四个问题。
基于上述构想，选择位移相关土压力模型，基于库仑土压力框架，结合原位测试方法和受限空间土压力修正解，建立复杂环境下基于CPTU的深基坑土压力统一计算模型。所构建模型通过与室内模型试验和离心试验结果对比，验证其合理性与正确性。而后，将所构建模型应用至深基坑近接开挖工程，并与现场土压力监测数据对比，进一步探讨模型的工程适用性。
1. 土压力统一计算模型构建
1.1 位移相关土压力模型建立
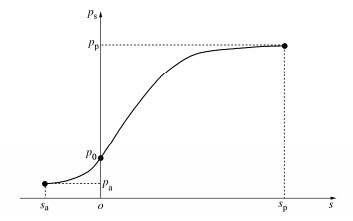
Mei等[11]基于土压力-位移测试数据（如图 1），结合边界条件，提出了从主动到被动状态下位移土压力模型，适用于不同支护结构位移模式。该模型被分别应用于求解刚/柔性地下结构侧向土压力[13-15]。其数学方程可表达为\$
ps=(k(φ′)1+e−b(sa,φ′)s−k(φ′)−42)p02。 (1) 式中：p0为静止土压力；φ′为有效土体内摩擦角；k(φ′)为土体内摩擦角函数；b(sa,φ′)为调动主动极限土压力所需位移和土体内摩擦的正函数。
根据图 1，模型下边界为主动极限土压力，对应主动极限位移，即ps = pa (s = sa < 0)；模型上边界为被动极限土压力，对应被动极限位移，即ps = pp (s = sp > 0)。需要指出，sp和sa均受土体类型、压实度和墙体位移模式等影响。一般情况下，sp要远大于sa。表 1给出了调动不同土体主动、被动土压力需要的位移大小。根据Clough等[28]试验结果，对于砂土和黏土均可假设sp = -10sa。基于土压力模型上限ps = pp（s = sp），定义A =e−bsa。根据式（1）可得
pp=(k1+e−bsp−k−42)p02=(k1+A−10−k−42)p02=KpK0p0。 (2) 土体类型 sa sp sp/sa 密砂 0.001H 0.01H 10 中密砂 0.002H 002H 10 松砂 0.004H 0.04H 10 硬黏土 — — — 软黏土 — — — 压实粉土 0.002H 0.02H 10 压实纯黏土 0.01H 0.05H 5 压实有机质黏土 0.01H 0.05H 5 注：H为支护结构高度。 式中：Kp和K0分别为被动和静止土压力系数。
已知b > 0和sa < 0，参数A > 1恒成立。因此A-10始终接近于0。因此，根据式（2）可得
k=4KpK0−4。 (3) 由土压力下限ps = pa (s = sa)可得
pa=(k1+e−bsa−k−42)p02=(k1+A−k−42)p02=KaK0p0。 (4) 联立式（3），（4）可得
A=Kp−KaKp−2K0+Ka， (5) 式中，Ka为主动土压力系数。
基于上述推导，位移相关土压力模型可表达为
ps=f(γ,K0,Ka,Kp,sa,s,z)。 (6) 1.2 库仑土压力框架拓展
库仑土压力理论分别给出了极限主动和被动土压力系数：
Ka=(cosφ′)2cosδ[1+√sinφ′(sinφ′+δ)cosδ]2， (7) Kp=(cosφ′)2cosδ[1−√sinφ′(sinφ′+δ)cosδ]2。 (8) 库仑土压力理论虽然考虑了土体内摩擦角和墙-土界面摩擦系数，但忽略了土体黏聚力。Ni等[13]采用等效抗剪强度概念，引入等效内摩擦角考虑黏聚力：
φ′ D=arctan(tanφ′+c′γH)。 (9) 考虑基坑开挖引起土体超固结比OCR的影响，土体静止土压力系数为
K0=(1−sinφ′)OCRsinφ′。 (10) 此外，为考虑复杂环境下深基坑邻近既有地下结构形成的地基土受限空间问题和墙后土拱效应，分别引入Lai等[26]和Li等[27]提出的基于库仑土压力理论的主动和被动土压力修正系数（βa和βp）。所引入土压力修正系数综合考虑了土体强度参数（c′和φ′）、土-结构界面摩擦角δ、地基土宽深比B/H（取决于基坑开挖深度、开挖宽度和围护结构插入比）：
βa=0.97+0.40BtanφH+2.34BtanδHtanφ−25.44cBγH2− 0.04μtanφ−0.77tanδtanφ， (11) βp=2.67tan2φ−5.78tanδtanφ+0.48(BH)2+ 0.11(cγH)2−3.76。 (12) 因此，考虑开挖引起土体工程性质演化和邻近既有地下结构的深基坑土压力统一计算模型可表述为
p=f(γ,K0,βaKa,βpKp,sa,s,z) =f(γ,c′,φ′,OCR,δ,B,H,sa,s,z)。 (13) 1.3 基于CPTU原位测试参数解译
根据式（13）可发现，所构建土压力模型考虑了受限空间地基土宽深比、土体黏聚力、土体内摩擦角、超固结比、土体重度、墙体变形等影响因素。其中，土体工程性质参数均由CPTU原位测试解译获取。
土体天然重度计算公式为
γ=[0.27lgRf+ 0.36lg(qt/pa) +1.236]γw。 (14) 式中：qt为修正锥尖阻力；破坏比Rf = 100 fs/qc，qc和fs分别为CPTU锥尖阻力和侧壁摩阻力；pa为大气压强，取100 kPa；γw为水的重度，γw= 10 kN/m3。
Mayne[29]提出土体有效黏聚力为
c′≈0.03σ′v0， (15) 式中，σ′v0为土层初始有效上覆应力。
土体有效内摩擦角的计算需要区分细颗粒土（主要为粉土和黏土）和粗颗粒土（砂土或杂填土等）[29-30]，计算公式分别为：
φ′=29.5B0.121q[0.256+0.336Bq+lgQ]， (16) φ′=17.6∘+11.1lg[(qc/pa)⋅(pa/σ′v0)0.5]， (17) 其中，
Bq=(u2−u0)/(qt−σv0)， (18) Q=(qt−σv0)/σ′v0。 (19) 式中：u0为静止孔隙水压力；σv0为天然上覆应力。
类似地，土体超固结比的计算也需要考虑区分细粒土和粗粒土[31-32]，计算公式如下：
OCR=0.33(qt−σv0)/σ′v0， (20) OCR=0.32(qt−σv0)0.72/σ′v0。 (21) 土-结构界面摩擦角无法通过原位测试方法直接获取。Potyondy[33]开展了大量室内直剪试验，探究了不同墙体材料和各类土体界面摩擦系数。试验结果表明，混凝土墙体与黏土或砂土界面摩擦系数tanδ/tanφ′介于0.65~1.0。在计算被动侧土压力时，已有研究[16]建议取δ = (1/3~1/2)φ′。为保守考虑，取δ =φ′/3；φ′由现场原位测试参数解译。
地基土位移大小决定了土压力的发挥程度，因此确定不同土层极限位移极其重要。如前所述，所构建土压力模型假设sp = -10sa。基于此，结合表 1；对于砂土，取sa = 0.001H；对于粉土，取sa = 0.002H；对于黏土，取sa = 0.01H。
1.4 模型实现
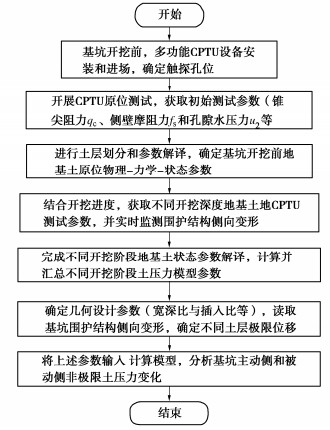
图 2给出了复杂环境下基于CPTU的基坑不同开挖深度土压力计算流程。首先，基坑开挖前，CPTU测试设备进场，确定静力触探孔位，并将探头与数据采集设备连接后开展CPTU原位测试试验，获取地层初始原位参数。根据所采集原位测试结果，进行土层划分和土体物理-力学-状态参数解译。在完成土层划分后，可确定不同土层所对应极限位移。结合开挖进度，进一步开展CPTU原位测试工作，获取基坑不同开挖深度下地基土原位测试参数。此外，所建立深基坑土压力模型的实现还需输入围护结构侧向变形。
![]()
图 2 基于CPTU的基坑土压力计算流程Figure 2. Flow chart to estimate earth pressures in deep excavations based on CPTU在汇总基坑不同开挖深度对应土体状态参数的同时，还应确定基坑几何设计参数。例如，对于相邻基坑围护结构主动区土压力计算（常指基坑外侧），当相邻双基坑围护结构净距较小时，可能导致地基土受限空间问题，需要计算对应宽深比B/H。对于围护结构被动土压力计算（常指基坑内侧），当基坑开挖宽度较小且围护结构插入比较大时，也容易造成地基土受限空间问题，详见文献[26]。最后，将上述参数分别输入所构建土压力模型，获取不同开挖阶段主动区和被动区土压力剖面。具体实施过程详见图 2。
2. 对比与验证
2.1 1g模型试验
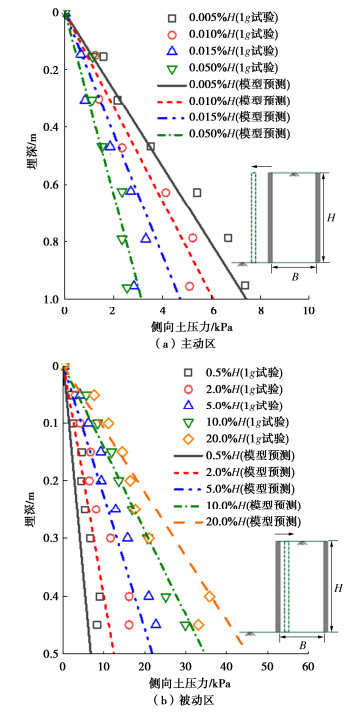
Fang等[4]通过1g室内模型试验，测量了刚性支护结构位移过程不同深度土体主动区土压力发挥过程。模型选择Ottawa石英干砂填料。支护结构高度为1.04 m，地基土埋深为1.015 m，宽度为1.8 m，对应宽深比B/H为1.77。Ottawa石英砂相对密实度Dr为24.8%（松砂），重度γ为15.4 kN/m3，内摩擦角φ′为34°，结构-土界面摩擦角δ为21.1°。根据表 1，确定主动极限位移sa = 0.004 m。在主动土压力试验的基础上，Fang等[3]开展了被动区土压力测试工作。类似地，基于室内模型试验，采用Ottawa石英干砂，对应γ为15.5 kN/m3，φ′为30.9°，δ为19.2°，H为0.5 m，B为2 m，对应B/H为4。根据表 1，换算被动极限位移为0.04 m。
图 3给出了1g模型试验与土压力模型预测结果的对比。如图 3所示，所构建土压力模型能够较好地反映模型试验主动区与被动区土压力大小与分布，验证了模型的合理性。需要指出的是，所构建模型基于库仑土压力框架拓展，因此所获土压力呈线性分布。模型试验反映出土拱效应，土压力呈非线性分布。在模型的底部，可观测到预测值与试验结果存在一定偏差。
![]()
图 3 1g试验与土压力模型预测结果对比Figure 3. Comparison of earth pressures obtained between 1g model tests and developed model2.2 离心机试验
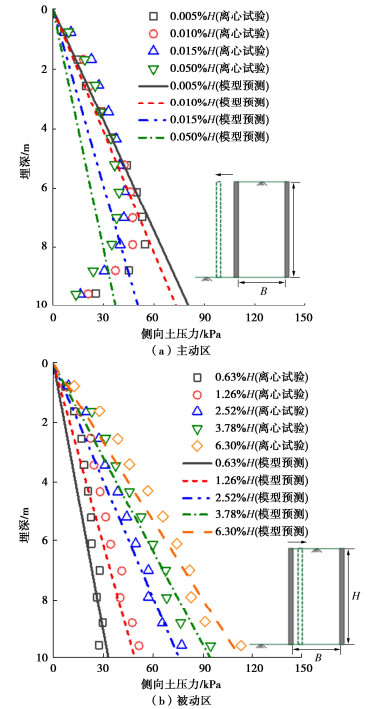
为进一步探讨所构建土压力模型的有效性，引入支护结构位移相关土压力离心试验结果进行对比。Deng等[5-6]开展了一系列40g离心机试验，研究了支护结构平动模式下无黏性土主动区和被动区土压力的变化规律。模型试验原型尺寸为：支护结构高度H为10 m，填土宽度B为22 m，对应地基土宽深比B/H为2.2。主动和被动土压力模型试验填料均选择Houstun砂，对应Dr为33%（松砂），γ为13.9 kN/m3，φ′为32.9°，δ为21.7°。
图 4对比了离心机试验结果和所构建模型预测结果。墙体主动位移初期，试验结果与所提模型预测结果吻合良好。随着墙体主动位移的增加至0.15%H，土拱效应充分发挥，土压力非线性增强，表现为结构底部土压力的减小。此时主动区土压力预测结果与试验结果的偏差随着墙体位移增加而逐渐增大，见图 4（a）。因此，基于库仑土压力框架所建立位移相关土压力模型不能完全反映土拱效应引起的非线性主动土压力分布。尽管如此，基于土拱效应和土压力合力而提出的修正系数βa和βp可保证理论解与试验土压力合力基本接近，在一定程度上弥补了该缺陷。图 4（b）说明，采用所构建模型能够较为准确地反映被动土压力分布。综上所述，所构建土压力模型可用于预测基坑围护结构土压力变化。
![]()
图 4 离心机试验与土压力模型预测结果对比Figure 4. Comparison of earth pressures obtained between centrifuge tests and developed model3. 工程应用
3.1 工程概况
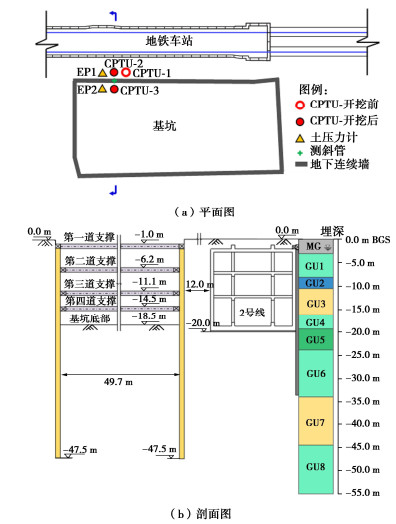
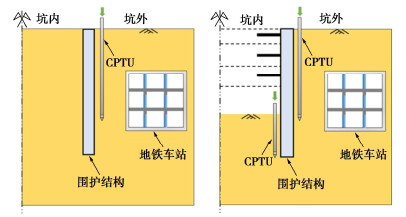
苏州市姑苏区某深基坑工程位于典型的太湖冲湖积相软土地层，邻近地铁车站开挖。地层自上而下分别为第①层杂填土，表示为“MG (Made Ground)”；第②层粉质黏土，表示为“GU1 (Geotechnical Unit 1)”；第③层黏质粉土(GU2)；第④层粉砂夹砂质粉土(GU3)；第⑤层粉质黏土(GU4)；第⑥层黏质粉土夹粉质黏土(GU5)；第⑦层粉质黏土(GU6)；第⑧层粉砂夹砂质粉土(GU7)；第⑨层粉质黏土(GU8)。基坑支护体系采用地下连续墙结合四道钢筋混凝土水平支撑。基坑开挖宽度Bp为49.7 m，开挖深度He为18.5 m，围护结构埋深为47.5 m，围护结构距地铁车站宽度Ba为12.0 m。地铁车站埋深为地表以下20 m，与坑底标高近似。基坑与邻近地铁车站几何尺寸、位置关系和地层分布见图 5。由此可见，基坑下覆深厚软土，开挖深度内广泛分布粉土和砂土，取样扰动大，难以通过室内单元试验准确预测基坑开挖引起原状土体参数变化。
![]()
图 5 深基坑与邻近地铁车站几何示意图及地层剖面Figure 5. Soil strata and layout of a deep excavation adjacent to a metro station总体而言，该工程施工环境复杂，基坑开挖后围护结构易发生侧向变形，但基坑变形控制要求高，使得土压力预测对围护结构的设计和优化更为重要。
3.2 现场原位测试方案
图 6给出了邻近既有地铁车站的深基坑CPTU测试方案。首先，在基坑围护结构安装结束但地层未开挖之前，获取围护结构外侧原位测试参数。假设地基土开挖前围护结构内外两侧土体工程性质参数基本一致。随着基坑开挖深度的增加，坑内土体移除导致周边土体卸荷，坑外土体逐渐进入主动状态，坑内土体则逐渐进入被动状态。与此同时，周边土体受到开挖扰动。为获得准确的土压力模型计算参数，需要分别在围护结构内、外侧开展CPTU原位测试试验。考虑测试成本，本次测试仅在基坑开挖至设计标高后开展坑内CPTU测试，可获得基坑开挖结束后土体力学和状态参数。图 7给出了邻近地铁车站深基坑CPTU测试现场。
![]()
图 6 邻近地铁车站深基坑CPTU测试方案Figure 6. Testing scheme of CPTU for a deep excavation adjacent to a metro station![]()
图 7 邻近地铁车站深基坑CPTU测试过程Figure 7. CPTU testing process of a deep excavation adjacent to a metro station现场在地下连续墙迎土侧埋设了测斜管，实时监测基坑开挖全过程围护结构侧向变形。此外，在变形监测剖面附近围护结构内、外侧埋设了振弦式土压力计（见图 5），可通过频率变化反算压应力值。土压力计埋设采用挂布法，即在围护结构钢筋笼安装过程，将土压力计绑扎至钢筋笼上，随后完成混凝土浇灌，使其形成整体后对土压力计进行校正。现场在地连墙每5 m深度内布设一个土压力计。需要注意，由于坑内土体移除后，开挖面以上的土压力计便无法再工作，因此仅在基坑内部设计标高以下布设土压力计，这与CPTU测试方案对应。图 8进一步给出了土压力计埋设过程。
![]()
图 8 邻近地铁车站深基坑土压力计埋设过程Figure 8. Installation process of earth pressure cells for a deep excavation adjacent to a metro station3.3 原位测试结果解译
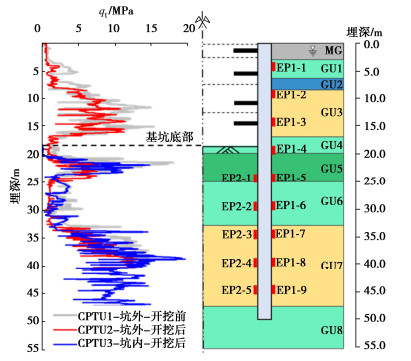
图 9给出了基坑开挖前后修正锥尖阻力qt分布曲线。基于开挖前CPTU1测孔建立地层模型，CPTU2和CPTU3分别对应开挖后坑内外测孔。图中，EP1-1~EP1-9沿B区基坑地连墙外侧布设，EP2-1~EP2-5沿B区基坑开挖面以下地连墙外侧布设。土压力测试结果将用于验证基于CPTU的土压力模型预测结果。
![]()
图 9 深基坑开挖前后CPTU测试结果对比Figure 9. Comparison of CPTU results for pre-excavation and post-excavation从图 9可以看出，基坑开挖导致地表和开挖面以下一定范围内的土体锥尖阻力降低。随着土体埋深的增加，锥尖阻力基本一致。这说明开挖对周边一定范围内的土体形成了扰动，降低了细粒土不排水抗剪强度或粗粒土排水抗剪强度，这与Lu等[25]结论一致。此外，锥尖阻力和竖向应力的降低还将导致土体超固结比发生改变，对土压力系数计算产生影响。后文将进一步分析。
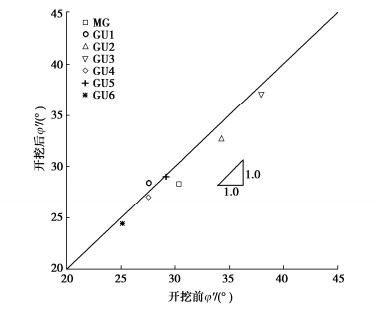
根据式（13）可以发现，所构建土压力模型的实现主要依赖于土体强度参数选取和不同状态下土压力系数计算。土体有效强度参数由黏聚力和有效内摩擦角组成。对于正常固结土，黏聚力一般为零，因此计算开挖前后的有效内摩擦角是关键。基于式（16），（17），选取基坑围护结构外侧土体开挖前后CPTU测试曲线，用以计算开挖对不同土层（细粒土和粗粒土）有效内摩擦角的影响，如图 10所示。
![]()
图 10 深基坑开挖前后坑外土体有效内摩擦角对比Figure 10. Comparison of CPTU results for pre-excavation and post-excavation从图 10可发现，开挖前后土体有效内摩擦角基本不改变，这说明开挖扰动不影响土体有效内摩擦角。Lunne等[34]和Blaker等[35]分别通过室内单元试验研究了挪威海相软土和低塑性天然粉土取样扰动的影响。试验结果证明取样扰动对土体有效内摩擦角影响可忽略不计。因此，可假设基坑开挖卸荷不改变土体有效内摩擦角。综上，采用所构建土压力模型计算基坑开挖前后围护结构土压力时，仅需输入开挖前土体有效内摩擦角，重点关注开挖前后土体超固结比OCR变化导致的静止土压力系数改变。
3.4 深基坑土压力预测
为预测基坑围护结构主动区和被动区土压力，基于CPTU曲线解译土层（层顶标高z）、土体天然重度γw及土层平均竖向应力σv、有效黏聚力c'、有效内摩擦角φ′、墙-土界面摩擦角δ及其开挖前后土体OCR值和静止土压力系数K0的变化。此外，根据基坑几何设计尺寸确定围护结构至地铁车站距离Ba、开挖深度He、墙体插入深度H和基坑开挖宽度Bp。
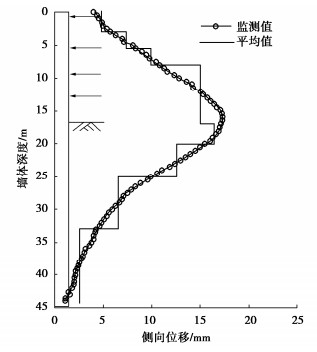
进一步根据不同土层给出主动极限位移sa和被动极限位移sp。由于基坑采用柔性地下连续墙作为围护结构，墙体变形模型表现为连续的鼓肚状曲线。根据土层分布，对墙体进行离散。为获取不同土层平均侧向位移savg，对同一土层所有测点水平位移作算术平均，将求得的平均值等效为平动模式下墙体侧向位移，从而可引入土压力修正系数βa和βp。据此，图 11给出了基坑开挖至设计标高后墙体侧向变形监测过程及各土层平均位移。
![]()
图 11 深基坑开挖至设计标高后墙体侧向变形Figure 11. Lateral deformations of diaphragm wall of deep excavation at designed level表 2给出了基于CPTU的基坑土压力模型参数。从表 2中可以看出，由于开挖导致坑外土体锥尖阻力降低，竖向应力保持不变，因此导致超固结比略有减小。值得注意的是，基坑开挖导致坑内土体竖向卸荷明显，锥尖阻力显著减小，OCR值则显著增大。这说明计算基坑土压力须考虑当前状态下的静止土压力系数变化。此外，表 2也给出了基坑几何设计参数。对于基坑主动土压力计算，填土宽深比B/H可能低至0.25左右，理论上不可能形成完整的库仑滑楔体，因此有必要对主动区土压力系数进行修正。对于被动土压力计算，坑内地基土宽深比为1.7左右，基坑可忽略地基土宽度的影响。
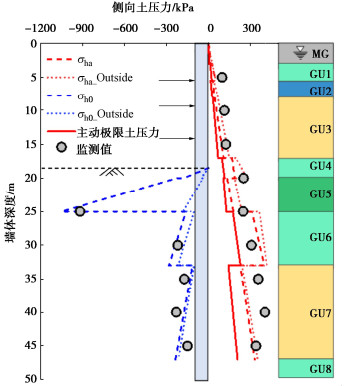
表 2 基坑土压力模型计算参数Table 2. Parameters of earth pressure model for a deep excavationGU z/m γw/(kN·m-3) σv/kPa c'/kPa φ′/(°) δ/(°) OCR K0 s/mm sa/mm sp/mm a b c a b c MG 0.0 17.1 25.7 0.0 30.3 10.1 1.0 1.0 — 0.50 0.50 — 4.9 3.0 30.0 GU1 3.0 17.0 72.5 2.2 27.5 9.2 1.2 1.0 — 0.59 0.54 — 7.3 30.0 300.0 GU2 5.5 18.0 116.2 0.0 34.2 11.4 1.2 0.9 — 0.49 0.41 — 9.9 4.0 40.0 GU3 8.0 19.1 224.7 0.0 37.9 12.6 1.6 1.4 — 0.52 0.47 — 15.1 8.0 80.0 GU4 17.0 17.5 337.0 10.1 27.5 9.2 2.1 1.4 — 0.76 0.63 —- 16.4 40.0 400.0 GU5 20.0 19.1 411.0 0.0 29.1 9.7 1.0 1.0 9.0 0.51 0.51 1.50 12.6 6.0 60.0 GU6 25.0 17.0 526.5 0.0 25.1 8.4 1.6 1.0 2.5 0.70 0.58 0.85 6.5 70.0 700.0 GU7 33.0 19.8 733.2 0.0 36.6 12.2 1.0 1.0 1.0 0.40 0.40 0.40 2.5 18.0 180.0 GU8 47.0 — — 0.0 — — — — — 0.50 0.50 0.50 — — — 注：OCR (a，b，c) = OCR (开挖前坑外土/开挖后坑外土/开挖后坑内土)，K0 (a，b，c) = K0 (开挖前坑外土/开挖后坑外土/开挖后坑内土)，Ba = 12.0 m，He = 18.5 m，H = 47.5 m，Bp = 49.7 m。 图 12给出了基于CPTU所构建土压力模型得到的土压力预测值和监测值对比结果。定义基坑围护结构外侧承受主动区土压力σha，内侧承受被动区土压力σhp。定义σha和外侧静止土压力σh0_Outside为正值，σhp和内侧静止土压力σh0_Inside为负值。
![]()
图 12 深基坑围护结构侧向土压力预测值与监测值对比Figure 12. Comparison between predicted and measured lateral earth pressures exerted onto diaphragm wall of a deep excavation如图 12所示，理论预测结果与现场监测数据基本吻合。由于坑内降水和施工荷载等影响，导致局部数据点发生偏离。对比主动、被动土压力值发现，主动区土压力预测效果较被动区土压力预测效果好。这可能是因为坑内土体扰动较为明显，土压力监测数据波动大，且坑底经降水处理后，CPTU解译精度也可能出现偏差，尤其是坑底面附近土体。另外，库仑土压力理论计算被动土压力时，三角形滑楔体假设与被动推力作用下的真实弧形滑楔体有一定差异，导致库仑土压力修正解出现误差较大。综上，认为基于CPTU的深基坑土压力计算模型可应用于复杂环境下深基坑围护结构土压力变化分析。
4. 结论
（1）综合考虑基坑几何尺寸、周边既有地下结构、土拱效应、地基土强度参数和土-结构界面摩擦系数以及开挖引起的土体工程性质参数演变，基于库仑土压力框架和CPTU原位测试，构建了深基坑土压力模型，并通过与室内1g试验和离心机试验结果进行对比，验证了所构建土压力模型的准确性与合理性。
（2）将所构建基于CPTU的土压力模型应用至邻近地铁车站的深基坑围护结构土压力预测，评价了深基坑开挖诱发土体工程性质演化规律；基于CPTU确定了土压力模型参数，并通过与现场监测数据对比，验证了基于CPTU土压力统一计算模型的工程适用性，建立了软土地层深基坑土压力变化分析方法。
（3）CPTU原位测试结果证明了深基坑开挖对坑内外土体形成了不同程度的扰动，坑内浅层土体锥尖阻力显著降低，土体超固结比显著改变，对土压力系数影响十分明显，但有效内摩擦角基本保持不变。
本文从原位土力学[36]的角度出发，有效避免了取样扰动对土体物理-力学-状态参数解译影响，证明了CPTU确定现场原位土工程特性的优势。通过探讨深基坑土压力问题，说明了CPTU原位测试可应用于复杂边值问题求解，有助于提高工程设计水平。但本文所建立统一土压力计算模型融合了多种因素，表达形式仍较为复杂，计算需求助于数学编程，有待进一步简化和完善。
-
![]()
图 2 基于CPTU的基坑土压力计算流程
Figure 2. Flow chart to estimate earth pressures in deep excavations based on CPTU
![]()
图 3 1g试验与土压力模型预测结果对比
Figure 3. Comparison of earth pressures obtained between 1g model tests and developed model
![]()
图 4 离心机试验与土压力模型预测结果对比
Figure 4. Comparison of earth pressures obtained between centrifuge tests and developed model
![]()
图 5 深基坑与邻近地铁车站几何示意图及地层剖面
Figure 5. Soil strata and layout of a deep excavation adjacent to a metro station
![]()
图 6 邻近地铁车站深基坑CPTU测试方案
Figure 6. Testing scheme of CPTU for a deep excavation adjacent to a metro station
![]()
图 7 邻近地铁车站深基坑CPTU测试过程
Figure 7. CPTU testing process of a deep excavation adjacent to a metro station
![]()
图 8 邻近地铁车站深基坑土压力计埋设过程
Figure 8. Installation process of earth pressure cells for a deep excavation adjacent to a metro station
![]()
图 9 深基坑开挖前后CPTU测试结果对比
Figure 9. Comparison of CPTU results for pre-excavation and post-excavation
![]()
图 10 深基坑开挖前后坑外土体有效内摩擦角对比
Figure 10. Comparison of CPTU results for pre-excavation and post-excavation
![]()
图 11 深基坑开挖至设计标高后墙体侧向变形
Figure 11. Lateral deformations of diaphragm wall of deep excavation at designed level
![]()
图 12 深基坑围护结构侧向土压力预测值与监测值对比
Figure 12. Comparison between predicted and measured lateral earth pressures exerted onto diaphragm wall of a deep excavation
土体类型 sa sp sp/sa 密砂 0.001H 0.01H 10 中密砂 0.002H 002H 10 松砂 0.004H 0.04H 10 硬黏土 — — — 软黏土 — — — 压实粉土 0.002H 0.02H 10 压实纯黏土 0.01H 0.05H 5 压实有机质黏土 0.01H 0.05H 5 注：H为支护结构高度。 
下载: 导出CSV
表 2 基坑土压力模型计算参数
Table 2 Parameters of earth pressure model for a deep excavation
GU z/m γw/(kN·m-3) σv/kPa c'/kPa /(°) δ/(°) OCR K0 s/mm sa/mm sp/mm a b c a b c MG 0.0 17.1 25.7 0.0 30.3 10.1 1.0 1.0 — 0.50 0.50 — 4.9 3.0 30.0 GU1 3.0 17.0 72.5 2.2 27.5 9.2 1.2 1.0 — 0.59 0.54 — 7.3 30.0 300.0 GU2 5.5 18.0 116.2 0.0 34.2 11.4 1.2 0.9 — 0.49 0.41 — 9.9 4.0 40.0 GU3 8.0 19.1 224.7 0.0 37.9 12.6 1.6 1.4 — 0.52 0.47 — 15.1 8.0 80.0 GU4 17.0 17.5 337.0 10.1 27.5 9.2 2.1 1.4 — 0.76 0.63 —- 16.4 40.0 400.0 GU5 20.0 19.1 411.0 0.0 29.1 9.7 1.0 1.0 9.0 0.51 0.51 1.50 12.6 6.0 60.0 GU6 25.0 17.0 526.5 0.0 25.1 8.4 1.6 1.0 2.5 0.70 0.58 0.85 6.5 70.0 700.0 GU7 33.0 19.8 733.2 0.0 36.6 12.2 1.0 1.0 1.0 0.40 0.40 0.40 2.5 18.0 180.0 GU8 47.0 — — 0.0 — — — — — 0.50 0.50 0.50 — — — 注：OCR (a，b，c) = OCR (开挖前坑外土/开挖后坑外土/开挖后坑内土)，K0 (a，b，c) = K0 (开挖前坑外土/开挖后坑外土/开挖后坑内土)，Ba = 12.0 m，He = 18.5 m，H = 47.5 m，Bp = 49.7 m。
下载: 导出CSV
-
[1] SCHWEIGER H F, TSCHUCHNIGG F. A numerical study on undrained passive earth pressure[J]. Computers and Geotechnics, 2021, 140: 104441. doi: 10.1016/j.compgeo.2021.104441
[2] 赖丰文, 刘松玉, 杨大禹, 等. 有限宽度填土挡墙主动土压力的普适解法[J]. 岩土工程学报, 2022, 44(3): 483-491. doi: 10.11779/CJGE202203010 LAI Fengwen, LIU Songyu, YANG Dayu, et al. Generalized solution to active earth pressure exerted onto retaining wall with narrow backfills[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(3): 483-491. (in Chinese) doi: 10.11779/CJGE202203010
[3] FANG Y S, CHEN T J, WU B F. Passive earth pressures with various wall movements[J]. Journal of Geotechnical Engineering, 1994, 120(8): 1307-1323. doi: 10.1061/(ASCE)0733-9410(1994)120:8(1307)
[4] FANG Y S, ISHIBASHI I. Static earth pressures with various wall movements[J]. Journal of Geotechnical Engineering, 1986, 112(3): 317-333. doi: 10.1061/(ASCE)0733-9410(1986)112:3(317)
[5] DENG C, HAIGH S K. Earth pressures mobilised in dry sand with active rigid retaining wall movement[J]. Géotechnique Letters, 2021, 11(3): 202-208. doi: 10.1680/jgele.20.00116
[6] DENG C, HAIGH S K. Sand deformation mechanisms and earth pressures mobilised with passive rigid retaining wall movements[J]. Géotechnique, 2022: 1-14.
[7] FAN X, XU C, LIANG L, et al. Analytical solution for displacement-dependent passive earth pressure on rigid walls with various wall movements in cohesionless soil[J]. Computers and Geotechnics, 2021, 140: 104470. doi: 10.1016/j.compgeo.2021.104470
[8] WANG L, XIAO S. Calculation method for displacement- dependent earth pressure on a rigid wall rotating around its base[J]. International Journal of Geomechanics, 2021, 21(8): 04021132. doi: 10.1061/(ASCE)GM.1943-5622.0002104
[9] NEJJAR K, DIAS D, CUIRA F, et al. Numerical modelling of a 32 m deep excavation in the suburbs of Paris[J]. Engineering Structures, 2022, 268: 114727. doi: 10.1016/j.engstruct.2022.114727
[10] NEJJAR K, DIAS D, CUIRA F, et al. Experimental study of the performance of a 32 m deep excavation in the suburbs of Paris[J]. Géotechnique, 2021: 1-11.
[11] MEI G, CHEN Q, SONG L. Model for predicting displacement-dependent lateral earth pressure[J]. Canadian Geotechnical Journal, 2009, 46(8): 969-975. doi: 10.1139/T09-040
[12] MEI G, CHEN R, LIU J. New insight into developing mathematical models for predicting deformation-dependent lateral earth pressure[J]. International Journal of Geomechanics, 2017, 17(8): 06017003. doi: 10.1061/(ASCE)GM.1943-5622.0000902
[13] NI P, MANGALATHU S, SONG L, et al. Displacement- dependent lateral earth pressure models[J]. Journal of Engineering Mechanics, 2018, 144(6): 04018032. doi: 10.1061/(ASCE)EM.1943-7889.0001451
[14] NI P, MEI G, ZHAO Y. Displacement-dependent earth pressures on rigid retaining walls with compressible geofoam inclusions: physical modeling and analytical solutions[J]. International Journal of Geomechanics, 2017, 17(6): 04016132. doi: 10.1061/(ASCE)GM.1943-5622.0000838
[15] NI P, SONG L, MEI G, et al. On predicting displacement- dependent earth pressure for laterally loaded piles[J]. Soils and Foundations, 2018, 58(1): 85-96. doi: 10.1016/j.sandf.2017.11.007
[16] POTTS D, FOURIE A. A numerical study of the effects of wall deformation on earth pressures[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1986, 10(4): 383-405. doi: 10.1002/nag.1610100404
[17] British Code BA42/96 The Design of Integral Bridges[S]. London: Highways Agency, 1996.
[18] DUNCAN J M, MOKWA R L. Passive earth pressures: theories and tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(3): 248-257. doi: 10.1061/(ASCE)1090-0241(2001)127:3(248)
[19] Transportation Officials, Subcommittee on Bridges. AASHTO Guide Specifications for LRFD Seismic Bridge Design[S]. AASHTO, 2011.
[20] 刘松玉, 吴燕开. 论我国静力触探技术(CPT) 现状与发展[J]. 岩土工程学报, 2004, 26(4): 553-556. http://cge.nhri.cn/cn/article/id/11468 LIU Songyu, WU Yankai. On the state-of-art and development of CPT in China[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 553-556. (in Chinese) http://cge.nhri.cn/cn/article/id/11468
[21] 蔡国军, 刘松玉, 童立元, 等. 现代数字式多功能CPTU与中国CPT对比试验研究[J]. 岩石力学与工程学报, 2009, 28(5): 914-928. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200905011.htm CAI Guojun, LIU Songyu, TONG Liyuan, et al. Comparative study of modern digital multifunctional CPTU and China's CPT tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(5): 914-928. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200905011.htm
[22] MAYNE P W, COOP M R, SPRINGMAN S M, et al. Geomaterial behavior and testing[C]// Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering. IOS Press, 2009: 2777-2872.
[23] LI H, LIU S, TONG L. Evaluation of lateral response of single piles to adjacent excavation using data from cone penetration tests[J]. Canadian Geotechnical Journal, 2019, 56(2): 236-248.
[24] 李赞, 刘松玉, 吴恺, 等. 基于多功能CPTU测试的基坑开挖扰动深度确定方法[J]. 岩土工程学报, 2021, 43(1): 181-187. doi: 10.11779/CJGE202101021 LI Zan, LIU Songyu, WU Kai, et al. Determination of the disturbance depth due to excavations using multifunctional CPTU tests[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(1): 181-187. (in Chinese) doi: 10.11779/CJGE202101021
[25] LU T, LIU S, CAI G, et al. Effect of excavation disturbance on clayey soil mechanical properties and pile capacity[J]. International Journal of Geomechanics, 2022, 22(7): 05022003.
[26] LAI F, ZHANG N, LIU S, et al. A generalised analytical framework for active earth pressure on retaining walls with narrow soil[J]. Géotechnique, 2022: 1-16.
[27] LI C, LAI F, SHIAU J, et al. Passive earth pressure in narrow cohesive-frictional backfills[J]. International Journal of Geomechanics, 2023, 23(1): 04022262.
[28] CLOUGH G, DUNCAN J. Foundation Engineering Handbook[M]. New York: Springer, 1991. [29] MAYNE P. Evaluating effective stress parameters and undrained shear strengths of soft-firm clays from CPT and DMT[J]. Australian Geomechanics Journal, 2016, 51(4): 27-55.
[30] OUYANG Z, MAYNE P W. Modified NTH method for assessing effective friction angle of normally consolidated and overconsolidated clays from piezocone tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(10): 04019067.
[31] MAYNE P W. Integrated Ground Behavior: In-Situ and Labtests[M]// London: Taylor & Francis, 2005.
[32] AGAIBY S S, MAYNE P W. CPT evaluation of yield stress profiles in soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(12): 04019104.
[33] POTYONDY J G. Skin friction between various soils and construction materials[J]. Géotechnique, 1961, 11(4): 339-353.
[34] LUNNE T, BERRE T, ANDERSEN K H, et al. Effects of sample disturbance and consolidation procedures on measured shear strength of soft marine Norwegian clays[J]. Canadian Geotechnical Journal, 2006, 43(7): 726-750.
[35] BLAKER Ø, DEGROOT D J. Intact, disturbed, and reconstituted undrained shear behavior of low-plasticity natural silt[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(8): 04020062.
[36] 杨光华. 土力学发展的四个阶段的思考[J]. 岩土工程学报, 2022, 44(9): 1730-1732. doi: 10.11779/CJGE202209018 YANG Guanghua. Thingking of four stages of development of soil mechanics [J]. Chinese Journal of Geotechnical Engineering, 2022, 44(9): 1730-1732. (in Chinese) doi: 10.11779/CJGE202209018
-
期刊类型引用(2)
1. 杨文杰，谢志强. 滨海地区砂土层连片式基坑土体加固技术应用. 建筑机械. 2024(11): 127-130 . 
百度学术
2. 刘松玉，蔡国军，赖丰文，黄明，程月红，鲁泰山. 基于CPTU/SDMT原位测试的软弱土HSS本构模型参数确定方法. 地基处理. 2024(06): 531-539 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 757
- HTML全文浏览量: 78
- PDF下载量: 205
- 被引次数: 3
