考虑强度速率衰减效应的地震滑坡SPH-FEM模拟

魏星; 程世涛; 谢相焱; 陈睿

doi:10.11779/CJGE20230463

考虑强度速率衰减效应的地震滑坡SPH-FEM模拟 English Version

魏星^1,,
程世涛²,
谢相焱^3, ,,
陈睿¹

1.
西南交通大学土木工程学院, 四川成都 610031
2.
四川交通职业技术学院, 四川成都 611130
3.
中铁二院昆明勘察设计研究院有限责任公司, 云南昆明 650200

基金项目:

国家自然科学基金项目 41977235

详细信息

作者简介:
魏星(1977—)，女，工学博士，副教授，主要从事岩土工程数值模拟、岩土本构理论方面的研究工作。E-mail: weixinghl@163.com

通讯作者:
谢相焱, E-mail: xiexiangyan163@163.com

中图分类号: TU435
计量
- 文章访问数: 322
- HTML全文浏览量: 40
- PDF下载量: 87
出版历程
- 收稿日期: 2023-05-23
- 网络出版日期: 2023-12-19
- 刊出日期: 2024-07-31

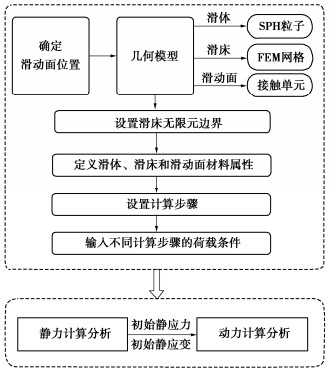
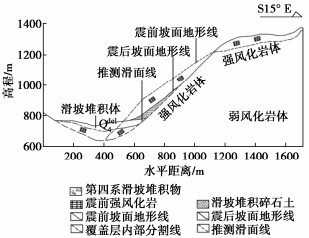
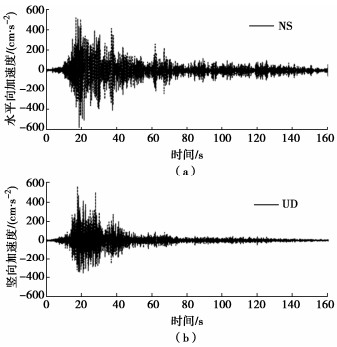
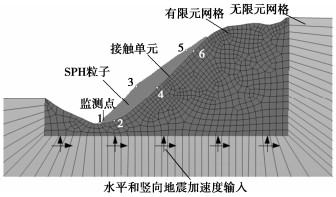
SPH-FEM simulation of landslide induced by earthquake considering velocity weakening effect of frictional strength

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
Sichuan Vocational and Technical College of Communications, Chengdu 611130, China
3.
Kunming Survey, Design and Research Institute Co. Ltd. of CREEC, Kunming 650200, China

摘要

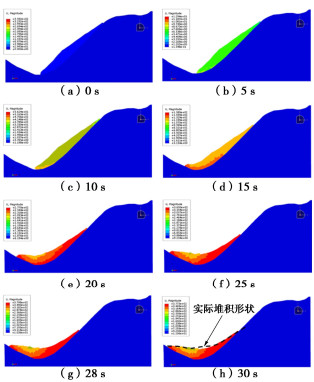
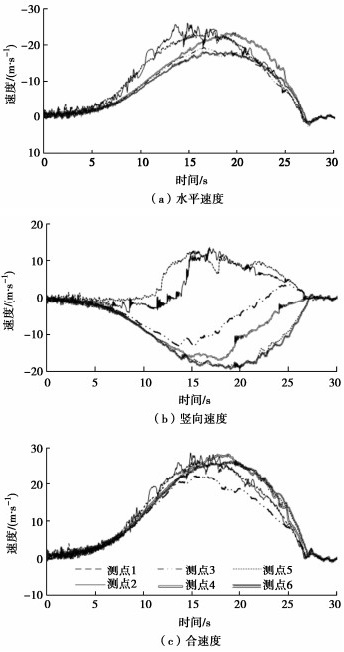
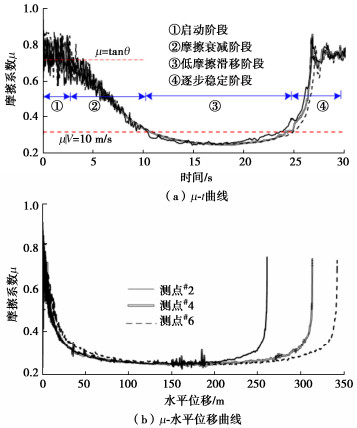
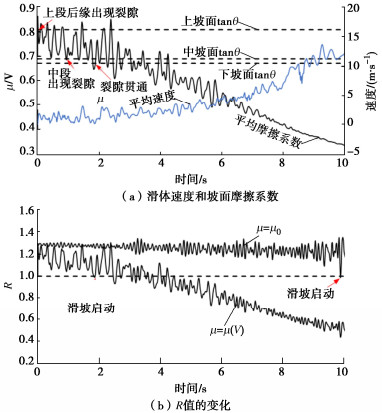
摘要: 基于SPH和FEM耦合的数值计算方法，引入滑动面摩擦强度的速率衰减模型，提出了一种能够模拟地震诱发滑坡破坏过程的数值模拟方法。基于所提数值方法模拟了唐家山地震滑坡，模拟结果与现场勘查结果及室内试验现象较为一致。基于模拟的滑动面上摩擦系数的演化过程，将唐家山滑坡的发生分为4个阶段：启动阶段、摩擦衰减阶段、低摩擦滑移阶段和逐步稳定阶段。模拟结果表明速度增加和摩擦强度衰减的相互促进，是触发滑体的高速运动的根本原因。提出采用滑体上作用的动摩擦力f_d和动下滑力T_d的比值R作为判别指标用于判断大型滑坡的启动，当首次出现R小于1时认为滑动面发生整体贯通并出现失稳启动。基于滑动面不同位置摩擦系数的演化，揭示了滑坡启动中滑动面摩擦强度衰减和滑动面的渐进贯通过程，解释了地震作用与滑动面摩擦参数速率衰减效应共同作用触发大型滑坡发生破坏的内在机理。
- 大型滑坡 /
- 滑动面 /
- 摩擦强度 /
- 速度衰减效应 /
- SPH-FEM耦合方法
Abstract: Based on the SPH-FEM coupling method, a frictional velocity weakening model for sliding surface is introduced and a numerical simulation method which can simulate the whole failure process of the landslides triggered by earthquake is proposed. The Tangjiashan landslide is simulated by the proposed method, and the simulated results are consistent with the on-site investigations and the laboratory test results. Based on the calculated frictional strength on the sliding surface, the whole failure process of the Tangjiashan landslide is divided into four stages: the triggering stage, the frictional weakening stage, the low frictional stage and the gradually stabilizing stage. The simulated results indicate that the high-speed movement of the sliding body is triggered by the interaction of the increase of the velocity and the decrease of the frictional strength. The parameter R defined by the ratio of the dynamic frictional force f_d to the dynamic sliding force T_d is suggested to evaluate the failure of large landslides. When R less than 1 occurs for the first time, the stress on the sliding surface reaches the shear strength and slope failure occurs. Based on the evolution of friction coefficient at different positions of the sliding surface, the frictional weakening of the sliding surface and the gradual failure of the landslide are revealed. The large-scale landslide is supposed to be triggered by the joint effects of the earthquake and the frictional velocity weakening.
- large-scale landslide /
- sliding surface /
- frictional strength /
- velocity weakening effect /
- SPH-FEM coupling method

HTML全文

0. 引言

潜水面上升可能诱发边坡失稳，艾伯凡矿灾^[1]（Aberfan Disaster）、沃楚西特水坝^[2]（Wachusett Dam）等就属于这一破坏模式。Brand^[3]建议研究边坡的破坏机理时，应该考虑边坡内土体单元的应力应变响应。边坡内潜水面上升的应力路径可以简化为等剪应力排水路径^[3-6]。针对等剪应力排水路径下土体的力学响应，研究者们进行了一系列工作^{[2, 6-7]}。Chu等^[2]通过试验证明了等剪应力排水路径下土体的非稳定态与边坡失稳存在相关性。Lashkari等^[7]利用离散元数值模拟等剪应力排水路径，发现松砂和密砂的非稳定态存在区别。此外，研究者还发现各向异性对等剪应力排水路径的非稳定态存在显著影响。Fanni等^[8]通过试验发现大主应力方向从垂直于沉积面旋转到45°时，非稳定态的应力比不断减小，指出在评估边坡稳定时不能忽略各向异性的影响。

一些研究者也在利用本构模型模拟该应力路径。Lashkari等^[7]采用了各向异性临界状态塑性本构模型^[9]模拟了不同孔隙比和剪应力值下的等剪应力排水试验，表明了模型具有模拟该应力路径的能力。但本构模型能否模拟各向异性条件下的等剪应力排水试验，目前仍然未知。

各向异性对砂土的力学响应有显著影响^[10-16]。如何用本构模型描述饱和砂土的力学响应是目前的研究热点之一。为总结各向异性对于砂土力学响应影响的规律，研究者们进行了大量物理试验和离散元数值试验。物理试验方面如Yoshimine等^[17]和Nakata等^[18]研究了不同加载方向和中主应力系数对丰浦砂应力应变关系的影响，发现当大主应力平行于沉积面、中主应力系数为1时，土样表现出更强的剪缩特性，更易发生静态液化。离散元数值试验方面如Fu等^[19]再现了直剪试验，研究各向异性砂土的峰值强度。这些试验为本构模型的建立和验证提供了基础和依据，各类模型通过模拟试验证明了自身的有效性^[20-23]。如Wang等^[22]通过离散元数值试验总结各向异性对塑性模量和剪胀的影响，在CycLiq本构模型^[24]的基础上加入了组构各向异性，并通过离散元试验和物理试验对新模型进行了验证。

本文利用Wang等^[22]提出的各向异性CycLiq本构模型，对Fanni等^[8]进行的一系列定轴不排水试验与定轴等剪应力排水试验进行了模拟，验证了该模型对于各向异性砂土在不同主应力方向下、不同应力路径力学响应的模拟能力，并研究了初始组构强度对于模型模拟定轴等剪应力排水试验结果的影响。

1. 各向异性CycLiq模型

1.1 本构模型

基于排水与不排水循环扭剪试验现象研究，张建民等^[25-26]将砂土的体应变 ${\varepsilon _\text{v}}$ 分解为有效球应力变化引起的弹性体应变 ${\varepsilon _\text{vc}}$ 和剪切引起的塑性体应变 ${\varepsilon _\text{vd}}$ ，又将剪切引起的塑性体应变 ${\varepsilon _\text{vd}}$ 进一步划分为可逆性剪切体应变 ${\varepsilon _\text{vd, re}}$ 与不可逆性剪切体应变 ${\varepsilon _\text{v, ir}}$ 。在此基础上，王刚等^[27]和Wang等^[24]建立了一个能够模拟饱和砂土液化前后应力应变响应的弹塑性循环本构模型，并在模型中引入了状态变量，使得模型能够统一描述砂土在不同状态下的静动力响应。为考虑各向异性，Wang等^[22]基于试验和离散元数值模拟总结的规律，对模型进行了改进，引入了组构张量，在塑性模量与剪胀率的计算中引入了各向异性的影响，使得模型能够描述不同主应力方向下的响应。

CycLiq模型的应力应变关系可以用下式来描述：

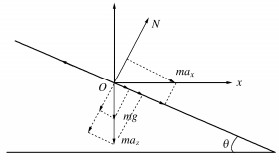
$\boldsymbol{\dot \varepsilon} = \frac{{p \boldsymbol{\dot r}}}{{2G}} + \left( {\frac{\boldsymbol{r}}{{2G}} + \frac{\boldsymbol{I}}{{3K}}} \right)\dot p + \left( {\boldsymbol{n} + \frac{D}{3}\boldsymbol{I}} \right)\left\langle L \right\rangle 。$

(1)

式中：p为有效球应力；r为偏应力张量s与球应力p之比；G和K为弹性剪切模量和体积模量；I为单位张量；n为塑性偏应变流动方向与加载方向；D为剪胀率；L为塑性加载指数。参数上加(·)表示增量；〈〉为Macaulay计算符，当x > 0时，〈x〉= x，当x ≤ 0时，〈x〉= 0。

弹性剪切模量和体积模量采用Richart等^[28]提出的线性弹性模量公式，在此不再赘述。塑性加载指数L通过下式计算：

$L = \frac{{p \boldsymbol{\dot r}:\boldsymbol{n}}}{H} 。$

(2)

式中：H为塑性模量。

砂土临界状态采用Been等^[29]提出的状态变量Ψ = $e - {e_\text{c}}$ ，但 ${e_\text{c}}$ 与p的关系采用了与Wang等^[22]所使用的指数关系^[30]不同的对数关系：

${e_\text{c}} = \varGamma - {\lambda _\text{e}}\ln (p) 。$

(3)

这一改动是因为Fanni等^[8]给出了本文模拟试样临界状态下试样的e-p曲线，并采用式（3）的对数关系进行了拟合，且e-p曲线的对数关系被广泛采用，许多模型采用了这种关系^[31-32]，因此对模型中的公式进行了替换。不过需要指出的是，在液化状态时，对数关系不再适用，因此砂土的动力本构模型大都采用指数关系^[33-34]。本文中不涉及液化内容，因此可以选取对数关系进行模拟。

为了考虑各向异性的影响，Wang等^[22]在模型中引入了组构张量 ${\boldsymbol{F}_\text{n}}$ ，并考虑了组构张量对于塑性模量与剪胀率的影响。组构张量 ${\boldsymbol{F}_\text{n}}$ 的演化采用了如下公式：

$\text{d}{\boldsymbol{F}_\text{n}} = \left\langle L \right\rangle c\left[ {\boldsymbol{n} - (1 + D){\boldsymbol{F}_\text{n}}} \right] 。$

(4)

式中：c为模量参数，代表组构张量演化的速率。通过总结离散元数值试验的规律，Wang等^[22]发现组构张量的模|| ${\boldsymbol{F}_\text{n}}$ ||与组构张量和加载方向的联合不变量A_n = ${\boldsymbol{F}_\text{n}}$ : n之差|| ${\boldsymbol{F}_\text{n}}$ ||-A_n可以作为一个良好的指标，以反映塑性模量和剪胀率随加载角度的变化。以水平沉积的试样在三轴压缩中的加载角度为0°，随着加载角度的增加，指标|| ${\boldsymbol{F}_\text{n}}$ ||-A_n不断增大，同时塑性模量不断减小，剪胀率从不断增加。因此，将|| ${\boldsymbol{F}_\text{n}}$ ||-A_n引入到了塑性模量与剪胀率的计算公式中：

$C = \exp \left[ { - {\Delta _1}{{(\left\| {{\boldsymbol{F}_\text{n}}} \right\| - {A_\text{n}})}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right] \text{，}$

(5)

$\begin{align}H = &\frac{2}{3}hg\left( \theta \right)G\exp ( - {n^p}\Psi ) \cdot \\& \left( {\frac{{M\exp ( - {n^{\rm{p}}}\Psi )}}{{{M_\text{m}}}}\frac{{\bar \rho }}{\rho } - \frac{1}{C}} \right) \text{，} \end{align}$

(6)

${D_\text{ir}} = \frac{{{d_\text{ir}} + {\Delta _2}(\left\| {{\boldsymbol{F}_\text{n}}} \right\| - {A_\text{n}})}}{{{d_\text{ir}}}}{D_\text{ir, iso}} 。$

(7)

式中：h，Δ₁，Δ₂，M，d_ir， ${n^{\rm{p}}}$ 为模型参数；g(θ)为形状函数，这里采用的是Zhang等^[35]建议的函数； ${M_\text{m}}$ 为历史最大应力比；D_{ir, iso}为各向同性条件下的不可逆剪胀率，详细公式可见Wang等^[24]。

1.2 参数标定

Fanni等^[8]试验中采用的砂为一种细硅砂，颗粒相对质量密度为2.64，平均粒径D₅₀为0.21 mm，均匀系数C_u为2.3，颗粒呈圆形至亚圆形。因缺乏相关试验，大部分参数参照了Wang等^[22]标定的丰浦砂参数，仅对部分可确定的临界状态参数（n^p，Γ， ${\lambda _\text{e}}$ ）进行了重新标定。标定结果如表 1所示。

其中，Γ和 ${\lambda _\text{e}}$ 由Fanni等^[8]根据试验拟合得到，在更换了Wang等^[22]模型中e_c与p的关系式后可直接使用。展示了 ${n^{\rm{p}}}$ 的标定方法，以Fanni等^[8]进行的一组定轴等剪应力排水试验（中主应力系数b = 0.2，加载角度α = 30°）结果参照进行标定。图中点代表试验所得试样到达非稳定态时的有效球应力与孔隙比，虚线和实线分别为n^p = 6和12时的模拟结果。可以看到当其他参数不变时， ${n^{\rm{p}}}$ 值越大，模拟得到的非稳定态时有效球应力随孔隙比变化越快，曲线更加陡峭。这是由于等剪应力排水路径中的非稳定态代表试样处于峰值应力比状态，而峰值应力比可由Mexp(- ${n^{\rm{p}}}$ Ψ)决定。

图 1 模型参数n^p的标定方法演示

Figure 1. Calibration method for model parameter n^p

下载: 全尺寸图片幻灯片

除了表 1中列出的模型参数外，初始组构强度，即初始组构张量的模||F_nin||，也是一个重要的参数。它代表了试样在试验开始时的各向异性程度，||F_nin||越大，试样的各向异性越强。不同的制样方式制得的试样往往有着不同的各向异性程度^[36]，因此需要取不同的初始组构强度。本次模拟中涉及两种不同的制样方式，湿装夯实法（moist tamped, MT）和干砂雨法（dry pluviated, DP），其中干砂雨法得到的试样孔隙比要小于湿装夯实法，结合Yang等^[37]、叶斌等^[38]通过物理试验与离散元模拟均发现干砂雨法的各向异性强于湿装夯实法，可以推测干砂雨法在制样中，由于受到重力影响，土颗粒的排列具有定向性，而湿装夯实法在制样中，土颗粒更倾向于随机排列，导致其各向异性相对较弱。最终，湿装夯实法制得的试样初始组构强度||F_nin||取为0.5，干砂雨法制得的试样初始组构强度||F_nin||取为0.7。

2. 不同主应力方向下模型的响应

2.1 定轴不排水剪切试验

Fanni等^[8]进行了一系列空心圆柱定轴不排水剪切试验。试验中，初始有效球应力均为171 kPa，大小主应力之差均为64 kPa，中主应力系数b分别为0，0.2，0.5，大主应力与沉积方向的夹角α分别为0°，22.5°，30°和45°，两种制样方法，即湿装夯实法和干砂雨法，各5组试验，如图 2，3所示。其中，湿装夯实法所得试样孔隙比在0.761~0.785，干砂雨法所得试样孔隙比在0.674~0.697。采用表 1中的模型参数对试验进行模拟，模拟结果如图 2，3所示。图 2（a），（b）中横纵坐标为Fanni等^[8]给出的八面体剪应变和八面体偏应力，图 3同理。

图 2 不同中主应力系数与主应力方向下湿装夯实法试样定轴不排水试验结果与模拟

Figure 2. Undrained torsional shear hollow cylinder tests and simulated results at different α and b of moist tamped loose sand

下载: 全尺寸图片幻灯片

图 3 不同中主应力系数与主应力方向下干砂雨法试样定轴不排水试验结果与模拟

Figure 3. Undrained torsional shear hollow cylinder tests and simulated results at different α and b of dry pluviated loose sand

下载: 全尺寸图片幻灯片

表 1 各向异性CycLiq模型参数

Table 1. Model parameters of anisotropic CycLiq model

G_o	κ	h	d_{re, 1}	d_{re, 2}	d_ir	α	γ_{d, r}	n^p	n^d	M	λ_e	Γ	Δ₁	Δ₂	c
100	0.008	4.0	0.7	30	0.3	30	0.05	12	2	1.2	0.008	0.761	1.35	0.8	5

下载: 导出CSV

| 显示表格

图 2展示了湿装夯实法试样定轴不排水试验结果与模拟。湿装夯实法得到的试样均为松砂，各试验和模拟均出现静态液化。总体上来看，随着b和α的增加，试验与模拟中试样的峰值偏应力均不断减小。从图 2（a），（c）中可以看出，试验中b = 0.2的3组曲线极为接近，甚至α = 30°的偏应力要高于α = 22.5°，这主要是试验中不同试样的孔隙比相差较大造成的，在模拟中该现象并不明显。此外，b = 0.5的模拟结果在加载初期剪应力出现了明显的减小，这主要是由于本构模型中组构对塑性模量的影响描述不够准确，在大孔隙比下放大了组构对塑性模量的影响。

图 3展示了干砂雨法试样定轴不排水试验结果与模拟。相比于湿装夯实法，干砂雨法得到的试样孔隙比更小，可认为密砂。各组模拟的曲线与试验结果均有较好的吻合。对于b = 0.2的3组试验和模拟，α = 22.5°时均表现出明显的剪胀，而在α = 45°时则表现出强烈的剪缩。对于b = 0，α = 0°和b = 0.2，α = 22.5°两组试验，试验和模拟的曲线在图 3（a），（b）均出现了交叉，这是由于两者的孔隙比相差较大，在孔隙比、中主应力系数、主应力方向三者的共同作用下出现了图中的效果。

2.2 定轴等剪应力排水试验

在定轴不排水剪切试验的基础上，Fanni等^[8]进行了一系列定轴等剪应力排水试验，以探究各向异性对等剪应力排水应力路径的影响。试验中采用了湿装夯实法（MT）和干砂雨法（DP）两种制样方法，初始有效球应力均为171 kPa，大小主应力之差均为64 kPa，中主应力系数b分别为0，0.2，主应力与沉积方向的夹角α分别为0°，22.5°和45°。每个夹角均用不同的孔隙比进行试验，对于湿装夯实法，b = 0，α = 0°组采用了6个不同的孔隙比，b = 0.2，α = 22.5°组采用了4个，b = 0.2，α = 45°组采用了10个；对于干砂雨法， b = 0.2，α = 22.5°组1个，b = 0.2，α = 45°组2个。采用表 1中的模型参数进行模拟，模拟中保持偏应力不变，当有效球应力无法再减小时，即试样达到峰值应力比时，认为此时试样处于非稳定态，模拟结束。

图 4给出了湿装夯实法试样在不同b和α下的定轴等剪应力排水试验结果与模拟。图中圆代表初始状态，三角形代表试样达到非稳定态，即处于峰值应力比状态。当相同b和α时，非稳定态的有效球应力p随孔隙比e的增加而增加，3组中模拟与试验均吻合较好。当孔隙比e不变、α增加时，模拟与试验得到的有效球应力均增加。

图 4 不同中主应力系数与主应力方向下湿装夯实法试样定轴等剪应力排水试验结果与模拟

Figure 4. Constant shear drained tests and simulated results at different α and b of moist tamped loose sand

下载: 全尺寸图片幻灯片

图 5给出了干砂雨法试样在不同b和α下的定轴等剪应力排水试验结果与模拟。b = 0.2，α = 45°组试验与模拟结果相近，规律也与湿装夯实法中一致；模拟结果在定量上与试验结果存在差距，推测这是由于模型参数或者初始组构强度不准确导致的。当α增加时，模拟与试验得到的有效球应力均增加，这与湿装夯实法中的规律是一致的。

图 5 不同主应力方向下干砂雨法试样定轴等剪应力排水试验结果与模拟

Figure 5. Constant shear drained tests and simulated results at different α and b of dry pluviated loose sand

下载: 全尺寸图片幻灯片

图 6给出了试验和模拟中非稳定态的结果与趋势线。可以看到试验得到的非稳定态在e-p空间内具有良好的线性关系，对模拟得到的非稳定态进行线性回归，得到R²均在0.99以上，表明模型对等剪应力比试验具有良好的模拟能力。对比湿装夯实法的3组试验，可以发现模拟得到的3条趋势线之间的间距要略小于试验所得，这主要受初始组构强度的影响，具体情况在下文中阐释。

图 6 不同中主应力系数、主应力方向下定轴等剪应力排水试验中非稳定态试验与模拟结果及各自的趋势线

Figure 6. Instability states of constant shear drained tests and simulations at different α and b

下载: 全尺寸图片幻灯片

为了说明初始组构强度对于定轴等剪应力排水条件下土体响应的影响，在数值模拟中对不同初始组构强度条件进行了分析。中给出了不同初始组构强度对非稳定态模拟结果的影响。从图中可以发现初始组构越强，不同主应力方向下的非稳定态差异越大，即峰值应力比差异越大。式（5），（6）中可以解释这一现象。试样达到峰值应力比时，有塑性模量H = 0。当初始组构强度增加，即|| ${\boldsymbol{F}_\text{n}}$ ||增加时，指标|| ${\boldsymbol{F}_\text{n}}$ ||-A_n = || ${\boldsymbol{F}_\text{n}}$ ||(1 – n_F: n)（其中n_F指组构张量的方向）的值域[0, 2|| ${\boldsymbol{F}_\text{n}}$ ||]随之扩大，式（5）所得C的值域也相应扩大。对于定轴试验，初始组构强度增加，导致了不同的b和α计算得到C值之间的差异增加，因H = 0，进而使得式（6）中历史最大峰值应力比M_m（即非稳定态时的应力比）的差异增加，在剪应力q不变的情况下，非稳定态时的球应力p之间的差异也就增加了。这些反映在图 7中即为趋势线之间的间距增加。

图 7 初始组构强度对定轴等剪应力排水试验非稳定态e-p关系的影响

Figure 7. Effects of initial fabric norm on instability state of constant shear drained loading at different α and b

下载: 全尺寸图片幻灯片

3. 结论

本文利用各向异性CycLiq本构模型，模拟了Fanni等^[8]进行的定轴不排水试验与定轴等剪应力排水试验，对比试验结果与模拟结果，可以得到以下3点结论。

（1）对于定轴不排水剪切试验，该模型与试验均表现为随着中主应力系数和加载角度的增加，土体剪缩增强，更易发生静态液化。在定量上，模型模拟的应力路径和应力应变曲线与试验也有较好的吻合。

（2）对于定轴等剪应力排水试验，模型与试验均表现为非稳定态时的平均有效应力随孔隙比和加载角度的增加而增加，且相同加载角度的非稳定态在e-p空间内呈线性分布。总体来说，CycLiq模型对各向异性下砂土等剪应力排水响应的模拟效果较好，具有运用到实际工程中的潜力。

（3）不同初始组构强度对于等剪应力排水试验的结果有显著的影响。初始组构强度越高，不同主应力方向作用下的非稳定态时平均有效应力相差越大。

图 1 SPH和FEM耦合的数值模拟方法流程图

Figure 1. Flow chart of coupled SPH and FEM numerical simulation method

下载: 全尺寸图片幻灯片

图 2 唐家山滑坡地质剖面图^[29]

Figure 2. Geological profile of Tangjiashan landslide^[29]

下载: 全尺寸图片幻灯片

图 3 汶川地震什邡八角镇地面加速度记录

Figure 3. Ground acceleration records of Bajiao Town, Shifang City during Wenchuan earthquake

下载: 全尺寸图片幻灯片

图 4 唐家山数值计算模型

Figure 4. Numerical model for Tangjiashan landslide

下载: 全尺寸图片幻灯片

图 5 模拟的不同时刻的滑坡形态和水平位移云图

Figure 5. Simulated landslide morphology and horizontal displacement at different time

下载: 全尺寸图片幻灯片

图 6 测点的速度的模拟结果

Figure 6. Simulated results of velocity at measuring points

下载: 全尺寸图片幻灯片

图 7 滑动面摩擦系数的变化曲线

Figure 7. Curves of frictional coefficient of sliding surface

下载: 全尺寸图片幻灯片

图 8 滑体受力示意图

Figure 8. Schematic diagram of force on sliding body

下载: 全尺寸图片幻灯片

图 9 滑动带摩擦系数变化和滑坡失稳启动

Figure 9. Variation of friction coefficient of sliding surface and failure of landslide

下载: 全尺寸图片幻灯片

表 1 唐家山滑坡的材料参数

Table 1 Material parameters of Tangjiashan landslide

滑坡 γ/(kN·m^-3) E/GPa $\nu$ c_p/MPa c_r/MPa φ_p/(°) φ_r/(°) η

滑体 24.0 2.63 0.2 1.28 0.60 40 28 400

滑床 26.5 12 0.1 2.65 2.65 40 40 0.0

下载: 导出CSV

参考文献(40)

[1]	FRANÇOIS L. The mobility of long-runout landslides[J]. Engineering Geology, 2002, 63(3): 301-331.
[2]	LUCAS A, MANGENEY A, AMPUERO J P. Frictional velocity-weakening in landslides on Earth and on other planetary bodies[J]. Nature Communications, 2014, 5(9): 3417.
[3]	YANG C M, YUA W L, DONG J J, et al. Initiation, movement, and run-out of the giant Tsaoling landslide-What can we learn from a simple rigid block model and a velocity-displacement dependent friction law[J]. Engineering Geology, 2014, 182(1): 158-181.
[4]	陈果, 钮志林, 樊晓一, 等. 高速远程滑坡沿程速度演化与冲击力分布研究—以三溪村滑坡为例[J]. 自然灾害学报, 2022, 31(3): 232-241. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH202203024.htm CHEN Guo, NIU Zhilin, FAN Xiaoyi, et al. Velocity evolution and impact force distribution of high-velocity and long-runout landslide debris flow along the way: a case study of Sanxi Village landslide[J]. Journal of Natural Disasters, 2022, 31(3): 232-141. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH202203024.htm
[5]	王鲁男, 晏鄂川, 宋琨, 等. 滑带土残余强度的速率效应及其对滑坡变形行为的影响[J]. 中南大学学报: 自然科学版, 2017, 48(12): 3350-3358. doi: 10.11817/j.issn.1672-7207.2017.12.028 WANG Lunan, YAN Echuan, SONG Kun, et al. Rate effect of residual strength of slip soils and its impact on deformation process of landslides[J]. Journal of Central South University (Science and Technology), 2017, 48(12): 3350-3358. (in Chinese) doi: 10.11817/j.issn.1672-7207.2017.12.028
[6]	WANG F, ZHANG Y, HUO Z, et al. Mechanism for the rapid motion of the Qianjiangping landslide during reactivation by the first impoundment of the Three Gorges Dam Reservoir, China[J]. Landslides, 2008, 5(4): 379-386. doi: 10.1007/s10346-008-0130-7
[7]	张卫杰, 余瑞华, 陈宇, 等. 强度指标影响下滑坡运动特征及参数反分析[J]. 岩土工程学报, 2022, 44(12): 2304-2311. doi: 10.11779/CJGE202212018 (ZHANG Weijie, YU Ruihua, CHEN Yu, et al. Post-failure movement characteristics and parameter back-analysis for landslides considering effect of strength parameters[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(12): 2304-2311. doi: 10.11779/CJGE202212018
[8]	SASSA K, FUKUOKA H, WANG G H, et al. Undrained dynamic-loading ring-shear apparatus and its application to landslide dynamics[J]. Landslides, 2004(1): 7-19.
[9]	胡明鉴, 汪发武, 程谦恭. 基于高速环剪试验易贡巨型滑坡形成原因试验探索[J]. 岩土工程学报, 2009, 31(10): 1602-1606. doi: 10.3321/j.issn:1000-4548.2009.10.020 HU Mingjian, WANG Fawu, CHENG Qiangong. Formation of tremendous Yigong landslide based on high-speed shear tests[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1602-1606. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.10.020
[10]	崔圣华, 裴向军, 王功辉, 等. 基于环剪试验的汶川地震大型滑坡启动机理探索[J]. 岩土工程学报, 2017, 39(12): 2268-2277. doi: 10.11779/CJGE201712016 CUI Shenghua, PEI Xiangjun, WANG Gonghui, et al. Initiation of a large landslide triggered by Wenchuan earthquake based on ring shear tests[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(12): 2268-2277. (in Chinese) doi: 10.11779/CJGE201712016
[11]	IKARI M J, MARONE C, SAFFERA D M. On the relation between fault strength and frictional stability[J]. Geology, 2011, 39(1): 83-86. doi: 10.1130/G31416.1
[12]	BEELER N M, TULLIS T E, GOLDSBY D L. Constitutive relationships and physical basis of fault strength due to flash heating[J]. Journal of Geophysical Research, 2008, 113: B01401.
[13]	TOGO T, SHIMAMOTO T, MA S, et al. High-velocity frictional behavior of Longmenshan fault gouge from Hongkou outcrop and its implications for dynamic weakening of fault during the 2008 Wenchuan earthquake[J]. Earthquake Science, 2011, 24(3): 267-281. doi: 10.1007/s11589-011-0790-6
[14]	汪发武. 地震诱发的高速远程滑坡过程中土结构破坏和土粒子破碎引起的两种不同的液化机理[J]. 工程地质学报, 2019, 27(1): 98-107. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201901011.htm WANG Fawu. Liquefactions caused by structure collapse and grain crushing of soils in rapid and long runout landslides triggered by earthquakes[J]. Journal of Engineering Geology, 2019, 27(1): 98-107. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201901011.htm
[15]	SASSA K, DANG K, HE B, et al. A new high-stress undrained ring-shear apparatus and its application to the 1792 Unzen–Mayuyama megaslide in Japan[J]. Landslides, 2014, 11: 827-842. doi: 10.1007/s10346-014-0501-1
[16]	KEEFER D K, WILSON R C. Predicting earthquake-induced landslides, with emphasis on arid and semi-arid environments[C]// Landslides Arid Semi-arid Environ. Yinchuan, 1989.
[17]	ROMEO R. Seismically induced landslide displacements: a predictive model[J]. Engineering Geology, 2000, 58(3): 337-351. doi: 10.3969/j.issn.1004-9665.2000.03.015
[18]	JIBSON R W. Methods for assessing the stability of slopes during earthquakes-a retrospective[J]. Engineering Geology, 2011, 122(1): 43-50.
[19]	DONG J J, LEE W R, LIN M L, et al. Effects of seismic anisotropy and geological characteristics on the kinematics of the neighboring Jiufengershan and Hungtsaiping landslides during Chi-Chi earthquake[J]. Tectonophysics, 2009, 466(3/4): 438-457.
[20]	YANG C M, HSU C H, DONG J J. Critical displacement of earthquake-triggered catastrophic landslides[C]// Advancing Culture of Living with Landslides. Cham, 2017.
[21]	曹琰波, 戴福初, 许冲, 等. 唐家山滑坡变形运动机制的离散元模拟[J]. 岩石力学与工程学报, 2011, 30(增刊1): 2878-2887. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2011S1039.htm CAO Yanbo, DAI Fuchu, XU Chong, et al. Discrete element simulation of deformation and movement mechanism for tangjiashan landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S1): 2878-2887. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2011S1039.htm
[22]	张迎宾, 董琰, 陈岩岩, 等. 基于强度衰减的Vajont滑坡运动特征非连续变形分析[J]. 西南交通大学学报, 2021, 56(6): 1205-1213. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT202106010.htm ZHANG Yingbin, DONG Yan, CHEN Yanyan, et al. Effects of strength degradation of sliding mass on movement of vajont landslide numerical simulation based on discontinuous deformation analysis[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1205-1213. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT202106010.htm
[23]	ZHANG W J, JI J, GAO Y F. SPH-based analysis of the post-failure flow behavior for soft and hard interbedded earth slope[J]. Engineering Geology, 2019, 267: 105446.
[24]	黄帅, 刘传正, GODA K. 光滑粒子流体动力学方法在饱和边坡地震滑移大变形中的适用性研究[J]. 岩土工程学报, 2023, 45(2): 336-344. doi: 10.11779/CJGE20211274 HUANG Shuai, LIU Chuanzheng, GODA K. Applicability of smooth particle hydrodynamics method to large sliding deformation of saturated slopes under earthquake action[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(2): 336-344. (in Chinese) doi: 10.11779/CJGE20211274
[25]	李云屹, 王睿, 张建民. 瑞利波作用下缓倾场地流滑大变形的SPH数值模拟[J]. 岩土工程学报, 2023, 45(7): 1333-1340. doi: 10.11779/CJGE20220489 LI Yunyi, WANG Rui, ZHANG Jianmin. Numerical simulation of Rayleigh wave-induced large lateral spreading deformation in gentle sloping ground using SPH[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(7): 1333-1340. (in Chinese) doi: 10.11779/CJGE20220489
[26]	钟祖良, 贺凯源, 宋宜祥, 等. 基于仿射速度矩阵改进物质点法的大位移滑坡研究[J]. 岩土工程学报, 2022, 44(9): 1626-1634. doi: 10.11779/CJGE202209007 ZHONG Zuliang, HE Kaiyuan, SONG Yixiang, et al. Large-displacement landslides based on affine velocity matrix-improved material point method[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(9): 1626-1634. (in Chinese) doi: 10.11779/CJGE202209007
[27]	ZHAO L H, QIAO N, HUANG D L, et al. Numerical investigation of the failure mechanisms of soil–rock mixture slopes by material point method[J]. Computers and Geotechnics, 2022, 150: 104898.
[28]	SOGA K, ALONSO E, YERRO A, et al. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method[J]. Géotechnique, 2016, 66(3): 1-26.
[29]	胡卸文, 黄润秋, 施裕兵, 等. 唐家山滑坡堵江机制及堰塞坝溃坝模式分析[J]. 岩石力学与工程学报, 2009, 28(1): 181-189. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200901027.htm HU Xiewen, HUANG Runqiu, SHI Yubing, et al. Analysis of blocking river mechanism of Tangjiashan landslide and dam-breaking mode of its barrier dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 181-189. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200901027.htm
[30]	李守定, 李晓, 张军, 等. 唐家山滑坡成因机制与堰塞坝整体稳定性研究[J]. 岩石力学与工程学报, 2010, 29(增刊1): 2908-2915. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1049.htm LI Shouding, LI Xiao, ZHANG Jun, et al. Study of geological origin mechanism of Tangjiashan landslide and entire stability of landslide dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2908-2915. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1049.htm
[31]	罗刚. 唐家山高速短程滑坡堵江及溃坝机制研究[D]. 成都: 西南交通大学, 2012. LUO Gang. Analysis of Blocking Mechanism of Tangjiashan High-Speed Short-Run Landslide and Dam-Breaking Mode of Tangjiashan Barrier Dam[D]. Chengdu: Southwest Jiaotong University, 2012. (in Chinese)
[32]	International Union of Geological Sciences Working Group on Landslides. A suggested method for describing the rate of movement of a landslide[J]. Bulletin of the International Association of Engineering Geology, 1995, 52(1): 75-78.
[33]	李坤, 程谦恭, 林棋文, 等. 高速远程滑坡颗粒流研究进展[J]. 地球科学, 2022, 47(3): 893-912. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202203012.htm LI Kun, CHENG Qiangong, LIN Qiwen, et al. State of the art on rock avalanche dynamics from granular flow mechanics[J]. Earth Science, 2022, 47(3): 893-912. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202203012.htm
[34]	董金玉, 赵志强, 郑珠光, 等. 大型地震滑坡高速滑动堵江机制的离散元数值模拟[J]. 华北水利水电大学学报(自然科学版), 2015, 36(6): 47-50. https://www.cnki.com.cn/Article/CJFDTOTAL-HBSL201506012.htm DONG Jinyu, ZHAO Zhiqiang, ZHENG Zhuguang, et al. Discrete element numerical simulation of the mechanism of the large-scale earthquake high-speed landslide's blocking the river[J]. Journal of North China University of Water Resources and Electric Power, 2015, 36(6): 47-50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HBSL201506012.htm
[35]	邬爱清, 林绍忠, 马贵生, 等. 唐家山堰塞坝形成机制DDA模拟研究[J]. 人民长江, 2008, 39(22): 91-95. https://www.cnki.com.cn/Article/CJFDTOTAL-RIVE200822036.htm WU Aiqing, LIN Shaozhong, MA Guisheng, et al. DDA simulation research for formation mechanism of Tangjiashan barrier lake[J]. Yangtze River, 2008, 39(22): 91-95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-RIVE200822036.htm
[36]	SONE H, SHIMAMOTO T. Frictional resistance of faults during accelerating and decelerating earthquake slip[J]. Nature Geoscience, 2009, 2(10): 705-708.
[37]	LIBERSKY L D, PETSCHEK A G, CARNEY T C, et al. High strain Lagrangian hydrodynamics[J]. Journal of Computational Physics, 1993, 109(1): 67-75.
[38]	MORRIS J P, FOX P J, ZHU Y. Modeling low Reynolds number incompressible flows using SPH[J]. Journal of Computational Physics, 1997, 136(1): 214-226.
[39]	DOMNIK B, PUDASAINI S P, KATZENBACH R, et al. Coupling of full two-dimensional and depth-averaged models for granular flows[J]. Journal of Non-Newtonian Fluid Mechanics, 2013, 201: 56-68.
[40]	CRESPO A J C, GOMEZ G M, DALRYMPLE R A. Boundary conditions generated by dynamic particles in SPH methods[J]. Computers Materials and Continua, 2007, 5(3): 173-184.