Scaling laws for quasi-static granular sand at critical state
-
摘要: 土的临界状态理论描述了土有效应力、抗剪强度与土密实度之间的对应关系,大量土力学试验还揭示了土体强度与加载速率存在相关性。考虑到颗粒物质是自然土体的实际载体,从颗粒物理本源出发,将流态颗粒惯性数I发展为考虑砂土密实程度(即初始颗粒体积分数ϕ0)的准静态颗粒物理惯性数Q=ϕ0[ln(I)+α]。以砂土的经典三轴试验数据为基础,探究了处于临界状态土的颗粒物理标度律,发现颗粒的摩擦系数μ与准静态颗粒惯性数Q之间满足简单的μ=ξQ线性关系。新建立的简单物理标度律能够统一刻画处于临界状态砂土的密实状态、剪切速率、围压和粒径等因素与土内摩擦角间复杂的经验关系。为描述受剪颗粒准静态变形的体变规律,进一步探索了临界状态下土颗粒体积分数与准静态颗粒惯性数间的相关性。对三维应力状态情况,引入一个新的无量纲量“中主应力数”对标度律进行拓展,可揭示中主应力对临界状态砂土摩擦特性的影响。Abstract: The critical state theory of soils describes the correspondence between effective stress, shear strength and soil density. Numerous soil mechanics experiments have also revealed a correlation between soil strength and loading rate. Considering that the granular matter is the actual medium of natural soils, a quasi-static inertia number is proposed, i.e., Q=ϕ0[ln(I)+α], for the granular soils considering the particle volume fraction. Based on the classical triaxial test data of soils, the scaling laws of quasi-static deforming sand at the critical state from the perspective of granular physics are explored, and a simple linear relationship i.e., μ=ξQ, is found between the friction coefficient and the quasi-static particle inertia number. The newly established scaling laws can quantitatively describe the influences of the volume fraction, shear rate, confining pressure and particle size on the frictional properties of sand when reaching the critical state. In addition, to quantify the volumetric deformation laws of sand under quasi-static shear, a correlation is obtained between the particle volume fraction ϕ at the critical state and the quasi-static inertia number Q. In attempt to characterize the scaling laws of the three-dimensional stress state, a new dimensionless number (i.e., the intermediate principal stress number) is defined to reveal the influences of the intermediate principal stress on the frictional properties. Thus, the scaling laws are extended.
-
Keywords:
- granular material /
- critical state /
- scaling law /
- Cambridge model /
- sand
-
0. 引 言
边坡、隧道、路基和地下工程的失稳垮塌机制复杂,岩土体是这些典型岩土工程灾变的主要赋存介质,深入掌握土的本构特性对工程安全分析十分必要。Rendulic[1]和Henkel[2]针对饱和正常固结黏土和具有相同先期固结压力的超固结土的三轴试验研究发现,不管是固结排水试验还是固结不排水试验,破坏前土体有效应力和孔隙比间存在唯一性关系,土破坏时孔隙比和强度间存在唯一性关系,且结果与试验类型及应力路径等无关。这就意味着土的抗剪强度与有效围压和土的孔隙比(反映了土的密实程度)之间存在着唯一性关系。
在上述研究基础上,Schofield等[3]、Muir Wood等[4]提出了土的剑桥模型(Cambridge Model Cam- clay),形成了经典的临界状态土力学理论,解释了黏土的临界土力学行为。经典剑桥模型是基于黏土试验数据总结提炼的,难以描述砂土在临界状态下的应力软化和剪胀行为。砂土的经典剪胀模型可反映土密实状态和围压等物理量对无黏性土摩擦强度的影响[5]。为完善临界土力学理论描述无黏性土,Jefferies[6]引入了状态量ψ(ψ=e−ecs,e为土的孔隙比,ecs为土临界状态下的孔隙比),假定应力增量与应变增量方向相同、应变增量方向与屈服面垂直,提出了一种砂土的修正剑桥模型,即Nor-Sand模型。
不管是黏土还是砂土,根据临界状态理论,土体能够在临界状态下发生无限变形,应力和孔隙比恒定,在常规三轴应力条件下,其数学表达式可表示为
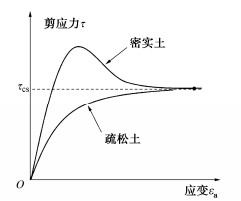
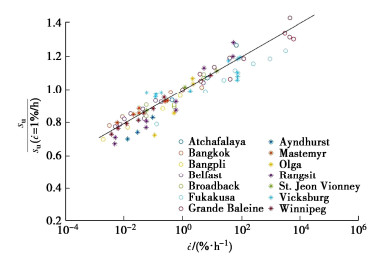
∂p∂εq=0, ∂q∂εq=0, ∂εv∂εq=0。 (1) 式中:p=(σ1+2σ3)/3;q=σ1−σ3;εq为剪应变,可表示为εq=2(ε1−ε3)/3。且当ψ→0时,εq→∞。在p-q-v三维空间坐标系下(其中v=1+e),临界土力学理论定义了物态边界面(罗斯柯面,State Boundary Surface),即以NCL(normal consolidation line,正常固结线)和CSL(critical state line,临界状态线)为边界的空间曲面,可定量化描述临界状态下土平均应力p、抗剪强度q与孔隙比e之间的关系。除了土临界状态理论所描述的土的抗剪强度与有效围压、密实度间的相关性,大量土力学试验发现,加载速率与土的不排水强度存在正相关关系(如图1)[7],一般的三轴试验会持续数十分钟或数小时,试验发现,低加载速率下测得的土体强度比高加载速率下小得多,最大可相差50%。尽管这种加载效应得到了广泛认识,其物理机理尚未明确。
采用堆石料和无黏性土在不同围压下开展三轴试验,试样开始发生应变硬化达到峰值强度,低围压下随后转为应变软化发展到临界状态[8-9]。总结试验数据发现[7],峰值摩擦角和临界状态摩擦角随着围压增大而减小,临界状态的摩擦角符合下列公式:
φcr=φ0−Δφlg(σ3pa)。 (2) 式中:pa为与围压σ3量纲相同的大气压力;φ0和Δφ为试验参数。
近百年土力学领域大量科研工作,揭示了土的内摩擦角(摩擦特性)与围压(外荷载大小)、孔隙比(体变特征)、加载速率(变形速率)等因素存在相关性,基于试验结果建立了各自变量相关性的经验公式。这种相关性需满足普适性的物理定律,即应该存在深层次的颗粒动力统一机制。考虑到颗粒物质是自然土体的实际载体,本研究从颗粒物理的视角出发,基于颗粒力学理论提出准静态颗粒惯性数的概念,基于大量三轴试验数据,建立临界状态下砂土摩擦特性、体变特征、剪切速率间的标度律,发展土力学的临界状态理论。从另一角度看,以大量既有三轴试验数据为支撑建立准静态颗粒的标度律,可为经典流态μ(I)颗粒流变准则的准静态修正以及颗粒材料统一准静态-流态本构法则的构建提供可行方案,也能够为深入剖析岩土灾变机理创造条件。
1. 颗粒物理理论与惯性数
1.1 流态颗粒的惯性数
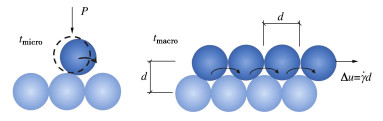
颗粒体的快速平板剪切试验是定量研究颗粒体在快速剪切状态下应力-应变行为的有效手段,Baran等[10]开展了三维颗粒体剪切试验,试验中对顶板施加恒定的压力P,在两板之间的颗粒(颗粒密度为ρs、粒径为d)以固定剪切速率˙γ受剪,上板可以垂向自由移动,试验中测出极限状态时恒定的体积分数ϕ和剪切应力τ。进而可以计算广义摩擦系数(friction coefficient)μ=τ/P。试验发现在稳态变形状态(steady-state,对应土的临界状态),可通过量纲分析确定颗粒的本构关系主要特征[11],该体系的性质受颗粒重分布微观时间尺度tmicro与剪切速率定义的宏观时间尺度的比值控制。颗粒体系从一个稳定的定向排列变形到下一个稳态(如图2),过程满足牛顿第二定律,即
md2zdt2=Fz。 (3) 考虑到m~ρsd3,d2z/dt2~d/t2以及Fz~Pd2,代入式(3)化简后,可得围压约束条件下颗粒重新排列时间t=tmicro,即
tmicro = d/√P/ρs。 (4) 又由相邻错动的两层颗粒相对变形速度Δu=˙γd,相邻颗粒间隙的距离为单倍粒径d(如图2),可得到特定颗粒从某粒间隙移动到相邻间隙的宏观时间为
tmacro=dΔu=d˙γd=˙γ−1。 (5) 式中:˙γ为剪应变速率。将微观时间尺度与宏观变形时间尺度作比,可综合表征颗粒变形的剧烈程度,可定义无量纲数I,又称为惯性数[12-13]
I=tmicrotmacro=|˙γ|d√P/ρs。 (6) 根据以上量纲分析的结果,并结合斜面上颗粒流试验[14]、三维颗粒体剪切数值试验[15]、二维颗粒体数值试验[16]、环剪数值试验[17],GDR[18]、Forterre等[19]定义了流态颗粒的广义摩擦系数μ、颗粒体积分数ϕ与惯性数I之间的相关性,拟合这些数据点可得到被广泛认可的μ(I)和ϕ(I)颗粒流变准则:
μ(I)=μs+μ2−μsI0/I0II+1, (7) ϕ=ϕmax (8) 式中:μs和μ2分别为广义摩擦系数的临界值(critical value)和极限值(limiting value),I0为试验参数。μs,μ2和I0与自然土颗粒的尺寸参数(长度、宽度、面积、周长)和形貌特征(长宽比、磨圆度、粗糙度)相关。试验参数ϕmax和ϕmin分别为颗粒体积分数的最大和最小值,对应颗粒体系最密实和最疏松两种状态。
目前关于μ,ϕ和 I 间相关性在数值计算、室内试验等方面的探究多是针对颗粒流态( I >10-3)状态下开展的。μ( I )和ϕ( I )颗粒流变准则揭示了颗粒摩擦强度μ,颗粒体积分数ϕ与外力作用P、剪应变速率\dot \gamma 、颗粒材料特性(d和ρs)的相关性。虽然 \mu (I) , \phi (I) 流变准则对流态( I >10-3)颗粒动力行为的刻画已得到广泛认可,但在分析准静态变形颗粒(I<10-3)时失效。为描述解析颗粒物质的准静态力学行为,Kamrin等[20]、Henann等[21]在塑性力学框架下,引入颗粒关联长度的概念修正塑性势函数,提出非局部流变准则;Bouzid等[22-23]通过I的空间梯度项表示其耗散作用,直接对摩擦系数进行修正,即非局部流变准则。这些修正方法较为复杂,与唯象的土力学理论存在应用鸿沟。
考虑到经典土力学三轴压缩试验中土样变形多处于准静态(I<10-3),近百年土力学研究积累了大量试验的三轴试验数据,本研究基于这些试验数据发展了颗粒惯性数概念,分析初始孔隙比、剪切速率、围压和粒径、中主应力等因素对颗粒摩擦特性和体变规律的影响,探讨颗粒准静态变形动力特征的物理标度律。
1.2 三轴试验中砂土的惯性数
土的三轴试验是土力学中最常用的经典试验方法,可完整地反映试样受力变形直到破坏的全过程,用作土体强度、应力应变关系分析。用三轴试验开展土的受力分析,与经典流态颗粒μ(I),ϕ(I)流变准则受力变形状态有所差别,惯性数有所不同,本节着重分析三轴试验中的颗粒惯性数。
经典μ(I),ϕ(I)颗粒流变准则是基于单剪物理和数值试验方法取得的,试样处于二维纯剪状态,即颗粒以均一的剪切速率发生剪切变形。为进一步描述复杂三维颗粒动力特征,假设颗粒在运动过程中保持体积不变(即不可压缩),基于偏应力张量与应变率张量共轴性假定(即线性相关),Jop等[24]将标量形式的μ(I)局部流变准则扩展成张量形式,推广了该准则在连续介质模型中的应用:
\boldsymbol{\sigma}=-P \boldsymbol{\delta}+\boldsymbol{\tau}, (9) \boldsymbol{\tau} = \eta (\left| {\boldsymbol{\dot \gamma} } \right|, P)\boldsymbol{\dot \gamma} \text{,} (10) \eta (\left| {\boldsymbol{\dot \gamma }} \right|, P) = \frac{{\mu (I)P}}{{\left| {\boldsymbol{\dot \gamma }} \right|}} 。 (11) 式中:\boldsymbol{\sigma} ,\boldsymbol{\tau} 和 \boldsymbol{\dot \gamma} 分别为应力张量、偏应力张量和应变率张量;\delta 为单位张量; \left| {\boldsymbol{\dot \gamma }} \right| = {\left( {\frac{1}{2}{{\boldsymbol{\dot \gamma }}_{ij}}{{\boldsymbol{\dot \gamma }}_{ji}}} \right)^{\frac{1}{2}}} 为应变率第二不变量。
在常规三轴试验过程中,施加围压后通过施加轴向力产生偏应力使得土样发生变形破坏。相对密实的土样会出现明显的剪切带,此时变形主要集中在剪切带区域,即土样发生局部剪切破坏。相对疏松土样的变形则比较均匀,无剪切带出现。需要说明的是,本文所取三轴试验数据均来自于局部剪切型破坏。对于三轴试验中的三维受剪土样建立物理模型,考虑到试样横向变形相对轴向较小,式(6)中定义应变率第二不变量主要受轴向变形速率控制,即为试样的剪切速率v与圆柱试样轴向尺寸H之比(即\dot \varepsilon =v/H)。此外,取试验围压定义P(即P = {\sigma _3}),天然土样的颗粒粒径d取平均粒径d50。根据式(6),可以得到三轴试验中砂土的惯性数为
I = \frac{{\left| {\boldsymbol{\dot \gamma }} \right|d}}{{\sqrt {P/{\rho _{\text{s}}}} }}{\text{ = }}\frac{{\left| {\dot \varepsilon } \right|{d_{50}}}}{{\sqrt {{\sigma _3}/{\rho _{\text{s}}}} }}。 (12) 2. 临界状态砂土的标度律
2.1 三轴试验中的摩擦系数和体积分数
土力学和颗粒物理领域常用内摩擦角或摩擦系数来描述土和颗粒的内摩擦特性。而通过试验得到的内摩擦角与颗粒材料摩擦系数间的关系与试验方法息息相关。例如,在重力驱动颗粒流动的斜槽试验中[14],摩擦系数可定义为临界滑动状态下平面倾斜角度的正切值,这个临界角度类似于准静态砂土休止角,可以用于评价砂土的摩擦属性。
临界状态理论[3]定义了在大变形条件下,材料达到一种临界状态(如图3所示),其特征为体积分数和剪应力(对应摩擦特性)均保持不变。由于试验数据均来源于三轴试验,因此本文中的摩擦系数均采用临界状态内摩擦角 {\varphi _{{\text{cs}}}} 进行计算,即 \mu = \tan {\varphi _{{\text{cs}}}} 。此外,为与颗粒物理描述表达保持一致,本研究将土力学里面的孔隙比e通过下式换算为颗粒体积分数ϕ:
\phi = \frac{{{V_{\text{s}}}}}{{{V_{\text{s}}} + {V_{\text{v}}}}} = \frac{1}{{1 + e}} 。 (13) 式中: {V_{\text{s}}} 为土体中土颗粒的体积; {V_{\text{v}}} 为土体中孔隙的体积。
2.2 临界状态砂土μ和I的相关关系
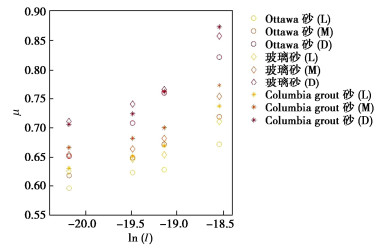
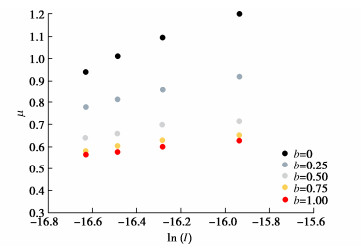
本研究选取代表性无黏性颗粒材料的三轴试验数据进行分析。Alshibli等[25]采用长宽比、磨圆度、粗糙度等形貌特征差别较大的3种砂在4种围压下进行了三轴排水压缩试验,部分试验物理指标如表1所示。每种试验材料设置了3种不同的密实度(松散L、中密M、密实D),中密和密实试样利用Al-Shibli等[26]的空气淋滤装置制备,松散的样品使用ASTM D4254(ASTM 2016b)等程序制备(手拿一个带有13 mm喷嘴的漏斗,从25 mm的落点高度沉积砂子)。圆柱形试验试样直径为71.1 mm,高度为142.2 mm,偏移应力以0.5 mm/min的恒定位移速率施加。虽然3种砂的Gs=2.65和d50=0.36 mm参数一致,但是电镜图像发现3种材料的长宽比、磨圆度、粗糙度等差别很大。Ottawa砂、玻璃砂和Columbia grout 砂的μ-ln(I)关系如图4所示。
表 1 试验材料的物理指标Table 1. Physical properties of test materials材料 Gs d50/mm 密实状态 e F-35 Ottawa 砂 2.65 0.36 疏松 0.733 中等 0.614 致密 0.494 #1玻璃砂 2.65 0.36 疏松 0.928 中等 0.778 致密 0.638 GS#40 Columbia grout砂 2.65 0.36 疏松 0.921 中等 0.762 致密 0.639 由图 4可以看出,3种砂的临界状态摩擦系数μ均与惯性数和颗粒的密实度相关。对于不同类型的土,土越密实摩擦系数越大。如果将采用颗粒物理中初始颗粒体积分数 {\phi _{\text{0}}} 来描述颗粒的密实程度,可以得到颗粒准静态变形摩擦特性μ、初始密实状态 {\phi _{\text{0}}} 和颗粒惯性数I间的标度律,符合线性关系,如图5示。
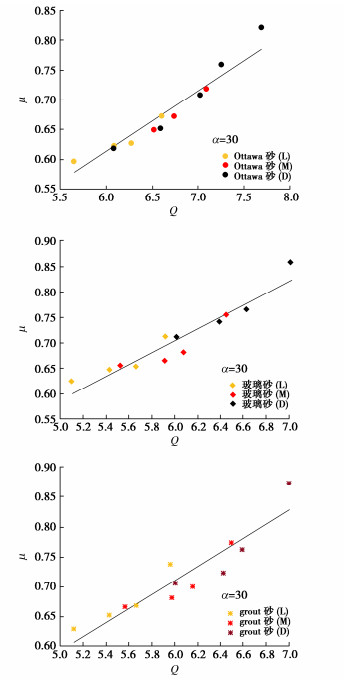
不同于流态颗粒运动状态下摩擦系数μ与惯性数I之间的一一对应关系,颗粒在高围压、准静态下,摩擦系数μ与 {\phi _{\text{0}}} [ln(I)+α]之间存在线性一一对应关系。其中,对于3种试验材料, \alpha 的数值均为 \alpha =30,这可能是因为3种材料的比重和中值粒径等参数相近。 {\phi _{\text{0}}} 这一变量的相关性表明颗粒体系的摩擦特性受其密实状态影响,土颗粒越密实内摩擦特征越显著。另一变量颗粒惯性数I表征了颗粒形变剧烈程度客观规律。将发现的规律看成是考虑密实程度的准静态颗粒惯性数,定义它为Q= {\phi _{\text{0}}} [ln(I)+α]。
临界土力学理论认为,在剪切的最终阶段,只有剪应变还持续增加,而土颗粒所受的有效应力和体积趋于不变。流态颗粒μ(I)和ϕ(I)流变准则认为摩擦系数μ分别与惯性数I和ϕ一一对应,对应的是达到临界状态后受力的变形特征。经典的颗粒μ(I),ϕ(I)流变准则在描述 I >10-3的密实均匀颗粒流时效果显著,但对颗粒准静态I<10-3动力特性描述时失效。发现的新标度律,揭示了颗粒准静态受力变形的本构法则。颗粒达到临界状态后产生流态化变形,ϕ(I)流变准则表明在固定的I条件下颗粒体积分数ϕ是定值,故颗粒的摩擦特性μ只反映出与颗粒惯性数I的对应关系。而在达到流态前的准静态变形状态,颗粒的摩擦特性还受体积分数 {\phi _{\text{0}}} 的影响: {\phi _{\text{0}}} 越大,准静态惯性数Q= {\phi _{\text{0}}} [ln(I)+α]越大,如图6示。也就意味着,颗粒在达到临界状态前发生准静态变形,对于同一种土,在同样的受力变形条件下(颗粒惯性数I相同,即外部围压(正应力)P和变形速率 \left| {\boldsymbol{\dot \gamma }} \right| 相同),更密实的土颗粒(更大的颗粒体积分数 {\phi _{\text{0}}} )表现出更强的摩擦强度特性,这与常理认知一致。
对线性关系进行标定,可得下列关系表达:
\mu = \xi Q 。 (14) 其中,拟合参数见表2所示。可以发现,ξ近似等于0.11。
从另一个角度来分析上述标度率所表征的体积分数对摩擦特性的影响,临界土力学定义了临界状态比 {M_{\text{c}}}
q = {M_{\text{c}}}p 。 (15) 这个固定的临界状态比与摩擦系数之间的关系为
{M_{\text{c}}} = 6\mu '/(3 - \mu ') 。 (16) 在固定的临界状态比(摩擦系数)条件下,正应力 {p_{\text{s}}} (=P)与颗粒体积分数的关系为[27-28]
{p_{\text{s}}} = a\frac{{\phi - {\phi _{{\text{rlp}}}}}}{{{\phi _{{\text{rcp}}}} - \phi }} 。 (17) 式中: {\phi _{{\text{rlp}}}} 为疏松颗粒临界状态下的体积分数; {\phi _{{\text{rcp}}}} 为密实颗粒临界状态下的体积分数;a为参数。
根据莫尔库仑准则,无黏性颗粒强度 \tau 可以表示为
\tau = \mu {p_{\text{s}}} 。 (18) 以莫尔库仑准则为纽带,提炼标度律所反映的体积分数与摩擦系数μ之间正相关的关系(P不变),与临界土力学给出的体积分数与正应力P间的关系是一致的,都反应了体积分数对颗粒强度正向影响。总的来讲,文章所分析的试验规律和新揭示的物理规律,把颗粒不同方面的性质,包括颗粒的强度μ、粒径d、颗粒密度ρs、密实状态ϕ0,正应力P和对应的变形速率 \left| {\boldsymbol{\dot \gamma }} \right| 有机的结合在一起,反应了颗粒重要的受力变形物理规律。
表 2 3种材料三轴试验数据获取标度律的拟合参数Table 2. Fitting parameters of scaling law for obtaining triaxial test data for three types of materials材料 ξ F-35 Ottawa砂 0.1021 #1 玻璃砂 0.1173 GS#40 Columbia grout砂 0.1179 2.3 考虑中主应力影响的相关关系
自然状态下的土体多处于三向应力状态,由于上述分析中p = ({\sigma _1} + 2{\sigma _3})/3只考虑了{\sigma _1} 和{\sigma _3} 的影响,需进一步考虑主应力{\sigma _2}的影响。Xiao等[29]采用120 mm×60 mm×120 mm试样开展真三轴固结排水试验,研究了在较低应力水平下中主应力对堆石颗粒材料强度影响。引入毕肖普常数b描述中主应力大小:
b = \frac{{{\sigma _2} - {\sigma _3}}}{{{\sigma _1} - {\sigma _3}}} 。 (19) 选取不同的毕肖普常数0,0.25,0.5,0.75,1开展独立试验。每次试验中,剪切过程中保持小主应力{\sigma _3}和b值不变,加载速率为恒定的1 mm/min。数据处理结果如图7所示。可以发现,在相同的试验条件下,摩擦系数μ随着b值的增大而减小。
土的三维莫尔库仑强度准则的表达形式为
p\sin \varphi - \frac{1}{{\sqrt 3 }}q\left[ {\frac{1}{{\sqrt 3 }}\sin \theta \sin \varphi + \cos \theta } \right] + c\cos \varphi = 0 。 (20) 其中应力罗德角θ与b之间符合下列关系
\tan \theta = \frac{{2b - 1}}{{\sqrt 3 }} 。 (21) 认为土达到临界状态与弹塑性材料达到屈服准则进入塑性区的力学特征一致,也就是认为临界内摩擦角满足屈服准则。对于砂土c=0,将μ=tanφcs代入上式,可得
p\mu - q\left( {\frac{1}{3}\sin \theta \mu + \frac{{\cos \theta }}{{\sqrt 3 }}} \right) = 0 。 (22) 土达到临界状态时,根据剑桥模型得
{M_{\text{c}}} = \frac{\mu }{{\frac{1}{3}\sin \theta \mu + \frac{{\cos \theta }}{{\sqrt 3 }}}}{\text{ = }}\frac{1}{{\frac{{\sin \theta }}{3} + \frac{{\cos \theta }}{{\sqrt 3 \mu }}}} 。 (23) 这里可以定义一个考虑应力罗德角(即中主应力影响)的摩擦系数 {\mu _\beta } 。考虑到Mc=6 {\mu _\beta } /( 3 - {\mu _\beta } ),其中 {\mu _\beta } =tanϕβ(cs)代入公式可得
{\mu _\beta } = \frac{1}{{2\left( {\frac{{\sin \theta }}{3} + \frac{{\cos \theta }}{{\sqrt 3 \mu }}{\text{ + }}\frac{1}{6}} \right)}} \text{,} (24) 该式子定义了应力罗德角对临界状态内摩擦强度的影响。
为定量描述中主应力(应力罗德角θ或毕肖普常数b)的影响,定义一个新的无量纲数“中主应力数”β= \mu /{\mu _\beta }
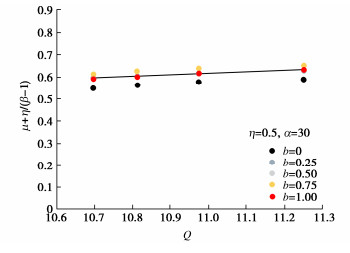
\beta = 2\mu \left( {\frac{{\sin \theta }}{3} + \frac{{\cos \theta }}{{\sqrt 3 \mu }}{\text{ + }}\frac{1}{6}} \right)。 (25) 引入新的无量纲数“中主应力数”用于试验数据分析,发现μ+η(β-1)与准静态惯性数Q=ϕ0[ln(I)+α]之间呈线性相关关系,如图8所示。常规三轴试验中b=0,则中主应力数β=1,此时标度律回归到不考虑中主应力的标度律(即式(14))。
2.4 临界状态砂土ϕ与I的相关关系
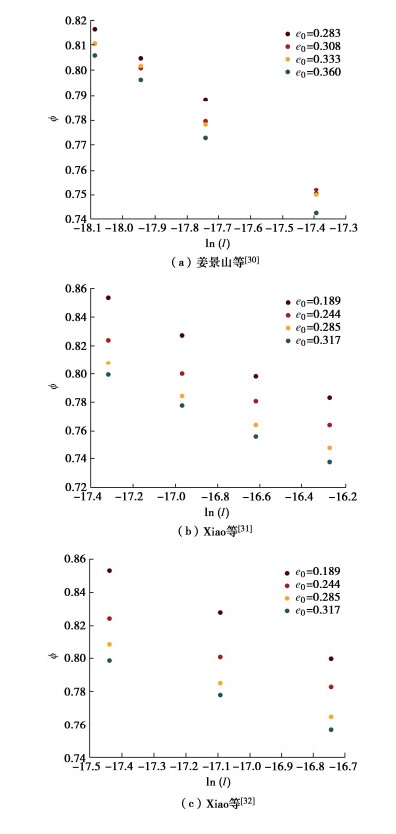
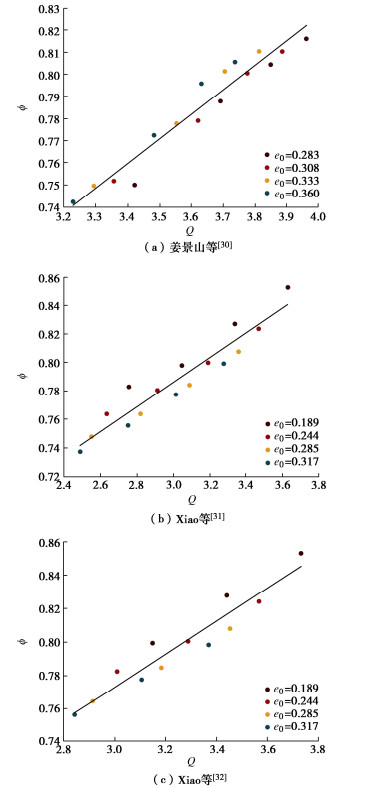
上节通过建立准静态颗粒惯性数Q,建立标度率描述临界状态砂土的摩擦特性,本节探讨临界状态体积分数与土摩擦系数μ、颗粒惯性数I、以及初始体积分数ϕ0间的临界状态标度律。选取姜景山等[30]、Xiao等[31-32]的固结排水常规三轴压缩试验(试验中使用土样的物理参数如表3所示),试验发现土达到临界状态后,初始孔隙比、剪切速率、颗粒粒径对临界状态体积分数有直接的影响。导入试验数据,可以初步得到ϕ-ln(I)相关关系,如图9所示。可以看到,初始体积分数越小(初始孔隙比越大),临界状态的体积分数也越小。
表 3 主要试验参数Table 3. Primary experimental parameters初始孔隙比 Gs d50/mm 剪切速率 0.360 2.72 14.39 0.6 mm/min 姜景山 等[30] 0.333 2.72 14.39 0.6 mm/min 0.308 2.72 14.39 0.6 mm/min 0.283 2.72 14.39 0.6 mm/min 0.189 2.69 26.48 1 mm/min Xiao 等[31] 0.224 2.69 26.48 1 mm/min 0.285 2.69 26.48 1 mm/min 0.317 2.69 26.48 1 mm/min 0.189 2.69 23.48 1 mm/min Xiao 等[32] 0.224 2.69 23.48 1 mm/min 0.285 2.69 23.48 1 mm/min 0.317 2.69 23.48 1 mm/min 引入本文建立的准静态颗粒惯性数Q,可以得到准静态变形颗粒在临界状态下,颗粒体积分数ϕ与初始ϕ0和颗粒惯性数I间的标度律,如图10示。发现临界状态的颗粒体积分数与准静态惯性数Q= ϕ0[ln(I)+α]呈线性关系,可知准静态颗粒惯性数Q对揭示临界状态砂土的体积特征同样关键。
3. 结 语
本研究从土的颗粒物理本源出发,采用3种无黏性土的试验数据获取标度律的数理表达,发现临界状态摩擦系数μ值与惯性数I、颗粒初始体积分数ϕ0相关:土体越密实,临界状态摩擦系数越大。为定量描述土力学试验所揭示的土体强度与加载速率的相关性,引入了初始颗粒体积分数ϕ0来描述颗粒的初始密实程度,提出了考虑初始密实程度的准静态颗粒惯性数Q=ϕ0[ln(I)+α],这样通过ϕ0可以反映密实状态对颗粒体系的摩擦特性的影响,同时发现摩擦系数μ与准静态颗粒惯性数Q之间满足μ=ξQ的简单线性关系。
经典的三轴试验还发现,体积分数越小(初始孔隙比越大),临界状态的颗粒体积分数也越小。为揭示临界状态土体的体变规律,采用本研究提出的准静态颗粒惯性数Q,得到了准静态变形的临界状态砂土,颗粒体积分数ϕ与初始体积分数ϕ0和颗粒惯性数I间的相关性。
需要说明的是,自然土形貌特征等性质复杂,本文在建模分析先是将土颗粒抽象概化为圆形颗粒,开展无量纲数的数理推导,在此建模分析中粒径、压力、密度被认为是最主要的控制因素。土颗粒的重排列时间实际还与颗粒的其他尺寸参数、形貌特征等因素相关。
此外,本研究基于多组试验数据定义的准静态颗粒惯性数Q=ϕ0[ln(I)+α]中,拟合参数值为α=30,过程中没有特意调整拟合参数,参数α的归一可能源自3种试验颗粒材料的基本性质相似。参数α对土类型和性质的依赖性,仍待进一步补充研究。考虑到研究所采用的三轴试验经典颗粒惯性数I>e -30,因此准静态颗粒惯性数Q恒大于零,符合定义的物理意义。对于I<e -30的情况,需要采用对应条件的试验数据拟合得到新的拟合参数α值。
-
表 1 试验材料的物理指标
Table 1 Physical properties of test materials
材料 Gs d50/mm 密实状态 e F-35 Ottawa 砂 2.65 0.36 疏松 0.733 中等 0.614 致密 0.494 #1玻璃砂 2.65 0.36 疏松 0.928 中等 0.778 致密 0.638 GS#40 Columbia grout砂 2.65 0.36 疏松 0.921 中等 0.762 致密 0.639 表 2 3种材料三轴试验数据获取标度律的拟合参数
Table 2 Fitting parameters of scaling law for obtaining triaxial test data for three types of materials
材料 ξ F-35 Ottawa砂 0.1021 #1 玻璃砂 0.1173 GS#40 Columbia grout砂 0.1179 表 3 主要试验参数
Table 3 Primary experimental parameters
初始孔隙比 Gs d50/mm 剪切速率 0.360 2.72 14.39 0.6 mm/min 姜景山 等[30] 0.333 2.72 14.39 0.6 mm/min 0.308 2.72 14.39 0.6 mm/min 0.283 2.72 14.39 0.6 mm/min 0.189 2.69 26.48 1 mm/min Xiao 等[31] 0.224 2.69 26.48 1 mm/min 0.285 2.69 26.48 1 mm/min 0.317 2.69 26.48 1 mm/min 0.189 2.69 23.48 1 mm/min Xiao 等[32] 0.224 2.69 23.48 1 mm/min 0.285 2.69 23.48 1 mm/min 0.317 2.69 23.48 1 mm/min -
[1] RENDULIC L. Das Grundgesetz der Tonmechanik und sein experimenteller Beweis[J]. Bauingenieur, 1937, 18: 31/32.
[2] HENKEL D J. The relationships between the effective stresses and water content in saturated clays[J]. Géotechnique, 1960, 10(2): 41-54. doi: 10.1680/geot.1960.10.2.41
[3] SCHOFIELD A N, WROTH P. Critical State Soil Mechanics[M]. New York: McGraw-Hill, 1968.
[4] MUIR WOOD D. Soil behaviour and critical state soil mechanics[M]. Cambridge: Cambridge University Press, 1990.
[5] LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449-460. doi: 10.1680/geot.2000.50.4.449
[6] JEFFERIES M G. Nor-Sand: a simple critical state model for sand[J]. Géotechnique, 1993, 43(1): 91-103. doi: 10.1680/geot.1993.43.1.91
[7] KULHAWY F H, MAYNE P W. Manual on Estimating Soil Properties for Foundation Design[R]. Electric Power Research Inst. , Palo Alto, CA (USA); Cornell Univ. , Ithaca, NY (USA). Geotechnical Engineering Group, 1990.
[8] FU Z, CHEN S, PENG C. Modeling cyclic behavior of rockfill materials in a framework of generalized plasticity[J]. International Journal of Geomechanics, 2014, 14(2): 191-204. doi: 10.1061/(ASCE)GM.1943-5622.0000302
[9] LADE P V. Assessment of test data for selection of 3-D failure criterion for sand[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(4): 307-333. doi: 10.1002/nag.471
[10] BARAN O, ERTAŞ D, HALSEY T C, et al. Velocity correlations in dense gravity-driven granular chute flow[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2006, 74(5 pt 1): 051302.
[11] IORDANOFF I, KHONSARI M M. Granular lubrication: toward an understanding of the transition between kinetic and quasi-fluid regime[J]. J Trib, 2004, 126(1): 137-145. doi: 10.1115/1.1633575
[12] SAVAGE S B. The mechanics of rapid granular flows[J]. Advances in Applied Mechanics, 1984, 24: 289-366.
[13] ANCEY C, COUSSOT P, EVESQUE P. A theoretical framework for granular suspensions in a steady simple shear flow[J]. Journal of Rheology, 1999, 43(6): 1673-1699. doi: 10.1122/1.551067
[14] POULIQUEN O, FORTERRE Y. Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane[J]. Journal of Fluid Mechanics, 2002, 453: 133-151. doi: 10.1017/S0022112001006796
[15] WANG C, DENG A, TAHERI A. Three-dimensional discrete element modeling of direct shear test for granular rubber–sand[J]. Computers and Geotechnics, 2018, 97: 204-216. doi: 10.1016/j.compgeo.2018.01.014
[16] DA CRUZ F, EMAM S, PROCHNOW M, et al. Rheophysics of dense granular materials: discrete simulation of plane shear flows[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2005, 72(2 pt 1): 021309.
[17] SAVAGE S B, SAYED M. Stresses developed by dry cohesionless granular materials sheared in an annular shear cell[J]. Journal of Fluid Mechanics, 1984, 142: 391-430. doi: 10.1017/S0022112084001166
[18] GDR M D. On dense granular flows[J]. The European Physical Journal E, 2004, 14: 341-365. doi: 10.1140/epje/i2003-10153-0
[19] FORTERRE Y, POULIQUEN O. Flows of dense granular media[J]. Annu Rev Fluid Mech, 2008, 40: 1-24. doi: 10.1146/annurev.fluid.40.111406.102142
[20] KAMRIN K, KOVAL G. Nonlocal constitutive relation for steady granular flow[J]. Phys Rev Lett, 2012, 108(17): 178301. doi: 10.1103/PhysRevLett.108.178301
[21] HENANN D L, KAMRIN K. A predictive, size-dependent continuum model for dense granular flows[J]. Proc Natl Acad Sci USA, 2013, 110(17): 6730-6735. doi: 10.1073/pnas.1219153110
[22] BOUZID M, TRULSSON M, CLAUDIN P, et al. Nonlocal rheology of granular flows across yield conditions[J]. Phys Rev Lett, 2013, 111(23): 238301. doi: 10.1103/PhysRevLett.111.238301
[23] BOUZID M, IZZET A, TRULSSON M, et al. Non-local rheology in dense granular flows[J]. The European Physical Journal E, 2015, 38(11): 1-15.
[24] JOP P, FORTERRE Y, POULIQUEN O. A constitutive law for dense granular flows[J]. Nature, 2006, 441(7094): 727-730. doi: 10.1038/nature04801
[25] ALSHIBLI K A, CIL M B. Influence of particle morphology on the friction and dilatancy of sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2018, 144(3): 04017118. doi: 10.1061/(ASCE)GT.1943-5606.0001841
[26] AL-SHIBLI K, MACARI E J, STURE S. Digital imaging techniques for assessment of homogeneity of granular materials[J]. Transportation Research Record, 1996, 1526(1): 121-128. doi: 10.1177/0361198196152600115
[27] JOHNSON P C, JACKSON R. Frictional-collisional constitutive relations for granular materials, with application to plane shearing[J]. Journal of fluid Mechanics, 1987, 176: 67-93. doi: 10.1017/S0022112087000570
[28] JOHNSON P C, NOTT P, JACKSON R. Frictional-collisional equations of motion for participate flows and their application to chutes[J]. Journal of Fluid Mechanics, 1990, 210: 501-535. doi: 10.1017/S0022112090001380
[29] XIAO Y, LIU H, LIU H, et al. Strength and dilatancy behaviors of dense modeled rockfill material in general stress space[J]. International Journal of Geomechanics, 2016, 16(5): 04016015. doi: 10.1061/(ASCE)GM.1943-5622.0000645
[30] 姜景山, 左永振, 程展林, 等. 围压和密度对粗粒料临界状态力学特性的影响[J]. 长江科学院院报, 2021, 38(5): 94-102. https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB202105018.htm JIANG Jingshan, ZUO Yongzhen, CHENG Zhanlin, et al. Effects of confining pressure and density on mechanical properties of coarse granular material under critical state[J]. Journal of Yangtze River Scientific Research Institute, 2021, 38(5): 94-102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB202105018.htm
[31] XIAO Y, LIU H, DING X, et al. Influence of particle breakage on critical state line of rockfill material[J]. International Journal of Geomechanics, 2016, 16(1): 04015031. doi: 10.1061/(ASCE)GM.1943-5622.0000538
[32] XIAO Y, LIU H, CHEN Y, et al. Bounding surface model for rockfill materials dependent on density and pressure under triaxial stress conditions[J]. Journal of Engineering Mechanics, 2014, 140(4): 04014002. doi: 10.1061/(ASCE)EM.1943-7889.0000702
-
期刊类型引用(1)
1. 万航,周跃峰,邓茂林,左永振,赵艺颖,王磊. 三轴加载条件下粗粒土剪切带的细观演化规律. 水力发电学报. 2025(01): 54-63 .  百度学术
百度学术
其他类型引用(0)
-
其他相关附件



 下载:
下载: