Calculation of rising height of capillary water based on fractal model for grain-size distribution
-
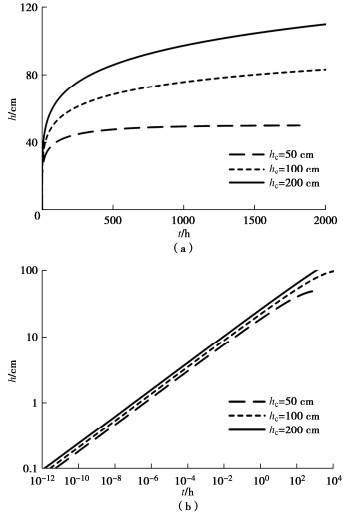
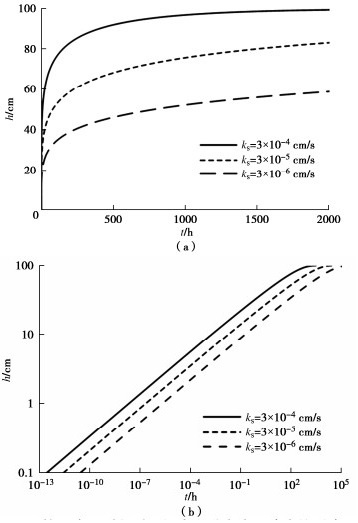
摘要: 由表面张力引起的弯液面两侧压力差推动毛细水上升,造成低路堤路基产生毛细水病害,毛细水上升高度是防治路基毛细水病害的关键所在。克服了毛细水上升高度测量试验的缺陷,基于土粒分布的分形模型,提出毛细水上升高度的计算方法。采用筛分试验计算粉土颗粒分布分维,建立粉土颗粒级配的分形模型,系统地分析分维、进气值、孔隙率、毛细水最大上升高度和饱和渗透系数对毛细水上升高度和速度的影响。计算结果表明:毛细水上升高度与时间呈幂函数正相关关系,毛细水上升高度随颗粒分布分维、进气值、毛细水最大上升高度和饱和渗透系数增大而增大,随孔隙率增大而减小;毛细水上升速度只与颗粒分布的分维有关,随颗粒分布分维增大而增大,不受进气值、孔隙率、毛细水最大上升高度和饱和渗透系数的影响。Abstract: The rising of capillary water, which is driven due to the pressure difference at both sides of the meniscus caused by surface tension, causes the phenomenon of mud boiling and mud seepage in the silt roadbed. The rising height of the capillary water is the key to preventing and controlling the mud boiling and mud seepage in the roadbed. A method for calculating the rising height of the capillary water based on the grain-size distribution is proposed, which overcomes the test defects in measuring the height of the capillary water. By using the sieving tests to calculated the grain-size distribution and fractal of silt, a fractal model is established to analyze the effects of the fractal dimension, air-entry value, porosity, the maximum rising height of the capillary water and saturated permeability coefficient on the rising height and velocity of the capillary water. The calculated results show that the rising height of the capillary water is positively correlated with the time as a power function, increases with the fractal dimension, air-entry value, the maximum rising height of the capillary water and saturated permeability coefficient, and decreases with the porosity. The rising speed of the capillary water is only related to the fractal dimension of the grain-size distribution and increases with the increase of the fractal dimension of the grain-size distribution but not related to the porosity, air-entry value and the saturated permeability coefficient.
-
Keywords:
- silt /
- capillary water /
- grain-size distribution /
- fractal /
- fractal dimension
-
0. 引言
泥水平衡盾构广泛应用于水下隧道建设中,其采用拌制的泥水悬浮液(泥浆)作为支护材料,通过泥浆渗透形成不透水泥膜,将泥水压力转化为有效支护力从而平衡开挖面水土压力[1]。盾构机在进行带压开舱作业时,泥膜还需要有较好的闭气保压能力。而在高渗透地层,由于地层孔隙大,普通的膨润土泥浆大量流失,泥膜质量差,往往无法满足闭气要求甚至无法成膜。
目前普遍采用向泥浆中添加粗颗粒的方法提高成膜成功率和泥膜质量,常用的粗颗粒材料有天然河砂、锯末和蛭石等,已在Zimmerberg Base Tunnel [2]、南京和燕路隧道[3]等工程中成功应用。核桃壳是一种生物质粗颗粒材料,其主要成分为木质素、纤维素和半纤维素[4],常应用于污水处理、砂浆改性等领域,在长期浸泡和酸碱盐浸渍条件下均有较好的耐久性[5]。由于核桃壳颗粒具有一定强度且吸水膨胀后可产生柔性变形,因此可同时承担骨架和填充变形作用[6],因而也是钻井液最常用的堵漏材料之一。近年来,由于核桃壳在满足工程经济性的基础上,拥有比砂子更好的地层适应性和泥浆匹配性,含核桃壳泥浆在高渗透地层的盾构施工中也开始应用。
明确泥浆流变性、渗透成膜特性是施工中相关参数设定的基础。在泥浆流变性方面,盾构泥浆被认为是一种塑性流体或屈服假塑性流体[7-8],泥浆中固相含量的增加对浆液的流变行为有显著影响,主要表现为黏度增加和流变曲线形状改变[9-10]。在泥浆渗透性方面,国内外众多学者通过室内泥浆渗透试验对泥浆渗透成膜进行全过程分析,把泥浆在地层中的渗透分为液相滤失和固相滞留两部分,提出了渗滤模型[11],并对颗粒的堵漏机制[12]、堆积形态[13]、颗粒与地层孔隙的匹配关系[14]开展了进一步研究。在带压开舱时,粗颗粒对泥膜闭气性也有明显影响,粗颗粒含量的适当增加可改善地层内部网架结构的稳定性,从而提高泥膜的闭气性能[15]。但以上研究主要针对含砂泥浆,对含核桃壳泥浆各项性质认识不足,导致施工中泵送压力、泥浆配比、闭气压力等参数的设定多依靠经验。
本文拟采用核桃壳作为盾构泥浆粗颗粒材料,研究添加核桃壳后泥浆流变性变化,同时进行高渗透地层下的泥浆渗透和泥膜闭气试验,对比含核桃壳泥浆和含砂泥浆的渗透成膜特性和泥膜闭气性,以期为高渗透地层的带压开舱泥浆配制提供施工指导和建议。
1. 试验材料与方法
1.1 试验材料
(1)地层材料
为了模拟高渗透地层的孔隙特征,泥浆渗透及泥膜闭气试验所用地层采用粒径范围为0.5~2 mm的连续级配砂土,地层平均孔径为0.205 mm。控制每次试验的地层干密度为1.441 g/cm3,地层孔隙率为0.461,采用常水头渗透试验测得地层渗透系数为9.04×10-3 m/s。
(2)泥浆材料
试验中采用的泥浆材料主要包括纯净水、钠基膨润土、羧甲基纤维素钠(CMC)、核桃壳和天然河砂。试验用基浆按1︰8的膨水比配置,并添加质量分数为1‰的CMC作为增黏剂。其中,钠基膨润土采用0.075 mm标准筛做筛分处理,以消除杂质的影响,粗粒材料粒径的选取依据Min等[16]提出地层匹配性准则。试验采用的核桃壳由废弃物中回收而来,通过清洗、破碎、分拣、筛分等工序,制备成不同大小的颗粒。泥浆配制完成后,充分膨化24 h后对其进行基本性质测定。试验采用相同配比基浆(LB0/ST0),添加不同种类、含量的粗颗粒进行泥浆配制,研究泥浆的流变性、渗透性和泥膜闭气性,试验组别安排与泥浆基本性质参数如表 1所示。其中,编号ST0-ST4的含核桃壳泥浆同时进行流变性测试和泥浆渗透及泥膜闭气试验,编号ST5-ST8的含砂泥浆仅进行泥浆渗透及泥膜闭气试验。
表 1 泥浆基本性质参数Table 1. Basic parameters and properties of slurry泥浆编号 粗颗粒材料 添加量/(g·L-1) 密度/(g·cm-3) 漏斗黏度/s 胶体率/% ST0 — 0 1.075 35 83.5 ST1 0.15~0.2 mm核桃壳 10 1.082 55 87.0 ST2 20 1.086 61 90.0 ST3 30 1.090 65 92.0 ST4 40 1.092 68 88.0 ST5 0.15~0.2 mm砂 10 1.082 49 81.0 ST6 20 1.093 52 87.0 ST7 30 1.100 57 90.0 ST8 40 1.106 51 88.4 1.2 试验装置
(1)NXS-11型旋转黏度计
泥浆流变性测试试验采用NXS-11型旋转黏度计,采用控制剪切速率的方式进行流变测试。黏度计共5组测量系统,可测量剪切速率范围为15.5~996.1 s-1,共15级转速可调。
(2)泥浆渗透及泥膜闭气试验系统
采用自制的泥浆渗透及泥膜闭气试验系统,由加压系统、渗透柱和渗透流量采集系统3部分组成,加压系统包括空压机、调压装置和压力表;渗透柱为内径10 cm高70 cm的有机玻璃柱;渗透流量采集系统包括高精度天平、滤液收集器及配套的数据采集软件,如图 1所示。
1.3 试验步骤
(1)泥浆流变性测试试验
试验前,根据试验泥浆的预估黏度选择合适的测量系统,本试验选用测量系统A(外筒内径4 cm,内筒外径3.846 cm)。安装仪器,外筒中倒入规定量待测浆液并按照顺序安装内、外筒。待仪器各部分安装完毕后将转子置于工作状态,转动旋钮调整转速,待指针摆动稳定后(±0.5格)读取对应的刻度盘读数,按下式计算得到某一剪切速率所对应的泥浆剪切应力及表观黏度:
τ=N⋅z,η=γτ。} (1) 式中:τ为剪切应力(Pa);N为刻度盘读数;z为转子常数,取0.2767 Pa/格;η为表观黏度(Pa·s);γ为剪切速(s-1)。
试验中采用两种不同的剪切速率加载方式。其中,加载曲线1用于测试泥浆在剪切速率分级增加和降低条件下的流动性变化,分别可得到流变上行曲线(即流变曲线)和下行曲线;加载曲线2用于测试泥浆在恒定剪切速率下长时间剪切的流动性变化,剪切速率加载曲线如图 2所示。
(2)泥浆渗透及泥膜闭气试验
首先进行地层填装,底部滤层采用6~8 mm白色砾石,高度为5 cm,试验地层采用粒径为1~2 mm的天然河砂,高度26 cm,自下向上进行地层饱和,完成后缓慢注入制备好的泥浆1000 ml,静止5 min后开始泥浆渗透试验。
试验采用分级加压,共50,100,150,200 kPa共4级压力,每级压力下保持3 min。待每级压力稳定后打开渗透柱底部的出水阀门,数据采集系统自动采集流量,采集间隔为1 s。试验结束后缓慢对渗透柱进行泄压,打开渗透柱侧壁的阀门将剩余泥浆排出,观察泥膜形态并测量泥膜厚度。
对泥浆渗透试验中形成稳定泥膜的泥浆组进行泥膜闭气试验,采用分级加压的方式测定泥膜的耐高气压能力,以30 kPa为增量逐级增压至泥膜破坏,每级压力下保持1 min。试验结束后取出泥膜,观察泥膜的破坏形态并进行电镜扫描。
2. 试验结果分析
2.1 核桃壳颗粒对盾构泥浆流变性影响分析
(1)泥浆流变曲线分析
对ST0~ST4共5组含核桃壳颗粒泥浆进行流变性测试,得到宽剪切范围下泥浆的剪切应力-剪切速率(τ-γ)曲线(上行曲线)和表观黏度-剪切速率(η-γ)曲线,其中表观黏度为剪切应力与其相对应的剪切速率之比。泥浆的τ-γ曲线如图 3所示,当核桃壳含量为0 g/L时,泥浆表现为典型的屈服假塑性流体。加入核桃壳后τ-γ曲线形态产生改变,低剪切速率时剪切应力增长较快,中剪切速率处出现剪切应力平台。
泥浆的η-γ曲线如图 4所示,在中低剪切速率段表观黏度迅速降低,并随剪切速率的增大逐渐趋于一定值,即表现为明显的剪切稀释性。加入核桃壳前后曲线形态并无明显变化,但核桃壳的添加使泥浆在低剪切速率下的初始黏度有明显提升,黏度降幅增大,剪切稀释特性更为显著。
由于τ-γ曲线中段剪切应力平台的出现,现有的流变模型均不能完整反映添加核桃壳后泥浆的流变行为。为准确表达含核桃壳泥浆的流变特点,基于泥浆在不同剪切速率下表现出的不同流动特性,将其分为中低剪切速率下的屈服假塑性区和高剪切速率下的塑性区,分别采用不同的流变模型进行拟合,以保持较高的拟合相关程度。
由于泥浆中胶体颗粒间的相互作用,泥浆内部形成较为稳定的空间网架结构。在低剪切速率区,泥浆的空间网架结构逐渐破坏,泥浆表观黏度迅速降低。达到某一剪切速率后,泥浆的网架结构基本被破坏,此时泥浆黏度的主要由流体内部摩擦决定,这种摩擦贡献逐渐趋于定值,泥浆达到稳定流动状态,表观黏度不再变化。基浆中以胶体颗粒为主,固体粗颗粒较少,泥浆可以在较低的剪切速率下达到稳定流动。加入核桃壳后,粗颗粒间的碰撞和无序运动延长了泥浆的不稳定流动段。随着剪切速率的继续增大,在高剪切速率区,粗颗粒运动产生的摩擦贡献逐渐趋于稳定,泥浆也达到稳定流动状态,黏度不再随剪切速率变化。
在中低剪切速率区,泥浆的流动符合屈服假塑性流体的特征,采用幂律模型对该段进行拟合,拟合相关度达到了0.83以上。其流变控制方程为τ=Kγn,其中K为稠度系数,反映泥浆的流动阻力,若K值过大,则泥浆泵送困难,过小则泥浆携渣能力不足;n为流动指数,反映流体的流动行为偏离牛顿行为的程度(当n<1时,流体表现为剪切稀释性),在施工过程中,一般希望泥浆有较低的n值,以便于泥浆流动与土渣携带,拟合结果参数见表 2。核桃壳颗粒的加入在降低泥浆流动指数的同时提升了泥浆的稠度,对工程中泥浆的泵送性和携渣能力均有正向贡献。
表 2 中低剪切速率区幂律模型拟合结果Table 2. Fitting results by power law model at low and medium shear rates核桃壳含量/(g·L-1) 幂律模型τ=Kγn n K/(Pa·s) R2 0 0.270 0.995 0.993 10 0.166 2.454 0.841 20 0.142 2.736 0.843 30 0.168 2.915 0.832 40 0.157 2.163 0.883 采用Bingham模型对泥浆稳定流动后高剪切速率下的塑性区进行拟合,拟合相关度达到了0.98以上。其流变控制方程为τ=τ0+μγ,其中τ0为泥浆的屈服应力,反映了泥浆内部各组分之间相互作用力的大小,亦即形成三维空间网架结构的能力;μ为泥浆的塑性黏度,该黏度不随剪切速率变化,与幂律模型中的稠度系数K具有相似的物理意义,反映泥浆稳定流动时的流动阻力,拟合参数结果如表 3所示。
表 3 高剪切速率区Bingham模型拟合结果Table 3. Fitting results by Bingham at high shear rates核桃壳含量/(g·L-1) Bingham模型τ=τ0+μγ τ0/Pa μ/(Pa·s) R2 0 2.024 0.0038 0.995 10 3.102 0.0059 0.998 20 3.444 0.0064 0.989 30 3.601 0.0067 0.982 40 3.360 0.0072 0.999 泥浆屈服应力τ0和塑性黏度μ随核桃壳含量的变化曲线如图 5所示,核桃壳颗粒的添加显著提高了泥浆的屈服应力,这表示核桃壳颗粒较好地嵌入了泥浆的三维网架结构,并提高了泥浆三维空间网架结构的稳定性。另外,随着核桃壳添加量的增加,总表面积增大,泥浆各组分间内摩擦力随之增加,宏观表现为泥浆塑性黏度的增大。
(2)泥浆的触变性分析
泥浆触变性是泥浆经剪切后变稀而静置后变稠的特性。膨润土泥浆作为典型的触变性非牛顿流体,主要特征为在剪切速率恒定的条件下,泥浆的剪切应力逐渐降低并趋于稳定,该值的大小和稳定时间与泥浆自身结构和剪切速率有关。该性能对于描述长时间输送后泥浆流变特性的变化具有重要意义。
经过计算,以盾构施工常用的泥浆输送系统为例,管径0.35 m、流量1000 m3/h的泥浆泵送设备的有效剪切速率约为124.75 s-1,因此采用旋转黏度计的第7级转速(105.1 s-1),在该转速下测试泥浆长时间剪切的流变性衰减,如图 6所示。虽然各组泥浆的初始黏度不同,但经过恒定剪切速率的长时间作用后,剪切应力趋于一个较为统一的稳定值,达到这一稳定值的时间也无较大区别。因此,核桃壳颗粒的加入对盾构泥浆固定速率下长时间剪切后的流变性并无明显改变。
触变性流体在流变曲线上的表现为剪切速率上行和下行曲线不重合,形成一个滞后圈,可采用滞后圈面积表示流体触变性[17]。触变滞后圈包含的面积被定义为使材料三维网格或凝胶结构被破坏所需要的能量,其量纲为能量/体积。
核桃壳添加量为0,30 g/L的泥浆滞后圈如图 7所示,添加核桃壳前后泥浆的滞后圈形态有较大差异,主要体现在上行曲线形态的改变和下行曲线斜率的不同。
通过积分计算各组泥浆滞后圈面积如图 8所示,加入核桃壳后泥浆滞后圈面积显著增加,随着核桃壳添加量的增加,泥浆滞后圈面积先增加后减小,在添加量为30 g/L时达到峰值。这表示核桃壳的加入提升了泥浆内部网架结构和凝胶结构强度,破坏该结构需要更多的能量,核桃壳添加量为30 g/L的泥浆具有的凝胶强度最高,触变性最好。
2.2 含核桃壳泥浆渗透特性分析
对添加核桃壳颗粒(ST1-4)和天然河砂(ST5-8)的九组泥浆开展高渗透砂层下的泥浆渗透试验,试验中的总渗透流量变化曲线分别如图 9,10所示。九组泥浆中,除了未添加粗颗粒的基浆外,均形成了稳定的泥膜+渗透带型低渗透区。由于高渗透砂层的地层孔径过大,基浆的液相和固相颗粒均穿过地层孔隙造成滤失,因此无法形成稳定的低渗透区;加入合适粒径粗颗粒后,一部分粗颗粒在地层内部滞留堵塞降低了地层渗透系数形成渗透带,另一部分粗颗粒在地层表面不断堆积形成泥膜,该过程中泥浆渗透流量逐渐降低并趋于稳定,这标志着不透水泥膜的形成。
图 11为泥浆渗透成膜的总渗透流量变化图,随着粗颗粒含量的增加,泥浆的成膜滤失量呈现出先减小后增加的趋势,且含核桃壳泥浆的成膜渗透流量大于传统含砂泥浆。另外,试验中发现,含核桃壳泥浆生成的泥膜厚度(约为8~10 mm)大于含砂泥浆(约为5~6 mm)。由于试验中的渗透方向为竖向渗透,砂颗粒比重较大,可以较快地沉积于地层表面,而核桃壳颗粒与泥浆比重相近,均匀分散悬浮于泥浆中,随泥浆缓慢渗透进入地层堵塞地层孔隙,因此在竖向渗透试验中含核桃壳泥浆的成膜时间较长,渗透流量较大。但在实际盾构施工中,泥浆为横向渗透,将不会出现此种渗透流量的差别。反而由于砂颗粒密度大,多聚集于开挖舱底部,上部由于缺乏堵漏材料而产生大量漏失,常出现泥膜质量不均匀甚至无法成膜的问题。
2.3 含核桃壳泥浆与含砂泥浆的泥膜耐高气压能力对比
在带压开舱时,泥水舱的空气压力经泥膜转化为有效应力用以平衡地层的水土压力,从而维持开挖面稳定。泥膜在一定气压下不被气体击穿并保持这种压力转化功能的能力即为泥膜的闭气性能。
对ST1-4、ST6-8共7组含粗颗粒泥浆渗透形成的泥膜进行耐高气压能力测试试验,试验过程中的渗透流量变化曲线分别如图 12,13所示。
渗透流量曲线在不同位置出现突变点,即泥膜的进气点。由于泥膜内部实际由许多孔隙连通形成毛管,研究中通常将此现象简化为多孔介质毛管模型进行解释:进气点之前,外气压与泥膜孔隙毛管中液体的表面张力形成平衡,此时渗透流量几乎为零,气舱压力无明显变化;随着气压的增大,毛管液体弯液面不断“下凹”,以获得更大的垂向张力来抵抗气压。当弯液面变为半球形时达到极限状态(即进气点),外气压瞬间完成对泥膜孔隙液体的驱替,渗透流量瞬间增大,泥膜表现为圆孔状击穿破坏,如图 14所示。
采用闭气值作为泥膜耐高气压能力的评价指标,闭气值是泥膜在压气条件下能维持闭气性能的最大压力值,闭气值越大,泥膜质量越好,在试验中取为泥膜进气点的前一级气压。泥膜闭气值随粗颗粒种类和含量的变化如表 4所示。对于同种粗颗粒材料,随着添加量的增加,泥膜闭气值逐渐增大,在30 g/L分别达到最大值120,90 kPa。随着含量的继续增加,过多的粗颗粒表面吸附了泥浆中大量的水,抑制膨润土颗粒水化的同时颗粒平均水化膜厚度变薄,泥膜各组分间的连接紧密性降低,宏观表现为泥膜耐高气压能力的降低。
表 4 泥膜闭气值汇总表Table 4. Threshold pressures of airtightness of filter cakes添加量/(g·L-1) 泥膜闭气值/kPa 核桃壳 砂 10 30 — 20 90 30 30 150 90 40 60 30 对于不同的粗颗粒材料,在相同质量含量条件下,含核桃壳泥浆的泥膜闭气值均高于含砂泥浆。两种泥浆均在粗颗粒添加量为30 g/L达到泥膜闭气的最优值,且含核桃壳泥浆的泥膜最优闭气值较含砂泥浆高30 kPa。因此,含核桃壳泥浆形成的泥膜具有更好的耐高气压能力。
3. 讨论
3.1 核桃壳对泥浆性质影响机理分析
盾构泥浆是一种多相分散体系,主要由膨润土或黏土等胶粒和分散介质(水)组成,胶体颗粒与分散介质的界面性质对泥浆的性质起关键作用[18]。表面负电性的膨润土颗粒和极性水分子通过物理吸附作用建立联系,形成以膨润土胶体颗粒为“节点”,以水化阳离子为“桥”的三维网架结构,在静止状态下泥浆保持均匀分散和稳定性。核桃壳的主要成分为纤维素、半纤维素、木质素等,且基本单元中含有糖类物质,富含极性羟基,因而具有较强的亲水性[18-19],可以通过化学连接和物理吸附作用吸引水化阳离子形成水化膜。因此,大量的膨润土胶体颗粒可以于核桃壳表面建立有效连接并将其包裹,使其较好地嵌入到泥浆的三维网架结构中,提高了结构的稳定性,宏观表现为泥浆胶体率和屈服应力的提高。通过电镜扫描试验对含核桃壳泥浆形成的泥膜进行细观分析,如图 15所示。颗粒表面与连接处均被叠状连接的膨润土胶粒包裹,形成致密的结构,颗粒界线轮廓已不明显。
3.2 核桃壳改善泥膜特性作用机理分析
泥浆在向地层中渗透的过程中,大部分液相滤失、固相则堆积成为泥膜。泥膜的基本单元体为骨架状结构,骨架间的孔隙是泥膜进气的“突破点”。含粗颗粒泥浆形成的泥膜主要以粗颗粒作为骨架结构,骨架孔隙中由膨润土颗粒和CMC大分子进行填充。由于粗颗粒刚度较大且稳定性强,泥膜高气压破坏的击穿圆孔多位于粗颗粒之间的孔隙处,因此,填充泥浆的凝胶强度和粗颗粒与填充物间的界面结合强度是泥膜耐高气压能力的关键影响因素。
传统泥浆常用的堵漏材料,如天然河砂,为刚性材料,颗粒之间为硬接触,如图 16(a)所示。而核桃壳颗粒吸水后表面会发生软化,可产生一定柔性变形和挤压,颗粒间为软接触,如图 16(b),因此颗粒间的孔隙明显小于刚性颗粒,孔隙中可平衡外气压的表面张力越大,泥膜越不容易被气体击穿,闭气值越大。
除此之外,结合2.1节中对含核桃壳泥浆流变性的测试结果,核桃壳粗颗粒的加入可提高泥浆黏度和在高剪切速率下的凝胶强度,触变性也有明显改善,这也使泥膜中颗粒间的黏结性更强、泥膜的三维空间网架结构更为稳定,不易被高气压冲破。
4. 结论
针对传统含砂泥浆在高渗透砂层带压开舱时遇到成膜困难及闭气性不足的问题,本文选用轻质有机颗粒核桃壳作为泥浆堵漏材料,进行流变性测试试验、泥浆渗透成膜及泥膜闭气试验,对含核桃壳泥浆的流变性和渗透成膜特性进行研究并分析其作用机理,主要得到4点结论。
(1)核桃壳可以增强泥浆的分散稳定性。核桃壳颗粒由于表面水化和吸附作用可以较好地嵌入泥浆的三维网架结构,提高胶体结构稳定性,泥浆黏度和胶体率均有所提升。
(2)核桃壳颗粒的添加会影响泥浆的流变性,在提升泥浆屈服应力和黏度的同时保持了较好的流动性。含核桃壳泥浆的流变曲线形态发生改变,可以分为中低剪切速率下的屈服假塑性区和高剪切速率下的塑性区,分别采用幂律模型和Bingham模型拟合的相关性较高。
(3)相同添加量下,含核桃壳泥浆较传统含砂泥浆的泥膜耐高气压能力更强。与砂子间的硬接触相比,核桃壳颗粒的软接触方式可以减少颗粒间孔隙尺寸、且泥浆流变性和触变性均有一定程度改善,使泥膜更加致密,耐高气压能力更强。
(4)盾构施工中,在泥浆性质方面,应尽量选用稳定性高、泵送性强、凝胶强度高的泥浆,在泥膜质量方面,应尽量选择闭气值高的泥膜。综合考虑各试验结果,采用核桃壳替代传统砂子可改善泥浆性质和泥膜质量,在渗透系数为9.04×10-3 m/s的高渗透性砂层中,推荐的添加量为30 g/L。
-
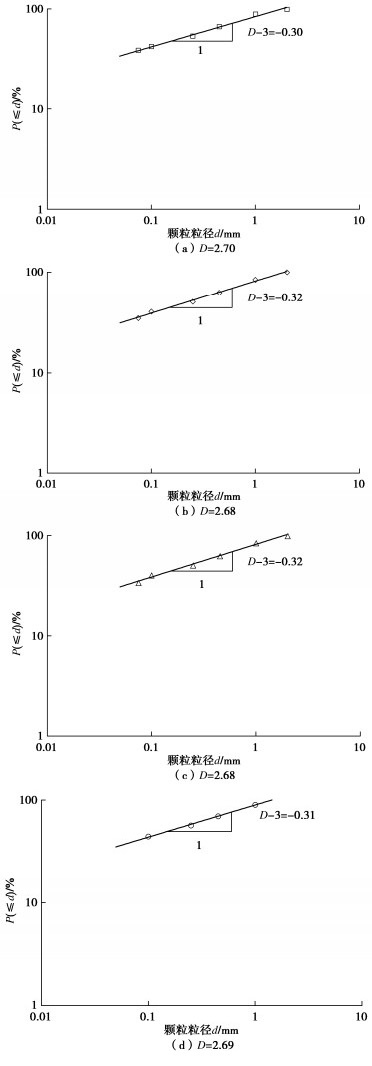
表 1 计算参数
Table 1 Calculation parameters
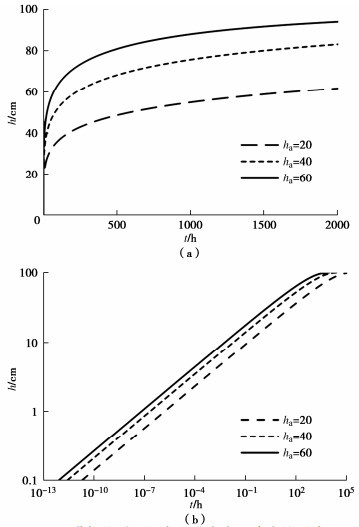
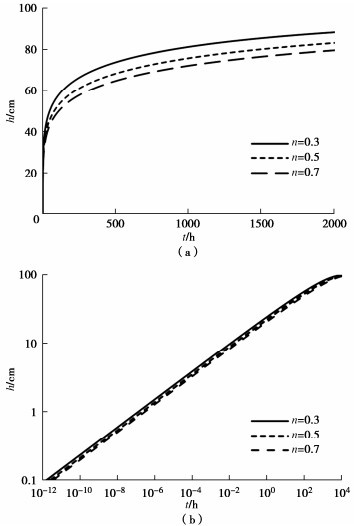
序号 D ha/m n ks/(10-7 m·s-1) hc/m 1 2.1,2.3,2.5,2.7,2.9 0.4 0.5 3 1.0 2 2.7 0.2,0.4,0.6 0.5 3 1.0 3 2.7 0.4 0.3,0.5,0.7 3 1.0 4 2.7 0.4 0.5 0.3,3,30 1.0 5 2.7 0.4 0.5 3 0.5,1.0,2.0 -
[1] 张睿, 徐永福, 于波. 交通荷载下低路堤高速公路路基沉降计算[J]. 地下空间与工程学报, 2016, 12(4): 952-957. ZHANG Rui, XU Yongfu, YU Bo. Cumulative settlement of highway subgrade with low embankment induced by traffic load[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(4): 952-957. (in Chinese)
[2] 张睿, 徐永福, 于波, 等. 低路堤高速公路路基路面处理措施分析[J]. 地下空间与工程学报, 2013, 9(增刊1): 1675-1680. ZHANG Rui, XU Yongfu, YU Bo, et al. Analysis of measures to reduce the traffic-load-settlement of low embankment highway[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(S1): 1675-1680. (in Chinese)
[3] 江国勤, 管同心, 徐永福. 天然软土地基上路堤临界高度分析[J]. 路基工程, 2011(2): 47-49. doi: 10.3969/j.issn.1003-8825.2011.02.015 JIANG Guoqin, GUAN Tongxin, XU Yongfu. Analysis on critical height of embankment on natural soft foundation[J]. Subgrade Engineering, 2011(2): 47-49. (in Chinese) doi: 10.3969/j.issn.1003-8825.2011.02.015
[4] 宋国森, 徐永福, 林飞, 等. 滨海盐渍土用于路基填料的关键技术研究[J]. 公路, 2013, 58(12): 56-60. doi: 10.3969/j.issn.0451-0712.2013.12.012 SONG Guosen, XU Yongfu, LIN Fei, et al. Study on key technology of coastal saline soil used as subgrade filler[J]. Highway, 2013, 58(12): 56-60. (in Chinese) doi: 10.3969/j.issn.0451-0712.2013.12.012
[5] 赵海, 周进华, 徐永福, 等. 低液限粉土路基填筑施工现场试验分析[J]. 中外公路, 2013, 33(2): 34-38. doi: 10.3969/j.issn.1671-2579.2013.02.009 ZHAO Hai, ZHOU Jinhua, XU Yongfu, et al. Field test analysis of low liquid limit silt subgrade filling construction[J]. Journal of China & Foreign Highway, 2013, 33(2): 34-38. (in Chinese) doi: 10.3969/j.issn.1671-2579.2013.02.009
[6] 陶涛, 陈志明, 徐永福, 等. 吹填海砂路基包边土厚度确定方法研究[J]. 中外公路, 2016, 36(1): 32-36. TAO Tao, CHEN Zhiming, XU Yongfu, et al. Study on the method of determining the thickness of wrapping soil for subgrade with blown sea sand[J]. Journal of China & Foreign Highway, 2016, 36(1): 32-36. (in Chinese)
[7] 胡明鉴, 张晨阳, 崔翔, 等. 钙质砂中毛细水高度与影响因素试验研究[J]. 岩土力学, 2019, 40(11): 4157-4164. HU Mingjian, ZHANG Chenyang, CUI Xiang, et al. Experimental study on capillary rise and influencing factors in calcareous sand[J]. Rock and Soil Mechanics, 2019, 40(11): 4157-4164. (in Chinese)
[8] 邓改革, 何建国, 康宁波. 基于多物理场耦合的毛细水高度研究[J]. 水土保持研究, 2021, 28(4): 136-141. DENG Gaige, HE Jianguo, KANG Ningbo. Research on capillary water height based on multi-physical field coupling[J]. Research of Soil and Water Conservation, 2021, 28(4): 136-141. (in Chinese)
[9] WASHBURN EW. The dynamics of capillary flow[J]. Physics Review, 1921, 17(3): 273-283. doi: 10.1103/PhysRev.17.273
[10] RICHARDS LA. Capillary conduction of liquids through porous mediums[J]. Physics, 1931, 1(5): 318-333. doi: 10.1063/1.1745010
[11] AGHAJANI H F, SOROUSH A, SHOURIJEH P T. An improved solution to capillary rise of water in soils[J]. Inter Journal of Civil Engineering, 2011, 9(4): 275-281.
[12] 张平, 吴昊, 殷洪建, 等. 颗粒级配对毛细水上升影响的研究[J]. 节水灌溉, 2010(7): 24-26. ZHANG Ping, WU Hao, YIN Hongjian, et al. Effect of particle size distribution on capillary water upward movement[J]. Water Saving Irrigation, 2010(7): 24-26. (in Chinese)
[13] 夏宁, 黄琴龙. 长江口细砂毛细水上升高度试验研究[J]. 粉煤灰综合利用, 2009, 22(6): 3-5. doi: 10.3969/j.issn.1005-8249.2009.06.001 XIA Ning, HUANG Qinlong. The experimental research of the capillarity water rising height of Changjiang delta fine sand[J]. Fly Ash Comprehensive Utilization, 2009, 22(6): 3-5. (in Chinese) doi: 10.3969/j.issn.1005-8249.2009.06.001
[14] 栗现文, 周金龙, 赵玉杰, 等. 高矿化度对砂性土毛细水上升影响[J]. 农业工程学报, 2011, 27(8): 84-89. doi: 10.3969/j.issn.1002-6819.2011.08.014 LI Xianwen, ZHOU Jinlong, ZHAO Yujie, et al. Effects of high-TDS on capillary rise of phreatic water in sand soil[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(8): 84-89. (in Chinese) doi: 10.3969/j.issn.1002-6819.2011.08.014
[15] 苗强强, 陈正汉, 田卿燕, 等. 非饱和含黏土砂毛细上升试验研究[J]. 岩土力学, 2011, 32: 327-333. MIAO Qiangqiang, CHEN Zhenghan, TIAN Qinyan, et al. Experimental study of capillary rise in unsaturated clayey sand[J]. Rock and Soil Mechanics, 2011, 32: 327-333. (in Chinese)
[16] 赵明华, 刘小平, 陈安. 非饱和土路基毛细作用分析[J]. 公路交通科技, 2008, 25(8): 26-30. ZHAO Minghua, LIU Xiaoping, CHEN An. Analysis of capillary action in unsaturated soil roadbeds[J]. Journal of Highway and Transportation Research and Development, 2008, 25(8): 26-30. (in Chinese)
[17] 王生平, 李涛. 非饱和土路基的毛细作用及其影响因素分析[J]. 公路, 2012, 57(6): 124-128. WANG Shengping, LI Tao. Analysis of capillary action and its influencing factors of unsaturated soil subgrade[J]. Highway, 2012, 57(6): 124-128. (in Chinese)
[18] 米海存, 何红曼, 段吉波. 风干砂毛细上升实验研究[J]. 节水灌溉, 2014(6): 26-28, 31. MI Haicun, HE Hongman, DUAN Jibo. Experimental study on aeolian sand capillary rise[J]. Water Saving Irrigation, 2014(6): 26-28, 31. (in Chinese)
[19] 袁玉卿, 李伟, 赵丽敏. 豫东黄泛区粉砂土毛细水上升研究[J]. 公路交通科技, 2016, 33(2): 33-38. YUAN Yuqin, LI Wei, ZHAO Limin. Study on capillary water rise in chalky sandy soils in the yellow floodplain of east Henan province[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 33-38. (in Chinese)
[20] 杜红普, 刘波, 王华军, 等. 基于土水特征曲线预测多孔介质毛细上升过程[J]. 工程地质学报, 2013, 21(3): 345-350. DU Hongpu, LIU Bo, WANG Huajun, et al. Prediction of capillary rise in porous media based on soil water characteristic curve[J]. Journal of Engineering Geology, 2013, 21(3): 345-350. (in Chinese)
[21] 肖红宇, 刘明寿, 彭鹏程, 等. 基于黏性土分形特征的毛细水上升高度研究[J]. 水文地质工程地质, 2016, 43(6): 48-52, 58. XIAO Hongyu, LIU Mingshou, PENG Pengcheng, et al. A study of the height of capillary water rise based on fractal characteristics of cohesive soil[J]. Hydrogeology & Engineering Geology, 2016, 43(6): 48-52, 58. (in Chinese)
[22] LAGO M, ARAUJO M. Capillary rise in porous media[J]. J Colloid Interface Sci, 2001, 234(1): 35-43.
[23] XU Y F. Fractal approach to unsaturated shear strength[J]. Journal of Geotechnical & Geoenvironmental Engineering, ASCE, 2004, 3: 264-274.
[24] 徐永福. 颗粒破碎对粗颗粒填料剪切强度的影响[J]. 固体力学学报, 2018, 39(5): 513-521. XU Yongfu. Effect of particle breakage on shear strength of coarse granular materials[J]. Chinese Journal of Solid Mechanics, 2018, 39(5): 513-521. (in Chinese)
[25] 徐永福. 考虑颗粒破碎影响的粗粒土的剪切强度理论[J]. 岩土工程学报, 2018, 40(7): 1171-1179. XU Yongfu. Theory of shear strength of granular materials based on particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(7): 1171-1179. (in Chinese)
[26] 徐永福. 固体颗粒破碎的分维演化规律[J]. 工程地质学报, 2017, 25(5): 1287-1292. XU Yongfu. Evolution of fractal dimension of particle breakage[J]. Journal of Engineering Geology, 2017, 25(5): 1287-1292. (in Chinese)
[27] OCHIAI M, OZAO R, YAMAZAKI Y. Self-similarity law of particle size distribution and energy law in size reduction of solids[J]. Physica A, 1992, 191: 295-300.
[28] KAPUR P C. Kinetics of granulation by non-random coalescence mechanism[J]. Chemical Engineering Science, 1972, 27(10): 1863-1869.
[29] AUSTIN L G, ROGERS R S C. Powder technology in industrial size reduction[J]. Powder Technology, 1985, 42(1): 91-109.
[30] FRANCES C, LINÉ A. Comminution process modelling based on the monovariate and bivariate direct quadrature method of moments[J]. AIChE Journal, 2014, 60(5): 1621-1640.
[31] MANDELBROT B B. The Fractal Geometry of Nature[M]. San Francisco: W H Freeman, 1982.
[32] 徐永福, 孙婉莹, 吴正根. 我国膨胀土的分形结构的研究[J]. 河海大学学报, 1997, 25(1): 18-25. XU Yongfu, SUN Wanying, WU Zhenggen. A study of the fractal structure of our expansive soils[J]. Journal of Hohai University, 1997, 25(1): 18-25. (in Chinese)
[33] 刘松玉, 方磊, 陈浩东. 论我国特殊土粒度分布的分形结构[J]. 岩土工程学报, 1993, 15(1): 23-30. LIU Songyu, FANG Lei, CHEN Haodong. On the fractal structure of particle size distribution of special soils in China[J]. Journal of Hohai University, 1993, 15(1): 23-30. (in Chinese)
[34] WATABE Y, LEROUEIL S, Le BIHAN J-P. Influence of compaction conditions on pore-size distribution and saturated hydraulic conductivity of a glacial till[J]. Can Geotech J, 2000, 37: 1184-1194.
[35] TERZAGHI K. Theoretical Soil Mechanics[M]. New York: Wiley, 1843.
[36] XU Y F, DONG P. Fractal approach to hydraulic properties in unsaturated porous media[J]. Chaos, Solitons & Fractals, 2004, 19(2): 327-337.
[37] XU Y F. Calculation of unsaturated hydraulic conductivity using a fractal model for the pore-size distribution[J]. Computers and Geotechnics, 2004, 31(7): 549-557.



 下载:
下载: