基于颗粒重组理论的水合物沉积物温-压耦合热力学模型

周瑞; 白冰; 杨光昌

doi:10.11779/CJGE20230246

基于颗粒重组理论的水合物沉积物温-压耦合热力学模型 English Version

周瑞^1,,
白冰^1, ,,
杨光昌²

1.
北京交通大学城市地下工程教育部重点实验室, 北京 100044
2.
北京科技大学土木与资源工程学院, 北京 100083

基金项目:

国家自然科学基金项目 52079003

北京市自然科学基金项目 8182046

详细信息

作者简介:
周瑞(1993—)，男，博士研究生，主要从事环境岩土工程等方面的研究工作。E-mail: 18121179@bjtu.edu.cn

通讯作者:
白冰, E-mail: bbai@bjtu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 223
- HTML全文浏览量: 72
- PDF下载量: 49
出版历程
- 收稿日期: 2023-03-21
- 网络出版日期: 2024-06-04
- 刊出日期: 2024-05-31

Thermodynamic model of coupled temperature and pressure effects for hydrate-bearing sediments within particle rearrangement theory

1.
Key Laboratory of Urban Underground Engineering of Ministry of Education, Beijing Jiaotong University, Beijing 100044, China
2.
School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China

摘要

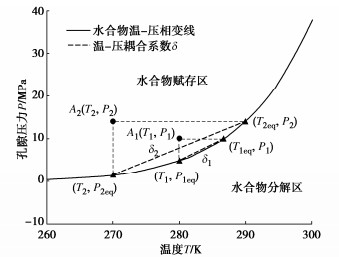
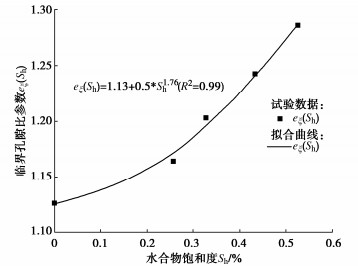
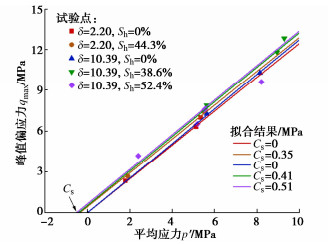
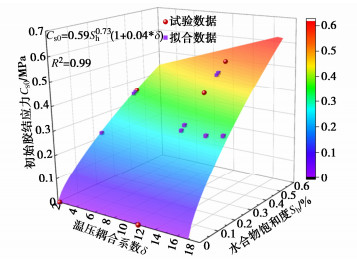
摘要: 水合物沉积物赋存时的温度和孔隙水压变化对沉积物的力学性质影响明显。基于颗粒重组理论，通过引入温-压耦合系数δ、剪应变和体应变胶结应力衰减方式( ${\lambda _{\text{v}}}$ ， ${\lambda _{\text{s}}}$ )和水合物饱和度影响下的剪胀方程d，建立了水合物沉积物温-压耦合热力学模型。利用数值模拟结果同室内试验结果的对比分析, 从宏观力学性质变化和微观作用机理两个角度探讨了围压、水合物饱和度和温-压耦合系数对沉积物力学特性的影响。最后，对模型中的刚度系数和体应变衰减参数进行敏感性分析。结果表明：引入温-压耦合系数的水合物沉积物模型能够很好的描述沉积物赋存的温度和水压同其力学特性变化关系。环境温度降低和水压增大增强了微观层面水合物的胶结强度和刚度，宏观表现为峰值强度、应变软化和剪胀性提高。刚度系数 $\gamma$ 通过增大沉积物初始刚度使得沉积物表现出更强的峰值强度。体应变衰减参数 ${\lambda _{\text{v}}}$ 通过提高胶结应力衰减速率增强沉积物的应变软化特性。
- 温-压耦合系数 /
- 颗粒重组理论 /
- 热力学模型 /
- 水合物沉积物 /
- 剪胀方程
Abstract: The mechanical properties of hydrate-bearing sediments are significantly influenced by changes in temperature and water pressure. Based on the particle rearrangement theory, a thermodynamic model that couples temperature and pressure, incorporating the dilation equation considering the effects of hydrate saturation and introducing the bond degradation parameters caused by shear and volumetric strains, is developed to describe the mechanical behaviors of hydrate-bearing sediments. The numerical simulation results are compared with the laboratory experiments to explore the effects of confining pressure, hydrate saturation and the temperature-pressure coupling coefficient on the mechanical properties of sediments from both macroscopic and microscopic perspectives. Finally, the sensitivity analyses are conducted on the stiffness coefficient and bond degradation parameter. The results indicate that the introduction of a temperature-pressure coupling coefficient in the model effectively describes the relationship between the mechanical properties of sediments and temperature and water pressure during deposition. Decreasing environmental temperature and increasing water pressure enhance the bond strength and stiffness of hydrates at the microscopic level, resulting in the increased peak strength, strain softening and shear dilation at the macroscopic level. Increasing the stiffness coefficient γ enhances the peak strength of sediments by increasing the initial stiffness of sediments. The bond degradation parameter enhances the strain-softening behaviors of sediments by increasing the rate of bond degradation.
- temperature-pressure coupling coefficient /
- particle rearrangement theory /
- thermodynamic model /
- hydrate-bearing sediment /
- dilation equation

HTML全文

0. 引言

地表局部地形对地震波的传播有显著影响，当地震波遇到高山、峡谷等，会产生散射波、入射波和反射波等复杂波场，并引起地面运动的放大或衰减，称为地形效应。目前针对地形效应已有了相应的研究（表 1），主要包含了数值模拟和解析分析两种。解析主要运用的是波函数展开法，Wong等^[1]提出了半圆形峡谷对地震SH波散射的波函数级数解，随后众多学者提出了多种圆弧形峡谷的解析解^[2-6]，Gao等^[7]提出了通过坐标变换求解V形对称峡谷引起的圆柱形SH波二维散射和衍射波函数的级数解。数值方法包含了有限差分法^[8]，谱元法等^[9]等，数值方法可实现复杂地形地震波传播模拟，具备边界和复杂几何处理的灵活性，但在计算精度方面往往需要解析解的校准。

表 1 复杂地形效应近场波动模拟研究现状

Table 1. Researches on near-field fluctuation problems

模拟方法	应用场景	时间	文献
解析法	平面SH波在半圆柱型峡谷的散射	1972年	[1]
	平面SH波在半圆柱型冲击峡谷的散射	1971年	[2]
	平面SH波在半椭圆形冲击峡谷的散射	1974年	[3]
	平面SH波在圆弧形峡谷的散射	2009年	[4]
	平面SH波在截断峡谷的散射	2009年	[5]
	U型峡谷引起的地形放大对地震波的影响	2012年	[6]
	柱面SH波在对称V型峡谷的反射和散射	2013年	[7]
有限差分法	极坐标尺度不规则地形FEM方法	2021年	[8]
谱元法	入射平面SV波作用下梯田形山丘的表面运动	2017年	[9]
PINN	近场波动数值模拟	2022年	[30]

下载: 导出CSV

| 显示表格

近场波动在数学上可归结为偏微分方程的初值、边值问题，偏微分方程的数值离散化在模拟多物理场问题方面取得了很大的进展，但通过使用经典的分析或计算工具来建模和预测非线性多尺度系统的演化较困难，面对复杂网络剖分、参数化偏微分方程控制的高维问题等。

近年来的研究发现，物理信息神经网络（PINN）可以用于对控制物理系统的偏微分方程进行建模，通过嵌入物理信息解决了传统神经网络算法对于求解方面的局限性，例如高度依赖数据驱动，缺乏物理可解释性、易陷入过拟合以及可获取数据的稀疏性等。PINN方法仅依赖于少量甚至零标记的数据集，并实现数据稀缺、物理约束的学习。嵌入物理公式为可训练参数提供约束，缓解过拟合问题，减少对大型训练数据集的需求，从而提高训练模型的鲁棒性，以实现可靠的预测。Raissi等^[10]利用深度学习神经网络（DNN）的强表达性，开发了通用PINN框架，解决了涉及小数据集甚至没有任何标记数据的非线性偏微分方程系统的正逆问题。最近几年PINN方法在地球物理学^[11-13]、固体力学^[14-16]、流体动力学^[17-20]、热传导^[21-22]等方面有了相应的研究。众多学者针对不同的偏微分方程，让PINN方法更好地适应不同的物理问题^[23-29]。也有了少数利用物理信息神经网络求解波动方程的工作，Rao等^[19]通过DNN复合方案以硬嵌入的方式强制满足初值、边值条件，在截断域的波传播问题上进行了模拟。陈苏等^[30]结合了数值模拟原理和物理驱动深度学习建立了波动模拟方法，提出了可以提高网络训练效率的迁移学习方法。

在前人研究的基础上，提出通过物理信息神经网络模拟圆柱形SH波在不规则地形下的散射和衍射方法。通过新的参数加载代理建模策略，在给定初始时刻稀疏地震位移波场，模拟地震波在半无限域的传播，通过对比解析解和PINN预测解来评估所提出的规则地形下PINN模型的性能。通过PINN模型模拟不规则地形下圆柱形SH波的二维散射和衍射，证明该方法具有良好的泛化性。

1. 物理驱动深度学习原理

深度学习神经网络（DNN）具备出色的计算表达能力，在图像识别和自然语言处理等领域获得了较多应用。前馈全连接神经网络可以假设为输入层、多个隐藏层和输出层的堆栈。相邻两层之间的连接，例如从第i−1层到第i层，可用张量的形式简单表示为

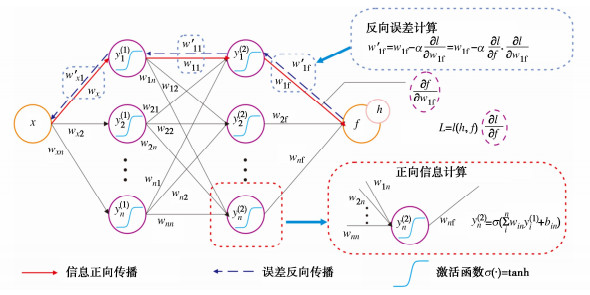
$\boldsymbol{Y}_i=\alpha\left(\boldsymbol{W}_i \boldsymbol{Y}_{i-1}+\boldsymbol{b}_i\right) \quad(1 \leqslant i \leqslant n+1) 。$

(1)

式中：n为隐层总数；σ(·)为按元素作用的激活函数； ${\boldsymbol{Y}_0}$ 和 ${\boldsymbol{Y}_{n + 1}}$ 分别为输入张量和输出张量； ${\boldsymbol{W}_i}$ ， ${\boldsymbol{b}_i}$ 为第i层的可训练权重矩阵和偏置向量。DNN作为弹性动力学问题的参数化近似解，其中时空位置X = (x, t)为自变量。通过最优逼近物理系统理论解，获取训练参数，需设计嵌入物理定律的损失函数作为训练目标，网络训练中需评估物理场对时空变量的偏导数，Tensorflow和Pytorch框架中可完成自动微分功能。以前馈神经网络为例，网络以变量x为输入，在式（1）中定义的非线性变换后输出f，表示第i个隐藏层中第j个神经元的输出。由于输出f可以表示为x的嵌套函数，应用链式法则，可以计算每一层之间的梯度关系，通过构建损失函数和误差的反向传播，每训练一步后更新权重和偏置，如图 1所示，权重和偏置的更新计算为

图 1 DNN网络自动微分简图

Figure 1. Automatic differential diagram of DNN network

下载: 全尺寸图片幻灯片

$\omega_{1 \mathrm{f}}^{\prime}=\omega_{1 \mathrm{f}}-\alpha \frac{\partial l}{\partial \omega_{1 \mathrm{f}}} ,$

(2)

$\frac{\partial l}{\partial \omega_{\mathrm{1f}}}=\frac{\partial l}{\partial f} \cdot \frac{\partial f}{\partial \omega_{\mathrm{1f}}},$

(3)

$f=\sigma\left(\sum_i^n \omega_{i \mathrm{f}} y_i^{(2)}+b_i\right),$

(4)

$\frac{\partial f}{\partial \omega_{1 \mathrm{f}}}=\sigma y_1^{(2)}。$

(5)

式中： $\alpha$ 为DNN网络的学习率；l为期望值h与网络输出值f构建的损失函数。

损失函数L可以求得 $\tfrac{{\partial l}}{{\partial f}}$ 的值，式（4）中节点 $y_1^{(2)}$ 与输出f之间关系可以求得 $\tfrac{{\partial f}}{{\partial {\omega _\text{1f}}}}$ ，再通过式（2），（3）求得更新后的权重 ${\omega '_\text{1f}}$ 。偏置 ${b'_\text{1f}}$ 的计算同理，网络参数更新过后采用梯度下降最快的策略，使得损失函数L减小到0，最终输出值f与期望值h以及两者的导数实现强形式的相等，如图 1所示。

从函数逼近论角度，具有单一隐藏层的神经网络可精确逼近任何线性或非线性连续函数，因此可以将神经网络作为非线性函数逼近器。Rassi等^[10]通过训练全连接神经网络来逼近偏微分方程的解，用神经网络逼近方程的各阶偏导数，实现将PDE残差以及初、边值条件作为正则项加入损失函数中。

以一维杆件中波的传播为例，介绍物理驱动深度学习方法求解偏微分方程的可行性。杆件长10 m，在杆左端施加Ricker子波，波速为1 m/s。一维标量波动方程形式为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\frac{{{\partial ^2}u}}{{{\partial ^2}x}} = 0{\text{ }}\left( {x \in [0, 10], t \in [0, 20]} \right),$

(6)

Ricker子波公式 $:$

$u_{\mathrm{r}}=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(7)

Ricker子波从x=0处输入，所以在x=0处的边界条件可以表示为

$u(0, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(8)

式中：c为波速， ${t_\text{s}}$ 为Ricker波的半周期，根据波动传播理论，得到

$u=f\left(t+\frac{x}{c}\right)=\left[\frac{2 \pi^2\left(t-t_\text{s}\right)^2}{t_\text{s}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_\text{s}\right)^2}{t_\text{s}^2}}。$

(9)

化简后易得上述波动方程解析解：

$u(x, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}}。$

(10)

此案例满足如下形式的偏微分方程：

$\left. \begin{array}{l}\begin{gathered} \boldsymbol{D}(u(x, t) ; \lambda)=f(x, t) \quad(x \in \varOmega, t \in[0, T]), \\ u(x, t)=\boldsymbol{B}_D(t) \quad\left(x \in \partial \varOmega_D, t \in[0, T]\right), \\ \nabla u(x, t)=\boldsymbol{B}_N(t) \quad\left(x \in \partial \varOmega_N, t \in[0, T]\right), \\ u(0, t)=\boldsymbol{B}_0(t) \quad(t \in[0, T]), \\ u(x, 0)=\boldsymbol{J}_0(x) \quad(x \in \varOmega) 。 \end{gathered}\end{array} \right\}$

(11)

式中： $u(x, t)$ 为偏微分方法的解； $\boldsymbol{D}( \cdot )$ 为带参数 $\lambda$ 的微分算子；x为域 $\varOmega \in {R^d}$ 中的空间变量， $d = 1, 2, \ldots n$ ；域边界 $\partial \varOmega$ 由Dirichlet边界 $\partial {\varOmega _D}$ 和Neumann边界 $\partial {\varOmega _N}$ 组成； $t \in [0, T]$ 为时间变量； ${\boldsymbol{B}_D}(t), {\boldsymbol{B}_N}(t)$ 分别为偏微分方程的初边值问题中的Dirichlet、Neumann边界条件函数； ${\boldsymbol{B}_0}(t)$ 为在x=0处的边界条件函数； ${\boldsymbol{J}_0}(x)$ 为初始条件函数。

对于这些初、边值函数，通过设计损失函数 $\sum (\theta )$ 架构并训练神经网络：

$\sum (\theta ) = {\sum _{\text{p}}}(\theta ) + {\sum _{{\text{bc}}}}(\theta ) + {\sum _{{\text{ic}}}}(\theta ) ,$

(12)

$\left. \begin{array}{l}\begin{aligned} \sum\nolimits_{\mathrm{bc}}(\theta)= & \frac{1}{N_{\mathrm{d}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_D(t)\right\|_{\partial \varOmega_D \times[0, T]}^2+ \\ & \frac{1}{N_{\mathrm{n}}} \sum\nolimits_i^{N_{\mathrm{n}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_N(t)\right\|_{\partial \varOmega_N \times[0, T]}^2, \\ \sum\nolimits_{\mathrm{ic}}(\theta)= & \frac{1}{N_{\mathrm{ic}}} \sum\nolimits_i^{N_{\mathrm{ic}}}\left(\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_0(t)\right\|_{\varOmega \times\{t=0\}}^2+\right. \\ & \left.\left\|\nabla \boldsymbol{N} \boldsymbol{N}_t\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_1(t)\right\|_{\varOmega \times\{t=0\}}^2\right), \\ \sum\nolimits_{\mathrm{p}}(\theta)= & \frac{1}{N_{\mathrm{p}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left(\left\|\boldsymbol{D}\left(\boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right) ; \lambda\right)-f\left(x_i\right)\right\|_{\varOmega \times[0, T]}^2\right.。 \end{aligned}\end{array} \right\}$

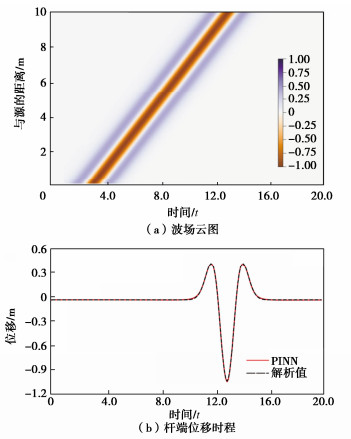
(13)

使用Sobol序列算法分别生成PDE残差损失项、初始条件损失项的时空采样点。采用8个隐藏层、每层20个神经元的全连接神经网络，使用Adam优化器训练40000步，波场云图及PINN的预测解与解析解对比如图 2所示，PINN预测值与解析解之间的绝对误差最大值为0.007 m，表明经过训练的神经网络已具备较强逼近波动方程真解的能力。

图 2 波场云图及PINN预测与解析对比图

Figure 2. Comparison of wavefield clouds and PINN prediction and resolution

下载: 全尺寸图片幻灯片

2. 物理驱动人工智能波动模拟方法

2.1 方法介绍

以SH波在平面内和地表及峡谷处的散射反射为例，二维波动方程为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\left( {\frac{{{\partial ^2}u}}{{{\partial ^2}x}} + \frac{{{\partial ^2}u}}{{{\partial ^2}z}}} \right) = f。$

(14)

式中： $u(x, z, t)$ 为出平面波动位移；c为介质物理波速； $f(x, z, t)$ 为外荷载，令 $f \equiv 0$ ，并通过给定初始波场等效施加外力。

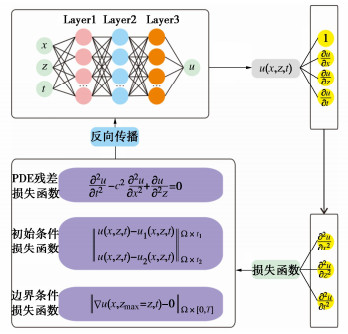
根据陈苏等^[30]提出的二维波动方程PINN求解框架，指定时空坐标 $X = (x, z, t)$ 的3个分量为网络的输入值，位移场 $Y = u(x, z, t)$ 为网络的输出值，通过Pytorch的自动微分功能，得到位移对于各分量的微分值，即 $\tfrac{{{\partial ^2}u}}{{{\partial ^2}t}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}x}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}z}}$ ，并构建损失函数。

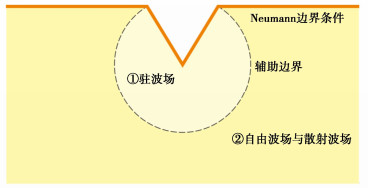
Gao等^[7]提出了对称V形峡谷引起的柱面SH波二维散射和衍射的波函数级数解。峡谷模型如所示，采用半径为a（峡谷壁长度）的圆弧作为辅助边界，将整个空间分成两个子区域。子区域①中为驻波波场，子区域②中包含没有牵引边界的自由波场和因为峡谷存在而产生的散射波场。要求波源的位置位于子区域②中，通过波函数展开法和坐标变换得到了此模型下二维圆柱SH波的反射结果，即半平面内的位移场 ${Y_\text{reli}} = {u_\text{reli}}(x, z, t)$ 。本文采用解析计算得到的 ${t_1}, {t_2}$ 时刻的两个早期位移场作为初始条件，通过两帧波场快照 ${\boldsymbol{u}_1}, {\boldsymbol{u}_2}$ 约束震源的位置、形状和SH波的传播方向。垂直地表的应力为零的边界条件可通过损失函数中的Neumann边界条件 $\nabla u(x, z = {z_\text{top}}, t) = 0$ 表示。

图 3 对称V型峡谷模型示意图

Figure 3. Schematic diagram of a symmetrical V-shaped canyon model

下载: 全尺寸图片幻灯片

$\boldsymbol{L}(\theta)=\lambda_1 \boldsymbol{L}_{\mathrm{p}}(\theta)+\lambda_2 \boldsymbol{L}_{\mathrm{bc}}(\theta)+\lambda_3 \boldsymbol{L}_{\mathrm{ic}}(\theta) ,$

(15)

$\left. \begin{array}{l}\boldsymbol{L}_{\text{p}}(\theta )=\frac{1}{{N}_{\text{p}}}{\displaystyle {\sum }_{i}^{{N}_{\text{p}}}}\Vert \frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {t}_{i}^{2}}-{c}_{i}^{2}(\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {x}_{i}^{2}}+\\ {\text{ }\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {z}_{i}^{2}})\Vert }_{\varOmega \times [0, T]}^{2}, \\ \boldsymbol{L}_{\text{ic}}(\theta )=\frac{1}{{N}_{\text{ic1}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic}1}}}\Vert {\Vert \stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel1}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{1}\}}^{2}+\\ {\text{ }\frac{1}{{N}_{\text{ic2}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic2}}}}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel2}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{2}\}}^{2}, \\ \boldsymbol{L}_{\text{bc}}(\theta )=\frac{1}{{N}_{\text{bc}}}{\displaystyle {\sum }_{i}^{{N}_{\text{bc}}}{\Vert \nabla \stackrel{⌢}{u}({x}_{i}, {z}_{i}={z}_\text{top}, {t}_{i})\Vert }_{\varOmega \times [0, T]}^{2}。}\end{array} \right\}$

(16)

式中： $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}$ 为PINN逼近的偏微分方程的解， $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} (x, z, t) =$ $\boldsymbol{NN}(x, z, t;\theta )$ 。

根据式（15），（16），在半无限区域的二维波动问题中，损失函数由PDE残差损失项、初始条件损失项和边界条件损失项组成，其中 ${\lambda _1}$ ， ${\lambda _2}$ ， ${\lambda _3}$ 为损失分配系数。求解二维波动方程的物理信息神经网络架构如图 4所示。选择Tanh激活函数作为神经网络的非线性激活函数，以确保网络非零二阶导数存在，并实现高效收敛。采用Adam和L-BFGS共同作用的优化策略。其中Adam优化算法可实现全域快速收敛，接L-BFGS优化获得高精度解。使用Xavier初始化对神经网络中的可训练参数进行初始化。

图 4 物理驱动神经网络架构图

Figure 4. Diagram of PINN architecture

下载: 全尺寸图片幻灯片

2.2 方法验证

半无限均匀介质内的SH波动模型如图所示，模型区域为宽1500 m，深1500 m，峡谷深度d=50 m，峡谷宽度b=150 m。介质物理波速c=3000 m/s，输入波位移时程采用主频为10 Hz的Ricker源时间函数，源位置处于模型中心x = 750 m， z = -750 m。

使用解析计算得到的 ${t_1} = 0.05{\text{ s}}$ ， ${t_2} = 0.1{\text{ s}}$ 的位移场作为初始条件参与训练，其余时刻的结果与PINN的计算结果进行对比验证。解析计算中时间步长为0.01 s，计算总时长为1 s。训练前根据模型的几何数据，定义顶部边界为宽150 m，深50 m的对称V型峡谷，在此边界上添加应力为0的Neumann边界条件。采用Sobol序列算法在整个域中生成用于计算PDE残差损失项的采样点和初始条件采样点。在V型峡谷处的采样点布设做局部加密，在顶部两侧水平边界布设200个采样点，在V型边界布设1000个采样点，删除峡谷上部PDE残差损失项采样点，调整后采样点数 ${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$ 。设置4个隐藏层，每层30个神经元的全连接神经网络。

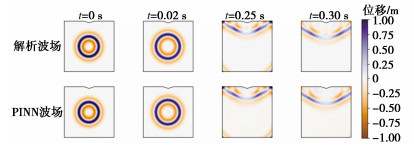
根据时间域分解策略，首先对模型采取预训练（热启动），波场时刻从 ${t_1} = 0.05{\text{ s}}$ 开始算起，预测总时间 $T = 0.1{\text{ s}}$ ，根据经验设置损失分配系数 ${\lambda _1} = {10^{ - 5}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ 。调用学习率为6×10^-3的Adam优化器训练20000步，再使用L-BFGS优化器训练200000步。损失分配系数的神经网络会根据初始条件项损失项、边界条件损失项、PDE残差损失项的顺序进行训练，预训练时的SH波还未传播到顶部边界，能够观测到PINN方法很好地预测了柱面SH波的传播过程。保存预训练后的网络结构进行二次训练，调整损失分配系数 ${\lambda _1} = {10^{ - 3}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ ，预测总时间 $T =$ $0.3{\text{ s}}$ 。调用L-BFGS优化器训练100000步，进一步优化PDE残差损失项，训练完成后保存网络结构进行最终训练，损失分配系数不变，设置预测总时间T=0.6 s，调用L-BFGS优化器训练200000步。训练完成后，可对任意分辨率下任意时空点的波动方程解及解的各阶偏导进行预测，图 5给出了4个时刻的PINN模拟波场和解析波场的对比。

图 5 半无限空间波动问题: PINN与解析波场快照对比

Figure 5. Semi-infinite space fluctuation problem: PINN vs. analytical wave snapshot

下载: 全尺寸图片幻灯片

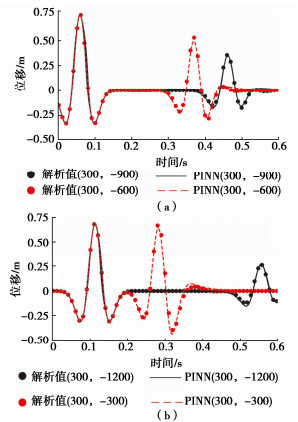
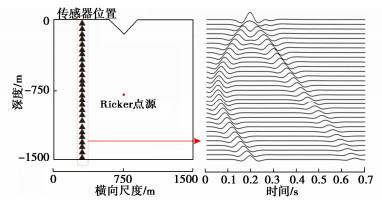
由于此模型的波源位于中心位置，所以可在 $x = 300$ 外布设传感器，观测入射波、反射波和散射波经过的过程，验证PINN在预测柱面SH波在半无限空间内传播和反射特性，给出x坐标同为300 m，z坐标关于 $z = - 750$ 对称点位的时程数据，其中z坐标600 m与z坐标900 m是相对于 $z = - 750$ 的对称坐标，由于t=0 s时刻区域内已存在点源散发出的波场，在0~0.6 s时刻内，在坐标 $z = - 600$ 处和 $z = - 900$ 处有入射波和反射波经过，可以看出PINN方法在此模型下的入射波传播和边界反射的预测值与解析真值基本一致。同时z坐标-300 m与z坐标-1200 m是相对于 $z = - 750$ 的对称坐标，在0~0.6 s时刻内，坐标 $z = - 300$ 处和 $z = - 1200$ 处除入射波和反射波外，还有因峡谷而产生的散射波，可以看出PINN方法在预测柱面SH波在峡谷出的散射值与解析真值基本一致。在 $x = 300$ 布设的位移传感器和预测位移时程结果图 7所示。

图 6 对称位置PINN与解析波场时程对比

Figure 6. Comparison of time histories of symmetrical position PINN and analytical wave field

下载: 全尺寸图片幻灯片

图 7 PINN模拟时程图（x=300）

Figure 7. Time histories of PINN analog (x=300)

下载: 全尺寸图片幻灯片

3. 不同工况深切峡谷波动模拟

为保证PINN方法在处理对称V型峡谷波动模拟问题的有效性，考虑不同波速、不同主频的Ricker波在V型半无限空间内的波动问题。模型区域为宽1500 m，高1500 m，峡谷深度d=50 m，峡谷宽度b=150 m，输入波位移时程采用Ricker源时间函数，源位置处于模型中心x = 750 m，z = -750 m。

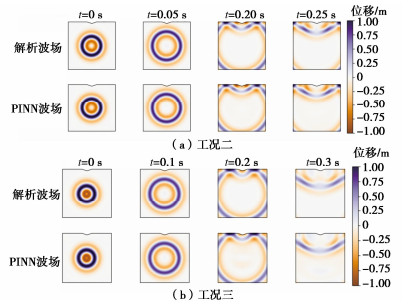
本文所有工况的模型参数和训练参数如表 2所示，工况二和工况三的预测结果与解析值的对比云图如图 8所示，由此可见PINN方法在对称V型峡谷的地形下，能够较好地预测不同频率不同波速下柱面SH波的反射和散射。

表 2 不同工况PINN模型参数

Table 2. Parameters of PINN model under different working conditions

参数	工况一（图 5）		工况二（图 8(a)）	工况三（图 8(b)）
主频 $\omega {\text{/Hz}}$		10	8	5
波速 $c{\text{/}}$ ${\text{(m}} \cdot {{\text{s}}^{ - 1}}{\text{)}}$		3000	3000	2000
第一帧快照时间 ${t_0}{\text{/s}}$		0.20	0.15	0.30
第二帧快照时间 ${t_1}{\text{/s}}$		0.22	0.20	0.40
传播时间 $T{\text{/s}}$		0.60	0.65	1.00
采样点	${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$
预训练损失分配系数	${\lambda _1} = {10^{ - 5}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
后续损失分配系数	${\lambda _1} = {10^{ - 3}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
优化策略	Adam20000步+ LBFGS500000步		Adam20000步+ LBFGS300000步	Adam20000步+ LBFGS300000步

下载: 导出CSV

| 显示表格

图 8 PINN预测与解析真值云图对比

Figure 8. Comparison of PINN prediction and ground truth under condition 3

下载: 全尺寸图片幻灯片

对比不同工况下的预测精度，定义在某一点PINN与解析波场之间的相对 ${L_2}$ 范数误差为

$\varepsilon (\boldsymbol{u}) = \frac{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i}) - {u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {{u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}。$

(17)

式中： ${x_0}$ ， ${z_0}$ 为采样点的坐标位置； $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i})$ 为PINN方法预测得到的该采样点的位移时程； ${u_{ref}}({x_0}, {z_0}, {t_i})$ 为相同位置的解析位移时程；N为计算点数。

给出3种工况预测模型在 $x = 300$ 不同位置的相对范数误差。在x相同时，相对 ${L_2}$ 范数误差与纵坐标z有关，越靠近地表，由于散射波和衍射波的叠加，相对 ${L_2}$ 范数误差会增大，但都保持在0.03以内。表明PINN方法处理对称V型峡谷反射波和散射波的有效性，可实现复杂地形模拟分析。分别给出不同频率下PINN预测的峡谷地表及附近各位置峰值位移分布。由可知：不同SH波（5，8，10 Hz）条件下，V型峡谷地形效应总体上呈现出“M”型分布，中心V型峡谷底端及邻区SH波发生衰减与振荡，在谷肩及地表SH波放大，峡谷边缘出现了显著放大。3种工况下地表处最大峰值位移的相对 ${L_2}$ 误差范数分别为0.0009，0.0006，0.001，由此可见PINN方法在预测低频SH波峡谷处地形效应时更为准确。

图 9 不同工况相对

${L_2}$ 范数误差（x=300）

Figure 9. Relative norm errors under different working conditions (x=300)

下载: 全尺寸图片幻灯片

图 10 地表峰值位移对比

Figure 10. Comparison of peak displacements on surface

下载: 全尺寸图片幻灯片

4. 结论

通过物理信息驱动神经网络（PINN）的自动微分功能求解了二维波动方程，并计算了柱面SH波在对称V型峡谷下的反射和散射。通过与解析值的对比，验证了PINN方法在求解波动问题上的精度。得到3点结论。

（1）物理驱动深度学习（PINN）方法可通过稀疏初始波场数据，模拟柱面SH波在对称V型峡谷下的反射和散射，具备“无网格、强耦合”等特性，可适应不同地形与波源。

（2）对比不同工况的训练结果，发现越靠近地表位置，波场叠加越复杂，相对 ${L_2}$ 误差范数也会越大。且同一模型下，相对 ${L_2}$ 范数误差与柱面SH波的主频关系不大。

（3）对比不同工况下解析与PINN预测的地表峰值位移大小关系，柱面SH波在V型峡谷底端发生衰减现象，在其他位置发生放大现象。其中在V型峡谷边缘处放大现象最明显，且PINN方法在预测低频SH波在峡谷处地形效应时更为准确。

图 1 水合物沉积物温-压耦合系数

Figure 1. Temperature-pressure coupling coefficient of hydrate- bearing sediments

下载: 全尺寸图片幻灯片

图 2 水合物饱和度与临界孔隙比参数关系

Figure 2. Relationship between hydrate saturation and critical void ratio parameters

下载: 全尺寸图片幻灯片

图 3 沉积物峰值强度与水合物饱和度和温-压耦合系数关系

Figure 3. Relationship among peak shear strength, hydrate saturation and temperature-pressure coupling coefficient

下载: 全尺寸图片幻灯片

图 4 初始胶结强度与水合物饱和度和温-压耦合系数关系

Figure 4. Relationship among initial cementation strength, hydrate saturation and temperature-pressure coupling coefficient

下载: 全尺寸图片幻灯片

图 5 水合物饱和度与临界应力比关系

Figure 5. Relationship between hydrate saturation and critical stress ratio

下载: 全尺寸图片幻灯片

图 6 不同围压下模拟值与试验值对比

Figure 6. Comparative results by proposed model and tests under different confining pressures

下载: 全尺寸图片幻灯片

图 7 不同水合物饱和度下模拟值与试验值对比

Figure 7. Comparative results by proposed model and tests under different hydrate saturations

下载: 全尺寸图片幻灯片

图 8 不同温-压耦合系数(温度引起)下模拟值与试验值对比

Figure 8. Comparative results by proposed model and tests under different temperature-pressure coupling coefficients caused by the temperatures

下载: 全尺寸图片幻灯片

图 9 不同温-压耦合系数(孔隙压力引起)下模拟值与试验值对比

Figure 9. Comparative results by proposed model and tests under different temperature-pressure coupling coefficients caused by the water pressures

下载: 全尺寸图片幻灯片

图 10 刚度系数γ对沉积物力学性质影响

Figure 10. Effects of stiffness coefficient on mechanical properties of sediments

下载: 全尺寸图片幻灯片

图 11 体应变衰减系数λ_v对沉积物力学性质影响

Figure 11. Effects of degradation coefficient of volumetric strain on mechanical properties of sediments

下载: 全尺寸图片幻灯片

参考文献(32)

[1]	INADA N, YAMAMOTO K. Data report: hybrid pressure coring system tool review and summary of recovery result from gas-hydrate related coring in the Nankai Project[J]. Marine and Petroleum Geology, 2015, 66: 323-345. doi: 10.1016/j.marpetgeo.2015.02.023
[2]	MAKOGON Y F. Natural gas hydrates—a promising source of energy[J]. Journal of Natural Gas Science and Engineering, 2010, 2(1): 49-59. doi: 10.1016/j.jngse.2009.12.004
[3]	颜荣涛, 韦昌富, 魏厚振, 等. 水合物形成对含水合物砂土强度影响[J]. 岩土工程学报, 2012, 34(7): 1234-1240. http://cge.nhri.cn/cn/article/id/14631 YAN Rongtao, WEI Changfu, WEI Houzhen, et al. Effect of hydrate formation on mechanical strength of hydrate-bearing sand[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1234-1240. (in Chinese) http://cge.nhri.cn/cn/article/id/14631
[4]	刘昌岭, 李彦龙, 孙建业, 等. 天然气水合物试采: 从实验模拟到场地实施[J]. 海洋地质与第四纪地质, 2017, 37(5): 12-26. https://www.cnki.com.cn/Article/CJFDTOTAL-HYDZ201805001.htm LIU Changling, LI Yanlong, SUN Jianye, et al. Gas hydrate production test: from experimental simulation to field practice[J]. Marine Geology & Quaternary Geology, 2017, 37(5): 12-26. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HYDZ201805001.htm
[5]	王维希, 张春生, 吴颜雄, 等. 联合深海地热开采天然气水合物技术展望[J]. 现代化工, 2021, 41(9): 17-21. https://www.cnki.com.cn/Article/CJFDTOTAL-XDHG202109004.htm WANG Weixi, ZHANG Chunsheng, WU Yanxiong, et al. Prospects on technology for combining deep-sea geothermal energy with exploitation of natural gas hydrate[J]. Modern Chemical Industry, 2021, 41(9): 17-21. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDHG202109004.htm
[6]	WU P, LI Y H, LIU W G, SUN X, KONG X J, SONG Y C. Cementation failure behavior of consolidated gas hydrate-bearing sand[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(1): e2019JB018623. doi: 10.1029/2019JB018623
[7]	LUO T T, LI Y H, MADHUSUDHAN B N, et al. Deformation behaviors of hydrate-bearing silty sediment induced by depressurization and thermal recovery[J]. Applied Energy, 2020, 276: 115468. doi: 10.1016/j.apenergy.2020.115468
[8]	MASUI A, MIYAZAKI K, HANEDA H, OGATA Y, AOKI K. Mechanical properties of natural gas hydrate bearing sediments retrieved from eastern Nankai trough[C]//Offshore Technology Conference. Houston, 2008.
[9]	LI Y H, SONG Y C, LIU W G, et al. Analysis of mechanical properties and strength criteria of methane hydrate-bearing sediments[J]. International Journal of Offshore and Polar Engineering, 2012, 22: 290-296.
[10]	SHEN S, SUN X, WANG L, et al. Effect of temperature on the mechanical properties of hydrate-bearing sand under different confining pressures[J]. Energy & Fuels, 2021, 35: 4106-4117.
[11]	HYODO M, NAKATA Y, YOSHIMOTO N, et al. Basic research on the mechanical behavior of methane hydrate-sediments mixture[J]. Soils and Foundations, 2005, 45(1): 75-85.
[12]	WINTERS W J, WAITE W F, MASON D H, et al. Methane gas hydrate effect on sediment acoustic and strength properties[J]. Journal of Petroleum Science and Engineering, 2007, 56(1/2/3): 127-135.
[13]	CHAOUACHI M, FALENTY A, SELL K, et al. Microstructural evolution of gas hydrates in sedimentary matrices observed with synchrotron X-ray computed tomographic microscopy[J]. Geochemistry, Geophysics, Geosystems, 2015, 16(6): 1711-1722. doi: 10.1002/2015GC005811
[14]	TOKUNAGA T. Physicochemical controls on adsorbed water film thickness in unsaturated geological media[J]. Water Resources Research, 2011, 47(8): W08514.
[15]	蒋明镜, 朱方园. 不同温压环境下深海能源土力学特性离散元分析[J]. 岩土工程学报, 2014, 36(10): 1761-1769. doi: 10.11779/CJGE201410001 JIANG Mingjing, ZHU Fangyuan. DEM investigation on mechanical properties of methane hydrate bearing soils under different temperatures and pore-water pressures[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(10): 1761-1769. (in Chinese) doi: 10.11779/CJGE201410001
[16]	颜荣涛, 张炳晖, 杨德欢, 等. 不同温-压条件下含水合物沉积物的损伤本构关系[J]. 岩土力学, 2018, 39(12): 4421-4428. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812016.htm YAN Rongtao, ZHANG Binghui, YANG Dehuan, et al. Damage constitutive model for hydrate-bearing sediment under different temperature and pore pressure conditions[J]. Rock and Soil Mechanics, 2018, 39(12): 4421-4428. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812016.htm
[17]	刘乐乐, 张旭辉, 刘昌岭, 等. 含水合物沉积物三轴剪切试验与损伤统计分析[J]. 力学学报, 2016, 48(3): 720-729. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201603021.htm LIU Lele, ZHANG Xuhui, LIU Changling, et al. Triaxial shear tests and statistical analyses of damage for methane hydrate-bearing sediments[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 720-729. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201603021.htm
[18]	YAMAGUCHI T, AOKI K, TENMA N, et al. A nonlinear elastic model for triaxial compressive properties of artificial methane-hydrate-bearing sediment samples[J]. Energies, 2012, 5(10): 4057-4075. doi: 10.3390/en5104057
[19]	UCHIDA S, SOGA K, YAMAMOTO K. Critical state soil constitutive model for methane hydrate soil[J]. Journal of Geophysical Research: Solid Earth, 2012, 117: B03209.
[20]	SÁNCHEZ M, GAI X R, SANTAMARINA J C. A constitutive mechanical model for gas hydrate bearing sediments incorporating inelastic mechanisms[J]. Computers and Geotechnics, 2017, 84: 28-46. doi: 10.1016/j.compgeo.2016.11.012
[21]	YANG G C, BAI B, LIU Y, et al. Constitutive modeling for undrained shear behavior of gassy sand considering energy dissipation at the mesoscopic level[J]. Ocean Engineering, 2021, 219: 108307. doi: 10.1016/j.oceaneng.2020.108307
[22]	BAI B, ZHOU R, CAI G Q, et al. Coupled thermo- hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics[J]. Computers and Geotechnics, 2021, 137: 104272. doi: 10.1016/j.compgeo.2021.104272
[23]	JIANG Y M, LIU M. Granular solid hydrodynamics[J]. Granular Matter, 2009, 11(3): 139-156. doi: 10.1007/s10035-009-0137-3
[24]	TEYMOURI M, SÁNCHEZ M, SANTAMARINA J C. A pseudo-kinetic model to simulate phase changes in gas hydrate bearing sediments[J]. Marine and Petroleum Geology, 2020, 120: 104519. doi: 10.1016/j.marpetgeo.2020.104519
[25]	GUPTA S, HELMIG R, WOHLMUTH B. Non-isothermal, multi-phase, multi-component flows through deformable methane hydrate reservoirs[J]. Computational Geosciences, 2015, 19(5): 1063-1088. doi: 10.1007/s10596-015-9520-9
[26]	YAN R T, WEI C F. Constitutive model for gas hydrate-bearing soils considering hydrate occurrence habits[J]. International Journal of Geomechanics, 2017, 17(8): 04017032. doi: 10.1061/(ASCE)GM.1943-5622.0000914
[27]	SHEN J, CHIU C F, NG C W W, et al. A state-dependent critical state model for methane hydrate-bearing sand[J]. Computers and Geotechnics, 2016, 75: 1-11. doi: 10.1016/j.compgeo.2016.01.013
[28]	DE LA FUENTE M, VAUNAT J, MARÍN-MORENO H. A densification mechanism to model the mechanical effect of methane hydrates in sandy sediments[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2020, 44(6): 782-802. doi: 10.1002/nag.3038
[29]	HYODO M, YONEDA J, YOSHIMOTO N, et al. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed[J]. Soils and Foundations, 2013, 53(2): 299-314. doi: 10.1016/j.sandf.2013.02.010
[30]	BEEN K, JEFFERIES M G. A state parameter for sands[J]. Geotechnique, 1985, 35(2): 99-112. doi: 10.1680/geot.1985.35.2.99
[31]	LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449-460. doi: 10.1680/geot.2000.50.4.449
[32]	HYODO M, LI Y H, YONEDA J, et al. Mechanical behavior of gas-saturated methane hydrate-bearing sediments[J]. Journal of Geophysical Research: Solid Earth, 2013, 118: 5185-5194. doi: 10.1002/2013JB010233