基于物质点-特征有限元耦合方法的向后侵蚀管涌模拟

王兆南; 王刚; 金伟

doi:10.11779/CJGE20230207

基于物质点-特征有限元耦合方法的向后侵蚀管涌模拟 English Version

王兆南^{1, 2,},
王刚^{1, 2},
金伟^{1, 3}

1.
山地城镇建设与新技术教育部重点实验室, 重庆 400045
2.
重庆大学土木工程学院, 重庆 400045
3.
中国电建集团成都勘测设计院有限公司, 四川成都 610072

基金项目:

国家自然科学基金面上项目 52079126

详细信息

作者简介:
王兆南(1994—)，男，博士研究生，主要从事岩土力学数值方法和本构模型等方面的研究工作。E-mail: znwang@cqu.edu.com

中图分类号: TU411
计量
- 文章访问数: 311
- HTML全文浏览量: 67
- PDF下载量: 82
出版历程
- 收稿日期: 2023-03-08
- 网络出版日期: 2024-06-04
- 刊出日期: 2024-05-31

Simulation of backward erosion piping based on coupled material point-characteristic finite element method

WANG Zhaonan^{1, 2,},
WANG Gang^{1, 2},
JIN Wei^{1, 3}

1.
Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400045, China
2.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
3.
Chengdu Engineering Corporation Limited, Power China, Chengdu 610072, China

摘要

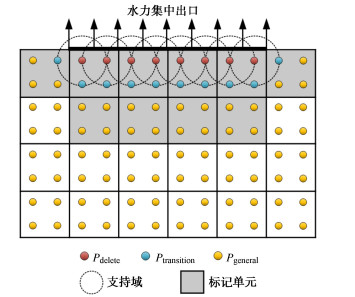
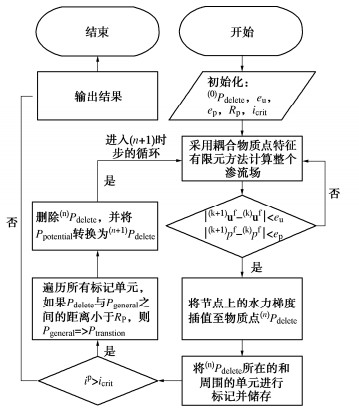
摘要: 向后侵蚀管涌是汛期堤坝中一种常见的渗透破坏形式，多发生在下游存在无保护出水口的二元结构堤基中。由于土体渗流在出水口处存在较高的水力梯度，使得固、液界面附近的土体极易被侵蚀带走，一旦侵蚀土体的上层存在不透水的黏土层时，便会形成不断向上游迎水侧发展的管涌通道，最终导致堤坝出现失稳破坏。基于向后侵蚀管涌的发展过程，采用局部水力梯度作为管涌发展的判别准则，结合饱和孔隙介质的耦合物质点-特征有限元法，发展了一个能够模拟向后侵蚀管涌的新方法。新方法将求解域内的物质点分为3种粒子类型，对满足管涌触发条件的粒子进行删除，以此表示被侵蚀带走的土颗粒。由于算法中的流体部分采用了广义的Navier-Stokes方程进行描述，因此新方法能够同时计算孔隙水渗流和管道流体的自由流动。通过对小尺度模型试验的计算，验证了新方法在向后侵蚀管涌问题中的适用性。
- 向后侵蚀管涌 /
- 耦合物质点-特征有限元法 /
- 临界水力梯度
Abstract: The backward erosion piping is a common form of seepage failure in embankments during flood seasons, and it mostly occurs in the dual-structure foundations with unprotected outlet downstream. Due to the high hydraulic gradient of the soil seepage at the water outlet, the soil near the solid-liquid interface is easy to be eroded away. Once there is an impervious clay layer on the upper layer of the eroded soil, a piping channel will be formed to continuously develop to the upstream side, and eventually lead to the instability and failure of the embankment. Based on the coupled material point - characteristic finite element method, a novel modeling approach for the backward erosion piping is developed by employing the local hydraulic gradient as the triggering criterion of piping. The novel approach divides the particles within the solution domain into three types, and deletes the particles that meet the triggering conditions of piping to represent the granular taken away by erosion. Since the fluid phase is described by the generalized Navier-Stokes equation, the proposed approach can simultaneously calculate the seepage of pore water and the free flow of piping channel. Finally, the small-scale erosion experiments are provided to perform the applicability of the proposed approach.
- backward erosion piping /
- coupled material point-characteristic finite element method /
- critical hydraulic gradient

HTML全文

0. 引言

浑水渗流是指含泥沙等细颗粒水体在多孔介质中的流动，其过程伴随着渗流介质孔隙淤堵、表层沉积等现象，流固耦合效应显著^[1]，是典型的非稳定渗流。浑水渗流对水利工程的反滤设计、浑水浇灌、堤坝渗流控制等方面有较大影响^[2-4]，但目前理论多采用稳定渗流计算方法，忽略了渗流过程中粗细颗粒与水体的耦合作用，使计算结果和工程措施均存在一定偏差。因此，研究浑水颗粒在粗粒土中运移、滞留及表层沉积等过程对于认清浑水渗流机理具有重要意义。

浑水渗流研究方面，Trzaska等^[5]分析了多孔介质中悬浮质的淤塞作用对悬浮液渗流动态的影响；党发宁等^[6]以达西定律为基础推导了浑水渗流计算公式，将淤积层与原土层分开研究，采用层状土渗透系数法进行求解，对变路径渗流分析有一定指导意义，但忽略了粗粒土充填淤堵下变渗透系数问题；姚锋杰^[7]基于上述表面沉积计算方法分析了某斜心墙土石坝渗流稳定机理。许尚杰等^[8]研究了浑水渗流在平原水库防渗方面的应用，但未考虑颗粒的运移影响。关于浑水中细颗粒在粗粒土的研究向相对较少，成果多集中在反滤层研究方面^[9~10]。其中，将反滤层颗粒与水中细颗粒粒径之比（d_ss/d_fs）作为指标^[11]反映滤层的滤土效果有重要借鉴意义；路莹等^[12]通过砂柱试验刻画了堵塞过程，但均选用小于0.075 mm颗粒，代表性较差；李时博等^[13]通过分次序添加淤堵材料研究了粗粒土的渗透性，采用等效粒径和有效孔隙直径两种判别方法对粗粒土淤堵模式进行定量判别。综上，已有计算方法忽略了原状土的变渗透系数问题，粒径或粒组相对单一，对浑水渗流过程多孔介质内部淤堵和表面沉积等规律的系统认识还缺乏指导性。

因此，通过自制试验装置，设置不同粗粒组土柱和浑水类型，研究不同工况下浑水在粗粒土中的渗流特性，推导变渗透系数渗流计算式，对比分析浑水中颗粒在不同粗粒土中的运移-沉积特性规律，以期进一步认识浑水渗流提供理论和技术支持。

1. 试验概况

1.1 装置及材料

研究表明当渗透仪直径与试样d₈₅尺寸比值大于8时，渗透系数接近真实值^[14]。因此，试验自制内径为140 mm的透明有机玻璃筒浑水渗流装置如图 1所示，以消除尺寸效应影响。系统由供水系统、水头控制区、填料区、流量收集器和数据采集装置组成。

图 1 试验装置

Figure 1. Test devices

下载: 全尺寸图片幻灯片

（1）粗粒土特性

土工试验规程规定粗粒组质量大于50%的土为粗粒土^[15]，为便于计算、监测和量化，试验采用石英砂烧制的球型陶瓷颗粒代替粗粒土，其质地坚硬、化学性质稳定如图 2所示。

图 2 球型陶瓷颗粒

Figure 2. Spherical ceramic particles

下载: 全尺寸图片幻灯片

配置不均匀系数C_u为1.24和5.09两组土样，代表均质和非均质粗粒土（下称粗粒土柱），其级配曲线如图 3所示。

图 3 粗粒土柱颗粒级配曲线

Figure 3. Grain-size distribution curves of coarse-grained soil

下载: 全尺寸图片幻灯片

粗粒土孔隙特性决定着浑水渗流的几何条件，也是试验设计中浑水颗粒组成的依据，采用等效颗粒粒径几何平均法计算^[13]：

${d_{\text{e}}} = \sqrt {{d_{\max }}{d_{\min }}} 。$

(1)

式中：d_e为颗粒等效粒径；d_max，d_min分别为粒径的最大值和最小值。

不均匀粗粒土等效颗粒粒径采用概率分析法^[16]：

${d_{\text{e}}} = {d_{20}} 。$

(2)

式中：d₂₀为土重占20%时对应的颗粒粒径。

粗粒土骨架颗粒形成的有效孔隙直径为

${D_{\text{e}}} = \frac{2}{{3{\alpha _1}}}\frac{{{n_0}}}{{1 - {n_0}}}{d_{\text{e}}} 。$

(3)

式中：D_e为有效孔隙直径；n₀为初始孔隙率；α₁当粗粒土为理想的砂砾石料时，取值1.5~1.9^[17]。

经试验和计算分析粗粒土物理参数如表 1所示。

表 1 粗粒土柱物理力学参数

Table 1. Physical and mechanical parameters of coarse-grained soil columns

工况	粒径	不均匀系数 C_u	等效颗粒粒径d_e/mm	干密度ρ_d/(g·cm^-3)	初始孔隙率n₀	有效孔隙直径D_e/mm	渗透系数k/(cm·s^-1)
土样1	2~3 mm	1.24	2.45	2.53	0.397	0.56~0.70	4.76
土样2	1~8 mm	5.09	1.72	2.40	0.357	0.36~0.46	2.97

下载: 导出CSV

| 显示表格

（2）浑水特性

根据《土工试验方法标准：GB/T 50123—2019》^[18]要求，小于0.5 mm颗粒满足有效孔径要求，浑水中土的粒组如图 4所示。

图 4 浑水中颗粒组成

Figure 4. Particle composition in muddy water

下载: 全尺寸图片幻灯片

从土的组粒划分来看，浑水中土粒径范围0.25~0.5 mm（图 4（a）），0.075~0.25 mm（图 4（b），（c））属于中砂和细砂组，均为粗粒组；粒径小于0.075 mm（图 4（d））的为粉粒和黏粒组，属于细粒组^[19]。已有研究表明土中粒径小于0.075 mm的颗粒具有黏聚效应^[19]，因此本试验将不大于0.075 mm粒径土作为控制指标（下称C_0.075），配置10种不同细粒含量的颗粒组分，级配曲线如图 5所示。

图 5 各组分颗粒级配曲线

Figure 5. Grain-size distribution curves of various particle component

下载: 全尺寸图片幻灯片

采用常水头试验和变水头试验测得各颗粒组分渗透系数；采用环刀法和排水法测得各颗粒组分干密度，结果如表 2。

表 2 各颗粒组分的干密度和渗透系数

Table 2. Dry densities and permeability coefficients of various particle components

C_0.075/%	干密度ρ_d/(g·cm^-3)	渗透系数k/(cm·s^-1)
0	2.41	3.00×10^-2
9.17	2.40	6.78×10^-3
18.73	2.37	1.09×10^-3
28.50	2.33	5.56×10^-4
38.96	2.31	5.09×10^-4
49.98	2.30	4.01×10^-4
58.13	2.25	9.68×10^-5
69.40	2.22	8.63×10^-5
79.48	2.18	6.27×10^-5
90.56	2.16	3.41×10^-5

下载: 导出CSV

| 显示表格

1.2 试验方法

（1）试验方案

浑水浓度为100 kg/m³，根据试验装置尺寸，将控制水头设置为120，50 cm，测得渗流速度分别为0.2，0.26 cm/s，满足水力条件^[20]，方案如下：①定水头作用下（设置水头120 cm），选取两种粗粒土柱进行浑水渗流试验，探析粗粒土柱不均匀系数对浑水渗流的影响；②粗粒土不均匀系数不变（C_u=1.24），研究水头变化下浑水渗流对粗粒土渗透性的影响；③上述工况中改变控制粒径含量，探究浑水中细粒组颗粒含量对粗粒土柱渗透性影响。

（2）试验步骤

试验步骤如下：①准备阶段。搅拌以保证浑水中水与土充分混合；分10层装填粗粒土柱，饱水振捣使其密实排气。②浑水渗流试验。控制水头，先进行清水渗流，确保土柱中粗粒土充分湿润后再浑水试验。③数据采集。采用多时段间隔记录流量，压力，淤积层厚度数据，前10 min每隔30 s记录，10~20 min每隔1 min记录，之后每隔2 min记录。④试验结束后提取粗粒土柱孔隙中沉积颗粒，分层取出，将0.5 mm以下的粗粒组和细粒组区分并烘干称重，分析孔隙率等。

2. 圆管中粗粒土渗流公式推导

假定圆管内径为D，内有长度为L₀均质粗粒土层，根据Darcy定律：

$q = kiA。$

(4)

式中：q为渗流量（cm³/s）；i为水力梯度；A为垂直渗流方向土体截面积（cm²）；k为渗透系数（cm/s）。

浑水中颗粒填充和淤积过程，是一个变渗透系数非稳定渗流过程^[6]，某时刻前通过单位面积渗流量为

$Q(t) = \int_0^T {k(t)i{\text{d}}t} 。$

(5)

式中：Q(t)为t时刻的流量（cm³/s）；k(t)为含淤积层和土柱实时整体平均渗透系数（cm/s）；T为渗流时长。

粗粒土顶部发生淤积后，假定顶部淤积层渗透系数为k₀，顶部淤堵过程中粗粒土层渗透系数为，t时刻粗粒土顶部淤积层厚度为L(t)，则

$k{\text{(}}t{\text{) = }}\frac{{L(t) + {L_0}}}{{\frac{{L(t)}}{{{k_0}}} + \frac{{{L_0}}}{{k'{\text{(}}t{\text{)}}}}}} 。$

(6)

式中：k₀为顶部淤积层渗透系数；L(t)表达式为

$L(t) = \beta \alpha Q{\text{(}}t{\text{)}} 。$

(7)

式中：β为沉积层厚度修正系数，取值范围为0~1；α为浑水的体积含砂量（g/cm³）。

粗粒土柱顶部封堵前，浑水颗粒不断进入土柱，随着孔隙堵塞和内部沉积，土柱段（不含淤积层）渗透系数k'(t)的表达式为

$k'{\text{(}}t{\text{) = }}C{d^2}(t)\frac{\gamma }{\mu } \text{，}$

(8)

$或 k'(t){\text{ = }}C{d^2}(t)\frac{\gamma }{\mu }n(t) 。$

(9)

式中：C为常数，圆管可取0.5^[21]，d(t)为填充过程中土柱颗粒平均粒径（cm）；μ为水的黏滞性（Pa·s）； $\gamma$ 为水的重度（N/cm³）；R为水力半径（cm）；对于半径为R₀的圆管，R=0.5R₀；n(t)为体积孔隙率。

由于粗粒土柱孔隙差异与浑水颗粒堵塞沉积要满足几何条件和水力条件，则原粗粒土的k到淤堵后的k´(t)变化范围会较大，甚至有多个数量级的差别。式（8），（9）中的d(t)，n(t)是实时变化的，计算时需要辅以室内渗透系数试验来验证和核对。

将式（7），（8）代入式（6），然后再代入式（5），得积分形式的浑水渗流方程为

$Q(t) = \int_0^T {\frac{{\beta \alpha Q(t) + {L_0}}}{{\frac{{\beta \alpha Q(t)}}{{{k_0}}} + \frac{{\mu {L_0}}}{{Cd{{(t)}^2}\gamma }}}}} i{\text{d}}t 。$

(10)

进一步推求式（10）的其微分形式，在一个微小的时间段内可以将浑水渗流问题看成稳定流问题，则该微小时间段内单位面积上的渗流量为

$Q(t + \Delta t) - Q(t) = k(t)i\Delta t。$

(11)

所以

$\frac{{Q(t + \Delta t) - Q(t)}}{{\Delta t}} = k(t)i。$

(12)

对Δt取极限得微分形式的浑水渗流方程

$\frac{{{\text{d}}Q(t)}}{{{\text{d}}t}} = k(t)i。$

(13)

将式（7）代入式（6）后再代入式（13）得浑水渗流微分方程的另一形式：

$Q(t) = \frac{{\beta \alpha Q(t) + {L_0}}}{{\frac{{\beta \alpha Q(t)}}{{{k_0}}} + \frac{{\mu {L_0}}}{{Cd{{(t)}^2}\gamma }}}}i 。$

(14)

式（14）即为粗粒土在浑水作用下的渗流微分方程，方程中βαQ(t)和d(t)均需要通过试验获得。

3. 结果分析

3.1 淤积规律分析

浑水中C_0.075含量影响着土柱整体特性变化，运移、沉积和淤积结果不同，但总体规律存在相似性。如不均匀系数C_u为1.24，水头为120 cm，不同C_0.075含量下土柱淤积情况如图 6所示。

图 6 不同控制粒径下土柱典型淤堵形态

Figure 6. Typical clogging forms of coarse-grained soil columns under different controlled particle sizes

下载: 全尺寸图片幻灯片

以粗粒土柱内淤积的颗粒质量来反映土柱的淤堵情况，计算式如下：

$Y = \frac{{{m_{\text{s}}}}}{M} \times 100\% 。$

(15)

式中：Y为土柱淤积率；m_s为烘干后淤积颗粒质量（g）；M为投入颗粒总质量（g）。

各工况下土柱表层淤积率如图 7所示。

图 7 各工况下淤积率变化规律

Figure 7. Variation laws of deposition rate under various working conditions

下载: 全尺寸图片幻灯片

由图 7可知，土柱淤积率Y随C_0.075含量的增加逐渐减小。图 7（a）显示Y随C_0.075含量变化分为4种：高淤积区、中间快速下降区、稳定区和弱淤积区。以120 cm水头为例，C_0.075含量小于20%时Y均大于80%，以表层淤积为主；在C_0.075为20%~60%区间时Y显著减小，相差可达61%，表现为表层淤积消减；在C_0.075为60%~80%时Y约为20%，表现为内部沉积；当C_0.075大于80%时Y为11.7%，浑水颗粒未对粗粒土柱产生有效堵塞，表现为暂态沉积后流失。综上，C_0.075含量变化对粗粒土淤堵形态分为4种，如表 3所示。

表 3 粗粒土淤堵形态判别

Table 3. Discrimination of clogging forms of coarse-grained soil

淤堵形态	表层淤积淤堵形态（S）	表层-内部双重淤堵形态（S-I）	内部孔隙淤堵形态（I）	暂态孔隙淤堵形态（P）
C_0.075	≤20%	20%~60%	60%~80%	＞80%

下载: 导出CSV

| 显示表格

此外，不均匀系数越大Y越高如图 7（b）所示，如C_0.075为58.13%时，C_u为1.24和5.09时Y分别为22%和46%。对上述各工况拟合后发现Y与C_0.075符合Boltzmann函数式：

$Y = 16.5 + \frac{{84.3\xi }}{{(1 + {{\text{e}}^{12.1({C_{0.075}} - 39.3\zeta )}})}}。$

(16)

式中：ξ为水头修正系数，120 cm取1.01，50 cm取0.98；ζ为C_u修正系数，C_u为1.24取0.84，C_u为5.09取1.16。

3.2 土柱孔隙特性分析

（1）水力条件对土柱相对孔隙率影响

采用相对孔隙率η来反映填充效果，表达式为

$\eta = \frac{{n{}_{\text{e}}}}{{{n_0}}}。$

(17)

式中：n_e为试验后的孔隙率。

η越小说明孔隙填充越好，测得两种水头下C_u为1.24时土柱孔隙沉积颗粒体积，得相对孔隙率如图 8所示。

图 8 不同水头下相对孔隙率变化曲线

Figure 8. Variation curves of relative porosity under different water heads

下载: 全尺寸图片幻灯片

由图 8可知，C_0.075增加使土柱相对孔隙率呈先减后增的规律。S比S-I型土柱相对孔隙率减小更快，S-I型末η值最小，I阶段η逐渐增大且比P型时增加幅度更大。表明S和S-I型下颗粒以运移和沉积为主，I和P型下颗粒易穿透土柱发生流失，在孔隙中沉积较少。另外，水头越大η越小，如C_0.075含量为69.4%时，在水头为50，120 cm时η相差0.07，说明水力条件改变了颗粒在孔隙中运移和沉积。

（2）C_u对土柱相对孔隙率的影响

图 9为120 cm水头下土柱相对孔隙率，可知两种土柱相对孔隙率随C_0.075含量先减小后增大，且C_u为5.09土柱的η较大。

图 9 两种粗粒土相对孔隙率变化曲线

Figure 9. Variation curves of relative porosity of two kinds of coarse-grained soil

下载: 全尺寸图片幻灯片

S型C_u越大η减小梯度趋缓，C_u等于5.09和1.24时，η值较C_0.075等于0时分别减小了2.15%和19.2%；P型C_u等于5.09且C_0.075为90.56%时，η降至0.87，而C_u为1.24时，该值却增至0.84，呈相反趋势；S-I和I型下两者η变化幅度基本相同。说明土柱不均匀系数越大，孔隙度越小，浑水颗粒在其中运移较困难，土柱填充性差，相对孔隙率较大。

（3）土柱不同深度相对孔隙率

以C_u等于1.24，水头为50 cm工况为例来说明土柱不同深度相对孔隙率变化规律，如图 10所示。

图 10 土柱不同深度相对孔隙率变化规律

Figure 10. Variation laws of relative porosity at different depths of soil columns

下载: 全尺寸图片幻灯片

图 10显示，随着C_0.075含量增加土柱不同深度η整体上呈现先减小后增大的规律，深度越大η值越大。S型时，C_0.075改变对土柱上部0~2 cm粗粒土R基本无影响，η值约为0.6；土柱2~20 cm的η明显降低，可见S型下浑水颗粒能较顺畅进入土柱中下部，并在其中沉积淤堵，使中下部相对孔隙率减小；S-I型时，C_0.075变化对土柱4~6 cm的η值基本无影响，土柱0~4 cm的η值减幅大于6~20 cm；I型时土柱4~6 cm的η值也未发生明显变化，0~4 cm和6~20 cm的η值均有所增大，前者增幅大于后者。

综上，S-I型C_0.075含量增加导致上部孔隙堵塞并阻碍浑水颗粒向下运移，存在临界深度，该深度以下的η减幅较小；I型C_0.075含量增加，颗粒能较顺利向下运移，同样存在一个临界深度，该深度以下η值增幅度大于上部。P型土柱各深度从上至下的最大变化幅度仅为0.07，表明仅在土柱局部产生少量沉积，浑水颗粒流失严重，土柱整体η值基本不变。

4. 土柱渗透性

4.1 各形态下土柱不同深度渗透系数

测试并计算土柱顶部封堵之前不同高度的渗透系数，以C_u为1.24在120 cm水头为例进行分析。S、S-I、I及P型分别选取代表工况进行分析，对应的C_0.075含量分别为0，28.5%，79.8%，90.13%，各典型工况渗透系数变化如图 11所示。

图 11 不同形态下土柱不同深度渗透系数变化规律

Figure 11. Variations law of permeability coefficient of soil columns at different depths under different forms

下载: 全尺寸图片幻灯片

S型土柱深度0~8 cm部分渗透系数在前1.5 min内基本不变，此后沿深度方向各层渗透系数逐渐下降，且越靠下部下降梯度越小（图 11（a））；在2~6 min期间，各层渗透系数自上而下分别下降了97%，90.6%，83.2%，58.6%。而8~20 cm部分的渗透系数基本无变化。说明该形态下，土柱从上而下颗粒沉积堵塞程度逐渐降低，导致上部渗透系数减小速率明显高于下部。

S-I型下土柱0~2 cm范围内渗透系数下降速率最快，土柱封堵时该范围内的渗透系数也最小，约为1.2×10^-2 cm/s（图 11（b））。自上而下2~4，4~6，6~8 cm范围内渗透系数下降速率依次趋缓，但该范围整体渗透系数减少量达两个数量级；同S型相似，土柱8~20 cm范围内渗透系数也无明显变化。该形态的主要特点表现为：浑水颗粒在土柱顶部暂时沉积并导致渗透系数快速减小，随后顶部沉积的颗粒在渗透力作用下逐渐向下部运移和沉积，所以下部渗透系数减小出现滞后现象。

I和S-I型的渗透系数存在相似之处，即下部渗透系数衰减速率滞后于上部，但8~12 cm范围内S-I型渗透系数（6.4×10^-2 cm/s）小于I型（8.5×10^-1 cm/s），说明I型颗粒沉积数量少，整体渗透系数偏大（图 11（c））。

P型下土柱0~8 cm范围内各层渗透系数随时间逐渐减小并最终趋于稳定，各层达到稳定状态所需时间随深度逐渐减小，如0~2 cm和6~8 cm渗透系数达到稳定所需时间分别为22.5，19.8 min，相差2.7 min。土柱8~20 cm的渗透系数不随时间发生变化。该形态上部浑水颗粒在土柱中运移最终达到平衡，渗透系数也趋于稳定，而在下部浑水颗粒几乎无滞留沉积现象，渗透系数也几乎不变。

4.2 土柱整体渗透性

（1）淤泥层厚度与整体渗透系数关系

与4.1节工况一致，分析土柱整体渗透系数的理论值、实测值及淤积层厚度关系，如图 12所示。

图 12 4种淤堵形态下整体渗透系数试验与理论值对比

Figure 12. Test and theoretical overall permeability curves under four clogging conditions

下载: 全尺寸图片幻灯片

由图 12知，根据各工况下浑水颗粒随时间在土柱中运移和沉积的现象不同，可将渗透系数随时间变化关系分为阶段1、2和3。其中阶段1浑水颗粒在土柱顶部未形成淤积层，在土柱孔隙中可自由运移，孔隙结构几乎无变化，渗透系数也基本不变；阶段2颗粒部分在土柱顶部和表层淤积，一部分在渗透力作用下仍能向下部运移，该阶段渗透系数减小速率快；阶段3颗粒在土柱孔隙中运移现象基本消失，仅在表层淤积。

对比发现S、S-I和I型均出现明显的3个阶段，而P型不存在阶段2和3。理论值和实测值在阶段1和阶段3拟合效果相对较好，而阶段2和P型后段二者有较大误差。

（2）计算值与试验结果对比

上述理论值与实测值误差主要原因是公式（14）在计算中无法实时获得土柱平均粒径d(t)，故无法获取动态渗透系数k'(t)，而是采用土柱初始渗透系数k来计算。采用相关系数R²和均方根误差RMSE误差指标来进行误差分析，结果如表 4。

表 4 土体计算参数

Table 4. Soil parameters

C_0.075	阶段	决定系数R²	均方根误差 RMSE
0	阶段1	0.99	0.04
	阶段2	0.85	0.404
	阶段3	0.98	0.086
28.5	阶段1	0.43	2.04
	阶段2	0.68	0.41
	阶段3	0.99	0
58.13	阶段1	-1.02	2.78
	阶段2	0.92	0.22
	阶段3	1.00	0
79.49	阶段1	-1.82	3.13
	阶段2	0.97	0.26
	阶段3	1.00	0
90.56	阶段1	-1.27	2.53
90.56	阶段2	0.98	0.27

下载: 导出CSV

| 显示表格

由表 4知，C_0.075含量为0%时阶段1、3线性回归精度较高，阶段2的R²较低，拟合精度差。其余形态下阶段1，2的RMSE大于0.2，反映其拟合度不高，而阶段3线性拟合度均较好。

4.3 渗透系数讨论

（1）C_0.075含量偏低时（小于18.73%）渗透系数

当浑水中细粒组含量偏低时，即C_0.075含量不大于18.73%，土柱淤堵形态为S型，淤堵后土柱渗透系数变化不大。k'(t)可采用式（18）计算：

$k'(t) = \sqrt {{k_1}{k_3}} 。$

(18)

式中：k₁，k₃分别为阶段1和阶段3的渗透系数。以C_0.075为0时，采用式（18）重新计算阶段2渗透系数并与实测值进行对比如图 13所示。

图 13 阶段2试验与式(18)改进渗透系数结果对比

Figure 13. Comparison between stage 2 tests and improved permeability coefficient results by Formula (18)

下载: 全尺寸图片幻灯片

图 13知，式（18）渗透系数计算值接近阶段2试验变化情况。两者误差指标计算结果见表 5。

表 5 改进式与试验渗透系数误差指标

Table 5. Error indexes of permeability coefficient by improved formula and tests

工况	阶段	R²	RMSE
未改进	阶段1	0.99	0.04
	阶段2	0.85	0.404
	阶段3	0.98	0.086
改进	阶段1	0.99	0.04
	阶段2	0.96	0.09
	阶段3	0.98	0.086

下载: 导出CSV

| 显示表格

由表 5知，改进后阶段2线性精度显著提高，可见采用阶段1和3渗透系数均方差来确定阶段2的渗透性，计算结果更加合理。

（2）C_0.075含量较高时渗透系数

浑水中C_0.075含量大于28.5%时，土柱淤堵形态表现为S-I、I和P型。3种形态的阶段1细颗粒在土柱孔隙中能自由运移并伴随极少量沉积，渗透系数几乎无变化，可用Darcy定律来计算；土柱整体渗透性系数较小，阶段2结束后，土柱整体渗透系数下降近2个数量级。此时土柱整体渗透系数主要由C_0.075土粒含量来决定，根据二者贡献率取加权平均值。

$k'(t) = a{k_1} + b{k_3}。$

(19)

式中：a，b为渗透系数权重并通过实测获取，a+b=1。

以C_0.075为58.13%工况为例，采用式（19）计算阶段2渗透系数与试验结果对比如图 14所示。

图 14 阶段2试验与式（19）改进渗透系数结果对比

Figure 14. Comparison between stage 2 tests and improved permeability coefficient results by Formula (19)

下载: 全尺寸图片幻灯片

图 14显示，采用式（19）对阶段2渗透系数进行计算，能与实测值较好吻合，改进前后误差分析指标如表（6）。

表 6 改进式与试验渗透系数误差指标

Table 6. Error indexes of permeability coefficient by improved formula and test

改进与未改进	阶段	R²	RMSE
未改进	阶段1	-1.02	2.78
	阶段2	0.92	0.22
	阶段3	1	0
改进	阶段1	1	0
	阶段2	0.99	0.008
	阶段3	1	0

下载: 导出CSV

| 显示表格

表 6知，改进后精度明显提高，说明公式（19）计算结果符合实际要求

式（19）渗透系数权重a可与C_0.075的线性拟合关系来确定，如C_u为1.24时二者拟合关系图 15。

图 15 权重系数与控制粒径的线性拟合关系

Figure 15. Linear fitting relationship between weight coefficient and control particle size

下载: 全尺寸图片幻灯片

图 15（a）知a随C_0.075增加而增大，水头越大对a的影响反而越小，主要因为高水头加速了浑水颗粒淤积的速度，渗透系数减小速率也增加，故a值较小。不均匀系数越大对应的直线斜率越大，说明权重系数变化的幅度越显著；而在相同C_0.075条件下，C_u为1.24时的权重系数高于5.09工况（图 15（b））。分析其原因是不均匀系数越大，孔隙度越小，渗流过程随C_0.075变化存在显著差异，造成渗透系数变化幅度较大。

5. 结论

（1）推导了圆管中粗粒土变非稳定渗流微分方程，与试验结果进行对比验证并提出修正方法。

（2）土柱中颗粒淤积率与控制粒径含量关系符合Boltzmann函数变化趋势。

（3）浑水中控制粒径C_0.075是重要的影响因子，颗粒在粗粒土柱的运移、沉积和淤堵形态过程大致可分为四种形态：表层堆积淤堵形态（S型）；表层-内部双重淤堵形态（S-I型）；内部孔隙淤堵形态（I型）；暂态孔隙淤堵形态（P型）。

（4）土柱不均匀系数越大，孔隙度越小，浑水颗粒运移较困难，土柱填充性差，相对孔隙率较大；水头加剧了浑水中颗粒在土柱内部的运移的速度，但也加速了颗粒在顶部的沉积并封堵。

（5）S型时土柱0~2 cm渗透系数下降速率最大，封堵时平均渗透系数最小，2 cm以下相对隙率及随深度逐渐减小；S-I和I型土柱下部渗透系数明显滞后于上部，相对孔隙率存在临界深度（约为4~6 cm）；P型时土柱整体相对孔隙率基本无变化。

图 1 管涌出口处不同的粒子类型

Figure 1. Different particle types at downstream outlet

下载: 全尺寸图片幻灯片

图 2 向后侵蚀管涌计算方法的流程图

Figure 2. Algorithm procedure of backward erosion piping

下载: 全尺寸图片幻灯片

图 3 数值模型的几何示意图

Figure 3. Geometric conditions of numerical model

下载: 全尺寸图片幻灯片

图 4 计算结束时的管涌通道和总水头分布

Figure 4. Piping channel and total head contours at the end of simulation

下载: 全尺寸图片幻灯片

图 5 不同网格尺寸和粒子数量下压力水头的分布

Figure 5. Pressure water heads under different mesh sizes and particle numbers

下载: 全尺寸图片幻灯片

图 6 含防渗墙砂土地基的几何示意图

Figure 6. Geometric conditions of sandy soil foundation with cutoff wall

下载: 全尺寸图片幻灯片

图 7 不同上游水头下管涌通道的长度

Figure 7. Lengths of piping channel under different water heads without cut-off wall

下载: 全尺寸图片幻灯片

图 8 含防渗墙地基中管涌通道和总水头分布

Figure 8. Contours of piping channels and total water head of foundation with cut-off wall

下载: 全尺寸图片幻灯片

图 9 含防渗墙地基顶部边界上的压力水头

Figure 9. Pressure water heads on top boundary of foundation with cut-off wall

下载: 全尺寸图片幻灯片

参考文献(30)

[1]	VAN BEEK V M, BEZUIJEN A, SELLMEIJER J B, et al. Initiation of backward erosion piping in uniform sands[J]. Géotechnique, 2014, 64(12): 927-941. doi: 10.1680/geot.13.P.210
[2]	ROBBINS B A, VAN BEEK V M, LÓPEZ-SOTO J F, et al. A novel laboratory test for backward erosion piping[J]. International Journal of Physical Modelling in Geotechnics, 2018, 18(5): 266-279. doi: 10.1680/jphmg.17.00016
[3]	VANDENBOER K, DOLPHEN L, BEZUIJEN A. Backward erosion piping through vertically layered soils[J]. European Journal of Environmental and Civil Engineering, 2019, 23(11): 1404-1412. doi: 10.1080/19648189.2017.1373708
[4]	ROBBINS B A, MONTALVO-BARTOLOMEI A M, GRIFFITHS D V. Analyses of backward erosion progression rates from small-scale flume experiments[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(9): 04020093. doi: 10.1061/(ASCE)GT.1943-5606.0002338
[5]	VANDENBOER K, VAN BEEK V M, BEZUIJEN A. 3D character of backward erosion piping[J]. Géotechnique, 2018, 68(1): 86-90. doi: 10.1680/jgeot.16.P.091
[6]	POL J C, KANNING W, BEEK V M, et al. Temporal evolution of backward erosion piping in small-scale experiments[J]. Acta Geotechnica, 2022, 17(10): 4555-4576. doi: 10.1007/s11440-022-01545-1
[7]	AKRAMI S, BEZUIJEN A, VAN BEEK V, et al. Analysis of development and depth of backward erosion pipes in the presence of a coarse sand barrier[J]. Acta Geotechnica, 2021, 16(2): 381-397. doi: 10.1007/s11440-020-01053-0
[8]	VANDENBOER K, VAN BEEK V M, BEZUIJEN A. Analysis of the pipe depth development in small-scale backward erosion piping experiments[J]. Acta Geotechnica, 2019, 14(2): 477-486. doi: 10.1007/s11440-018-0667-0
[9]	VAN BEEK V M, VAN ESSEN H M, VANDENBOER K, et al. Developments in modelling of backward erosion piping[J]. Géotechnique, 2015, 65(9): 740-754. doi: 10.1680/geot.14.P.119
[10]	BRIAUD J L, GOVINDASAMY A V, SHAFII I. Erosion charts for selected geomaterials[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(10): 04017072. doi: 10.1061/(ASCE)GT.1943-5606.0001771
[11]	周晓杰, 丁留谦, 姚秋玲, 等. 悬挂式防渗墙控制堤基渗透变形发展模型试验[J]. 水力发电学报, 2007, 26(2): 54-59. doi: 10.3969/j.issn.1003-1243.2007.02.011 ZHOU Xiaojie, DING Liuqian, YAO Qiuling, et al. Laboratory model test for evolution of seepage deformation controlled by means of suspended cut-off wall in foundation of dike[J]. Journal of Hydroelectric Engineering, 2007, 26(2): 54-59. (in Chinese) doi: 10.3969/j.issn.1003-1243.2007.02.011
[12]	ZHOU X J, JIE Y X, LI G X. Numerical simulation of the developing course of piping[J]. Computers and Geotechnics, 2012, 44: 104-108. doi: 10.1016/j.compgeo.2012.03.010
[13]	FASCETTI A, OSKAY C. Dual random lattice modeling of backward erosion piping[J]. Computers and Geotechnics, 2019, 105: 265-276. doi: 10.1016/j.compgeo.2018.08.018
[14]	ROBBINS B A, GRIFFITHS D V. A two-dimensional, adaptive finite element approach for simulation of backward erosion piping[J]. Computers and Geotechnics, 2021, 129: 103820. doi: 10.1016/j.compgeo.2020.103820
[15]	LIANG Y, YEH T C J, WANG J J, et al. An auto-adaptive moving mesh method for the numerical simulation of piping erosion[J]. Computers and Geotechnics, 2017, 82: 237-248. doi: 10.1016/j.compgeo.2016.10.011
[16]	WANG Y A, NI X D. Hydro-mechanical analysis of piping erosion based on similarity criterion at micro-level by PFC^3D[J]. European Journal of Environmental and Civil Engineering, 2013, 17(S1): 187-204.
[17]	TRAN D K, PRIME N, FROIIO F, et al. Numerical modelling of backward front propagation in piping erosion by DEM-LBM coupling[J]. European Journal of Environmental and Civil Engineering, 2017, 21(7/8): 960-987.
[18]	FROIIO F, CALLARI C, ROTUNNO A F. A numerical experiment of backward erosion piping: kinematics and micromechanics[J]. Meccanica, 2019, 54(14): 2099-2117 doi: 10.1007/s11012-019-01071-7
[19]	RAHIMI M, SHAFIEEZADEH A. Coupled backward erosion piping and slope instability performance model for levees[J]. Transportation Geotechnics, 2020, 24: 100394. doi: 10.1016/j.trgeo.2020.100394
[20]	ROTUNNO A F, CALLARI C, FROIIO F. A finite element method for localized erosion in porous media with applications to backward piping in levees[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(1): 293-316. doi: 10.1002/nag.2864
[21]	FUJISAWA K, MURAKAMI A, NISHIMURA S I. Numerical analysis of the erosion and the transport of fine particles within soils leading to the piping phenomenon[J]. Soils and Foundations, 2010, 50(4): 471-482. doi: 10.3208/sandf.50.471
[22]	ZHANG X S, WONG H, LEO C J, et al. A thermodynamics-based model on the internal erosion of earth structures[J]. Geotechnical and Geological Engineering, 2013, 31(2): 479-492. doi: 10.1007/s10706-012-9600-8
[23]	WEWER M, AGUILAR-LÓPEZ J P, KOK M, et al. A transient backward erosion piping model based on laminar flow transport equations[J]. Computers and Geotechnics, 2021, 132: 103992. doi: 10.1016/j.compgeo.2020.103992
[24]	LEI X Q, HE S M, CHEN X Q, et al. A generalized interpolation material point method for modelling coupled seepage-erosion-deformation process within unsaturated soils[J]. Advances in Water Resources, 2020, 141: 103578. doi: 10.1016/j.advwatres.2020.103578
[25]	LIANG D F, ZHAO X Y, SOGA K. Simulation of overtopping and seepage induced dike failure using two-point MPM[J]. Soils and Foundations, 2020, 60(4): 978-988. doi: 10.1016/j.sandf.2020.06.004
[26]	CECCATO F, YERRO A, GIRARDI V, et al. Two-phase dynamic MPM formulation for unsaturated soil[J]. Computers and Geotechnics, 2021, 129: 103876. doi: 10.1016/j.compgeo.2020.103876
[27]	王兆南, 王刚. 饱和孔隙介质的耦合物质点-特征有限元方法[J]. 岩土工程学报, 2023, 45(5): 1094-1102. doi: 10.11779/CJGE20220332 WANG Zhaonan, WANG Gang. Coupled material point method and characteristic finite element method for saturated porous media[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(5): 1094-1102. (in Chinese) doi: 10.11779/CJGE20220332
[28]	ZIENKIEWICZ O C, TAYLOR R L, NITHIARASU P. The Finite Element Method for Fluid Dynamics (Seventh Edition)[M]. Oxford: Butterworth-Heinemann, 2014.
[29]	ABAQUS G. Abaqus 6.11[M]. Providence: Dassault Systemes Simulia Corporation, 2011.
[30]	ROBBINS B A, VAN BEEK V M, POL J C, et al. Errors in finite element analysis of backward erosion piping[J]. Geomechanics for Energy and the Environment, 2022, 31: 100331. doi: 10.1016/j.gete.2022.100331