考虑毛细与吸附作用的黏土干缩开裂过程离散元模拟

邓云鹏; 彭镝; 董梅; 徐日庆; 傅榆涵

doi:10.11779/CJGE20230189

考虑毛细与吸附作用的黏土干缩开裂过程离散元模拟 English Version

邓云鹏^1,,
彭镝²,
董梅^1, ,,
徐日庆¹,
傅榆涵¹

1.
浙江大学滨海和城市岩土工程研究中心, 浙江杭州 310058
2.
中国建筑科学研究院有限公司地基基础研究所, 北京 100013

基金项目:

浙江省“尖兵”“领雁”研发攻关计划项目 2022C03180

详细信息

作者简介:
邓云鹏(1999—)，男，硕士，主要从事土的工程性质等方面的研究工作。E-mail: yunpeng_deng@zju.edu.cn

通讯作者:
董梅, E-mail: mdong@zju.edu.cn

中图分类号: TU431
计量
- 文章访问数: 314
- HTML全文浏览量: 80
- PDF下载量: 76
出版历程
- 收稿日期: 2023-03-05
- 网络出版日期: 2024-08-11
- 刊出日期: 2024-07-31

DEM simulation of desiccation cracking in clay considering capillarity and adsorption

1.
Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China
2.
Institute of Foundation Engineering, China Academy of Building Research Co., Ltd., Beijing 100013, China

摘要

摘要: 黏土干缩开裂过程中土颗粒间的作用非常复杂，导致难以从颗粒层面对干缩裂缝的形成机理开展定量研究。基于非饱和土中的吸应力曲线，明确区分黏土中的毛细与吸附作用，在此基础上建立考虑黏土颗粒间吸引力随含水率变化的离散元接触模型，开展黏土干缩开裂的数值模拟，并与室内试验结果进行对比。结果表明，数值模拟得到的裂缝形态、裂缝发育历程、土样应变均与室内试验较为吻合，验证了离散元接触模型的可靠性。对模拟结果的进一步分析发现：①在黏土干缩开裂过程中，毛细与吸附作用共同发挥效果。随着含水率的降低，吸附作用的影响逐渐超过毛细作用。在吸附作用占优阶段，模拟土样的土颗粒沿裂缝分布方向的平均位移为最终位移值的73%。②土颗粒间总接触数量随含水率的降低先减少后增加。③在毛细/吸附作用占优阶段，土颗粒间的物理接触力会迅速增加并引起应力集中，土颗粒间接触因此集中断开进而形成裂缝。
- 黏土 /
- 非饱和土 /
- 干缩开裂 /
- 离散单元法 /
- 毛细作用 /
- 吸附作用
Abstract: The interaction between clay particles during the process of desiccation cracking is highly complex, making it challenging to conduct quantitative researches on the formation mechanism of cracks at the particle level. The capillarity and adsorption in clay is distinguished based on the suction stress characteristic curve (SSCC) in unsaturated soils. A contact model of discrete element method (DEM) that accounts for the change of attraction between clay particles with water content is then established, and the numerical simulation of desiccation cracking in clay is carried out. The simulated results are compared with those of laboratory tests, and the findings indicate that the crack morphology, crack development history and strain of the soil sample obtained by the DEM simulation are in good agreement with the laboratory results, verifying the reliability of the DEM model. Further analysis of the simulated results reveals that: (1) The capillarity and adsorption both play a role in the desiccation cracking process of clay. With the decrease of water content, the effects of adsorption gradually exceed those of capillarity. At the dominant stage of adsorption, the average displacement of simulated soil particles along the crack distribution direction accounts for 73% of its final value. (2) The total contact number between soil particles initially decreases and then increases as water content decreases. (3) The physical contact force between soil particles will increase rapidly at the dominant stage of capillarity/adsorption, resulting in stress concentration, and the contact between soil particles will be centralized and cracks will be formed. The proposed DEM contact model is of significant physical implications and can offer valuable insights into the underlying mechanisms of desiccation cracking in clay at the particle level.
- clay /
- unsaturated soil /
- desiccation cracking /
- discrete element method /
- capillarity /
- adsorption

HTML全文

0. 引言

潜水面上升可能诱发边坡失稳，艾伯凡矿灾^[1]（Aberfan Disaster）、沃楚西特水坝^[2]（Wachusett Dam）等就属于这一破坏模式。Brand^[3]建议研究边坡的破坏机理时，应该考虑边坡内土体单元的应力应变响应。边坡内潜水面上升的应力路径可以简化为等剪应力排水路径^[3-6]。针对等剪应力排水路径下土体的力学响应，研究者们进行了一系列工作^{[2, 6-7]}。Chu等^[2]通过试验证明了等剪应力排水路径下土体的非稳定态与边坡失稳存在相关性。Lashkari等^[7]利用离散元数值模拟等剪应力排水路径，发现松砂和密砂的非稳定态存在区别。此外，研究者还发现各向异性对等剪应力排水路径的非稳定态存在显著影响。Fanni等^[8]通过试验发现大主应力方向从垂直于沉积面旋转到45°时，非稳定态的应力比不断减小，指出在评估边坡稳定时不能忽略各向异性的影响。

一些研究者也在利用本构模型模拟该应力路径。Lashkari等^[7]采用了各向异性临界状态塑性本构模型^[9]模拟了不同孔隙比和剪应力值下的等剪应力排水试验，表明了模型具有模拟该应力路径的能力。但本构模型能否模拟各向异性条件下的等剪应力排水试验，目前仍然未知。

各向异性对砂土的力学响应有显著影响^[10-16]。如何用本构模型描述饱和砂土的力学响应是目前的研究热点之一。为总结各向异性对于砂土力学响应影响的规律，研究者们进行了大量物理试验和离散元数值试验。物理试验方面如Yoshimine等^[17]和Nakata等^[18]研究了不同加载方向和中主应力系数对丰浦砂应力应变关系的影响，发现当大主应力平行于沉积面、中主应力系数为1时，土样表现出更强的剪缩特性，更易发生静态液化。离散元数值试验方面如Fu等^[19]再现了直剪试验，研究各向异性砂土的峰值强度。这些试验为本构模型的建立和验证提供了基础和依据，各类模型通过模拟试验证明了自身的有效性^[20-23]。如Wang等^[22]通过离散元数值试验总结各向异性对塑性模量和剪胀的影响，在CycLiq本构模型^[24]的基础上加入了组构各向异性，并通过离散元试验和物理试验对新模型进行了验证。

本文利用Wang等^[22]提出的各向异性CycLiq本构模型，对Fanni等^[8]进行的一系列定轴不排水试验与定轴等剪应力排水试验进行了模拟，验证了该模型对于各向异性砂土在不同主应力方向下、不同应力路径力学响应的模拟能力，并研究了初始组构强度对于模型模拟定轴等剪应力排水试验结果的影响。

1. 各向异性CycLiq模型

1.1 本构模型

基于排水与不排水循环扭剪试验现象研究，张建民等^[25-26]将砂土的体应变 ${\varepsilon _\text{v}}$ 分解为有效球应力变化引起的弹性体应变 ${\varepsilon _\text{vc}}$ 和剪切引起的塑性体应变 ${\varepsilon _\text{vd}}$ ，又将剪切引起的塑性体应变 ${\varepsilon _\text{vd}}$ 进一步划分为可逆性剪切体应变 ${\varepsilon _\text{vd, re}}$ 与不可逆性剪切体应变 ${\varepsilon _\text{v, ir}}$ 。在此基础上，王刚等^[27]和Wang等^[24]建立了一个能够模拟饱和砂土液化前后应力应变响应的弹塑性循环本构模型，并在模型中引入了状态变量，使得模型能够统一描述砂土在不同状态下的静动力响应。为考虑各向异性，Wang等^[22]基于试验和离散元数值模拟总结的规律，对模型进行了改进，引入了组构张量，在塑性模量与剪胀率的计算中引入了各向异性的影响，使得模型能够描述不同主应力方向下的响应。

CycLiq模型的应力应变关系可以用下式来描述：

$\boldsymbol{\dot \varepsilon} = \frac{{p \boldsymbol{\dot r}}}{{2G}} + \left( {\frac{\boldsymbol{r}}{{2G}} + \frac{\boldsymbol{I}}{{3K}}} \right)\dot p + \left( {\boldsymbol{n} + \frac{D}{3}\boldsymbol{I}} \right)\left\langle L \right\rangle 。$

(1)

式中：p为有效球应力；r为偏应力张量s与球应力p之比；G和K为弹性剪切模量和体积模量；I为单位张量；n为塑性偏应变流动方向与加载方向；D为剪胀率；L为塑性加载指数。参数上加(·)表示增量；〈〉为Macaulay计算符，当x > 0时，〈x〉= x，当x ≤ 0时，〈x〉= 0。

弹性剪切模量和体积模量采用Richart等^[28]提出的线性弹性模量公式，在此不再赘述。塑性加载指数L通过下式计算：

$L = \frac{{p \boldsymbol{\dot r}:\boldsymbol{n}}}{H} 。$

(2)

式中：H为塑性模量。

砂土临界状态采用Been等^[29]提出的状态变量Ψ = $e - {e_\text{c}}$ ，但 ${e_\text{c}}$ 与p的关系采用了与Wang等^[22]所使用的指数关系^[30]不同的对数关系：

${e_\text{c}} = \varGamma - {\lambda _\text{e}}\ln (p) 。$

(3)

这一改动是因为Fanni等^[8]给出了本文模拟试样临界状态下试样的e-p曲线，并采用式（3）的对数关系进行了拟合，且e-p曲线的对数关系被广泛采用，许多模型采用了这种关系^[31-32]，因此对模型中的公式进行了替换。不过需要指出的是，在液化状态时，对数关系不再适用，因此砂土的动力本构模型大都采用指数关系^[33-34]。本文中不涉及液化内容，因此可以选取对数关系进行模拟。

为了考虑各向异性的影响，Wang等^[22]在模型中引入了组构张量 ${\boldsymbol{F}_\text{n}}$ ，并考虑了组构张量对于塑性模量与剪胀率的影响。组构张量 ${\boldsymbol{F}_\text{n}}$ 的演化采用了如下公式：

$\text{d}{\boldsymbol{F}_\text{n}} = \left\langle L \right\rangle c\left[ {\boldsymbol{n} - (1 + D){\boldsymbol{F}_\text{n}}} \right] 。$

(4)

式中：c为模量参数，代表组构张量演化的速率。通过总结离散元数值试验的规律，Wang等^[22]发现组构张量的模|| ${\boldsymbol{F}_\text{n}}$ ||与组构张量和加载方向的联合不变量A_n = ${\boldsymbol{F}_\text{n}}$ : n之差|| ${\boldsymbol{F}_\text{n}}$ ||-A_n可以作为一个良好的指标，以反映塑性模量和剪胀率随加载角度的变化。以水平沉积的试样在三轴压缩中的加载角度为0°，随着加载角度的增加，指标|| ${\boldsymbol{F}_\text{n}}$ ||-A_n不断增大，同时塑性模量不断减小，剪胀率从不断增加。因此，将|| ${\boldsymbol{F}_\text{n}}$ ||-A_n引入到了塑性模量与剪胀率的计算公式中：

$C = \exp \left[ { - {\Delta _1}{{(\left\| {{\boldsymbol{F}_\text{n}}} \right\| - {A_\text{n}})}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right] \text{，}$

(5)

$\begin{align}H = &\frac{2}{3}hg\left( \theta \right)G\exp ( - {n^p}\Psi ) \cdot \\& \left( {\frac{{M\exp ( - {n^{\rm{p}}}\Psi )}}{{{M_\text{m}}}}\frac{{\bar \rho }}{\rho } - \frac{1}{C}} \right) \text{，} \end{align}$

(6)

${D_\text{ir}} = \frac{{{d_\text{ir}} + {\Delta _2}(\left\| {{\boldsymbol{F}_\text{n}}} \right\| - {A_\text{n}})}}{{{d_\text{ir}}}}{D_\text{ir, iso}} 。$

(7)

式中：h，Δ₁，Δ₂，M，d_ir， ${n^{\rm{p}}}$ 为模型参数；g(θ)为形状函数，这里采用的是Zhang等^[35]建议的函数； ${M_\text{m}}$ 为历史最大应力比；D_{ir, iso}为各向同性条件下的不可逆剪胀率，详细公式可见Wang等^[24]。

1.2 参数标定

Fanni等^[8]试验中采用的砂为一种细硅砂，颗粒相对质量密度为2.64，平均粒径D₅₀为0.21 mm，均匀系数C_u为2.3，颗粒呈圆形至亚圆形。因缺乏相关试验，大部分参数参照了Wang等^[22]标定的丰浦砂参数，仅对部分可确定的临界状态参数（n^p，Γ， ${\lambda _\text{e}}$ ）进行了重新标定。标定结果如表 1所示。

其中，Γ和 ${\lambda _\text{e}}$ 由Fanni等^[8]根据试验拟合得到，在更换了Wang等^[22]模型中e_c与p的关系式后可直接使用。展示了 ${n^{\rm{p}}}$ 的标定方法，以Fanni等^[8]进行的一组定轴等剪应力排水试验（中主应力系数b = 0.2，加载角度α = 30°）结果参照进行标定。图中点代表试验所得试样到达非稳定态时的有效球应力与孔隙比，虚线和实线分别为n^p = 6和12时的模拟结果。可以看到当其他参数不变时， ${n^{\rm{p}}}$ 值越大，模拟得到的非稳定态时有效球应力随孔隙比变化越快，曲线更加陡峭。这是由于等剪应力排水路径中的非稳定态代表试样处于峰值应力比状态，而峰值应力比可由Mexp(- ${n^{\rm{p}}}$ Ψ)决定。

图 1 模型参数n^p的标定方法演示

Figure 1. Calibration method for model parameter n^p

下载: 全尺寸图片幻灯片

除了表 1中列出的模型参数外，初始组构强度，即初始组构张量的模||F_nin||，也是一个重要的参数。它代表了试样在试验开始时的各向异性程度，||F_nin||越大，试样的各向异性越强。不同的制样方式制得的试样往往有着不同的各向异性程度^[36]，因此需要取不同的初始组构强度。本次模拟中涉及两种不同的制样方式，湿装夯实法（moist tamped, MT）和干砂雨法（dry pluviated, DP），其中干砂雨法得到的试样孔隙比要小于湿装夯实法，结合Yang等^[37]、叶斌等^[38]通过物理试验与离散元模拟均发现干砂雨法的各向异性强于湿装夯实法，可以推测干砂雨法在制样中，由于受到重力影响，土颗粒的排列具有定向性，而湿装夯实法在制样中，土颗粒更倾向于随机排列，导致其各向异性相对较弱。最终，湿装夯实法制得的试样初始组构强度||F_nin||取为0.5，干砂雨法制得的试样初始组构强度||F_nin||取为0.7。

2. 不同主应力方向下模型的响应

2.1 定轴不排水剪切试验

Fanni等^[8]进行了一系列空心圆柱定轴不排水剪切试验。试验中，初始有效球应力均为171 kPa，大小主应力之差均为64 kPa，中主应力系数b分别为0，0.2，0.5，大主应力与沉积方向的夹角α分别为0°，22.5°，30°和45°，两种制样方法，即湿装夯实法和干砂雨法，各5组试验，如图 2，3所示。其中，湿装夯实法所得试样孔隙比在0.761~0.785，干砂雨法所得试样孔隙比在0.674~0.697。采用表 1中的模型参数对试验进行模拟，模拟结果如图 2，3所示。图 2（a），（b）中横纵坐标为Fanni等^[8]给出的八面体剪应变和八面体偏应力，图 3同理。

图 2 不同中主应力系数与主应力方向下湿装夯实法试样定轴不排水试验结果与模拟

Figure 2. Undrained torsional shear hollow cylinder tests and simulated results at different α and b of moist tamped loose sand

下载: 全尺寸图片幻灯片

图 3 不同中主应力系数与主应力方向下干砂雨法试样定轴不排水试验结果与模拟

Figure 3. Undrained torsional shear hollow cylinder tests and simulated results at different α and b of dry pluviated loose sand

下载: 全尺寸图片幻灯片

表 1 各向异性CycLiq模型参数

Table 1. Model parameters of anisotropic CycLiq model

G_o	κ	h	d_{re, 1}	d_{re, 2}	d_ir	α	γ_{d, r}	n^p	n^d	M	λ_e	Γ	Δ₁	Δ₂	c
100	0.008	4.0	0.7	30	0.3	30	0.05	12	2	1.2	0.008	0.761	1.35	0.8	5

下载: 导出CSV

| 显示表格

图 2展示了湿装夯实法试样定轴不排水试验结果与模拟。湿装夯实法得到的试样均为松砂，各试验和模拟均出现静态液化。总体上来看，随着b和α的增加，试验与模拟中试样的峰值偏应力均不断减小。从图 2（a），（c）中可以看出，试验中b = 0.2的3组曲线极为接近，甚至α = 30°的偏应力要高于α = 22.5°，这主要是试验中不同试样的孔隙比相差较大造成的，在模拟中该现象并不明显。此外，b = 0.5的模拟结果在加载初期剪应力出现了明显的减小，这主要是由于本构模型中组构对塑性模量的影响描述不够准确，在大孔隙比下放大了组构对塑性模量的影响。

图 3展示了干砂雨法试样定轴不排水试验结果与模拟。相比于湿装夯实法，干砂雨法得到的试样孔隙比更小，可认为密砂。各组模拟的曲线与试验结果均有较好的吻合。对于b = 0.2的3组试验和模拟，α = 22.5°时均表现出明显的剪胀，而在α = 45°时则表现出强烈的剪缩。对于b = 0，α = 0°和b = 0.2，α = 22.5°两组试验，试验和模拟的曲线在图 3（a），（b）均出现了交叉，这是由于两者的孔隙比相差较大，在孔隙比、中主应力系数、主应力方向三者的共同作用下出现了图中的效果。

2.2 定轴等剪应力排水试验

在定轴不排水剪切试验的基础上，Fanni等^[8]进行了一系列定轴等剪应力排水试验，以探究各向异性对等剪应力排水应力路径的影响。试验中采用了湿装夯实法（MT）和干砂雨法（DP）两种制样方法，初始有效球应力均为171 kPa，大小主应力之差均为64 kPa，中主应力系数b分别为0，0.2，主应力与沉积方向的夹角α分别为0°，22.5°和45°。每个夹角均用不同的孔隙比进行试验，对于湿装夯实法，b = 0，α = 0°组采用了6个不同的孔隙比，b = 0.2，α = 22.5°组采用了4个，b = 0.2，α = 45°组采用了10个；对于干砂雨法， b = 0.2，α = 22.5°组1个，b = 0.2，α = 45°组2个。采用表 1中的模型参数进行模拟，模拟中保持偏应力不变，当有效球应力无法再减小时，即试样达到峰值应力比时，认为此时试样处于非稳定态，模拟结束。

图 4给出了湿装夯实法试样在不同b和α下的定轴等剪应力排水试验结果与模拟。图中圆代表初始状态，三角形代表试样达到非稳定态，即处于峰值应力比状态。当相同b和α时，非稳定态的有效球应力p随孔隙比e的增加而增加，3组中模拟与试验均吻合较好。当孔隙比e不变、α增加时，模拟与试验得到的有效球应力均增加。

图 4 不同中主应力系数与主应力方向下湿装夯实法试样定轴等剪应力排水试验结果与模拟

Figure 4. Constant shear drained tests and simulated results at different α and b of moist tamped loose sand

下载: 全尺寸图片幻灯片

图 5给出了干砂雨法试样在不同b和α下的定轴等剪应力排水试验结果与模拟。b = 0.2，α = 45°组试验与模拟结果相近，规律也与湿装夯实法中一致；模拟结果在定量上与试验结果存在差距，推测这是由于模型参数或者初始组构强度不准确导致的。当α增加时，模拟与试验得到的有效球应力均增加，这与湿装夯实法中的规律是一致的。

图 5 不同主应力方向下干砂雨法试样定轴等剪应力排水试验结果与模拟

Figure 5. Constant shear drained tests and simulated results at different α and b of dry pluviated loose sand

下载: 全尺寸图片幻灯片

图 6给出了试验和模拟中非稳定态的结果与趋势线。可以看到试验得到的非稳定态在e-p空间内具有良好的线性关系，对模拟得到的非稳定态进行线性回归，得到R²均在0.99以上，表明模型对等剪应力比试验具有良好的模拟能力。对比湿装夯实法的3组试验，可以发现模拟得到的3条趋势线之间的间距要略小于试验所得，这主要受初始组构强度的影响，具体情况在下文中阐释。

图 6 不同中主应力系数、主应力方向下定轴等剪应力排水试验中非稳定态试验与模拟结果及各自的趋势线

Figure 6. Instability states of constant shear drained tests and simulations at different α and b

下载: 全尺寸图片幻灯片

为了说明初始组构强度对于定轴等剪应力排水条件下土体响应的影响，在数值模拟中对不同初始组构强度条件进行了分析。中给出了不同初始组构强度对非稳定态模拟结果的影响。从图中可以发现初始组构越强，不同主应力方向下的非稳定态差异越大，即峰值应力比差异越大。式（5），（6）中可以解释这一现象。试样达到峰值应力比时，有塑性模量H = 0。当初始组构强度增加，即|| ${\boldsymbol{F}_\text{n}}$ ||增加时，指标|| ${\boldsymbol{F}_\text{n}}$ ||-A_n = || ${\boldsymbol{F}_\text{n}}$ ||(1 – n_F: n)（其中n_F指组构张量的方向）的值域[0, 2|| ${\boldsymbol{F}_\text{n}}$ ||]随之扩大，式（5）所得C的值域也相应扩大。对于定轴试验，初始组构强度增加，导致了不同的b和α计算得到C值之间的差异增加，因H = 0，进而使得式（6）中历史最大峰值应力比M_m（即非稳定态时的应力比）的差异增加，在剪应力q不变的情况下，非稳定态时的球应力p之间的差异也就增加了。这些反映在图 7中即为趋势线之间的间距增加。

图 7 初始组构强度对定轴等剪应力排水试验非稳定态e-p关系的影响

Figure 7. Effects of initial fabric norm on instability state of constant shear drained loading at different α and b

下载: 全尺寸图片幻灯片

3. 结论

本文利用各向异性CycLiq本构模型，模拟了Fanni等^[8]进行的定轴不排水试验与定轴等剪应力排水试验，对比试验结果与模拟结果，可以得到以下3点结论。

（1）对于定轴不排水剪切试验，该模型与试验均表现为随着中主应力系数和加载角度的增加，土体剪缩增强，更易发生静态液化。在定量上，模型模拟的应力路径和应力应变曲线与试验也有较好的吻合。

（2）对于定轴等剪应力排水试验，模型与试验均表现为非稳定态时的平均有效应力随孔隙比和加载角度的增加而增加，且相同加载角度的非稳定态在e-p空间内呈线性分布。总体来说，CycLiq模型对各向异性下砂土等剪应力排水响应的模拟效果较好，具有运用到实际工程中的潜力。

（3）不同初始组构强度对于等剪应力排水试验的结果有显著的影响。初始组构强度越高，不同主应力方向作用下的非稳定态时平均有效应力相差越大。

图 1 典型的SSCC

Figure 1. Typical SSCC

下载: 全尺寸图片幻灯片

图 2 考虑吸引力的离散元法向接触模型

Figure 2. DEM normal contact model considering attraction

下载: 全尺寸图片幻灯片

图 3 室内试验平行组土样干缩开裂后的典型裂缝图像^[29]

Figure 3. Typical crack images after desiccation cracking of clay sample in parallel laboratory tests^[29]

下载: 全尺寸图片幻灯片

图 4 Bioley粉土的SWRC ^[15]与实测质量含水率^[29]

Figure 4. SWRC^[15] of Bioley silt and measured mass water content^[29]

下载: 全尺寸图片幻灯片

图 5 Bioley粉土的吸应力-基质吸力曲线

Figure 5. Suction stress-matric suction curve of Bioley silt

下载: 全尺寸图片幻灯片

图 6 Bioley粉土的SSCC

Figure 6. SSCC of Bioley silt

下载: 全尺寸图片幻灯片

图 7 离散元模拟生成的初始土样

Figure 7. Initial soil sample generated by DEM simulation

下载: 全尺寸图片幻灯片

图 8 离散元模拟得到的不同含水率情况下土颗粒的轴向位移

Figure 8. Axial displacements of soil particles under different water contents obtained by DEM simulation

下载: 全尺寸图片幻灯片

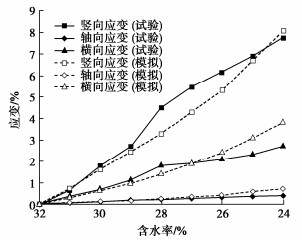
图 9 室内试验^[29]与离散元模拟的土样应变-含水率关系

Figure 9. Strain-water content relationship of soil samples in laboratory tests and DEM simulation

下载: 全尺寸图片幻灯片

图 10 土颗粒轴向位移绝对值的最大值、平均值的归一化百分比

Figure 10. Normalized percentages of maximum value and average value of absolute axial displacement of soil particles

下载: 全尺寸图片幻灯片

图 11 土颗粒间总接触数量与含水率的关系

Figure 11. Relationship between total contact number of DEM soil samples and water content

下载: 全尺寸图片幻灯片

图 12 干缩过程吸应力与含水率的关系

Figure 12. Relationship between suction stress and water content during desiccation

下载: 全尺寸图片幻灯片

图 13 土颗粒间接触力与含水率的关系

Figure 13. Relationship between contact force of soil particles and water content

下载: 全尺寸图片幻灯片

图 14 土颗粒间物理接触力力链与含水率的关系

Figure 14. Relationship between physical contact force chain of soil particles and water content

下载: 全尺寸图片幻灯片

表 1 离散元模拟参数取值

Table 1 Values of parameters for DEM simulation

参数	变量	取值
初始颗粒半径/m	${R_0}$	$1.0 \times {10^{-3}}$
阻尼系数	$\beta$	0.7
颗粒法向刚度/(N·m^-1)	$k_{\text{n}}^{{\text{ball-ball}}}$	$1.0 \times {10^6}$
颗粒切向刚度/(N·m^-1)	$k_{\text{s}}^{{\text{ball-ball}}}$	$8.0 \times {10^5}$
颗粒-墙法向刚度/ (N·m^-1)	$k_{\text{n}}^{{\text{ball-wall}}}$	$1.0 \times {10^7}$
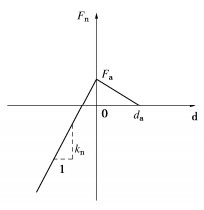
颗粒-墙切向刚度/ (N·m^-1)	$k_{\text{s}}^{{\text{ball-wall}}}$	$8.0 \times {10^6}$
颗粒摩擦系数	${\mu ^{{\text{ball-ball}}}}$	0.20
颗粒-墙摩擦系数	${\mu ^{{\text{ball-wall}}}}$	0.0
吸引力/N	${F_{\text{a}}}$	$d_{50}^2{\sigma _{\text{s}}}$
吸引力作用范围/m	${d_{\text{a}}}$	$1.0{R_{\text{w}}}$

下载: 导出CSV

参考文献(32)

[1]	唐朝生, 施斌, 崔玉军. 土体干缩裂隙的形成发育过程及机理[J]. 岩土工程学报, 2018, 40(8): 1415-1423. doi: 10.11779/CJGE201808006 TANG Chaosheng, SHI Bin, CUI Yujun. Behaviors and mechanisms of desiccation cracking of soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1415-1423. (in Chinese) doi: 10.11779/CJGE201808006
[2]	TANG C S, ZHU C, CHENG Q, et al. Desiccation cracking of soils: A review of investigation approaches, underlying mechanisms, and influencing factors[J]. Earth-Science Reviews, 2021, 216: 103586. doi: 10.1016/j.earscirev.2021.103586
[3]	殷宗泽, 袁俊平, 韦杰, 等. 论裂隙对膨胀土边坡稳定的影响[J]. 岩土工程学报, 2012, 34(12): 2155-2161. http://cge.nhri.cn/cn/article/id/14958 YIN Zongze, YUAN Junping, WEI Jie, et al. Influences of fissures on slope stability of expansive soil[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2155-2161. (in Chinese) http://cge.nhri.cn/cn/article/id/14958
[4]	ALBRECHT B A, BENSON C H. Effect of desiccation on compacted natural clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(1): 67-75. doi: 10.1061/(ASCE)1090-0241(2001)127:1(67)
[5]	RAYHANI M H T, YANFUL E K, FAKHER A. Physical modeling of desiccation cracking in plastic soils [J]. Engineering Geology, 2008, 97(1-2): 25-31. doi: 10.1016/j.enggeo.2007.11.003
[6]	TANG C S, SHI B, LIU C, et al. Influencing factors of geometrical structure of surface shrinkage cracks in clayey soils [J]. Engineering Geology, 2008, 101(3/4): 204-217.
[7]	TANG C S, CUI Y J, TANG A M, et al. Experiment evidence on the temperature dependence of desiccation cracking behavior of clayey soils[J]. Engineering Geology, 2010, 114(3/4): 261-266.
[8]	TRABELSI H, JAMEI M, ZENZRI H, et al. Crack patterns in clayey soils: Experiments and modeling[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(11): 1410-1433. doi: 10.1002/nag.1060
[9]	林朱元, 唐朝生, 曾浩, 等. 土体干缩开裂过程的边界效应试验与离散元模拟[J]. 岩土工程学报, 2020, 42(2): 372-380. doi: 10.11779/CJGE202002019 LIN Zhuyuan, TANG Chaosheng, ZENG Hao, et al. Laboratory characterization and discrete element modeling of desiccation cracking behavior of soils under different boundary conditions[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(2): 372-380. (in Chinese) doi: 10.11779/CJGE202002019
[10]	GUO Y, HAN C J, YU X. Laboratory characterization and discrete element modeling of shrinkage and cracking in clay layer[J]. Canadian Geotechnical Journal, 2018, 55(5): 680-688. doi: 10.1139/cgj-2016-0674
[11]	沈珠江, 邓刚. 黏土干湿循环中裂缝演变过程的数值模拟[J]. 岩土力学, 2004, 25(增刊2): 1-6, 12. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2004S2000.htm SHEN Zhujiang, DENG Gang. Numerical simulation of crack evolution in clay during drying and wetting cycle[J]. Rock and Soil Mechanics, 2004, 25(S2): 1-6, 12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2004S2000.htm
[12]	WANG X N, YU P, YU J L, et al. Simulated crack and slip plane propagation in soil slopes with embedded discontinuities using XFEM[J]. International Journal of Geomechanics, 2018, 18(12): 04018170. doi: 10.1061/(ASCE)GM.1943-5622.0001290
[13]	SANCHEZ M, MANZOLI O L, GUIMARAES L J N. Modeling 3-D desiccation soil crack networks using a mesh fragmentation technique[J]. Computers and Geotechnics, 2014, 62: 27-39. doi: 10.1016/j.compgeo.2014.06.009
[14]	YAN C Z, WANG T, KE W H, et al. A 2D FDEM-based moisture diffusion-fracture coupling model for simulating soil desiccation cracking [J]. Acta Geotechnica, 2021, 16(8): 2609-2628. doi: 10.1007/s11440-021-01297-4
[15]	PERON H, DELENNE J Y, LALOUI L, et al. Discrete element modelling of drying shrinkage and cracking of soils [J]. Computers and Geotechnics, 2009, 36(1-2): 61-69. doi: 10.1016/j.compgeo.2008.04.002
[16]	EL YOUSSOUFI M S, DELENNE J Y, RADJAI F. Self-stresses and crack formation by particle swelling in cohesive granular media [J]. Physical Review E, 2005, 71(5): 051307. doi: 10.1103/PhysRevE.71.051307
[17]	SIMA J, JIANG M J, ZHOU C B. Numerical simulation of desiccation cracking in a thin clay layer using 3D discrete element modeling [J]. Computers and Geotechnics, 2014, 56: 168-180. doi: 10.1016/j.compgeo.2013.12.003
[18]	司马军, 蒋明镜, 周创兵. 黏性土干缩开裂过程离散元数值模拟[J]. 岩土工程学报, 2013, 35(增刊2): 286-291. http://cge.nhri.cn/cn/article/id/15396 SIMA Jun, JIANG Mingjing, ZHOU Chuangbing. Numerical simulation of desiccation cracking of clay soils by DEM[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 286-291. (in Chinese) http://cge.nhri.cn/cn/article/id/15396
[19]	LIN Z Y, WANG Y S, TANG C S, et al. Discrete element modelling of desiccation cracking in thin clay layer under different basal boundary conditions[J]. Computers and Geotechnics, 2021, 130: 103931. doi: 10.1016/j.compgeo.2020.103931
[20]	LE T C, LIU C, TANG C S, et al. Numerical simulation of desiccation cracking in clayey soil using a multifield coupling discrete-element model[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2022, 148(2): 04021183. doi: 10.1061/(ASCE)GT.1943-5606.0002747
[21]	MITCHELL J K, SOGA K. Fundamentals of Soil Behaviour[M]. Hoboken, New Jersey: John Wiley & Sons, Inc, 2005.
[22]	施斌, 唐朝生, 王宝军, 等. 黏性土在不同温度下龟裂的发展及其机理讨论[J]. 高校地质学报, 2009, 15(2): 192-198. doi: 10.3969/j.issn.1006-7493.2009.02.007 SHI Bin, TANG Chaosheng, WANG Baojun, et al. Development and mechanism of desiccation cracking of clayey soil under different temperatures[J]. Geological Journal of China Universities, 2009, 15(2): 192-198. (in Chinese) doi: 10.3969/j.issn.1006-7493.2009.02.007
[23]	LU N, LIKOS W J. Suction stress characteristic curve for unsaturated soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(2): 131-142. doi: 10.1061/(ASCE)1090-0241(2006)132:2(131)
[24]	ZHANG C, LU N. Unified effective stress equation for soil [J]. Journal of Engineering Mechanics, 2020, 146(2): 04019135. doi: 10.1061/(ASCE)EM.1943-7889.0001718
[25]	ZHANG C, LI J Z, ZHANG Y X, et al. Experimental and discrete element modeling study on suction stress characteristic curve and soil-water characteristic curve of unsaturated reticulated red clay [J]. Bulletin of Engineering Geology and the Environment, 2022, 81(9): 363. doi: 10.1007/s10064-022-02834-5
[26]	GUO L, CHEN G, DING L, et al. Numerical simulation of full desiccation process of clayey soils using an extended DDA model with soil suction consideration [J]. Computers and Geotechnics, 2023, 153: 105107. doi: 10.1016/j.compgeo.2022.105107
[27]	VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. doi: 10.2136/sssaj1980.03615995004400050002x
[28]	LU N, GODT J W, WU D T. A closed-form equation for effective stress in unsaturated soil [J]. Water Resources Research, 2010, 46(5): 567-573.
[29]	PERON H, LALOUI L, HUECKEL T, et al. Experimental study of desiccation of soil [M]. Unsaturated Soils 2006. ASCE geotechnical special publication 147. 2006: 1073-1084.
[30]	YAO M. Three-Dimensional Discrete Element Method Analysis of Cohesive Soil[D]. Baltimore: The Johns Hopkins University, 2002.
[31]	YAO M, ANANDARAJAH A. Three-dimensional discrete element method of analysis of clays [J]. Journal of Engineering Mechanics, 2003, 129(6): 585-596. doi: 10.1061/(ASCE)0733-9399(2003)129:6(585)
[32]	SOULIE F, CHERBLANC F, EL YOUSSOUFI M S, et al. Influence of liquid bridges on the mechanical behaviour of polydisperse granular materials[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(3): 213-228. doi: 10.1002/nag.476