考虑小应变刚度特性的软土边界面模型与应用

梁发云; 郑瀚波; 李林; 王如路; 闫静雅

doi:10.11779/CJGE20230187

考虑小应变刚度特性的软土边界面模型与应用 English Version

1.
同济大学地下建筑与工程系, 上海 200092
2.
长安大学公路学院, 陕西西安 710064
3.
上海申通地铁集团有限公司, 上海 200070

基金项目:

上海市优秀技术带头人计划资助项目 21XD1430900

详细信息

作者简介:
梁发云(1976— )，男，博士，教授，主要从事土力学与基础工程的教学科研工作。E-mail: fyliang@tongji.edu.cn

中图分类号: TU43
计量
- 文章访问数: 347
- HTML全文浏览量: 36
- PDF下载量: 107
出版历程
- 收稿日期: 2023-03-02
- 网络出版日期: 2024-05-14
- 刊出日期: 2024-04-30

Bounding surface constitutive model for soft soils considering characteristics of small-strain stiffness and its application in engineering

1.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
2.
Highway College, Chang'an University, Xi'an 710064, China
3.
Shanghai Shentong Metro Group Co., Ltd., Shanghai 200070, China

摘要

摘要: 基坑开挖导致周边土体经历复杂的加卸载应力路径，传统的本构模型难以同时反映此过程中土体的超固结和小应变刚度特性。在现有的边界面模型中，引入土体小应变刚度特性，提出软土边界面模型小应变刚度修正方法。基于一种高效的半隐式应力更新算法，将改进后的边界面模型采用UMAT子程序二次开发嵌入有限元软件ABAQUS中，并应用于某地铁车站深基坑开挖工程的数值模拟。分析结果表明，采用改进模型准确地反映了上海地区典型土层的小应变状态本构关系和土体的应变刚度相关性；由于改进的边界面模型能够同时反映土体超固结和小应变刚度特性，计算的围护结构变形与现场监测数据吻合较好。
- 边界面模型 /
- 小应变刚度 /
- 半隐式应力更新算法 /
- 深基坑工程
Abstract: The construction of an excavation pit induces complex loading-unloading stress paths in the surrounding soils, while the commonly used constitutive models are insufficient to reflect the over-consolidation and small-strain stiffness characteristics during excavation. In this study, a modified bounding surface model considering the over-consolidation and strain-stiffness relationship of soft soils is proposed by modifying the shear modulus under small-strain state. Based on the user defined material subroutine (UMAT), the modified bounding surface model is developed into the finite element software ABAQUS through an accurate and efficient semi-implicit stress update algorithm, and the numerical simulation is carried out for a deep excavation of underground station. The constitutive relationship of typical Shanghai soil under small-strain state is well predicted by the proposed model. The stress-strain curve results show that the proposed model reflects the relationship between soil strain and stiffness reasonably. Since the modified bounding surface model reasonably reflect the over-consolidation and small-strain stiffness characteristics of soil in the same time, the numerical simulation results by the proposed model satisfy the field data.
- bounding surface model /
- small-strain stiffness /
- semi-implicit stress update algorithm /
- deep excavation engineering

HTML全文

0. 引言

注浆是裂隙岩体加固防渗的主要手段，在基础工程设施领域得到了广泛应用^[1-2]。深入了解浆液在岩体裂隙中的运移规律对于工程实践具有重要指导意义。

试验是研究注浆扩散机理的重要途径，国内外学者在该领域开展了大量研究工作。Funehag等采用亚克力板制作了单裂隙平板注浆试验装置，研究了宾汉姆浆液黏度、屈服应力和扩散特性^[3]。Sui等利用单裂隙模型试验台，通过正交试验研究了动水条件下裂隙宽度、初始水流速度、浆液胶凝时间、注浆量等对注浆堵漏效率的影响^[4]。李术才等^[5]、刘人太等^[6]研制了大尺寸平板裂隙注浆模型试验系统，开展了裂隙岩体动水注浆模型试验研究，对浆液扩散性能和封堵效果进行了定量评价。Wang等^[7]设计了一种微裂隙注浆试验系统，采用多种超细水泥浆液，进行不同裂隙开度条件下注浆试验，揭示了注浆压力和注浆量对注浆加固效果的影响。Liang等^[8]设计了倾斜裂隙模型试验装置，研究了不同裂隙倾角条件下，注浆对水砂混合物排放控制效果的影响。总体来看，上述研究主要针对水泥、水玻璃等常密度浆液，所得结论不适用于解释具有自膨胀特性的高聚物注浆材料的扩散行为。

近年来，具有自膨胀特性的聚氨酯类高聚物注浆材料及其高压注射技术在国际上发展十分迅速，成为岩土工程领域较为活跃的发展方向之一^[9]。高聚物浆液具有反应速度快、膨胀率高、防水抗渗、安全环保等特点，成为综合性能较优的注浆材料，在地下工程水害防治等领域得到广泛应用^[10]。为揭示高聚物材料裂隙注浆扩散机理，Hao等^[11]和Li等^[12]设计了单裂隙平板注浆模型试验装置，测试了不同注浆量条件下高聚物浆液在裂隙中的扩散特性和压力分布。Liang等^[13]研究了高聚物浆液在竖向裂隙中的膨胀扩散特性。

一些学者已注意到高聚物浆液反应过程中的高放热现象，石明生等研究了双组分聚氨酯高聚物材料在固化过程中的温度变化规律^[14]。郝梅美^[15]研究发现，在相同环境温度下，高聚物膨胀速率随浆液预热温度的升高而增大，原因在于提高预热温度能够加快浆液化学反应速度，加速体系升温和物理发泡剂气化，从而使浆液膨胀速率加快。

可以推断，当浆液流动过程中与周围介质之间由于温差发生热传导时将改变浆液温度场分布，进而影响其反应速率和扩散过程。尤其对于裂隙注浆，由于裂隙面延展范围大、开度小，浆液与裂隙壁接触面积大，因温差产生的热传导对浆液温度场及其扩散过程的影响无疑会更加显著。但目前关于温度和热传导效应对高聚物裂隙注浆扩散行为的影响仅限于定性了解，缺乏系统深入的试验研究。

基于这一背景，本文设计了平板裂隙注浆模型试验装置，以一种工程中常用的聚氨酯高聚物浆液为对象，开展了系列注浆试验，测试不同条件下高聚物浆液在平板裂隙中的扩散特性，分析浆液预热温度、环境温度、注浆量等因素对浆液扩散行为的影响，研究高聚物扩散过程浆液温度场变化及分布特征，旨在深化对高聚物裂隙注浆扩散机理的认识，为高聚物注浆工艺设计和施工方案制定提供参考依据。

1. 裂隙注浆试验介绍

1.1 试验装置

试验装置由可视化裂隙注浆平台，温度采集系统，高聚物注浆系统3部分组成，试验装置组成如图 1所示。

图 1 试验装置示意图

Figure 1. Schematic plot of test device

下载: 全尺寸图片幻灯片

裂隙注浆平台由上下两块1.2 m×1.2 m×15 mm尺寸透明亚克力板，加固装置及垫片构成，如图 2所示。在上板表面中心处钻直径10 mm圆孔作为注浆孔。为避免亚克力板在浆液膨胀压力下产生过大变形，在上、下板外侧分别放置4根1.5 m×50 mm×30 mm钢条，利用螺栓将钢条与亚克力板固定，提升亚克力板抵抗变形能力。通过在上、下板间放置长条状垫片形成裂隙空间。为安设温度传感器，以注浆孔为中心，在上板面沿两垂直中轴线方向钻直径2 mm圆孔，相邻两孔间隔10 cm，其中，^#1~^#15孔钻透板底，^#16~^#20孔钻深7.5 mm（上板厚度一半）。

图 2 可视化裂隙注浆平台

Figure 2. Visual fracture grouting platform

下载: 全尺寸图片幻灯片

温度采集系统如图 3所示，包含温度采集仪和K型热电偶。温度采集仪为慧谱TCP-X多路温度采集仪，能够精确快速、稳定可靠地记录高聚物膨胀扩散过程中的温度变化。把K型热电偶探头插入预先布好的钻孔中，在孔周围涂抹热熔胶将其黏结固定。如图 4所示，^#1~^#10号探头悬浮于裂隙中，用于测量高聚物浆液温度，^#11~^#15号探头紧贴亚克力板内侧，用于测量浆液扩散过程中高聚物与亚克力板的接触温度，^#16~^#20号探头位于亚克力板内部，用于测量亚克力板壁面内温度。

图 3 温度采集系统

Figure 3. Temperature acquisition system

下载: 全尺寸图片幻灯片

图 4 热电偶布置示意图

Figure 4. Schematic plot of thermocouple layout

下载: 全尺寸图片幻灯片

高聚物注浆系统采用重大基础设施检测修复技术国家地方联合工程实验室开发的集成式多功能注浆系统。该系统主要由供料子系统和注射子系统组成，供料子系统将高聚物A，B两种原料按一定比例吸入其内部，利用加热器将两种原料加热至设定的预热温度后通过输料管送入注射子系统中，经注射枪高速混合后高压输出，完成注浆过程。

1.2 试验材料

试验采用的聚氨酯高聚物浆液由A，B两种组分构成，A组分为多亚甲基多苯基多异氰酸酯，B组分主要由多元醇、催化剂、发泡剂等构成。A，B两种组分的质量混合比为1.1∶1，材料配比组成见表 1。高聚物浆液黏度在初凝前基本保持稳定（小于0.8 Pa·s），接近初凝时黏度急剧升高；浆液固化体抗压强度和抗拉强度随材料密度的增大而增大，当材料密度为0.9 g/cm³时，抗压和抗拉强度分别达到36 MPa和13 MPa；浆液固化体具有较好的抗渗性能，渗透系数为1×10^-8~1×10^-9 cm/s。

表 1 高聚物浆液材料配比

Table 1. Proportioning of polymer slurry materials

组分	原料	质量分数/%
A组分	多亚甲基多苯基多异氰酸酯	100
B组分	硬泡聚醚多元醇体系	35
	聚酯多元醇（PS-3152）	15
	阻燃剂（磷酸三乙酯）	10
	催化剂体系	2
	表面活性剂（L6950）	0.5
	物理发泡剂	5
	化学发泡剂	0.5
	其它	32

下载: 导出CSV

| 显示表格

该浆液的固化过程主要包括两个化学反应——凝胶反应和发泡反应。异氰酸酯和多元醇反应生成聚氨酯的过程被称为凝胶反应，其反应方程式为

\begin{aligned} n N C O - R - N C O + n H O - R^{'} - O H \to \\ - {[O - R^{'} - O - C O N H - R - N H C O]}_{n} - 。 \end{aligned}

$\begin{aligned} & n \mathrm{NCO}-\mathrm{R}-\mathrm{NCO}+n \mathrm{HO}-\mathrm{R}^{\prime}-\mathrm{OH} \rightarrow \\ & \quad\quad-\left[\mathrm{O}-\mathrm{R}^{\prime}-\mathrm{O}-\mathrm{CONH}-\mathrm{R}-\mathrm{NHCO}\right]_n-。 \end{aligned}$

(1)

在采用水作为化学发泡剂的情况下，异氰酸酯和水反应生成脲和二氧化碳的反应被称为发泡反应，其反应方程式为

2 R - N C O + H_{2} O \to R - N H - C O - N H - R + {C O}_{2} ↑ 。

$2 \mathrm{R}-\mathrm{NCO}+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{R}-\mathrm{NH}-\mathrm{CO}-\mathrm{NH}-\mathrm{R}+\mathrm{CO}_2 \uparrow 。$

(2)

在高聚物浆液被注入裂隙后，迅速发生化学反应，释放大量热能，一方面促使浆液体系温度不断上升，加速反应进行，另一方面，使浆液中溶解的液态物理发泡剂逐渐气化形成大量微小闭孔气泡悬浮于浆液中，连同发泡反应生成的二氧化碳气体，促使浆液体积膨胀，驱动浆体流动。

1.3 试验过程

首先组装裂隙注浆试验平台，然后连接K型热电偶与温度采集仪，待环境温度达到设定值之后开始注浆试验。利用高聚物注浆系统将预热至设定温度的浆液通过注射枪高压（注浆压力7 MPa）注入裂隙中，此后注浆压力撤去，高聚物浆液依靠其自身的化学反应膨胀，驱动浆液流动扩散，观察高聚物扩散过程，同步记录温度变化。重复上述步骤，依次开展试验，试验各影响因素取值列于表 2中。

表 2 试验各影响因素取值

Table 2. Values of influencing factors of tests

编号	注浆量/g	浆液预热温度/℃	环境温度/℃
^#1	500	30	20
^#2	625	40	30
^#3	750	50	—

下载: 导出CSV

| 显示表格

2. 试验结果分析

2.1 高聚物浆液扩散形态及温度变化和分布特征

图 5所示为裂隙开度7 mm，注浆量500 g，预热温度40℃，环境温度30℃条件下高聚物浆液在裂隙中的扩散过程，高聚物浆液被注入裂隙后开始发生化学反应，浆液以圆饼状向周围迅速膨胀扩散，由最初的透明液态逐渐转变为淡黄色固态。图 6，7分别为对应工况r=10，20 cm测点处浆液温度随时间变化曲线和不同时刻浆液温度沿径向分布情况，可以看到，高聚物浆液温度在反应过程中先快速升高，达到峰值后逐渐降低，温度下降速度低于上升速度；充填区域内的浆液温度分布随时间不断变化，任一时刻，在注浆孔中心处温度最高，沿径向逐渐降低。

图 5 高聚物浆液在裂隙中扩散过程

Figure 5. Fracture diffusion process of polymer slurry

下载: 全尺寸图片幻灯片

图 6 注浆量500 g，预热温度40℃，环境温度30℃不同测点处高聚物温度随时间变化曲线

Figure 6. Variation curves of polymer temperature with time at different measuring points under grouting amount 500 g, preheating temperature 40℃ and ambient temperature 30℃

下载: 全尺寸图片幻灯片

图 7 注浆量500 g，预热温度40℃，环境温度30℃不同时刻高聚物浆液温度沿径向变化曲线

Figure 7. Radial variation curves of polymer temperature with time at different time under grouting amount 500 g, preheating temperature 40℃ and ambient temperature 30℃

下载: 全尺寸图片幻灯片

2.2 预热温度对浆液膨胀扩散过程的影响

裂隙开度7 mm，环境温度30℃，预热温度分别为30℃，40℃和50℃条件下，注浆量为500，625 g时浆液扩散半径随时间的变化如图 8所示，对应工况的浆液最终扩散半径如图 9所示。从图 8可以看出，不同注浆量条件下，浆液扩散过程均表现出相似特征，预热温度越高，浆液扩散速率越快，初凝时间越早，预热温度30℃时的扩散速率和初凝时间显著低于40℃和50℃时的测试结果。当注浆量为500 g，浆液预热温度30℃，40℃，50℃时，其扩散平均速率分别为1.09，2.03，2.31 cm/s，初凝时间分别为22，18，16 s。注浆量625 g，预热温度30℃，40℃，50℃时的平均扩散速率分别为1.04，2.25，2.73 cm/s，分别在24，18，15 s时达到初凝，与500 g时对应预热温度条件下的初凝时间较为接近。

图 8 不同预热温度条件下高聚物扩散半径随时间变化曲线

Figure 8. Variation curves of polymer diffusion radius with time under different preheating temperature conditions

下载: 全尺寸图片幻灯片

图 9 不同注浆量时高聚物扩散半径-预热温度变化柱状图

Figure 9. Histograms of polymer diffusion radius-preheating temperature change under different grouting amounts

下载: 全尺寸图片幻灯片

从图 9中可以发现，预热温度为40℃和50℃时浆液扩散范围较为接近，而预热温度30℃时的浆液最终扩散半径远小于前两者。注浆量500 g时，预热温度30℃，40℃，50℃条件下浆液的最终扩散半径分别为24，36.5，37 cm；注浆量625 g时，3种预热温度条件下浆液最终扩散半径分别为25，40.5，41 cm。分析其原因在于，当预热温度为30℃时，化学反应速率较慢，浆液反应不充分，体系温度较低，物理发泡剂未充分气化，导致体积膨胀倍率较低。从试验结果来看，预热温度40℃以上时浆液反应已较为充分，物理发泡剂充分气化，因此随着温度的继续升高浆液扩散半径不再显著增加。

裂隙开度为7 mm，环境温度为30℃，预热温度为50℃，注浆量分别为500，625 g时高聚物扩散半径及温度随时间变化曲线如图 10所示。可以看到，当注浆量为500 g时，浆液在14 s时达到初凝，此后扩散范围不再增大，但温度仍继续上升，19 s时达到峰值（132℃），之后逐渐下降。注浆量625 g时的试验结果表现出类似特征，表明高聚物浆液化学反应进程与其扩散过程并不同步，浆液化学反应终止时间晚于其初凝时间。

图 10 不同注浆量时高聚物扩散半径、温度随时间变化曲线

Figure 10. Variation curves of polymer diffusion radius and temperature with time under different grouting amounts

下载: 全尺寸图片幻灯片

2.3 预热温度对浆液温度的影响

图 11为注浆量750 g，裂隙开度7 mm，环境温度30℃，预热温度30℃，40℃，50℃条件下，距离注浆孔10，20 cm测点处高聚物浆液温度随时间变化曲线；图 12为预热温度40℃，50℃条件下，t=20，40 s时浆液温度沿径向分布情况。可以看出，不同工况下高聚物温度变化均呈现先升高后下降的趋势。预热温度越高，浆液温度变化速率越快，达到峰值的时刻越早。在10 cm测点处，当预热温度为30℃，40℃，50℃时，浆液温度分别在68，34，20 s达到峰值，峰值温度分别为105℃，129℃，151℃。在温度下降阶段，预热温度30℃工况下浆液温度下降速度慢于其他两种工况，分析其原因可能是由于该工况下浆液扩散范围较小，与裂隙壁接触面积小，因此受热传导效应影响小，使浆液温度下降速率相对较慢。在其它条件相同的情况下，同一时刻预热温度越高，对应测点处浆液温度越高。

图 11 注浆量750 g不同预热温度、不同位置处浆液温度随时间变化曲线

Figure 11. Variation curves of slurry temperature with time at different preheating temperatures and different positions under grouting amount 750 g

下载: 全尺寸图片幻灯片

图 12 注浆量750 g不同预热温度、不同时刻浆液温度沿径向分布曲线

Figure 12. Distribution curves of slurry temperature along radial direction at different preheating temperatures and different time under grouting amount 750 g

下载: 全尺寸图片幻灯片

2.4 环境温度对浆液温度的影响

裂隙开度7 mm，注浆量750 g，预热温度50℃，环境温度20℃和30℃条件下，r=10，20 cm测点处浆液温度随时间变化曲线和t=30，60 s时高聚物温度径向分布情况分别如图 13，14所示。可以看出，环境温度越高，浆液温度上升速率越快，达到峰值的时刻越早，环境温度30℃时的浆液温度和上升速率始终高于环境温度20℃时的试验结果；10 cm测点处，前者浆液温度在20 s时达到峰值151℃，而后者在22 s时才达到峰值133℃；同一时刻注浆孔中心处浆液温度最高，沿径向逐渐降低，在不同位置处，浆液温度随着环境温度的升高而增大。

图 13 注浆量750 g，预热温度50℃不同环境温度不同位置处浆液温度随时间变化曲线

Figure 13. Variation curves of slurry temperature with time at different ambient temperatures and different positions under grouting amount 750 g and preheating temperature 50℃

下载: 全尺寸图片幻灯片

图 14 注浆量750 g，预热温度50℃不同环境温度不同时刻浆液温度沿径向分布曲线

Figure 14. Distribution curves of temperature along radial direction at different ambient temperatures and different time under grouting amount 750 g and preheating temperature 50℃

下载: 全尺寸图片幻灯片

2.5 高聚物浆液与裂隙壁热传导效应

预热温度50℃，环境温度30℃，裂隙开度7 mm，注浆量750 g时，r=10，20 cm测点处高聚物温度、接触面温度及裂隙壁内温度随时间变化曲线及t=30，50 s时以上3类温度的径向分布情况分别如图 15，16所示。从图 15可以看出，高聚物温度与接触面温度随时间变化趋势基本保持同步，先升高然后逐渐降低，几乎同时达到峰值，受热传导作用影响，过峰值后两者温度逐渐下降，但相同位置处接触面温度始终低于高聚物温度。在10 cm测点处，高聚物和接触面峰值温度分别为151℃，93℃，在20 cm测点处，两者的峰值温度分别为129℃，80℃。裂隙壁内温度在初始时刻与环境温度相同，然后随时间缓慢升高，在测试时间范围内始终低于接触面温度。200 s时10 cm测点处温度达到33.8℃，20 cm测点处温度达到32.07℃。其原因在于，在测试时间范围内浆液温度始终高于裂隙壁面温度，受热传导效应影响，裂隙壁内温度逐渐上升。

图 15 注浆量750 g，预热温度50℃，环境温度30℃时高聚物温度、接触面温度及裂隙壁内温度随时间变化曲线

Figure 15. Variation curves of polymer temperature, contact surface temperature and wall temperature with time under grouting amount 750 g, preheating temperature 50℃ and ambient temperature 30℃

下载: 全尺寸图片幻灯片

图 16 注浆量750 g，预热温度50℃，环境温度30℃时不同时刻高聚物温度、接触面温度及壁面内温度沿径向分布曲线

Figure 16. Distribution curves of polymer temperature, contact surface temperature and wall temperature along radial direction under grouting amount 750 g, preheating temperature 50℃ and ambient temperature 30℃

下载: 全尺寸图片幻灯片

从图 16可以看出，裂隙壁内温度始终低于高聚物温度和接触面温度。由于热传导效应，50 s时裂隙壁内不同测点处温度均高于30 s时对应位置测试结果。

2.6 温度和热传导效应对高聚物浆液在裂隙中扩散过程影响机制分析

高聚物浆液被高速混合注入裂隙后，迅速发生化学反应，释放大量热能，促使浆液温度不断上升，使浆液中溶解的液态物理发泡剂达到沸点温度后逐渐气化，连同发泡反应生成的气体，驱动浆液体积快速膨胀并持续扩散。由于温度是影响浆液化学反应速率的重要因素，因此温度变化尤其是浆液预热温度的改变对浆液扩散过程产生较显著影响。

浆液反应过程中温度不断升高与裂隙壁间形成较大温差，因温差产生的热传导使一部分热能通过接触面由浆液传递到裂隙壁内，导致浆液温度减小，改变了温度场分布，降低浆液反应速度和扩散速率。环境温度的变化改变浆液与裂隙壁间的温差，影响两者间热传导效应和温度场变化速率，间接对浆液反应速度和扩散过程产生影响。

3. 结论

（1）浆液预热温度对高聚物扩散过程具有重要影响。相同注浆量条件下，预热温度越高，浆液扩散速率越快，初凝时间越早，浆液扩散半径越大，当预热温度升高至一定值时，浆液扩散范围基本不再变化。

（2）浆液扩散过程与其化学反应进程不完全同步，化学反应终止时间晚于初凝时间。不同注浆量条件下浆液扩散半径、温度随时间变化趋势基本一致，其峰值随着注浆量的增大而增大。

（3）高聚物浆液温度时空演变过程具有明显规律性。不同测点处浆液温度随时间均呈现先升高后下降，变化速率由快到慢的演化特征；在体系温度达到平衡前，注浆孔中心处温度最高，沿径向逐渐递减。

（4）随着预热温度和环境温度的升高，浆液整体温度增大，升温速度加快，峰值温度增高，达到峰值点的时刻变早。与预热温度相比，环境温度对浆液温度变化速率影响相对较小。

（5）受高聚物与裂隙壁温差影响，浆液在裂隙内扩散过程中存在明显热传导效应，使得浆液温度达到峰值后逐渐下降，当两者温度达到平衡前，浆液温度高于接触面温度，接触面温度高于裂隙壁内温度。

围绕温度对高聚物浆液在裂隙中扩散行为影响采用可视化平板裂隙模型开展了初步研究，尚未考虑裂隙壁面粗糙度、起伏度等因素的耦合影响，未来将进一步完善试验装置，使试验工况最大限度逼近真实工程场景，为现场注浆施工提供更有效的指导。

图 1 基坑开挖周边不同位置土体应力路径示意图

Figure 1. Stress paths of soils at different locations around excavation

下载: 全尺寸图片幻灯片

图 2 边界面模型示意图

Figure 2. Diagram of bounding surface model

下载: 全尺寸图片幻灯片

图 3 ABAQUS二次开发UMAT子程序调用原理

Figure 3. Calling mechanism of UMAT subroutine in ABAQUS

下载: 全尺寸图片幻灯片

图 4 半隐式应力更新算法示意图

Figure 4. Diagram of semi-implicit stress updating algorithm

下载: 全尺寸图片幻灯片

图 5 小应变下模型预测应力-应变关系与试验对比结果

Figure 5. Comparison of stress-strain curves between predicted and test results under small-strain state

下载: 全尺寸图片幻灯片

图 6 三轴排水剪切试验预测结果对比

Figure 6. Comparison between predicted and test results of drained triaxial shear tests

下载: 全尺寸图片幻灯片

图 7 基坑开挖施工剖面及土层分布示意图

Figure 7. Diagram of profile and soil layers of excavation

下载: 全尺寸图片幻灯片

图 8 开挖至不同水平时挡墙水平位移沿深度分布曲线

Figure 8. Lateral displacements of retaining wall versus depth after different excavation steps

下载: 全尺寸图片幻灯片

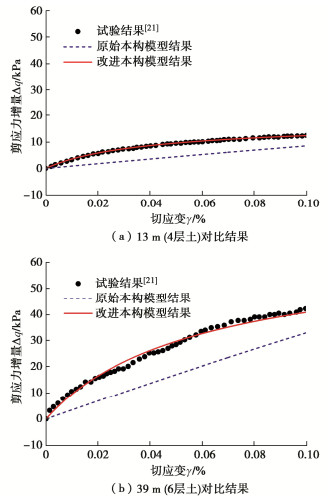
表 1 土体参数取值

Table 1 Soil parameters

土体参数	13 m (4层土)	39 m (6层土)
$M$	1.10	1.15
$\nu$	0.35	0.35
$\lambda$	0.155	0.07
$\kappa$	0.02	0.013
${e_0}$	0.86	0.66
$R$	2.72	2.72
$h$	10	10
$m$	0.02	0.02
${\gamma _{0.7}}$	1.8×10^-4	2.8×10^-4

下载: 导出CSV

表 2 各土层模型参数取值表

Table 2 Model parameters of soil layers

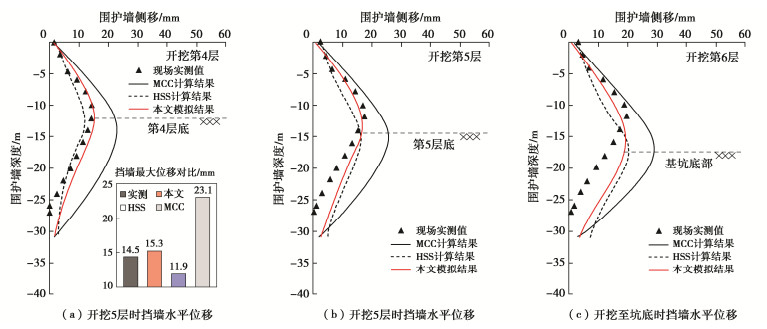
土层\参数	$M$	$\nu$	$\lambda$	$\kappa$	${e_0}$	$R$	$h$	$m$	${\gamma _{0.7}}$ /10^-4
①填土，②黏土	1.20	0.3	0.044	0.009	0.807	2.72	50	0.02	3.2
②₃砂质粉土	1.31	0.3	0.031	0.014	0.728	2.72	50	0.02	3.2
④淤泥质黏土	0.78	0.35	0.081	0.020	1.315	2.72	50	0.02	3.2
⑤₁黏土	1.20	0.3	0.041	0.014	0.882	2.72	50	0.02	3.2
⑤₂粉质黏土	1.29	0.3	0.017	0.003	0.982	2.72	50	0.02	3.9
⑦粉细砂，⑧粉质黏土	1.38	0.3	0.010	0.002	0.965	2.72	50	0.02	3.9

下载: 导出CSV

表 3 基坑开挖分析步设置

Table 3 Construction steps of excavation

分析步	分析步工况描述
Initial	ABAQUS内置初始分析步
1	激活地应力场，地应力平衡计算
2	施工围护结构并激活相应接触对
3	激活第一道砼支撑，完成第一层土体开挖
4	完成第二层土体开挖，激活第二道钢支撑
5	完成第三层土体开挖，激活第三道钢支撑
6	完成第四层土体开挖，激活第四道钢支撑
7	完成第五层土体开挖，激活第五道钢支撑
8	完成最后一层土体开挖，结束计算

下载: 导出CSV

参考文献(36)

[1]	BURLAND J B. Ninth Laurits Bjerrum Memorial Lecture: "Small is beautiful"—the stiffness of soils at small strains[J]. Canadian Geotechnical Journal, 1989, 26(4): 499-516. doi: 10.1139/t89-064
[2]	ATKINSON J H, SALLFORS G. Experimental determination of stress-strain-time characteristics in laboratory and in situ tests[J]. Proceedings of the International Conference on Soil Mechanics and Foundation Engineering, 1991, 3: 915-956.
[3]	上海市住房和城乡建设管理委员会. 基坑工程技术标准: DG/TJ 508—61—2018[S]. 上海: 同济大学出版社, 2018. Ministry of Housing and Urban-rural Development of Shanghai City. Technical Code for Excavation Engineering: DG/TJ 508—61—2018[S]. Shanghai: Tongji University Press, 2018. (in Chinese)
[4]	YIMSIRI S, SOGA K. Micromechanics-based stress-strain behaviour of soils at small strains[J]. Géotechnique, 2000, 50(5): 559-571. doi: 10.1680/geot.2000.50.5.559
[5]	MAŠÍN D. Clay hypoplasticity model including stiffness anisotropy[J]. Géotechnique, 2014, 64(3): 232-238. doi: 10.1680/geot.13.P.065
[6]	BENZ T. Small-strain Stiffness of Soils and its Numerical Consequences[D]. Stuttgart: University of Stuttgart, 2007.
[7]	BRINKGREVE R B J, KUMARSWAMY S, SWOLFS W M, et al. PLAXIS 2016[R]. Delft: PLAXIS, 2016.
[8]	褚峰, 李永盛, 梁发云, 等. 土体小应变条件下紧邻地铁枢纽的超深基坑变形特性数值分析[J]. 岩石力学与工程学报, 2010, 29(增刊1): 3184-3192. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1087.htm CHU Feng, LI Yongsheng, LIANG Fayun, et al. Numerical analysis of deformation of deep excavation adjacent to metro considering small-strain stiffness of soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 3184-3192. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1087.htm
[9]	顾晓强, 吴瑞拓, 梁发云, 等. 上海土体小应变硬化模型整套参数取值方法及工程验证[J]. 岩土力学, 2021, 42(3): 833-845. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103026.htm GU Xiaoqiang, WU Ruituo, LIANG Fayun, et al. On HSS model parameters for Shanghai soils with engineering verification[J]. Rock and Soil Mechanics, 2021, 42(3): 833-845. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103026.htm
[10]	梁发云, 贾亚杰, 丁钰津, 等. 上海地区软土HSS模型参数的试验研究[J]. 岩土工程学报, 2017, 39(2): 269-278. doi: 10.11779/CJGE201702010 LIANG Fayun, JIA Yajie, DING Yujin, et al. Experimental study on parameters of HSS model for soft soils in Shanghai[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 269-278. (in Chinese) doi: 10.11779/CJGE201702010
[11]	王卫东, 王浩然, 徐中华. 上海地区基坑开挖数值分析中土体HS-Small模型参数的研究[J]. 岩土力学, 2013, 34(6): 1766-1774. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201306037.htm WANG Weidong, WANG Haoran, XU Zhonghua. Study of parameters of HS-Small model used in numerical analysis of excavations in Shanghai area[J]. Rock and Soil Mechanics, 2013, 34(6): 1766-1774. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201306037.htm
[12]	李连祥, 刘嘉典, 李克金, 等. 济南典型地层HSS参数选取及适用性研究[J]. 岩土力学, 2019, 40(10): 4021-4029. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201910038.htm LI Lianxiang, LIU Jiadian, LI Kejin, et al. Study of parameters selection and applicability of HSS model in typical stratum of Jinan[J]. Rock and Soil Mechanics, 2019, 40(10): 4021-4029. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201910038.htm
[13]	武朝军. 上海浅部土层沉积环境及其物理力学性质[D]. 上海交通大学, 2016. WU Chaojun. Depositional Environment and Geotechnical Properties for the Upper Shanghai Clays [D]. Shanghai: Shanghai Jiao Tong University 2016. (in Chinese)
[14]	张锋. 计算土力学[M]. 北京: 人民交通出版社, 2007. ZHANG Feng. Computational Soil Mechanics[M]. Beijing: China Communications Press, 2007. (in Chinese)
[15]	郑颖人. 岩土塑性力学的新进展: 广义塑性力学[J]. 岩土工程学报, 2003, 25(1): 1-10. doi: 10.3321/j.issn:1000-4548.2003.01.001 ZHENG Yingren. New development of geotechnical plastic mechanics-generalized plastic mechanics[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(1): 1-10. (in Chinese) doi: 10.3321/j.issn:1000-4548.2003.01.001
[16]	DAFALIAS Y F. The concept and application of the bounding surface in plasticity theory[M]//Physical Non-Linearities in Structural Analysis. Berlin: Springer Berlin Heidelberg, 1981: 56-63.
[17]	DAFALIAS Y F. Bounding surface plasticity: Ⅰ mathematical foundation and hypoplasticity[J]. Journal of Engineering Mechanics, 1986, 112(9): 966-987. doi: 10.1061/(ASCE)0733-9399(1986)112:9(966)
[18]	YAO Y P, HOU W, ZHOU A N. UH model: three- dimensional unified hardening model for overconsolidated clays[J]. Géotechnique, 2009, 59(5): 451-469. doi: 10.1680/geot.2007.00029
[19]	ASAOKA A, NAKANO M, NODA T. Superloading yield surface concept for highly structured soil behavior[J]. Soils and Foundations, 2000, 40(2): 99-110. doi: 10.3208/sandf.40.2_99
[20]	YAO Y P, QU S, YIN Z Y, et al. SSUH model: a small-strain extension of the unified hardening model[J]. Science China Technological Sciences, 2016, 59(2): 225-240. doi: 10.1007/s11431-015-5914-0
[21]	张硕, 叶冠林, 甄亮, 等. 考虑小应变下刚度衰减特征的软土本构模型[J]. 上海交通大学学报, 2019, 53(5): 535-539. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201905006.htm ZHANG Shuo, YE Guanlin, ZHEN Liang, et al. Constitutive model of soft soil after considering small strain stiffness decay characteristics[J]. Journal of Shanghai Jiao Tong University, 2019, 53(5): 535-539. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201905006.htm
[22]	ZHAO J D, SHENG D C, ROUAINIA M, et al. Explicit stress integration of complex soil models[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2005, 29(12): 1209-1229. doi: 10.1002/nag.456
[23]	刘艳秋, 胡存, 刘海笑. 一种适用于饱和黏土循环动力分析边界面塑性模型的隐式积分算法[J]. 岩土力学, 2013, 34(12): 3617-3624. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312042.htm LIU Yanqiu, HU Cun, LIU Haixiao. An implicit integration algorithm in the bounding-surface plasticity model for cyclic behaviors of saturated clay[J]. Rock and Soil Mechanics, 2013, 34(12): 3617-3624. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312042.htm
[24]	陈超斌, 武朝军, 叶冠林, 等. 小应变三轴试验方法及其在上海软土的初步应用[J]. 岩土工程学报, 2015, 37(增刊2): 37-40. doi: 10.11779/CJGE2015S2008 CHEN Chaobin, WU Chaojun, YE Guanlin, et al. Small-strain triaxial test method and its preliminary application in Shanghai soft clay[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 37-40. (in Chinese) doi: 10.11779/CJGE2015S2008
[25]	SANTOS J A, CORREIA A G. Reference threshold shear strain of soil its application to obtain a unique strain-dependent shear modulus curve for soil[C]// 15th International Conference on Soil Mechanics and Geotechnical Engineering. Istanbul, 2001.
[26]	DAFALIAS Y F, HERRMANN L R. Bounding surface plasticity: Ⅱ application to isotropic cohesive soils[J]. Journal of Engineering Mechanics, 1986, 112(12): 1263-1291. doi: 10.1061/(ASCE)0733-9399(1986)112:12(1263)
[27]	KALIAKIN V N, DAFALIAS Y F. Simplifications to the bounding surface model for cohesive soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1989, 13(1): 91-100. doi: 10.1002/nag.1610130108
[28]	徐中华. 上海地区支护结构与主体地下结构相结合的深基坑变形性状研究[D]. 上海: 上海交通大学, 2007. XU Zhonghua. Deformation Behavior of Deep Excavations Supported by Permanent Structure in Shanghai Soft Deposit[D]. Shanghai: Shanghai Jiao Tong University, 2007. (in Chinese)
[29]	SLOAN S W, ABBO A J, SHENG D C. Refined explicit integration of elastoplastic models with automatic error control[J]. Engineering Computations, 2001, 18(1/2): 121-194. doi: 10.1108/02644400110365842
[30]	TAN Y, WEI B, DIAO Y P, et al. Spatial corner effects of long and narrow multipropped deep excavations in Shanghai soft clay[J]. Journal of Performance of Constructed Facilities, 2014, 28(4): 04014015. doi: 10.1061/(ASCE)CF.1943-5509.0000475
[31]	吴瑞拓, 顾晓强, 高广运, 等. 基于HSS模型的上海地铁深基坑开挖变形分析[J]. 建筑科学与工程学报, 2021, 38(6): 64-70. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG202106010.htm WU Ruituo, GU Xiaoqiang, GAO Guangyun, et al. Analysis of deep excavation deformation of Shanghai metro station using HSS model[J]. Journal of Architecture and Civil Engineering, 2021, 38(6): 64-70. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG202106010.htm
[32]	徐中华, 王建华, 王卫东. 上海地区深基坑工程中地下连续墙的变形性状[J]. 土木工程学报, 2008, 41(8): 81-86. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200808015.htm XU Zhonghua, WANG Jianhua, WANG Weidong. Deformation behavior of diaphragm walls in deep excavations in Shanghai[J]. China Civil Engineering Journal, 2008, 41(8): 81-86. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200808015.htm
[33]	邵羽, 江杰, 陈俊羽, 等. 基于HSS模型与MCC模型的深基坑降水开挖变形分析[J]. 水利学报, 2015, 46(增刊1): 231-235. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB2015S1044.htm SHAO Yu, JIANG Jie, CHEN Junyu, et al. Deformation of deep foundation pits due to excavation and dewatering based on HSS model and Modified Cam-Clay Model[J]. Journal of Hydraulic Engineering, 2015, 46(S1): 231-235. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB2015S1044.htm
[34]	徐中华, 王卫东. 敏感环境下基坑数值分析中土体本构模型的选择[J]. 岩土力学, 2010, 31(1): 258-264, 326. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201001045.htm XU Zhonghua, WANG Weidong. Selection of soil constitutive models for numerical analysis of deep excavations in close proximity to sensitive properties[J]. Rock and Soil Mechanics, 2010, 31(1): 258-264, 326. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201001045.htm
[35]	宋广, 宋二祥. 基坑开挖数值模拟中土体本构模型的选取[J]. 工程力学, 2014, 31(5): 86-94. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201405013.htm SONG Guang, SONG Erxiang. Selection of soil constitutive models for numerical simulation of foundation pit excavation[J]. Engineering Mechanics, 2014, 31(5): 86-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201405013.htm
[36]	LIM A, OU C Y, HSIEH P G. Evaluation of clay constitutive models for analysis of deep excavation under undrained conditions[J]. Journal of GeoEngineering, 2010, 5(1): 9-20.