Evolution analysis of over-consolidated state with UH model and verification of hypergravity centrifuge experiments
-
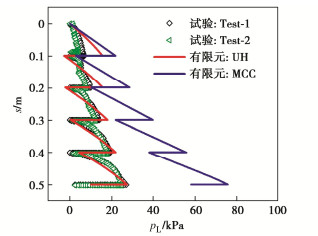
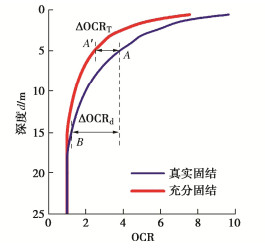
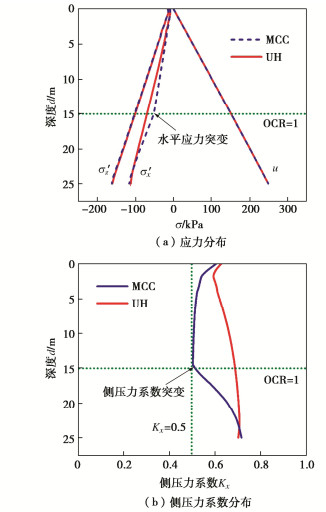
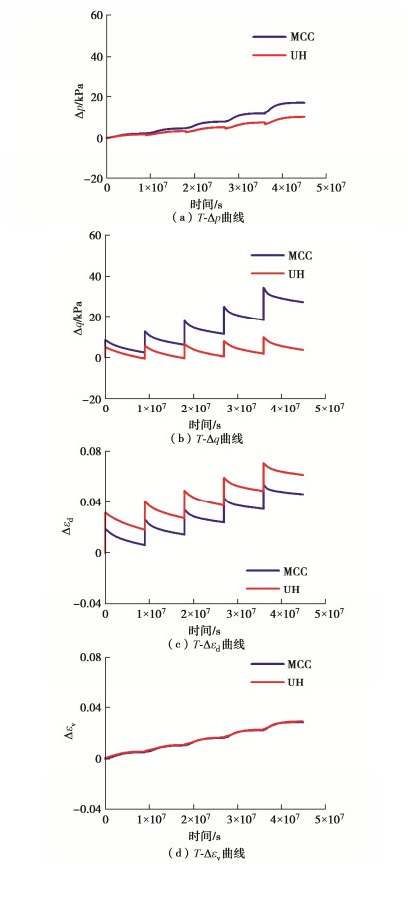
摘要: 本构模型是土力学求解强度变形问题的关键。研究揭示了剑桥模型在超临界侧强度过高、超固结状态下无法应力三维化、应力应变关系发生突变等存在的问题,分析了UH模型建立的超固结状态耦合演化机制及在弹塑性理论框架下实现的超固结状态与正常固结状态计算理论的统一,并基于三轴试验预测证明了UH模型能更加合理地描述超固结状态下土的应力应变关系。通过开展载荷板离心模型试验以及数值模拟验证可以发现,相较于剑桥模型,UH模型计算的地基土荷载变形曲线、侧压力系数分布更加准确,其本质是单元的应力应变关系更加科学、合理。研究证明UH模型的应用能显著提高超固结状态土体强度变形计算的准确性和实用性,对复杂岩土工程问题的计算求解具有重要理论价值和实践意义。Abstract: Development of a proper constitutive model is the key to solving the strength and deformation problem in soil mechanics. It is revealed that the conventional Cam-clay model would exhibit unrealistically high strength on the supercritical side and sudden changes in stress-strain relations, and it is incapable of extending the stress tensor to three dimensions at the over-consolidated state. The coupling evolution mechanism in the over-consolidated state is introduced in a state-of-the-art UH constitutive model and the unification of calculation formulas in the over-consolidated and normal-consolidated states based on the elastoplastic theory. Through comparisons with the triaxial compression test results, it is verified that the UH model can satisfactorily describe the stress-strain relations of the over-consolidated soil. The validations against supergravity tests on the vertical behaviour of a circular plate, in terms of the load-deformation curve and lateral pressure coefficient distribution of the soil, demonstrate the significant advantage of the UH model over the Cam-clay model. The essence is that the stress-strain relations of the soil element can be described in a more scientific and rational manner in the UH model. It is well proved that the UH model significantly improves the accuracy and practicability in assessing the strength and deformation problems of the over-consolidated soil, thus capturing important theoretical value and practical significance in solving complex geotechnical engineering problems.
-
0. 引言
螺旋桩是一种由钢制桩身连杆和焊接在其上的螺旋叶片构成的基础。由于螺旋桩外形的特殊性,可以通过在桩顶施加的扭矩和压力将其旋转按压至土体内。螺旋桩安装所需设备轻便,安装过程快速且噪音小[1];其安装在位后,桩身连杆和螺旋叶片协同承载,提供的抗拔承载力明显大于传统单桩基础[2-3];同时,可通过施加反向扭矩实现螺旋桩的回收利用[4]。基于以上优势,螺旋桩被视作一种有广泛应用价值的海上风电基础形式。
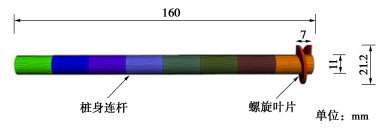
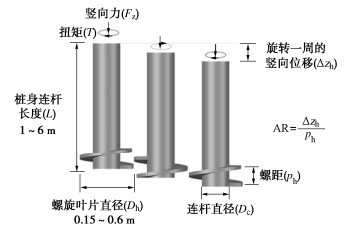
目前,螺旋桩基础常用于锚固或支撑近岸及陆上小型结构[5-6],螺旋叶片直径约0.15~0.6 m,桩身连杆长约1~6 m[7],可以提供的抗拔承载力约为50~300 kN。典型单叶片螺旋桩的外形及安装参数如图 1所示。在极端海况下,典型8 MW四腿导管架海上风电结构若采用螺旋桩作为其单腿基础,其桩长和螺旋叶片直径需分别达30,2 m以上[8]。相比于陆上螺旋桩,应用于海洋工程中的螺旋桩其尺寸需要大幅提升,安装过程需要的压力和扭矩也需要大幅增加。因此,如何准确预测安装螺旋桩所需的压力和扭矩是其应用于海上风电工程中的关键问题之一。许多学者提出螺旋桩安装过程所受力和扭矩的预测模型[9-10],这些预测模型的共同点在于将螺旋桩各部件所受的力和扭矩分别计算。Ghaly等[9]和Sakr[11]预测螺旋桩分别在砂土和无黏性土中安装所受的扭矩时,都将螺旋桩安装扭矩分为作用在桩身连杆、螺旋叶片上下表面、螺旋叶片侧壁等部分产生的扭矩。Therar[12]提出的CPT法预测螺旋叶片受力时,将其分为螺旋叶片底部摩擦力、螺旋叶片侧向摩擦力和螺旋叶片刃口承载力。现有的螺旋桩安装扭矩及压力的预测方法都是在推进比为1的前提下提出的[10]。推进比作为用来描述螺旋桩的安装的重要参数,其计算公式为螺旋桩旋转一周的竖向位移Δzh与螺旋叶片螺距ph的比值。推进比AR的建议取值为1±0.2[13-14],即螺旋桩每旋转一周向下推进约一个螺距,这样的安装形式被称为“螺距匹配”式安装。现有的螺旋桩施工规范建议采用这样安装方式是为了减少安装过程对土体的扰动。
然而,史旦达等[13]通过室内模型试验发现减小AR可以显著降低螺旋挤扩钻具贯入时的竖向阻力以及扭矩。Wang等[15]和Sharif等[14]通过模型试验及离散元数值模拟发现在螺旋桩的安装过程中存在相似的结果。Sharif等[14]应用离散元方法模拟了螺旋桩在不同AR下的安装和上拔,发现在显著减小螺旋桩安装所需竖向力的同时,减小AR可以显著增大螺旋桩的上拔承载力。Cerfontaine等[16]通过离心机实验进一步表明在AR < 0.25时,螺旋桩的整个安装过程都受到土体的下拉作用,即不需要提供额外的竖向压力便可将螺旋桩安装到位。对于海上大型螺旋桩而言,AR对于其施工设备选型以及螺旋桩安装工作能否顺利进行起着关键性作用。
此外,学者们对于螺旋桩安装过程对其周围土体的影响进行了研究。Shi等[17]通过离散元方法模拟螺旋桩在不同AR下的安装过程,发现AR较大时螺旋桩周围土体的孔隙率降低更明显,即螺旋桩安装引起的土体压实效应更强。Sharif等[14]应用离散元方法研究了螺旋桩安装完成后AR对桩周土体残余应力的影响,观察到在较高AR值下安装导致螺旋桩下方产生较大的残余应力且这些应力随AR的增加而增加的现象。史旦达等[13]通过模型试验研究了不同AR下安装螺旋挤扩钻具时周围土体的组构演化,发现接触法向各向异性程度随着AR的减小而减小。螺旋桩安装过程对桩周土体影响的研究对理解螺旋桩与土的相互作用具有重要意义。
综上所述,业内学者已关注到AR对螺旋桩安装所需条件以及安装后承载性能的影响,并对螺旋桩安装过程中土体所受响应进行了一定研究。但目前有关螺旋桩在不同AR下的安装受力研究,仅将螺旋桩的受力分为连杆受力与螺旋叶片受力两部分[18]。要准确预测螺旋桩在不同AR下安装时所需扭矩和力,还需将连杆与螺旋叶片所受的反力和扭矩进一步细分。
本文目的是通过离散元方法模拟螺旋桩在不同AR下的安装过程,研究螺旋桩在不同AR下安装时的桩身受力情况及对周围土体的影响。宏观上,分析了螺旋桩各部件的受力情况,相较于之前学者的研究进行了进一步细化:将连杆受力进一步划分为连杆侧壁及端部受力,将螺旋叶片受力进一步划分为螺旋叶片上下表面受力;细观上,研究了螺旋桩安装前后土体孔隙率、配位数、应力等方面的变化。研究螺旋桩与土之间的相互作用,从侧面解释螺旋桩各部件受力在不同AR下发生变化的内在原因。
1. 离散元模型建立
本文涉及到的螺旋桩模型依据Cerfontaine等[16]的离心机试验建立。在50g的条件下,Cerfontaine等在HST95砂中开展了螺旋桩的安装试验,研究了不同AR对螺旋桩安装力的影响。螺旋桩模型与其离心机试验中的平底螺旋桩模型的几何参数一致,并模拟其在50g条件下的安装过程。
1.1 螺旋桩模型
螺旋桩通过离散元中的墙单元模拟,建立过程如下:首先在AutoCAD软件中构建螺旋桩的三维模型,然后导入PFC3D中生成由三角形面单元组成的整个螺旋桩模型。螺旋桩模型的叶片上下表面、连杆端部和连杆侧面分别赋予不同的识别id,以便后续研究螺旋桩安装过程中各部位的受力情况。螺旋桩模型尺寸如图 2所示,螺旋叶片直径Dh和桩身连杆直径Ds分别为21.2,11 mm。螺旋叶片的厚度和螺距分别为1.4,7 mm。桩身连杆长度为160 mm。
1.2 土样及边界
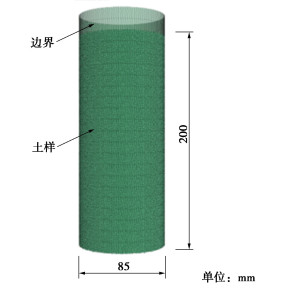
离散元模型中所使用的土体颗粒以HST95砂土为原型,该砂土的物理力学性质[18-21]如表 1所示。为在保证计算精度的前提下尽可能缩减离散元模拟的时间,离散元颗粒的特征粒径(d10,d50和d100)扩大为HST95砂土粒径的10倍。螺旋桩桩身连杆直径Dc(11 mm)与放大后颗粒中值粒径d50(1.4 mm)的比值约为7.8,大于Arroyo等[22]建议的Dc与d50的最小比值2.69,与Shi等[17]和Cerfontaine等[18]采用的比值近似(分别为8,7.8),因此,认为放大后的颗粒粒径不会对计算结果精度产生影响。选用球形颗粒并限制其旋转以模拟异形砂土颗粒间的咬合力。采用Ciantia等[23]提出的颗粒胞元复制法(PCRM)生成目标孔隙率为0.38的试样,此孔隙率对应于HST95砂土的相对密度为52%,与原型试验[18]中所用砂土的相对密实度一致。该方法首先生成一个颗粒数较少但符合目标应力状态、孔隙率和配位数的胞元,随后通过复制胞元来填充目标模型区域,最后通过修改颗粒间接触力使模型内应力分布满足目标地应力场。通过复制“胞元”生成的模型收敛速度快,密度分布均匀且初始应力状态容易控制。该成样方法适用于生成颗粒数目较多且同时需要控制水平土压力系数的离散元模型。本文中的模型所生成的总颗粒数目约为70万。模型中的土样及边界条件如图 3所示。模型边界的设置对颗粒数目、计算成本以及边界效应都起到关键性作用。如果采用位置固定的水平向边界(无限刚度),在有限的土体范围内将导致颗粒受到的径向约束过大;如果采用恒应力(零刚度)边界条件将会因颗粒的无限制运动而导致径向应力的低估。因此,模型的水平向环状边界采用了20个直径为85 mm、沿深度分布的恒定刚度的环状边界。每个环状边界的径向位移根据其当时的径向位置进行伺服控制,即环状墙单元会随着所受接触力的增加或减少发生扩张或收缩,以此达到更合理的模拟土体受到的径向约束,同时减小边界效应的目的。
表 1 HST95砂物理力学参数Table 1. Physical and mechanical parameters of HST95 sand物理力学参数 对应值 最小孔隙比emin 0.467 最大孔隙比emax 0.769 临界状态摩擦角φ/(°) 32 颗粒密度ρs/(kg·m-3) 2650 有效粒径d10 /mm 0.09 中值粒径d50 /mm 0.14 静止土压力系数K0 0.47 环状墙单元的扩张(或收缩)刚度通过圆柱孔在弹性介质中的扩张理论计算得到[24],其中涉及到的土体剪切模量Gsand [18]为
Gsand=17.3(p′100)0.548。 (1) 式中:p’为平均有效围压。
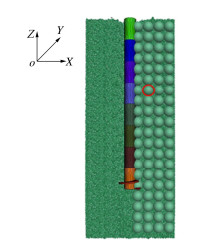
为了记录螺旋桩安装过程对其周围土体的影响,在螺旋桩一侧生成80个测量球。测量球直径为5 mm,其在X-Z面上的分布如图 4所示。
1.3 接触模型
本文模拟中采用Hertz接触模型[25],接触模型参数如表 2所示。其中颗粒间的接触模型参数大小采用Sharif等[14]根据HST95砂的三轴试验结果所标定的Hertz模型微观参数。钢–土界面摩擦系数采用Lauder等[21]通过直接剪切试验确定的砂土与钢制螺旋桩之间的摩擦系数。离散元颗粒与边界墙之间的摩擦系数由砂的峰值摩擦角计算得到[18, 23]。
1.4 螺旋桩安装
在模拟螺旋桩的安装时,在保证螺旋桩附近土体处于准静态状态的同时尽可能降低计算成本,本模拟中采用Da等[26]提出的惯性数I来控制极限安装速度。惯性数I是通常用作确定离散元模型是否以处于准静态的指标。通常假设惯性数保持在某个阈值Imax以下时,离散元模型处于准静态状态。相关文献中对该阈值的建议值并不固定,常用取值在0.001[26-27]~0.01[28]。模拟采用0.01作为惯性数的阈值,并根据此阈值与Cerfontaine等[18]推导公式计算螺旋桩安装过程中的最大允许贯入速率:
vz,max=min(4phAR,3Dh)Imaxd50√σ3ρs。 (2) 式中:ph为螺旋叶片螺距;Dh为螺旋叶片直径;d50为颗粒中值粒径;σ3为初始围压;ρs为颗粒密度。
根据AR的定义,螺旋桩的旋转速率为
{w_{\max }} = \frac{{2{\rm{\mathsf{π}}} \cdot {v_{\text{z}}}_{,{\text{max}}}}}{{AR \cdot {p_{\text{h}}}}} 。 (3) 由式(2)可知,最大允许贯入速率随初始围压 {\sigma _{\text{3}}} 的增加而增大。因此,随着螺旋桩安装深度的增加,其最大允许贯入速率也相应增加[10, 14]。为减少模拟时间,本模拟中采用变速率的方式来安装螺旋桩。根据式(2),当螺旋桩的安装AR为0.5时,保证模型处于准静态的螺旋桩的最大贯入速率与深度的关系如表 3所示。
表 3 AR=0.5时螺旋桩贯入速率与深度的关系Table 3. Relationship between penetration rate and depth of screw pile when AR=0.5深度范围/m 最大贯入速率/(m·s-1) 0.0~0.01 0.6958 0.01~0.02 1.2052 0.02~0.04 1.7045 0.04~0.06 2.2005 0.06~0.1 2.7834 0.1~0.16 3.5481 1.5 模拟汇总
为了对比不同AR下螺旋桩的安装对土体的扰动,分别模拟了AR为1,0.5,0.25时螺旋桩的安装过程。在拥有两颗Intel Xeon Scalable Platinum 8358(32核,64线程)芯片的工作站上同时模拟3种AR下螺旋桩安装至0.16 m深度处,总用时32 d。
2. 螺旋桩受力分析
螺旋桩各部件所受到的竖向力可通过记录该部件所受接触力的垂直分量来获得,扭矩可通过各部件所受接触力水平分量与该部件中心与旋转轴之间距离的积来获得。
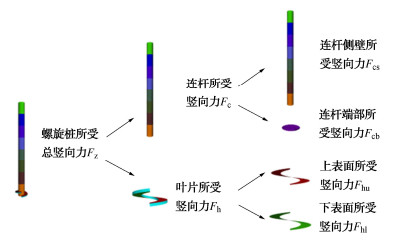
螺旋桩各部件受力按照图 5进行划分。将螺旋桩安装过程中所受的竖向力通过下式划分为连杆受力及叶片受力:
{F_{\text{z}}} = {F_{\text{c}}} + {F_{\text{h}}} 。 (4) 式中:Fc为安装过程中桩身连杆所受竖向力;Fh为安装过程中叶片所受竖向力。
将螺旋桩连杆及叶片所受竖向力进一步细分:
{F_{\text{c}}} = {F_{{\text{cs}}}} + {F_{{\text{cb}}}} \text{,} (5) {F_{\text{h}}} = {F_{{\text{hu}}}} + {F_{{\text{hl}}}} 。 (6) 式中:Fcs为桩身连杆侧壁所受竖向摩擦力;Fcb为连杆端部所受竖向力;Fhu为螺旋叶片上表面所受竖向力;Fhl为螺旋叶片下表面所受竖向力。
2.1 螺旋桩所受竖向力及扭矩
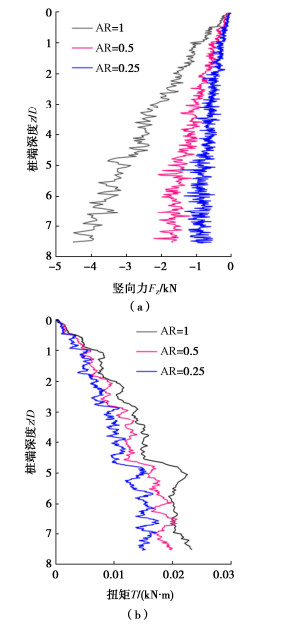
螺旋桩整体所受竖向力及扭矩随安装深度的变化如图 6所示。图 6(a)中横坐标为螺旋桩安装过程中所受的竖向力,负号表示螺旋桩受力方向与螺旋桩运动方向相反,即竖直向上。纵坐标为螺旋桩桩端深度与螺旋叶片外径比。从图 6(a)中可以看出,在同一AR下,随着螺旋桩安装深度的增加,其受到的竖向阻力也随之增大。此外,随着AR的减小螺旋桩安装过程中受到的竖向力明显降低,从AR=1至AR=0.25,竖向力降低近80%。使用低AR安装模式(AR < 1)可以有效减小螺旋桩的安装阻力,这与目前已有的试验和数值模拟结果一致[14]。
图 6(b)中横坐标为螺旋桩安装过程中所受的扭矩。从图 6(b)中可以看出,在同一AR下,随着螺旋桩安装深度的增加,其受到的扭矩也随之增大。随着AR的减小,螺旋桩安装过程中受到的扭矩随之降低。这一现象说明采用低AR安装模式既可减小螺旋桩的竖向安装力,也可减小安装扭矩,对安装设备的要求也将显著降低。图 6中安装扭矩随AR的减小幅度小于竖向安装力,这与Cerfontaine等[18]离心机实验所反映的规律一致。
2.2 螺旋桩连杆及叶片所受竖向力
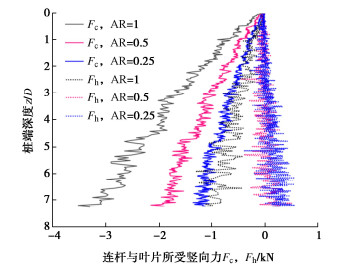
按照图 5所示,对螺旋桩安装过程中各部件受力情况分别进行分析。螺旋桩连杆及叶片受力随安装深度变化如图 7所示。
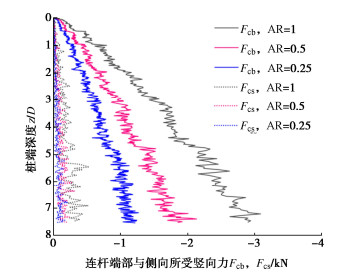
从图 7可以看出,螺旋桩安装过程所受的竖向力主要来自桩身连杆(Fc),在AR=1时,桩身连杆的受力约占总竖向力的76%。在AR < 1时,螺旋桩叶片的受力为正,即与螺旋桩运动方向相同,不再阻碍螺旋桩的安装,且AR为0.5,0.25时,螺旋叶片上的受力基本一致。连杆端部及侧向所受竖向力随安装深度变化如图 8所示。
从图 8中可以看出,桩身连杆上的受力几乎全部来自连杆端部,且其受力随AR的减小而减小,这一现象将在后文中进行详细解释。同时,图 8说明连杆侧向所受竖向力较小。连杆侧向在安装过程中主要受摩擦力的作用,该力的大小与桩–土摩擦系数以及螺旋桩在土中的深度有关。对于本文中所研究的安装深度较浅的螺旋桩,侧摩阻力明显低于端阻力。此外,螺旋桩所受摩擦力方向与桩–土相对运动方向相反:在AR=1时,摩擦力方向与叶片倾角方向一致;随着AR的减小,摩擦力的方向更接近水平方向;当AR=0时,螺旋桩在土中仅发生旋转而没有竖向位移,摩擦力方向沿水平向。因此,安装过程中桩身连杆所受摩擦力对竖向安装阻力贡献随AR的减小而减小,但其对安装扭矩的贡献随AR的减小而增大。桩身连杆侧向所受竖向安装阻力大小与螺旋桩的几何形式和安装模式有关。
图 9中对比了不同的AR情况下螺旋叶片上下表面受力随安装深度的变化,在AR=1时,叶片上表面受到十分小的外力作用,下表面受大小为负的竖向力,即叶片上的安装阻力主要来源于叶片下表面与土的相互作用力。在AR为0.5,0.25时,螺旋叶片下表面受微小力,上表面所受力向下,即螺旋叶片所受合外力为安装推动力。这表明叶片在AR=1与AR<1两种安装情况下受力机制存在明显的差异,这一差异是螺旋桩安装阻力随AR变化的主要原因之一。
综上所述,安装过程中螺旋桩所受竖向阻力主要由桩身连杆端部力Fcb和叶片上的作用力Fh构成。桩身连杆端部力随AR的减小而减小;叶片下表面接触力(方向向上,阻力)随AR减小而减小,而上表面接触力(方向向下,推动力)随AR减小而增大。桩身连杆端部的受力的方向主要竖直向上,且桩身连杆端部上的作用力矩理论上是0,因此对安装扭矩的贡献很小;螺旋叶片上作用力的力矩较大,这部分力是安装扭矩的主要来源,且作用于螺旋叶片上下表面的力均产生阻碍螺旋桩旋转的扭矩,因此AR发生变化时螺旋叶片上的受力变化对安装扭矩的变化影响较小;随着AR的减小,连杆侧壁上的摩擦力方向逐渐靠近水平方向,对安装扭矩的贡献增大。以上3个因素共同作用导致了图 6中安装扭矩随着AR的变化幅度小于竖向安装力变化幅度的现象。
2.3 叶片上下表面颗粒运动及接触力分布
为了进一步分析造成AR=1与AR<1时受力机制差异的原因,分别研究了螺旋桩在AR为1,0.5两种模式下安装至0.16 m(7.5D)深度时,螺旋叶片附近土体颗粒的运动以及叶片上下表面的受力分布变化。AR为0.25,0.5两种情况下的颗粒运动和叶片受力情况大致相同,因此省略了AR=0.25的模拟结果。
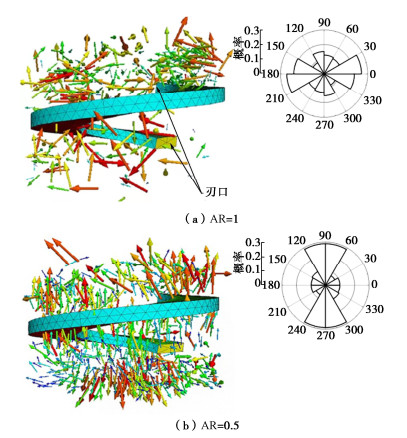
图 10显示了不同AR下叶片附近相同区域内的颗粒速度矢量图,图中箭头的大小代表颗粒速度的大小,箭头的方向为颗粒运动的方向。为突出显示叶片上下表面的颗粒运动方向,图 10中删除了部分位于叶片刃口位置的移动速度大的颗粒。从图 10中可以看出,在AR=1时,叶片上方颗粒主要沿水平方向运动。而在AR=0.5时,叶片上方颗粒主要沿竖直方向运动,因此颗粒对螺旋叶片的反作用力是竖直向下的。
为了更直观的表示叶片上表面颗粒速度方向,此处考虑将颗粒速度均投影到X-Z平面上。同时,将所有速度矢量划分到12个相同大小的角度区间中,分别计算速度方向位于各个区间内的颗粒数目,以此获得颗粒速度在X-Z平面上的概率分布。叶片上表面同一区域内颗粒速度方向概率分布如图 10所示。从中可以明显看出,AR=1时螺旋叶片上表面颗粒速度方向更多的偏向水平方向。AR=0.5安装模式下螺旋叶片上表面颗粒速度方向更多的偏向竖直方向。图 10解释了图 9中叶片上表面受力随AR变化的原因。
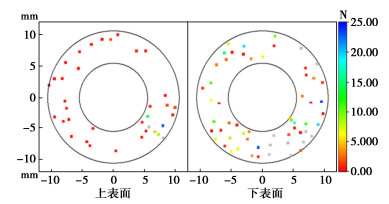
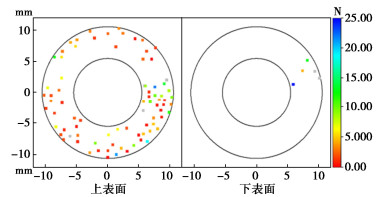
图 11,12分别为AR为1,0.5的安装模式下叶片上的颗粒接触力的作用位置在水平面上的投影图。图中点的位置为颗粒与叶片接触点在水平面上的投影,点的颜色表示总接触力的大小。从图 11,12可以看出,在AR=1时叶片上表面接触点的个数明显小于AR=0.5时,且接触力的值大多小于2 N。对于叶片下表面,在AR=1时接触点的个数明显多于AR=0.5时。这与图 9所示的结果一致。
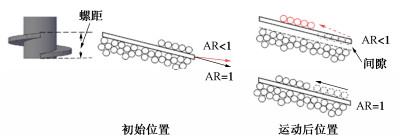
为了更好的理解不同AR下螺旋桩与其周围土体间的相互作用,图 13将三维空间中的螺旋叶片展开到二维平面上。根据AR的定义,在AR=1时,螺旋叶片的运动方向将与螺旋叶片倾角方向一致,即叶片表面处的土颗粒与螺旋叶片发生沿螺旋叶片倾角方向的相对滑动。在AR<1时,螺旋叶片的运动方向更靠近水平向,导致叶片上表面的颗粒在发生沿叶片倾角方向的相对滑动的同时产生向上的位移;随着螺旋桩的旋转,叶片下表面与土颗粒之间的挤压作用减弱,甚至可能产生一定的间隙,使得叶片下表面受到的力小于AR=1时对应的情况。图 13说明AR影响了螺旋桩叶片与土之间的相对运动方向,从而导致螺旋叶片上下表面受力随AR的变化。
3. 微观结果分析
微观结果侧重于分析螺旋桩模型在不同AR下安装对周围土体造成的影响,通过螺旋桩一侧土体中孔隙率、配位数和应力变化等方面进一步分析,以研究螺旋桩在不同AR进行安装时对周围土体的扰动。
3.1 孔隙率与配位数变化
离散颗粒体在外荷载作用下的密度变化可通过孔隙率的变化直接反映。此外,配位数也常被用作离散颗粒体堆积密度的量度,其变化受颗粒组构和土体密实度的共同影响。配位数为某离散颗粒体中平均每个颗粒所分配的接触个数,其计算公式为
{Z_{\text{c}}} = {\text{2}}\frac{{{N_{\text{c}}}}}{{{N_{\text{p}}}}} 。 (7) 式中:Nc为接触的总数;Np为颗粒的数量。
为研究螺旋桩安装过程对其周围土体密度的影响,选取了离散元模型中深度为0.065 m(3.1D)、距螺旋桩中心0.017 m的测量球,研究了该测量球中土体孔隙率和配位数变化,测量球位置在图 4中用红色圆圈标出。该测量球距螺旋桩通过区域较近,其内的土体响应较为明显。测量球内土体孔隙率和配位数随螺旋桩安装深度的变化如图 14所示。
从图 14(a)中可以看出,当螺旋桩安装深度达到测量球中心所在位置时,孔隙率增大至一峰值。螺旋桩端远离测量球后孔隙率开始减小,稳定后的孔隙率相较于初始值有所减小,且减小幅度随AR的减小而增加。这表明螺旋桩的安装导致了土体密实度的增大,且AR越小这一密实效应越强。这一现象说明在中等密实砂土中采用AR < 1的安装模式不仅不会导致原土体的扰动,反而对土体有一定的加固效果。低AR安装条件下螺旋桩上拔承载力的提升或许与这一加固效果有关。此外,从图 14(a)中可以看出,螺旋桩安装对孔隙率的影响范围约为桩端上下1D。
从图 14(b)中可以看出,当螺旋桩安装深度达到测量球中心所在位置时,配位数减小至3左右。螺旋桩端远离测量球后配位数开始回升,稳定后的配位数相较于初始值有所减小,且减小幅度随AR的减小而减小;在AR=0.25时配位数最终又回到初始值。从图 14(b)中可以看出,螺旋桩的安装过程对配位数的影响范围约为桩端上下2D。
对比图 14左右两部分,可以发现在螺旋桩安装过程中,螺旋桩周围的土体出现了密度增加但是配位数减小的情况,这与螺旋桩安装过程中土体组构的变化有关[29]。
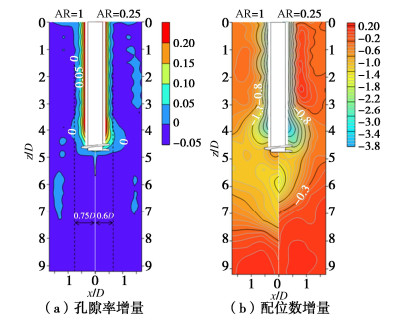
为研究螺旋桩安装过程对不同区域土体密度变化的影响,图 15中对比了螺旋桩在AR为1,0.25两种模式安装时,离散元模型中孔隙率和配位数增量在X-Z平面上的分布。图 15(a)中对比了AR为1,0.25时螺旋桩安装导致的桩周土体孔隙率的变化分布,图 15(b)中对比了AR为1,0.25螺旋桩安装导致的桩周土体配位数的变化分布。由于测量球的分布位置情况,螺旋桩一侧的小部分区域数值由插值所得,故将其覆盖。
图 15为螺旋桩安装至0.1 m深度(4.7D)时孔隙率与配位数的增量分布云图。从图 15(a)中可以看出,孔隙率仅在螺旋桩周围一定范围内增大。在此范围外孔隙率减小,即土体密实度增加。这与从图 14所得到的:AR越小土体密实效应越强的结论一致,而与Shi等[17]通过离散元数值模拟所获得的结论相反。这可能与所模拟的螺旋桩类型以及土体的初始密实程度有关。
从图 15(b)中可以看出,桩周的土体内配位数相较于初始值几乎都有所减小。对比土体内相同位置配位数在AR为1,0.25时的变化,发现在AR=1时配位数的减小效果更为显著,与图 14中配位数变化相呼应。
3.2 应力变化
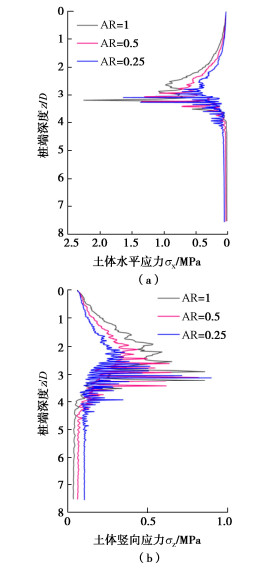
选取图 4所示位置测量球研究螺旋桩安装过程对其周围土体应力的影响。该测量球内土体水平应力及竖向应力随螺旋桩安装深度的变化如图 16所示。
从图 16可以看出,当螺旋桩安装深度达到测量球中心所在位置时,土体水平应力和竖向应力都增大至一峰值,相同条件下土体水平应力峰值明显大于土体竖向应力峰值。这是因为选取的测量球位于螺旋桩外侧,当测量球内应力达峰值时,螺旋桩的桩端与测量球中心处于同一水平位置,故测量球内土体受到水平向的影响效果更明显。
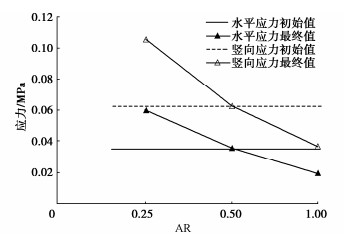
为进一步分析螺旋桩安装前后土体残余应力的变化,将上述测量球内土体水平应力及竖向应力在螺旋桩安装前后的数值大小绘制于图 17中。从图 17中可以看出,在AR=1时,螺旋桩一侧测量球内土体水平应力与竖向应力最终值均低于初始值,即残余应力为负值。随着AR的减小,残余应力增大。在AR=0.5时残余应力几乎为0,而在AR=0.25时残余应力为正值。这表明螺旋桩一侧土体残余应力随着AR的减小而增大。Sharif等[14]模拟观察到螺旋桩下方土体残余应力随着AR的增大而增大,这与所研究区域的位置有关。
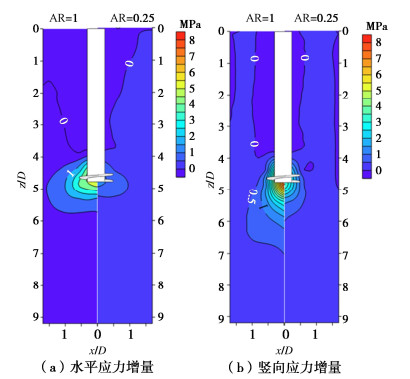
下文通过对比螺旋桩在AR为1,0.25安装时离散元模型中应力增量在X-Z平面上的分布,以研究螺旋桩安装过程对不同区域土体应力的影响。
图 18为螺旋桩安装至0.1 m深度(4.7D)时应力增量分布云图。图 18(a)中对比了AR为1,0.25时螺旋桩安装导致的土体水平应力变化分布,图 18(b)中对比了AR为1,0.25时螺旋桩安装导致的土体竖向应力变化分布。从图 18(a)可以看出,桩身连杆周围土体的水平应力减小,而螺旋叶片周围土体水平应力增大。并且,螺旋桩在AR=1安装时螺旋桩连杆周围土体水平应力减小的范围和螺旋叶片周围土体水平应力增大的范围都大于在AR=0.25时。在图 18(b)中可以看出竖向应力也存在相同的现象。
由2.2节可知,螺旋叶片随着AR的减小呈现两种不同的安装机制,AR=1时,螺旋叶片与土体之间的相互作用阻碍螺旋桩的安装,螺旋叶片下表面土体应力增长幅度最大,导致连杆端部在AR=1时所受阻力最大。随着AR的减小,螺旋叶片上所受合外力为安装推动力,螺旋叶片下表面与土颗粒之间的挤压作用减弱,螺旋叶片下部土体应力增长幅度减小,使得连杆端部受力也随之减小。这可以很好地解释图 8中桩身连杆端部受力随AR的减小而减小的现象。
4. 结论
基于离散元分析方法,分别分析了螺旋桩在AR为1,0.5,0.25下的安装过程,研究了螺旋桩安装过程中其各个部件的受力及螺旋桩与周围土体的相互作用。得到5点结论。
(1)在螺旋桩安装过程中,螺旋桩受到的竖向力与扭矩均随着AR的减小而降低且扭矩随AR的减小幅度小于竖向力的减小幅度。
(2)螺旋桩在AR=1与AR<1时存在两种不同的安装机制:AR=1时,螺旋叶片表面处的土颗粒与螺旋叶片发生沿螺旋叶片倾角方向的相对滑动;螺旋叶片上表面所受竖向力很小,下表面所受的竖向力为负值。在AR<1时,螺旋叶片的运动方向更接近水平向,叶片上表面颗粒在发生沿叶片倾角方向相对滑动的同时产生向上位移;在AR≤0.5时,螺旋叶片上表面所受竖向力为正值,下表面所受竖向力很小。
(3)螺旋桩安装过程中所受竖向力由桩身连杆和螺旋叶片所受竖向力组成,桩身连杆所受竖向力占比大于螺旋叶片所受竖向力。桩身连杆所受竖向力几乎全部来自桩身连杆端部受力。
(4)螺旋桩的安装导致其周围土体孔隙率降低,且随着AR的减小,螺旋桩周土体孔隙率减小更为显著,即密实效应更加明显。这与部分学者所观察到的现象不一致,桩型与土体相对密实度对螺旋桩安装前后土体中孔隙率变化的影响还需进一步的研究。
(5)随着AR的减小,螺旋桩周围土体的附加竖向应力与水平应力都降低,螺旋桩连杆端部受力随AR的减小与这一现象有关。螺旋桩安装完成后,周围土体内的残余应力随着AR的减小而增大。
致谢: 感谢浙江大学超重力研究中心孔德琼、赵宇、闫子壮、李桢懿等对离心模型试验的帮助与配合。 -
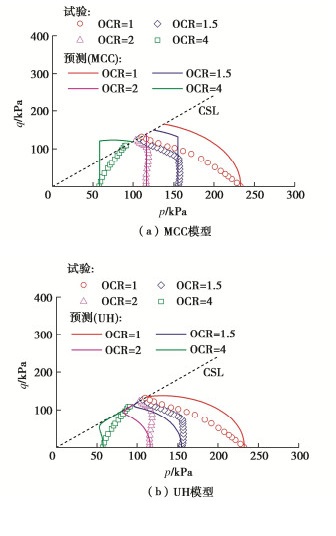
表 1 地基土本构模型参数
Table 1 Constitutive model parameters of foundation soil
参数 M υ κ λ N UH模型 0.9 0.33 0.079 0.244 2.335 剑桥模型 0.9 0.33 0.079 0.244 2.335 -
[1] ROSCOE K H, SCHOFIELD A N, WROTH C. On the yielding of soils[J]. Géotechnique, 1958, 8: 22-53. doi: 10.1680/geot.1958.8.1.22
[2] ROSCOE K H, SCHOFIELD A N, THURAIRAJAH A. Yielding of clays in states wetter than critical[J]. Géotechnique, 1963, 13(3): 211-240. doi: 10.1680/geot.1963.13.3.211
[3] SCHOFIELD A N, WROTH P. Critical State Soil Mechanics[M]. New York: McGraw-Hill, 1968.
[4] YAO Y P, HOU W, ZHOU A N. UH model: three-dimensional unified hardening model for overconsolidated clays[J]. Géotechnique, 2009, 59(5): 451-469. doi: 10.1680/geot.2007.00029
[5] YAO Y P, ZHANG K. Innovations of the UH model associated with a clue of stress-strain chain[J]. Transportation Geotechnics, 2022, 37: 100836. doi: 10.1016/j.trgeo.2022.100836
[6] YAO Y P, LIU L, LUO T. A constitutive model for granular soils[J]. Science China Technological Sciences, 2018, 61(10): 1546-1555. doi: 10.1007/s11431-017-9205-8
[7] YAO Y P, ZHOU A N. Non-isothermal unified hardening model: a thermo-elasto-plastic model for clays[J]. Géotechnique, 2013, 63(15): 1328-1345. doi: 10.1680/geot.13.P.035
[8] 姚仰平, 田雨, 周安楠, 等. 土的统一硬化函数的构造[J]. 中国科学: 技术科学, 2019, 49(1): 26-34. https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK201901003.htm YAO Yangping, TIAN Yu, ZHOU Annan, et al. Unified hardening law for soils and its construction[J]. Scientia Sinica (Technologica), 2019, 49(1): 26-34. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK201901003.htm
[9] YAO Y P, SUN D A. Application of Lade's criterion to Cam-clay model[J]. Journal of Engineering Mechanics, 2000, 126(1): 112-119. doi: 10.1061/(ASCE)0733-9399(2000)126:1(112)
[10] YAO Y P, WANG N D. Transformed stress method for generalizing soil constitutive models[J]. Journal of Engineering Mechanics, 2014, 140(3): 614-629. doi: 10.1061/(ASCE)EM.1943-7889.0000685
[11] 姚仰平, 张丙印, 朱俊高. 土的基本特性、本构关系及数值模拟研究综述[J]. 土木工程学报, 2012, 45(3): 127-150. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201203020.htm YAO Yangping, ZHANG Bingyin, ZHU Jungao. Behaviors, constitutive models and numerical simulation of soils[J]. China Civil Engineering Journal, 2012, 45(3): 127-150. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201203020.htm
[12] 陈云敏, 马鹏程, 唐耀. 土体的本构模型和超重力物理模拟[J]. 力学学报, 2020, 52(4): 901-915. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202004001.htm CHEN Yunmin, MA Pengcheng, TANG Yao. Constitutive models and hypergravity physical simulation of soils[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(4): 901-915. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202004001.htm
[13] 陈云敏, 韩超, 凌道盛, 等. ZJU400离心机研制及其振动台性能评价[J]. 岩土工程学报, 2011, 33(12): 1887-1894. http://cge.nhri.cn/cn/article/id/14444 CHEN Yunmin, HAN Chao, LING Daosheng, et al. Development of geotechnical centrifuge ZJU400 and performance assessment of its shaking table system[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1887-1894. (in Chinese) http://cge.nhri.cn/cn/article/id/14444
[14] CHEN Y M, TANG Y, LING D S, et al. Hypergravity experiments on multiphase media evolution[J]. Science China Technological Sciences, 2022, 65(12): 2791-2808. doi: 10.1007/s11431-022-2125-x
[15] 沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. SHEN Zhujiang. Theoretical Soil Mechanics[M]. Beijing: China Water & Power Press, 2000. (in Chinese)
[16] ANTONIO G. Stress-strain and Strength Characteristics of a Low Plasticity Clay[D]. London: Imperial College London, 1982.
[17] POTTS D M, ZDRAVKOVIC L. Finite Element Analysis in Geotechnical Engineering: Theory[M]. London: Thomas Telford, 1999.
[18] YAO Y P, LU D C, ZHOU A N, et al. Generalized non-linear strength theory and transformed stress space[J]. Science in China Series E: Technological Sciences, 2004, 47(6): 691-709. doi: 10.1360/04ye0199
[19] GHANTOUS I B. Prediction of in Situ Consolidation Parameters of Boston Blue Clay[D]. Cambridge: Massachusetts Institute of Technology, 1982.
[20] CHOWDHURY E Q, NAKAI T. Consequences of the tij-concept and a new modeling approach[J]. Computers and Geotechnics, 1998, 23(3): 131-164. doi: 10.1016/S0266-352X(98)00017-2
-
其他相关附件



 下载:
下载: