0.   引言

月球作为世界各国深空探测的首要目标，在完成绕、落、回三期探月工程的背景下，中国已全面启动第四期探月工程，其中月表资源原位利用工程将面临大量资源勘探及开采的任务。但当前缺乏对真实月表环境下月壤物理力学特性的认识，相关理论和分析方法不够成熟，难以准确预测在月表资源勘探和开采中月壤的物理力学响应，这将阻碍月表资源原位利用工程的实施。

相较于中国探月工程，美国阿波罗计划探月任务期间同样获取了部分月壤表层土样及测定了部分表层月壤的物理性质及力学响应^[1-6]，但由于月壤的稀缺性，鲜有针对月壤进行损伤性室内试验的研究成果。为了弥补这一缺陷，在采用非损伤测试技术探明月壤的矿物构成后，月壤模拟物可用于初步探明表层月壤的力学性质。例如美国研制了LSS1~LSS5、MLS-1、MLS-1A、MLS-2、JPL-1、JSC-1、JSC-1A、JSC-1AF、JSC-1AVF、JSC-1AC等多种模拟月壤模拟物^[7-9]；日本研制了MKS-1、FJS-1两种类型的月壤模拟物^[10]；中国学者也开展了模拟月壤的研制工作，用于满足中国探月工程的需要，Jiang等^[11]研制的TJ-1模拟月壤与已知月壤的力学特性吻合较好；Zheng等^[12]以辉南火山渣为原料，研制了模拟月壤CAS-1用于月壤微波辐射特性的研究；李建桥等^[13]一系列模拟月壤用于月球着陆相关试验研究。Zhou等^[14]考虑月球表面温度和真空环境的影响开发BH-1、BH-2系列月壤，用于探究太空环境下月壤力学性质的演化规律。Li等^[15]通过使用新的模拟月壤CUMT-1探究了低重力条件下月壤的力学响应特点。

除去室内试验方面的研究，数值模拟的手段同样被用于探究月壤的力学响应，以弥补室内试验不足。在已报道的月球风化层的离散元模拟中^[16]，从微观力学的角度出发，一定程度上表征了表层月壤的力学性质，但是将具有复杂形状的月壤颗粒理想化建模仍有一定缺陷。为考虑颗粒形状的影响，早期有学者采用椭圆形颗粒证实了粒形在颗粒材料的力学性质中扮演着重要角色，随后Soltanbeigi等^[17]以颗粒簇的形式，通过球体的堆积形成不规则颗粒簇进行离散元模拟。为了考虑月壤颗粒形态特征，Katagiri等^[18]通过CT扫描技术对月壤颗粒进行无损伤检测，获取月壤的颗粒集合特征，建立三维不规则形态的颗粒模型用于离散元模拟，该方法虽然较大程度上考虑了颗粒形状特征，但在计算算力方面有较大的需求。基于此，Jiang等^[19]将颗粒粒形特征与粒间转动阻力相结合，在将颗粒球形理想化的基础上考虑了颗粒的粒形特征同时降低了计算效率与模型仿真真实度的冲突。该方法同样被Rorato等^[20]利用Hostun砂的粒形特征进行数值模拟与室内试验结果对比，证实了该方法的有效性。

因此，本文提出一种基于图像考虑中国月壤粒形特征的离散元模拟方法，为在月球环境下运用地球环境的物理知识及研究手段提供思路。通过中国月壤颗粒形态图像数据，提取粒形特征及尺寸数据，建立颗粒尺寸、粒形特征与抗转动程度的对应关系；结合本团队开发的三维月壤接触模型^[21]，考虑颗粒形状对颗粒材料整体力学行为的影响，引入抗转动系数，以此为桥梁将月壤的颗粒形状影响考虑到试样的整体计算中；通过构建月壤颗粒形状及尺寸特征的数据库，一方面为后期指导制备月壤模拟物，另一方面用于建立考虑中国月壤粒形特征的离散元数值样，研究开展更加贴近真实月表环境的月壤物理力学特性，为中国月球资源勘探及相关设备开发利用提供数值研究基础。

1.   嫦娥五号月壤颗粒形态特征

如图 1所示，本文研究所使用的月壤样本来自中国探月工程嫦娥五号任务中获取的表层月壤，是迄今为止采样纬度最高的一个新区域。月壤表层颗粒主要有不规则的棱角形、次棱角形及表面粗糙的角砾岩组成^[23]。

图  1  部分月球表面颗粒^[22]

Figure  1.  Multiple lunar regolith particles^[22]

下载: 全尺寸图片 幻灯片

Rorato等^[24]认为与球体或球体的相似性用于描述颗粒的形状特征较为合适，因此本文采用球度作为评价标准用于描述中国月壤颗粒的粒形特征；真球度（true sphericity）定义为等效球形体积的表面积与真实颗粒的表面积之比，但计算不规则颗粒的表面积仍有一定的难度，且结合当前所能获取的月壤颗粒图像属于二维图像特征；因此，本文以2D图像框架的内对月壤颗粒粒形进行捕捉，通过颗粒2D圆度特征反演对三维空间下颗粒球度^[25]，用于评价月壤颗粒粒形在三维空间下的特征。其中颗粒2D圆度特征如下式：

式中：${p_{\text{c}}}$为和颗粒面积相同的圆的周长；${p_{\text{s}}}$为颗粒周长。

粒形3D球度（$\psi$）和2D圆度（${S_{\text{p}}}$）关系如下式：

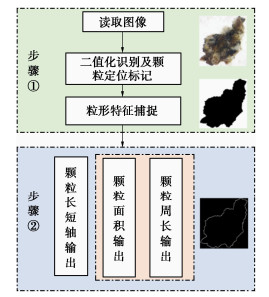
如图 2所示，依据上述二维成像来考虑月壤的颗粒粒形的定义，月壤的颗粒粒形的数据捕获整体分为两部分：①通过对月壤图像进行月壤图像进行二值化识别及相关颗粒特征的捕获；②依据二维球度的定义计算输出颗粒粒径尺寸、颗粒面积、颗粒周长等相关信息。在获取月壤颗粒数值尺度后，应参照标尺换算真实颗粒尺度。

图  2  基于图像识别月壤粒形特征捕获流程图

Figure  2.  Implementation of lunar soil particle shape feature capture based on image processing

下载: 全尺寸图片 幻灯片

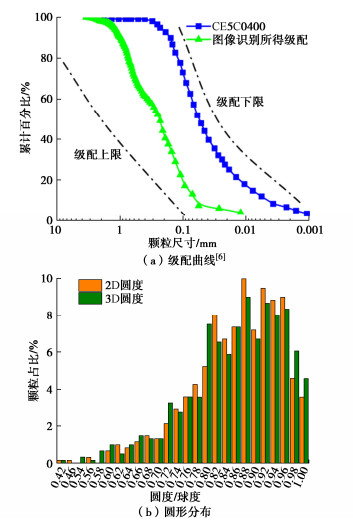
如图 3所示，通过收集当前已发表的中国月壤相关文献[26~34]及尚未发表正在研究的月壤颗粒粒形图像，依照图 2所述流程，对所获取的近612个月壤颗粒图像进行分析，用于探究中国月壤的颗粒圆度特征及级配分布。由图 3（a）所示，在已知美国Apollo系列月壤级配^[6]背景下，嫦娥五号样品CE5C0400^[35]及本文图像识别获取的月壤颗粒级配，结果表明二者级配均在月壤级配范围内。此外，进一步观察表明，在1~10 um粒径范围内，颗粒数目占比增长缓慢，有研究^[34]表明在1~10 um粒径范围内存在大量的细粉尘。而现有的月壤文献研究中，关于该粒径范围月壤粒形特性研究稍有不足。

图  3  嫦娥五号月球样品的颗粒形状和尺寸分布

Figure  3.  Particle shape and size distributions of Chang'E lunar sample

下载: 全尺寸图片 幻灯片

此外，相较于嫦娥样本CE5C0400级配曲线，本文所获取颗粒级配曲线则表现出较为明显的间断感，导致该现象的原因本文归纳为2类：①当前所发表的文献中颗粒所能收集到的数目较少，且对1~10 um区间范围的月壤颗粒粒径的研究稍有不足；②由于科学研究的目的不同，嫦娥月壤样品差异性过高，导致其整合后，级配曲线在不同粒径区间表现形式不同。尽管综合多个月壤研究样本后的级配曲线有一定间断，但所获取的月壤样本同属一批嫦娥五号探月计划任务返回样，且整合所得级配曲线落入美国阿波罗探月计划所获取的月壤级配上下限范围内，从另一方面佐证了本文研究数据的合理性。如图 3（a）所示：当前收集月壤颗粒粒径主要以小于1 mm粒径的小颗粒为主，其中小于1 mm的颗粒数目占总数目的90%。在此基础上依据球度对月壤的颗粒粒形特征进行定量分类，在考虑颗粒粒径的情况下，对其球度特征进行描述。如图 3（b）所示，当前所收集月壤颗粒平均球度0.851，其中大部分月壤颗粒球度集中0.8~0.97，嫦娥月壤样本CE5C0400获取颗粒平均球度0.875^[36]。其中有25%的颗粒球度小于0.8，35%的颗粒球度大于0.9，10%的颗粒球度大于0.95。基于此，拟将月壤的颗粒形态分为6类，如表 1所示。

表  1  月壤的颗粒形态分布表

Table  1.  Representative particle morphologies of lunar particles

球度范围	颗粒占比/%	代表性颗粒形态
${S_{\text{p}}}$ < 0.6	1.3
0.6 < ${S_{\text{p}}}$ < 0.7	5.8
0.7 < ${S_{\text{p}}}$ < 0.8	18.1
0.8 < ${S_{\text{p}}}$ < 0.9	39.27
0.9 < ${S_{\text{p}}}$ < 0.94	18.3
0.94 < ${S_{\text{p}}}$ < 1.0	17.18

下载: 导出CSV 

| 显示表格

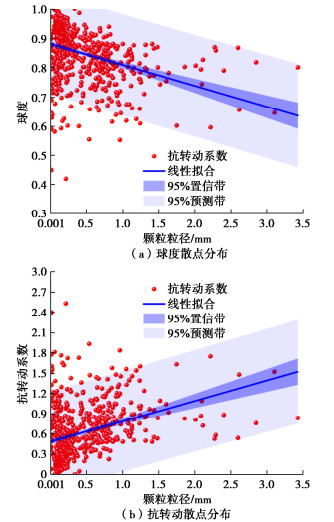
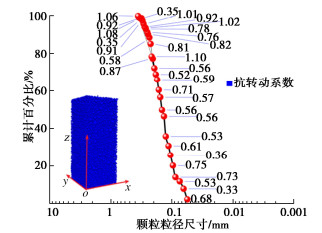
如图 4（a）所示，在考虑粒径的情况下，对其球度特征进行描述，当前中国月壤粒形圆度分布呈现出随粒径增大，颗粒圆形度呈下降趋势。基于此，造成颗粒圆度随粒径降低现象的结果主要可以归纳解释为：①以当前已发表的能够获取的月壤粒形特征中，由于设备的原因难以捕获细小月壤颗粒的特征，导致在进行粒径数据统计时难以精准统计其平面特征，进而影响球度分布；②在月壤形成过程中，受颗粒间相互作用的结果，颗粒本身棱角进行磨损，导致其球度过高；③在太空真空环境及微重力影响下，有部分质量小且属于熔融状态冷却后的月壤颗粒表现出良好的球形，圆度较高，接近于圆形。

图  4  月壤颗粒球度和抗转动的散点分布

Figure  4.  Scatter distribution of sphericity and rolling resistances of lunar soil particles

下载: 全尺寸图片 幻灯片

为考虑月壤粒形在DEM模拟中的影响，本文参考Rorato等^[20]提出的球度（true sphericty）与颗粒的抗转动性存在相关性的概念。假设一个完美的球体（ψ=1）在与另一个任意形状的物体接触时可能不会产生任何旋转阻力，而一个立方体应该具有较高的滚动摩擦值取0.8^[24]。正方形球度计算反演立方体球度为0.806。本文基于线性方程建立球度与抗转动的关系：

式中：$\beta$为抗转动系数；$\psi$为由式（2）转换求得三维球度。其抗转动系数分布如图 4（b）所示。由于本文简单认为颗粒球度与其抗转动系数呈线性对应关系，则颗粒抗转动系数分布形式与球度分布形式相左，离散程度较高，且由于较大尺度下，月壤颗粒粒径图像获取清晰，则球度较小，对应的抗转动系数对应较高，也近似表现出随颗粒粒径增加，颗粒抗转动系数呈正相关趋势。为简单计算，本文对粒径相近颗粒球度及抗转动系数进行统计求均值用于后续的离散元模拟中。

2.   考虑粒形特征的粒间接触模型

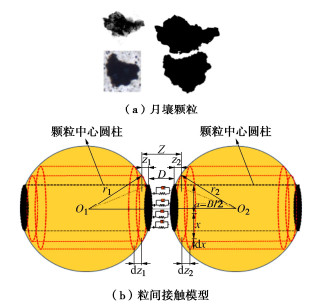
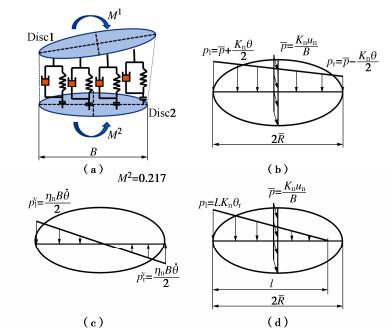
如图 5（a）所示，月壤颗粒多表现为形状不规则，粒间以面-面接触居多，表现为“互锁效应”，具有一定的抗转动能力。在考虑颗粒形状的影响后，不规则颗粒所导致的摩擦和剪胀的影响随之产生^[36]。如图 5（b）所示，本文通过在颗粒接触处引入抗转动力矩和局部破碎系数，分别考虑不规则颗粒所带来的影响，以及加载过程中颗粒破碎的现象^[19]，本文主要介绍如何将颗粒形状引入粒间接触计算。通过球体（3D）和单位长度与变形平面（2D）正交的圆盘（矩形）两个相对的圆形平面接触区域来模拟粒子间接触行为，如图 6所示。

图  5  月壤粒间接触示意图

Figure  5.  Schematic diagram of lunar soil particle contact

下载: 全尺寸图片 幻灯片

图  6  考虑抗转动影响的粒间演化规律

Figure  6.  Contact evolution between particles considering resistance rotation coefficient

下载: 全尺寸图片 幻灯片

式中：B为接触尺度；r为颗粒半径分别为${r}_{1}，{r}_{2}$相互接触颗粒的共同半径；$\beta$作为无量纲的形状参数，即公式（3），用以映射颗粒形态特征来考虑颗粒形态对试样剪切强度的影响。

如图 6所示，先定义一个标准单元（basic element）用于阐述抗转动参数的在接触模型中扮演的意义。首先假设两个颗粒球体接触点处分布无限多个法向及切向元器件，用以描述单元体在滚动和扭转方向上的接触行为，如图 6（a）所示。对接触截面（如图 6（b））进一步分析，其中基本力学响应如下：

式中：${K_{\text{n}}}$(N/m²)及${\eta _{\text{n}}}$(N_s/m²)分别为基本单元的法向刚度系数和黏滞阻尼系数；${k_{\text{n}}}$为法向刚度接触系数；${c_{\text{n}}}$为法向阻尼系数。

在法向力作用下使两个颗粒球在竖向截面内发生旋转，其转动角度可以由下式表示

式中：$\dot \Theta$为相对转动率；${\dot \theta _1}$及${\dot \theta _2}$为颗粒球1，2在$\Delta t$时间竖向平面内的转动率。

基于此，颗粒接触面中力学响应可以分为两方面影响因素产生（如图 6（b）所示）：①颗粒接触；②颗粒转动。其中单位长度上的不考虑颗粒转动平均接触力（$\bar p$）为

式中：${\mu _{\text{n}}}$颗粒间重叠量。

上式说明，当粒间接触宽度B保持不变时，面上法向接触力保持线性分布并产生抗转动的力矩，随着颗粒发生转动（如图 6（c）），接触面上的左右两端的接触力和阻尼力发生变化，开始达到第二个阶段：

在式（9）~（12）中，${P_{{\text{left}}}}$，${\text{ }}{P_{{\text{right}}}}$为接触面左右两端的接触力；$p_{{\text{left}}}^{\text{v}}$，$p_{{\text{right}}}^{\text{v}}$为接触力两端的阻尼力。${M^{{\text{left}}}}$，${\text{ }}{M^{{\text{left}}\_{\text{v}}}}$分别为由接触力和阻尼力所产生的弯矩。式（12）中的转动抗度${K_{\text{m}}}$和转动黏滞阻尼系数${c_{\text{r}}}$也与颗粒的粒形特征进行联系，如下所示：

随着转角的逐渐增大，计算单元左侧的接触力逐渐增大，而计算单元右侧的接触力逐渐减小，如图 6（d）所示，直在颗粒旋转的过程中，其应力和弯矩分别为

由式（14），（15）可知，在类似图 6（d）的阶段，粒间接触的应力、弯矩计算由线性关系转变非线性关系，这大大增加了数值模拟计算难度。因此，假设在该阶段力矩为常数，等于临界状态的力矩。具体应力计算如下所示：

综上所述，通过嫦娥五号月壤图像获取的颗粒形态数据，将月壤的颗粒形状特征纳入离散元计算的接触模型中，同时结合月壤颗粒级配曲线，建立颗粒形态特征与级配相结合的数值样，将模拟结果与已知月壤试验结果对比验证其可靠性。在考虑了月壤颗粒形状影响的同时，避免了采用不规则颗粒计算所带来的计算时间的难题，为揭示月壤复杂宏观力学特性和开展月球资源勘探及开发利用研究提供基础。

3.   离散元数值模拟试验

本文通过在软件PFC3D 6.0中植入团队开发的三维离散元月壤接触模型，结合Fish语言编码以实现在数值样中考虑月壤粒形的影响。

3.1   离散元样制备

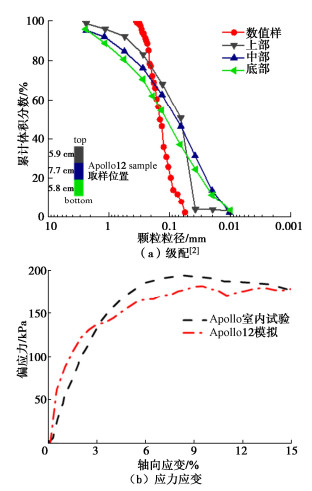
土体颗粒级配是土体力学和工程特性的重要物理参数^[37]，为避免科研目的不同导致样品中月壤级配差异性过大，进而影响到数值样的物理力学性质。在DEM模拟中，仅采用CE5C0400样品通过图像识别所获取的颗粒级配，通过对月壤二维颗粒图片识别获取相对粒径下的抗转动系数，并与美国阿波罗探月工程计划^[6]中获取的月壤级配区间以及现有的中国探月工程嫦娥五号部分样品的月壤级配^[35]进行比较，结合图 3，7，所获得月壤颗粒级配曲线均分布于已知的月壤颗粒级配曲线上下限范围内，从侧面反映了基于图像识别获取月壤级配曲线的可行性。

图  7  DEM模拟颗粒级配曲线及抗转动参数

Figure  7.  DEM simulation of grain grading curve and corresponding resistance rotation coefficient

下载: 全尺寸图片 幻灯片

如图 7所示，采用由28种不同粒径球形颗粒组成颗粒级配结合相应抗转动系数，用以制备离散元数值样。其中相关参数设置如下：颗粒等效模量及法切向刚度比可以经由以往Apollo系列获取月壤的弹性模量和泊松比进行标定，但同时需要考虑刚度过小会造成颗粒重叠量过大，从而使计算失真。因此根据团队已有参数选取经验^[21]，选择颗粒等效模量为800 MPa，颗粒法切向刚度比选为5，颗粒间摩擦系数是土体颗粒固有属性，通过试错法选为0.5。其他参数设置详见表 2，进行数值样的制备主要分为以下几个步骤：

表  2  离散元模拟参数^[21]

Table  2.  Parameters used in DEM simulations

接触类型	细观参数		取值
球-球		颗粒密度/(kg·m-3)	2320
		有效模量Ep/MPa	800
		法向与切向刚度比$\zeta$	5
		抗转动系数$\beta$	见图 7
		局部破碎系数	4
		颗粒摩擦系数	0.5
		局部阻尼	0.7

下载: 导出CSV 

| 显示表格

（a）试样制备：采用Jiang等^[38]提出的分层欠压法，分10层制备初始孔隙比为0.85的试样，试样高径比1∶2，总颗粒数为21400。

（b）施加接触模型，并基于刚性边界条件的伺服机制对试样进行初始固结，固结过程中，以有效应力的形式施加固结压力，使其达到目标固结状态12.5 kPa保持稳定。

（c）将试样置于目标应力下进行等向固结并保持稳定。

（d）将试样置于1%/min应变速率下进行剪切，当轴向应变达到20%时，结束加载。

为了在单元试验中准确地获得土壤的力学性能，需要确保样品经受均匀的宏观目标应力。在地质实验室中，三轴压缩试验通常使用高度为8 cm的圆柱体样品，这导致样品顶部和底部之间由于重力而产生的垂直应力差异，与围压相比可忽略不计。在DEM模拟中，通过简单地将重力设置为零，理想地实现了无重力条件，消除了重力对力学行为的影响。

3.2   数值结果对比验证

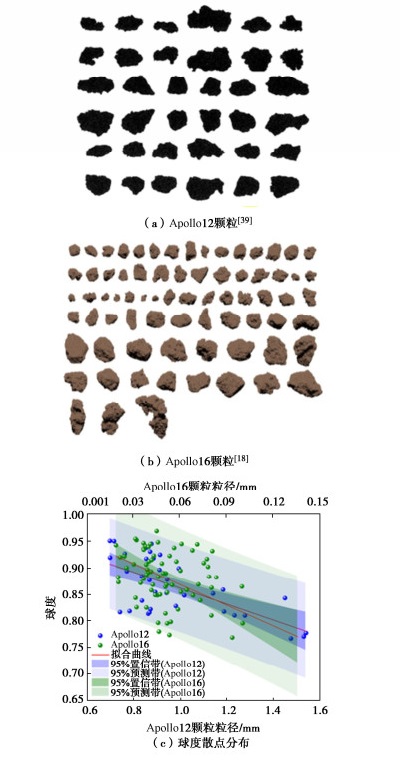
月壤颗粒粒形特征的角度对比验证：其中如图 8（a），（b）所示，Apollo 12/16获取的部分月壤颗粒的颗粒形态^[39]与中国嫦娥五号任务获取颗粒形态（见图 1）基本类似，由于试验方案设计原因，Apollo 12/16样品均经过筛分取样，导致其颗粒粒径分布相对集中。如图 8（c）所示，在仅有颗粒形态数目下，统计分析其样品球度特征演变规律与嫦娥五号系列（见图 4（a））基本一致，从颗粒形态的角度佐证了数值样和试验样品的相似性。

图  8  Apollo 12/16月壤颗粒形态特性

Figure  8.  Morphological characteristics of soil particles in Apollo 12/16 mission

下载: 全尺寸图片 幻灯片

颗粒级配及力学响应的角度对比验证：由图 9（a）所示，美国Apollo12颗粒级配范围高于本文所使用的月壤级配，但二者d₅₀较为接近。由图 9（b）可知，数值样的模拟结果与室内试验的应力应变趋势基本一致，佐证了DEM模拟的有效性。模拟曲线与试验曲线之间差别的原因主要可归结为两方面：①在基于图像对月壤颗粒捕获时存在误差，尤其是小颗粒的粒形特征难以精确捕捉；②收集颗粒数目的限制，颗粒数目较小，在表征试样整体特征方面尚有不足。基于上述应力应变响应所标定的参数下的三轴离散元模拟试样能较好地反映月壤的宏微观应力应变响应。

图  9  数值模拟与室内试验对比

Figure  9.  Comparison between numerical simulations and laboratory tests

下载: 全尺寸图片 幻灯片

3.3   三轴试验模拟宏观结果对比及讨论

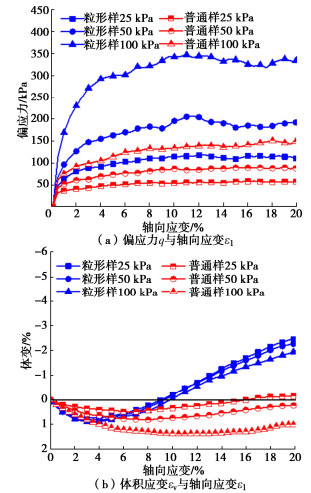
依照上文提及的数值样制备方法，本文制备2组孔隙比为0.85的数值样进行三轴剪切试验用以探究月壤粒形对其力学性质的影响。如图 7所示，不同颗粒尺寸结合相应的抗转动系数，命名为粒形样，未考虑粒形影响，命名为普通样，其他参数保持一致。在不考虑太空环境及重力的影响下，通过不同有效应力水平下（25，50，100 kPa）三轴压缩实验，探究月壤粒形的影响。

如图 10（a）所示，在应力应变关系曲线中，在不同有效围压下，二者均表现出松样应变硬化的剪切特征，此外，明显可以看出在同一有效围压下，考虑粒形样的峰值强度明显高于普通样，且随着有效围压的增高，二者之间的差距加强，该现象说明颗粒形状在试样力学性质中扮演着重要的角色^[19]，一定程度上佐证了考虑月壤粒形特征的合理性。此外对考虑月壤粒形样的结果进行线性拟合，在$\tau {\text{ - }}\sigma$平面内粒形样的强度破坏包线，所得黏聚力约为7.6 kPa，内摩擦角约为31.6°，这符合之前的文献研究中获取月壤黏聚力（1~10 kPa）、内摩擦角（30°~50°）^[3]的研究范围。

图  10  不同围压下试样三轴试验结果

Figure  10.  Results of conventional triaxial tests under different confining pressures

下载: 全尺寸图片 幻灯片

如图 10（b）所示，土体的剪胀性作为反映土体物理特性的重要指标。在不考虑颗粒粒形的情况下，普通样的体变曲线与普通砂土松样的体变曲线形状基本一致。在整个剪切过程中试样均处于减缩过程中，粒形样则表现出明显不同，且有效围压的影响在试样体变演化过程中不明显。此外，在剪切过程中，粒形样则无松砂样的剪切特征，反而体积剪胀的现象被观察到。上述现象可解释为：由于在剪切过程中颗粒会发生相对位置的错动或转动，在考虑颗粒粒形的产生的抗转动效应的影响下，颗粒发生错动或转动的情况较为困难，在内能积攒到一定情况后，产生较大范围的翻动，进而产生的体积膨胀，在有效围压较小时该现象较明显。

3.4   三轴试验模拟细观结果对比及讨论

为了进一步探究剪切过程中月壤数值样内部的演化规律，引入平均纯转动率（averaged pure rotation rate，简称APR）、力学配位数来表征试样剪切过程中的内部机理。Jiang等^[40]认为颗粒间的能量消散与滑动转动量相关，而滑动转动量可以分解为与颗粒中心平动部分及与颗粒转动和颗粒尺寸相关（纯转动率（pure rotation rate），简称PR），后者表达式为

式中：${r_1}$，${r_2}$分别为相接触的颗粒1和颗粒2的半径；${\dot \theta _1}$，${\dot \theta _2}$分别为颗粒1和颗粒2的相对转动率；r为两个颗粒的平均半径，其表达式为

当考虑某颗粒群的平均纯转动率（APR），可以作为连接砂土宏微观研究的变量；本文引用APR变量，将颗粒的转动特性加以利用，用以描述砂土的剪切带演化机理，其计算公式如下：

式中：N为接触点总数；${r_k}$为第k个接触点相互接触颗粒的平均半径。

力学配位数^[41]通过计算颗粒平均拥有的有效的接触数目及扣除接触数量小于等于一个的颗粒后的配位数具体计算可参考下式：

式中：Z为配位数；${N_{\text{c}}}$为接触数目；${N_{\text{p}}}$为颗粒数目；${N_{{\text{p0}}}}$和${N_{{\text{p1}}}}$分别是接触数目为0和1的数目。

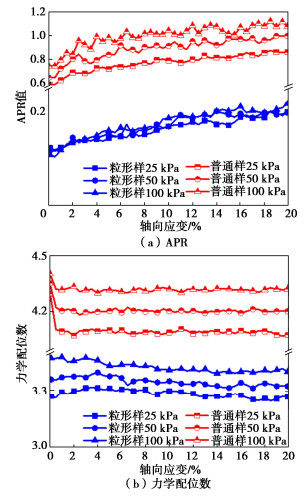
由图 11（a）可知，在不同围压下普通样的APR值远大于粒形样的结果，且普通样的APR值明显表现出与有效围压呈正相关的联系。该现象表明，考虑颗粒粒形的影响能够有效的降低了颗粒在剪切过程中的转动效应，从侧面反映了理想球形颗粒在模拟土体力学行为的局限性。力学配位数表征颗粒平均拥有的有效的接触数目，用以表征试样的密实程度。如图 11（b）所示，在不同有效围压下，普通样的力学配位数大于粒形样的配位数，且在三轴剪切的过程中，普通样力学配位数随轴向应变增加基本保持不变，粒形样则表现出随轴向应变增加颗粒配位数减少的负相关规律；这表明在剪切过程中，普通样密实度基本保持不变，而粒形样密实度随轴向应变的增加逐渐降低，这与上文所观察到的体变现象基本一致。综上可知，颗粒粒形特征在试样的力学性质及体变特征扮演重要角色。

图  11  剪切过程中力学配位数及APR演化规律

Figure  11.  Evolution of mechanical coordination number and porosity during shearing

下载: 全尺寸图片 幻灯片

4.   结论与展望

本文将月壤颗粒特征与抗转动特性结合起来，提出一种考虑中国月壤颗粒形态特征的离散元模拟方法。主要得到以下3点结论。

（1）通过图像识别手段对月壤颗粒特征进行识别捕捉，获取其粒形特征及尺寸信息，初步建立1~3040 um粒径范围下嫦娥五号月壤粒形特征与尺寸数据库，从不同尺寸范围内颗粒映射对应的形态特征，在获取足够多的月壤粒形及级配相关信息后，可以用于指导月壤模拟物的制备、对月壤真实力学性能、边值问题的研究。

（2）确立月壤粒形特征与其抗转动特性的对应关系，并结合本团队研发的三维月壤接触模型，进而考虑粒形特征的影响，通过与已知月壤试验结果进行对比验证其有效性。

（3）以月壤粒形为影响因素，模拟不同有效围压下的三轴剪切试验，结果表明了月壤粒形对其宏微观性质的有重要的影响，也佐证了在探究月表物理力学性质的过程中考虑粒形特性的必要性。

最后需要指出，本文所提出的考虑月壤粒形特征的数值模拟是依据近612颗嫦娥五号月壤颗粒的相关形态特征进行建模，所使用的颗粒数目仍然较少，代表性有所不足。其次，由于技术的限制，本文基于二维图像对月壤颗粒形态特征进行捕获，虽然降低了数据处理的难度，但反演颗粒三维球度信息仍存在一定误差。要想更加精细准确的模拟中国月壤的粒形特征，可以考虑采用CT扫描技术从三维全息角度进行突破，并且从多角度对细观尺度下的相关参数进行标定，不仅仅停留在宏观试验结果的对比上。