波流耦合影响下分层海床隧道周围砂土渗流孔压及液化分析

张治国; 陈金芃; 朱正国; PANY T; 孙苗苗

doi:10.11779/CJGE20230008

波流耦合影响下分层海床隧道周围砂土渗流孔压及液化分析 English Version

张治国^{1, 2, 3, 4, 5, 6,},
陈金芃¹,
朱正国²,
PANY T⁴,
孙苗苗^{5, 6}

1.
上海理工大学环境与建筑学院, 上海 200093
2.
石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室, 河北石家庄 050043
3.
国家海洋局北海预报中心山东省海洋生态环境与防灾减灾重点实验室, 山东青岛 266061
4.
新加坡国立大学土木与环境工程系, 新加坡 119077
5.
浙大城市学院土木工程系, 浙江杭州 310015
6.
城市基础设施智能化浙江省工程研究中心, 浙江杭州 310015

基金项目:

国家自然科学基金项目 42177145

国家自然科学基金项目 41977247

省部共建交通工程结构力学行为与系统安全国家重点实验室课题项目 KF2022-07

山东省海洋生态环境与防灾减灾重点实验室课题项目 201703

城市基础设施智能化浙江省工程研究中心课题项目 IUI2022-YB-01

详细信息

作者简介:
张治国（1978—），男，博士，博士后，教授，博士生导师，主要从事岩土地下工程方面的研究工作。E-mail：zgzhang@usst.edu.cn

中图分类号: TU443
计量
- 文章访问数: 699
- HTML全文浏览量: 100
- PDF下载量: 249
出版历程
- 收稿日期: 2023-01-05
- 网络出版日期: 2024-04-09
- 刊出日期: 2024-03-31

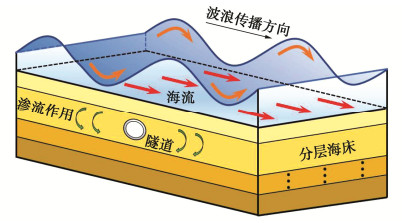
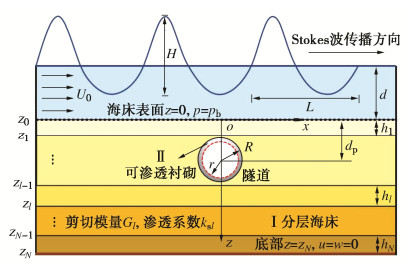
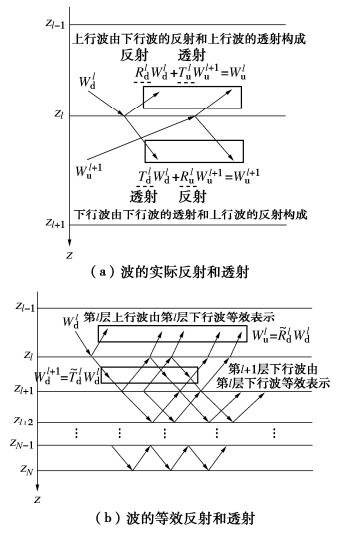
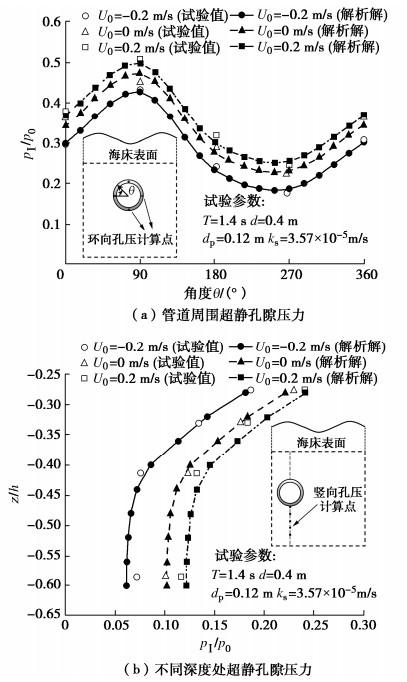
Sand liquefaction and seepage pore pressure around shield tunnels in multilayered seabed under action of waves and currents

ZHANG Zhiguo^{1, 2, 3, 4, 5, 6,},
CHEN Jinpeng¹,
ZHU Zhengguo²,
PAN Y T⁴,
SUN Miaomiao^{5, 6}

1.
School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China
2.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
3.
Shandong Provincial Key Laboratory of Marine Ecological Environment and Disaster Prevention and Mitigation, North Sea Marine Forecast Center of State Oceanic Administration, Qingdao 266061, China
4.
Department of Civil and Environmental Engineering, National University of Singapore, Singapore 119077
5.
Department of Civil Engineering, Hangzhou City University, Hangzhou 310015, China
6.
Zhejiang Engineering Research Center of Intelligent Urban Infrastructure, Hangzhou 310015, China

摘要

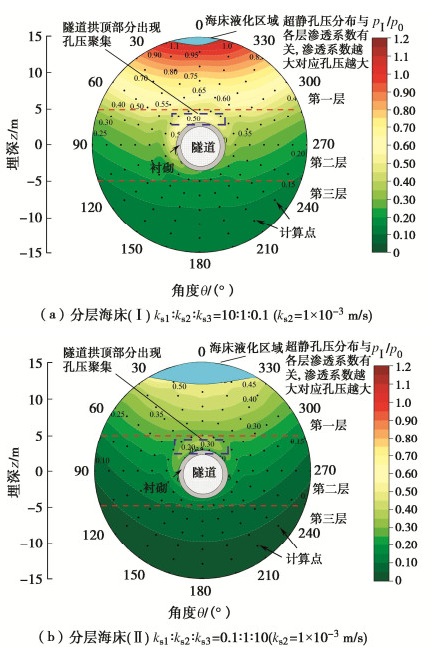
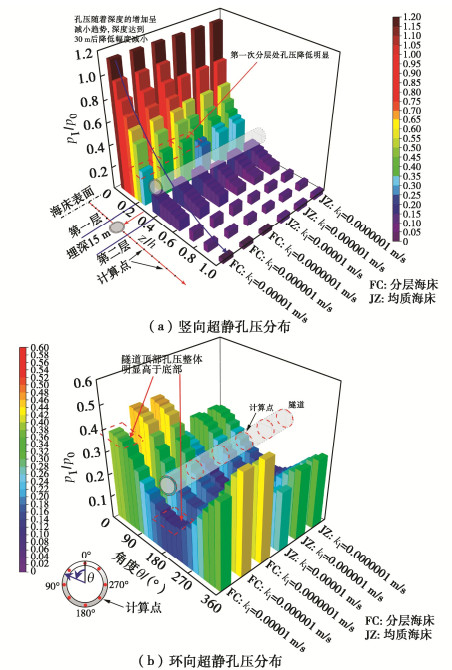
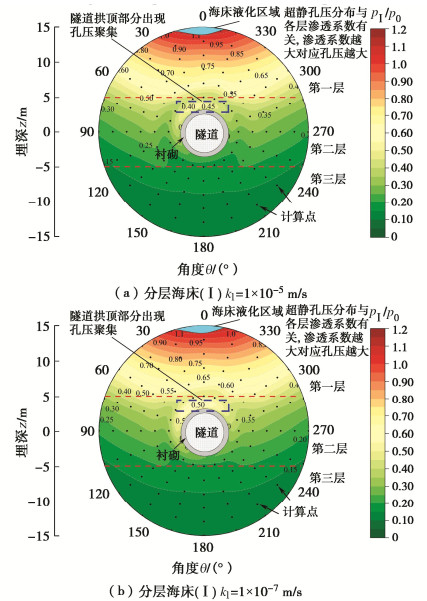
摘要: 目前针对波浪作用下海底盾构隧道周围渗流场的既有理论研究一般将衬砌考虑为不透水介质，较少考虑隧道衬砌的渗透性，尤其是较少考虑波浪与海流共同作用对隧道的影响。此外，既有理论一般将海床视为均质且各向同性工况，忽略了实际情况下分层海床的影响。首先，基于波流共同作用下的海床表面的动力边界条件，采用传递-反射矩阵法得到波流共同作用下自由分层海床的孔压响应；其次，采用镜像法建立了由于隧道存在引起的砂土摄动压力控制方程，并利用砂土与衬砌间渗流连续条件获得了该方程的Fourier级数展开解析解；接着，采用叠加原理得到了波流共同作用下分层海床中隧道周围砂土的渗流压力响应及液化判定解答。最后，将理论解析解与数值结果及已有的试验结果进行对比，获得了较好的一致性。此外，针对海床渗透性和隧道衬砌渗透性进行了影响因素分析。结果表明：海流顺流会增大海床中的孔压和液化程度，逆流会减小海床中的孔压并抑制海床的液化，且流速相同时海床对逆流响应的相对差异总体上也大于顺流；当分层海床上层渗透系数较大时（k_s＞1×10^-2 m/s），海床整体孔压较大，且第一次分层处孔压变化明显；当隧道衬砌渗透系数较小时（k_l＜1×10^-6 m/s），隧道对超静孔隙水压在海床内传播“阻挡”效应明显。
- 海底盾构隧道 /
- 分层海床 /
- 波流耦合 /
- 渗流孔压 /
- 传递-反射矩阵法
Abstract: At present, the existing theoretical studies on the seepage field around subsea shield tunnels under wave action generally consider the linings as an impermeable medium, and seldom consider the permeability of the tunnel linings, especially the influences of the coupling action of waves and currents on the tunnel. In addition, the existing theories generally regard the seabed as being homogeneous and isotropic, ignoring the influences of multilayered seabed. Firstly, based on the dynamic boundary conditions of seabed surface under wave-current interaction, the pore water pressure response of pure seabed under wave-current interaction is obtained by the transmission and reflection matrix method. Secondly, the mirror image method is introduced to establish the governing equation for the excess pore water pressure caused by the existence of tunnel, and the analytical solution of the equation is obtained by the Fourier series expansion under the continuous seepage between sand and linings. Then, based on the superposition principle, the seepage pressure of the sand around the tunnel in multilayered seabed under the action of waves and currents is obtained. Finally, the theoretical analytical solution is compared with the numerical results and the existing experimental results, and a good agreement is obtained. In addition, the influencing factors for the permeabilites of seabed and tunnel linings are analyzed. The results show that the following currents will increase the pore pressure in the seabed and the liquefaction degree of the seabed, while the opposing currents will reduce the pore pressure in the seabed and the liquefaction of the seabed. The relative difference of the seabed response to the opposing currents at the same velocity is generally greater than that of the following currents. When the permeability coefficient of the upper seabed is large (k_s > 1×10^-2 m/s), the overall pore pressure of the seabed is large, and the pore pressure at the first stratification changes significantly. When the permeability coefficient of tunnel linings is small (k_l < 1×10^-6 m/s), the tunnel has an obvious "block" effects on the propagation of the excess pore pressure in the seabed.
- subsea shield tunnel /
- multilayered seabed /
- wave-current coupling /
- seepage pore pressure /
- transmission and reflection matrix method

HTML全文

0. 引言

土体导热系数是表征地下热量传导效率的重要热物理参数，也是土体热力学性质的重要指标之一，其大小影响着地下空间传、蓄热过程。深入了解土体导热系数的影响因素及其内在机制对于许多热工项目的传热分析、建模和合理设计具有重要意义，例如人工冻结法在地下工程施工中的应用^[1]，核废料深地质处置的导热问题^[2-3]，深部矿产与地热资源的开发利用^[4]，埋地高压电缆的散热^[5]以及垃圾填埋场衬垫系统的设计^[6]等。为此，国内外学者对土体导热系数开展了大量的研究探讨，发现影响岩土体导热系数的因素较多，主要包括矿物成分、颗粒大小与级配、含水率、孔隙率、饱和度、盐分、有机质、微观结构和温度等^[7-9]。然而，研究中对土体导热系数的测试大多是在室温下进行，对于不同温度下土体导热系数的测试及其预测研究较少，需引起重视。

由于土体是由固、液、气三相组成的复合多孔介质，温度变化时土中液相会发生迁移和相变，比如温度变化引起的水分迁移^[10]、冻融循环^[11]以及水汽潜热传输^[7]等过程，影响了土体的导热系数。与低温循环引起冻融过程的影响相比，高温引起的水汽潜热传输作用对土体导热系数的影响表现得更为突出。陆森等^[12]利用单针热脉冲技术测试了3~81℃下壤土的导热系数，发现当试样温度升至81℃时，其导热系数约为22℃下的（2~4）倍。研究表明，室温范围（0~40 ℃）非饱和土中热量传递主要通过土中各相的接触热传导进行；较高温度（40~90℃）影响下，非饱和土中还存在水汽潜热传输作用的传热机制，且该机制甚至占据主导作用^[13]。目前，由于水汽潜热传输作用的量化仍比较困难，因此考虑温度影响的导热系数预测模型还较少。

De ^[14]最早建立了考虑水汽扩散强化传热影响的导热系数预测模型，但该模型含有较多参数，其关键参数的取值具有较大不确定性。为此，一些学者对De Vries模型进行简化和修正，提出了Campbell模型^[15]、De Ⅴ-1和De Ⅴ-2模型^[16]。Tarnawski等^[17]以Johansen模型为基础，将标准化函数扩展成关于饱和度和温度的函数，建立了Tarnawski经验模型，但该模型拟合参数较多，不实用。Tarnawski等^[18]和Leong等^[19]提出了考虑温度影响的粒间接触传热模型，该模型是以自洽近似理论为基础，同时考虑了土颗粒间接触热阻对传热过程的影响，但计算过程过于复杂。就目前而言，由于缺少不同温度下土体导热系数的实测数据，现有考虑温度影响的预测模型尚缺乏可靠的试验验证。同时，由于温度作用下非饱和土体内部热传递是一个传热传质耦合过程，使得现有预测模型的形式普遍比较复杂，存在一定局限性。

本文利用热探针法测试了4种土体导热系数的温度效应，探讨温度对土体导热系数影响的内在机理。在此基础上，基于广义几何平均法建立了考虑温度影响的土体导热系数预测模型，并与传统预测模型进行比较。为进一步检验新模型的有效性和可靠性，利用该模型预测干密度和含水率对土体导热系数温度效应的影响，结果表明新模型具有较好的预测性能。

1. 试验材料与方法

1.1 试验材料

试验用土包括红黏土、粉质黏土、软土以及GMZ07膨润土，红黏土和粉质黏土取自广西桂林市雁山镇广西师范大学新校区内，软土取自上海地区，GMZ07膨润土产自内蒙古兴和县高庙子地区。在进行试验之前，先将所取土样风干、碾散、过筛，均匀混合后备用。通过室内试验，获取了4种供试土样的基本物性指标和矿物成分，如表 1，2所示。

表 1 供试土样的基本物性指标

Table 1. Physical property indexes of soil samples

土样	相对质量密度	液限/ %	塑限/%	塑性指数	颗粒级配/%
土样	相对质量密度	液限/ %	塑限/%	塑性指数	砂粒2~0.05 mm	粉粒0.05~0.002 mm	黏粒 < 0.002 mm
红黏土	2.74	61.8	38.1	23.7	7.89	47.02	45.09
粉质黏土	2.72	27.6	16.5	11.1	27.10	52.54	20.36
软土	2.73	40.6	20.5	20.1	3.75	69.44	26.81
GMZ07膨润土	2.76	163.0	32.0	131.0	—	56.40	43.60

下载: 导出CSV

| 显示表格

表 2 供试土样的矿物成分

Table 2. Mineral compositions of soil samples 单位: %

土样	蒙脱石	高岭石	伊利石	长石	石英	其他
红黏土	—	50.7	12.0	9.9	12.7	14.7
粉质黏土	—	51.0	19.0	—	11.5	18.5
软土	—	—	31.2	—	23.0	45.8
GMZ07膨润土	62.0	—	—	11.0	10.0	17.0

下载: 导出CSV

| 显示表格

1.2 土体导热系数测定

为研究温度、含水率和干密度对土体导热系数的影响，本次试验设置试样温度分别为5，20，40，60，80，90℃，含水率为0.5%~40.3%，干密度为1.10~1.80 g/cm³。为满足导热系数测定设备的尺寸要求，确定试样直径为7.0 cm，高为5.2 cm。

采用喷雾法和静压法制备不同含水率和干密度试样，具体的制备过程如下：①取适量土体置于塑料袋内，利用喷雾法湿润土样至目标含水率；②扎紧塑料袋并密封静置7 d，直至湿土样内水分均匀分布；③将均化后的湿土样倒入不锈钢模具内，静压至目标干密度，并静置一定时间直至试样不发生回弹。

土体导热系数的测定采用KD2 Pro型热特性分析仪，优点是能够快速完成热性质的测定。KD2 Pro型热特性分析仪主要由控制器和热探针组成，其测试原理是基于线热源理论，可归结为在无限大介质中一恒定线热源径向一维导热的求解问题^[20]。测量过程中，热探针会产生热脉冲并对样品进行加热，随后控制器将会采集热电偶对热脉冲产生的温度响应，最后利用该过程中热探针温度变化的监测数据来计算样品的导热系数。本次试验利用SH-1型热探针进行导热系数测定，其长度和直径分别为30，1.28 mm，双针间隔为6 mm，测试精度为±5%，可在-50~150℃环境温度下正常使用。为保证不同温度下导热系数测定时试样内水分维持恒定，利用保鲜膜和胶布将试样包裹严实，随后将密封好的试样放置恒温箱内静置至目标温度（分别为5，20，40，60，80，90 ℃），再利用SH-1型热探针竖直插入试样进行测定，即可获取不同温度试样的导热系数，测试过程如图 1所示。为保证试验的测试精度，每个试样测定3次，土体最终的导热系数取多次测定结果的平均值。

图 1 不同温度下试样的导热系数测试

Figure 1. Measurement of thermal conductivity of samples subjected to different temperatures

下载: 全尺寸图片幻灯片

1.3 考虑温度影响的土体导热系数预测模型

（1）Tarnawski（2000）模型

Tarnawski等^[17]以Johansen模型^[21]为基础，将标准化函数Ke扩展成关于饱和度S_r 和摄氏温度T的函数，建立了考虑温度影响的导热系数K预测模型，即Tarnawski经验模型：

$\operatorname{Ke}\left(S_{\mathrm{r}}, T\right)=\frac{K-K_{\text {dry }}}{\left(K_{\text {sat }}-K_{\text {dry }}\right)} \quad \ \ \ 。$

(1)

式中：K_sat，K_dry分别为完全干燥和饱和状态下土体的导热系数（W/mK）。

干燥状态下土体的导热系数K_dry可由下式进行计算：

$K_{\mathrm{dry}}=\frac{0.137 \rho_{\mathrm{d}}+64.7}{\rho_{\mathrm{p}}-0.947 \rho_{\mathrm{d}}} \ \ \ 。$

(2)

式中：ρ_d为干密度；ρ_p为颗粒密度，取2650 kg/m³。

饱和状态下土体的导热系数K_sat可由广义几何平均关系式进行计算：

$K_{\text {sat }}=K_{\mathrm{w}}^n K_{\mathrm{s}}^{1-n} \quad \ \ \ 。$

(3)

式中：n为孔隙率；K_w，K_s分别为水和固体颗粒的导热系数，K_w在20℃下取0.594 W/mK；

$K_{\mathrm{s}}=K_{\mathrm{q}}^{\theta_{\mathrm{q}}} K_{\mathrm{o}}^{1-\theta_{\mathrm{q}}} \quad \ \ \ 。$

(4)

式中： $\begin{array}{ll}K_{\mathrm{q}}, \quad \theta_{\mathrm{q}}\end{array}$ 分别为石英的导热系数和体积分数，K_q=7.7 W/mK；K_o为除石英外其它矿物成分的等效导热系数，当 $\theta_{\mathrm{q}} \leqslant 0.2$ 时，K_o =3 W/mK；当 $\theta_{\mathrm{q}}>0.2$ 时，K_o=2 W/mK。

Ke是关于饱和度S_r和温度T的函数：

$\operatorname{Ke}\left(S_{\mathrm{r}}, T\right)=\frac{a+b T+c S_{\mathrm{r}}+d S_{\mathrm{r}}^2}{1+e T+f S_{\mathrm{r}}+g S_{\mathrm{r}}^2} \ \ \ 。$

(5)

式中：a~g为拟合参数，由任一温度下的实测数据进行拟合获取，进而用于预测其它温度下土体的导热系数。为使该模型更易于推广使用，现采用20℃下导热系数的实测结果来拟合获取参数a~g，由此可预测其它温度下土体的导热系数：

$K=K_{\text {dry } 20^{\circ} \mathrm{C}}+\left(K_{\text {sat } 20^{\circ} \mathrm{C}}-K_{\text {dry }, 20^{\circ} \mathrm{C}}\right) \operatorname{Ke}\left(S_{\mathrm{r}}, T\right) \ \ \ 。$

(6)

（2）Gori（2002）模型

Gori等^[22]将土体概化为由各组分构成的立方体单元空间，且立方固体颗粒处于土体单元中心。在此基础上，将土体单元水饱和过程划分成以下3个阶段：①在完全干燥条件下，孔隙中由空气充满；②含湿（非饱和）状态下，土中水先通过吸附和毛细作用赋存在固体颗粒四周，随着水分的继续增加，“水桥”开始形成并逐渐扩张；③在完全饱和状态下，土中孔隙充满水。针对水饱和过程的不同阶段，土体的导热系数计算方法不同。

a）完全干燥状态下，土体的导热系数K由干空气和固体颗粒的导热系数计算求得：

$\frac{1}{K}=\frac{\beta-1}{K_{\mathrm{da}} \beta}+\frac{\beta}{K_{\mathrm{s}}+K_{\mathrm{da}}\left[\beta^2-1\right]} \quad\ \ \ 。$

(7)

b）类似地，完全饱和状态下，土体的导热系数可由下式计算求得：

$\frac{1}{K}=\frac{\beta-1}{K_{\mathrm{w}} \beta}+\frac{\beta}{K_{\mathrm{s}}+K_{\mathrm{w}}\left[\beta^2-1\right]}\ \ \ 。$

(8)

式中：K_s，K_w和K_da分别为固体颗粒、水和干空气的热传导系数；参数β与孔隙率n有关：

$\beta=\sqrt[3]{\frac{1}{1-n}} \quad \ \ \ 。$

(9)

K_w，K_da均为温度T的函数：

$K_{\mathrm{w}}=0.569+1.88 \times 10^{-3} T-7.72 \times 10^{-7} T^2 \text {, }$

(10)

$K_{\mathrm{da}}=2.408 \times 10^{-2}+7.92 \times 10^{-5} \mathrm{~T} \text { 。 }$

(11)

固体颗粒的导热系数K_s为各矿物组分的加权平均，但该方法过于复杂，为便于比较不同预测模型的可靠性，K_s也按式（4）计算取值。

非饱和状态下，热传导系数计算的前提是求取临界含水率 $\theta_{\mathrm{c}}$ ：

$\theta_{\mathrm{c}}=0.375 \theta_{\mathrm{PWP}} \quad \ \ \ 。$

(12)

式中： $\theta_{\mathrm{PWP}}$ 为土粒间开始形成“水桥”时的体积含水率，可利用Rawls等^[23]的线性回归公式估算：

$\theta_{\mathrm{PWP}}=0.026+0.005 m_{\text {clay }} \text { 。 }$

(13)

式中：m_clay为黏粒含量。

c）含湿状态下，当体积含水率 $\theta_{\mathrm{w}}<\theta_{\mathrm{c}}$ 时，非饱和土体的导热系数为

$\begin{gathered} \frac{1}{K}=\frac{\beta-1-\delta / 3}{K_{\mathrm{app}} \beta}+\frac{\beta \delta}{3\left[K_{\mathrm{w}}+K_{\mathrm{app}}\left(\beta^2-1\right)\right]}+ \\ \frac{\beta}{K_{\mathrm{s}}+\frac{2}{3} \delta K_{\mathrm{w}}+\left(\beta^2-1-\frac{2}{3} \delta\right)} \end{gathered}\ \ \ 。$

(14)

式中：K_app为空气的表观热传导系数，可由干空气的导热系数K_da和饱和水蒸汽的导热系数K_da计算求得

$K_{\mathrm{app}}=K_{\mathrm{da}}+h \cdot K_{\mathrm{vs}} \cdot \xi \ \ \ 。$

(15)

式中： $\xi$ 为传质增强因子，按文献[24]建议取1；h为气相相对湿度，

$h=\exp \left(\frac{\psi M_{\mathrm{w}}}{\rho_{\mathrm{w}} R T_{\mathrm{K}}}\right) \quad \text { 。 }$

(16)

式中: $\psi$ 为土壤水势, $M_{\mathrm{w}}$ 为水的摩尔质量; $\rho_{\mathrm{w}}$ 为水的密度; $R$ 为绝对气体常数; $T_{\mathrm{K}}$ 为开尔文温度。

饱和水蒸汽的热传导系数K_vs为

$K_{\mathrm{vs}}=\frac{H_{\mathrm{L}} D M_{\mathrm{W}}}{R T_{\mathrm{K}}} \cdot \frac{p_{\mathrm{b}}}{p_{\mathrm{b}}-p_{\mathrm{vs}}} \cdot \frac{\mathrm{d} p_{\mathrm{vs}}}{\mathrm{d} T_{\mathrm{K}}}\ \ \ 。$

(17)

式中: $p_{\mathrm{b}}$ 为大气压; $H_{\mathrm{L}}$ 为汽化潜热, $H_{\mathrm{L}}=2503000-$ $2300 T$ 。

饱和蒸汽压p_vs与温度T有关：

$\ln p_{\mathrm{vs}}=\sum\limits_{l=-1}^3 g_l T^l+g_4 \ln T \ \ \ \ 。$

(18)

式中：g_l为形状因子，l=-1~4。g_-1 =-5800.22，g₀ =0.01，g₁=-0.05，g₂ = 0.42 ×10^-4，g₃ = -0.14 × 10^-7，g₄ =6.55。

式（17）中，D为水蒸气在空气中的扩散系数，与开尔文温度T_K有关：

$D=2.25 \times 10^{-5}\left[\frac{T_{\mathrm{K}}}{273.15}\right]^{1.72} \ \ \ \ 。$

(19)

参数δ为关于体积含水率θ_w和孔隙率n的函数：

$\delta=\frac{\theta_{\mathrm{w}}}{1-n} \ \ \ \ 。$

(20)

d）当体积含水率θ_w > θ_c，且长度比γ_f < 1时，土体的导热系数可由下式求得：

$\begin{aligned} \frac{1}{K}= & \frac{\beta^2-\beta \gamma}{K_{\text {app }}\left(\beta^2-\gamma_f^2\right)+K_{\mathrm{w}} \cdot \gamma_f^2}+\frac{\beta \gamma-\beta}{K_{\text {app }}\left(\beta^2-\gamma^2\right)+K_{\mathrm{w}} \cdot \gamma^2}+ \\ & \frac{\beta-\beta \gamma_f}{K_{\text {app }}\left(\beta^2-\gamma^2\right)+K_{\mathrm{w}} \cdot\left(\gamma^2-1\right)+\lambda_{\mathrm{s}}}+ \\ & \frac{\beta \gamma_f}{K_{\mathrm{s}}+K_{\mathrm{w}} \cdot\left(\gamma^2-1+2 M\right)+K_{\text {app }}\left(\beta^2-\gamma^2-2 M\right)} \ \end{aligned}\ \ \ \ 。$

(21)

式中：参数 $\gamma$ 为

$\gamma=\sqrt[3]{\frac{V_{\mathrm{w}}}{V_{\mathrm{s}}}-\frac{V_{\mathrm{wf}}}{V_{\mathrm{s}}}+1} \quad \ \ \ 。$

(22)

式中：V_wf，V_s分别为毛细水和固体颗粒的体积；V_s可由基本物性指标计算求得。

$\frac{V_{\mathrm{wf}}}{V_{\mathrm{s}}}=\left[0.183+\frac{0.226-0.183}{0.4764-0.2595} \cdot(0.4764-n)\right] \cdot\left(\beta^3-1\right) \text { 。 }$

(23)

长度比γ_f本质上也与体积含水率有关：

$\gamma_{\mathrm{f}}=\sqrt{\frac{V_{\mathrm{wf}} / V_{\mathrm{s}}}{3(\beta-\gamma)}} \quad \text {。 }$

(24)

e）当体积含水率θ_w > θ_c，且长度比γ_f > 1时，土体的导热系数可由下式求得：

$\begin{aligned} \frac{1}{K}= & \frac{\beta^2-\beta \gamma}{K_{\text {app }}\left(\beta^2-\gamma_f^2\right)+K_{\mathrm{w}} \cdot \gamma_{\mathrm{f}}^2}+\frac{\beta \gamma-\beta \gamma_f}{K_{\text {app }}\left(\beta^2-\gamma^2\right)+K_{\mathrm{w}} \cdot \gamma^2}+ \\ & \frac{\beta \gamma_{\mathrm{f}}-\beta}{K_{\text {app }}\left(\beta^2-\gamma^2-2 M\right)+K_{\mathrm{w}} \cdot\left(\gamma^2+2 M\right)}+ \\ & \frac{\beta}{K_{\mathrm{s}}+K_{\mathrm{w}} \cdot\left(\gamma^2-1+2 M\right)+K_{\text {app }}\left(\beta^2-\gamma^2-2 M\right)}。 \end{aligned}$

(25)

（3）Leong（2005）模型

Leong模型^[19]是以自洽近似法为基础，即假定土体是由土颗粒和均质体构成，该均质体是由具有相似性状的组分（包括土颗粒、水和空气）组成（见图 2）。由此，土体的等效导热系数可由迭代公式计算求得：

图 2 Leong模型的结构原理图

Figure 2. Structural diagram of Leong model

下载: 全尺寸图片幻灯片

$K_{\mathrm{eff}}=\frac{1}{3}\left[\sum\limits_{i=1}^3 \frac{\theta_i}{2 K_{\mathrm{eff}}+K_i}\right]^{-1} \text { 。 }$

(26)

式中： ${K_i}$ 和 ${\theta _i}$ 分别为土中各单相的导热系数和体积分数。

固相（ ${\theta _1}$ ）、液相（ ${\theta _2}$ ）和气相（ ${\theta _3}$ ）的体积分数可由下式计算求得：

${\theta _1} = \frac{{{V_{\text{s}}}}}{{{V_{\text{v}}} + {V_{\text{s}}}}} = \frac{{{\rho _{\text{d}}}}}{{{\rho _{\text{w}}}{G_{\text{s}}}}} \text{，}$

(27)

${\theta _2} = \frac{{{V_{\text{w}}}}}{{{V_{\text{v}}} + {V_{\text{s}}}}} = \frac{{{{\text{S}}_{\text{r}}}({G_{\text{s}}} - {\rho _{\text{d}}}/{\rho _{\text{w}}})}}{{{G_{\text{s}}}}} \text{，}$

(28)

${\theta _3} = \frac{{{V_{\text{a}}}}}{{{V_{\text{v}}} + {V_{\text{s}}}}} = 1 - ({\theta _1} + {\theta _2}) \ \ \ 。$

(29)

式中： ${V_{\text{s}}}$ ， ${V_{\text{w}}}$ 和 ${V_{\text{v}}}$ 分别为固体颗粒、水和土中孔隙的体积； ${\rho _{\text{d}}}$ 为土体的干密度（g/cm³）； ${\rho _{\text{w}}}$ 为水的密度； ${G_{\text{s}}}$ 为土粒相对质量密度。

固相的导热系数 ${K_1}$ 可由下式计算求得：

${K_1} = \alpha {K_{\text{s}}} \ \ \ 。$

(30)

式中： ${K_{\text{s}}}$ 为固体颗粒的导热系数，可利用式（4）计算求解； $\alpha$ 是传质校正因子，反映了土颗粒间接触热阻（TCR）对传热过程影响程度的大小，数值越大，土颗粒间接触情况越良好，故土颗粒的导热系数越大。在水饱和过程中，土颗粒间的接触情况受饱和度的影响，因而传质校正因子 $\alpha$ 与饱和度 ${S_{\text{r}}}$ 有关：

$\alpha = Ke({\alpha _{{\text{sat}}}} - {\alpha _{{\text{dry}}}}) + {\alpha _{{\text{dry}}}} \text{，}$

(31)

$Ke = 0.7\lg {{\text{S}}_{\text{r}}} + 1 \ \ \ 。$

(32)

式中： ${\alpha _{{\text{dry}}}}$ ， ${\alpha _{{\text{sat}}}}$ 分别为完全干燥和饱和状态下的传质校正因子，

${\alpha _{{\text{dry}}}} = \frac{1}{{(\beta /{K_{\text{s}}} + (1 - \beta )/{K_{{\text{da}}}}){K_{\text{s}}}}} \text{，}$

(33)

${\alpha _{{\text{sat}}}} = \frac{1}{{(\beta /{K_{\text{s}}} + (1 - \beta )/{K_2}){K_{\text{s}}}}} \ \ \ 。$

(34)

式中： ${K_{{\text{da}}}}$ ， ${K_2}$ 分别为干空气和液相（水）的导热系数，均是关于温度T的函数：

${K_{{\text{da}}}} = 2.408 \times {10^{ - 2}} + 7.92 \times {10^{ - 5}}T \text{，}$

(35)

${K_{\text{2}}} = 0.569 + 1.88 \times {10^{ - 3}}T - 7.72 \times {10^{ - 7}}{T^2} \ \ \ 。$

(36)

式（5），（6）中，参数 $\beta$ 为土颗粒间有效接触率，与孔隙率（ $n$ ）有关：

$\beta = 1 - 0.12833n + 0.06461{n^2} + 0.06491{n^3} \ \ \ 。$

(37)

气相的导热系数 ${K_3}$ 可由干空气 ${K_{{\text{da}}}}$ 和饱和水蒸汽 ${K_{{\text{vs}}}}$ 的导热系数求得：

${K_3}{\text{ = }}{K_{{\text{da}}}} + h{K_{{\text{vs}}}} \ \ \ 。$

(38)

式中：h为气相的相对湿度，可利用式（16）计算求得； ${\lambda _{{\text{vs}}}}$ 可利用式（17）计算求得。

（4）加权几何平均模型

本文基于加权几何平均法^[25]，建立考虑温度影响的土体导热系数预测模型，导热系数K可由各组分的加权几何平均关系式计算求得：

$K{\text{ = }}\prod\limits_i^n {K_i^{{\theta _i}}} \ \ \ 。$

(39)

式中： ${K_i}$ ， ${\theta _i}$ 分别为各组分的导热系数和体积分数。

利用加权几何平均法建立预测模型时，需作如下假定：①温度梯度作用下，视岩土体为固、液、气组成的3相混合均质体；②土体孔隙由空气填充，随着土中水分的增加，孔隙中的空气逐渐被水分取代。据此，非饱和土的导热系数可由下式进行计算：

$K = K_{\text{s}}^{{\theta _{\text{s}}}}K_{\text{w}}^{{\theta _{\text{w}}}}K_{\text{g}}^{{\theta _{\text{g}}}}\text{，}$

(40)

${\theta _{\text{s}}} = 1 - n = {\rho _{\text{d}}}/{\rho _{\text{p}}}\text{，}$

(41)

${\theta _{\text{w}}} = n{S_{\text{r}}}\text{，}$

(42)

${\theta _{\text{g}}} = n(1 - {S_{\text{r}}})\text{，}$

(43)

${\theta _{\text{s}}} + {\theta _{\text{w}}} + {\theta _{\text{g}}} = 1\ \ \ 。$

(44)

式中：固、液、气相的导热系数和体积分数分别为 ${K_{\text{s}}}$ ， ${K_{\text{w}}}$ ， ${K_{\text{g}}}$ 和 ${\theta _{\text{s}}}$ ， ${\theta _{\text{w}}}$ ， ${\theta _{\text{g}}}$ ； ${S_{\text{r}}}$ ，n分别为土的饱和度以及孔隙率； ${\rho _{\text{d}}}$ 为干密度； ${\rho _{\text{p}}}$ 为颗粒密度。

已有研究表明，干燥状态下温度对土体导热系数的影响较微弱^{[7, 12-13]}。为此，固相导热系数采用式（4）进行估算，即不考虑温度对其导热系数的影响。为考虑温度对液、气相导热系数的影响，利用Leong模型中式（36），（38）来分别计算不同温度下液、气相的导热系数。

需要说明的是，若不考虑温度变化的影响，土中主要传热方式是通过接触传导，而温度作用下压实非饱和土中各单相之间的接触情况比较复杂，土中还存在水蒸汽相，虽然Leong模型引入传质校正因子 $\alpha$ 用于表征土颗粒间接触热阻对传热过程的影响，但忽略了水蒸汽对土颗粒间接触热阻的影响，且该影响还可能与温度有关，目前较难进行量化。为此，引入模型拟合参数m和p用于综合考虑上述因素对土体传热的影响，对加权几何平均模型作进一步修正如下：

$K = K_{\text{s}}^{m(1 - n)}{(K_{\text{w}}^{{S_{\text{r}}}}K_{\text{g}}^{(1 - {S_{\text{r}}})})^{pn}}\ \ \ 。$

(45)

2. 试验结果及分析

2.1 含水率对土体导热系数温度效应的影响

图 3表示不同含水率w下土体导热系数K随温度T的变化。由图可知，土体导热系数随着温度和含水率的增大而增大。不同含水率条件下，温度对土体导热系数的影响程度不同。对于干燥和饱和试样，温度对土体导热系数的影响比较微弱。对于非饱和试样，温度对土体导热系数的影响随着含水率的增加呈先增大后减小的变化趋势。例如，初始干密度为1.30 g/cm³，含水率分别为0.5%（饱和度为1.2%，）和40.3%（饱和度为99.7%）时，温度对红黏土试样导热系数的影响明显较小（图 3（a））。而当试样的温度大于40℃时，温度对非饱和土体导热系数的影响开始显著，且随着试样含水率的增加，温度对土体导热系数的影响越显著，随着试样含水率的继续增加，温度对土体导热系数的影响呈下滑趋势，直至试样处于饱和状态时，温度对土体导热系数的影响极小。

从土体三相构成角度来分析，由于温度对干试样的导热系数几乎没影响（图 3），表明土中固相和气相部分的导热系数受温度变化的影响较小。已有研究表明，土中水的导热系数随温度的变化也较小，当水温从2℃升至92℃时，土中水导热系数的增加不超过0.1 W/mK^[26]。换言之，仅从土中各单相导热系数与温度的变化关系无法较好的解释温度对土体导热系数的影响。在较高环境温度下，由于非饱和含湿土样（多孔多相材料）内部孔隙结构（包含孔隙大小、形状、分布以及迂曲情况等）、孔隙中水分形态（结合水、自由水以及水蒸汽）、含量及分布情况均比较复杂，在孔隙尺度上可能会存在一定的温度梯度，导致土样内部发生水汽潜热传输效应。研究表明，在温度梯度作用下，土中水在“液岛”两端会发生蒸发和凝结交替存在的潜热传输作用（即相变热量的传递），并在热扩散作用下进一步强化土壤内部的热传导，即为水汽潜热传输效应^[27]。对膨润土持水特性的研究发现，膨润土的持水特性随着温度的升高反而变弱^[28-29]。在土体导热系数测试过程中，由于试样的含水率始终保持不变，因而吸力会随着温度的升高而减小，对土中水的约束减小，也就更有利于水汽潜热传输的发生，导热系数随之增大。王平全等^[30]采用热失重法确定了黏土中结合水类型、界限以及相对含量，发现土样温度升至75~120℃时，土中弱结合水转变为自由水。随着试样温度升高至一定范围内，部分土中弱结合水将转变成自由水，导致由温度引起的土中水分子热运动增强，也为水汽潜热传输提供了良好的物质条件。据此，本文认为温度对土体传热过程的影响可能取决于水汽潜热传输作用的变化，且比较依赖于温度、土中水分含量和水汽运移通道。这也就解释了非饱和土体导热系数的温度效应在中等饱和度范围内最为显著，而在干燥和完全饱和状态时，温度对土体导热系数的影响较小。

图 3 不同含水率试样导热系数随温度的变化

Figure 3. Change in thermal conductivity of samples with different water contents with temperature

下载: 全尺寸图片幻灯片

2.2 干密度对土体导热系数温度效应的影响

为不同干密度 ${\rho _{\text{d}}}$ 下压实试样导热系数K随温度T的变化。由图可知，相同含水率下，土体导热系数随着温度和干密度的增大而增大，且温度对土体导热系数的影响还与干密度有关。随着压实干密度的增大，温度对试样导热系数的影响明显减小。因而，尽管室温下（20~40℃）较高干密度试样的导热系数更大，但在高温（如90℃）条件下，较低干密度试样的导热系数也可能大于较高干密度试样。由“液岛”理论可知，良好的物质条件（土中水）和顺畅的传热通道（孔隙或裂隙）是水汽潜热传输作用的前提基础。换言之，土体内部可供潜热传输的水分和传热通道数越多，水汽潜热传输越显著，温度对土体导热系数的影响也就更明显。这就可以解释图 4中的试验结果，随着干密度的增大，土中孔隙空间被压缩，尤其是大孔隙，致使水汽潜热传输作用受阻，因此土体导热系数的温度效应随干密度的增大而减小。

图 4 不同干密度试样导热系数随温度的变化

Figure 4. Change in thermal conductivity of samples with different dry densities with temperature

下载: 全尺寸图片幻灯片

3. 预测模型验证及评估

利用实测的土体导热系数，图 5对比了4种模型的预测性能。由图可知，本文提出的加权几何平均模型预测性能最优，特别是对于膨润土，其预测值与实测值的偏差基本在±10%以内。Gori模型的预测效果不佳，其在高温条件下预测值普遍偏大，主要原因在于：①该理论模型中关键参数（如临界含水率θ_c）取值存在不确定性，需要通过间接估算获取（见式（12），（13）），且该关键参数较难通过实测获得；②Gori模型视土体为立方体单元，其固体颗粒位于土体单元中心，并将土体单元水饱和过程划分成3个阶段来预测导热系数，这些假定不可避免存在不同程度的偏差和不确定性。此外，Gori模型形式上也最为复杂，难以满足工程设计要求。Tarnawski模型和Leong模型的预测效果较好，偏差基本小于±30%。其中，采用Tarnawski模型对不同温度下土体导热系数进行计算时，模型参数a~g仅由20℃下的实测结果拟合获得，若模型参数a~g由不同温度下的实测结果拟合获取，Tarnawski模型预测效果应更好，但计算起来也比较繁琐，不利于该模型的推广使用。由式（15），（38）可知，传质增强因子ξ是用以反映水汽潜热传输过程水蒸汽扩散速率的影响，Gori模型和Leong模型中气相导热系数计算时并未考虑该因素的影响（即取ξ=1），忽略土中水蒸汽热扩散作用的影响。据此，本文认为Gori模型和Leong模型的预测偏差可能还与传质增强因子ξ的取值有关，今后需深入探究。

图 5 导热系数模型预测值和实测值对比

Figure 5. Comparison of measured and predicted thermal conductivities of soil

下载: 全尺寸图片幻灯片

为进一步检验加权几何平均模型对其它不同质地土壤的预测性能，利用该模型（加权几何平均模型）对文献[14]中细砂和粉砂质黏壤土的导热系数进行预测分析，结果如图 6所示。由图可知，加权几何平均模型对细砂和粉砂质黏壤土的预测效果均较好。实测结果表明，温度对红黏土热传导系数的影响与干密度和含水率均有关（图 3，4）。为此，利用加权几何平均模型预测含水率和干密度变化对土体导热系数温度效应的影响，进一步检验加权几何平均模型的可靠性。

图 6 平均几何模型预测值和实测值对比

Figure 6. Comparison between predicted and measured values of average geometric model

下载: 全尺寸图片幻灯片

图 7，8分别为含水率和干密度对土体导热系数温度效应影响的预测结果。由图可知，对于干燥和饱和土体，温度对其导热系数的影响很微弱。对于非饱和含湿土体，温度对其导热系数的影响显著。随着干密度的增大，土体的导热系数均随之增大，但温度对土体传热的影响还受干密度的约束，这与实测结果的分析是一致的。因此，本文提出的加权几何平均模型可较好预测土体导热系数温度效应与含水率和干密度间的关系，具有良好的预测性能。

图 7 含水率对土体导热系数温度效应影响的预测

Figure 7. Prediction of influences of water content on temperature effects of thermal conductivity of soil

下载: 全尺寸图片幻灯片

图 8 干密度对土体导热系数温度效应影响的预测

Figure 8. Prediction of influences of dry density on temperature effects of thermal conductivity of soil

下载: 全尺寸图片幻灯片

4. 结论

本文利用热探针法测试了不同温度条件下红黏土、粉土、软土和膨润土的导热系数，对土体导热系数的温度效应进行分析。在此基础上，建立了考虑土体导热系数温度效应的加权几何平均模型，并与传统的预测模型进行对比分析，主要得出3点结论。

（1）土体导热系数随着温度的增加而增大，其温度效应随干密度的增大而减小，温度对非饱和含湿土体导热系数的影响较大，对于干燥和饱和土体导热系数的影响比较微弱。

（2）基于加权几何平均法，建立考虑温度影响的导热系数预测模型，该模型同时考虑了水分和干密度对土体导热系数温度效应的影响。基于6种土体导热系数的实测结果，对加权几何平均模型和传统模型进行了对比分析，模型的计算结果表明，本文提出的加权几何平均模型预测性能最好，Tarnawski模型和Leong模型预测性能略低于加权几何平均模型，Gori模型预测效果最差。

（3）温度对土体导热系数的影响可能取决于水汽潜热传输作用的变化，该作用较依赖于温度、土中水分含量和水汽运移通道，当土中可提供潜热传输的水分和水汽运移通道越多，水汽潜热传输作用将越强，温度对土体导热系数的影响也越显著。

图 1 波流共同作用下海底隧道示意图

Figure 1. Schematic diagram of subsea tunnel under combined wave-current interaction

下载: 全尺寸图片幻灯片

图 2 分层海床-隧道作用计算模型

Figure 2. Computational model for multilayered seabed-tunnel interaction

下载: 全尺寸图片幻灯片

图 3 传递-反射矩阵法中波的反射和透射

Figure 3. Reflection and transmission of waves for transmission and reflection matrix method

下载: 全尺寸图片幻灯片

图 4 镜像法示意图

Figure 4. Diagram of mirror image method

下载: 全尺寸图片幻灯片

图 5 模型试验布置^[20]

Figure 5. Layout of model tests ^[20]

下载: 全尺寸图片幻灯片

图 6 管道周围超静孔隙压力对比

Figure 6. Comparison of excess pore pressures around pipeline

下载: 全尺寸图片幻灯片

图 7 三维数值模型

Figure 7. 3D numerical model

下载: 全尺寸图片幻灯片

图 8 隧道外超静孔隙水压响应对比

Figure 8. Comparison of excess pore water pressure responses outside tunnel

下载: 全尺寸图片幻灯片

图 9 不同海床渗透系数下隧道外水压响应对比

Figure 9. Comparison of external water pressure responses of tunnel for different seabed permeability coefficients

下载: 全尺寸图片幻灯片

图 10 不同海床渗透系数下隧道周围超静孔隙水压响应

Figure 10. Response of excess pore water pressure around tunnel for different seabed permeability coefficients

下载: 全尺寸图片幻灯片

图 11 不同隧道衬砌渗透系数下水压响应对比

Figure 11. Comparison of external water pressure responses for different tunnel lining permeability coefficients

下载: 全尺寸图片幻灯片

图 12 不同隧道衬砌渗透系数下隧道周围超静孔隙水压响应

Figure 12. Response of excess pore water pressure around tunnel for different tunnel lining permeability coefficients

下载: 全尺寸图片幻灯片

表 1 数值模型海床参数

Table 1 Seabed parameters of numerical model

海床	各层厚度h_l/m	泊松比 ${\nu _{\text{s}}}$	孔隙率n_s	剪切模量G/MPa	渗透系数k_s/(m·s^-1)	重度 ${\gamma _{\text{s}}}$ /(kN·m^-3)	饱和度S_r
第1层	10	0.35	0.41	15.8	1.53×10^-2	15.3	1.0
第2层	10	0.35	0.43	18.3	6.20×10^-3	19.1	1.0
第3层	30	0.35	0.47	22.4	1.20×10^-4	19.3	1.0

下载: 导出CSV

表 2 数值模型波流和隧道参数

Table 2 Wave currents and tunnel parameters of numerical model

波流							隧道
水深d/m	波高H/m	波长L/m	周期T/s	海流流速U₀/(m·s^-1)			埋深d_p/m	外径R/m	衬砌厚度(R-r)/m	剪切模量 ${G_{\text{l}}}$ /GPa	孔隙率 ${n_{\text{l}}}$	泊松比 ${\nu _{\text{l}}}$	渗透系数k_l/(m·s^-1)
20	5	100	9	2	0	-2	15	3	0.3	12.5	0.03	0.2	1.0×10^-6

下载: 导出CSV

参考文献(21)

[1]	BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. doi: 10.1063/1.1712886
[2]	BIOT M A. Theory of propagation of elastic waves in a fluid-Saturated porous solid: I low-Frequency range[J]. The Journal of the Acoustical Society of America, 2005, 28(2): 168.
[3]	BIOT M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482-1498. doi: 10.1063/1.1728759
[4]	ZIENKIEWICZ O C, CHANG C T, BETTESS P. Drained, undrained, consolidating and dynamic behaviour assumptions in soils[J]. Géotechnique, 1980, 30(4): 385-395. doi: 10.1680/geot.1980.30.4.385
[5]	TOKUO Y, KONING H L, HANS S, et al. On the response of a poro-elastic bed to water waves[J]. Journal of Fluid Mechanics, 1978, 87(1): 193-206. doi: 10.1017/S0022112078003006
[6]	ULKER M B C, RAHMAN M S, JENG D S. Wave-induced response of seabed: Various formulations and their applicability[J]. Applied Ocean Research, 2009, 31(1): 12-24. doi: 10.1016/j.apor.2009.03.003
[7]	GATMIRI B. Simplified finite element analysis of wave-induced effective stresses and pore pressures in permeable sea beds[J]. Géotechnique, 1990, 40(1): 15-30. doi: 10.1680/geot.1990.40.1.15
[8]	THOMAS S D. A finite element model for the analysis of wave induced stresses, displacements and pore pressures in an unsaturated seabed: II model verification[J]. Computers and Geotechnics, 1995, 17(1): 107-132. doi: 10.1016/0266-352X(95)91305-N
[9]	OZGUR KIRCA V S, SUMER B M, FREDSØE J. Influence of clay content on wave-induced liquefaction[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2013, 140(6): 4014024.
[10]	刘晓磊, 贾永刚, 郑杰文. 波浪导致黄河口海床沉积物超孔压响应现场试验研究[J]. 岩土力学, 2015, 36(11): 3055-3062. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201511003.htm LIU Xiaolei, JIA Yonggang, ZHENG Jiewen. In situ experiment of wave-induced excess pore pressure in the seabed sediment in Yellow River Estuary[J]. Rock and Soil Mechanics, 2015, 36(11): 3055-3062. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201511003.htm
[11]	QI W G, LI C F, JENG D S, et al. Combined wave-current induced excess pore-pressure in a sandy seabed: flume observations and comparisons with theoretical models[J]. Coastal Engineering, 2019, 147(5): 89-98.
[12]	ZHOU X L, XU B, WANG J H, et al. An analytical solution for wave-induced seabed response in a multi-layered poro-elastic seabed[J]. Ocean Engineering, 2011, 38(1): 119-129. doi: 10.1016/j.oceaneng.2010.10.003
[13]	QI H F, CHEN Z L, LI Y C, et al. Wave and current-induced dynamic response in a multilayered poroelastic seabed[J]. Bulletin of Engineering Geology and the Environment, 2020, 79(1): 11-26. doi: 10.1007/s10064-019-01553-8
[14]	ZHOU X L, JENG D S, YAN Y G, et al. Wave-induced multi-layered seabed response around a buried pipeline[J]. Ocean Engineering, 2013, 72(11): 195-208.
[15]	ZHU C W, YING H W, GONG X N, et al. Analytical solution for wave-induced hydraulic response on subsea shield tunnel[J]. Ocean Engineering, 2021, 228(5): 108924.
[16]	ZIMMERMAN C, STERN M. Scattering of plane compressional waves by spherical inclusions in a poroelastic medium[J]. The Journal of the Acoustical Society of America, 1998, 94(1): 527.
[17]	HSU H C, CHEN Y Y, HUS J R C, et al. Nonlinear water waves on uniform current in Lagrangian coordinates[J]. Journal of Nonlinear Mathematical Physics, 2009, 16(1): 47-61.
[18]	DERESIEWICZ H, SKALAK R. On uniqueness in dynamic poroelasticity[J]. Bulletin of the Seismological Society of America, 1963, 53(4): 783-788. doi: 10.1785/BSSA0530040783
[19]	ZEN K, YAMAZAKI H. Mechanism of wave-induced liquefaction and densification in seabed[J]. Soils and Foundations, 1990, 30(4): 90-104. doi: 10.3208/sandf1972.30.4_90
[20]	CHEN H, ZHANG J S, TONG L L, et al. Experimental study of soil responses around a pipeline in a sandy seabed under wave- current load[J]. Applied Ocean Research, 2023, 130(1): 103409.
[21]	常方强. 波浪作用下黄河口海底滑坡研究[D]. 青岛: 中国海洋大学, 2009. CHANG Fangqiang. Study on Mechanism of Wave-Induced Submarine Landslide at the Yellow River Estuary[D]. Qingdao: Ocean University of China, 2009. (in Chinese)

施引文献(7)

期刊类型引用(4)

1.	马殷军，杜腾飞，栾恩铭，张寿红，董江龙. 环境温度对青海湖地区含盐土水热变化规律试验研究. 水利与建筑工程学报. 2025(01): 55-60+79 . 百度学术
2.	孔纲强，常洪林，王天赐，杨庆. 区域尺度地埋管地源热泵与能源地下结构开采浅层地热能评价综述. 岩土力学. 2024(05): 1265-1283 . 百度学术
3.	唐少容，殷磊，杨强，柯德秀. 微胶囊相变材料改良粉砂土的导热系数及预测模型. 中国粉体技术. 2024(03): 112-123 . 百度学术
4.	褚召祥，王一鸣，李晓昭，董凯军，顾晓滨，贾国圣. 岩土热导率预测正三棱柱-准内切球单元结构模型. 岩土工程学报. 2024(12): 2580-2590 . 本站查看