非达西流影响的超长桩荷载传递研究

张恩祥; 赵天时; 王正振; 戴国亮; 周勇; 龙照; 杨阳

doi:10.11779/CJGE2022S1038

非达西流影响的超长桩荷载传递研究 English Version

张恩祥^{1, 2,},
赵天时^3, ,,
王正振^{3, 4},
戴国亮⁴,
周勇³,
龙照^{1, 2},
杨阳⁵

1.
甘肃中建市政工程勘察设计研究院有限公司, 甘肃兰州 730000
2.
中国市政工程西北设计研究院有限公司, 甘肃兰州 730000
3.
兰州理工大学土木工程学院, 甘肃兰州 730050
4.
东南大学土木工程学院, 江苏南京 210000
5.
陇东学院土木工程学院, 甘肃庆阳, 745000

基金项目:

国家自然科学基金项目 52068048

甘肃省自然科学基金项目 21JR11RM052

甘肃省高等学校青年博士基金项目 2022QB-045

甘肃省住房和城乡建设厅项目 JK2022-04

详细信息

作者简介:
张恩祥(1963—)，男，本科，正高级工程师，主要从事桩基础工程和地基处理等方面的工程设计与研究工作。E-mail: zex@vip.163.com

通讯作者:
赵天时, E-mail: 363669609@qq.com

中图分类号: TU473
计量
- 文章访问数: 109
- HTML全文浏览量: 26
- PDF下载量: 23
出版历程
- 收稿日期: 2022-09-27
- 网络出版日期: 2023-02-06
- 刊出日期: 2022-11-30

Load transfer of super-long piles considering influences of non-Darcy flow

1.
Gansu CSCEC Municipal Engineering Investigation and Design Institute Co., Ltd, Lanzhou 730000, China
2.
China Municipal Northwest Design and Research Institute Co., Ltd., Lanzhou 730000, China
3.
School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China
4.
School of Civil Engineering, Southeast University, Nanjing 210000, China
5.
School of Civil Engineering, Longdong University, Qingyang 745000, China

摘要

摘要: 为建立黄土地区超长桩的荷载传递计算方法，基于非达西流定律以及中心差分法推导出了在非达西流作用下的孔隙水压力计算公式，进而推导得出土体沉降量计算方法；然后以传统荷载传递法为基础，得出桩土相对位移计算模型，推导了大厚度黄土地区超长桩的下拉荷载理论计算方法；最后结合某桩基础试验，将计算结果与传统的达西定律推导出的结果以及试验结果进行对比。结果表明：①理论计算方法所得出的桩侧土体沉降与桩基侧摩阻力及轴力分布与试验结果吻合较好，能很好地反映出超长桩的荷载传递规律；②传统达西流计算得出的流速较大，导致孔隙水压力在未固结的某一时间点消散速度快于非达西流计算结果，这是达西流计算结果存在偏差的主要原因；③与非达西流动结果相比，传统达西定律推算得出的桩侧正摩阻力值偏小，未能充分发挥桩侧正摩阻力和桩基础承载力，造成较大浪费，故在计算桩侧阻力及分析桩周土变形规律时考虑非达西流影响十分必要。
- 桩基工程 /
- 超长桩 /
- 非达西流 /
- 荷载传递法 /
- 侧摩阻力
Abstract: In order to establish the load transfer method for the super-long piles in loess areas, based on the non-Darcy flow law and the central difference method, the formula for calculating pore water pressure under the action of non-Darcy flow is deduced, and the method for soil settlement is derived. Then, based on the traditional load transfer method, the model for the relative displacement of pile-soil is obtained, and the theoretical method for the pull-down loads on the super-long piles in thick loess areas is deduced. Finally, by combining with a pile foundation test, the calculated results are compared with those derived from the traditional Darcy's law and the test. The results show that: (1) The soil settlement at the pile side, side friction and axial force distribution of the pile calculated by the proposed theoretical method are in good agreement with the test results, and can well reflect the load transfer law of the super-long piles; (2) The velocity calculated by the traditional Darcy flow is large, which leads to that the dissipation speed of pore water pressure at a certain time point of unconsolidated flow is faster than that calculated by the non-Darcy flow, and this is why the calculated results by the Darcy flow are deviated. (3) Compared with that by the non-Darcy flow, the value of the normal friction at the pile side calculated according to the traditional Darcy law is small, which can not give full play to the positive frictional resistance of the pile side and the bearing capacity of the pile foundation, resulting in a great waste. Therefore, it is very necessary to consider the influences of non-Darcy flow when calculating the side resistance of the pile and analyzing the deformation law of soils around the pile.
- pile foundation engineering /
- super-long pile /
- non-Darcy flow /
- load transfer method /
- side friction

HTML全文

0. 引言

桩基础作为一种常见的建筑物基础形式其荷载传递形式、内力响应分析、桩土相互作用、桩侧摩阻力分析等问题一直以来都是研究的热点问题^[1-12]，准确掌握桩侧阻力、桩端阻力、桩身轴力及桩周土沉降量等响应指标对桩基础的设计至关重要。相关学者近年来对该问题进行了深入研究，取得了广泛的成果，但相关研究在计算或试验当中考虑桩土固结位移时均按经典达西定律考虑土体固结沉降，并未考虑土中孔隙水压力的非达西流性质。

近年来，针对非达西流动的土体固结沉降研究越来越引起学者的重视。于光明等^[13]基于非达西流动定律推导得出一维固非线性方程，得出超孔隙水压数值解答，建立了桩周土体固结沉降计算模型，进而通过荷载传递法得出桩基础的各项响应指标；刘忠玉等^[14]通过引入非达西定律修正了砂井地基固结方程，用隐式有限差分法进行了数值求解；刘忠玉等^[15]为讨论黏性土变形的黏弹塑性和非达西流影响效应，引入了统一硬化本构模型和非达西定律，修正了一维太沙基固结方程，并给出了数值解答；于光明等^[16]通过引入非达西定律建立了考虑固结和流变共同作用下的软土地基变形沉降计算模型，研究结果表明考虑固结流变共同作用对单桩承载力的不利影响非常重要。

针对目前在黄土地区鲜有考虑土体非达西流性质的情况，本文通过引入非达西流定律，并考虑桩周土层的非线性，建立改进的一维太沙基固结方程，进而通过荷载传递法求解超长桩的桩侧阻力、桩身轴力等，并通过某桩基础浸水试验对本文提出的计算方法进行验证分析。

1. 考虑非达西流的分层土沉降力学模型建立

1.1 基本假定

本文假设：①桩周土体假设为各向同性的非均质土；②孔隙水压力不可压缩，且仅考虑在径向渗流；③桩周土体为弹性体，不考虑塑性和蠕变特性；④桩侧剪应力微段内均匀分布；⑤桩体为弹性体；⑥土体固结过程中孔隙水按非达西流体考虑。

1.2 考虑非达西流的孔隙水压力计算

当土中水力梯度较低时，土中的水流流动不符合传统的达西定律，而是按照非达西流定律进行流动。本文在前人研究的基础上拟采用的非达西流定律^[17]，其计算流速的方程为

$v = - k[i - {i_0}(1 - {{\text{e}}^{\frac{{ - i}}{{{i_0}}}}})]\text{，}$

(1)

式中，v为渗流流速，k为土渗透系数，i为水力梯度，i₀为临界水力梯度。

非达西流定律描述的问题可以归结为：当土中水利梯度小于临界水力梯度时，土中水的渗流体现为非达西流规律；当大于或等于临界水利，该模型即退化为达西定律。

水力梯度和孔隙水压力的关系为

$i = \frac{1}{{{\gamma _{\text{w}}}}}\frac{{\partial u}}{{\partial z}}。$

(2)

将式（1）代入式（2）中，即可得到一组关于孔隙水压力和土中水流速的关系：

$v = - k\left[ {\frac{1}{{{\gamma _{\text{w}}}}}\frac{{\partial u}}{{\partial z}} - {i_0}(1 - {{\text{e}}^{ - \frac{{{i_0}}}{{{\gamma _w}}}\frac{{\partial u}}{{\partial z}}}})} \right]。$

(3)

根据单位时间内单元土体排水量等于单位土体体积与流速沿深度方向速度的变化量的乘积，

${\text{d}}q = \frac{{\partial v}}{{\partial z}}\Delta V\text{，}$

(4)

式中，ΔV为单位土体体积。

而单位体积土体内的流量差为

$\frac{{\partial V}}{{\partial t}} = \frac{{\Delta V}}{{1 + e}}{a_{\text{v}}}\frac{{\partial u}}{{\partial t}}。$

(5)

最后，在一维固结且只考虑径向渗流的情况下，令式（4），（5）相等，得到：

$\frac{{\partial v}}{{\partial z}}\Delta V = \frac{{\Delta V}}{{1 + e}}{a_{\text{v}}}\frac{{\partial u}}{{\partial t}}。$

(6)

将式（3）代入到式（6）当中得

$- k\left( {\frac{1}{{{\gamma _{\text{w}}}}}\frac{{{\partial ^2}u}}{{\partial {z^2}}} + \frac{{i_0^2}}{{{\gamma _{\text{w}}}}}\frac{{{\partial ^2}u}}{{\partial {z^2}}}{{\text{e}}^{ - \frac{{{i_0}}}{{{\gamma _{\text{w}}}}}\frac{{\partial u}}{{\partial z}}}}} \right)\Delta V = \frac{{\Delta V}}{{1 + e}}{a_{\text{v}}}\frac{{\partial u}}{{\partial t}}\text{，}$

(7)

式中，k为土体渗透系数， ${\gamma _{\text{w}}}$ 为水的重度，i₀为临界水力梯度，e为土体的孔隙比， ${a_{\text{v}}}$ 为土体的压缩系数ΔV为土体微元体积， ${a_{\text{v}}}$ =ΔxΔyΔz。

式（7）即为考虑非达西流影响的土中孔隙水压力的计算表达式。

根据泰勒展开式原理，现对式（7）进行简化。参照泰勒展开式处理ex=1-x的原理，式（7）可表示为

$\frac{{ - ki_0^3}}{{\gamma _{\text{w}}^2}}\frac{{{\partial ^3}u}}{{\partial {z^3}}} - \left( {\frac{k}{{{\gamma _{\text{w}}}}} + \frac{{ki_0^2}}{{{\gamma _{\text{w}}}}}} \right)\frac{{{\partial ^2}u}}{{\partial {z^2}}} - \frac{{{a_{\text{v}}}}}{{1 + e}}\frac{{\partial u}}{{\partial t}} = 0。$

(8)

由于已假定孔隙水压力不可压缩，且仅考虑径向渗流，故可考虑孔隙水压力仅与径向与时间相关，记为u(z, t)，并令 $\frac{{ - ki_0^3}}{{\gamma _{\text{w}}^2}} = A$ ， $- \left( {\frac{k}{{{\gamma _{\text{w}}}}} + \frac{{ki_0^2}}{{{\gamma _{\text{w}}}}}} \right) = B$ ， $- \frac{{{a_{\text{v}}}}}{{1 + e}} = C$ ，则式（8）转化为

$A\frac{{{\partial ^3}u(z, t)}}{{{\text{d}}{z^3}}} + B\frac{{{\partial ^2}u(z, t)}}{{{\text{d}}{z^2}}} + C\frac{{\partial u(z, t)}}{{{\text{d}}t}} = 0。$

(9)

式（9）为一个三阶偏微分方程，整理后可得

$\frac{{\partial u(z, t)}}{{{\text{d}}t}} = - \frac{A}{C}\frac{{{\partial ^3}u(z, t)}}{{{\text{d}}{z^3}}} - \frac{B}{C}\frac{{{\partial ^2}u(z, t)}}{{{\text{d}}{z^2}}}。$

(10)

可考虑采用中心差分法对上述孔隙水压力关于时间和空间的偏导数进行近似代替后变为

${u_{i, j + 1}} = - \frac{{\Delta (t)}}{{C{h^2}}}\left\{ {\frac{A}{h}\left[ {{u_{i + 2, j}} - 3({u_{i + 1, j}} - {u_{i, j}}) - {u_{i - 1, j}}} \right]} \right. + \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ B({u}_{i+1, j}-2{u}_{i, j}+{u}_{i-1, j})\begin{array}{l}\\ \end{array}\}\text{+}{u}_{i, j}\text{ }\text{，}$

(11)

式中，u_{i, j}为沿土层深度方向第i点在第j时刻的孔隙水压力，Δ(t)为一个时间增量，h为任一土层的厚度。

根据现场试验的地质条件，可认为场地排水条件为单面排水（上部排水，下部不排水）本计算方法拟定的初始条件及边界条件为

$\left. \begin{array}{l} u(0, t)=0\text{，}\\ u(z, 0)=q\text{，}\\ \frac{\partial u(z, t)}{\partial z}(z=H, t)=0。\end{array} \right\}$

(12)

根据通解（11）及边界初始条件（12），即可求解土中任意点的孔隙水压力值。

1.3 土体固结沉降计算

根据土体沉降的定义，可认为土体的最终沉降量是基于沿桩身长度所有单位土体应变量的总和，而根据基本假设，认为桩周土体为弹性体，故土体的应力应变关系符合胡克定律，

${w_{\text{c}}} = \int_0^H {{\varepsilon _z}(z, t){\text{d}}z} 。$

(13)

将土体沉降连续方程根据土层的分布情况离散化，即认为

${w_{\text{c}}} = \int_0^H {{\varepsilon _z}(z, t){\text{d}}z} = \mathop \sum \limits_{i = 1}^n {\varepsilon _z}(z, t)h 。$

(14)

而土体在某一时刻、某一深度处的应变可以根据胡克定律表示为

$\mathop \sum \limits_{i = 1}^n {\varepsilon _z}(z, t) = \mathop \sum \limits_{i = 1}^n \frac{{{{\sigma '}_i}(z, t)}}{{{E_i}}}\text{，}$

(15)

式中，n为桩周土层数， ${\sigma '_i}(z, t)$ 为桩周土体有效应力，根据有效应力原理， ${\sigma '_i}(z, t)$ 可表示为

${\sigma '_i}(z, t) = q - u(z, t)。$

(16)

将式（11）代入式（16）即得土体有效应力，再将式（16）代入式（15）得土体的分层应变总和，最后将式（15）代入式（14）即获得土体的最终沉降量。

2. 超长桩荷载传递分析

2.1 桩侧荷载传递基本方程

依据桩土相对位移的定义：

${w_{\text{p}}} - {w_{\text{c}}} = \tau {r_0}\int_{{r_0}}^{{r_{\text{m}}}} {\frac{{{\text{d}}z}}{{{G_{{\text{s}}1}}z}}} 。$

(17)

对式（17）进行简单处理后得

$\tau = k({w_{\text{p}}} - {w_{\text{c}}})\text{，}$

(18)

式中，k为桩侧剪切刚度， $k = \frac{{{G_{{\text{s}}1}}}}{{{r_0}{\text{ln}}({r_{\text{m}}}/{r_0})}}$ ，r₀为桩身半径，r_m为桩的最大影响半径。其计算方法按区分端承桩^[18]与摩擦桩^[19]进行确定。

然后根据桩身轴向荷载与桩单元变形之间的平衡关系：

$\frac{{\partial {w_{\text{p}}}(z)}}{{\partial z}} = - \frac{{P(z)}}{{{E_{\text{p}}}{A_p}}}。$

(19)

根据桩身单元平衡关系，任取一个桩身单元，其上下截面桩身压缩量与轴力合力之间的关系：

${w_{\text{p}}}(i) - {w_{\text{p}}}(i + 1) = \frac{{(P(i) + P(i + 1)){h_i}}}{{2{E_{\text{p}}}{A_{\text{p}}}}}\text{，}$

(20)

式中，h_i为任取桩单元的厚度。代入到式（18）中即得桩侧剪切应力函数式（20）。

2.2 桩侧阻力平衡方程

根据选定的任意桩单元平衡关系，侧阻力和桩身轴力之间的关系为

$\frac{{\partial P(z)}}{{\partial z}} = - 2{{\rm{\mathsf{π} }}}{r_0}\tau (z)。$

(21)

对式（21）进行积分，并根据任意桩单元平衡关系，可得式（21）的离散表达形式：

$P(i + 1) - P(i) = - 2{{\rm{\mathsf{π} }}}{r_0}\int_{{z_i}}^{{z_{i + 1}}} {\tau (z){\text{d}}z} 。$

(22)

然后，依据式（18）得出的桩侧剪切函数代入到式（22）中，即可得出桩身任意截面出的轴力表达式。至此，桩身的荷载传递关系全部得出。

3. 试验概况及结果分析

3.1 场地条件

本试验场地地层均匀且简单，桩长范围内主要为黄土状粉土，具有Ⅱ~Ⅳ级自重湿陷性，湿陷系数为0.001~0.065；粉土层下部为砂砾和泥岩，各土层主要性质如表 1所示。

表 1 场地土层特性

Table 1. Properties of soils

土层名称	厚度/m	压缩模量/MPa	地基承载力特征值/kPa
黄土状粉土层1	20左右	3.5~7.5	100~120
黄土状粉土层2	10左右	11.5	160
砂砾层	2.8~4.9	25.0	320
泥岩	未穿透	38.0	400

下载: 导出CSV

| 显示表格

3.2 试验布置及传感器埋设情况

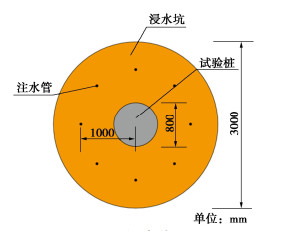
本试验用桩桩径0.8 m，桩长26 m。以试验桩为中心设置一个直径约为3.0 m的浸水坑，坑深约1.0 m，浸水试验时水头基本与地表平行，为加速浸水速率，在桩周每45°设置一个PVC注水管，管上钻有注水孔，试验布置如图 1所示。

图 1 浸水装置

Figure 1. Immersion device

下载: 全尺寸图片幻灯片

为监测浸水状态下的桩身响应，沿试桩深度共计布置22组钢筋应力计，15组混凝土应变计；在桩端均匀布置4个压力盒；在0~-14.5 m范围内每隔2 m布置一个分层沉降计，共计布置7组（图 2，3）。

图 2 浸水试验

Figure 2. Immersion tests

下载: 全尺寸图片幻灯片

图 3 传感器埋设

Figure 3. Embedment of sensors

下载: 全尺寸图片幻灯片

试验过程中先进行了静载试验，之后进行浸水试验，由于本文理论只计算非达西渗流的负摩阻力，故下文中的摩阻力和轴力变化曲线均为静载试验之后与浸水试验之后的差值曲线。

3.3 试验结果与理论计算结果对比

（1）土体沉降计算对比

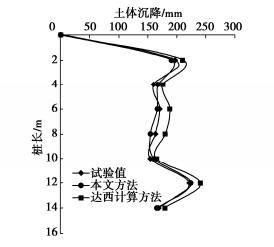
由于试验采用桩顶浸水和桩周注水孔分段渗透导致桩周土分段湿陷，故随着土层深度的增加，土体的沉降规律出现了多峰值状态。因此，在计算分析过程中可按照分段计算的原则来提高计算精度，即可认为将桩分割成为多段桩进行分析。由于本次试验的分层沉降计只设置到桩顶向下14 m处，故为保持与理论计算数值的一致性，图 4中并未标出14~22 m处的土体沉降数值。试验选取的曲线为第13天时土体最大沉降量时的曲线。

图 4 土体沉降沿深度变化曲线

Figure 4. Variation curves of soil settlement along depth

下载: 全尺寸图片幻灯片

由图 4可以看出，依据非达西流计算方法得出的土体沉降曲线与试验所得结果基本一致，误差较小。依据非达西流计算方法得出的最大值为223.78 mm，试验最大值为220.72 mm，而依据达西流计算方法得出的最大值为240.12 mm。由此可以看出依据达西流计算方法得出的数值最大，这是由于虽然非达西定律只对孔隙水压力消散的快慢有影响，对最终固结完成时的孔隙水压力消散没有影响，但在浸水至第13天时，土体并未完成固结沉降，而达西定律对孔隙水压力的消散要快于非达西定律，故而产生的土体沉降在此时要大于非达西定律产生的土体沉降。

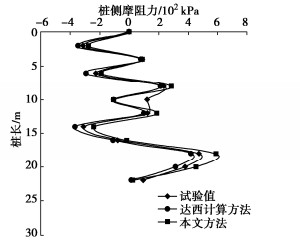
（2）桩身侧摩阻力计算对比

由于浸水方式的特殊性，本试验结果与传统的桩侧摩阻力分布结果不同。本试验结果显示：侧摩阻力沿桩身存在多个零点，即负摩阻力沿桩长呈现出多峰值状，导致正、负摩阻力出现交错分布状，其负摩阻力峰值分别为314，228，312 kPa；其正摩阻力峰值分别为87.4，235，121，473 kPa。同样选取浸水第13天的桩身侧摩阻力进行分析。

图 5为桩侧摩阻力沿深度变化曲线。由图 5可以看出，依据达西流定律计算得出的桩侧负摩阻力最大，峰值分别为348，295，104，368 kPa，正摩阻力最小，峰值分别为78.4，212，101，421 kPa；依据非达西流定律计算得出的桩侧正摩阻力最大，峰值分别为90.4，288，185，589 kPa，负摩阻力最小，其峰值分别为278，192，102，242 kPa。这主要是由于在桩周土体并未达到固结状态下，依据达西流定律计算得出的土体沉降量最大，故而产生的下拉荷载最大，对桩周产生的负摩阻力峰值也就最大；反之，依据非达西流定律计算得出的土体沉降量最小，桩土相对位移最小，故而产生的负摩阻力峰值也就最小，正摩阻力峰值最大。

图 5 桩侧摩阻力沿深度变化曲线

Figure 5. Variation curves of side friction of pile along depth

下载: 全尺寸图片幻灯片

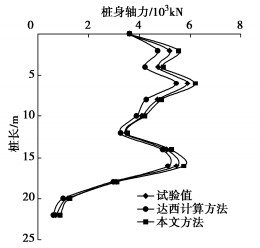
（3）桩身轴力计算对比

图 6为桩身轴力沿深度的变化曲线由。图 6可以看出，桩身最大轴力发生在中性点处，其分布曲线由于土体沉降为分段沉降，进而也出现了多个峰值状态，这主要是由于黄土遇水湿陷后，不同土层先后发生湿陷，导致出现多个湿陷层，因而出现了多个轴力的峰值点即轴力的极值点，极值分别发生在4，7，12.5，16 m深度处，其峰值分别为5180，5890，3490，5450 kN。

图 6 桩身轴力沿深度变化曲线

Figure 6. Variation curves of axial force of pile along depth

下载: 全尺寸图片幻灯片

依据达西流定律计算得出的桩身轴力最大，这主要是由于按照达西定律计算得出的桩侧负摩阻力最大，故而产生的下拉荷载也最大，故而其轴力也最大，其峰值分别为5540，6210，3510，5740 kN。依据非达西流定律得出的桩身轴力最小，其变化趋势依然是多峰值状态，其峰值分别为4710，5450，3250，5120 kN。这是由于在土体未达到固结状态下的某一时间点，依据非达西流定律得出的孔隙水压力最小，孔隙水压力消散速度慢于按照达西流定律的计算结果，故其土体的有效应力较小，进而导致土体沉降量较小，桩侧负摩阻力较小，故而下拉荷载较小，最终导致桩身的轴力也较小。

4. 结论

（1）本文建立的考虑非达西流影响下的侧摩阻力曲线与现场试验结果吻合性较好，证明本文提出的计算方法合理可行，可为类似地区桩基础设计提供参考。

（2）传统达西流计算得出的流速较大，导致孔隙水压力在未固结的某一时间点消散速度快于非达西流计算结果，这是达西流计算结果存在偏差的主要原因。

（3）与非达西流动结果相比，传统达西定律推算得出的桩侧正摩阻力值偏小，未能充分发挥桩侧正摩阻力和桩基础承载力，造成较大浪费，故在计算桩侧阻力及分析桩周土变形规律时考虑非达西流影响十分必要。

图 1 浸水装置

Figure 1. Immersion device

下载: 全尺寸图片幻灯片

图 2 浸水试验

Figure 2. Immersion tests

下载: 全尺寸图片幻灯片

图 3 传感器埋设

Figure 3. Embedment of sensors

下载: 全尺寸图片幻灯片

图 4 土体沉降沿深度变化曲线

Figure 4. Variation curves of soil settlement along depth

下载: 全尺寸图片幻灯片

图 5 桩侧摩阻力沿深度变化曲线

Figure 5. Variation curves of side friction of pile along depth

下载: 全尺寸图片幻灯片

图 6 桩身轴力沿深度变化曲线

Figure 6. Variation curves of axial force of pile along depth

下载: 全尺寸图片幻灯片

表 1 场地土层特性

Table 1 Properties of soils

土层名称	厚度/m	压缩模量/MPa	地基承载力特征值/kPa
黄土状粉土层1	20左右	3.5~7.5	100~120
黄土状粉土层2	10左右	11.5	160
砂砾层	2.8~4.9	25.0	320
泥岩	未穿透	38.0	400

下载: 导出CSV

参考文献(19)

[1]	陈仁朋, 周万欢, 曹卫平, 等. 改进的桩土界面荷载传递双曲线模型及其在单桩负摩阻力时间效应研究中的应用[J]. 岩土工程学报, 2007, 29(6): 824–830. doi: 10.3321/j.issn:1000-4548.2007.06.006 CHEN Ren-peng, ZHOU Wan-huan, CAO Wei-ping, et al. Improved hyperbolic model of load-transfer for pile-soil interface and its application in study of negative friction of single piles considering time effect[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(6): 824–830. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.06.006
[2]	孔纲强, 杨庆, 郑鹏一, 等. 考虑时间效应的斜桩基负摩阻力室内模型试验研究[J]. 岩土工程学报, 2009, 31(4): 617–621. doi: 10.3321/j.issn:1000-4548.2009.04.020 KONG Gang-qiang, YANG Qing, ZHENG Peng-yi, et al. Model tests on negative skin friction for inclined pile considering time effect[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 617–621. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.04.020
[3]	孔纲强, 杨庆, 郑鹏一, 等. 考虑时间效应的群桩负摩阻力模型试验研究[J]. 岩土工程学报, 2009, 31(12): 1913–1919. doi: 10.3321/j.issn:1000-4548.2009.12.017 KONG Gang-qiang, YANG Qing, ZHENG Peng-yi, et al. Model tests on negative skin friction for pile groups considering time effect[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1913–1919. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.12.017
[4]	杨庆, 孔纲强, 郑鹏一, 等. 堆载条件下单桩负摩阻力模型试验研究[J]. 岩土力学, 2008, 29(10): 2805–2810. doi: 10.3969/j.issn.1000-7598.2008.10.040 YANG Qing, KONG Gang-qiang, ZHENG Peng-yi, et al. Model test study of negative skin friction for single pile under surface load[J]. Rock and Soil Mechanics, 2008, 29(10): 2805–2810. (in Chinese) doi: 10.3969/j.issn.1000-7598.2008.10.040
[5]	齐静静, 徐日庆, 龚维明. 湿陷性黄土地区桩侧负摩阻力问题的试验研究[J]. 岩土力学, 2006, 27(增刊2): 881–884. doi: 10.16285/j.rsm.2006.s2.072 QI Jing-jing, XU Ri-qing, GONG Wei-ming. Experimental study on negative skin friction resistance on piles in collapsible loess area[J]. Rock and Soil Mechanics, 2006, 27(S2): 881–884. (in Chinese) doi: 10.16285/j.rsm.2006.s2.072
[6]	陈福全, 龚晓南, 马时冬. 桩的负摩阻力现场试验及三维有限元分析[J]. 建筑结构学报, 2000, 21(3): 77–80. doi: 10.3321/j.issn:1000-6869.2000.03.012 CHEN Fu-quan, GONG Xiao-nan, MA Shi-dong. Field test and three-dimensional finite element analysis of negative friction of pile[J]. Journal of Building Structures, 2000, 21(3): 77–80. (in Chinese) doi: 10.3321/j.issn:1000-6869.2000.03.012
[7]	夏力农, 雷鸣, 聂重军. 桩顶荷载对负摩阻力性状影响的现场试验[J]. 岩土力学, 2009, 30(3): 664–668. doi: 10.3969/j.issn.1000-7598.2009.03.016 XIA Li-nong, LEI Ming, NIE Chong-jun. Field test of influences of load at pile top on negative skin friction behaviors[J]. Rock and Soil Mechanics, 2009, 30(3): 664–668. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.03.016
[8]	黄雪峰, 陈正汉, 哈双, 等. 大厚度自重湿陷性黄土中灌注桩承载性状与负摩阻力的试验研究[J]. 岩土工程学报, 2007, 29(3): 338–346. doi: 10.3321/j.issn:1000-4548.2007.03.005 HUANG Xue-feng, CHEN Zheng-han, HA Shuang, et al. Research on bearing behaviors and negative friction force for filling piles in the site of collapsible loess with big thickness[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 338–346. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.03.005
[9]	王兰民, 孙军杰, 黄雪峰, 等. 黄土场地震陷时桩基负摩阻力的现场试验研究[J]. 岩土工程学报, 2008, 30(3): 341–348. doi: 10.3321/j.issn:1000-4548.2008.03.006 WANG Lan-min, SUN Jun-jie, HUANG Xue-feng, et al. Field tests on negative skin friction along piles caused by seismic settlement of loess[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(3): 341–348. (in Chinese) doi: 10.3321/j.issn:1000-4548.2008.03.006
[10]	朱彦鹏, 赵天时, 陈长流. 桩基负摩阻力沿桩长变化的试验研究[J]. 岩土力学, 2013, 34(增刊1): 265–272. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2013S1041.htm ZHU Yan-peng, ZHAO Tian-shi, CHEN Chang-liu. Field tests on changes of pile negative friction along its length[J]. Rock and Soil Mechanics, 2013, 34(S1): 265–272. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2013S1041.htm
[11]	孔纲强, 周杨, 彭怀风. 负摩阻力作用下桩基中性点位置、下拽力及下拽位移与时间的关系[J]. 中南大学学报(自然科学版), 2016, 47(11): 3884–3889. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201611035.htm KONG Gang-qiang, ZHOU Yang, PENG Huai-feng. Relationship of neutral point position, dragload or downdrag of pile versus time under negative skin friction[J]. Journal of Central South University (Science and Technology), 2016, 47(11): 3884–3889. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201611035.htm
[12]	贺成斌, 赵明华, 雷勇. 基于荷载传递法的嵌岩桩负摩阻力计算研究[J]. 工程力学, 2014, 31(11): 110–115. doi: 10.6052/j.issn.1000-4750.2013.05.0441 HE Cheng-bin, ZHAO Ming-hua, LEI Yong. Negative friction computational research of rock-socketed pile based on load transfer method[J]. Engineering Mechanics, 2014, 31(11): 110–115. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.05.0441
[13]	于光明, 龚维明, 戴国亮. 考虑非达西流固结土体中桩基承载时间效应研究[J]. 中南大学学报(自然科学版), 2020, 51(8): 2132–2142. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202008009.htm YU Guang-ming, GONG Wei-ming, DAI Guo-liang. Research on bearing time effect of pile foundation in consolidation soil considering non-Darcy flow[J]. Journal of Central South University (Science and Technology), 2020, 51(8): 2132–2142. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202008009.htm
[14]	刘忠玉, 崔鹏陆, 范智铖, 等. 基于非牛顿指数渗流和分数阶Merchant模型的理想砂井地基径向固结分析[J]. 兰州大学学报(自然科学版), 2020, 56(4): 545–552. https://www.cnki.com.cn/Article/CJFDTOTAL-LDZK202004016.htm LIU Zhong-yu, CUI Peng-lu, FAN Zhi-cheng, et al. Analysis of radial consolidation of an ideal sand-drained ground with a non-Darcian flow described by the non-Newtonian index and fractional-order Merchant's model[J]. Journal of Lanzhou University (Natural Sciences), 2020, 56(4): 545–552. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LDZK202004016.htm
[15]	刘忠玉, 黄家涛, 夏洋洋, 等. 基于非牛顿指数渗流的饱和黏土一维流变固结分析[J]. 土木工程与管理学报, 2020, 37(3): 1–7. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCJ202003001.htm LIU Zhong-yu, HUANG Jia-tao, XIA Yang-yang, et al. One-dimension rheological consolidation analysis of saturated clay with Non-Darcian flow based on Non-Newtonian index[J]. Journal of Civil Engineering and Management, 2020, 37(3): 1–7. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WHCJ202003001.htm
[16]	于光明, 龚维明, 戴国亮, 等. 考虑固结流变的软土地基单桩下拉荷载计算[J]. 东南大学学报(自然科学版), 2020, 50(4): 606–615. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX202004002.htm YU Guang-ming, GONG Wei-ming, DAI Guo-liang, et al. One-dimentional rheological consolidation analysis of saturated clay with non-Darcian flow based on non-Newtonian index[J]. Journal of Southeast University (Natural Science Edition), 2020, 50(4): 606–615. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX202004002.htm
[17]	SWARTZENDRUDER D. Modification of Darcy's law for the flow of water in soils[J]. Soil Science, 1962, 93(1): 22–29.
[18]	FLEMING K, WELTMAN A, RANDOLPH M, et al. Piling engineering[M]. London, CRC Press, 2008: 129–139.
[19]	RANDOLPH M, WROTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of Geotechnical and Geoenvironmental, 1978, 104(12): 1465–1488.