0.   引言

石漠化边坡存在着一些严重阻碍植被恢复的难题，例如水土流失、地表缺土或者土层浅薄致使水分会快速流失，还常出现蒸发量大于降水量的干燥期，都会造成土壤季节性干旱。近年来，国内外学者提出了框格梁填土复绿护坡技术、植被水泥土等边坡生态恢复方法^[1]。本课题组提出在石漠化边坡框格内填水泥土并预留植株孔的技术，降雨在植被水泥土中的入渗情况直接影响边坡植被土层的稳定性与植被存活率。降雨入渗情况可以通过模型试验、数值模拟与降雨入渗解析模拟等方法开展研究。

为了研究边坡土体的降雨入渗，叶万军等^[2]通过室内模型试验研究黄土边坡的降雨入渗规律。潘振辉等^[3]用Hydrus-1D软件研究了土水特征曲线参数与边界条件变化对黄土中水分入渗的影响。经典降雨入渗模型主要有Green-Ampt模型、Horton模型和Philip模型等。Green-Ampt模型^[4]因其具有物理意义明确、形式简单和模型参数少等优点而被多数学者广泛应用改进。郭向红等^[5]建立了能模拟不同入渗水头对入渗影响的改进Green-Ampt模型。Chen等^[6]通过扩展G-A模型，成功地应用到斜坡降雨入渗中。雷文凯等^[7]能模拟不同边坡倾角对入渗影响的改进Green-Ampt模型。范严伟等^[8]针对夹砂层土壤量化了上层土壤的导水程度来改进Green-Ampt入渗模型。王文焰等^[9]根据黄土土壤水分剖析面改进了Green-Ampt模型。彭振阳等^[10]针对沙土特性在分层Green-Ampt入渗模型基础上调整了分层假定中的湿润区形状。

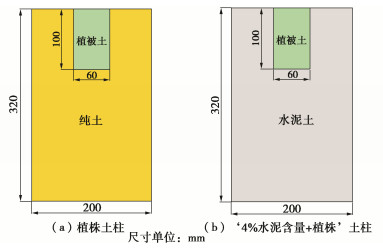
本课题组^[11]曾开展了5组叠合式土柱的降雨入渗试验，如图 1所示，包括纯土、纯土+植株孔、2%和4%水泥含量土、4%水泥含量土+植株孔5组土柱，针对传统Green-Ampt入渗模型仅将土柱分为饱和区与非饱和区，与土柱试验中植株孔优先蓄水入渗产生的非饱和区前的过渡区情况不符，本文将土柱降雨入渗模型分为饱和区、湿润过渡区和非饱和区。在分层假设的基础上，对Green-Ampt入渗模型进行了改进，研究了植被水泥土的累计入渗深度、累计入渗量等随时间变化规律，并结合试验结果对改进后的模型进行分析。

图  1  蓄水型植被水泥土联合格构护坡技术示意图

Figure  1.  Slope protection technology for water storage vegetated cement-soil combined project

下载: 全尺寸图片 幻灯片

1.   Green-Ampt模型及其改进模型

1.1   Green-Ampt模型

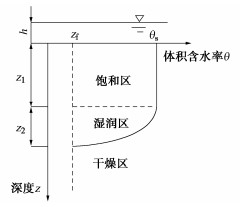
Green-Ampt模型是描述非饱和土中水分瞬时入渗的经典模型，该模型通过干燥土柱的积水入渗试验，直接采用达西定律求解土壤水分入渗速率，很好地描述了薄层积水条件下水分的入渗过程，因其阶梯状湿润锋锋面，所以又被称为活塞入渗模型。该模型的基本假定是：①土体表面至湿润锋锋面之间的水分均匀连续分布；②土体表面至湿润锋锋面区域含水率为饱和含水率$ {\theta _{\text{s}}} $，干土层含水率为初始含水率$ {\theta _{\text{t}}} $。传统的Green-Ampt模型示意图如图 2所示。

图  2  传统的Green-Ampt模型示意图^[4]

Figure  2.  Diagram of traditional Green-Ampt model^[4]

下载: 全尺寸图片 幻灯片

在Green-Ampt模型中，

式中i为入渗率（cm/min）；$ {K_{\text{S}}} $为土壤饱和导水率（cm/min）；${z_{\text{f}}}$为湿润锋深度（cm）；${s_{\text{f}}}$为湿润锋平均基质吸力（cm）；h为地表积水深度（cm）；I为累计入渗量（cm）；$ {\theta _{\text{s}}} $，$ {\theta _{\text{t}}} $分别为土壤饱和含水率与初始含水率。

累计入渗量对时间的导数即为入渗速率，根据式（1），（2）可推导出时间与湿润锋深度、累计入渗量关系，如式（3），（4）所示：

1.2   改进的Green-Ampt模型

Green-Ampt入渗模型假定湿润锋前面为干燥区，湿润锋后面湿润层为饱和区，与一般的土柱试验结果不符。王文焰等^[9]针对黄土的Green-Ampt入渗模型作了如下假定：①在积水入渗过程中，任意时刻的土壤水分剖面均概化为两部分，即将饱和层与传导层统一视为饱和区，其导水率为$ {K_{\text{s}}} $，而含水率变化较大的湿润层仍视为非饱和区；②土壤含水率由饱和含水率$ {\theta _{\text{s}}} $至初始含水率$ {\theta _{\text{i}}} $的剖面分布以椭圆曲线示之；③湿润区深度近似实际湿润锋深度的一半，即${z_1} = {z_2}$。王文焰模型将湿润区深度假设为实际湿润锋深度的一半是基于黄土入渗的水分剖面分布特征而来的，不同土体的含水率的剖面分布不一致，因此本文引入系数m，定义$m$为非饱和区厚度与饱和区厚度的比值，即$m = {{{z_2}} \mathord{\left/ {\vphantom {{{z_2}} {{z_1}}}} \right. } {{z_1}}}$，如图 3所示。当$m = 0$时，改进的Green- Ampt模型为传统Green-Ampt模型；当$m = 1$时，改进的Green-Ampt模型为王文焰模型。

图  3  改进的Green-Ampt模型分区示意图

Figure  3.  Zoning of improved Green-Ampt model

下载: 全尺寸图片 幻灯片

根据以上假定，由达西定律可写出入渗水流的地表通量$q$为

同时由水量平衡原理可知，在任一时刻$dt$内地表入渗通量$q$应等于土体内饱和区与湿润区的水分增量之和，即

将式（5）代入式（6）经整理后为

对上式积分，并整理可得时间与湿润锋运移深度的关系式：

在取得以上各基本关系式的基础上，累计入渗量可由下式求得

将式（9）代入式（8）得到时间与累计入渗量的关系如下所示：

上述式子中各参数的物理意义与式（1）和式（2）相同。

2.   改进的Green-Ampt模型参数取值及计算分析

2.1   模型参数的确定

在G-A模型中，$ {K_{\text{s}}} $和${s_{\text{f}}}$是两个关键参数，不少学者对这两个参数的取值进行了研究，一般而言G-A模型中的渗透系数小于饱和渗透系数，本文根据Bouwer^[12]的建议，取湿润锋后的导水率为饱和渗透系数${K_{\text{b}}}$的一半，湿润锋处基质吸力的取值同样取土壤进气压力值的一半，由式（11），（12）计算。

式中，${K_{\text{b}}}$为土柱饱和渗透系数（cm/min），${P_{\text{b}}}$为土柱的土壤进气压力值（kPa），$\rho $为水密度，取1000 kg/m³，g为重力加速度，取10 N/kg。

饱和渗透系数${K_{\text{b}}}$由土柱试验数据得出，土壤进气压力值${P_{\text{b}}}$通过不同土体的土水特征曲线根据传统图解法得出。传统图解法获得的进气吸力值与潘登丽等^[13]提出的单峰SWCC基本参数的确定方法计算结果接近。对于含植株的土柱，其饱和渗透系数和土壤进气压力值采用体积加权法求得，由式（13），（14）计算，含植株土柱概化模型图如图 4所示。

图  4  含植株土柱的概化模型

Figure  4.  Generalized model for vegetated soil columns

下载: 全尺寸图片 幻灯片

式中${K_{{\text{b, i}}}}$为各类土的饱和渗透系数（cm/min）；${P_{{\text{b, i}}}}$为各类土的土壤进气压力值（kPa）；${V_{\text{i}}}$为各类土体积（cm³）；${K_{\text{b}}}$和${P_{\text{b}}}$的物理意义与式（11），（12）相同。

通过传统图解法、文献[13]中的单峰SWCC基本参数的确定方法得出水泥土和植被土的土壤进气吸力值，再联合式（12），（14）计算出湿润锋基质吸力值${s_{\text{f}}}$，结果如表 1所示。

表  1  土壤进气吸力值和湿润锋基质吸力值的确定

Table  1.  Determination of soil suction value and matrix suction value of wetting front

土柱	传统图解法$ {P_{\text{b}}} $/kPa	文献[13]中方法$ {P_{\text{b}}} $/kPa	$ {s_{\text{f}}} $ /cm
纯土	1.84	2.22	9.20
纯土+植株	1.75	2.04	8.75
2%水泥含量	2.34	2.44	11.70
4%水泥含量	3.53	4.37	17.65
4%水泥含量+植株	3.43	4.06	17.20

下载: 导出CSV 

| 显示表格

将土柱试验得到的饱和渗透系数代入式（11），（13）计算出各组土柱饱和导水系数${K_{\text{s}}}$。另外，模型中积水水头h为实际入渗的水头高度3 cm，初始体积含水率和饱和体积含水率根据制样完成后和入渗结束时各传感器的监测结果取平均值，如表 2所示。

表  2  改进的G-A模型参数取值

Table  2.  Parameters of improved Green-Ampt model

土柱	$ {\theta _{\text{i}}} $	$ {\theta _{\text{s}}} $	$ {K_{\text{s}}} $/(cm·min-1)	$ {s_{\text{f}}} $/cm
纯土	0.14	0.30	0.011	9.20
纯土+植株	0.15	0.30	0.012	8.75
2%水泥含量	0.13	0.32	0.069	11.70
4%水泥含量	0.14	0.30	0.018	17.65
4%水泥含量+植株	0.14	0.30	0.017	17.20

下载: 导出CSV 

| 显示表格

改进的G-A模型中的系数m通过实测的湿润锋和时间的数据点进行拟合得到，不同土柱由于土体性质的差异，入渗特性不同，饱和区与湿润区厚度所占的比例也不同。由MATLAB软件1stOpt非线性曲线拟合软件得到各土柱m系数的取值如表 3所示。

表  3  系数m拟合结果（$ m = {z_2}/{z_1} $）

Table  3.  Fitting results of coefficient m ($ m = {z_2}/{z_1} $)

参数	纯土	纯土+植株	2%水泥含量	4%水泥含量	4%水泥含量+植株
m	0.635	1.64	0.283	0.478	0.784
相关系数R2	0.996	0.986	0.993	0.981	0.997

下载: 导出CSV 

| 显示表格

2.2   改进G-A模型的计算分析

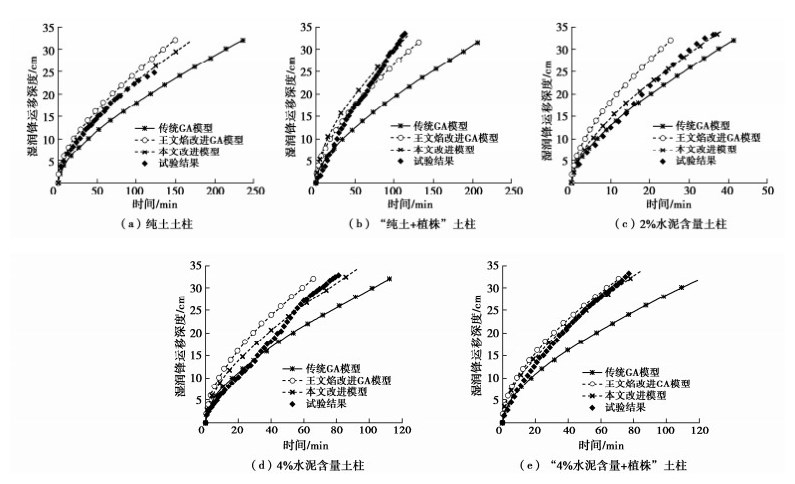
各组土柱改进G-A模型的湿润锋运移深度随时间变化的计算结果与传统G-A模型、王文焰改进的G-A模型计算结果比较如图 5所示。可以看出，除了“纯土+植株”土柱，本文改进的G-A模型的模拟结果介于Green-Ampt模型（m=0）和王文焰改进的G-A模型（m=1）之间。改进的G-A模型和王文焰改进模型的湿润锋模拟结果与试验结果相比都普遍偏高，采用传统G-A模型计算得到的结果则偏低。本文改进模型相较于传统G-A模型和王文焰改进的G-A模型，与试验结果的拟合效果最佳。在同一时刻，Green-Ampt入渗模型的湿润锋运移深度一般小于本文改进模型的湿润锋运移深度和试验结果，这是由于Green-Ampt入渗模型假定存在缺陷导致的，改进入渗模型考虑了实际入渗的情况，本文改进模型的湿润锋运移深度的解析解，更加贴近试验结果。

图  5  不同计算模型湿润锋运移深度随时间变化曲线

Figure  5.  Curves of migration depth of wetting front with time by different models

下载: 全尺寸图片 幻灯片

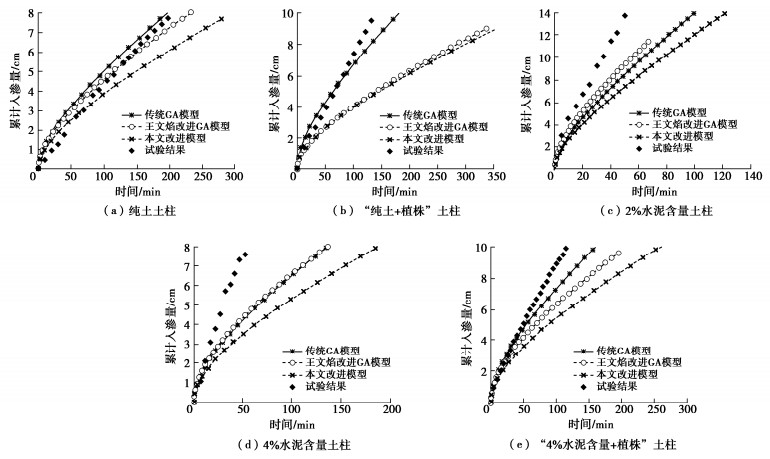
各组土柱改进G-A模型的累计入渗量随时间变化的计算结果与原模型、王文焰改进模型计算结果、试验结果比较如图 6所示。

图  6  不同计算模型累计入渗量随时间变化曲线

Figure  6.  Curves of cumulative infiltration with time by different models

下载: 全尺寸图片 幻灯片

从图 6可以看出，除了纯土中传统G-A模型模拟结果大于试验结果，其他所有模拟结果都小于试验结果。本文改进模型的计算结果不再介于Green-Ampt模型（m=0）和王文焰改进的G-A模型（m=1）之间，而是低于其值，计算结果偏保守。

3.   结论

（1）经典Green-Ampt入渗模型假定土柱表面至湿润锋面为饱和区，与含有植株土柱入渗存在湿润过渡区的情况不符，而基于分层假定的王文焰修正的G-A模型假设湿润过渡区与饱和区比值为1，与试验结果不符，因此本文假设过渡湿润区与饱和区的比值为m。针对植被土与水泥土在入渗特性上的不同，采用体积加权法计算含植株土柱的改进G-A模型参数。

（2）通过对比分析传统G-A模型、王文焰模型、本文改进的G-A模型与土柱试验结果，可以看出改进G-A模型计算结果和土柱试验结果较一致。对于湿润锋运移深度，改进后的G-A模型最贴近实测值，在同一时刻，除“纯土+植株”土柱改进模型计算值大于王文焰模型，其余土柱的改进模型计算值均小于王文焰模型，大于传统G-A模型。对累计入渗量而言，相较于试验结果，改进的G-A模型的计算值普遍偏低，改进的G-A模型计算累计入渗量时偏保守。

（3）植被水泥土可以抑制旱季表土开裂、减少土壤水分蒸发，而植株孔能够增加降雨入渗起到蓄水漏斗的作用，有利于植被恢复。改进G-A模型通过室内试验确定参数，针对石漠化边坡格构内植被水泥土生态恢复技术进行入渗分析，具有一定的工程实用价值。