Creep characteristics of lacustrine sedimentary peaty soil
-
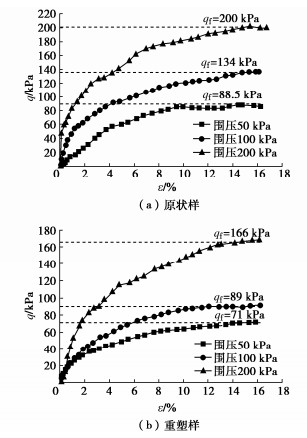
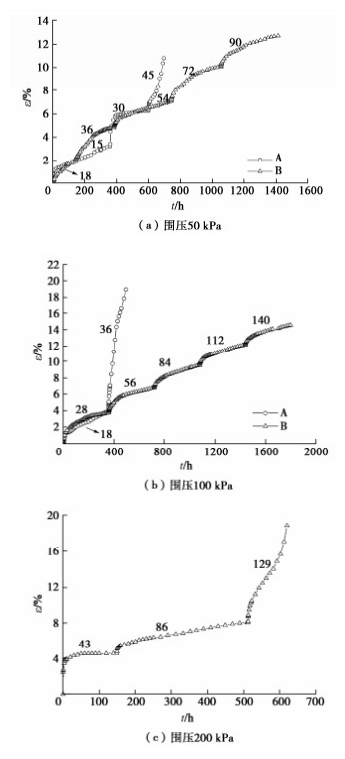
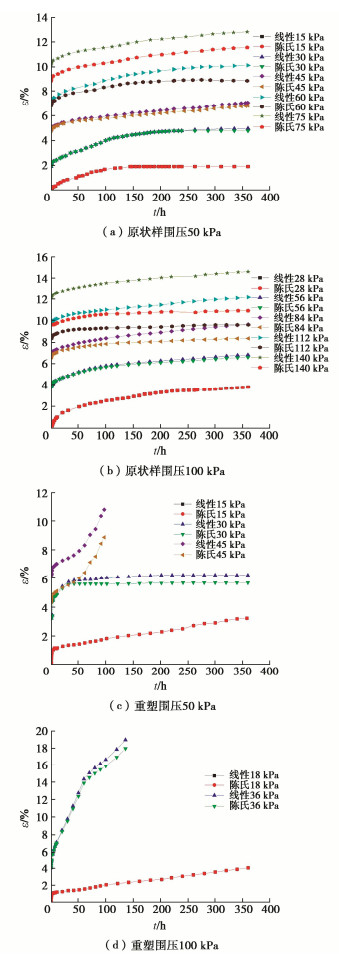
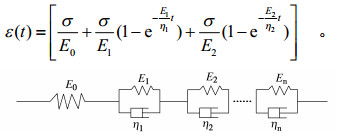
摘要: 利用SLB-1型应力应变控制式三轴剪切渗透试验仪，对湖相沉积泥炭质土进行三轴固结不排水蠕变试验，研究泥炭质土在不同围压及偏应力条件下的蠕变过程，并通过“陈氏法”得到分级加载下蠕变曲线。三轴蠕变试验研究表明：原状样在围压为50，100 kPa时，应变时间关系呈现明显的衰减蠕变特征，而当围压为200 kPa，偏应力为129 kPa时表现为明显的非衰减蠕变特征；重塑较原状样能承受的加荷等级少；“陈氏法”较Boltzmann线性叠加法更加适用于处理蠕变数据。以围压100 kPa下的蠕变试验曲线为例，结合最小二乘法的拟合分析，建立了广义kelvin模型与改进分数阶Maxwell蠕变模型，得到的蠕变模型具有参数少、适用性较强的特点。Abstract: By using the SLB-1 stress-strain controlled triaxial shear permeability tester, the triaxial consolidation undrained creep tests on lacustrine sedimentary peaty soil are carried out to study its creep process under different confining pressures and partial stresses, and the creep curve under graded loading is obtained by the Chen's method. The results of the triaxial creep tests show that the strain-time relationship of the undisturbed samples exhibits obvious attenuation creep characteristics when the confining pressure is 50 and 100 kPa, while it exhibits obvious non attenuation creep characteristics when the confining pressure is 200 kPa and the deviating stress is 129 kPa. The remolded sample can bear less loads than the original one. The Chen's method is more suitable for processing the creep data than the Boltzmann's linear superposition method. Taking the creep tests under the confining pressure of 100 kPa as an example, by combining with the fitting analysis of the least square method, the generalized Kelvin model and the improved fractional Maxwell creep model are established. The obtained creep model has the characteristics of few parameters and strong applicability.
-
Keywords:
- peaty soil /
- triaxial creep /
- creep property /
- creep model
-
0. 引言
随着大城市地铁工程建设发展，呈现大量深基坑开挖问题，主要表现为基坑周边建筑物沉降及沉降差加大，进而出现墙面开裂，管道漏水，结构承载能力下降等现象，影响了建（构）筑物的正常使用性能。为合理控制坑周地层位移以及保护环境，蒋洪胜等[1]提出的“时空效应法”的基本思想是设计过程中应考虑现场实际的基坑施工方法与工艺，进而提高设计和施工配合程度。
软土地区深基坑工程的变形、轴力特点显著。Goldberg等[2]分析了多个基坑工程的实测数据，发现有65%的软土地层深基坑围护墙体位移大于1%的基坑深度。曹雪山等[3]对南京某深基坑工程进行变形监测，发现围护墙体位移达137 mm，约0.86%的基坑深度。蒋洪胜等[1]提出了软土地区深基坑开挖过程中支撑轴力数据离散性大、规律性不清，认为具有显著的时空效应；陈保国等[4]通过模型试验研究了内支撑体系、地连墙和墙后土体之间的协调变形特性；金亚兵等[5]研究了内支撑–支护桩–土相互作用且变形协调过程中的温度应力的影响。2004年新加坡Nicoll Highway地铁基坑失事过程中监测到第九道支撑因失效而轴力下降，第八道支撑轴力急剧上升，增加1倍多，第七道略有下降，变化量约10%, 而第九道支撑失效是基坑坍塌的直接原因[6]。综上，目前研究成果显示深基坑的变形与内支撑轴力之间存在内支撑–支护桩–土的相互作用；要解决深基坑变形问题，必须掌握支撑轴力变化规律；支撑轴力、围护墙位移及弯矩等直接关联着基坑安全，由此研究钢支撑设计问题具有重要的工程意义。
为探索钢支撑轴力变化规律，本文以南京某车站基坑开挖过程为研究对象，结合监测数据开展了数值模拟，研究了深基坑内支撑轴力变化规律及影响因素，为进一步提高深基坑工程设计与施工水平提供技术支撑。
1. 钢支撑的设置与功能
围护墙与内支撑共同组成支护系统，其中内支撑的设置与功能较为特殊。基坑围护墙是挡土的主体结构，而内支撑是辅助挡土的附属结构。对于重力式挡墙、悬臂式挡土墙，没有内支撑，围护墙也能确保基坑开挖稳定。但深基坑的内支撑结构，通过承受由围护墙传递的荷载，调整围护墙的弯矩和变形，进而改善围护墙的挡土功能。《建筑基坑支护技术规程》[7]定义了内支撑的轴向压力设计值，是由围护墙荷载组合后计算所得，属于荷载效应的设计值。设计时，因Ø609 mm，壁厚t=16 mm的钢支撑构件承载力不低于3200 kN[8]，所以支撑轴力设计值小于3200 kN时，设计文件通常选用该型号的钢支撑。国家监测规范[9]规定轴力控制值取“构件承载能力设计值”的60%~80%，江苏省地方规程[10]则将轴力控制值取“支撑轴力设计值”的60%~80%，条文说明注释了“支撑轴力设计值”即为支撑荷载效应设计值。虽然构件承载力设计值与荷载效应设计值不是一个概念，但基于构件承载力设计值不小于荷载效应设计值，这两部规范所表达的意图相同，执行时取小值。这表明工程界重视了支撑受力后的安全性能，而未提及支撑对围护墙的设置效果要求，进而可能导致支撑辅助作用的削弱，进而形成“钢支撑轴力实测值小于设计值就表示工程安全”的片面性理念，忽略钢支撑轴力与围护墙位移、弯矩的关联性。
钢支撑结构组成及施工工艺是特殊的。钢支撑由钢管杆件、活络头以及钢围檩组成，虽然各组成部分对承载力均有影响，但施工工艺的预加轴力工序是特有的，文献[7]规定内支撑预加轴力宜取（0.5~0.8）倍的轴力标准值，但基坑开挖过程中的钢支撑预加轴力实测值多数小于设计值。李书银等[11]报道了昆明地铁#4线大唐子站基坑扩大段的设计预加力的5%~69%，小于30%的居多；标准段为22%~56%，其中以小于40%的居多。曹雪山等[8]报道的南京地铁某车站施工段15个钢支撑预加轴力仅1个达到设计要求。产生这种现象的主要原因是多方面的，例如出现钢围檩、钢榫截面变形，围护墙面不平整等，这些均属于施工质量问题[11]。设计文件仅给出一个轴力预加值，而未考虑预加轴力衰减现象的存在，没有规定预加轴力目标值与施加值，导致缺乏相应预加轴力值的质量评定标准。再者较大的预加轴力对应的支撑轴力也略大[12]，相对于固定的预警值而言，更易产生轴力预警问题。然而轴力增大对变形控制有效。Clough等[13]通过有限元研究发现当预加力为（0.2~0.4）倍的静土压力时，围护墙位移量可比无预加力时减小50%以上；2020年6月后监测国家标准[14]新增了支撑预加轴力的最小轴力预警。综上，目前的钢支撑施工技术水平与设计成果很不匹配。引发这一问题的关键是对钢支撑轴力变化规律认识不清。因此需要深入研究钢支撑轴力变化规律，以充分发挥钢支撑的功能，进一步提高内支撑设计水平。
2. 深基坑开挖过程的模拟分析
2.1 基坑设计与监测概况
南京某地铁车站设计情况如图 1所示。场地地层由上至下为人工填土、淤泥质粉质黏土、粉质黏土夹粉砂等组成。其中淤泥质粉质黏土（②-2b4），全场区分布，厚度为24.80~32.40 m、平均26.90 m。车站主体大部分位于该层中。基坑围护墙为厚度0.8 m的地下连续墙，标准段宽度20.0 m，开挖深度16.0 m，竖向设四道支撑（第一道为砼支撑，其余为Ф609 mm，t=16 mm钢支撑）。坑底采用三轴搅拌桩抽条基底加固，抽条宽度3 m，间距3 m。
如图 1（a）所示，研究区位于标准段，距离端部盾构井段约8 m；研究区的监测点为墙体测斜CX02、CX03及对面墙内的CX16，对应的轴力为ZL03；如图 1（b），第二—第四道支撑均为钢管支撑，对应的轴力测点分别为ZL03-2，ZL03-3，ZL03-4。图 2为基坑开挖过程中的墙体变形与轴力监测结果。图 2（a）~2（c）显示随着开挖深度加大，向坑内的墙体变形量相应增大，最大值位置深度下移；且3个测点测量值相近，变化趋势相同。图 2（d）显示3个测点轴力测试值虽然波动，但共同规律是前期的快速增大、后期的逐渐平缓的发展过程。
2.2 模型建立与施工阶段的模拟计算
地铁车站深基坑呈现狭长型，这是典型的平面应变问题，而支撑与围护墙之间的作用状态具有显著的三维特性，于是本文以轴力ZL03为中心取纵向长度25.5 m的标准施工段建立基坑开挖模型。模型总宽度80 m，即坑内宽度20 m，坑外向两侧各延伸30 m。地连墙深度38 m，模型深度80 m。为了展示土层开挖对轴力的影响，土层开挖时计算厚度为1 m。计算模型如图 3所示。
基坑开挖模拟计算采用Midas GTS NX软件的总应力法进行。土体本构为修正摩尔库仑模型。考虑地铁基坑开挖速度较快，参数选用场地的地质勘察报告及设计图纸中的快剪强度指标，具体岩土参数详见表 1。基坑支护结构参数详见表 2。商业程序的非线性刚度参数：$ E_{{\text{50}}}^{{\text{ref}}} $为标准三轴实验的割线刚度，$ E_{{\text{oed}}}^{{\text{ref}}} $为固结试验的切线刚度，$ E_{{\text{ur}}}^{{\text{ref}}} $为卸载/重新加载刚度。弹性模量的取值按地区软土比例系数经验确定。
表 1 土层模型计算参数Table 1. Parameters for soil model土层 弹性模量/MPa 泊松比 饱和重度/(kN·m-3) 初始孔隙比 黏聚力/kPa 内摩擦角/(°) $ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ 杂填土 4.1 4.1 16.4 0.34 19.0 0.9 10 9.0 素填土 4.1 4.1 16.4 0.34 18.8 0.9 15 5.4 淤泥质粉质黏土 3.3 3.3 13.2 0.41 18.2 1.1 12 5.7 粉质黏土夹粉砂 3.7 3.7 16 0.34 18.7 1.0 14 8.4 表 2 支护结构材料参数Table 2. Parameters for support structures结构名称 单元类型 弹性模量/GPa 泊松比 重度/(kN·m-3) 尺寸/mm 地下连续墙 板 31.5 0.2 26.0 厚度t=800 钻孔灌注桩 梁 31.5 0.2 26.0 桩径1000 格构柱 梁 200.0 0.3 78.5 方箱480, t=20 钢筋混凝土支撑 梁 31.5 0.2 26.0 矩形100×800 钢支撑 梁 200.0 0.3 78.5 ¬609, t=16 结合现场实际的施工开挖与支护顺序，模型计算时按16层土，22步，11个施工阶段模拟基坑开挖全过程，具体步骤如表 3所示。钢支撑初始预加轴力根据实测值施加。
表 3 基坑开挖模拟步骤Table 3. Simulation steps of excavation序号 施工阶段 单元处理 1 初始应力分析 激活所有土体、自重、边界约束；位移清零 2 围护墙施工 激活围护墙、围护墙旋转约束 3—4 开挖第1—第2层土 逐步钝化第1—第2层土 5 架设第一道支撑 激活第一道钢筋混凝土支撑 6—10 开挖第3—第7层土 逐步钝化第3—第7层土 11 架设第二道支撑 激活第二道钢支撑 12—15 开挖第8—第11层土 逐步钝化第8—第11层土 16 架设支撑3 激活第三道钢支撑 17—19 开挖第12—第14层土 逐步钝化第12—第14层土 20 架设支撑4 激活第四道钢支撑 21—22 开挖第15—第16层土 逐步钝化第15—第16层土 2.3 计算模型适用性验证
软土基坑开挖的最大问题是变形大，所以基坑变形规律的数值研究时[8, 15]通常由围护墙体位移计算值与实测值吻合性来验证模型适用性；但是深基坑的支护系统中的支撑结构对围护墙位移的影响显著[13]，同时围护墙位移与支撑轴力分别属于不同范畴，因此本文提出了围护墙体位移与支撑轴力双元参数组合的验证方法。根据基坑在不同开挖深度处的围护墙体位移及支撑轴力的实测值，拟合模型计算参数。拟合结果如图 4，5所示，拟合的相对误差如表 4所示。
![]()
图 4 围护墙体位移模拟值和实测值对比图Figure 4. Comparison between simulated and measured values of wall deflection![]()
图 5 基坑开挖过程中的钢支撑轴力模拟值与实测值对比图Figure 5. Comparison between simulated and measured values of axial forces of steel struts during excavation表 4 模拟值与实测值相对误差汇总表Table 4. Summary of relative errors between simulated and measured values/% 测项 模拟值与实测值相对误差 开挖7 m 开挖11 m 开挖14 m 开挖16 m 围护墙体位移 1 -6 -1 4 第二道轴力 12 17 9 5 第三道轴力 — 14 22 20 第四道轴力 — — 5 8 支撑抗压刚度决定于其截面积。钢支撑Ø609 mm，壁厚16 mm，截面积0.030 m2，而活络头连接部位矩形钢榫接触面积最大0.016 m2，正反楔组合体的受力面积可能更小，这些均可能是造成支撑刚度减小的原因。雷霆等[16]通过模型计算，发现钢支撑刚度仅有理论值的38%。本文模拟的钢支撑刚度是根据实测的位移、支撑轴力拟合确定，三道钢支撑模拟刚度分别为钢管横截面抗压刚度理论值的34%，34%，30%。
基坑开挖深度为7，11，14 m时，分别在6，10，13 m架设第2，第3，第4层钢支撑，开挖基底为深度16 m。图 4表明对于各开挖阶段围护墙体位移（CX16），计算值与模拟值大小分布形态，位移的最大数值及位置相近；图 5反映了第二道支撑架设完成后不同开挖深度时支撑轴力的计算值与模拟值对比关系，显然，规律吻合性好，总体趋势一致。表 4表明了围护墙体位移的相对误差较小，而轴力相对误差略大，这与支撑轴力测试精度及显著的时空效应相关[1]。总之，本文通过围护墙体位移与支撑轴力双元参数组合的方法验证了计算模型与现场实体吻合性，效果良好，这表明计算模型能合理地反映出基坑开挖过程中墙体变形和支撑轴力的变化规律。
2.4 计算成果分析
图 4反映了随基坑开挖深度增加，围护墙体位移不断增大的趋势。根据《建筑基坑工程监测技术标准》[14]，本段基坑的围护墙体位移预警值为30~50 mm，与基坑设计深度H的控制相对值为0.3%~0.4%，设计文件取小值，即分别为30 mm和0.3%。但如图 6所示，随着基坑开挖深度加大，不同开挖阶段的围护墙体位移最大值及相对值的不断加大是必然的。当开挖深度为10 m时已经达到预警控制值，之后的变形发展均表示基坑处于危险状态。这种现象，在场地软土层厚、开挖深度大的基坑中不是个别案例，具有普遍性，如表 5所示。为此，曹雪山等[3]提出了新的基坑安全预警方法，包含预警提醒、事故警告、事故征兆及事故发生4个阶段，旨在提高预警方法与措施的设计与施工配合程度，以进一步保障基坑安全。
![]()
图 6 基坑开挖过程中的围护墙体位移最大值及相对值Figure 6. Maximum and relative values of wall deflection during excavation表 5 软土基坑的围护墙位移Table 5. Wall deflections of excavation in soft soil area图 5反映的钢支撑轴力发展规律主要有3点。
（1）钢支撑架设后，随土层开挖，该道支撑轴力有一个从线性增加至基本稳定的发展过程，轴力变化的转折点是下道支撑所形成的阻隔作用。开挖深度为7 m时，第二道钢支撑预加力施加完成后，随着基坑开挖深度增大，支撑轴力线性增加，至开挖深度11 m时增速变缓；在第三道支撑预加轴力施加后，第三道支撑轴力随开挖深度线性增长，而第二道轴力不再明显增加，进入基本稳定状态，其原因是第三道支撑对第二道支撑起到了阻隔作用；同样，在第四道支撑预加轴力施加完成后，开挖深度的增加引起第四道支撑轴力的线性增加，而第二、三道支撑轴力趋向基本稳定。开挖过程中各部位支撑的不同轴力发展过程造成支撑轴力实测值离散[1]的重要原因，且与支撑的阻隔效果相关。
（2）钢支撑轴力与开挖深度相关性很好。图 5所示的第二—第四道钢支撑，每道支撑轴力增量均与支撑下土层开挖深度有线性增大趋势，且相关性很好。从图 7中的第二—第四道钢支撑轴力总和与基坑开挖深度的关系，也是线性增长的发展规律。
![]()
图 7 基坑开挖过程中的钢支撑轴力及其总和Figure 7. Axial forces and sum of steel structs during excavation（3）支撑轴力大小分布与阶段变形量相似，均是第三道支撑及其对应变形最大，第二道其次，第四道最小。图 8显示第二—第四道的钢支撑轴力总和与围护墙体位移之间的相关性很好。
![]()
图 8 围护墙体位移最大值与钢支撑轴力总和的关系Figure 8. Relationship between maximum wall deflection and sum of axial force of steel struts因此，钢支撑轴力变化规律应考虑该支撑所在部位、基坑开挖深度位置及下道支撑的阻隔作用等影响因素，同时应包含钢支撑轴力总和的变化趋势。
3. 钢支撑轴力影响因素分析
3.1 单道钢支撑预加轴力的影响
基坑施工过程中普遍存在钢支撑预加轴力不足的情况，本工程中预加轴力仅为30%~60%的预加设计值。根据设计文件所提供的初始预加轴力值，施工人员将此换算成千斤顶油压值来实现。由于忽视了钢支撑预加轴力的衰减现象，各道各根钢支撑的轴力衰减均独立发生，进而形成了实际预加轴力值不足的随机性。为了搞清某道钢支撑预加轴力不足对基坑变形、轴力的影响，将模型中第二道支撑的预加轴力计算值分别取0.3Fy，0.8Fy，Fy，Fs，1.5Fs；本基坑第二道轴力设计值Fs为2313 kN，预加轴力设计值Fy为1050 kN，是轴力设计值的0.45；计算时第三，第四道支撑预加轴力取实际预加值，分别为300，500 kN。计算结果如图 9所示。
![]()
图 9 第二道钢支撑预加轴力对轴力及墙体位移的影响Figure 9. Influences of preloading of secondary steel structs on axial forces and wall deflection从图 9（a）看出，由于预加轴力值明显低于轴力设计值，所以随开挖深度变化，低于设计值的预加轴力对轴力的影响很不明显；只有当预加轴力达到设计轴力值，甚至150%的设计轴力值时，第二道轴力才稍大的增长。图 9（b）展示了钢支撑的轴力特征值：预加轴力、初始轴力及最大轴力三者之间的关系。预加轴力是指计算前施加于支撑的外荷载；初始轴力是指该支撑激活后作用于模型结构，首次计算完成时所具有的轴力；最大轴力是指在支撑运行时所具有的轴力最大值。因此三者为不同支护结构状态下支撑轴力的特征量。随预加轴力增大，初始轴力、最大轴力相应增大，线性相关性系数 > 0.99；从变化率看，以预加轴力变化梯度为1，则初始轴力、最大轴力的变化梯度分别为0.32，0.21。综合图 9（a）~（d），说明预加轴力对轴力有影响但并不显著[8, 12]，其中原因是支护结构具有自身调节功能。
图 9（e）反映了第二道支撑预加轴力的加大对变形的影响。当预加轴力不大于设计值时，围护墙体位移相差量可忽略不计，但预加轴力达到设计轴力值及150%的设计轴力值，由于第二道支撑所在位置处位移减小，导致围护墙体位移在基底附近的最大值反而增大。分析原因是对于多道支撑的深基坑，因相邻支撑具有阻隔作用，所以每道支撑的作用范围为相邻支撑所围成的区域。在图 9（e）中，当第二道支撑预加轴力大于设计轴力时，虽然第二支撑处围护墙体位移减小了，但第四支撑处及围护结构最大变形却增大了，其力学作用机制是第三道支撑起到了变形曲线的拐点作用。所以对于多道支撑的基坑，不能盲目地增大单道支撑的预加轴力，避免对变形控制产生不利的影响。这与陈保国等[4]在室内试验所发现的单道上部支撑变形控制效果差的观点相近，同时给出了预加轴力不宜过大的一个解释。
3.2 两道钢支撑预加轴力的影响
将钢支撑第二、第三道分别施加预加轴力1600，3000 kN，而第四道仍施加1050 kN，计算预加轴力对轴力及变形的影响。计算结果如图 10所示。
![]()
图 10 改变第二、第三道钢支撑预加轴力Figure 10. Influences of preloading axial force on struts No. 2 and No. 3图 10表明两道钢支撑预加轴力均较大，轴力随基坑开挖的“线性增长到基本稳定”的发展过程规律仍不变。并且图 10（a）还显示第三道支撑施加预加轴力后，对第二支撑轴力起到了明显的卸载作用，而第四道支撑施加预加轴力对第三道支撑轴力的卸载作用不明显。图 10（b）显示预加力再大幅增加，则初始轴力有增加，对第二道支撑轴力的卸荷作用更加显著。这说明开挖时支撑对邻近支撑有阻隔作用外，较大的预加轴力还会对邻近支撑有卸荷作用。
表 6给出第二、第三道支撑预加轴力对支撑轴力的影响。较大的预加轴力所引起的初始轴力也较大，并且尽管支撑下土层开挖仍会使轴力增加，但较大的预加轴力会使轴力增量略小些。第二道支撑轴力在该支撑下土层开挖完成时最大，原因是第三道支撑在预加轴力施加结束后对第二支撑产生的较大卸载作用导致第二支撑的最终轴力降低；而第三、第四道支撑轴力的最大值与最终值相等，原因是第四道支撑预加轴力值小，且轴力也较小，对第三道支撑轴力无明显的卸荷和阻隔作用，表现为第四道支撑下土层开挖时第四道支撑轴力在增长，第三道支撑轴力也有增长。
表 6 第二、第三道钢支撑预加轴力影响Table 6. Influences of preloading axial force on struts No.2 and No.3计算模式 预加轴力/kN 初始轴力/kN 最大轴力/kN 最终轴力/kN 设计轴力/kN 方案Ⅰ 第二道 1600 1787 2610 2285 2313 第三道 1600 1701 2800 2800 1543 第四道 1050 999 1215 1215 1915 方案Ⅱ 第二道 3000 2014 2806 1988 2313 第三道 3000 2499 3340 3340 1543 第四道 1050 968 1182 1182 1951 总之，钢支撑轴力虽然有显著的时空效应，但其变化规律还是明确的。由于最终轴力不一定是最大轴力，而支撑受力安全性决定于最大轴力，因此设计轴力应理解为最大轴力，而不是最终轴力，支撑型号选择标准也应是最大轴力。
图 11，12给出第二、第三道支撑预加轴力为1600，3000 kN时对围护墙体位移、弯矩的影响，表明较大的预加轴力对位移控制效果好，且弯矩无明显变化。与单道支撑工况相比，第二、第三道支撑均有较大的预加轴力时，显著扩大了影响范围；并且此时第四道支撑轴力的拐点作用不明显，围护墙刚度得到了显著提高，变形控制能力加强；围护墙体位移从第二道支撑至基底范围内基本上整体减小，这就体现支撑对围护墙的刚度提高、变形控制的作用。
![]()
图 11 第二、第三道支撑不同预加轴力下围护墙体位移Figure 11. Comparison of wall deflection under different preloading axial forces on struts No. 2 and No. 3![]()
图 12 第二、第三道支撑不同预加轴力下围护墙体弯矩Figure 12. Comparison of wall moment under different preloading axial forces on struts No. 2 and No. 3所以对于多道支撑的基坑预加轴力施加方法，两道支撑施加效果明显不同于单道支撑，这也解释了各道按比例增加预加轴力[8]、等位移变化[4]的变形控制效果佳的结论。
3.3 支撑架设条件对钢支撑轴力的影响
基坑开挖过程中，钢支撑轴力与支撑下土层所开挖的深度成线性增长比例，直到下道支撑的阻隔作用才改变。为了探索轴力增长的时空效应，根据支撑与即将开挖土层顶面关系，确定了悬挂架设、常规架设及超挖1 m后架设的钢支撑3种模式，如图 13所示。
钢支撑常规架设是指基坑开挖至钢支撑位置下1 m后架设，支撑下1 m空间是用于支承钢围檩、钢支撑的三角牛腿及坑中部立柱横向联系梁等架设需要的；悬挂架设是指开挖至钢支撑底面即开始架设，由于此时三角牛腿及坑中部立柱横向联系梁没有架设空间，所以只能采用围护墙预埋钢构件，通过悬挂结构固定钢支撑；超挖1 m是因出土过量导致开挖面过低，低于常规架设的开挖面1 m所形成的特殊工况。工程中常规架设钢支撑施工工艺成熟，工效高；而悬挂架设属于新技术，如采用钢支撑下开槽施工，则工效低，难度大，很难推广；超挖情况一般不会发生，出现时表明工程管理存在问题，其结果是工效低且还有高空架设问题。
以计算模型为基础，对不同支撑架设条件的基坑开挖进行模拟计算，计算结果如图 14所示。
![]()
图 14 不同架设条件下钢支撑轴力值变化Figure 14. Variation of axial force of steel structs under different erection conditions支撑轴力受架设条件影响很大，相应的支撑风险也增大。由图 14（a）可知，首先对初始轴力值的影响。虽然预加轴力值一样，但不同架设条件下支护结构所处状态不同，导致支撑激活后作用于围护结构，首次计算所得支撑轴力也不同。悬挂式最小，而超挖1 m时最大。其次是开挖过程中轴力变化规律不同。第二道支撑位置为基坑深度6 m处，无论开挖深度与支撑位置的深度差是多大，当开挖深度增大时，第二支撑轴力均有线性增长趋势，所不同的是支撑轴力增长幅度随深度差增大而增大。支撑采用悬挂架设，深度差为零，轴力增长幅度最小，而超挖1 m时架设的轴力增长幅度最大；至下道支撑架设时开挖深度增长量相同，但所累计的轴力相差很大，如表 7所示，超挖1 m条件下架设支撑轴力达到4026 kN，是常规架设时支撑轴力的180%，此时对于支撑量程为3200 kN的φ609 mm，t=16 mm的常规钢支撑，极易引发支撑轴力失效，进而引发基坑事故[6, 20]；悬挂架设支撑轴力最小，是常规架设时支撑轴力的69%。图 14（b）显示第三道支撑轴力对超挖1 m条件下最小，这与第二道轴力过大直接相关；图 14（c）中第四道支撑轴力在超挖1 m条件下再次达到最大，与第三道轴力过小相关；常规架设条件下最小，与第三道轴力过大相关；只有悬挂架设的轴力增长最平稳，相应风险最小。
表 7 各架设条件下钢支撑最大轴力值Table 7. Maximum axial forces of steel struts under various erection conditions(kN) 项目 第二道 第三道 第四道 悬挂架设 1544 1893 2266 常规架设 2228 3182 997 超挖1 m 4026 1159 3904 设计方案 2313 1543 1951 实际方案 2015 2627 926 基坑开挖深度不同，轴力差异幅度也有差异。图 14显示，开挖深度小于10 m的基坑，仅架设了第二道支撑，则各种支撑架设条件的影响不明显，即使发生超挖1 m工况，支撑轴力最大达2000 kN；但如基坑开挖深度约13 m，要架设第三道支撑，则超挖1 m条件下第二道支撑轴力可能达到3893 kN，风险很大；而常规架设时风险相对要小些。
综上，支撑架设条件对支撑轴力的变化具有显著影响。基坑工程实施开挖过程中，由于每阶段开挖深度没有质量评定要求，必然存在开挖面深度的随机性差值，进而引起轴力实测值离散[1]。根据钢支撑轴力增长与变形的相关性[7]，由支撑架设时间延迟也会引发围护结构变形增长，进而导致上道支撑轴力变化，加剧轴力实测值离散性。多种因素共同作用是目前轴力变化规律不清[6]的关键，因此需要进一步细化施工过程管控指标，强化施工工艺精细控制，以达到预防基坑事故的功效。
支撑架设条件对围护墙位移、弯矩的影响分别如图 15，16所示。围护墙体位移和弯矩在悬挂架设条件下均最小，而超挖条件下均最大。这说明围护墙位移、弯矩与支撑轴力是密切相关的，悬挂架设的钢支撑轴力总和最小，对应的墙体位移、弯矩均最小；而超挖1 m条件下钢支撑轴力总和最大，对应的墙体位移、弯矩也是最大的。
![]()
图 15 不同支撑架设条件下围护墙体位移Figure 15. Wall deflections under different strut erection conditions![]()
图 16 不同支撑架设条件下围护墙弯矩图Figure 16. Wall moments under different strut erection conditions另外，图 15，16还表明具有厚层软土的深基坑变形控制的优化方向。表 8展示了不同支撑架设条件下围护墙体位移及弯矩的变化情况。在超挖1 m条件下进行支撑架设的基坑风险最大，不仅体现于变形过大，而且正负弯矩也是最大的；相比常规架设条件，墙体位移增大95%，而正弯矩增大39%，负弯矩增大91%，所以此工况必须严格杜绝；反之，悬挂架设条件下围护墙体位移小、正负弯矩均得到显著减小，应大力发展。
表 8 不同支撑架设条件下围护墙位移、弯矩最大值Table 8. Wall deflections and maximum moments under different strut erection conditions项目 最大位移/mm 最大正弯矩/(kN·m) 最大负弯矩/(kN·m) 悬挂架设 68 1729 -603 常规架设 110 2412 -1045 超挖1 m 204 3354 -1996 4. 结论
（1）支护系统中的钢支撑可显著提高围护墙的挡土功能，减小位移、弯矩等，因此揭示钢支撑轴力变化规律，具有重要的工程意义。
（2）提出了围护墙体位移与支撑轴力双元组合的计算模型验证方法。在围护墙体位移拟合基础上，通过将第二—第四道钢支撑的实际刚度分别折减为理论刚度的34%，34%，30%后，计算轴力值与实测值较为接近；本文的双元组合验证法不仅提高了模型适用性、计算参数合理性，还能更好地反映出基坑开挖过程中围护墙的变形和支撑轴力的发展规律。
（3）揭示了随基坑开挖深度增加，围护墙体位移增长规律。对于具有厚层软土的深基坑，墙体位移大可使围护墙体位移最大值及相对值均超控制值的现象不是个别案例，具有普遍性，应进一步加强监测预警的设计与施工配合程度。
（4）揭示了钢支撑轴力变化规律。钢支撑架设后，随土层开挖，该道支撑轴力有一个从线性增加至基本稳定的发展过程，轴力变化的转折点是下道支撑的阻隔作用。因此，钢支撑轴力变化规律应考虑该支撑所在部位、基坑开挖深度位置及下道支撑的阻隔作用等影响因素，同时应包含钢支撑轴力总和的变化趋势。
（5）揭示了预加轴力、支撑架设条件对钢支撑轴力变化的影响规律。预加值大小及施加方式、支撑架设条件等不改变轴力发展过程的变化趋势，但较大轴力预加值具有对上道支撑轴力的卸荷调整作用，增大本道轴力初始值、减小线性增加幅度等影响。
（6）多道支撑的基坑，单道钢支撑预加轴力施加对墙体变形控制产生不利的影响；而双道钢支撑预加轴力对变形控制有利，因此建议轴力伺服系统应用时应不少于2道支撑。
（7）支撑架设条件对支撑轴力、围护墙位移和弯矩的影响很大。相对于常规架设条件，超挖后支撑架设引起支撑轴力、围护墙体位移及正负弯矩均显著增大，显著加大基坑安全风险，应严禁超挖；而悬挂架设则使支撑轴力、围护墙体位移及正负弯矩均显著减小，应大力发展悬挂架设。
钢支撑是深基坑工程内支撑的一种重要结构，优点突出，应用广泛，但使用效果并不突出，因此需要精细化施工，强化设计与施工的配合程度，通过更多的典型工程案例完善钢支撑轴力变化规律，这对具有厚层软土深基坑的变形设计控制具有重要的工程意义。
-
![]()
图 2 原状样与重塑样三轴剪切结果
Figure 2. Triaxial shear results of undisturbed and remolded samples
![]()
图 3 原状样与重塑样三轴蠕变分级加载全过程
Figure 3. Whole process of triaxial creep graded loading of undisturbed and remolded samples
![]()
图 4 原状及重塑样三轴分级加载蠕变曲线
Figure 4. Creep curves of undisturbed and remolded samples under triaxial loading
表 1 试验加载方案
Table 1 Loading schemes for tests
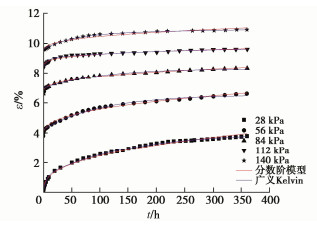
土样状态 σ3/kPa (σ1−σ3)/kPa 原状 50 18 36 54 72 90 100 28 56 84 112 140 200 43 86 129 172 215 重塑 50 15 30 45 60 75 100 18 36 54 72 90 
下载: 导出CSV
表 2 广义Kelvin模型参数拟合结果
Table 2 Fitting results of parameters of generalized Kelvin model
荷载/kPa A1 A2 A3 A4 A5 28 0.074 2.908 0.007 1.065 0.147 56 4.068 23.019 1.380×10-4 1.424 0.023 84 6.74 1.266 0.008 0.389 0.132 112 8.461 0.643 0.074 1.121 0.002 140 9.572 1271.520 5.520×10-7 1.082 0.020
下载: 导出CSV
表 3 分数阶模型参数拟合结果
Table 3 Fitting results of parameters of fractionals order model
荷载/kPa E0/MPa ξ/(MPa·hβ) β R2 28 8.16×102 70.23 0.37 0.992 56 16.36 111.31 0.30 0.996 84 12.80 345.40 0.32 0.993 112 13.57 376.66 0.24 0.993 140 14.88 718.47 0.34 0.967
下载: 导出CSV
-
[1] MESRI G, AJLOUNI M. Engineering properties of fibrous peats[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(7): 850–866. doi: 10.1061/(ASCE)1090-0241(2007)133:7(850)
[2] 阮永芬, 刘岳东, 王东, 等. 昆明泥炭与泥炭质土对建筑地基的影响[J]. 昆明理工大学学报(理工版), 2003, 28(3): 121–124. doi: 10.3969/j.issn.1007-855X.2003.03.030 RUAN Yong-fen, LIU Yue-dong, WANG Dong, et al. Effect of kunming's peat & peaty soil on the building foundation[J]. Journal of Kunming University of Science and Technology, 2003, 28(3): 121–124. (in Chinese) doi: 10.3969/j.issn.1007-855X.2003.03.030
[3] 王志良, 瞿嘉安, 申林方, 等. 泥炭质土层盾构施工扰动引起隧道长期沉降的研究[J]. 岩土工程学报, 2017, 39(8): 1416–1424. doi: 10.11779/CJGE201708008 WANG Zhi-liang, QU Jia-an, SHEN Lin-fang, et al. Long-term settlement of tunnel caused by shield tunneling in peaty soil[J]. Journal of Geotechnical Engineering, 2017, 39(8): 1416–1424. (in Chinese) doi: 10.11779/CJGE201708008
[4] 刘伟, 赵福玉, 杨文辉, 等. 安嵩线草海段泥炭质土的特征及性质[J]. 岩土工程学报, 2013, 35(增刊2): 671–674. http://cge.nhri.cn/cn/article/id/15467 LIU Wei, ZHAO Fu-yu, YANG Wen-hui, et al. Features and properties of peaty soil in Caohai section of Anning-Sonming line[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 671–674. (in Chinese) http://cge.nhri.cn/cn/article/id/15467
[5] GUO yi-peng, WANG xiao-nan, LAI zheng-fa, et al. Analysis on rheological properties of peat soil in Kunming area[J]. Applied Mechanics and Materials, 2012, 204/205/206/207/208: 722–726.
[6] GEMANT A. A method of analyzing experimental results obtained from elasto‐viscous bodies[J]. Physics, 1936, 7(8): 311–317. doi: 10.1063/1.1745400
[7] 殷德顺, 任俊娟, 和成亮, 等. 一种新的岩土流变模型元件[J]. 岩石力学与工程学报, 2007, 26(9): 1899–1903. doi: 10.3321/j.issn:1000-6915.2007.09.024 YIN De-shun, REN Jun-juan, HE Cheng-liang, et al. A new rheological model element for geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(9): 1899–1903. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.09.024
[8] 孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999. SUN Jun. Rheology of Geotechnical Materials and Its Engineering Application[M]. Beijing: China Architecture & Building Press, 1999. (in Chinese)
[9] 刘浩. 湖相软土物理力学特性及蠕变特性研究[D]. 长沙: 中南大学, 2011. LIU Hao. Study on Physical and Mechanical Properties and Creep Properties of Lake Soft Soil[D]. Changsha: Central South University, 2011. (in Chinese)
[10] NONNENMACHER T F, METZLER R. On the Riemann-liouville fractional calculus and some recent applications[J]. Fractals, 1995, 3(3): 557–566. doi: 10.1142/S0218348X95000497
[11] JIANG Q H, QI Y J, WANG Z J, et al. An extended Nishihara model for the description of three stages of sandstone creep[J]. Geophysical Journal International, 2013, 193(2): 841–854. doi: 10.1093/gji/ggt028
[12] 吴斐, 刘建锋, 边宇, 等. 盐岩的分数阶导数蠕变模型[J]. 四川大学学报(工程科学版), 2014, 46(5): 22–27. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201405004.htm WU Fei, LIU Jian-feng, BIAN Yu, et al. Fractional derivative creep model of salt rock[J]. Journal of Sichuan University (Engineering Science Edition), 2014, 46(5): 22–27. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201405004.htm
[13] 钱家欢, 殷宗泽. 土工原理与计算[M]. 2版. 北京: 中国水利水电出版社, 1996. QIAN Jia-huan, YIN Zong-ze. Geotechnical Principle and Calculation[M]. 2nd ed. Beijing: China Water Power Press, 1996. (in Chinese)
[14] 周光泉, 刘孝敏. 黏弹性理论[M]. 合肥: 中国科学技术大学出版社, 1996. ZHOU Guang-quan, LIU Xiao-min. Theory of Viscoelasticity[M]. Hefei: University of Science and Technology of China Press, 1996. (in Chinese)
-
期刊类型引用(12)
1. 郭瑞，吴德志，杜宁泽，梁融智，刘梦梦，周海贵，蒋阳阳. 盖挖法下的钢支撑架设施工技术研究. 工程与建设. 2025(01): 184-187 . 
百度学术
2. 唐伟华，林军. 基于二阶P-Δ弹性分析法的装配式钢管支撑结构稳定性分析. 勘察科学技术. 2024(01): 1-5+37 . 百度学术
3. 肖靖，朱俊涛，李德杰，饶为胜，曾旭涛. 超大深基坑支护结构设计及稳定性分析. 土工基础. 2024(04): 592-594+603 . 百度学术
4. 曹亮，李云鹤，陈帅，刘顺涛，刘伟. 基坑开挖变形特征和影响规律研究. 测绘通报. 2024(08): 160-164 . 百度学术
5. 赵升峰，汪敏营，邬喜春，李明东. 全钢结构基坑支护若干问题分析. 江苏建筑. 2024(05): 105-109 . 百度学术
6. 赵升峰，汪敏营，邬喜春，李明东. 不同深度基坑中桩加支撑支护特性研究. 江苏建筑. 2024(06): 112-115+129 . 百度学术
7. 邵根才，黄程翔，徐琳，周雪峰，谢李中，曹成功. 钢支撑预加轴力对温州软土基坑变形的影响. 中国水运(下半月). 2023(05): 128-130 . 百度学术
8. 毛学墙. 深基坑开挖过程中钢围堰-土相互作用机理研究. 施工技术(中英文). 2023(12): 74-79 . 百度学术
9. 彭力，肖敏. 水下钻孔爆破振动对桥梁的影响分析. 中国水运. 2023(10): 148-150 . 百度学术
10. 魏建华，鹿存亮，罗成恒，尹骥. 软土深基坑预应力混凝土伺服支撑设计与实践. 岩土工程技术. 2023(06): 737-743 . 百度学术
11. 李海涛，任光明，沈国卓，范荣全，曾文慧，董斌. 复杂环境下多种组合支护深基坑的变形控制及响应研究. 成都理工大学学报(自然科学版). 2023(06): 744-755 . 百度学术
12. 魏焕卫，李传斌，种记鑫，郑晓. 局部超挖对内支撑结构的施工效应. 计算机辅助工程. 2023(04): 56-65 . 百度学术
其他类型引用(6)
计量
- 文章访问数: 124
- HTML全文浏览量: 25
- PDF下载量: 28
- 被引次数: 18
