0.   引言

在天然沉积作用以及沉积后各种地质营力作用下，土颗粒间会产生一定的胶结作用力并呈现特定的排列方式^[1]，从而对土体变形、强度、固结、渗流产生重要影响^[2]，这种性质称为土的结构性。结构性土的力学特性与重塑土相比有较大差别。试验表明，在相同应力状态下，达到屈服前结构性土的刚度显著大于重塑土，比重塑土具有更高的孔隙比；达到屈服后，结构开始破坏，结构性土的压缩线斜率明显增大^[3-5]。此外，结构性土的剪切特性受应力历史、排水条件及围压等因素影响^[6]。

自然界中大多数土都兼具非饱和特性和结构性，基质吸力的存在使土颗粒间的联结作用加强，增强了土骨架的稳定性，这种由吸力产生的联结作用和由颗粒间矿物成分组成的胶结物质产生的联结作用是土体在宏观上呈现结构性的主要因素^[7]。

近年来，国内外众多学者分别基于不同的思想和理论，开展了结构性土本构模型的研究。从建模方法上看，大体可分为4类：①第一类是基于扰动状态理论建立的本构模型，如方祥位等^[8]、金旭等^[9]；②第二类是依据损伤理论建立的本构模型，如杨超等^[10]、蒋明镜等^[11]、李潇旋等^[12]；③第三类是在经典弹塑性框架内引入结构性参数，如黄茂松等^[13]、姚志华等^[14]；④第四类是基于四维空间理论建立的本构模型，如Liu等^[15]通过引入附加孔隙比建立的SCC模型。

依据四维空间理论建立的本构模型，从结构性土的变形特征出发，能有效描述结构性土的压缩行为，但目前国内外利用此方法建立的本构模型通常是针对饱和土的，鲜有适用于描述不同吸力下非饱和土变形行为的本构模型。

本文将SCC模型中饱和结构性土的体变方程拓展至非饱和状态，分别引入了结构性参数和结构强度，用以描述压缩过程中结构的退化规律和吸力对强度的强化作用，在边界面塑性理论框架下建立了一个能考虑结构性的非饱和土边界面本构模型。基于伊朗东北部非饱和原状黄土和西安非饱和原状Q₂黄土的试验数据，开展了模型参数标定和验证，结果表明所建立模型能有效描述结构性非饱和土的变形和强度特性。

1.   本构模型建立

1.1   体变方程

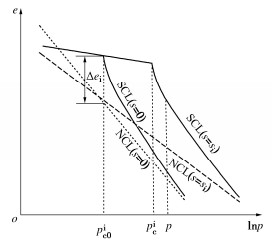
众多饱和结构性土等向压缩的试验结果^[16-17]表明，在相同应力状态下，结构性土比重塑土具有更高的孔隙比，当围压达到屈服应力后，结构逐渐发生破坏，产生不可恢复的塑性变形，其压缩曲线(structural compression line, SCL) 从上方不断趋近于重塑土的正常固结压缩曲线(normal compression line, NCL)，见图 1。

图  1  结构性土各向同性压缩曲线概念图

Figure  1.  Conceptual diagram of structural clay during isotropic compression

下载: 全尺寸图片 幻灯片

本文基于Liu等^[15]的思路，认为达到初始屈服应力$p_{\rm{c}}^{\rm{i}}$后，结构性开始破坏，压缩曲线(SCL, s=s₁) 不断趋近于重塑土正常固结压缩线(NCL, s=s₁)。

由上述分析可得，结构性非饱和土的孔隙比可采用下式表示：

式中，$e*$为非饱和重塑土的孔隙比，$\Delta e$为相同应力状态下结构性土与重塑土的孔隙比之差，

其中，$\Delta {e_i}$为$p = p_{\rm{c}}^{\rm{i}}$时的初始附加孔隙比，b为解构指数，表征结构性破坏的大小和速率。本文近似认为非饱和状态下的初始附加孔隙比与饱和状态时相同。

非饱和重塑土在正常固结过程中的体变方程可以采用下式表示：

式中，${e_0}$为初始孔隙比，$\lambda (s)$为重塑土的压缩线斜率。

将式（2），（3）代入式（1），可得结构性非饱和土的正常固结压缩曲线方程为

1.2   屈服方程

本文引入BBM模型中的LC屈服面来描述结构性非饱和土中屈服应力随基质吸力s的变化规律，LC屈服面方程如下：

式中，${p^{{\rm{c}}}}$为参考应力，${p_{{{\rm{c}}0}}}$为饱和状态时先期固结压力，${p_{{\rm{c}}}}$为非饱和状态时的先期固结压力，$\lambda (s)$为$e$–$\ln p$平面内非饱和土的正常固结线斜率，其值随吸力s的增加而逐渐降低，且有

其中，$\lambda (0)$为饱和状态时正常固结线斜率，r与土体的最大刚度有关，β控制土体刚度随吸力变化的速率。

1.3   结构强度和衰减规律

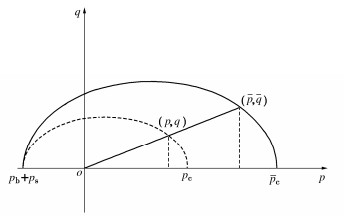
本文引入结构强度${p_{\rm b}}$来表征结构对黏聚力的影响，在$p$–$q$平面表示为屈服面与横轴的左交点，如图 2所示。

图  2  p–q–s空间内的边界面

Figure  2.  Bounding surface in p–q–s space

下载: 全尺寸图片 幻灯片

在剪切过程中，土颗粒的排列改变并且胶结物质发生破碎，结构强度${p_{\rm{b}}}$随之减小。基于Suebsuk等^[18]的思路，本文认为${p_{\rm{b}}}$只与塑性剪应变有关，衰减规律如下：

式中，${p_{{\rm{b}0}}}$为初始结构强度，可根据$p$–$q$平面的峰值强度进行标定。

1.4   边界面

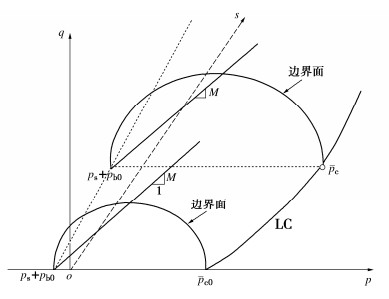
选取修正剑桥模型的椭圆屈服面作为边界面，将BBM模型中的LC屈服线作为p–s平面的边界线，图 4为边界面在p–q–s空间的示意图。${p_{\rm{s}}}$表示随吸力增大导致土体的黏结强度增加，${p_{{\rm{b}0}}}$为初始结构强度。初始边界面与$p$轴的左交点为$({p_{\rm{s}}} + {p_{{\rm{b}0}}})$，右交点为饱和结构性土先期固结压力${\bar p_{\rm{c}0}}$，当土体应力状态位于边界面且发生塑性变形时，边界面不断发生硬化扩张，与$p$轴的右交点不断右移。

图  3  映射准则

Figure  3.  Mapping criteria

下载: 全尺寸图片 幻灯片

图  4  等向压缩预测结果与试验数据对比

Figure  4.  Comparison between model predictions and experimental data during isotropic compression test

下载: 全尺寸图片 幻灯片

土体的边界面方程为

式中，$\bar p$，$\bar q$，${\bar p_c}$分别为边界面上的净应力、剪应力和屈服应力，M为临界状态线的斜率。

1.5   流动法则

模型采用相关联流动法则，塑性应变增量采用边界面塑性理论计算：

式中，$H$，${\bar H_j}$分别为当前应力点和边界面上映射点对应的塑性模量，${\boldsymbol n_{\rm Q}}$，$\boldsymbol n_{\rm F}^{\rm T }$分别为塑性势面和边界面上的单位法向量，代表塑性流动方向和加载方向。

1.6   硬化法则

在塑性加载过程中，边界面的大小与结构性饱和土前期固结压力有关，并且由塑性体变决定。根据1.1节的式（4）可推导出硬化法则为

边界面的一致性条件为

1.7   映射准则

通过映射准则可建立当前应力点的塑性模量与边界面上像应力点塑性模量的关系。suebsuk等^[19]针对结构性黏土建立了一个简单有效的径向映射法则，以坐标原点为映射中心，如图 3所示。塑性模量插值函数的形式如下：

式中，${\bar H_{j,i}}$为像应力点的初始塑性模量，$h$为无量纲参数，表征材料特性对塑性模量的影响，$\alpha$为像应力比，

其中，0≤α≤1，像应力点坐标$\left( {\bar p,\bar q} \right)$可以根据几何关系求出。

弹性应变增量根据胡克定律计算：

式中，${\boldsymbol C^e}$为弹性柔度矩阵。

2.   模型参数及确定方法

在三维应力状态下，模型共有15个参数。其中，b，Δe_i为结构性参数，可通过结构性土和重塑土的饱和正常固结压缩曲线拟合获得。Κ，λ(0)，p_c0为饱和土弹塑性参数，可通过重塑土在饱和状态下的各向同性压缩试验获得。$c'$，$\varphi '$，${\varphi ^{\rm b}}$用于确定土体的初始结构强度，可根据不同基质吸力下p–q平面的强度包线计算得出。h为材料参数，用来表征材料特性对塑性硬化模量的影响，可通过不同基质吸力下的剪切应力–应变曲线拟合得到。其余参数的确定方法与BBM模型一致。

3.   模型验证

3.1   原状非饱和黄土等向压缩试验验证

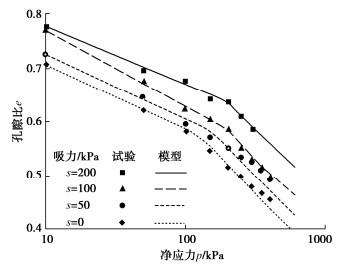
Horpibulsuk等^[19]为探究非饱和湿陷性黄土中的体积压缩行为，对伊朗东北部的原状黄土开展了一系列等向压缩试验。试验开始前，首先对试样进行吸力平衡，使吸力分别达到0，50，100，200 kPa，随后分别在恒定吸力下等向压缩至400 kPa，本文对相应的试验数据进行模型验证，采用的参数：κ=0.05，λ(0)= 0.1，r =0.8471，β=0.0076 kPa，p^c =40 kPa，k =0.2，p_c0= 150 kPa，b=1，Δe_i=0.03，h=100，e₀=0.77，M =1.15，G =6000 kPa，$c'$=20.2 kPa，$\varphi '$=26.2°，${\varphi ^{\rm b}}$= 12.5°。

图 4为等向压缩试验的模型预测与试验数据的对比，可以看出模型能较好的预测不同吸力下非饱和原状黄土在等向压缩过程中的体积变化规律。相同净应力下，吸力越大，孔隙比越大，即压缩过程中产生的变形越小。此外，图 4也进一步说明了本文模型采用边界面理论的优越性，由于加载全过程均有塑性变形产生，所以不存在达到屈服之后弹性到塑性阶段的明显转折点。

3.2   原状非饱和黄土三轴剪切试验验证

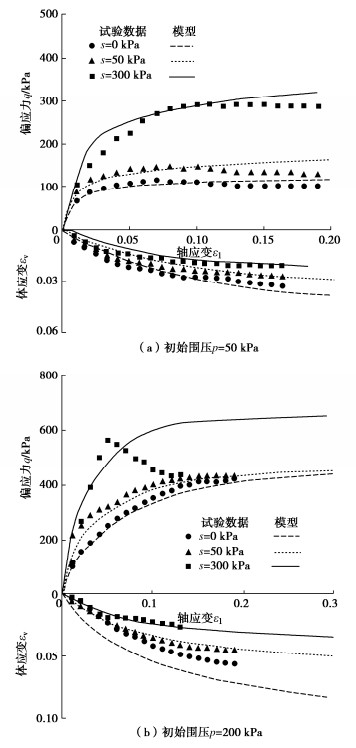
Haeri等^[20]分别对原状黄土和重塑黄土开展了两组等围压下的湿化试验和控制吸力的三轴剪切试验。本文分别选取初始围压为50，200 kPa，基质吸力为0，50，300 kPa的试验数据进行验证。

图 5为模型预测结果与试验数据的对比，可以看出，本文模型对剪切行为的预测结果与试验数据吻合度较高，偏应力和体应变随轴应变的增加而增大。随着初始围压的增大，剪切过程中产生的体变不断增加，也说明在加载的过程中结构不断破坏，土颗粒间的胶结作用逐渐退化。

图  5  三轴剪切预测结果与试验数据对比

Figure  5.  Comparison between model predictions and experimental data during triaxial shear test

下载: 全尺寸图片 幻灯片

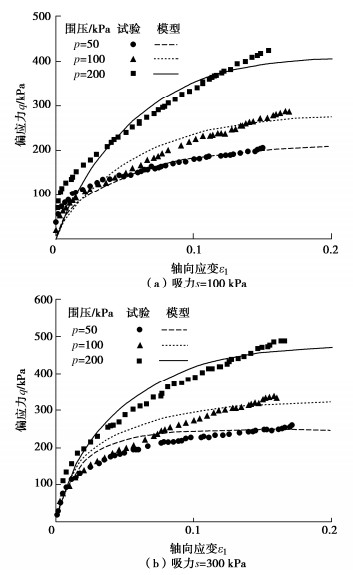
Q₂黄土具有明显的结构性且为典型的非饱和土，方祥位等^[21]针对非饱和Q₂原状黄土，控制吸力为100，300 kPa，分别在50，100，200 kPa的初始围压下开展三轴排水剪切试验。本文对以上两组试验数据进行验证，模型参数：κ=0.22，λ(0)= 0.1298，r =0.51，β=0.015 kPa，p^c =40 kPa，k =0.28，p_c0=68 kPa，b =1，Δe_i =0.03，h =100，e₀=0.86，M =0.88，G =4500 kPa，$c'$=37.6 kPa，$\varphi '$=25.1°，${\varphi ^{\rm b}}$=3.2°。

从图 6可以看出本文模型预测结果和试验结果吻合较好。在加载过程中，表现出了明显的硬化和剪缩特性，吸力越大，峰值强度越高。从图 6中可以看出，当施加的剪应力较小时，土体产生的应变较小，在剪切的前期刚度较大，这是由于土中存在较强的结构性，即存在一部分结构强度。同一吸力下，初始围压越大，前期结构强度越大，随着剪切的进行，结构逐渐破坏，结构性对抗剪强度的贡献逐渐降低。

图  6  模型预测结果与试验数据对比

Figure  6.  Comparison of model prediction results with experimental data

下载: 全尺寸图片 幻灯片

4.   结论

本文通过引入结构性参数，将饱和状态的结构性土压缩曲线方程拓展至非饱和状态，建立了可以考虑基质吸力影响的结构性土本构模型，得到3点结论。

（1）在Liu等^[15]提出的饱和结构性土压缩曲线方程的基础上，结合BBM模型中的LC屈服线，建立了结构性非饱和土的压缩曲线方程，通过附加孔隙比的变化可以描述等向压缩过程中结构的衰减。

（2）将修正剑桥模型的椭圆屈服面作为p–q平面的边界面，将LC曲线作为p–s平面的右边界线，将结构以及基质吸力产生的抗拉强度${p_s} + {p_b}$作为左边界线，利用边界面塑性理论对土体的变形进行了更加合理的预测。

（3）利用Matlab计算软件编写了计算程序，对伊朗东北部Gorgan地区的原状黄土和西安非饱和Q₂原状黄土的试验数据进行了参数标定及模型验证，结果表明，所建立模型能有效预测各向同性压缩以及三轴剪切条件下结构性非饱和土的变形特性。