单粒组冻结砂土三轴压缩颗粒破碎规律研究

陈榕; 孙鹤; 郝冬雪; 武智勇; 高宇聪

doi:10.11779/CJGE2022S1017

单粒组冻结砂土三轴压缩颗粒破碎规律研究 English Version

陈榕^{1, 2,},
孙鹤^{1, 3},
郝冬雪^{1, 2, ,},
武智勇^{1, 2},
高宇聪^{1, 2}

1.
东北电力大学, 建筑工程学院, 吉林吉林 132012
2.
东北电力大学, 吉林省电力基础设施安全评估与灾害防治重点实验室, 吉林吉林 132012
3.
贵州电网有限责任公司贵阳供电局, 贵州贵阳 550001

基金项目:

国家自然科学基金项目 52078108

吉林省科技厅中青年科技创新领军人才及团队项目 20210509058RQ

吉林省教育厅科学研究项目 JJKH20210103KJ

详细信息

作者简介:
陈榕(1979—)，男，辽宁沈阳人，博士，教授，主要从事土工合成材料加筋特性及软弱地基加固处理方法等方面的教学和科研工作。E-mail: lg1316cih@126.com

通讯作者:
郝冬雪, E-mail: haodongxue2005@126.com

中图分类号: TU432
计量
- 文章访问数: 123
- HTML全文浏览量: 24
- PDF下载量: 21
出版历程
- 收稿日期: 2022-09-21
- 网络出版日期: 2023-02-06
- 刊出日期: 2022-11-30

Particle breakage characteristics of frozen ideal uniform sands under triaxial compression

CHEN Rong^{1, 2,},
SUN He^{1, 3},
HAO Dong-xue^{1, 2, ,},
WU Zhi-yong^{1, 2},
GAO Yu-cong^{1, 2}

1.
School of Civil Engineering and Architecture, Northeast Electric Power University, Jilin 132012, China
2.
Key Lab of Electric Power Infrastructure Safety Assessment and Disaster Prevention of Jilin Province, Northeast Electric Power University, Jilin 132012, China
3.
Guiyang Power Supply Bureau of Guizhou Power Grid, Guiyang 550001, China

摘要

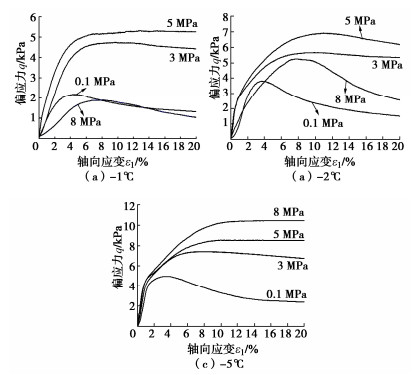
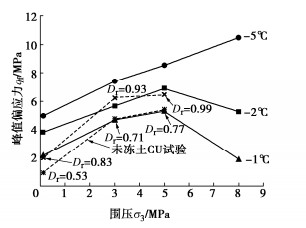
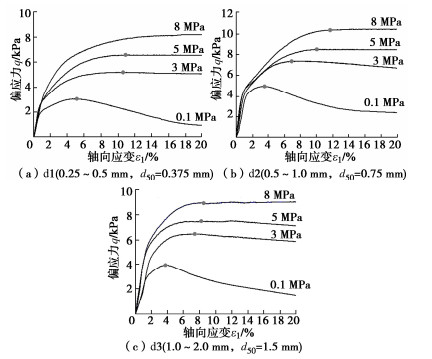
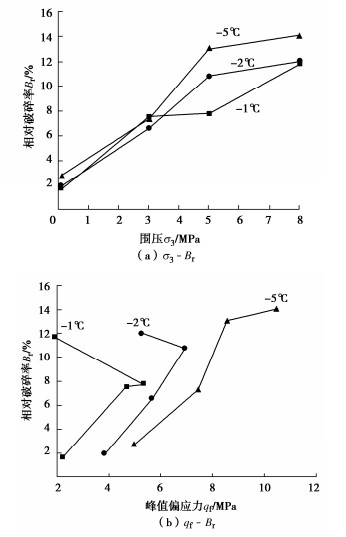
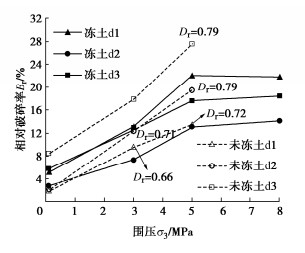
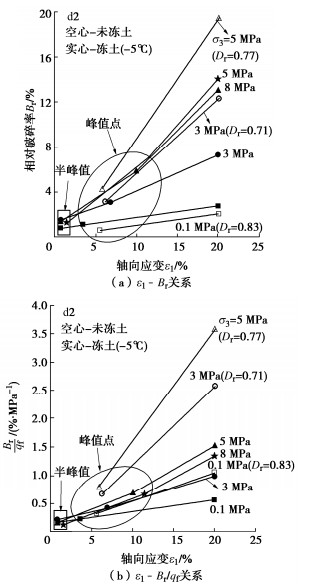
摘要: 针对三种不同粒径的单粒组冻结砂土开展三轴剪切试验，重点研究剪切过程中冻结砂土颗粒破碎演化规律及粒径对冻土颗粒破碎的影响。结果表明：冻结温度为-1℃和-2℃时，围压 ${\sigma _3}$ ≥5 MPa情况下冻结砂土出现明显压融，并且在-1℃时由于局部快速压融导致冻结砂土出现抗剪强度低于未冻土现象；冻结砂土在剪切过程中出现颗粒破碎现象，颗粒破碎率随轴向应变增大持续增长，在高围压（ ${\sigma _3}$ ≥5 MPa）下甚至出现加速增长趋势；冻结砂土颗粒破碎率规律与未冻砂土不同，小粒组冻结砂土颗粒破碎率最大，该现象可能与冻土内部不同部位的冰晶作用有关。
- 冻结砂土 /
- 粒径影响 /
- 围压 /
- 颗粒破碎
Abstract: The triaxial shear tests on three groups of frozen ideal sands are carried out to investigate the evolution rules of particle breakage during shearing process and the effects of particle size on the particle breakage. It is shown that obvious pressure melting of sand samples takes place under -1℃ ~ -2℃ when σ₃ ≥5 MPa, and the strength of frozen sands is even less than the unfrozen strength due to rapid melting near shearing rupture plane at -1℃. The particle breakage of frozen sands occurs during shearing. The particle breakage rate continues to increase with the increase of the axial strain, and even develops with the acceleration after the peak strength under high confining pressure (σ₃ ≥5 MPa). The influences of the particle size of frozen sands on the breakage rate is different from those of unfrozen sands. The particle breakage rate of the frozen sands of small particle group is the largest, which may be related to the action of ice crystals in different parts of frozen soils.
- frozen sand /
- particle-size influence /
- confining pressure /
- particle breakage

HTML全文

0. 引言

在气候变化及人类活动的影响下，非饱和土体内部的水分场和温度场会逐渐改变，劣化土体工程性质，进而诱发一系列工程地质问题，如不均匀沉降和路基稳定性问题等^[1]。实际过程中，土体中的水分和热量迁移存在复杂的耦合作用。因此，研究近地表非饱和土的水热耦合特性和工程响应，对于防控土体水热场变化引起的各类岩土工程问题具有重要的现实意义^[2]。

早期Philip等^[3]于1957年首次引入水分相变过程，并建立相应的水热耦合计算模型。在此基础上，国内外学者围绕非饱和多孔介质中水热耦合理论、试验研究和数值计算做了大量工作^[4-6]。需要指出的是，目前岩土工程界关于水热耦合设计体系都重视液态水的影响，在计算过程中关于重力项和水分相变等问题大多作简化处理^[2]。如Sellers等^[7]在水热耦合数值计算过程中，仅分别考虑了液态水流动对水分分布和热传导过程对温度分布影响，忽略了水汽运动对土体水热场的影响。陈佩佩等^[8]基于光滑粒子流体动力学（SPH）方法计算了不同热扩散系数等热物理参数对热源条件下的非饱和土水热场分布特征的影响，忽略了水-汽相变和水汽运动的影响。

综上，在非饱和土水热耦合问题中忽略自重项等因素能简化计算，但在一定程度上会影响数值求解的准确性^[2]。为系统研究如自重项等简化因子的影响，本文采用已有的水热耦合模型^[3-5]，充分考虑了热传导、相变、温度梯度、水分梯度和重力势耦合作用，采用FreeFem⁺⁺有限元软件^[9]自主编制了计算程序并求解。在此基础上，进一步考虑了表层蒸发、降雨入渗和干湿循环的不同工况，探讨了蒸发潜热项、自重项、水汽运动和渗透系数等因子在水热耦合问题简化计算中的合理性。

1. 非饱和土水热耦合理论模型

1.1 水分迁移方程

在非饱和土中，分子扩散引起的孔隙蒸汽质量通量可以用菲克定律来描述，蒸汽总通量可表示为^[3]

${q_{\text{v}}} = - {D_{{\text{atm}}}}v\alpha a\nabla {\rho _{\text{v}}}{, }$

(1)

式中，是梯度算子，q_v为蒸汽通量密度，D_atm为水蒸气在空气中的分子扩散率，v为质量流动因子，α为土体曲率因子，a为体积空气含量，ρ_v为水蒸气密度。

基于非饱和达西定律，液态水分通量密度表示为

$\frac{{{q_{\text{l}}}}}{{{\rho _{\text{l}}}}} = - K\nabla \phi {, }$

(2)

式中，q_l为液态水的通量密度，ρ_l为液体密度，K为非饱和土渗透系数，ϕ为总水势。总水势由基质势φ和重力势z组成，故式（2）可改写为

。

$\frac{{{q_l}}}{{{\rho _l}}} = - K\left( {\frac{{\partial \varphi }}{{\partial \theta }}} \right)\nabla \theta - K\left( {\frac{{\partial \varphi }}{{\partial T}}} \right)\nabla T - K\nabla z。$

(3)

根据水分通量质量守恒，可得

$\frac{{\partial \theta }}{{\partial t}} = \frac{{\partial {\theta _{\text{l}}}}}{{\partial t}} + \frac{{\partial {\theta _{\text{v}}}}}{{\partial t}} = - \nabla \left( {\frac{{{q_{\text{l}}}}}{{{\rho _{\text{l}}}}}} \right) - \nabla \left( {\frac{{{q_{\text{v}}}}}{{{\rho _{\text{l}}}}}} \right){, }$

(4)

式中，θ_l，θ_v分别为非饱和土液态水体积含水率和水蒸汽体积含水率，t为时间。

结合式（1），（3），（4），可得非饱和土水分运移的控制方程为

$\frac{{\partial \theta }}{{\partial t}} = \nabla \left( {{D_\theta }\nabla \theta } \right) + \nabla \left( {{D_{\text{T}}}\nabla T} \right) + \nabla \left( {K\nabla z} \right)。$

(5)

式中，D_T为温度诱致水分扩散系数，D_θ为等温水分扩散系数。

1.2 热量迁移方程

非饱和土中的热通量是由热传导、蒸汽运动引起的潜热、水蒸汽和液态水中的显热传递4部分组成。在Philip等^[3]模型中，根据热量守恒，可表示为

$C\frac{{\partial T}}{{\partial t}} + {L_0}{\rho _{\text{l}}}\frac{{\partial {\theta _{\text{v}}}}}{{\partial t}} = \nabla (\lambda \nabla T) - \nabla ({L_0}{q_{\text{v}}}){, }$

(6)

式中，C为土体比热容， $\lambda$ 为导热系数，L₀为参考温度T₀条件下水的蒸发潜热。

为更好的描述蒸汽流动，Thomas^[5]在Philip等^[3]水热耦合模型基础上引入相变系数ε来考虑气液相变：

$\frac{{{d_{\text{i}}}({\rho _{\text{l}}}{\theta _{\text{l}}})}}{{{d_{\text{e}}}({\rho _{\text{l}}}{\theta _{\text{l}}})}} = \frac{\varepsilon }{{1 - \varepsilon }}。$

(7)

当ε=1时，意味着水分转移是以蒸汽的形式发生的；当ε=0时，则表明是仅以液态形式发生。

最后基于水蒸汽的质量与液体的质量相比是可以忽略不计的假设，可得热流控制微分方程：

$\begin{array}{l} C\frac{{\partial T}}{{\partial t}} = \nabla \cdot (\lambda + {L_0}\varepsilon {\rho _{\text{l}}}{D_{\text{T}}})\nabla T + \nabla \cdot ({L_0}\varepsilon {\rho _{\text{l}}}{D_\theta })\nabla \theta +\\ \ \ \ \ \ \ \ \ \ \ {L_0}\varepsilon {\rho _{\text{l}}}\frac{{\partial K}}{{\partial z}}。 \end{array}$

(8)

2. 分析讨论

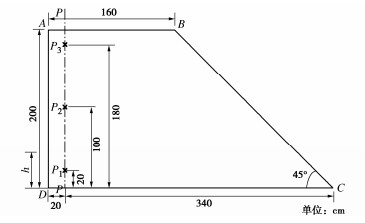
为系统研究边坡水热耦合计算模型中蒸发潜热项、自重项、水汽运动和渗透系数等因子对非饱和土体水热响应的影响，本文选取非饱和细砂土，基于上述水热耦合模型对各影响因子展开分析讨论。土体的热物理参数具体如表 1所示^[5]，考虑区域为图 1中ABCD区域。

表 1 细砂土的热物理参数^[5]

Table 1. Thermal physical parameters of unsaturated soils^[5]

参数	符号	取值
体积热容/(calžcm^-3ž℃^-1)	C	0.48
导热系数/(calžcm^-1žs^-1ž℃^-1)	λ	0.02
水的蒸发潜热/(calžg^-1)	L₀	540
温度诱致水分扩散系数/(cm²žs^-1ž℃^-1)	D_T	1×10^-5
相变系数	ε	0.3
等温水分扩散系数/(cm²žs^-1)	D_θ	0.01
非饱和渗透系数/(cmžs^-1)	K	1×10^-5
比水容量/(m^-1)	∂θ/∂φ	0.1

下载: 导出CSV

| 显示表格

图 1 二维简易坡体示意图^[5]

Figure 1. Schematic diagram of two-dimensional slope^[5]

下载: 全尺寸图片幻灯片

实际上，土体内部的渗透和导热特性与含水率密切相关，其内部的水热迁移还受地下水位、表层蒸发以及降雨入渗等外界条件的影响。为更贴合实际边坡工况，基于van Genuchten^[10]渗透系数计算模型和Côté等^[11]提出的导热系数计算模型，分别为

$K = {K_{\text{s}}} \cdot {S_{\text{e}}}^{0.5}{\left[ {1 - {{(1 - {S_{\text{e}}}^{1/{m_1}})}^{{m_1}}}} \right]^2} {, }$

(9)

$\lambda = {\text{(}}{\lambda _{{\text{sat}}}} - {\lambda _{{\text{dry}}}}{\text{)}} \times {\lambda _{\text{r}}} + {\lambda _{{\text{dry}}}}{, }$

(10)

式中，K_s为饱和渗透系数，K_s=1.35×10^-5 cm/s，S_e为饱和度，系数m₁=0.5，λ_sat为饱和状态导热系数，λ_sat=0.025 cal/cm/s/℃，λ_dry为干燥状态导热系数，λ_dry=5×10^-4 cal/cm/s/℃， ${\lambda _{\text{r}}} =$ $\frac{{3.55 \times {S_{\text{e}}}}}{{1 + (3.55 - 1){S_{\text{e}}}}}$ 。

初始温度、初始体积含水率和边界条件具体如表 2所示。在截面P上选取3个点P₁（h=20 cm）、P₂（h=100 cm）和P₃（h=180 cm）作为特征点来分析不同位置土体的水热特性。为研究如重力项等因素在水热耦合模型中的时间效应，如表 3所示，选取蒸发边界的蒸发速率为1×10^-5 cm/s，降雨入渗边界的入渗速率为1×10^-6 cm/s，干湿循环边界为上述蒸发和降雨入渗速率各一天依次交替，计算时间为60 d。

表 2 初始状态和边界条件

Table 2. Initial states and boundary conditions

初始状态	边界条件
初始状态	AB，BC	CD	AD
T₀=10 ℃, θ₀=0.5-y/100	蒸发/降雨入渗/干湿循环边界, T=25 ℃, 隔热边界	θ=0.5, 不透水隔热边界	不透水隔热边界

下载: 导出CSV

| 显示表格

表 3 模拟工况

Table 3. Simulated conditions

模拟工况	边界水分通量/(cm·s^-1)	持续时常
蒸发	-1×10^-5	60 d
降雨	1×10^-6	60 d
干湿循环	-1×10^-5 / 1×10^-6	各1 d依次交替，合计60 d

下载: 导出CSV

| 显示表格

2.1 蒸发潜热项对水热耦合过程的影响

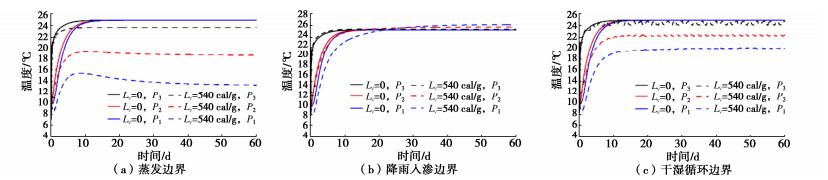
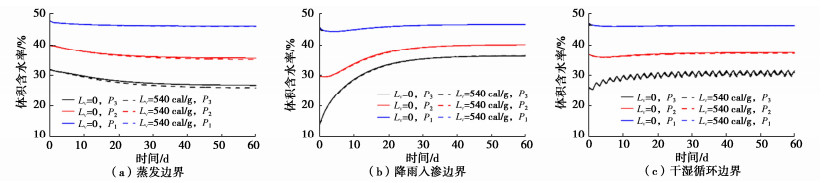
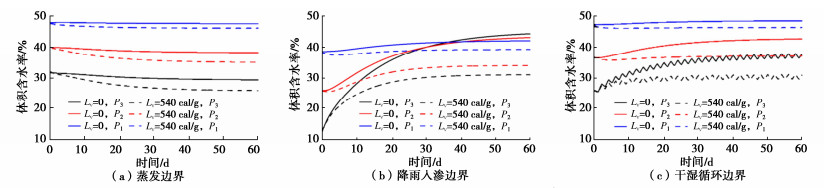
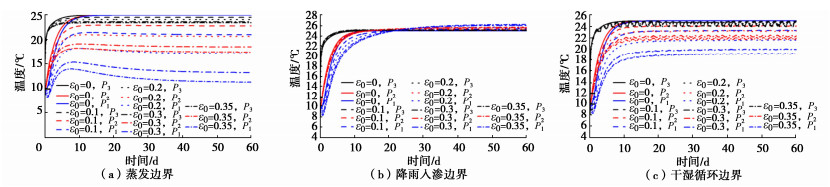
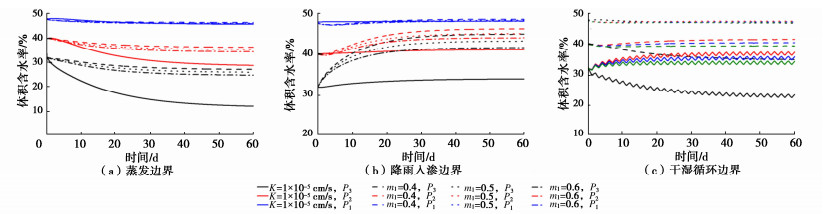
为分析水分蒸发引起的潜热变化对土体水热场的影响，在上述蒸发、降雨和干湿循环条件下，分别对考虑蒸发潜热项（L₀=540 cal/g）和不考虑蒸发潜热项（L₀=0）两种情况下的水热场分布进行数值计算，计算结果如图 2，3所示。对比图 2可以看出，在3种边界条件下，考虑蒸发潜热项与否会显著影响特征点温度随时间的变化特征及温度稳定值，由于水分蒸发吸收热量会使得考虑蒸发潜热时的计算值滞后于不考虑蒸发潜热时的温度场变化，其影响程度与边界条件有关，表现为降雨入渗 < 干湿循环 < 蒸发，这是由于水分入渗会加速热量扩散，该作用显著强于蒸发潜热的影响，使得稳定时的温度逐渐上升。

图 2 蒸发潜热项对温度场时空演化特征的影响

Figure 2. Effects of latent heat of evaporation on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 3 蒸发潜热项对水分场时空演化特征的影响

Figure 3. Effects of latent heat of evaporation on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

从图 3可以看出，在上述边界作用下，各特征点的含水率向稳定值缓慢变化。在本文的干湿循环条件下，仅P₃处体积含水率随时间呈波动变化。蒸发潜热项考虑与否对各特征点在不同时间上的含水率值及其变化特征并无显著区别，但在蒸发条件下其影响随高度和时间增加而稍有增强（在P₃处最大变化仅为3.2%）。说明蒸发潜热项对土体温度变化的影响极大，但对于含水率的影响几乎可以忽略不计。

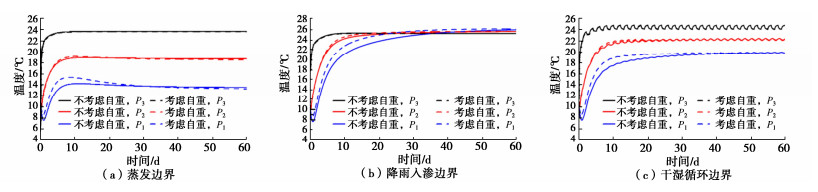
2.2 自重项对水热耦合过程的影响

为验证自重在水热耦合问题中的重要性，对于上述3种边界条件下的土体温度场和水分场在考虑及不考虑重力项两种情况下的分布进行了数值计算，计算结果分别如图 4，5所示。由图 4可知，自重项对温度场的影响随着高度的增加而减小，但仅表现在稳定前的时间段，如在蒸发条件下该阶段随高度增加时温度值的最大增幅依次为15.7%，2.5%和0.8%，这是由于水分场急剧变化导致的热量扩散，但并不会显著影响稳定时的温度场分布特征，各特征点稳定温度变化幅度最大仅为1.8%。从图 5可以看出，考虑自重项与否对于各特征点含水率变化及其稳定含水率存在显著区别，如在蒸发条件下其稳定含水率随高度增加依次为0.46，0.35，0.26，较小于不考虑自重项时的0.48，0.38，0.30。这是由于土体内部的水分迁移主要由自重、温度梯度和含水率梯度引起，当不考虑自重时，水分在温度和含水率梯度的共同作用下由底部高含水率处向上层低含水率处迁移。而自重则是引起水分向下迁移的动力，阻碍底部水分向上迁移，因此，在表层蒸发条件下，考虑自重时的稳定含水率更低。

图 4 自重对温度场时空演化特征的影响

Figure 4. Effects of gravity on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 5 自重对水分场时空演化特征的影响

Figure 5. Effects of gravity on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

2.3 相变系数对水热耦合过程的影响

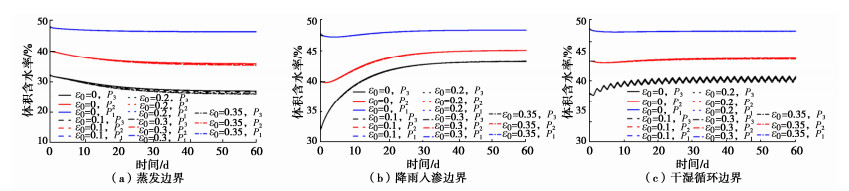
为研究水分蒸发相变系数（蒸汽流动）对非饱和土温度场及水分场的影响，设定相变系数ε分别为0（不考虑蒸汽流动），0.1，0.2，0.3，0.35，分别讨论了上述边界条件下各特征点的温度场及水分场的变化趋势，结果分别如图 6，7所示。由图 6可知，在不同相变系数条件下各特征点的温度变化趋势均呈先增加后逐渐稳定变化，在蒸发和干湿循环条件下，随着相变系数的增加，各特征点的稳定温度值逐渐降低，并且随着高度的增加，对温度的影响逐渐减弱，如在蒸发条件下P₁处，稳定温度值随设定相变系数的增加依次为25.0，21.1，17.2，13.3，11.4 ℃。但在降雨条件下，相变系数仅会影响前期温度变化，对稳定阶段的影响较小，最终的稳定值也不呈梯度分布。图 7为3种边界条件下各特征点含水率随时间变化的对比。

图 6 相变系数对温度场时空演化特征的影响

Figure 6. Effects of phase change coefficient on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 7 相变系数对水分场时空演化特征的影响

Figure 7. Effects of phase change coefficient on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

可见，相变系数的取值对土体体积含水率的影响并不显著，仅稳定含水率存在微小差异。该差异在蒸发条件下更为显著，尽管如此，相较于ε=0时，蒸发条件下不同相变系数的稳定含水率最大减幅在P3处仅有3.7%。说明相变系数取值对土体温度变化的影响极大，但对于含水率的影响几乎可以忽略不计，即对于非饱和土水热耦合问题时，相变系数取值是否合理会显著影响土体温度的计算值。

2.4 渗透系数对水热耦合过程的影响

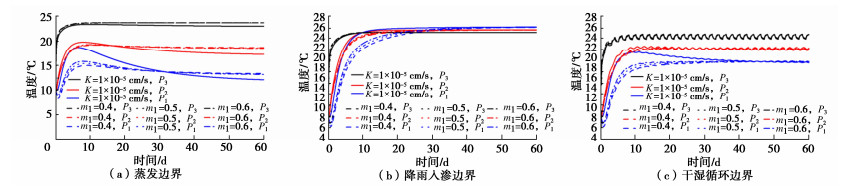
渗透系数是土体渗透性表征指标，反映了水在土体孔隙中渗透流动的性能。为研究非饱和土体渗透系数取值对其温度场及水分场演化的影响，将渗透系数分别设定为常数1×10^-5 cm/s，m₁=0.4，m₁=0.5和m₁=0.6，渗透系数与体积含水率的关系曲线如图 4所示。计算了土体温度场和水分场的演化特征，结果分别如图 8，9所示。由图 8可知，不同渗透系数条件下各特征点的温度变化趋势均呈先增加后逐渐稳定变化，m₁的取值对土体温度的影响随着高度的增加而逐渐减弱，如在蒸发条件下，相较于m₁=0.4，m₁=0.5时随高度增加最大增幅依次为5.0%，0.6%和0.3%，m₁=0.6时随高度增加最大增幅依次为10.4%，1.1%和0.7%，但对其稳定温度值的影响较小。图 9为不同渗透系数时特征点含水率随时间变化的对比。可见，m₁的取值并不会显著影响各特征点含水率的整体变化趋势，但对表层土体含水率时空演化过程的影响更为显著，并且特征点的稳定含水率随着m₁的取值而变化，如蒸发条件下P₃处，m₁=0.5和m₁=0.6相较于m₁=0.4的稳定含水率的减幅分别为4.1%，8.5%。随着m₁取值的增大，渗透系数增大，土体内部水分下渗加强而减弱底部向上的水分补给，土体的稳定含水率逐渐减小，并且在土体表层变化更为显著。此外，在上述3种边界条件下，当渗透系数为常数时，土体的水热场变化特征会显著区别于基于van Genuchten模型拟合的渗透系数。

图 8 渗透系数对温度场时空演化特征的影响

Figure 8. Effects of permeability on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 9 渗透系数对水分场时空演化特征的影响

Figure 9. Effects of permeability on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

3. 结论

（1）在蒸发、降雨入渗和干湿循环边界条件下，蒸发潜热项考虑与否和相变系数取值大小会显著影响土体内部温度场的分布特征，其影响程度随高度增加而逐渐减弱，但对水分迁移的影响并不显著。

（2）土体内部的水分迁移主要由温度梯度和水压梯度引起，其中，自重是引起水分向下迁移的动力，渗透系数增大也会加强土体内部水分下渗作用，二者均会在一定程度上阻碍底部水分向上部的迁移过程。因此，考虑自重和渗透系数较大时两种情况下的土体水分向下迁移更快，影响地下水对上层土体的补给和降雨入渗过程。自重项考虑与否与渗透系数选取还会在一定程度上影响温度场的变化，但仅表现在温度稳定前的时间段。

（3）自重等因子对非饱和土水热场的影响与边界条件有关，水分迁移会引起热量扩散，温度变化又会进一步影响水分场的分布。稳定时的温度梯度随着边界水分补给而逐渐减小，即降雨入渗边界条件下稳定时的温度梯度 < 干湿循环边界 < 蒸发边界。

（4）采用van Genuchten模型拟合的渗透系数更符合实际非饱和土的渗透特性，其水热场变化特征显著区别于常渗透系数情况。

不同温度下砂样d2的q– ${\varepsilon _1}$ 关系

Curves between q and ${\varepsilon _1}$ under different temperatures (Sample d2)

下载: 全尺寸图片幻灯片

不同温度下 ${q_{\text{f}}}$ 与 ${\sigma _3}$ 关系曲线（砂样d2）

Relationship between ${q_{\text{f}}}$ and ${\sigma _3}$ under different temperatures (Sample d2)

下载: 全尺寸图片幻灯片

三种粒径冻结砂土q– ${\varepsilon _1}$ 关系曲线

Relationship between q and ${\varepsilon _1}$ for frozen sands with different d₅₀

下载: 全尺寸图片幻灯片

图 4 不同温度下剪切结束后的颗粒相对破碎率

Figure 4. Values of B_r under different frozen temperatures ( ${\varepsilon _1}$ =20%)

下载: 全尺寸图片幻灯片

图 5 三种粒组砂样的颗粒相对破碎率

Figure 5. Relative breakage rates of three sand samples

下载: 全尺寸图片幻灯片

图 6 不同围压下相对破碎率的发展

Figure 6. Development of B_r under various confining pressures

下载: 全尺寸图片幻灯片

表 1 石英砂物理参数

Table 1 Physical parameters of quartz sand

砂样粒径范围d/mm d₅₀/mm e_max e_min e

d1 0.25~0.50 0.375 0.949 0.648 0.708

d2 0.50~1.00 0.75 0.804 0.552 0.602

d3 1.00~2.00 1.5 0.768 0.534 0.581

下载: 导出CSV

参考文献(18)

[1]	ARENSON L U, JOHANSEN M M, SPRINGMAN S M. Effects of volumetric ice content and strain rate on shear strength under triaxial conditions for frozen soil samples[J]. Permafrost and Periglacial Processes, 2004, 15(9): 261–271.
[2]	牛亚强, 赖远明, 王旭, 等. 初始含水率对冻结粉质黏土变形和强度的影响规律研究[J]. 岩土力学, 2016, 37(2): 499–506. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201602026.htm NIU Ya-qiang, LAI Yuan-ming, WANG Xu, et al. Research on influences of initial water content on deformation and strength behaviors of frozen silty clay[J]. Rock and Soil Mechanics, 2016, 37(2): 499–506. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201602026.htm
[3]	杜海民, 马巍, 张淑娟, 等. 围压与含水率对冻结砂土破坏应变能密度影响特性研究[J]. 岩土力学, 2017, 38(7): 1943–1950. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201707013.htm DU Hai-min, MA Wei, ZHANG Shu-juan, et al. Effects of confining pressure and water content on failure strain energy density for frozen silty sands[J]. Rock and Soil Mechanics, 2017, 38(7): 1943–1950. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201707013.htm
[4]	王大雁, 马巍, 常小晓. K₀固结后卸载状态下冻土应力–应变特性研究[J]. 岩石力学与工程学报, 2004, 23(8): 1252–1256. doi: 10.3321/j.issn:1000-6915.2004.08.004 WANG Da-yan, MA Wei, CHANG Xiao-xiao. Study on behavior of stress-strain for frozen soils subjected to K₀ consolidation by unloading triaxial shear tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1252–1256. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.08.004
[5]	吴超, 张淑娟, 周志伟, 等. 围压路径对冻结粉质砂土变形行为及强度的影响研究[J]. 冰川冻土, 2016, 38(6): 1575–1582. https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT201606014.htm WU Chao, ZHANG Shu-juan, ZHOU Zhi-wei, et al. A study of the effect of confining pressure path on strength and deformation of frozen silty sand[J]. Journal of Glaciology and Geocryology, 2016, 38(6): 1575–1582. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT201606014.htm
[6]	赖远明, 程红彬, 高志华, 等. 冻结砂土的应力–应变关系及非线性莫尔强度准则[J]. 岩石力学与工程学报, 2007, 26(8): 1612–1617. doi: 10.3321/j.issn:1000-6915.2007.08.011 LAI Yuan-ming, CHENG Hong-bin, GAO Zhi-hua, et al. Stress-strain relationships and nonlinear Mohr strength criterion of frozen sand clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1612–1617. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.08.011
[7]	QI J, MA W. A new criterion for strength of frozen sand under quick triaxial compression considering effect of confining pressure[J]. Acta Geotechnica, 2007, 2(3): 221–226. doi: 10.1007/s11440-007-0034-z
[8]	张德, 刘恩龙, 刘星炎, 等. 基于修正Mohr-Coulomb屈服准则的冻结砂土损伤本构模型[J]. 岩石力学与工程学报, 2018, 37(4): 978–986. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804020.htm ZHANG De, LIU En-long, LIU Xing-yan, et al. A damage constitutive model for frozen sandy soils based on modified Mohr-Coulomb yield criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 978–986. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804020.htm
[9]	张家铭, 汪稔, 张阳明, 等. 土体颗粒破碎研究进展[J]. 岩土力学, 2003, 24(增刊2): 661–665. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2003S2157.htm ZHANG Jia-ming, Wang Ren, ZHANG Yang-ming, et al. Advance in studies of soil grain crush[J]. Rock and Soil Mechanics, 2003, 24(S2): 661–665. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2003S2157.htm
[10]	蒙进, 屈智炯. 高压下冰碛土的颗粒破碎及应力应变关系[J]. 成都科技大学学报, 1989, 21(1): 17–22, 56. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH198901002.htm MENG Jin, QU Zhi-jiong. Stress-strain behavior of glacial till under high confining pressure[J]. Journal of Chengdu University of Technology, 1989, 21(1): 17–22, 56. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH198901002.htm
[11]	张季如, 胡泳, 张弼文, 等. 石英砂砾破碎过程中粒径分布的分形行为研究[J]. 岩土工程学报, 2015, 37(5): 784–791. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505004.htm ZHANG Ji-ru, HU Yong, ZHANG Bi-wen. Fractal behavior of particle-size distribution during particle crushing of quartz sand and gravel[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 784–791. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201505004.htm
[12]	马巍, 吴紫汪, 常小晓, 等. 围压作用下冻结砂土微结构变化的电镜分析[J]. 冰川冻土, 1995, 17(2): 152–158. https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT502.008.htm MA Wei, WU Zi-wang, CHANG Xiao-xiao, et al. Analysis of microstructural changes in frozen sandy soil under confining pressures by using scaning electronic microscope[J]. Journal of Glaciology and Geocryology, 1995, 17(2): 152–158. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT502.008.htm
[13]	马玲, 齐吉琳, 余帆, 等. 冻结砂土三轴试验中颗粒破碎研究[J]. 岩土工程学报, 2015, 37(3): 544–550. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201503023.htm MA Ling, QI Ji-lin, YU Fan, et al. Particle crushing of frozen sand under triaxial compression[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(3): 544–550. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201503023.htm
[14]	罗飞, 何俊霖, 朱占元, 等. 考虑颗粒破碎的冻结砂土非线性本构模型研究[J]. 地质力学学报, 2018, 24(6): 871–878. https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX201806023.htm LUO Fei, HE Jun-lin, ZHU Zhan-yuan, et al. A study on nonlinear constitutive model of frozen sand considering particle breakage[J]. Chinese Journal of Geomechanics, 2018, 24(6): 871–878. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX201806023.htm
[15]	郝冬雪, 岳冲, 陈榕, 等. 常压至高压下中砂剪切特性及应力–剪胀关系[J]. 岩土工程学报, 2020, 42(4): 765–772. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004027.htm HAO Dong-xue, YUE Chong, CHEN Rong, et al. Shear characteristics and stress-dilation relation of medium sand under normal to high pressures[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(4): 765–772. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004027.htm
[16]	耿爽. 高应力条件下中密砂和密砂颗粒破碎规律试验研究[D]. 吉林: 东北电力大学, 2020. GENG Shuang, Experimental Study on Particles Breakage Rules of Medium and Dense Sand Under High Pressure[D]: Jilin: Northeast Electric Power University, 2020. (in Chinese)
[17]	马巍, 吴紫汪, 张立新, 等. 高围压下冻土强度弱化机理分析[J]. 冰川冻土, 1999, 21(1): 27–31. https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT199901005.htm MA Wei, WU Zi-wang, ZHANG Li-xin, et al. Mechanisms of strength of frozen soils under high confining pressure[J]. Journal of Glaciology and Geocryology, 1999, 21(1): 27–31. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT199901005.htm
[18]	EINAV I. Breakage mechanics–part Ⅰ: theory[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(6): 1274–1297.

施引文献(10)

期刊类型引用(6)

1.	白雪. 煤矿顶管掘进参数实测分析与控制方法研究. 煤矿机械. 2025(02): 65-68 . 百度学术
2.	李博，刘宇翔，陈建国，杨耀红，张哲. 基于物理信息神经网络的长距离顶管施工顶力预测. 人民长江. 2025(01): 147-155 . 百度学术
3.	钟祖良，米朝阳，范一飞，李超，刘新荣. 软岩蠕变作用下顶管顶力计算方法研究. 岩石力学与工程学报. 2025(02): 292-302 . 百度学术
4.	钟祖良，杜传烨，刘新荣，李超. 岩石顶管穿越深大断层破碎带摩阻力计算方法研究. 岩土力学. 2025(03): 943-954 . 百度学术
5.	叶生华，陆俊，明攀，王涛，聂叙平. 复杂岩溶地层大口径DRCP顶管施工试验研究. 人民长江. 2024(08): 166-173 . 百度学术
6.	钱朋亮. 三圆咬合顶管顶推力计算方法研究. 铁道建筑技术. 2024(10): 71-76 . 百度学术