Method and characteristics of band gap of periodic pile row structures based on domain decomposition and nullspace technology
-
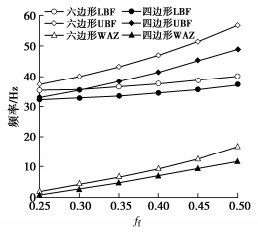
摘要: 针对传统能量法求解周期排桩结构带隙时位移型函数构造复杂、计算成本高、因桩土参数畸变而导致的波形拟合困难等问题,基于区域分解思路对传统能量法进行改进,将桩与土分别在独立坐标系下建模,克服桩土参数畸变问题;再结合零空间技术处理各类边界约束,克服了型函数构造中边界依赖问题,且大幅提高了计算效率。研究结果表明,相较于波数有限元法,该方法不仅同样准确、可靠,还具有效率优势。此外,土体弹性模量与排桩填充率是影响带隙的主要因素;相较于正方形布置的周期排桩,六边形布置时可以获得较高的起始频率、截止频率和带隙宽度。Abstract: Aiming at the problems such as complex structure of displacement function, high calculation cost, and difficulty in waveform fitting caused by the distortion of pile-soil parameters when the traditional energy method is used to solve the band gap of periodic row pile structures, the traditional energy method is improved based on the idea of regional decomposition, and the pile and the soil are modeled separately in independent coordinate systems to overcome the distortion of pile-soil parameters. Then the nullspace technology is used to deal with various boundary constraints, which overcomes the boundary dependency problem in type function construction and greatly improves the computational efficiency. The results show that compared with the wave number finite element method, the proposed method is accurate and reliable, and has efficiency advantages. In addition, the elastic modulus of soil and the filling ratio of row piles are the main factors affecting the band gap. Compared with the square periodic row piles, the hexagonal arrangement can obtain higher starting frequency, cut-off frequency and band gap width.
-
Keywords:
- periodic pile arrangement /
- energy method /
- region decomposition /
- nullspace technology /
- band gap
-
0. 引言
高水平放射性废物(以下简称高放废物)的安全处置,是能源、生态可持续发展不可忽视的重要研究内容,受到了核工业国家的高度重视。目前高放废物地质处置库多采用包含处置罐(贮存高放废物)、缓冲材料以及围岩(即包容地质处置设施的稳定地质体或岩层)的“多重屏障系统”进行设计[1],其中围岩对工程的长期稳定和安全具有关键的控制作用。由于地质构造运动的影响,围岩中不可避免地会存在各种随机分布的天然裂隙。另外处置工程在建设过程中也会导致围岩中产生裂隙或原生裂隙的扩展,形成开挖损伤区,对长久安全地封存放射性废物产生不利影响。因此,含裂隙围岩的力学行为特性研究,是高放废物地质处置工程稳定性和安全性评价的重要课题。
工程岩体中所存在的大量裂隙会很大程度地降低岩体的强度,而地下工程的失稳破坏也与裂隙的扩展、贯通密切相关[2-3]。针对含节理灰岩试样,王在泉等[4]通过加轴压、卸围压的应力控制试验和三轴压缩试验,研究了节理岩体的强度、变形特征和破坏特征。结合声发射监测技术,王强等[5]对含弱面的辉绿岩开展了单轴压缩试验研究,分析了含不同角度弱面试件的变形、强度特性和声发射特征。针对天然裂隙试样取样困难、试验可重复性差等缺点,国内外学者通过采用激光切割、水射流等方法在真实的完整岩石的基础上预制裂隙,制成裂隙岩体,并开展了大量的研究工作[6-9]。罗丹旎等[10]通过真三轴岩爆试验,研究了不同产状预制单裂隙花岗岩的破坏模式、强度变形和声发射特征,得出了裂隙花岗岩的剪切破裂型和张拉板裂型的两种岩爆机制。Wong等[11]通过含三维表面裂隙的大理岩单轴压缩试验,研究了裂隙倾角、深度等参数对裂纹扩展的影响规律。谢其泰等[12]针对预制单裂隙砂岩试样开展了单轴压缩试验研究,分析了裂隙倾角对裂纹扩展机制的影响规律。综合而言,机械切割法或高压水射流法是制备预制裂隙的常用方法,但采用这两种方法制备的非贯通裂隙往往不可避免地存在一定的开度。由于原岩材料的刚度较大、具有较强的抗变形能力,导致外力即使达到了抗压强度,其预制裂隙也可能无法发生闭合。再者,通过切割机或高压水刀制成的裂隙切口较为平整,难以反映裂隙表面粗糙度对岩体力学强度的影响。
本文以中国高放废物地质处置首选候选围岩甘肃北山花岗岩为研究对象,通过对压裂法获得的含不同倾角贯通单裂隙的花岗岩试样开展单轴压缩及三轴压缩试验研究,结合空间三维点云扫描信息,揭示了围压和裂隙倾角对花岗岩力学行为的影响规律,提出了沿裂隙面滑移破坏试样抗压强度与滑移前后裂隙面分形维数差值之间的经验关系式。
1. 试验方法
本文针对完整花岗岩和含不同倾角预制单裂隙的花岗岩试样,开展了单轴压缩试验以及围压为2,5,10 MPa条件下的三轴压缩试验。试验设备为法国TOP公司所生产的岩石高温三轴流变试验系统,该系统额定荷载1500 kN;最大围压和渗透压均为60 MPa;试验最高温度达200℃。试验所用花岗岩取自甘肃北山新场地表,为中细粒花岗闪长岩。根据相关试验规程及试验方法标准,首先将岩样加工成Φ50 mm×H100 mm的标准试样,作为本文中的完整试样。随后,选取部分完整试样放置于自行研制的岩石试样通透裂隙制造模具中,通过压裂的方法制备含倾角30°,45°,60°贯通单裂隙的花岗岩试样若干,如图 1所示。通过对完整岩石压裂的方法制备的贯通裂隙面具有一定的粗糙度,并且裂隙面上下两个部分能够自然耦合接触,即使是大倾角也不会发生滑落。
为降低预制裂隙面初始闭合可能引起较大变形的影响,试验开始前首先采用20 MPa左右的偏应力将试样预压紧。但考虑到倾角60°裂隙试样的单轴抗压强度较低,因此对该预制裂隙面的预压紧是在装样时人工完成的。试验过程中,首先采用5 MPa/min的加载速率将围压加载至预定值并保持不变,随后采用2 MPa/min的速率施加轴向荷载,直至试样残余变形阶段。试样的轴向变形采用2个线性位移传感器进行测量,横向变形采用环向位移引伸计测量。此外,试验前后采用Handy SCAN 3D 700便携式高速激光扫描设备对试样表面及预制裂隙面进行扫描建模,以获得不同试验条件下的裂纹分布特征。
2. 试验结果
2.1 破坏特征
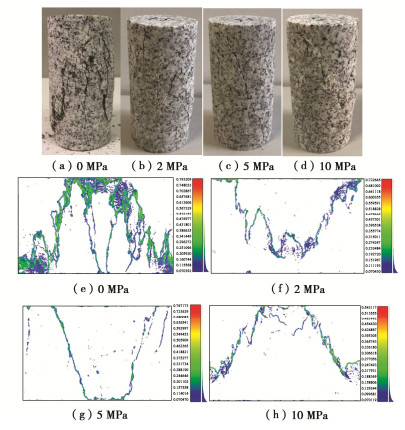
图 2~5为完整花岗岩及不同倾角裂隙花岗岩在单轴和三轴压缩试验后的试样照片,以及通过三维激光扫描获得的试样表面的裂纹分布特征。可以看出,完整花岗岩在单轴压缩条件下主要发生的是脆性的张拉劈裂破坏,试样表面分布诸多的竖向裂纹。2 MPa围压条件下的破坏是劈裂破坏和剪切破坏共存,但仍以劈裂破坏占主导地位,与单轴条件下不同的是,试样表面的裂纹数量显著减少。当围压超过5 MPa时,试样的破坏形式由劈裂破坏过渡到剪切破坏,且剪切破裂面和最大主应力之间的夹角随围压的增大而有所增加。
倾角30°裂隙花岗岩单轴和三轴条件下的破坏形式与完整岩石的破坏形式有诸多相似之处(图 3)。新生裂纹穿过预制裂隙面沿加载方向向试样两端扩展,最终在试样表面形成两条较为显著的主裂纹。在单轴条件下主要为竖向的劈裂破坏;在5 MPa和10 MPa围压条件下为典型的剪切破坏;而在2 MPa的低围压条件下,是以劈裂破坏为主,劈裂破坏和剪切破坏并存的一种破坏方式。不同的是,当微裂纹扩展至预制裂隙面时,预制裂隙面的存在导致试样在受压过程中能量释放面的增大,因此裂隙花岗岩试样表面的次生裂纹数量明显减少。
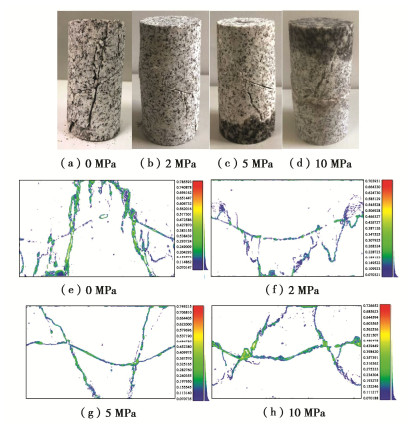
对于倾角45°的裂隙花岗岩(图 4),单轴条件下的新生裂纹少量穿过预制裂隙面,但未贯通至试样上下两个端面。新生主裂纹主要分布于预制裂隙面靠近试样端面的区域,两侧的主裂纹未直接连通,而是由预制裂隙面隔开呈现倾斜的“Z”字型。在围压2 MPa和5 MPa条件下,新生主裂纹穿过预制裂隙面贯通至试样两端,在试样表面形成较为规则的剪切面。而当围压升高至10 MPa条件时,破坏形式发生转变,呈现出与单轴条件下相似的倾斜“Z”字型的剪切-张拉破坏,破坏形式为穿裂隙面破坏和沿裂隙面滑移并存的复合破坏模式。
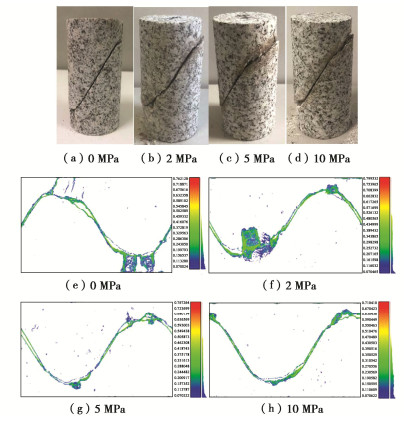
对于倾角60°的裂隙花岗岩(图 5),在单轴和三轴条件下的破坏形式较为统一,均是沿预制裂隙面发生滑移破坏。在单轴及低围压(2 MPa)条件下,仅在预制裂隙面靠近试样端部的区域观测到少许裂纹,这是由于在预制裂隙面摩擦滑移的过程中,预制裂隙长轴端部位置可能形成薄弱的凌空面,从而发生岩片的脱落。而在高围压条件下,升高的围压会对试样薄弱面的张拉剥落产生制约作用,因此破坏后试样表面除预制裂隙外几乎观测不到新生裂纹。
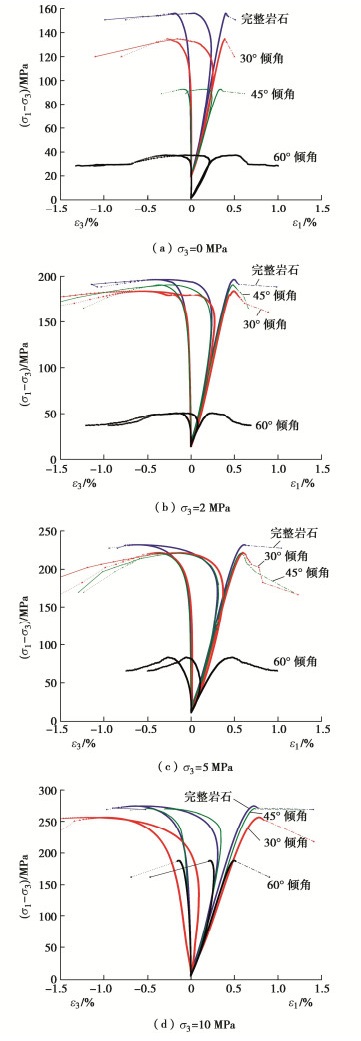
2.2 变形特征
图 6为不同围压条件下完整及裂隙花岗岩变形破坏过程中的应力-应变曲线。单轴条件下,倾角30°裂隙花岗岩发生穿裂隙面破坏,应力-应变曲线的弹性阶段缩小,较早地进入裂纹稳定扩展阶段。当轴向应力约为试件峰值应力的81.67%时,体积应变开始呈现出由压缩向膨胀的过渡,试样进入裂纹不稳定发展阶段。峰后阶段应力迅速回落,表明30°倾角裂隙的存在没有改变试样脆性劈裂破坏的属性,试样的变形主要为岩石材料的压缩变形。倾角60°裂隙花岗岩峰前的变形呈现出明显的屈服阶段,损伤应力非常接近峰值应力,平均约为峰值应力的88.43%。但在由该应力水平发展至峰值应力的时间段内,轴向及环向变形迅速增加,滑移特征明显。峰值后应力水平未出现立即跌落,倾角60°的预制裂隙面使试样在峰值滑移破坏后仍是两个单独承载的块体,这两个块体继续滑移致使轴向、横向变形的迅速增长和轴向荷载的缓慢下降,试样的变形主要为结构面的变形。
对于倾角45°裂隙花岗岩,其破坏形式较为复杂,呈现出穿裂隙面破坏和沿裂隙面滑移并存的复合破坏模式。对应在应力-应变曲线上,倾角45°裂隙花岗岩的变形也介于30°和60°裂隙花岗岩的变形之间,其变形特征更是揉合了之前二者的变形特征,试样的变形是包含了岩石的压缩变形和结构面变形的耦合变形。首先,倾角45°裂隙花岗岩的峰前变形特征更接近于倾角30°裂隙花岗岩的变形,只是塑性变形阶段更为明显。但倾角45°裂隙花岗岩的损伤应力也非常接近峰值应力,平均值约为峰值应力均值的88.67%,这一点与倾角60°裂隙花岗岩的变形特征更为相似,不同的是倾角60°裂隙花岗岩的损伤应力后试件的轴向应变和横向应变在很短的时间发生了较大的变形。其次,倾角45°裂隙花岗岩的峰后的变形特征与倾角60°的更为接近,峰后未出现应力水平的立刻跌落。
在三轴应力条件下,低倾角(30°,45°)裂隙花岗岩最终的破坏特征与完整岩石的破坏模式相似,其变形发展曲线与完整花岗岩的变形发展特征也相近,说明围压的存在限制了预制裂隙面的劣化影响,试样变形的主控因素为岩石材料的压缩变形。随着围压的增加,完整及低倾角裂隙花岗岩的变形逐渐从脆性向塑性转化。对于倾角60°裂隙花岗岩,三轴压缩条件下试样变形的主控因素为结构面的变形,峰值附近的非线性变形阶段随围压的升高显著减弱。与单轴条件下相比,2 MPa和5 MPa围压条件下损伤应力占峰值应力的比值显著降低,分别为73.91%和63.54%,当围压升高至10 MPa时,该比值又上升为83.32%。
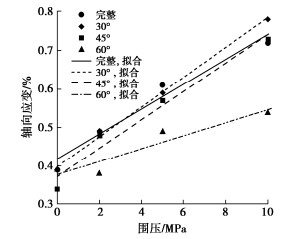
基于试样的应力-应变曲线,获得不同围压条件下试样的峰值应力对应的轴向应变,如图 7所示。
结果表明,裂隙花岗岩峰值破坏时的轴向应变随围压的升高呈现出线性增加的趋势。低倾角裂隙花岗岩峰值破坏时的轴向应变与完整岩石的相差不大,在围压0,2,5,10 MPa条件下该值约为0.38%,0.49%,0.59%和0.75%。但当裂隙倾角增大至60°时,该值在前述围压条件下分别为0.39%,0.38%,0.49%,0.54%,三轴条件下峰值破坏时的轴向应变与完整及低倾角裂隙花岗岩相比存在一个明显的下降,且围压越高,下降越显著。
2.3 强度特征
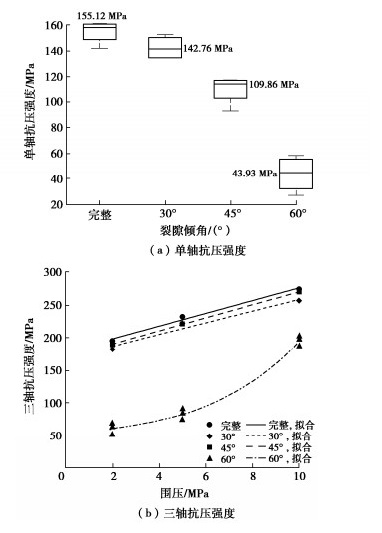
不同围压条件下裂隙花岗岩的抗压强度如图 8所示。单轴压缩条件下(图 8(a)),完整花岗岩及不同倾角的裂隙花岗岩各开展了4组试样的测试。测试所得完整花岗岩的平均单轴抗压强度为155.12 MPa,倾角30°,45°,60°裂隙花岗岩的平均单轴抗压强度分别为142.76,109.86,43.93 MPa,裂隙倾角越大,抗压强度越低。结果还发现,对于完整花岗岩和低倾角(30°和45°)裂隙花岗岩,不同试样的抗压强度的差异性并不显著。但对于倾角60°的裂隙花岗岩,不同试样的抗压强度的差异性较大。鉴于此,在三轴压缩时,完整花岗岩和低倾角裂隙花岗岩在各个围压条件下仅开展了1组测试,但倾角60°裂隙花岗岩分别开展了3组测试。
结果表明(图 8(b)),完整花岗岩及低倾角裂隙花岗岩的三轴抗压强度随围压升高呈现出线性增长的趋势,且围压的存在限制了裂隙对岩石强度的劣化作用,导致三轴压缩条件下低倾角裂隙花岗岩的抗压强度略低于完整岩石的抗压强度但整体相差不大,试样三轴抗压强度的平均值在2,5,10 MPa围压条件下分别为189.84,225.20,267.28 MPa。此时试样的破坏模式与完整岩石的三轴破坏模式相似,新生裂纹大多是穿过裂隙面贯通至试样的上下两个端面。当裂隙倾角增大至60°时,在前述围压条件下的三轴抗压强度分别为60.54,82.94,195.78 MPa。试样的抗压强度随围压升高呈现出非线性增长的趋势,且各围压条件下的抗压强度均显著低于完整花岗岩及低倾角裂隙花岗岩的抗压强度,相对应地试样发生的是沿裂隙面滑移的破坏模式。此外,由于围压的限制作用,不同试样抗压强度的差异性有所降低。
3. 裂隙面分形维数
图 9~11为裂隙花岗岩单轴及单轴压缩试验后预制裂隙面的状态。除试样表面呈现出分布特征不同的裂隙以外,试样内部的预制裂隙面也呈现出显著的变化。为分析预制裂隙面粗糙度的变化特征,在试验前后分别采用三维激光扫描仪对预制裂隙面进行了扫描,获得了预制裂隙面的三维点云数据。
由于低倾角裂隙花岗岩试样表面的新生裂纹或穿过预制裂隙面贯通至试样上下两个端面,或由预制裂隙面隔开形成倾斜的“Z”字型,对应的预制裂隙面上的裂纹为张拉型或剪切型。因此预制裂隙面在单轴压缩条件下通常较为破碎,而在三轴条件下裂隙面又较宽,在拆样的过程中不可避免地会造成预制裂隙面上细碎岩块的脱落,从而对三维激光扫描结果造成误差,直接影响了试验后分形维数计算的准确性,因此本研究中未给出倾角30°和45°裂隙面的分形维数。而对于倾角60°的裂隙花岗岩,其破坏模式为沿裂隙面滑移破坏,试验后预制裂隙面较完整,有利于定量衡量试验前后粗糙度的变化。另外,在上一节的分析中提到,不同倾角60°裂隙花岗岩试样的抗压强度的差异性较大,因此本节基于三维激光扫描结果,重点对倾角60°预制裂隙面粗糙度的变化进行分析。
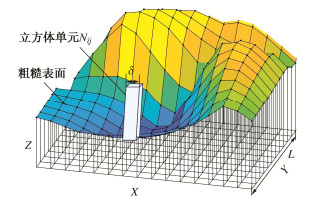
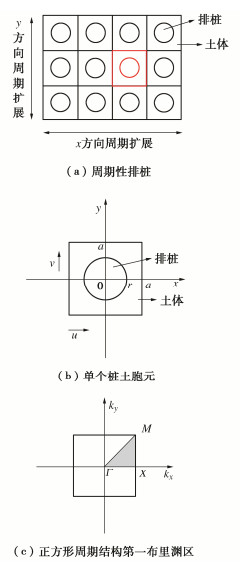
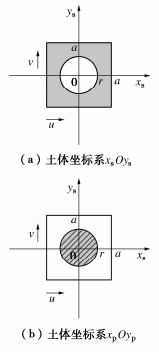
关于裂隙面几何特征的表征方法,较为经典的是Barton提出的经典剖面法,包括用于确定结构面粗糙度系数JRC的10条标准剖面[13]。但由于采用该方法来比照衡量被测表面的几何形貌时,可能会因为较强的主观性而导致判断结果产生比较大的偏差。于是,相关领域的学者在此基础上提出了不同的JRC描述方法[14-16]。在定量化描述裂隙岩体结构面几何特征方面,20世纪70年代创立的分形几何,又为裂隙面的衡量提供了一个启示性的理论方法和手段[17]。根据以往的研究结果,分形维数可以作为描述岩体中裂隙面几何形貌特征复杂程度的定量指标[18-21]。与经典几何相比,分形维数具有无标度的特点,其描述的裂隙面的几何特征不受测量尺度和精度的限制。基于上述分析,本研究采用Zhou等[22]提出的立方体覆盖法计算试验前后预制裂隙面的分形维数,探讨裂隙面抗压强度与其破坏特征之间的关系。如图 12所示,通过改变单元格边长δ的大小,得到不同覆盖立方体的个数N(δ)。如果裂隙面的粗糙度表现出分形特征,则边长δ与个数N(δ)之间存在如下关系:
N(δ)∼δ−Df。 (1) 式中:Df为表征裂隙面粗糙度的分形维数。
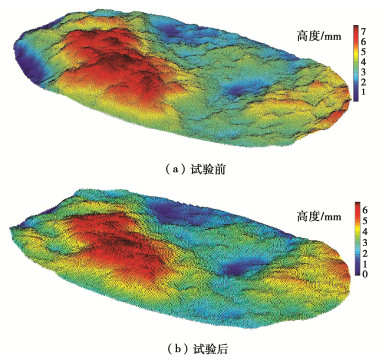
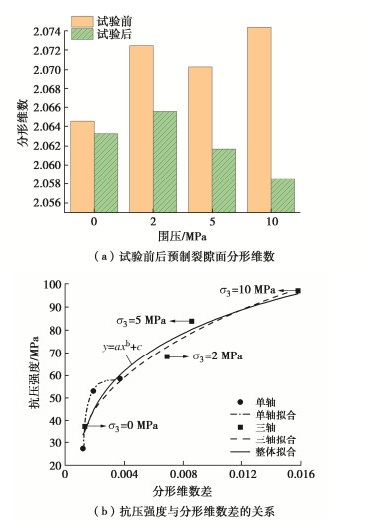
单轴压缩或三轴压缩试验后,倾角60°预制裂隙面上均可观测到大片的摩擦滑移区,对应于三维点云图中(图 13),可明显地看出试验后预制裂隙面变得更加平缓。采用图 12的立方体覆盖法计算试验前后预制裂隙面的分形维数,结果如图 14所示。研究表明,不同围压条件下,预制裂隙面发生摩擦滑移破坏后其分形维数与试验前相比均有所下降;且围压越高,试验前后预制裂隙面的分形维数差值越大,说明摩擦滑移破坏后预制裂隙面粗糙度的变化越显著。图 14(b)为单轴及三轴压缩条件下试样抗压强度与试验前后裂隙面分形维数差的关系。研究发现,试样的抗压强度与试验前后的分形维数差值符合幂函数y=axb+c的增长关系,式中变量y和x分别代表抗压强度和试验前后裂隙面的分形维数差值,参数a,b,c为拟合参数。分形维数相差越大,试样的抗压强度越高,这也从侧面解释了相同试验条件下不同倾角60°裂隙花岗岩试样抗压强度存在差异性的原因。
4. 结论
本文通过完整花岗岩和含不同倾角预制裂隙的花岗岩试样的单轴压缩和三轴压缩试验研究,揭示了围压及裂隙倾角对花岗岩力学行为的影响机制,得到以下3点结论。
(1)花岗岩的破坏形式受围压与裂隙倾角双重因素的共同影响。完整花岗岩的破坏形式随围压的升高由劈裂破坏向剪切破坏过渡,且围压越高剪切破裂面和最大主应力之间的夹角越大。倾角30°裂隙花岗岩的新生裂纹穿过预制裂隙面向试样两端扩展形成穿裂隙面的破坏模式,与完整花岗岩的破坏形式相近但裂隙数量明显减少。倾角60°裂隙花岗岩在0~10 MPa围压条件下均发生沿预制裂隙面的摩擦滑移破坏,试样表面除预制裂隙外几乎观测不到新生裂纹。倾角45°裂隙花岗岩在2 MPa和5 MPa围压条件下,新生主裂纹穿过预制裂隙面贯通至试样两端,在试样表面形成较为规则的剪切面;但在单轴及10 MPa围压条件下,新生主裂纹沿预制裂隙面呈现出倾斜“Z”字型,破坏形式为穿裂隙面破坏和沿裂隙面滑移并存的复合破坏模式。
(2)单轴压缩条件下,裂隙倾角越大,试样峰值破坏前的非线性屈服特征越明显。围压的存在限制了预制裂隙面的劣化作用。在三轴应力条件下,低倾角裂隙花岗岩的变形发展曲线与完整花岗岩的变形发展特征相近,试样峰值破坏时的轴向应变在围压0,2,5,10 MPa条件下分别约为0.38%,0.49%,0.59%,0.75%。对于倾角60°裂隙花岗岩,随围压的升高,峰值附近的非线性变形阶段显著减弱,且峰值破坏时对应的轴向应变与完整及低倾角裂隙花岗岩相比存在一个明显的下降,且围压越高,下降越显著。
(3)倾角越大,裂隙花岗岩的单轴抗压强度越低。三轴压缩条件下低倾角裂隙花岗岩的抗压强度略低于完整岩石的抗压强度,但整体相差不大。倾角60°裂隙花岗岩的抗压强度随围压升高呈现出非线性增长的趋势,且各围压条件下的抗压强度均显著低于完整及低倾角裂隙花岗岩的抗压强度。倾角60°预制裂隙面发生摩擦滑移破坏后分形维数有所下降;且围压越高,试验前后预制裂隙面的分形维数差值越大。试样的抗压强度与试验前后的分形维数差值符合幂函数增长关系,分形维数相差越大,试样的抗压强度越高。
-
表 1 桩土材料参数
Table 1 Parameters of pile-soil materials
材料 ρ/(kg·m-3) E/Pa μ 土 1900 2×107 0.35 混凝土 2500 3×1010 0.20 表 2 计算时长结果对比
Table 2 Comparison of calculation time results
序号 单元结构类型 ρ/(kg·m-3) E/Pa 填充率p 扫描波数 时长/s 土 混凝土 土/107 混凝土/1010 有限元 区域分解 1 正方形 1900 2500 2.0 3 0.35 30 38 10.6 2 六边形 1900 2500 2.0 3 0.35 30 43 12.1 3 正方形 2000 2600 2.5 4 0.40 60 72 20.5 4 六边形 2000 2600 2.5 4 0.40 60 76 22.7 5 正方形 2100 2700 3.0 5 0.45 100 131 31.5 6 六边形 2100 2700 3.0 5 0.45 100 167 41.9 -
[1] RICHART F E, HALL J R, WOODS R D. Vibrations of Soils and Foundations[M]. Englewood Cliffs, NJ: Prentice-Hall, 1970.
[2] KATTIS S E, POLYZOS D, BESKOS D E. Structural vibration isolation by rows of piles[C]// Seventh International Conference on Soil Dynamics and Earthquake Engineering (SDEE 95), Crete, Greece, 1995: 509-516.
[3] 孟庆娟, 石志飞. 基于周期理论和COMSOL PDE的排桩减振特性研究[J]. 岩土力学, 2018, 39(11): 4251-4260. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201811042.htm MENG Qingjuan, SHI Zhifei. Ambient vibration attenuation by periodic pile barriers using periodic theory and COMSOL PDE method[J]. Rock and Soil Mechanics, 2018, 39(11): 4251-4260. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201811042.htm
[4] 巴振宁, 刘世朋, 吴孟桃, 等. 周期分布群桩屏障对平面弹性波隔振效应的解析求解[J]. 岩石力学与工程学报, 2020, 39(7): 1468-1482. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202007015.htm BA Zhenning, LIU Shipeng, WU Mengtao, et al. Analytical solution for isolation effect of periodically distributed pile-group barriers against plane elastic wave[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(7): 1468-1482. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202007015.htm
[5] ZHENG G, WANG F J, DU Y M, et al. The efficiency of the ability of isolation piles to control the deformation of tunnels adjacent to excavations[J]. International Journal of Civil Engineering, 2018, 16(10): 1475-1490. doi: 10.1007/s40999-018-0335-7
[6] CHEN M, JIN G, ZHANG Y, et al. Three-dimensional vibration analysis of beams with axial functionally graded materials and variable thickness[J]. Composite Structures, 2019, 207: 304-322. doi: 10.1016/j.compstruct.2018.09.029
[7] 华洪良, 廖振强, 张相炎. 轴向移动悬臂梁高效动力学建模及频率响应分析[J]. 力学学报, 2017, 49(6): 1390-1398. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201706020.htm HUA Hongliang, LIAO Zhenqiang, ZHANG Xiangyan. An efficient dynamic modeling method of an axially moving cantilever beam and frequency response analysis[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(6): 1390-1398. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201706020.htm
[8] QU Y, WU S, CHEN Y, et al. Vibration analysis of ring-stiffened conical–cylindrical–spherical shells based on a modified variational approach[J]. International Journal of Mechanical Sciences, 2013, 69: 72-84. doi: 10.1016/j.ijmecsci.2013.01.026
[9] 唐豪, 陈晓斌, 唐孟雄, 等. 基于复频散曲线特征的周期结构高铁路基减振研究[J]. 岩土工程学报, 2021, 43(12): 2169-2179. doi: 10.11779/CJGE202112003 TANG Hao, CHEN Xiaobin, TANG Mengxiong, et al. Vibration reduction of high-speed railway subgrade with periodic structures based on complex dispersion curves[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(12): 2169-2179. (in Chinese) doi: 10.11779/CJGE202112003
[10] WANG T, SHENG M P, QIN Q H. Multi-flexural band gaps in an Euler–Bernoulli beam with lateral local resonators[J]. Physics Letters A, 2016, 380(4): 525-529. doi: 10.1016/j.physleta.2015.12.010
[11] 张文学, 寇文琦, 陈盈, 等. 基于能量法的斜拉桥纵向1阶自振周期简化计算[J]. 中国公路学报, 2017, 30(7): 50-57. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201707007.htm ZHANG Wenxue, KOU Wenqi, CHEN Ying, et al. Simplified calculation of first-order longitudinal natural vibration period of cable-stayed bridges based on energy method[J]. China Journal of Highway and Transport, 2017, 30(7): 50-57. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201707007.htm
[12] WANG T, QIN Q H, ZHU X. Reaction force and power flow analysis of an acoustic metamaterial beam with multi-band gaps[J]. Acoustics Australia, 2019, 48(1): 59-67.
[13] 宋婷婷, 郑玲, 邓杰. 基于高斯展开法的周期声学黑洞宽频能量回收特性研究[J]. 振动与冲击, 2022, 41(10): 186-195. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202210024.htm SONG Tingting, ZHENG Ling, DENG Jie. Gaussian expansion method used in a nalysing the broadband energy harvesting characteristics of periodic acoustic black holes[J]. Journal of Vibration and Shock, 2022, 41(10): 186-195. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202210024.htm
[14] 冯青松, 杨舟, 郭文杰, 等. 基于人工弹簧模型的周期结构带隙计算方法研究[J]. 力学学报, 2021, 53(6): 1684-1697. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202106015.htm FENG Qingsong, YANG Zhou, GUO Wenjie, et al. Research on band gap calculation method of periodic structure based on artificial spring model[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1684-1697. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202106015.htm
[15] GUO Wenjie, YANG Zhou, FENG Qingsong, et al. A new method for band gap analysis of periodic structures using virtual spring model and energy functional variational principle[J]. Mechanical Systems and Signal Processing, 2022, 168: 108634. doi: 10.1016/j.ymssp.2021.108634
[16] TANG L, CHENG L. Broadband locally resonant band gaps in periodic beam structures with embedded acoustic black holes[J]. Journal of Applied Physics, 2017, 121: 194901. doi: 10.1063/1.4983459
[17] 孟庆娟, 乔京生. 饱和土中周期性排桩隔离体波的性能研究[J]. 振动与冲击, 2020, 39(24): 179-186. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202024026.htm MENG Qingjuan, QIAO Jingsheng. Vibration isolation of body waves by periodic pile barriers in saturated soil[J]. Journal of Vibration and Shock, 2020, 39(24): 179-186. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202024026.htm
[18] DENG J, XU Y X, ORIOL G, et al. Nullspace technique for imposing constraints in the Rayleigh-Ritz method[J]. Journal of Sound and Vibration, 2022, 527: 116812. doi: 10.1016/j.jsv.2022.116812
[19] HUANG J K, SHI Z F. Application of periodic theory to rows of piles for horizontal vibration attenuation[J]. International Journal of Geomechanics, 2013, 13(2): 132-142. doi: 10.1061/(ASCE)GM.1943-5622.0000193
-
期刊类型引用(2)
1. 黄勇钧,李世文,刘先林,邵羽,翁剑,任中俊,吕玺琳. 裂隙花岗岩力学特性试验及破坏条件理论模型. 力学季刊. 2025(01): 162-172 .  百度学术
百度学术
2. 戎虎仁,曹海云,董浩,王占盛,张佳瑶. 双孔洞倾角对红砂岩强度及其破裂分形特征影响. 公路交通科技. 2024(10): 173-183 .  百度学术
百度学术
其他类型引用(1)
-
其他相关附件




 下载:
下载: