Dynamic settlement characteristics of piles based on stick-slip mechanism between piles and soils
-
摘要: 基于桩基运动控制方程,对荷载作用下的桩基沉降动态特性进行了研究。首先,考虑桩土间黏滞与滑动两种接触状态,建立了一种考虑侧阻软化及侧阻恢复的桩土相互作用模型;然后采用该模型及修正三折线模型分别模拟桩与桩侧土以及桩端土间的相互作用,结合有限差分法建立了考虑桩土间黏滑机制的桩基沉降分析方法;最后,基于建立的桩基受荷沉降分析方法,研究了桩基沉降的黏滑动态特性以及桩身的力学特性,并讨论了桩土相互作用模型中的参数对桩基沉降动态特性的影响。结果表明:当桩顶荷载接近桩基单级加载极限值,桩基沉降表现出黏滞位移与快速滑动位移交替的动态特性;桩身力学响应表现出加载路径相关性,与单级加载相比,分级加载时桩侧摩阻力能得到更好发挥,桩基极限承载力更高;提出的分析方法能够较好地模拟桩基静载试验沉降过程。Abstract: The dynamic characteristics of the pile settlement under loads are studied based on the motion control equation for piles. Firstly, a pile-soil interaction model, considering the softening and recovery of resistance, is established by considering two contact states between piles and soils: sticking and slipping. Then, the established model and a modified tri-linear model are used to simulate the pile-side soil interaction and pile-tip soil interaction, respectively. A method for settlement of pile foundation considering the stick-slip mechanism between piles and soils is established in combination with the finite difference method. Finally, the stick-slip dynamic characteristics of the pile settlement and the mechanical characteristics of the pile are investigated based on the analysis method. The effects of the parameters of pile-soil interaction model on the dynamic characteristics of pile settlement are also analyzed. The results show that the dynamic characteristics of pile foundation with alternating sticking movement and rapid slipping movement are observed when the loads are close to the ultimate value of single-stage loading. The mechanical responses of piles are related to the loading path. Compared with those under single-stage loading, the shaft resistance of the pile can be better mobilized and the ultimate bearing capacity of the pile is higher under gradation loading. The proposed method can be used to simulate the settlement process of static loading tests on the piles.
-
0. 引言
准确计算桩基的承载力与控制桩基变形是确保桩基正常服役的关键,对控制上部结构变形及防止结构开裂,使桩基处于正常使用极限状态内具有重要的意义。桩基沉降计算作为桩基沉降分析领域里的主要研究内容,在桩土相互作用关系、桩侧摩阻力时效性、桩周土体蠕变固结等方面进行了大量的研究。
桩基在承受上部荷载时,因承载力自上到下的逐步发挥以及桩周土体的流变与固结等效应,沉降是在一定时间内逐渐产生的,因而具有时效性[1-2]。常用的桩基沉降计算方法如荷载传递法[3]、剪切位移法[4],一般把桩基沉降计算当作静力学的问题考虑,直接得到最终沉降量,忽略了沉降的时间效应。已有的考虑桩基沉降时效性的研究一般包括两个方面:①考虑不同土体流变模型进行的准静力平衡分析[5-6];②考虑桩身位移与速度动态特性的桩基沉降研究[1, 7]。然而,目前对桩周土体阻力发挥过程中桩基位移动态特性的研究仍然很少,实际上,考虑到桩基沉降的时效性,研究桩基沉降发展过程中桩身位移的发展特性以及桩土间接触状态的变化规律,对进一步了解桩基沉降的位移动态特性与侧阻发挥机制具有重要的意义。
考虑桩身的位移与速度特性以及桩土之间的接触状态,对桩基进行时域分析通常在沉桩与桩基动力响应的研究领域内进行。在沉桩方面,Smith等[8]提出了考虑理想弹塑性土体静阻力的一维波动方程数值解法求解锤击打桩过程;Holeyman等[9]提出了振动沉桩过程中与桩身加速度相关的桩侧摩阻力弱化模型。桩基动力响应方面,Nogami等[10]使用串联Voigt体研究了桩顶冲击荷载作用下的桩基时域响应;吴鹏等[11]研究了在竖向地震激励下,桩土间可能存在相对滑移时的桩基动力响应特性。与桩基动力响应同为动态过程,桩基受荷沉降发展过程中,桩土间接触状态发生变化,桩侧摩阻力弱化,以及桩基振动响应导致桩土间反向剪切等情况,还未得到充分的考虑,应该在桩基沉降分析的过程中加以重视。
综上所述,动态考虑桩基受荷沉降过程,对桩身位移发展特性,桩土间接触状态变化等的研究还有待深入。本文从桩基运动控制方程出发,对桩基受荷沉降的动态特性进行了研究。完善了桩基受荷沉降中对桩身位移的考虑,在考虑黏滞与相对滑动两种桩土接触状态的基础上,结合考虑桩侧摩阻力的时效性,提出一种能考虑侧阻软化以及侧阻恢复的桩土相互作用模型;然后,结合桩基运动控制方程和建立的桩土相互作用模型,分析了理想均质土层中单桩的黏滑沉降特性和力学响应特性;最后基于两个桩基静载试验实例,验证了所提计算方法的有效性。
1. 桩基受荷沉降动态特性计算模型
1.1 桩基受荷沉降的黏滑动态模型
考虑桩基自重的条件下,分析桩身单元体的受力平衡条件,得到桩基沉降的运动控制方程如下:
∂2u(x,t)∂x2=1v2⋅∂2u(x,t)∂t2−gv2+2Er0⋅R。 (1) 式中:u为桩体的位移;x为桩身的纵坐标;t为时间;v=√E/ρ为桩身波速, 其中E为桩身弹性模量,ρ为桩身材料密度;g为重力加速度;r0为桩基半径;R为桩侧土体对桩身的阻力,考虑桩土间的黏性阻尼,R=τ+cs⋅∂u(x,t)/∂t,其中τ为桩侧摩阻力,cs为阻尼系数。
建立如图 1所示的桩基受荷沉降黏滑动态模型,桩基离散成由一系列弹簧和质量块组成的系统,用一个由塑性摩擦键和弹簧串联后再和阻尼器并联的组件来模拟桩身与桩侧土体之间的相互作用,用一个弹簧来模拟桩端与桩端土体之间的相互作用。
1.2 桩土相互作用模型
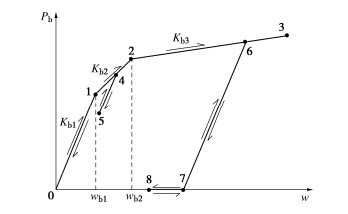
本文在三折线模型的基础上,考虑桩端与桩端土体之间的加/卸载,建立了如图 2所示的桩端土体阻力Pb与桩端位移w间的关系。
桩端与桩端土体之间的加载阶段可以分为不同的桩端土体压缩阶段(图 2中的0—1初始弹性压缩段以及1—2和2—3压缩段)以及桩端土体处于弹性的卸载后再压缩阶段(图 2中的5—4段和7—6段),加载阶段中的桩端土体阻力与桩端位移之间的关系表示为
Pb=Kb1⋅w(0<w⩽ (2) 式中: {K_{{\text{b1}}}} , {K_{{\text{b2}}}} , {K_{{\text{b3}}}} 为不同加载阶段的桩端土刚度; {w_{{\text{b1}}}} , {w_{{\text{b2}}}} 为不同阶段间的界限位移; {P_{{\text{breload}}}} 为再压缩阶段开始时的桩端阻力; {w_{{\text{reload}}}} 为再压缩阶段开始时的桩端位移。
桩端与桩端土体之间的卸载阶段可以分为桩端土弹性卸载阶段(图 2中的1—0段和4—5段)以及桩端土脱离阶段(图 2中的7—8和8—7段),处于卸载阶段的桩端土体阻力与桩端位移之间的关系表示为
\left.\begin{array}{ll} P_{\mathrm{b}}=P_{\mathrm{bunload}}+K_{\mathrm{b} 1} \cdot\left(w-w_{\mathrm{unload}}\right) & (\text { 弹性卸载段 }), \\ P_{\mathrm{b}}=0 & \text { (脱离段)。 } \end{array}\;\;\;\right\} (3) 式中: {P_{{\text{bunload}}}} 为弹性卸载阶段开始时的桩端阻力; {w_{{\text{unload}}}} 为弹性卸载阶段开始时的桩端位移。
桩身与桩侧土体之间摩阻力的值用桩土黏滞接触和相对滑动接触下不同的关系进行定义,考虑到同一深度处的桩侧摩阻力随着桩入土深度的增加在增加到某一值后有减小的趋势[12],以及桩基承载力随时间存在增长趋势[13],假定桩侧摩阻力与桩身点位移之间的关系如图 3所示。图 3中, {\tau _{\text{p}}} = c + {K_{\text{l}}} \cdot {\sigma _{\text{v}}} \cdot \tan \varphi 为峰值桩侧摩阻力, {\tau _{\text{r}}} = \xi \cdot {\tau _{\text{p}}} 为残余桩侧摩阻力,其中, c 为桩土界面黏聚力, {K_{\text{l}}} 为侧向土压力系数, {\sigma _{\text{v}}} 为原位土体竖向有效应力, \varphi 为极限摩擦角, \xi 为侧阻衰减系数。图 3中其余的变量以及符号在下文进行说明。
考虑桩土间的两种黏滞接触状态,分别为初始黏滞接触状态(图 3中的0—1段,点1对应的位移 u_{\max }^e 为桩土处于极限初始黏滞接触状态时的桩身极限初始黏滞位移),以及经过相对滑动接触状态后重新进入的桩身位移回弹/再沉降黏滞接触状态(如图 3中的2—3—4段),假定桩土间的黏滞摩阻力 {\tau _{{\text{stick}}}} 与黏滞接触状态下的桩身点位移之间满足线性的关系:
{\tau }_{\text{stick}}={\tau }_{\text{ss1}}+{K}_{\text{stick}}\cdot (u-{u}_{\text{ss1}})\text{,}{\tau }_{\text{stick}}\le {\tau }_{\text{stickmax}} 。 (4) 式中: {\tau _{{\text{ss1}}}} 为黏滞接触阶段开始时的桩侧摩阻力, {u_{{\text{ss1}}}} 为黏滞接触阶段开始时的桩身位移。考虑初始黏滞段桩侧土刚度 {K_{{\text{s1}}}} 和桩身位移回弹/再沉降黏滞段桩侧土刚度 {K_{{\text{s2}}}} , {K_{{\text{s1}}}} 参考Randolph等[4]的取值,黏滞接触段桩侧土刚度 {K_{{\text{stick}}}} 可以表示为
K_{\text {stick }}=\left\{\begin{array}{ll} K_{\mathrm{s} 1}=\frac{G}{r_0} \cdot \frac{1}{\ln \frac{r_{\mathrm{m}}}{r_0}} & (\text{初始黏滞段}) \\ K_{\mathrm{s} 2}=r \cdot K_{\mathrm{s} 1} & (\text {回弹/再沉降黏滞段}) \end{array} \;\;\;\;\;\;\;\;\;\;。\right. (5) 式中:G为桩侧土的剪切模量; {r_{\text{m}}} 为影响半径, {r_{\text{m}}} = 2.5L{\text{(}}1 - {\nu _{\text{s}}}{\text{)}}{\rho _{\text{g}}} , {\rho _{\text{g}}} 为桩L/2深度处土与桩底处土剪切模量的比值, {\nu _{\text{s}}} 为土的泊松比; r 为 {K_{{\text{s1}}}} 与 {K_{{\text{s2}}}} 的比值,考虑相同的 {K_{{\text{s1}}}} 与 {K_{{\text{s2}}}} 值, r 的值取1。
考虑桩土间处于黏滞接触状态时,桩土间极限黏滞摩阻力 {\tau _{{\text{stickmax}}}} 会随黏滞接触时间的增加指数恢复,如图 4所示,极限黏滞摩阻力与黏滞接触时间之间的关系表示为
{\tau _{{\text{stickmax}}}} = {\tau _{\text{p}}} - {\text{(}}{\tau _{\text{p}}} - {\tau _{\text{r}}}{\text{)}} \cdot {{\text{e}}^{\left( {\frac{1}{{T_0^a}}\ln \frac{{0.1{\tau _{\text{p}}} - 0.1{\tau _{\text{r}}}}}{{{\tau _{\text{p}}} - {\tau _{\text{r}}}}}} \right) \cdot {{\left( {{T_{\text{z}}} + \Delta {T_{\text{T}}}} \right)}^a}}} 。 (6) 式中: {T_0} 和 a 为侧阻力随时间恢复曲线的形状参数, {T_0} 为从残余桩侧摩阻力 {\tau _{\text{r}}} 恢复90%损失强度( 0.9{\text{(}}{\tau _{\text{p}}} - {\tau _{\text{r}}}{\text{)}} )至( 0.9{\tau _{\text{p}}} + 0.1{\tau _{\text{r}}} )所需的时间,假定砂土的情况下,从残余桩侧摩阻力 {\tau _{\text{r}}} 恢复90%损失强度需15 d,此时 {T_0} = 1296000{\text{ s}} ; a 为表征侧阻力恢复快慢的整体形状参数, a 取1; \Delta {T_{\text{T}}} 为本次黏滞的时间,定义对应于黏滞开始时的极限黏滞摩阻力 {\tau _{{\text{ssmax}}}} 的等效黏滞时间参数 {T_z} 为
{T_z} = {T_0}{\left( {\frac{{\ln \frac{{{\tau _{\text{p}}} - {\tau _{{\text{ssmax}}}}}}{{{\tau _{\text{p}}} - {\tau _{\text{r}}}}}}}{{\ln \frac{{0.1{\tau _{\text{p}}} - 0.1{\tau _{\text{r}}}}}{{{\tau _{\text{p}}} - {\tau _{\text{r}}}}}}}} \right)^{\frac{1}{a}}} \;\;。 (7) 当桩土间处于相对滑动接触状态时(如图 3中的1—2段和5—6段),假定桩土间的滑动摩阻力 {\tau _{{\text{slip}}}} 随着相对滑动接触状态下桩身点位移的发展指数衰减,两者间的关系为
{\tau _{{\text{slip}}}} = {\tau _{\text{r}}} + ({\tau _{\text{p}}} - {\tau _{\text{r}}}) \cdot {{\text{e}}^{ - A{{\left( {{u_{{\text{ss2}}}} + \Delta u - u_{\max }^{\text{e}}} \right)}^B}}} \;\;。 (8) 式中:A和B为侧阻力衰减弱化曲线的形状参数,表征摩阻力衰减的快慢程度,密砂情况下,达到残余侧摩阻力的剪切位移一般在10 mm左右,拟合得到的A和B值对于密砂一般分别可以取为200和0.8~0.9; \Delta u 为相对滑动接触阶段中桩身点的位移增量,定义对应于相对滑动接触状态开始时的侧摩阻力 {\tau _{{\text{ss2}}}} 的等效滑动位移 {u_{{\text{ss2}}}} 为
{u_{{\text{ss2}}}} = u_{{\text{max}}}^{\text{e}} + {\left( {\frac{1}{A}\ln \frac{{{\tau _{\text{p}}} - {\tau _r}}}{{{\tau _{{\text{ss2}}}} - {\tau _r}}}} \right)^{\frac{1}{B}}} \;\;。 (9) 当 {\tau _{{\text{ss2}}}} = {\tau _{\text{p}}} 时,式(8)即表示由初始黏滞接触状态转变为相对滑动接触状态的情况。
1.3 桩基沉降运动控制方程的差分求解
采用有限差分法求解桩基沉降的运动控制微分方程,式(1)中的位移对深度采用Crank-Nicolson差分,位移对时间采用中心差分,得到桩基沉降运动控制微分方程的离散格式:
\begin{array}{l} \frac{1}{2 \Delta x^2} u_{m-1}^{n+1}-\left(\frac{1}{\Delta x^2}+\frac{1}{v^2 \Delta T^2}+\frac{c_{\mathrm{s}}}{E r_0 \Delta T}\right) u_m^{n+1}+\frac{1}{2 \Delta x^2} u_{m+1}^{n+1} \\ =-\frac{1}{2 \Delta x^2} u_{m-1}^{n-1}+\left(\frac{1}{\Delta x^2}+\frac{1}{v^2 \Delta T^2}-\frac{c_{\mathrm{s}}}{E r_0 \Delta T}\right) u_m^{n-1}-\frac{1}{2 \Delta x^2} u_{m+1}^{n-1}- \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{2}{v^2 \Delta T^2} u_m^n-\frac{g}{v^2}+\frac{2}{E r_0} \cdot \tau_m^n\;\;。 \end{array} (10) 式中, u_m^n 表示 (n - 1)\Delta T 时刻 (m - 1)\Delta x 位置网格处的桩身点位移值。结合桩基的初始条件与边界条件,即可求得任意时刻时的桩体位移。
2. 桩顶荷载作用下桩基沉降特性分析
利用一个埋设在理想匀质砂土地基场地中的模型单桩受荷沉降案例对本文建立的桩基沉降计算黏滑动态模型的性能进行检验。模型桩桩长 L = 20{\text{ m}} ,半径 {r_0} = 0.3{\text{ m}} ,桩体弹性模量 E = 3 \times {10^{10}}{\text{ Pa}} ,桩身密度 \rho = 2500{\text{ kg/}}{{\text{m}}^{\text{3}}} 。理想匀质地基土层的重度为 \gamma ' = 17.5{\text{ kN/}}{{\text{m}}^{\text{3}}} ,侧向土压力系数为 {K_{\text{l}}} = 0.9 ,泊松比为0.3。桩侧土剪切模量在地面处为30 MPa,桩底处为70 MPa,沿深度线性分布。黏性阻尼系数 {c_{\text{s}}} = 10 {\text{kPa}} \cdot {\text{s/m}} ,所选取的桩土相互作用参数见表 1,为了简化分析起见,桩端土不妨考虑为理想弹塑性模型, {K_{{\text{b2}}}} = {K_{{\text{b3}}}} = 0{\text{ kN/m}} , {w_{{\text{b}}2}} = {w_{{\text{b1}}}} 。
表 1 桩土相互作用参数Table 1. Parameters of pile-soil interactionc/kPa \tan \varphi \xi A B r {T_0} a {K_{{\text{b1}}}}{\text{/}} (kN·m-1) {w_{{\text{b1}}}}{\text{/}} m 0 0.4 0.7 200 0.8 1 1296000 1 60000 0.005 2.1 桩顶单级荷载作用下桩基的沉降特征
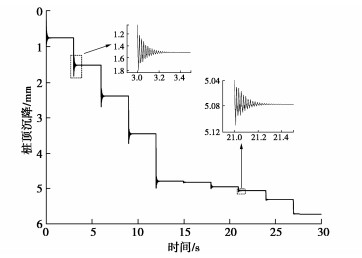
图 5给出了桩顶1800 kN单级荷载作用下,桩身不同位置处的位移-时间关系曲线。从图 5中可知,在桩顶1800 kN的单级荷载作用下,桩顶沉降达到稳定前,桩身不同位置处在位移过程中都出现了一定时间内沉降缓慢发展的黏滞位移阶段,表现出黏滞位移阶段与快速滑动位移阶段交替出现的位移模式,本文将这种位移模式称为黏滑沉降位移模态。从图 5桩顶和5 m桩身处黏滞位移阶段的局部放大图中可以看出,处于快速滑动位移阶段的桩顶与桩身在经过速度转向点(图 5局部放大图中的点A和点B)后进入黏滞位移阶段,桩身与土之间的接触状态也从相对滑动接触转化为黏滞接触;黏滞位移阶段的桩身与桩侧土体主要处于动态的黏滞接触状态,桩身产生数次速度转向,不断发生小型回弹/再向下位移的震荡(图 5局部放大图中的过程3)。在黏滞位移阶段结束后,桩身重新进入快速滑动位移阶段(图 5局部放大图中的过程5)。
图 6为不同桩顶单级荷载作用下的桩顶沉降-时间关系曲线,当桩顶单级荷载超过1820 kN时,桩顶沉降已不能达到稳定,1820 kN即为该模型桩单级加载时的极限加载值。从图 6中可以看出,当桩顶单级加载较小时,桩顶一开始会产生超过最终稳定沉降值的初始位移,随着时间的发展,桩顶位移在最终稳定沉降值附近波动,最后趋近于稳定沉降值。从图 6中还可看出,随着桩顶单级荷载的增大,桩顶沉降的位移模态由波动形式逐渐转变为黏滞位移阶段与快速滑动位移阶段交替的黏滑沉降位移模态,并且在单级加载的极限加载值处,桩身的黏滞位移阶段表现出一定的斜率。极限单级加载时桩身黏滞位移阶段的斜率可能是由于桩身与桩侧土体之间更加难以保持完全黏滞接触,导致相对滑动位移逐渐累积产生的。
2.2 桩顶单级荷载作用下桩身轴力与桩侧摩阻力分布特性
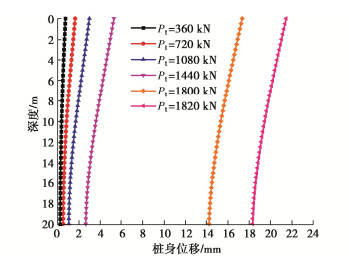
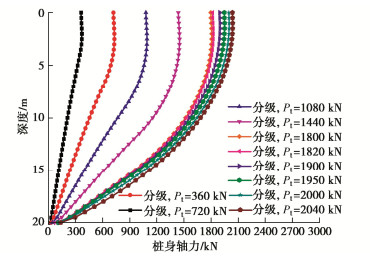
图 7, 8给出了桩顶单级荷载作用一定时间(3 s),桩顶沉降达到稳定时,桩身侧摩阻力和桩身轴力沿桩身的分布情况。图 9给出了不同桩顶单级荷载作用下,桩顶沉降稳定时桩身位移沿桩身的分布。
从图 7中可以看出,随着桩顶荷载作用增加,桩身临界截面逐渐下移,当桩顶单级荷载大于1440 kN时,桩身所有位置几乎都已脱离初始黏滞接触状态,桩身不再有明显的临界截面。从图 7中还可以看出,桩身上部脱离初始黏滞接触状态后,因为侧阻软化以及桩身回弹引起的侧摩阻力下降,部分位置可能会进入侧摩阻力反向的状态;而与桩周土体保持初始黏滞接触的下部桩身,也因为回弹导致的侧摩阻力下降,使得临界截面处的桩侧摩阻力并不等于该深度处的极限侧摩阻力。从图 8中也可见,由于桩身上部负摩阻力和桩身自重的影响,上部桩身轴力表现出一定程度的增加。总体而言,随着桩顶单级荷载作用的增加,桩顶沉降稳定时桩侧摩阻力逐渐向残余侧摩阻力接近,桩身轴力随深度的增加总体呈现减小的趋势。
2.3 桩顶荷载加载路径的影响
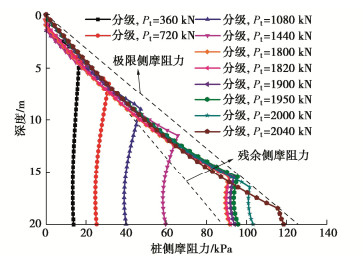
图 10给出了在桩顶“360—720—1080—1440—1800—1820—1900—1950—2000—2040 kN”分级荷载,每一级加载3 s下桩顶的沉降-时间关系曲线。图 11, 12给出了桩顶分级加载下,每一级荷载加载3 s时桩身侧摩阻力和桩身轴力沿桩身的分布情况。
从图 10可知,分级加载的每一级荷载作用下,桩顶的沉降表现为在一定时间的波动后达到该级荷载下的稳定值,与桩顶较小单级加载时的沉降表现一致,这是因为分级加载每一级的起点都是从上一级荷载沉降稳定时的状态开始的,较小的荷载增量下,桩身产生的速度响应较小,使得桩顶的沉降表现与桩基受到较小的单级荷载时的位移特性一致。分级加载荷载大于2040 kN时,桩顶沉降不能再达到稳定,因此该模型桩的极限承载力为2040 kN,该模型桩桩顶单级加载的极限值只有分级加载极限值的90%左右。
对比图 7, 11可知,桩顶荷载的加载路径对桩基的力学响应存在影响。从图 11中可知,桩顶荷载值较小时,分级加载桩顶附近的低摩阻力区域较单级加载时小,且几乎不再有进入负摩阻力的区域;施加相同桩顶荷载值时,分级加载产生的临界深度小于单级加载的情况,并且随着每一级荷载的施加,临界深度处的侧摩阻力逐渐向极限侧摩阻力靠近。从图 11中还可看出,与桩顶极限单级加载时桩侧摩阻力趋近于残余摩阻力不同,桩顶分级加载至极限承载力状态时,桩身上部的侧摩阻力趋近于残余侧摩阻力,而桩身底部的摩阻力则近于完全发挥。
导致桩身在桩顶分级加载与单级加载时力学响应不同的原因在于单级加载时,桩身产生的速度响应较大。当桩顶荷载较小时,桩身下部桩土间仍处于初始黏滞接触,速度响应的差异使得单级加载情况下的下部桩身位移比分级加载大,因此单级加载的桩基底部侧摩阻力以及端阻更大,而桩身上部各位置处则因为产生的回弹位移较大存在较大的低侧阻区域。当桩顶荷载进一步增大时(1440~1820 kN),单级加载桩身即已全部进入回弹/再沉降黏滞段,桩土之间的接触状态愈发接近相对滑动状态线,桩侧摩阻力也愈发接近高位移下的滑动摩阻力,而分级加载较小的桩身速度响应使得下部桩身位移与端阻均较小,桩基承载中桩身下部的侧摩阻力占比更大,桩身下部的侧摩阻力能得到更好的发挥。
3. 参数分析
经过计算,桩土间初始黏滞接触段桩侧土体刚度 {K_{{\text{s1}}}} 的变化对桩基受力沉降动态的影响较小,为简化起见,接下来仅分析桩端土体刚度 {K_{\text{b}}} ,表征侧阻弱化特性的侧阻衰减系数 \xi 对理想匀质砂土地基中模型单桩沉降特性的影响。计算时取桩顶单级加载方式,分析时除变化的参数外,其余参数同表 1。
3.1 桩端土参数对桩受力沉降动态的影响
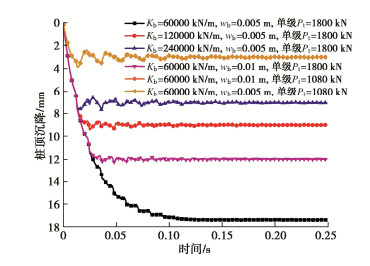
图 13为不同桩端土刚度以及桩端土界限位移下,桩顶单级加载时的桩顶沉降-时间关系曲线图。从图 13中可看出,桩端土刚度与桩端土界限位移对桩顶沉降稳定值均存在影响,当桩端土界限位移相同时,随着桩端土刚度增大,相同桩顶单级荷载作用下,桩顶沉降的稳定值减小,且桩基的沉降动态表现为桩顶一开始即产生较大的沉降位移,桩顶的位移在最终稳定沉降值附近波动趋近的行为;而当桩端土刚度相同,界限位移发生变化时,桩顶荷载较小时的桩顶沉降-时间关系曲线图相同,界限位移主要在桩顶荷载增大,桩端位移超过桩端界限位移时发挥作用。
3.2 桩土间残余摩阻力对桩受力沉降动态的影响
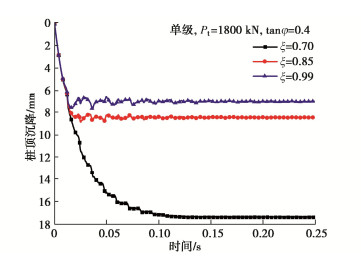
图 14给出了不同侧阻衰减系数 \xi 对桩顶受力沉降的影响。从图 14中可看出,桩土间的侧阻衰减系数 \xi 越大,即桩侧摩阻力衰减的程度越低时,相同桩顶单级荷载作用下,桩顶沉降稳定值越小。实际上 \xi 越大时,图 7中残余侧摩阻力线越接近极限侧摩阻力线,桩基单级加载时的极限加载值越大,因此桩顶相同单级加载下桩基的沉降表现与 \xi 较小的桩基在桩顶荷载作用较小时的沉降动态表现是一致的。
4. 桩基黏滑沉降计算模型的验证算例
使用文献[14,15]中的两个现场桩基静载试验的荷载-沉降实测数据对所建立的计算方法进行验证。
4.1 钻孔灌注桩算例一
文献[14]中给出了一根长 L = 10.6{\text{ m}} ,直径 D = 0.915{\text{ m}} 的钻孔灌注桩案例,场地的土层特性如表 2所示,地下水位在7.3 m处。缺少桩土间的摩擦角数据,桩土间的极限摩擦角 \varphi 取为29°;对于标贯击数较小的松散和稍密砂层( N \leqslant 15 ),忽略侧阻的弱化效应,侧阻衰减系数取 \xi = 0.99 ,对于中密和密实砂层( N>15 ),考虑70%极限摩阻力大小的残余摩阻力, \xi = 0.7 ;桩侧土剪切模量在地面取为20 MPa,桩底处取100 MPa,沿深度线性分布;侧向土压力系数按照THE FHWA 1999法[16]由下式求得:
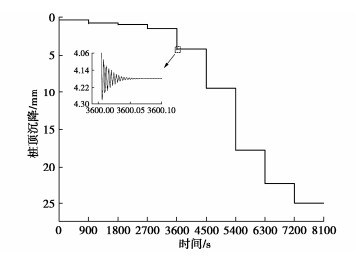
\left.\begin{array}{ll} K_1=\left(1.5-0.135 \cdot Z^{0.5}\right) / \tan 29^{\circ} & (N \geqslant 15), \\ K_1=\frac{N}{15}\left(1.5-0.135 \cdot Z^{0.5}\right) / \tan 29^{\circ} & (N <15)。 \end{array}\right\} (11) 表 2 算例一土层参数Table 2. Parameters of soil layers in Example 1土层编号 名称 土层深度/m 重度 \gamma {\text{/}} (kN·m-3) 标贯击数 内摩擦角/(°) 1 粉砂 0~4 20.0 15 34 2 净砂 4~8 17.0 19 31 3 含黏粒砂 8~13.5 18.3 22 — 式中: N 为标贯击数; Z 为土层深度,以英尺为单位。最终计算所采用的参数如表 3所示。计算采用分级加载,每一级加载15 min。
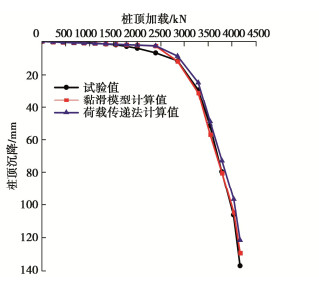
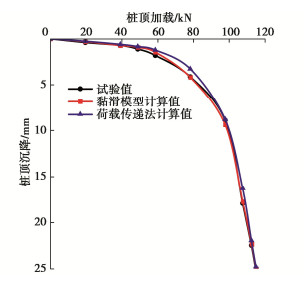
表 3 算例一计算参数Table 3. Parameters in Example 1土层 c/kPa \tan \varphi \xi A B r {T_0} 土层1 0 0.5543 0.99 200 09 1 129600 土层2 0 0.5543 0.7 200 0.9 1 129600 土层3 0 0.5543 0.7 200 0.9 1 129600 土层 a {K_{{\text{b1}}}}{\text{/}} (kN·m-1) {w_{{\text{b1}}}}{\text{/m}} {K_{{\text{b2}}}}{\text{/}} (kN·m-1) {w_{{\text{b2}}}}{\text{/m}} {K_{{\text{b3}}}} /(kN·m-1) 土层1 1 — — — — — 土层2 1 — — — — — 土层3 1 120000 0.011 10500 0.1 4000 图 15给出了算例一实测荷载-沉降曲线与理论计算荷载-沉降曲线之间的对比。图 16给出了算例一的桩顶计算沉降-时间关系曲线。从图 15中可以看出,本文所提黏滑模型的计算沉降值能较好地拟合实测数据。从图 15中还可以看出,在桩长较大/极限承载力较高的情况下,当桩顶加载值较小,荷载传递法与黏滑模型的计算沉降值几乎相同,当桩顶加载值进一步增大直到极限承载力,两者的计算结果都出现了一定的差异,与黏滑沉降计算模型相比,荷载传递法的计算沉降值偏小约6%,黏滑沉降模型由于考虑了加载时桩身的速度响应,在桩顶荷载增大时,每一级加载值下的桩身侧阻力较荷载传递法小,而得到的计算沉降值更大,计算结果更接近实测数据且偏向于安全,对实际工程的安全更有利。
4.2 小型钻孔灌注桩算例二
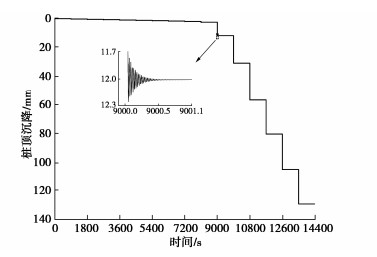
文献[15]中给出了一根长 L = {\text{2}}{\text{.25 m}} ,直径 D = 0.{\text{101 m}} 的小型钻孔灌注桩案例,场地的土层特性如表 4所示,在桩的埋深范围内没有地下水。由于桩长较小,桩侧土剪切模量沿深度统一取30 MPa,地基场地为超固结的微弱胶结砂,界面黏聚力 c = {\text{20 kPa}} ,最终计算所采用的参数如表 5所示,计算采用分级加载,每一级加载15 min。
表 4 算例二土层参数Table 4. Parameters of soil layers in Example 2土层编号 名称 土层深度/m 重度 \gamma {\text{/}} (kN·m-3) 标贯击数 内摩擦角/(°) 1 中密粉砂 0~4.5 18.0 20 35 2 致密粉砂 4.5~底部 19.5 > 69 43 表 5 算例二计算参数Table 5. Parameters in Example 2c/kPa \tan \varphi \xi A B r {T_0} a 20 0.5543 0.7 200 0.9 1 1296000 1 {K_{{\text{b1}}}}{\text{/}} (kN·m-1) {w_{{\text{b1}}}}{\text{/}} m {K_{{\text{b2}}}}{\text{/}} (kN·m-1) {w_{{\text{b2}}}}{\text{/m}} {K_{{\text{b3}}}}{\text{/}} (kN·m-1) G/MPa {K_{\text{l}}} 14000 0.004 1500 0.015 900 30 4.5 图 17给出了算例二实测荷载-沉降曲线与理论计算荷载-沉降曲线之间的对比。图 18给出了算例二的桩顶计算沉降-时间关系曲线。从图 17中可以看出,计算结果与实测数据之间的拟合也较好,在桩长较小/极限承载力较低的情况下,与黏滑沉降计算模型相比,荷载传递法的计算沉降值只在中等的加载值处出现一定程度与实测数据的偏离,在靠近极限承载力的加载值处,两种方法的计算沉降值均接近沉降实测数据,差异不大。
5. 结论
(1)桩顶单级荷载作用下,桩基沉降过程中会出现黏滞位移阶段与快速滑动位移阶段交替的黏滑位移模态,其中黏滞阶段是一个桩身不断发生小型回弹/再向下位移震荡的过程。
(2)桩顶单级荷载作用下,桩身与桩周土体间脱离初始黏滞接触状态后,因为侧阻软化以及桩身回弹,桩身上部会出现低摩阻区域。随着桩顶加载增加,桩顶沉降稳定时桩侧摩阻力逐渐向残余侧摩阻力接近,桩身轴力随深度的增加呈现减小的趋势。
(3)桩身的应力分布具有加载路径相关性。桩顶荷载作用值相同时,分级加载产生的临界深度小于单级加载的情况。桩顶分级加载时,桩身下部侧摩阻力能得到更多发挥,极限承载力大于单级加载极限值。
(4)桩端土刚度和桩土间残余摩阻力增大时,单级加载的极限承载力增大,桩顶在相同单级荷载作用下的沉降表现与桩端土刚度和桩土间残余摩阻力较小的桩基在桩顶荷载作用较小时的沉降特性相同。
-
表 1 桩土相互作用参数
Table 1 Parameters of pile-soil interaction
c/kPa (kN·m-1) m 0 0.4 0.7 200 0.8 1 1296000 1 60000 0.005 表 2 算例一土层参数
Table 2 Parameters of soil layers in Example 1
土层编号 名称 土层深度/m 重度(kN·m-3) 标贯击数 内摩擦角/(°) 1 粉砂 0~4 20.0 15 34 2 净砂 4~8 17.0 19 31 3 含黏粒砂 8~13.5 18.3 22 — 表 3 算例一计算参数
Table 3 Parameters in Example 1
土层 c/kPa A B r 土层1 0 0.5543 0.99 200 09 1 129600 土层2 0 0.5543 0.7 200 0.9 1 129600 土层3 0 0.5543 0.7 200 0.9 1 129600 土层 a (kN·m-1) (kN·m-1) /(kN·m-1) 土层1 1 — — — — — 土层2 1 — — — — — 土层3 1 120000 0.011 10500 0.1 4000 表 4 算例二土层参数
Table 4 Parameters of soil layers in Example 2
土层编号 名称 土层深度/m 重度(kN·m-3) 标贯击数 内摩擦角/(°) 1 中密粉砂 0~4.5 18.0 20 35 2 致密粉砂 4.5~底部 19.5 > 69 43 表 5 算例二计算参数
Table 5 Parameters in Example 2
c/kPa A B r a 20 0.5543 0.7 200 0.9 1 1296000 1 (kN·m-1) m (kN·m-1) (kN·m-1) G/MPa 14000 0.004 1500 0.015 900 30 4.5 -
[1] 胡育佳. 桩基非线性静动力学特性研究[D]. 上海: 上海大学, 2008. HU Yujia. The Research on Nonlinear Static and Dynamic Characteristics of Piles[D]. Shanghai: Shanghai University, 2008. (in Chinese)
[2] 李林, 李镜培, 孙德安, 等. 考虑时效性的静压桩荷载-沉降关系预测方法[J]. 岩土工程学报, 2017, 39(12): 2327-2334. doi: 10.11779/CJGE201712023 LI Lin, LI Jingpei, SUN De'an, et al. Prediction method for time-dependent load-settlement relationship of a jacked pile[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(12): 2327-2334. (in Chinese) doi: 10.11779/CJGE201712023
[3] KRAFT L M Jr, RAY R P, KAGAWA T. Theoretical t - z curves[J]. Journal of the Geotechnical Engineering Division, 1981, 107(11): 1543-1561. doi: 10.1061/AJGEB6.0001207
[4] RANDOLPH M F, WROTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of the Geotechnical Engineering Division, 1978, 104(12): 1465-1488. doi: 10.1061/AJGEB6.0000729
[5] 贺武斌. 静荷载下单桩沉降的时间效应研究[D]. 杭州: 浙江大学, 2003. HE Wubin. Studies on the Time Effect of the Settlement of Single Pile under Static Load[D]. Hangzhou: Zhejiang University, 2003. (in Chinese)
[6] 王东栋, 孙钧. 基于广义剪切位移法的桥梁桩基长期沉降分析[J]. 岩土工程学报, 2011, 33(增刊2): 47-53. http://cge.nhri.cn/cn/article/id/14319 WANG Dongdong, SUN Jun. Long-term settlement of pile foundation of bridges based on generalized shear displacement method[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 47-53. (in Chinese) http://cge.nhri.cn/cn/article/id/14319
[7] 李振亚, 王奎华, 吕述晖, 等. 考虑桩侧土体非线性的静荷载作用下的单桩沉降时间效应研究[J]. 岩石力学与工程学报, 2015, 34(5): 1022-1030. LI Zhenya, WANG Kuihua, LÜ Shuhui, et al. Time effect of settlement of single pile under static loading considering nonlinear characteristics of soil around pile[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 1022-1030. (in Chinese)
[8] SMITH I M, TO P. Numerical studies of vibratory pile driving[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1988, 12(5): 513-531. doi: 10.1002/nag.1610120506
[9] HOLEYMAN A. An analytical model-based computer program to evaluate the penetration speed of vibratory driven sheet piles[J]. Géotechnique, 1993, 43(18): 65-78.
[10] NOGAMI T, KONAGAI K. Time domain axial response of dynamically loaded single piles[J]. Journal of Engineering Mechanics, 1986, 112(11): 1241-1252. doi: 10.1061/(ASCE)0733-9399(1986)112:11(1241)
[11] 吴鹏, 任伟新. 竖向激励场下考虑桩土滑移的单桩动力性态[J]. 土木工程学报, 2009, 42(6): 92-96. WU Peng, REN Weixin. Response of single piles to vertical excitation with pile-soil slip[J]. China Civil Engineering Journal, 2009, 42(6): 92-96. (in Chinese)
[12] 张昭. 砂土中桩基础沉降机理宏细观研究[D]. 上海: 同济大学, 2007. ZHANG Zhao. Macro-Scale and Meso-Scale Study of Settlement Mechanism of Pile Foundations in Sand[D]. Shanghai: Tongji University, 2007. (in Chinese)
[13] 王伟, 卢廷浩, 宰金珉. 桩承载力的时间效应机理分析[C]//中国土木工程学会第九届土力学及岩土工程学术会议论文集(上册). 北京, 2003: 6755-658. WANG Wei, LU Tinghao, ZAI Jinmin. Time effect mechanism of pile bearing capcity[C]// Proceedings of 9th National Conference on Soil Mechanics and Geotechnical Engineering, China Civil Engineering Society, Beijing, 2003: 6755-658. (in Chinese)
[14] FELLENIUS B H. Determining the true distributions of load in instrumented piles[C]//Deep Foundations 2002. Reston V A: American Society of Civil Engineers, 2002.
[15] O'NEIL M, REESE L. Drilled Shafts: Construction Procedures and Design Methods[R]. Washington: Federal Highway Administration, 1999.
[16] ISMAEL N F. Axial load tests on bored piles and pile groups in cemented sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(9): 766-773. doi: 10.1061/(ASCE)1090-0241(2001)127:9(766)
-
期刊类型引用(1)
1. 叶帅华,辛亮亮. 基于桩-土界面剪切特性的单桩沉降和承载问题研究. 岩土力学. 2024(05): 1457-1471 .  百度学术
百度学术
其他类型引用(1)
-
其他相关附件




 下载:
下载: