0.   引言

中国基础设施建设日新月异，而软岩作为一种复杂岩体力学介质，在特定条件下会产生显著塑性变形、且具有明显的时间累积损伤效应^[1]。具体而言，在工程开挖建设过程中：一方面，开挖卸荷导致的应力重分布形成卸荷损伤；另一方面，软岩富含黏土矿物、水稳定性差、极易水化崩解^[2]。这二者综合作用导致工程软岩开挖卸荷后在水-岩作用下持续变形，最终失稳破坏，威胁工程运行安全^[3]。

为此，许多学者针对岩体损伤、水-岩作用等展开了一系列的理论及试验研究。在岩体损伤方面，陈静等^[4]研究了开挖卸荷对大理岩变形破坏特征；王宇等^[5]研究了非贯通裂隙软岩下裂缝发育破坏特征规律；邱士利等^[6]研究了初始损伤程度深埋大理岩卸荷变形破坏规律的控制作用。

在水-岩作用方面，郭宏云等^[7]、黄宏伟等^[8]、谢小帅等^[9]分别对泥岩、页岩、板岩等各类软岩在水-岩作用下的宏细观特征劣化规律进行了研究；潘艺等^[10]、周翠英等^[11]表征了水-岩作用下软岩的界面特征，创建了水岩动力学模型；刘驰等^[12]提出了界面胶结连接结构的概念，建立了软岩软化过程中的水-岩界面演化模型；Ciantia等^[13]提出了支撑岩石宏观稳定性的成岩黏结结构和沉积黏结结构的概念，建立了软岩软化过程的水-岩界面演化模型。

在损伤-水次序作用方面，邓华锋等^[14]分析了库岸边坡消落带节理软岩在水-岩和重复剪切次序作用下的累积损伤演化规律；张文达等^[15]分析了深埋花岗岩在高温酸性环境水-岩作用、三轴压缩次序作用下的力学强度劣化机制；窦子豪等^[16]分析了花岗岩在水岩和室内直剪次序作用下剪切损伤体积随浸水时长的演化规律。

综合目前损伤软岩的水-岩作用研究来看，主要侧重于分析水-岩作用下的软岩劣化效应，部分学者开展了水-岩和剪切、三轴压缩等次序作用下的岩体劣化规律，但尚未见考虑初始损伤（如卸荷损伤）对软岩在水-岩作用下损伤劣化累积放大效应的相关研究。

基于此，以典型软岩—三峡库区巴东组红层泥岩为研究对象，进行卸荷损伤-水次序作用试验，分析泥岩宏细观特征参数随水-岩作用时间的变化规律，研究泥岩在卸荷损伤-水次序作用下的累积损伤劣化规律，并基于非线性动力学理论，创建卸荷损伤泥岩在水-岩系统内的劣化模型。

1.   试验概况

1.1   试样制备及基本物理力学参数

试验所用红层泥岩取自巴东隧道某辅洞，岩块质地均匀细密，无风化现象，总体连续性、完整性好，密封处理后运回。严格按照国际岩石力学与工程学会（ISRM）标准将其制成高度100 mm，直径50 mm的标准试样备用。选取外观一致，体积、质量、纵波波速等参数较为接近的试样开展试验。

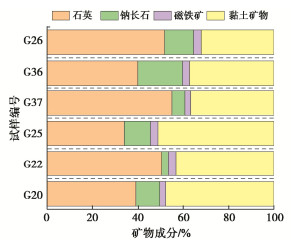
通过典型泥岩X射线衍射分析（XRD）可知泥岩矿物成分包含石英、钠长石、赤铁矿和黏土矿物，各试样的矿物成分占比如图 1所示。

图  1  试样矿物成分种类及占比

Figure  1.  Types and proportions of mineral composition of samples

下载: 全尺寸图片 幻灯片

1.2   泥岩卸荷损伤模拟试验

试验在RMT-150C岩石力学试验系统上进行，首先按静水压力条件以0.05 MPa/s的加载速率逐步施加${\sigma _1} = {\sigma _3}$至5 MPa（${\sigma _1}$为轴向压力，${\sigma _3}$为初始围压）；保持围压不变，继续以0.05 MPa/s的加载速率加轴向压力至24.69 MPa（约为极限抗压强度的80%）；然后保持${\sigma _1}$恒定，以0.05 MPa/s的卸荷速率卸围压，设计的围压卸荷量分别为30%，50%，60%，70%，90%，100%，其计算公式为

式中：${\sigma _3}$为初始围压值；${\sigma '_3}$为卸围压设计值；${\sigma _{\text{d}}}$为试样卸荷破坏时的围压值；$\Delta {\sigma _3}$为围压卸荷量。

1.3   水-岩作用试验

首先，用K946水中胶将4个应变片分两组紧密贴合在已完成卸荷损伤模拟试验的试样表面，分别监测其在水-岩作用下的轴向及侧向应变。

各宏细观特征参数测试中，质量m测试采用托盘天平，待试样在称重台上稳定后记录读数，重复3~4次计算平均值。纵波波速P测试采用GTJ-U920非金属超声检测仪，纵波换能器的频率为250 kHz，换能器与试样间采用适量凡士林耦合，每次测试前用标准铝块对仪器进行标定，确保其发射信号的稳定性。轴向应变${\varepsilon _1}$和侧向应变${\varepsilon _3}$测试采用应变片固定在被测物体上，使其随着被测对象的应变一起伸长或者缩短，应变片的电阻也会随之变化的原理，通过万用表测量应变片电阻值进而间接得到试样的应变，测量前选用合适的电阻量程并对万用表进行调零处理，然后用红黑表笔测量轴向应变片（^#1，^#2）和侧向应变片（^#3，^#4）电阻值并记录读数，重复测量^#3，^#4次计算平均值。试样的应变计算公式为

式中：$R$为应变片的原电阻值；$\Delta R$为应变片伸长或压缩引起的电阻变化值；$r$为应变片比例常数；$\varepsilon$为应变。

试样放入容器中进行自由饱水，测量记录每个试样在饱水0，6，12，24，…，132 h的m，P，${\varepsilon _1}$和${\varepsilon _3}$，并进行试样表面裂纹的拍照描图，同时将试样崩解时的试样碎片保存，一部分制成薄片用于偏光显微镜观察，一部分进行喷金用于SEM拍摄，并基于SEM图片计算分形维数K。

2.   泥岩卸荷损伤试验成果分析

2.1   应力-应变分析

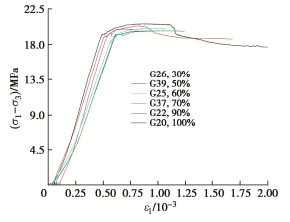
图 2为泥岩恒轴压卸围压应力-应变曲线（图例为试样编号，围压卸荷量$\Delta {\sigma _3}$）。可以看出，不同围压卸荷量下应力-应变曲线在线弹性段基本吻合，且偏应力达到恒定后轴向应变持续增大。当$\Delta {\sigma _3}$≤70%，试样仅出现塑性变形，未发生宏观破裂；而当$\Delta {\sigma _3}$＞70%时，试样在塑性变形后期出现显著应力跌落，产生宏观贯通破裂。

图  2  泥岩恒轴压卸围压应力-应变曲线

Figure  2.  Stress-strain curves of mudstone under constant axial pressure and unloading confining pressure

下载: 全尺寸图片 幻灯片

2.2   宏观裂纹特征分析

图 3为卸荷损伤试样，其中，围压卸荷量为30%，50%的试样表面微裂纹数量较少，整体性较好，相较于卸荷损伤前几乎没有变化；围压卸荷量为60%的试样有一条细长的表观张拉裂纹，试样未发生破坏；围压卸荷量为70%的试样表观裂纹显著增多，包含若干条剪切及张拉裂纹，但试样仍未发生贯通破坏；而围压卸荷量为90%，100%的试样则整体破坏，有贯通的剪切破坏主裂纹一条及张拉裂纹若干。由此可见，随着围压卸荷量增大，泥岩卸荷损伤程度随之增大。

图  3  卸荷损伤试样

Figure  3.  Unloading-damaged samples

下载: 全尺寸图片 幻灯片

2.3   细观结构特征分析

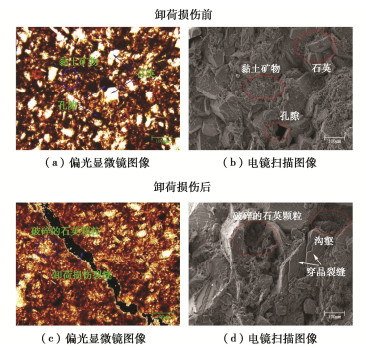
利用偏光显微镜和扫描电镜获取泥岩卸荷损伤前后的细观结构特征。如图 4所示。限于篇幅，以试样G22为例。

图  4  卸荷损伤前后泥岩细观图像

Figure  4.  Micro-images of mudstone before and after damage

下载: 全尺寸图片 幻灯片

由4（a）可知，所取试样主要由黏土矿物、石英颗粒和原生孔隙组成，黏土矿物中混有少量石英；由4（b）可知，试样中的石英颗粒被黏土矿物包裹，石英颗粒之间的连接方式有直接连接，也有间接连接，颗粒之间同样存在大量空隙；由4（c）可知，在经过三轴卸荷损伤试验损伤后，偏光图像内部出现一条裂缝，石英颗粒发生破坏；由4（d）可知，试样内部有石英颗粒发生破碎，产生沟壑，还有的石英颗粒产生穿晶裂缝，颗粒间孔隙变大。总体来看，卸荷损伤造成泥岩细观结构破坏，产生裂缝，矿物颗粒之间的黏结性和稳定性变差，从而导致泥岩宏观力学性质的改变。

2.4   卸荷损伤变量计算

为定量表征泥岩卸荷损伤程度，为后续卸荷损伤程度对泥岩水-岩作用下的宏细观参数劣化影响规律分析提供依据，利用弹性模量法^[17]计算泥岩卸荷损伤程度，结果如表 1所示。

表  1  不同围压卸荷量下泥岩卸荷损伤程度

Table  1.  Unloading damage degrees of mudstone under different confining pressure unloading quantities

试样	$\Delta {\sigma _3}$/%	E/GPa	$\bar E$/GPa	D
G26	30	35.46	25.54	0.28
G39	50	31.19	20.15	0.35
G25	60	32.42	18.69	0.42
G37	70	31.36	15.91	0.49
G22	90	37.24	11.14	0.70
G20	100	39.37	8.86	0.78
注：E为卸荷起始点处的弹性模量；$\bar E$为卸荷损伤试验结束时的变形模量；D为卸荷损伤程度。

下载: 导出CSV 

| 显示表格

3.   水-岩作用下卸荷损伤泥岩宏观参数变化规律

3.1   质量m

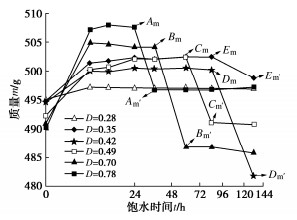
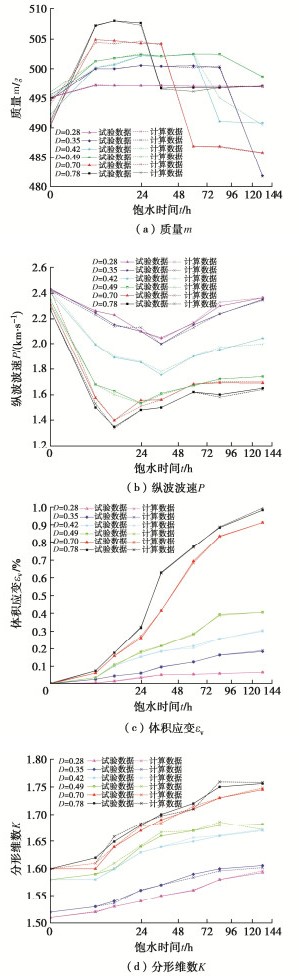
图 5为试样质量随饱水时间变化曲线（曲线中标记的${A_{\text{m}}}$~${E_{\text{m}}}$和${A'_{\text{m}}}$~${E'_{\text{m}}}$为质量崩解前后的点），可以看出曲线大致表现为先上升，保持稳定一段时间后陡然下降，最后稳定不变的趋势，即初期质量迅速增加至完全饱水后达到稳定，随着水溶液浸泡时间持续增加，泥岩内部孔隙、裂缝持续扩大，颗粒间胶结程度急剧下降，导致试样局部崩解，质量陡然下降，然后水化反应趋于稳定，质量不再显著变化。可以看出，随着卸荷损伤程度D增大，试样崩解时间变早。

图  5  质量随饱水时间变化曲线

Figure  5.  Variation curves of mass with water saturation time

下载: 全尺寸图片 幻灯片

3.2   纵波波速${V_{\text{P}}}$

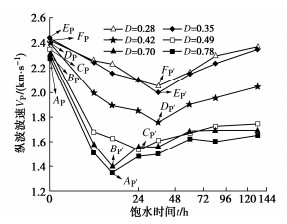
图 6是试样纵波波速随饱水时间变化曲线（曲线中标记的${A_{\text{P}}}$~${F_{\text{P}}}$为初始纵波波速，${A'_{\text{P}}}$~${F'_{\text{P}}}$为最低纵波波速）。由图 6可知，曲线总体表现为先下降后上升的趋势。这主要是由于在饱水初期，水分子沿孔隙裂缝快速渗入泥岩内部导致矿物颗粒间胶结程度降低，纵波波速随之减小；随着饱水时间持续增加，水溶液取代空气充满了试样孔隙、裂缝空间，使水溶液与试样骨架之间的自由空间减小，整个试样变为岩石颗粒与水介质的耦合体，造成纵波波速增大。

图  6  纵波波速随饱水时间变化曲线

Figure  6.  Variation curves of longitudinal wave velocity with water saturation duration

下载: 全尺寸图片 幻灯片

不仅如此，在下降阶段，D≥0.49后，各曲线纵波波速的最小值随卸荷损伤程度增加而变小，且最小值点对应的时间也越来越早。这主要是由于较高的卸荷损伤程度下试样存在表观裂缝，水分子的快速入渗导致其纵波波速下降更快，程度更高。在上升阶段，D≥0.49后，由于试样整体破坏程度更高，导致试样变为矿物颗粒与水介质的耦合体所需要的时间更长，因而纵波波速总体上升缓慢，数值较小。

3.3   体积应变${\varepsilon _{\text{v}}}$

测得卸荷损伤泥岩不同饱水时长的轴向和侧向应变，进而计算相应体积应变${\varepsilon _{\text{v}}}$为

式中：${\varepsilon _1}$为轴向应变；${\varepsilon _3}$为侧向应变。

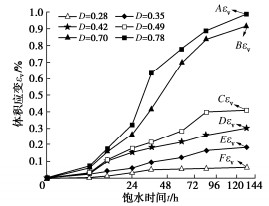
图 7给出体积应变随饱水时间变化曲线(曲线中标记的${A_{{\varepsilon _{\text{v}}}}}$~${F_{{\varepsilon _{\text{v}}}}}$为饱水结束时的体积应变)，可以看出，当D=0.28，0.35时，体积应变随饱水时间增长变化较小，最终体积应变值在0.1%左右，表明卸荷损伤程度很低时，水-岩作用下的体积应变主要是由泥岩中的黏土矿物吸水导致的微膨胀性产生；而当D=0.42，0.49，0.70，0.78时，体积应变的增长幅度更为显著，且D=0.49时，在饱水60 h后体积应变突增，D=0.70，0.78时，体积应变也分别在饱水36，24 h时发生突增，对比发现体积应变突增点与图 5中的质量跌落点对应时间基本一致。

图  7  体积应变随饱水时间变化曲线

Figure  7.  Variation curves of volume strain with saturation time

下载: 全尺寸图片 幻灯片

由于黏土矿物颗粒小、亲水性强，当水分子沿着孔隙、裂缝进入泥岩内部后，黏土矿物的吸附水膜便会增厚，从而引起岩石颗粒的体积膨胀。同时卸荷损伤D导致泥岩内部微观结构发生破坏、形成更多的裂纹和孔隙，使更多的黏土矿物暴露，加快了水分子的进一步入侵，进而引起了泥岩体积应变发生突增。且卸荷损伤程度D越大，体积应变随饱水时间的增长幅度越大，突增阶段来的越早。

3.4   宏观参数变化率与卸荷损伤程度的关系

根据各宏观参数随饱水时间变化曲线，可计算其变化速率为

式中：$\Delta {v_{\text{m}}}$为质量变化速率；${B_{\text{m}}}$为崩解前质量；${B'_{\text{m}}}$为崩解后质量；${t_{{B_{\text{m}}}}}$为崩解开始的时间；${t_{{{B'}_{\text{m}}}}}$为崩解结束的时间；$\Delta {v_{\text{P}}}$为纵波波速变化速率；${B_{\text{P}}}$为初始纵波波速；${B'_{\text{P}}}$为最低点纵波波速；${t_{{B_{\text{P}}}}}$为开始的时间；${t_{{{B'}_{\text{P}}}}}$为最低点时间；$\Delta {v_{{\varepsilon _{\text{v}}}}}$为体积应变变化速率；${B_{{\varepsilon _{\text{v}}}}}$为最终体积应变；${t_{{B_{{\varepsilon _{\text{v}}}}}}}$为最大体积应变时间；${t_0}$为初始时间。

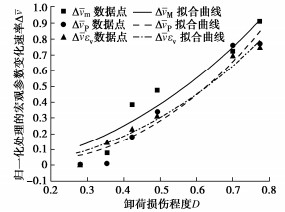
图 8是归一化处理的宏观参数变化速率与卸荷损伤程度关系曲线，可以看出，$\Delta {\bar v_{\text{m}}}$，$\Delta {\bar v_{\text{P}}}$，$\Delta {\bar v_{{\varepsilon _{\text{v}}}}}$随卸荷损伤程度增大呈幂函数增加，且D≥0.49后，各宏观参数变化速率大幅度增加，即试样更加快速的崩解，纵波波速降低的速度更快，体积应变增加的幅度越大。这实际是由于卸荷损伤程度较高时，试样表观及内部裂纹更多，在水分子入渗过程中，大量裂纹迅速由无序状态转化为有序的失稳状态，最后富集成核，在宏观上表现为裂缝进一步扩展贯通，试样劣化更为迅速。

图  8  各参数变化速率与卸荷损伤程度关系曲线

Figure  8.  Relation curves between variation rate of each parameter and unloading damage degree

下载: 全尺寸图片 幻灯片

3.5   宏观裂纹发育特征

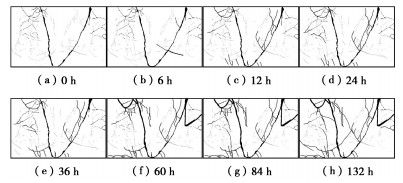
图 9为饱水过程中泥岩表观裂纹发育描图，限于篇幅，以试样G22为例进行定性描述。可以看出，试样卸荷损伤后存在一组剪切破坏面，伴随大量张拉裂纹，在水溶液浸泡过程中，裂纹持续发育扩展，部分转化为贯通破坏裂缝。

图  9  试样饱水过程中裂纹发育描图

Figure  9.  Crack growth profile during saturation of sample

下载: 全尺寸图片 幻灯片

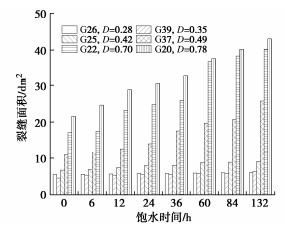
统计试样不同饱水时长裂缝面积如图 10所示，可以看出，试样表面的裂缝面积随饱水时间持续变大。当D≤0.49时，试样裂缝面积增长率仅为8%，几乎没有变化；而当D≥0.49后，裂缝面积增长明显加快，最大增长率为49%。表明卸荷损伤程度较大的试样，内部结构发生局部破坏，其在水溶液长期浸泡下，孔隙裂缝发育扩展更为迅速。

图  10  不同饱水时长裂缝面积分布

Figure  10.  Distribution of long fissure area under different saturation conditions

下载: 全尺寸图片 幻灯片

4.   水-岩作用下卸荷损伤泥岩细观结构特征变化规律

4.1   细观结构定性分析

卸荷损伤泥岩不同饱水时长下的SEM图像如图 11所示。可以看出，未饱水时泥岩中的黏土矿物颗粒相互交织定向排列聚集成了较大的块状、板状结构，且由于卸荷损伤作用，表面存在破碎的矿物颗粒，孔洞发育；饱水6 h后，破碎的矿物颗粒开始脱落，部分颗粒表面在水侵蚀下变得光滑平整；饱水12 h后，破碎的矿物颗粒完全流失，大量颗粒表面变得光滑平整；当饱水时长达到24 h后，颗粒边缘开始虚化，颗粒间胶结物流失严重，颗粒间孔隙变大、变多；当饱水36 h后，矿物颗粒直径进一步变小，孔隙开始相互连通，矿物颗粒由面-面连接变为点-面连接。饱水60 h后，矿物颗粒各自独立，颗粒直径也在水分子作用下溶蚀变小，颗粒间孔隙进一步加大；饱水时长增加到84 h后，矿物颗粒流失产生的孔隙和原生孔隙相互连通，形成孔洞，部分结构破坏，稳定性变差；继续饱水到132 h后，出现片状矿物，孔洞半径变大直至相互贯通，形成裂缝。

图  11  不同饱水时间下卸荷损伤泥岩的电镜扫描图像

Figure  11.  SEM images of unloading-damaged mudstone at different saturation durations

下载: 全尺寸图片 幻灯片

整体而言，在卸荷损伤泥岩饱水劣化过程中，细观上由原有胶结性强、孔隙度低的结构逐渐演变为胶结性弱、孔隙度高的结构，从致密程度好、强度高向强度低、疏松多孔不规则的堆积结构转化。

4.2   细观结构定量分析

（1）孔隙数量N

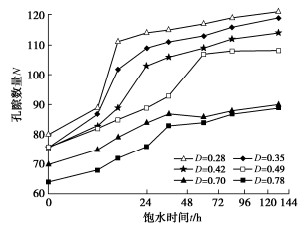
利用Image-Pro Plus软件对共6个试样，8个饱水时间节点，48张放大倍数为2000倍的SEM图像进行孔隙特征提取，发现泥岩孔隙尺寸主要分布在0.5 ${\text{μ m}}$左右，因此统计尺寸在0.3~0.7 ${\text{μ m}}$的孔隙数量随饱水时间的变化关系曲线如图 12所示。

图  12  孔隙数量随饱水时间变化曲线

Figure  12.  Variation curves of pore quantity with saturation time

下载: 全尺寸图片 幻灯片

可知，各试样孔隙数量均随饱水时间增长而增多，最后逐步趋于稳定。另外，随着卸荷损伤程度D的增大，孔隙数量急剧增长的时间越早，如：D= 0.49时，饱水36 h的孔隙数量增长率为15%，D=0.35时，饱水12 h的孔隙数量增长率为15%，而D=0.70，0.78时，饱水6 h的孔隙数量增长率就达到了17%和25%。由此可见，随着卸荷损伤程度增大，初始裂隙发育增多，导致饱水过程中水与颗粒间胶结物反应更为迅速，胶结物水化溶解，孔隙数量急剧增多，而在饱水后期（48 h后），颗粒间胶结物的水化反应基本完成，后续主要为矿物颗粒在水作用下的缓慢溶蚀过程，故而孔隙数量增长变缓，并逐渐趋于稳定。

（2）分形维数K

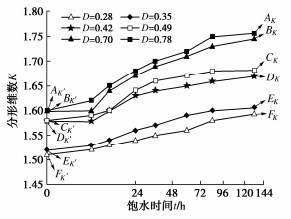
利用MATLAB计算机程序采用盒维数法，计算泥岩在不同饱水时间下的分形维数，结果如图 13所示。图 13中，A~F为不同损伤程度试样分形维数最大值，A^′~F^′为不同损伤程度试样分形维数初始值。

图  13  分形维数随饱水时间变化曲线

Figure  13.  Variation curves of fractal dimension with saturation time

下载: 全尺寸图片 幻灯片

从图 13中可以看出，泥岩的分形维数随饱水时间增加呈先增长后稳定趋势，D=0.28，0.35的曲线增长速率较为一致。0.70，0.78的曲线增长速率几乎一致。泥岩的分形维数在0~6 h增长率最小，为0.6%，在6~12 h增长率最大，为2.48%。原因是随着饱水时间的不断增加，导致试样内部的孔隙发育，直至相互连通形成裂缝，孔隙半径变大，小孔隙数量减少，大孔隙数量增多，细观结构更加破坏，致使分形维数增大。

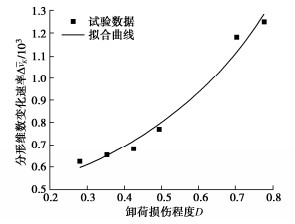
图 14是泥岩分形维数变化速率与卸荷损伤程度的关系曲线，其中分形维数变化速率$\Delta {v_K}$为

图  14  分形维数变化速率与卸荷损伤程度关系曲线

Figure  14.  Relation curves between variation rate of fractal dimension and damage degree

下载: 全尺寸图片 幻灯片

式中：${B_K}$为分形维数最大值；${B'_K}$为分形维数初始值；${t_{{B_K}}}$为最终饱水时间；${t'_{{B_K}}}$为初始饱水的时间。

可以看出，分形维数变化速率与损伤程度同样呈幂函数关系，随着卸荷损伤程度的增加逐渐增大，分形维数的速率增长越快。原因是卸荷损伤造成泥岩内部矿物颗粒破碎，从有序变为无序的状态，又在水溶液中长期浸泡发生水化反应，导致胶结物溶解，矿物颗粒溶蚀，致使内部结构更加容易混乱破坏，分形维数增长速率加快。

5.   卸荷损伤泥岩在水-岩作用过程中的非线性动力学模型构建及验证

5.1   泥岩在卸荷损伤-水次序作用下的损伤演化过程

泥岩为典型沉积岩，该类岩石通过沉积搬运、孔隙排水、风化、压实、胶结等作用，由散体变为岩石。胶结类型大致可以分为基底式胶结、孔隙式胶结、接触式胶结、悬挂式胶结、镶嵌式胶结5种^[18]。

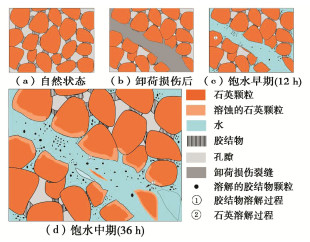
结合图 4可知，所用泥岩的胶结方式以接触式胶结为主，矿物颗粒相互接触，或各自独立，中间由胶结物填充。为研究泥岩在卸荷损伤及水次序作用下的内部结构演化规律，基于图 4，11，以试样G22为例，绘制其演化过程示意如图 15所示。

图  15  演化过程示意图

Figure  15.  Schematic diagram of mudstone evolution process

下载: 全尺寸图片 幻灯片

图 15反映了泥岩在卸荷损伤及水次序作用下的4个典型阶段：①自然状态下，泥岩的整体性良好，矿物骨架主要通过黏土矿物进行胶结，内部孔隙分布较为均匀；②卸荷损伤后，泥岩结构局部破坏，矿物颗粒及其间的胶结物断裂松动，产生微裂缝；③饱水早期（12 h），水分子通过孔隙裂缝进入泥岩内部，吸附在胶结物表面，导致其黏结力降低最终从矿物颗粒表面脱落，溶解至水中；④饱水中期（36 h），随着胶结物不断从矿物颗粒表面脱落，水分子入渗更快，使得泥岩内部孔隙裂缝急剧增多，并相互贯通，进而导致石英等矿物颗粒在水作用下溶蚀甚至脱落，宏观表现为试样质量陡降，出现局部崩解。总体而言，卸荷损伤裂缝促进了泥岩在水作用下的损伤劣化进程。

5.2   非线性动力学理论

将泥岩与水溶液长时间相互作用的系统视为一个开放的系统，其系统状态随着时间推移会从不稳定向新的稳定状态演化^[19]。从数学角度可认为水岩的长期相互作用问题是一个高度非线性问题，因而，可假设卸荷损伤泥岩在水环境作用下的系统状态随时间演化的物理规律为

式中，函数${f_i}$为${q_1},{q_2},{q_3}, \cdots ,{q_n}$的一般非线性函数。

根据物理系统的性质, 将${f_i}$设为某种非线性函数，并用反演方法确定具体形式和各参数值。

设${f_i}({q_1},{q_2},{q_3}, \cdots ,{q_n})$中有${G_K}$项和相应的${R_K}$个参数，写成矩阵形式为

其中，

式中：W，G均为非线性多项式变量，可用试验数据求得。即在式（7）中除了向量R未知，其他均为已知。

通过求得试验数据W与理论计算值GR的误差向量，得到其残差平方和S，即

并对其取最小值，使得假设的非线性函数与实际情况最接近，则方程需要满足以下等式关系：

若${\boldsymbol{G}^{\text{T}}}\boldsymbol{G}$为非奇异矩阵时，则有

5.3   变量选取及模型构建

5.1节中的研究表明，泥岩在卸荷损伤及水溶液长期浸泡过程中伴随着孔洞裂缝发育扩展、胶结物弱化溶解以及矿物颗粒溶蚀脱落等现象。因此，本文选取质量m、纵波波速度${V_{\text{P}}}$、体积应变${\varepsilon _{\text{v}}}$、分形维数K 4个宏细观参数的试验值作为理论方程的特解，经过变量均匀化，建立非线性动力学模型来描述卸荷损伤泥岩与水溶液相互作用系统的变量。

文献[20]中对于式（6），在大多数情况下总可以通过改变参数${a_k}$，${b_k}$，${c_k}$，将任意函数的值表达为

根据非线性动力学的观点，系统在一定的周期或准周期内的演化过程的稳定可以用动力学方程来描述^[21]。因此，可以认为卸荷损伤泥岩在水溶液长期浸泡作用下的系统时间尺度内，系统的动力学方程具有不变的形式，可以用一系列常参数和变量的一次、二次项在数值上表达出系统的动力学方程。

基于上分析，假设系统的方程为

结合非线性动力学理论，将m，${V_{\text{P}}}$，${\varepsilon _{\text{v}}}$和K的试验值代入，得矩阵W和G，经运算可得动力学方程各系数值（a_i，b_i，c_i，d_i），代入式（13）可得

为定量比较方程各项对系统动态演化的相对贡献大小，对各项的相对方差贡献进行计算，计算公式为

式中：h为饱水时长；T_i为方程组中的各项。限于篇幅，以分形维数K为例，给出其方程各项方差贡献值，如表 2所示。

表  2  各项的方差贡献

Table  2.  Variance contribution of each item

方程项	${d_1}m$	${d_2}{V_{\text{P}}}$	${d_3}{\varepsilon _{\text{v}}}$	${d_4}K$
${R_i}$	0.3×10-7	0.55	1.8×10-4	0.45
方程项	${d_5}{m^2}$	${d_6}{V_{\text{P}}}^2$	${d_7}\varepsilon _{\text{v}}^{\text{2}}$	${d_8}{K_2}$
${R_i}$	4.50×10-13	9.72×10-4	2.82×10-4	1.12×10-3
方程项	${d_9}m{V_{\text{P}}}$	${d_{10}}m\varepsilon _{\text{v}}^{}$	${d_{11}}mK$	${d_{12}}{V_{\text{P}}}\varepsilon _{\text{v}}^{}$
${R_i}$	1.66×10-6	8.57×10-8	1.66×10-6	6.86×10-4
方程项	${d_{13}}{V_{\text{P}}}K$	${d_{14}}\varepsilon _{\text{v}}^{}K$
${R_i}$	7.79×10-5	6.30×10-3

下载: 导出CSV 

| 显示表格

可以看出有的方程项对方差贡献较大，而有些方程项的贡献几乎为零，其中无关项的系数对比其他数据小于4个数量级以上^[22]。据此，剔除4个方程项中那些系统中的无关项，得到简化后的方程为

5.4   模型验证

运用MATLAB计算机程序对式（16）进行数值积分，求出各变量对应的时间节点理论计算值，并将其与试验数据进行对比，结果如图 16所示。

图  16  试验数据与计算数据的对比

Figure  16.  Comparison between test and calculated data

下载: 全尺寸图片 幻灯片

可以看出，基于非线性动力学模型的理论计算结果与试验数据基本一致，计算可知相对误差基本不超过3%。模型计算结果存在的波动性主要由于试验环境、试验试样离散性导致，但总体而言，非线性动力学模型能较好地预测卸荷损伤泥岩在水溶液长期浸泡下的演化规律及劣化机制。

6.   结论

（1）通过卸荷损伤-水次序作用试验得到了不同卸荷损伤程度泥岩质量、纵波波速和体积应变随饱水时长的变化规律，且各参数的变化速率均随卸荷损伤程度D增大呈非线性增加。

（2）卸荷损伤导致泥岩表观裂纹发育，随着饱水时长增加，裂纹进一步扩展，泥岩裂缝面积随饱水时长增加而持续增大，且当卸荷损伤程度D≥0.49时，裂隙面积占比增长率显著增加。

（3）卸荷损伤后泥岩试样内部孔洞、裂隙发育，其后随着饱水时长增加，黏土颗粒脱落，矿物颗粒表面变得光滑、边缘虚化，部分脱落流失。孔隙数量和分形维数随饱水时长增加而持续变大，且分形维数增长率随卸荷损伤程度D增大呈幂函数增加。

（4）泥岩在卸荷损伤-水次序作用下的演化规律表明，卸荷损伤泥岩在水-岩作用下的劣化过程具有明显的非线性动力学特征，因此，选取质量、纵波波速、体积应变和分形维数作为描述卸荷损伤泥岩与水溶液相互作用系统的变量，建立卸荷损伤泥岩在水-岩作用下的非线性动力学模型，并验证了模型的合理性。