基于等效零时刻点的水平层状场地黏弹性边界方法研究

贾忠明; 赵伯明; 王子珺; 赵天次; 冯俊

doi:10.11779/CJGE202212020

基于等效零时刻点的水平层状场地黏弹性边界方法研究 English Version

贾忠明^{1, 2,},
赵伯明^{1, 2, ,},
王子珺^{1, 2},
赵天次^{1, 2},
冯俊^{1, 2}

1.
北京交通大学城市地下工程教育部重点实验室，北京 100044
2.
北京交通大学土木建筑工程学院，北京 100044

基金项目:

国家自然科学基金项目 51778046

国家自然科学基金项目 51808035

国家自然科学基金重点项目 U1434210

详细信息

作者简介:
贾忠明(1996—)，男，博士研究生，主要从事结构抗震方面的研究。E-mail：zhmjia@bjtu.edu.cn

通讯作者:
赵伯明, E-mail: bmzhao@bjtu.edu.cn

中图分类号: TU435
计量
- 文章访问数: 119
- HTML全文浏览量: 34
- PDF下载量: 21
出版历程
- 收稿日期: 2021-10-25
- 网络出版日期: 2022-12-13
- 刊出日期: 2022-11-30

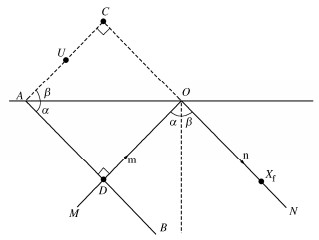
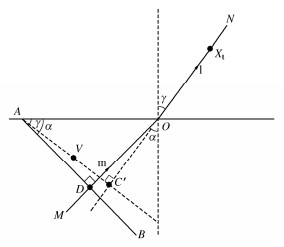
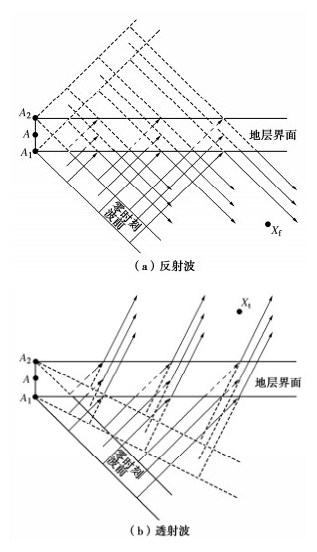
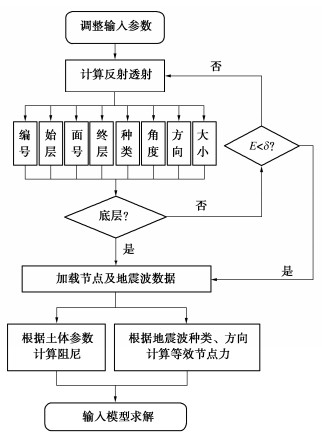
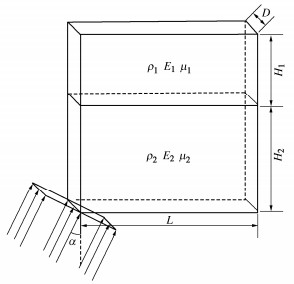
Viscoelastic boundary method of horizontal layered site based on equivalent zero-time point

JIA Zhong-ming^{1, 2,},
ZHAO Bo-ming^{1, 2, ,},
WANG Zi-jun^{1, 2},
ZHAO Tian-ci^{1, 2},
FENG Jun^{1, 2}

1.
Key Laboratory of Urban Underground Engineering, Ministry of Education, Beijing Jiaotong University, Beijing 100044, China
2.
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China

摘要

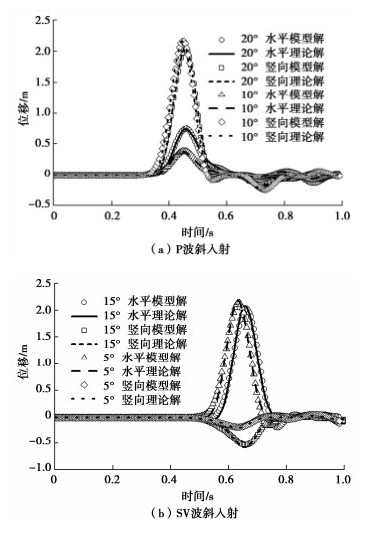
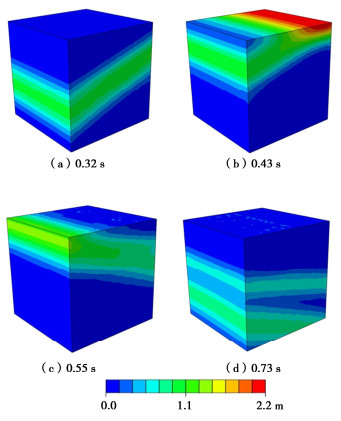
摘要: 针对黏弹性边界下水平层状场地地震动输入中的时间延迟计算问题，提出了水平层状场地的等效零时刻点迭代时间延迟计算方法，并依托斯涅尔方程及地震波在分层界面上的连续性条件推导了人工边界上等效节点力的计算公式，得出了黏弹性边界下的水平层状场地斜入射地震动输入方法。建立两层地层三维有限元计算模型，进行动力响应分析，并将计算结果与理论值进行对比，验证了方法的有效性和实用性。应用方法进行等效节点力计算的过程中，可根据所求目标地震波的具体信息及其所在地层的具体条件直接求解，无需对所求地震波的全部来源依次进行分析，使得公式更为统一，在简化计算的同时保证计算精度及准确性，并拓展了黏弹性边界理论在水平层状场地斜入射地震动上的应用。
- 地震波斜入射 /
- 水平层状场地 /
- 黏弹性边界 /
- 时间延迟
Abstract: An equivalent zero-time point iterative time delay method for horizontal layered strata is proposed to solve the problem of time delay calculation in ground motion input of layered strata under viscoelastic boundary. It assignes an equivalent zero-time plane to each generated seismic wave. An appropriate point on the plane can be selected as the equivalent zero-time point, and the time delay can be calculated. Based on the Snell equation and the continuity condition of seismic waves at the layered interface, the formula for calculating the equivalent nodal force of the artificial boundary is derived, and the viscoelastic boundary input method for oblique incidence ground motion of the layered strata under the viscoelastic boundary is deduced. The finite element model for a double-layer horizontal layered stratum is established for dynamic response analysis. The calculated results are compared with the theoretical values. The deviation between them is relatively small, which shows the effectiveness and practicability of the method. By using the method it can be solved directly according to the specific information of the seismic wave and the stratum, without analyzing all the sources of the desired seismic wave in turn, which makes the formula unified. It is a way to simplify the calculation without affecting the accuracy. Meanwhile, it can extend the application of the viscoelastic boundary to the oblique incidence ground motion of layered stratum.
- oblique incidence of seismic wave /
- layered stratum /
- viscoelastic boundary /
- time delay

HTML全文

0. 引言

在气候变化及人类活动的影响下，非饱和土体内部的水分场和温度场会逐渐改变，劣化土体工程性质，进而诱发一系列工程地质问题，如不均匀沉降和路基稳定性问题等^[1]。实际过程中，土体中的水分和热量迁移存在复杂的耦合作用。因此，研究近地表非饱和土的水热耦合特性和工程响应，对于防控土体水热场变化引起的各类岩土工程问题具有重要的现实意义^[2]。

早期Philip等^[3]于1957年首次引入水分相变过程，并建立相应的水热耦合计算模型。在此基础上，国内外学者围绕非饱和多孔介质中水热耦合理论、试验研究和数值计算做了大量工作^[4-6]。需要指出的是，目前岩土工程界关于水热耦合设计体系都重视液态水的影响，在计算过程中关于重力项和水分相变等问题大多作简化处理^[2]。如Sellers等^[7]在水热耦合数值计算过程中，仅分别考虑了液态水流动对水分分布和热传导过程对温度分布影响，忽略了水汽运动对土体水热场的影响。陈佩佩等^[8]基于光滑粒子流体动力学（SPH）方法计算了不同热扩散系数等热物理参数对热源条件下的非饱和土水热场分布特征的影响，忽略了水-汽相变和水汽运动的影响。

综上，在非饱和土水热耦合问题中忽略自重项等因素能简化计算，但在一定程度上会影响数值求解的准确性^[2]。为系统研究如自重项等简化因子的影响，本文采用已有的水热耦合模型^[3-5]，充分考虑了热传导、相变、温度梯度、水分梯度和重力势耦合作用，采用FreeFem⁺⁺有限元软件^[9]自主编制了计算程序并求解。在此基础上，进一步考虑了表层蒸发、降雨入渗和干湿循环的不同工况，探讨了蒸发潜热项、自重项、水汽运动和渗透系数等因子在水热耦合问题简化计算中的合理性。

1. 非饱和土水热耦合理论模型

1.1 水分迁移方程

在非饱和土中，分子扩散引起的孔隙蒸汽质量通量可以用菲克定律来描述，蒸汽总通量可表示为^[3]

${q_{\text{v}}} = - {D_{{\text{atm}}}}v\alpha a\nabla {\rho _{\text{v}}}{, }$

(1)

式中，是梯度算子，q_v为蒸汽通量密度，D_atm为水蒸气在空气中的分子扩散率，v为质量流动因子，α为土体曲率因子，a为体积空气含量，ρ_v为水蒸气密度。

基于非饱和达西定律，液态水分通量密度表示为

$\frac{{{q_{\text{l}}}}}{{{\rho _{\text{l}}}}} = - K\nabla \phi {, }$

(2)

式中，q_l为液态水的通量密度，ρ_l为液体密度，K为非饱和土渗透系数，ϕ为总水势。总水势由基质势φ和重力势z组成，故式（2）可改写为

$\frac{{{q_l}}}{{{\rho _l}}} = - K\left( {\frac{{\partial \varphi }}{{\partial \theta }}} \right)\nabla \theta - K\left( {\frac{{\partial \varphi }}{{\partial T}}} \right)\nabla T - K\nabla z。$

(3)

根据水分通量质量守恒，可得

$\frac{{\partial \theta }}{{\partial t}} = \frac{{\partial {\theta _{\text{l}}}}}{{\partial t}} + \frac{{\partial {\theta _{\text{v}}}}}{{\partial t}} = - \nabla \left( {\frac{{{q_{\text{l}}}}}{{{\rho _{\text{l}}}}}} \right) - \nabla \left( {\frac{{{q_{\text{v}}}}}{{{\rho _{\text{l}}}}}} \right){, }$

(4)

式中，θ_l，θ_v分别为非饱和土液态水体积含水率和水蒸汽体积含水率，t为时间。

结合式（1），（3），（4），可得非饱和土水分运移的控制方程为

$\frac{{\partial \theta }}{{\partial t}} = \nabla \left( {{D_\theta }\nabla \theta } \right) + \nabla \left( {{D_{\text{T}}}\nabla T} \right) + \nabla \left( {K\nabla z} \right)。$

(5)

式中，D_T为温度诱致水分扩散系数，D_θ为等温水分扩散系数。

1.2 热量迁移方程

非饱和土中的热通量是由热传导、蒸汽运动引起的潜热、水蒸汽和液态水中的显热传递4部分组成。在Philip等^[3]模型中，根据热量守恒，可表示为

$C\frac{{\partial T}}{{\partial t}} + {L_0}{\rho _{\text{l}}}\frac{{\partial {\theta _{\text{v}}}}}{{\partial t}} = \nabla (\lambda \nabla T) - \nabla ({L_0}{q_{\text{v}}}){, }$

(6)

式中，C为土体比热容， $\lambda$ 为导热系数，L₀为参考温度T₀条件下水的蒸发潜热。

为更好的描述蒸汽流动，Thomas^[5]在Philip等^[3]水热耦合模型基础上引入相变系数ε来考虑气液相变：

$\frac{{{d_{\text{i}}}({\rho _{\text{l}}}{\theta _{\text{l}}})}}{{{d_{\text{e}}}({\rho _{\text{l}}}{\theta _{\text{l}}})}} = \frac{\varepsilon }{{1 - \varepsilon }}。$

(7)

当ε=1时，意味着水分转移是以蒸汽的形式发生的；当ε=0时，则表明是仅以液态形式发生。

最后基于水蒸汽的质量与液体的质量相比是可以忽略不计的假设，可得热流控制微分方程：

$\begin{array}{l} C\frac{{\partial T}}{{\partial t}} = \nabla \cdot (\lambda + {L_0}\varepsilon {\rho _{\text{l}}}{D_{\text{T}}})\nabla T + \nabla \cdot ({L_0}\varepsilon {\rho _{\text{l}}}{D_\theta })\nabla \theta +\\ \ \ \ \ \ \ \ \ \ \ {L_0}\varepsilon {\rho _{\text{l}}}\frac{{\partial K}}{{\partial z}}。 \end{array}$

(8)

2. 分析讨论

为系统研究边坡水热耦合计算模型中蒸发潜热项、自重项、水汽运动和渗透系数等因子对非饱和土体水热响应的影响，本文选取非饱和细砂土，基于上述水热耦合模型对各影响因子展开分析讨论。土体的热物理参数具体如表 1所示^[5]，考虑区域为图 1中ABCD区域。

表 1 细砂土的热物理参数^[5]

Table 1. Thermal physical parameters of unsaturated soils^[5]

参数	符号	取值
体积热容/(calžcm^-3ž℃^-1)	C	0.48
导热系数/(calžcm^-1žs^-1ž℃^-1)	λ	0.02
水的蒸发潜热/(calžg^-1)	L₀	540
温度诱致水分扩散系数/(cm²žs^-1ž℃^-1)	D_T	1×10^-5
相变系数	ε	0.3
等温水分扩散系数/(cm²žs^-1)	D_θ	0.01
非饱和渗透系数/(cmžs^-1)	K	1×10^-5
比水容量/(m^-1)	∂θ/∂φ	0.1

下载: 导出CSV

| 显示表格

图 1 二维简易坡体示意图^[5]

Figure 1. Schematic diagram of two-dimensional slope^[5]

下载: 全尺寸图片幻灯片

实际上，土体内部的渗透和导热特性与含水率密切相关，其内部的水热迁移还受地下水位、表层蒸发以及降雨入渗等外界条件的影响。为更贴合实际边坡工况，基于van Genuchten^[10]渗透系数计算模型和Côté等^[11]提出的导热系数计算模型，分别为

$K = {K_{\text{s}}} \cdot {S_{\text{e}}}^{0.5}{\left[ {1 - {{(1 - {S_{\text{e}}}^{1/{m_1}})}^{{m_1}}}} \right]^2} {, }$

(9)

$\lambda = {\text{(}}{\lambda _{{\text{sat}}}} - {\lambda _{{\text{dry}}}}{\text{)}} \times {\lambda _{\text{r}}} + {\lambda _{{\text{dry}}}}{, }$

(10)

式中，K_s为饱和渗透系数，K_s=1.35×10^-5 cm/s，S_e为饱和度，系数m₁=0.5，λ_sat为饱和状态导热系数，λ_sat=0.025 cal/cm/s/℃，λ_dry为干燥状态导热系数，λ_dry=5×10^-4 cal/cm/s/℃， ${\lambda _{\text{r}}} =$ $\frac{{3.55 \times {S_{\text{e}}}}}{{1 + (3.55 - 1){S_{\text{e}}}}}$ 。

初始温度、初始体积含水率和边界条件具体如表 2所示。在截面P上选取3个点P₁（h=20 cm）、P₂（h=100 cm）和P₃（h=180 cm）作为特征点来分析不同位置土体的水热特性。为研究如重力项等因素在水热耦合模型中的时间效应，如表 3所示，选取蒸发边界的蒸发速率为1×10^-5 cm/s，降雨入渗边界的入渗速率为1×10^-6 cm/s，干湿循环边界为上述蒸发和降雨入渗速率各一天依次交替，计算时间为60 d。

表 2 初始状态和边界条件

Table 2. Initial states and boundary conditions

初始状态	边界条件
初始状态	AB，BC	CD	AD
T₀=10 ℃, θ₀=0.5-y/100	蒸发/降雨入渗/干湿循环边界, T=25 ℃, 隔热边界	θ=0.5, 不透水隔热边界	不透水隔热边界

下载: 导出CSV

| 显示表格

表 3 模拟工况

Table 3. Simulated conditions

模拟工况	边界水分通量/(cm·s^-1)	持续时常
蒸发	-1×10^-5	60 d
降雨	1×10^-6	60 d
干湿循环	-1×10^-5 / 1×10^-6	各1 d依次交替，合计60 d

下载: 导出CSV

| 显示表格

2.1 蒸发潜热项对水热耦合过程的影响

为分析水分蒸发引起的潜热变化对土体水热场的影响，在上述蒸发、降雨和干湿循环条件下，分别对考虑蒸发潜热项（L₀=540 cal/g）和不考虑蒸发潜热项（L₀=0）两种情况下的水热场分布进行数值计算，计算结果如图 2，3所示。对比图 2可以看出，在3种边界条件下，考虑蒸发潜热项与否会显著影响特征点温度随时间的变化特征及温度稳定值，由于水分蒸发吸收热量会使得考虑蒸发潜热时的计算值滞后于不考虑蒸发潜热时的温度场变化，其影响程度与边界条件有关，表现为降雨入渗 < 干湿循环 < 蒸发，这是由于水分入渗会加速热量扩散，该作用显著强于蒸发潜热的影响，使得稳定时的温度逐渐上升。

图 2 蒸发潜热项对温度场时空演化特征的影响

Figure 2. Effects of latent heat of evaporation on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 3 蒸发潜热项对水分场时空演化特征的影响

Figure 3. Effects of latent heat of evaporation on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

从图 3可以看出，在上述边界作用下，各特征点的含水率向稳定值缓慢变化。在本文的干湿循环条件下，仅P₃处体积含水率随时间呈波动变化。蒸发潜热项考虑与否对各特征点在不同时间上的含水率值及其变化特征并无显著区别，但在蒸发条件下其影响随高度和时间增加而稍有增强（在P₃处最大变化仅为3.2%）。说明蒸发潜热项对土体温度变化的影响极大，但对于含水率的影响几乎可以忽略不计。

2.2 自重项对水热耦合过程的影响

为验证自重在水热耦合问题中的重要性，对于上述3种边界条件下的土体温度场和水分场在考虑及不考虑重力项两种情况下的分布进行了数值计算，计算结果分别如图 4，5所示。由图 4可知，自重项对温度场的影响随着高度的增加而减小，但仅表现在稳定前的时间段，如在蒸发条件下该阶段随高度增加时温度值的最大增幅依次为15.7%，2.5%和0.8%，这是由于水分场急剧变化导致的热量扩散，但并不会显著影响稳定时的温度场分布特征，各特征点稳定温度变化幅度最大仅为1.8%。从图 5可以看出，考虑自重项与否对于各特征点含水率变化及其稳定含水率存在显著区别，如在蒸发条件下其稳定含水率随高度增加依次为0.46，0.35，0.26，较小于不考虑自重项时的0.48，0.38，0.30。这是由于土体内部的水分迁移主要由自重、温度梯度和含水率梯度引起，当不考虑自重时，水分在温度和含水率梯度的共同作用下由底部高含水率处向上层低含水率处迁移。而自重则是引起水分向下迁移的动力，阻碍底部水分向上迁移，因此，在表层蒸发条件下，考虑自重时的稳定含水率更低。

图 4 自重对温度场时空演化特征的影响

Figure 4. Effects of gravity on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 5 自重对水分场时空演化特征的影响

Figure 5. Effects of gravity on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

2.3 相变系数对水热耦合过程的影响

为研究水分蒸发相变系数（蒸汽流动）对非饱和土温度场及水分场的影响，设定相变系数ε分别为0（不考虑蒸汽流动），0.1，0.2，0.3，0.35，分别讨论了上述边界条件下各特征点的温度场及水分场的变化趋势，结果分别如图 6，7所示。由图 6可知，在不同相变系数条件下各特征点的温度变化趋势均呈先增加后逐渐稳定变化，在蒸发和干湿循环条件下，随着相变系数的增加，各特征点的稳定温度值逐渐降低，并且随着高度的增加，对温度的影响逐渐减弱，如在蒸发条件下P₁处，稳定温度值随设定相变系数的增加依次为25.0，21.1，17.2，13.3，11.4 ℃。但在降雨条件下，相变系数仅会影响前期温度变化，对稳定阶段的影响较小，最终的稳定值也不呈梯度分布。图 7为3种边界条件下各特征点含水率随时间变化的对比。

图 6 相变系数对温度场时空演化特征的影响

Figure 6. Effects of phase change coefficient on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 7 相变系数对水分场时空演化特征的影响

Figure 7. Effects of phase change coefficient on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

可见，相变系数的取值对土体体积含水率的影响并不显著，仅稳定含水率存在微小差异。该差异在蒸发条件下更为显著，尽管如此，相较于ε=0时，蒸发条件下不同相变系数的稳定含水率最大减幅在P3处仅有3.7%。说明相变系数取值对土体温度变化的影响极大，但对于含水率的影响几乎可以忽略不计，即对于非饱和土水热耦合问题时，相变系数取值是否合理会显著影响土体温度的计算值。

2.4 渗透系数对水热耦合过程的影响

渗透系数是土体渗透性表征指标，反映了水在土体孔隙中渗透流动的性能。为研究非饱和土体渗透系数取值对其温度场及水分场演化的影响，将渗透系数分别设定为常数1×10^-5 cm/s，m₁=0.4，m₁=0.5和m₁=0.6，渗透系数与体积含水率的关系曲线如图 4所示。计算了土体温度场和水分场的演化特征，结果分别如图 8，9所示。由图 8可知，不同渗透系数条件下各特征点的温度变化趋势均呈先增加后逐渐稳定变化，m₁的取值对土体温度的影响随着高度的增加而逐渐减弱，如在蒸发条件下，相较于m₁=0.4，m₁=0.5时随高度增加最大增幅依次为5.0%，0.6%和0.3%，m₁=0.6时随高度增加最大增幅依次为10.4%，1.1%和0.7%，但对其稳定温度值的影响较小。图 9为不同渗透系数时特征点含水率随时间变化的对比。可见，m₁的取值并不会显著影响各特征点含水率的整体变化趋势，但对表层土体含水率时空演化过程的影响更为显著，并且特征点的稳定含水率随着m₁的取值而变化，如蒸发条件下P₃处，m₁=0.5和m₁=0.6相较于m₁=0.4的稳定含水率的减幅分别为4.1%，8.5%。随着m₁取值的增大，渗透系数增大，土体内部水分下渗加强而减弱底部向上的水分补给，土体的稳定含水率逐渐减小，并且在土体表层变化更为显著。此外，在上述3种边界条件下，当渗透系数为常数时，土体的水热场变化特征会显著区别于基于van Genuchten模型拟合的渗透系数。

图 8 渗透系数对温度场时空演化特征的影响

Figure 8. Effects of permeability on temporal and spatial evolution characteristics of temperature

下载: 全尺寸图片幻灯片

图 9 渗透系数对水分场时空演化特征的影响

Figure 9. Effects of permeability on temporal and spatial evolution characteristics of volumetric water content

下载: 全尺寸图片幻灯片

3. 结论

（1）在蒸发、降雨入渗和干湿循环边界条件下，蒸发潜热项考虑与否和相变系数取值大小会显著影响土体内部温度场的分布特征，其影响程度随高度增加而逐渐减弱，但对水分迁移的影响并不显著。

（2）土体内部的水分迁移主要由温度梯度和水压梯度引起，其中，自重是引起水分向下迁移的动力，渗透系数增大也会加强土体内部水分下渗作用，二者均会在一定程度上阻碍底部水分向上部的迁移过程。因此，考虑自重和渗透系数较大时两种情况下的土体水分向下迁移更快，影响地下水对上层土体的补给和降雨入渗过程。自重项考虑与否与渗透系数选取还会在一定程度上影响温度场的变化，但仅表现在温度稳定前的时间段。

（3）自重等因子对非饱和土水热场的影响与边界条件有关，水分迁移会引起热量扩散，温度变化又会进一步影响水分场的分布。稳定时的温度梯度随着边界水分补给而逐渐减小，即降雨入渗边界条件下稳定时的温度梯度 < 干湿循环边界 < 蒸发边界。

（4）采用van Genuchten模型拟合的渗透系数更符合实际非饱和土的渗透特性，其水热场变化特征显著区别于常渗透系数情况。

图 1 反射波时间延迟计算示意图

Figure 1. Time delay calculation of reflected waves

下载: 全尺寸图片幻灯片

图 2 透射波时间延迟计算示意图

Figure 2. Time delay calculation of transmission waves

下载: 全尺寸图片幻灯片

图 3 三维模型时间延迟计算示意图

Figure 3. Time delay calculation of 3D model

下载: 全尺寸图片幻灯片

图 4 计算流程图

Figure 4. Flow chart of calculation

下载: 全尺寸图片幻灯片

图 5 计算模型示意图

Figure 5. Computational model

下载: 全尺寸图片幻灯片

图 6 输入位移时程曲线

Figure 6. Time histories of input displacement

下载: 全尺寸图片幻灯片

图 7 MD5计算结果

Figure 7. Results of MD5

下载: 全尺寸图片幻灯片

图 8 地表中点处的位移时程

Figure 8. Time histories of displacement at midpoint of surface

下载: 全尺寸图片幻灯片

图 9 不同时刻位移场云图

Figure 9. Cloud diagram of displacement field at different time

下载: 全尺寸图片幻灯片

参考文献(24)

[1]	胡聿贤. 地震工程学[M]. 北京: 地震出版社, 2006. HU Yu-xian. Earthquake Engineering[M]. Beijing: Seismological Press, 2006. (in Chinese)
[2]	耿萍. 铁路隧道抗震计算方法研究[D]. 成都: 西南交通大学, 2012. GENG Ping. Research on the Seismic Calculation Method of Railway Tunnel[D]. Chengdu: Southwest Jiaotong University, 2012. (in Chinese)
[3]	刘晶波, 杜义欣, 闫秋实. 黏弹性人工边界及地震动输入在通用有限元软件中的实现[J]. 防灾减灾工程学报, 2007, 27(增刊1): 37–42. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-OGTY200703001009.htm LIU Jing-bo, DU Yi-xin, YAN Qiu-shi. Implementation of viscoelastic artificial boundary and ground motion input in general finite element software[J]. Journal of Disaster Prevention and Mitigation Engineering, 2007, 27(S1): 37–42. (in Chinese) https://cpfd.cnki.com.cn/Article/CPFDTOTAL-OGTY200703001009.htm
[4]	刘晶波, 谷音, 杜义欣. 一致黏弹性人工边界及黏弹性边界单元[J]. 岩土工程学报, 2006, 28(9): 1070–1075. doi: 10.3321/j.issn:1000-4548.2006.09.004 LIU Jing-bo, GU Yin, DU Yi-xin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070–1075. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.09.004
[5]	何建涛, 马怀发, 张伯艳, 等. 黏弹性人工边界地震动输入方法及实现[J]. 水利学报, 2010, 41(8): 960–969. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201008014.htm HE Jian-tao, MA Huai-fa, ZHANG Bo-yan, et al. Method and realization of seismic motion input of viscous-spring boundary[J]. Journal of Hydraulic Engineering, 2010, 41(8): 960–969. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201008014.htm
[6]	XING J, MECHANICS L Z O E, SSB, et al. Statistical research on S-wave incident angle[J]. Earthquake Research in China, 1994, 8(1): 121–131.
[7]	TAKAHIRO S, TAKESHI U, RYOICHI T, et al. Estimation of earthquake motion incident angle at rock site[C]//Proc of 12th World Conference Earthquake Engineering, NZ National Society for Earthquake Engineering. Auckland. 2000.
[8]	杜修力, 黄景琦, 赵密, 等. SV波斜入射对岩体隧道洞身段地震响应影响研究[J]. 岩土工程学报, 2014, 36(8): 1400–1406. doi: 10.11779/CJGE201408004 DU Xiu-li, HUANG Jing-qi, ZHAO Mi, et al. Effect of oblique incidence of SV waves on seismic response of portal sections of rock tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1400–1406. (in Chinese) doi: 10.11779/CJGE201408004
[9]	王文晖. 地下结构实用抗震分析方法及性能指标研究[D]. 北京: 清华大学, 2013. WANG Wen-hui. Research on Practical Seismic Analysis Methods and Performance Index of Underground Structures[D]. Beijing: Tsinghua University, 2013. (in Chinese)
[10]	刘晶波, 王东洋, 谭辉, 等. 整体式反应位移法的理论推导及一致性证明[J]. 土木工程学报, 2019, 52(8): 18–23. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201908003.htm LIU Jing-bo, WANG Dong-yang, TAN Hui, et al. Theorectical derivation and consistency proof of the integral response deformation method[J]. China Civil Engineering Journal, 2019, 52(8): 18–23. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201908003.htm
[11]	赵密, 欧阳文龙, 黄景琦, 等. P波作用下跨断层隧道轴线地震响应分析[J]. 岩土力学, 2019, 40(9): 3645–3655. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909039.htm ZHAO Mi, OUYANG Wen-long, HUANG Jing-qi, et al. Analysis of axis dynamic response of rock tunnels through fault fracture zone under P waves of earthquake[J]. Rock and Soil Mechanics, 2019, 40(9): 3645–3655. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909039.htm
[12]	刘晶波, 王艳. 成层介质中平面内自由波场的一维化时域算法[J]. 工程力学, 2007, 24(7): 16–22. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200707006.htm LIU Jing-bo, WANG Yan. A 1d time-domain method for in-plane wave motion of free field in layered media[J]. Engineering Mechanics, 2007, 24(7): 16–22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200707006.htm
[13]	刘晶波, 王艳. 成层半空间出平面自由波场的一维化时域算法[J]. 力学学报, 2006, 38(2): 219–225. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB200602010.htm LIU Jing-bo, WANG Yan. A 1-d time-domain method for 2-d wave motion in elastic layered half-space by antiplane wave oblique incidence[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 219–225. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB200602010.htm
[14]	赵密, 杜修力, 刘晶波, 等. P-SV波斜入射时成层半空间自由场的时域算法[J]. 地震工程学报, 2013, 35(1): 84–90. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201301012.htm ZHAO Mi, DU Xiu-li, LIU Jing-bo, et al. Time-domain method for free field in layered half space under P-SV waves of oblique incidence[J]. China Earthquake Engineering Journal, 2013, 35(1): 84–90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201301012.htm
[15]	ZHAO M, YIN H Q, DU X L, et al. 1D finite element artificial boundary method for layered half space site response from obliquely incident earthquake[J]. Earthquakes and Structures, 2015, 9(1): 173–194.
[16]	尹侯权. 地震波斜入射时成层半空间场地反应分析方法及其应用[D]. 北京: 北京工业大学, 2015. YIN Hou-quan. A Method for Layered Half-Space Site Response Under Obliquely Incident Earthquake and its Application[D]. Beijing: Beijing University of Technology, 2015. (in Chinese)
[17]	王笃国, 赵成刚. 地震波斜入射下考虑场地非线性、地形效应和土结动力相互作用的大跨连续刚构桥地震响应分析[J]. 工程力学, 2017, 34(4): 32–41. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201704005.htm WANG Du-guo, ZHAO Cheng-gang. Seismic analysis of long-span continuous rigid frame bridge considering site nonlinearity, topography effect and soil-structure dynamic interaction under oblique incidence[J]. Engineering Mechanics, 2017, 34(4): 32–41. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201704005.htm
[18]	王笃国, 赵成刚. 地震波斜入射时二维成层介质自由场求解的等效线性化方法[J]. 岩土工程学报, 2016, 38(3): 554–561. doi: 10.11779/CJGE201603020 WANG Du-guo, ZHAO Cheng-gang. Two- dimensional equivalent linear seismic analysis of free field in layered half-space due to oblique incidence[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 554–561. (in Chinese) doi: 10.11779/CJGE201603020
[19]	黄景琦. 岩体隧道非线性地震响应分析[D]. 北京: 北京工业大学, 2015. HUANG Jing-qi. Study on Nonlinear Seismic Response of Rock Tunnels[D]. Beijing: Beijing University of Technology, 2015. (in Chinese)
[20]	徐海滨, 杜修力, 赵密, 等. 地震波斜入射对高拱坝地震反应的影响[J]. 水力发电学报, 2011, 30(6): 159–165. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201106031.htm XU Hai-bin, DU Xiu-li, ZHAO Mi, et al. Effect of oblique incidence of seismic waves on seismic responses of high arch dam[J]. Journal of Hydroelectric Engineering, 2011, 30(6): 159–165. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201106031.htm
[21]	刘云贺, 张伯艳, 陈厚群. 拱坝地震输入模型中黏弹性边界与黏性边界的比较[J]. 水利学报, 2006, 37(6): 758–763. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200606019.htm LIU Yun-he, ZHANG Bo-yan, CHEN Hou-qun. Comparison of spring-viscous boundary with viscous boundary for arch dam seismic input model[J]. Journal of Hydraulic Engineering, 2006, 37(6): 758–763. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200606019.htm
[22]	李明超, 张佳文, 张梦溪, 等. 地震波斜入射下混凝土重力坝的塑性损伤响应分析[J]. 水利学报, 2019, 50(11): 1326–1338, 1349. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201911005.htm LI Ming-chao, ZHANG Jia-wen, ZHANG Meng-xi, et al. Plastic damage response analysis of concrete gravity dam due to obliquely incident seismic waves[J]. Journal of Hydraulic Engineering, 2019, 50(11): 1326–1338, 1349. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201911005.htm
[23]	WEI X C, CHEN T S. Joint PP and PS AVO inversion based on Zoeppritz equations[J]. Earthquake Science, 2011, 24(4): 329–334.
[24]	傅淑芳, 刘宝诚. 地震学教程[M]. 北京: 地震出版社, 1991. FU Shu-fang, LIU Bao-cheng. Seismology Tutoria[M]. Beijing: Scismic Press, 1991. (in Chinese)

施引文献(10)

期刊类型引用(6)

1.	白雪. 煤矿顶管掘进参数实测分析与控制方法研究. 煤矿机械. 2025(02): 65-68 . 百度学术
2.	李博，刘宇翔，陈建国，杨耀红，张哲. 基于物理信息神经网络的长距离顶管施工顶力预测. 人民长江. 2025(01): 147-155 . 百度学术
3.	钟祖良，米朝阳，范一飞，李超，刘新荣. 软岩蠕变作用下顶管顶力计算方法研究. 岩石力学与工程学报. 2025(02): 292-302 . 百度学术
4.	钟祖良，杜传烨，刘新荣，李超. 岩石顶管穿越深大断层破碎带摩阻力计算方法研究. 岩土力学. 2025(03): 943-954 . 百度学术
5.	叶生华，陆俊，明攀，王涛，聂叙平. 复杂岩溶地层大口径DRCP顶管施工试验研究. 人民长江. 2024(08): 166-173 . 百度学术
6.	钱朋亮. 三圆咬合顶管顶推力计算方法研究. 铁道建筑技术. 2024(10): 71-76 . 百度学术