水合物注热开采影响下海底斜坡动态稳定性评价

年廷凯; 宋晓龙; 张浩; 荣泽

doi:10.11779/CJGE202212003

水合物注热开采影响下海底斜坡动态稳定性评价 English Version

大连理工大学海岸和近海工程国家重点实验室, 辽宁大连 116024

基金项目:

国家自然科学基金项目 52079020 & 51879036

辽宁省兴辽英才计划项目 XLYC2002036

详细信息

作者简介:
年廷凯(1971—)，男，教授，博士生导师，主要从事海洋岩土力学、能源岩土工程及工程地质灾害领域的教学和科研工作。E-mail: tknian@dlut.edu.cn

中图分类号: TU432
计量
- 文章访问数: 289
- HTML全文浏览量: 47
- PDF下载量: 34
出版历程
- 收稿日期: 2021-11-14
- 网络出版日期: 2022-12-13
- 刊出日期: 2022-11-30

Dynamic stability evaluation of submarine slopes with hydrate reservoir under influences of heat injection exploitation

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China

摘要

摘要: 注热开采会破坏水合物储层的温压平衡，引发水合物分解、储层孔隙压力激增，进而可能诱发海底斜坡沿水合物层发生失稳滑动甚至大规模海底滑坡，因此研究开采影响下水合物储层的动态响应和海底斜坡实时稳定性十分重要。首先推导了一种考虑热-水-化(THC)耦合作用的实时超孔压求解格式，建立水合物饱和度与超孔压之间的内在关系；进一步，基于无限坡极限平衡理论，发展水合物注热开采下海底斜坡动态稳定性的简化评价方法，并开发相应的数值模拟及计算程序。利用该方法对中国南海北部陆坡第二次水合物试采区开展了深入分析，探究了注热开采过程中海底斜坡的温度剖面、水合物饱和度剖面和动态稳定性安全系数等演变特征，并提出了合理化的开采建议。研究成果为深刻认识水合物分解引起的海底斜坡失稳破坏机理、实现水合物的安全可持续开发和海洋地质灾害风险的科学评估提供了重要依据。
- 水合物开采 /
- 海底斜坡动态 /
- 稳定性 /
- THC耦合 /
- 超孔压演化 /
- 南海北部陆坡
Abstract: The heat injection exploitation will destroy the temperature and pressure balance of hydrate reservoirs, cause hydrate dissociation, lead to the dramatic increase of pore pressure of strata, and then induce the instability of submarine slopes along the hydrate reservoirs or even a large-scale submarine landslide. Therefore, it is very important to investigate the dynamic response of the hydrate reservoirs and the real-time stability of the submarine slopes after environmental changes. First, a solving equation for calculating the real-time excess pore pressure considering thermo-hydro-chemical (THC) coupling is derived, and the internal relation between the hydrate saturation and the excess pore pressure is also established. Further, a simplified evaluation approach for the dynamic stability of the submarine slopes under the influences of heat injection exploitation of the hydrate reservoirs is proposed based on the theory of infinite slope limit equilibrium analysis, and the corresponding numerical simulation and calculation code are developed. This approach is employed to analyze the submarine slope in the second hydrate extraction area on the northern continental slope of the South China Sea. The evolution characteristics of the submarine slopes in the process of heat injection exploitation of the hydrate reservoirs, such as the temperature profile, hydrate saturation profile and dynamic stability factors, are explored, and the reasonable mining suggestions are put forward. The research results provide an important basis for understanding the mechanism of instability of submarine slopes caused by hydrate dissociation, realizing the safe and sustainable development of the hydrate reservoirs and the scientific assessment of marine geological disaster risks.
- marine hydrate exploitation /
- submarine slope /
- dynamic stability /
- thc coupling /
- evolution of excess pore pressure /
- northern continental slope of South China Sea

HTML全文

0. 引言

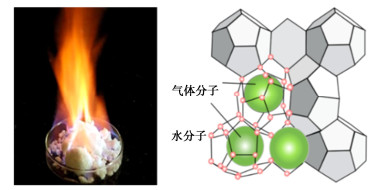
天然气水合物是一种笼形晶状化合物（图 1），具有能量密度高、储量巨大等特点，其中97%以上分布在海底沉积物中^[1-2]。据估算，全球天然气水合物中含碳量相当于全球已探明传统化石燃料总碳量的两倍，被普遍认为是21世纪最具潜力的新型清洁能源之一^[2]。目前世界很多国家都开展了水合物勘探和试采工作，例如美国JIP计划^[3]、日本MHR & DP项目^[4]，挪威GANS项目^[5]。另外，俄罗斯、德国、韩国、印度等国家都相继开展了水合物相关的研究项目和开发计划^[6]。中国在水合物领域的研究起步较晚，但取得了重要成果。在南海北部陆坡圈定了6个水合物成矿远景区，19个成矿区带，25个有利区块和24个钻探目标区^[7-8]。特别是在神狐、东沙等海域钻探获取了水合物实物样品，发现了多种类型的高品位水合物储层，锁定了试采目标^[9]。并于2017年和2020年成功完成了两次水合物试采工作，取得了突破性进展^[10-11]。

图 1 水合物实物与分子结构图^[2]

Figure 1. Physical and molecular structural diagrams of hydrate

下载: 全尺寸图片幻灯片

目前水合物领域的研究主要集中在资源储量勘探评估、水合物开发技术和水合物地层稳定性评价3个方面。其中水合物地层稳定性评价是水合物安全可持续生产的前提条件，特别是考虑开采影响下水合物储层的动态响应及海底斜坡稳定性问题。通过海洋工程地质调查、室内模型试验和数值模拟研究发现，含水合物储层的海底斜坡失稳破坏，往往与水合物分解后产生的超孔隙压力有关^[12-14]。因此，近年来专家学者对与水合物分解相关的超孔压计算模型进行了深入研究。例如，Nixon等^[15]提出一个数学模型，通过假定水合物的分解比例，量化了不排水条件下水合物分解产生的超孔压。在此基础上，Xiong等^[16]考虑甲烷的溶解度对孔隙压力的影响，对模型进行了改进。Zhang等^[17]通过RK方程计算了真实甲烷气体的压缩系数，并将此系数引入到上述模型。Chen等^[18]利用此模型，通过考虑水合物分解过程中压力和温度的平衡，计算了水合物分解的最大超孔隙压力。此外，刘锋等^[19]、Grozic^[20]、Zhu等^[21]进行了相关研究。然而，这些研究中所采用的孔隙压力模型很少考虑水合物储层的热-水-化(THC)耦合作用，导致无法准确获取瞬态超孔隙压力及其演化特征，因此很难准确评价海底斜坡的实时动态稳定性。

本文考虑水合物注热开采的影响，发展了一种热-水-化（THC）耦合作用下海底斜坡动态稳定性简化评价方法，并自主开发了相应的数值计算程序，建立了水合物饱和度与超孔隙压力间的内在关系；进而获取了多物理场耦合作用下水合物分解引发的瞬态超孔压演化特征及储层的动态响应；并利用改进的极限平衡法对海底斜坡稳定性进行动态评价；最后以南海北部陆坡水合物试采区典型斜坡为目标，研究了水合物注热开采影响下水合物储层动态响应及实时稳定性演化。

1. 考虑THC耦合作用的超孔压确定方法

1.1 THC耦合方程

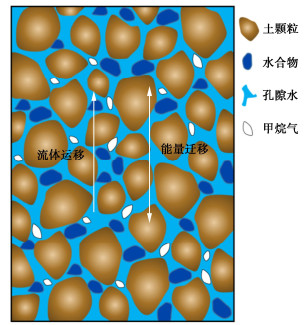
含水合物沉积物可视为由多组分（土骨架、水、水合物）和多相（固、液、气）组成的动态系统（图 2）。根据地质调查^[22]，海底水合物大多储存于相对封闭的沉积地层中，其形成由沉积物沉积、孔隙流体流动及底部甲烷供给等因素决定，且这类储层中一般缺乏明显的横向变化，因此只需考虑竖向的流体运移和能量迁移。基于此，采用Xu等^[23]提出的一维简化THC耦合模型描述海底水合物地层的赋存特性。该模型通过求解质量、能量和甲烷守恒方程，给出了水合物储层边界的计算公式，并推导了初始地层温度–压力分布和水合物聚集的表达式。

图 2 水合物沉积物多组分多相孔隙介质示意图

Figure 2. Schematic diagram of multi-component multi-phase porous sediments containing gas hydrate

下载: 全尺寸图片幻灯片

首先，根据质量守恒给出一维简化情况下流体运移的控制方程：

$- \frac{{k{\rho _{\text{l}}}}}{{{\mu _{\text{l}}}}}\left( {\frac{{{\text{d}}P}}{{{\text{d}}z}} + {\rho _{\text{l}}}g} \right) = {q_{\text{f}}}\text{，}$

(1)

式中，k为渗透率，ρ_l，μ_l分别为液体相的密度和动态黏度，P为地层压力，z为空间坐标，g为重力加速度，q_f为总质量通量。

其次，水合物储存系统的能量迁移可通过能量守恒方程描述，其简化模式为

$- \lambda \frac{{{\text{d}}T}}{{{\text{d}}z}}{\text{ + }}{q_{\text{f}}}{C_{{\text{pl}}}}T{\text{ = }}{q_{\text{e}}}\text{，}$

(2)

式中，λ为有效导热系数，T为地层温度，C_pl为水合物的比热容，q_e为总能量通量。

最后，储存系统中的甲烷运移可由甲烷介质的质量守恒方程描述：

$- \phi {K_{\text{m}}}{S_{\text{l}}}\frac{{{\text{d}}{M_{\text{l}}}}}{{{\text{d}}z}}{\text{ + }}{q_{\text{f}}}{M_{\text{l}}}{\text{ = }}{q_{\text{m}}}\text{，}$

(3)

式中，ϕ为沉积物孔隙度，K_m为扩散系数，S_l为液体相饱和度，M_l为液体相中甲烷浓度，q_m为与深度相关的甲烷通量。

以上3组基本控制方程间的耦合作用，其具体的建立过程为对式（1），（2）进行积分，可得到关于压力剖面P和地层温度剖面T的函数表达式：

$P - {P_0} = - \left( {\frac{{{q_{\text{f}}}{\mu _{\text{l}}}}}{{k{\rho _{\text{l}}}}}{q_{\text{f}}} + {\rho _{\text{l}}}g} \right)z\text{，}$

(4)

$T= \begin{cases}-\left(\xi-T_0\right) \mathrm{e}^{\frac{q_{\mathrm{e}}}{\lambda \cdot \xi} z}+\xi & \left(q_{\mathrm{f}} \neq 0\right) \\ -\frac{q_{\mathrm{e}}}{\lambda} z+T_0 & \left(q_{\mathrm{f}}=0\right)\end{cases}\text{，}$

(5)

式中，ξ为参数，ξ=q_e/(q_fC_pl)，P₀，T₀为海底面处的压力和温度。联立式（4），（5），可以得到任意深度z处的压力与温度之间的关系式。

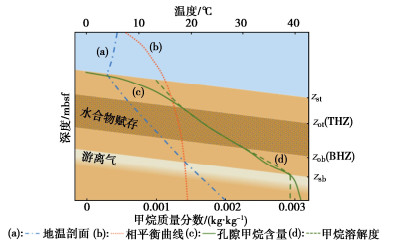
水合物的形成需要适当的温压条件，地层温度剖面和水合物相平衡曲线共同确定了水合物的理论稳定区间，如图 3所示。Sloan等^[24]通过试验测定了甲烷水合物的相平衡曲线，表达为

$T_{\mathrm{diss}}=\left\{\begin{array}{ll} 9.6349 \ln P+197.65 & (P \geqslant 2576.74 \mathrm{kPa}) \\ 0.0158 P+232.7 & (P<2576.74 \mathrm{kPa}) \end{array},\right.$

(6)

图 3 水合物理论稳定区域与生成区域的空间关系示意图^[26]

Figure 3. Schematic diagram of spatial relationship between hydrate stability zone and hydrate formation zone

下载: 全尺寸图片幻灯片

式中，T_diss为水合物分解的相平衡温度。

将式（4）~（6）联立，可得到水合物理论稳定区域的上边界z_st和下边界z_sb：

${z_{{\text{st}}}} = 0 \text{，}$

(7)

$z_{\mathrm{sb}}=\left\{\begin{array}{ll} -\frac{\lambda}{q_{\mathrm{f}} C_{\mathrm{pl}}} \ln \left(\frac{q_{\mathrm{e}}-q_{\mathrm{f}} C_{\mathrm{pl}} T_0}{q_{\mathrm{e}}-q_{\mathrm{f}} C_{\mathrm{pl}} T_{\mathrm{diss}}}\right) & \left(q_{\mathrm{f}} \neq 0\right) \\ -\frac{\lambda}{q_{\mathrm{e}}}\left(T_{\mathrm{diss}}-T_0\right) & \left(q_{\mathrm{f}}=0\right) \end{array},\right.$

(8)

式中，上边界z_st和下边界z_sb见图 3右侧标注。另外，水合物的生成不仅需要适宜的温度和压力，还取决于孔隙中甲烷的可用量。只有当孔隙中甲烷含量大于或等于甲烷溶解度时，才可能在孔隙中形成水合物，如图 3曲线（c）和曲线（d）所示。在水合物生成区域内部，多余的甲烷会与水结合形成水合物，因此孔隙甲烷含量等于甲烷溶解度，可由下式描述：

${M_{{\text{sl}}}}(T) = {M_{{\text{sl,diss}}}}({T_{{\text{diss}}}},P,S) \cdot \exp \left( {\frac{{T - {T_{{\text{diss}}}}}}{\beta }} \right)\text{，}$

(9)

式中，M_sl为任意温度、压力及孔隙中盐浓度影响下的甲烷溶解度，M_{sl, diss}(T_diss, P, S)为甲烷溶解度关于相平衡温度T_diss、压力P和盐度S的函数，由试验测定^[25]，β=14.4 ℃为经验常数。

而在水合物生成区域上部，孔隙中甲烷含量小于其溶解度，甲烷介质以溶质赋存于孔隙中，可由式（3）描述。为确定水合物生成区域的上边界z_ot和下边界z_ob(图 3右侧标注)，在0→z_ot区间内对式（3）进行积分，并辅以式(4)，(5)，(9)可得

$z_{\mathrm{ot}}= \begin{cases}-\frac{\phi K_{\mathrm{m}}}{q_{\mathrm{f}}} \ln \left(\frac{q_{\mathrm{mt}}-q_{\mathrm{f}} M_0}{q_{\mathrm{mt}}-q_{\mathrm{f}} M_{\mathrm{sl}}\left(z_{\mathrm{ot}}\right)}\right) & \left(q_{\mathrm{f}} \neq 0\right) \\ -\frac{\phi K_{\mathrm{m}}}{q_{\mathrm{mt}}}\left(M_{\mathrm{sl}}\left(z_{\mathrm{ot}}\right)-M_0\right) & \left(q_{\mathrm{f}}=0\right)\end{cases} \text{，}$

(10)

${z_{{\text{ob}}}}: - \phi {K_{\text{m}}}{\left( {\frac{{{\text{d}}{M_{{\text{sl}}}}}}{{{\text{d}}z}}} \right)_{z = {z_{{\text{ob}}}}}}{\text{ + }}{q_{\text{f}}}{M_{{\text{sl}}}}({z_{{\text{ob}}}}){\text{ = }}{q_{\text{m}}} \text{，}$

(11)

式中，M₀为海底面处的甲烷含量，q_mt为z_ot处的甲烷通量。

综合考虑式（7），（8），（10），（11），同时满足水合物理论稳定区域条件和水合物生成区域条件即可得出水合物真实赋存区域，其上边界THZ和下边界BHZ如图 3所示。

进一步，考虑水合物形成的时间尺度和空间分布与甲烷供应有关，可给出确定整个水合物储层初始水合物饱和度的表达式^[23]。甲烷水合物填充孔隙度ϕ到任意平均饱和度S_h所需的时间t₀近似为

${t_0} \approx {S_{\text{h}}}{\left( {\frac{{\partial {S_{\text{h}}}}}{{\partial t}}} \right)^{ - 1}}\text{，}$

(12)

式中，t为时间，∂S_h/∂t为水合物的积累速率，

$\frac{{\partial {S_{\text{h}}}}}{{\partial t}} = \frac{1}{{\phi ({\rho _{\text{h}}}{M_{\text{h}}} - {\rho _{\text{l}}}{M_{{\text{sl}}}})}}\left( {\phi {K_{\text{m}}}\frac{{{{\text{d}}^2}{M_{{\text{sl}}}}}}{{{\text{d}}{z^2}}} - {q_{\text{f}}}\frac{{{\text{d}}{M_{{\text{sl}}}}}}{{{\text{d}}z}}} \right) \text{，}$

(13)

其中，ρ_h，M_h为水合物密度和水合物中甲烷的质量分数。综上，由式（1）~（13）构建了一套完整的控制方程，可用于计算地层初始状态下的温度、压力剖面和水合物饱和度剖面。

1.2 超孔压计算

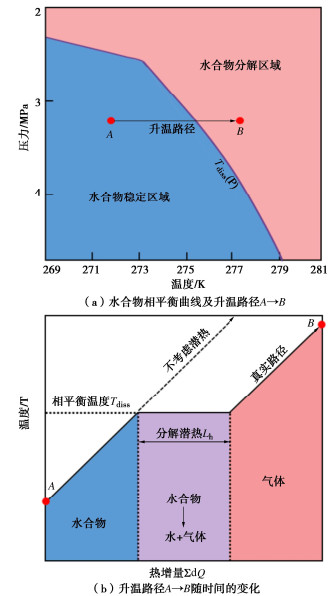
水合物储层注热开采会破坏地层中温度的动态平衡，一旦地层中的温度T超过水合物的相平衡温度T_diss，水合物会产生分解。地层温度剖面T的演化可以用一维热传导方程描述：

$\frac{{\partial T(z,t)}}{{\partial t}} = \kappa \frac{{{\partial ^2}T}}{{\partial {z^2}}} + s(z,t)\text{，}$

(14)

式中，κ为地层有效热扩散系数，假设为常量，这是因为水合物的导热系数接近于水（相差 < 10%）^[27]，s(z，t)为源项，用以考虑可能的热量增加和消耗。需要注意的是，在地层升温过程中（见图 4（a），A→B），一旦温度超出水合物的稳定区域，水合物会发生分解。这其中包含水合物的相变过程，因此需要消耗一定的潜热。这意味着当地层温度T_{i, j}（下标i代表时间步，j代表某地层深度）达到T_diss后，随着热量的增加，温度会保持T_diss不变，这会延迟温度在地层中的传播（见图 4（b））。

图 4 注热开采导致的地层温度变化路径示意图

Figure 4. Schematic diagram of change path of stratum temperature caused by hydrate heat injection exploitation

下载: 全尺寸图片幻灯片

为了计算潜热的消耗，采用热积分法^[28]进行简化。具体实施过程：首先利用有限差分法求解式(14)，计算在任意时间步i时地层深度j的温度T_{i, j}。在水合物分解区域将此温度修正为T_diss，进而会产生一个温度增量dQ_{i, j}=C_ph(T_ij-T_diss)，此温度增量会根据时间步和深度更新。将每一时间步所产生的热量累计求和，可以计算出地层深度j增加的总增量∑dQ_{i, j}。一旦累积的总热量超过水合物的分解潜热，则意味着相变完成，地层温度重新按照式（14）升高。在此过程中，位于深度j处，时刻i时的水合物饱和度S_{h i, j}为

${S_{{\text{h}} i,j}} = {S_{{\text{h}} j}} \times \frac{{{L_{\text{h}}} - \Sigma {\text{d}}{Q_{i,j}}}}{{{L_{\text{h}}}}}\text{，}$

(15)

式中，S_{h, j}为深度j处的初始饱和度，L_h为水合物的分解潜热。

根据式（15）可得出在地层温度变化过程中水合物的分解量，

$\Delta {S_{{\text{h }}i{\text{,}}j}} = \Sigma ({S_{{\text{h }}i{\text{,}}j}} - {S_{{\text{h }}i - 1{\text{,}}j}})。$

(16)

最后，利用气体非逃逸方法计算温度升高过程中瞬态超孔隙压力及其演化。此方法由Nixon等^[15]首先提出，后续不少学者对该方法进行了完善^[16-21]。这里在前人工作的基础上，充分考虑水合物赋存系统的THC耦合作用，获取水合物实时分解量(式(16))，并引入到该方法中，实现升温后地层中的真实超孔隙压力演化。其中做了如下假设：①依据中国南海水合物试采区的地质调查结果，其水合物储层沉积物以细粒为主，渗透系数较小^[9]，因此忽略水合物分解后气体的渗流；②水合物赋存区的孔隙水在水合物分解前已处于甲烷饱和状态，因此忽略分解后生成甲烷在孔隙水中的溶解；③相对于气体的压缩量其余介质的压缩量很小，忽略不计。

基于以上假设，单位水合物分解后沉积物的体积变化等于生成气体的体积∆V_unit，即

$\Delta {V_{{\text{unit}}}} = {V_{\text{g}}} + {V_{{\text{wh}}}} - 1\text{，}$

(17)

式中，V_g为水合物分解产生的气体体积，V_g=164.6P_atmT_nat/(T_atmP_nat)，P，T分别为地层压力和温度，下标atm和nat分别为标准条件和地层真实条件，V_wh为水合物分解产生水的体积。故沉积物总体积变化为

$\Delta V = \phi \Delta {S_{{\text{h}}i,j}}V(\frac{{164.6{p_{{\text{atm}}}}{T_{{\text{nat}}}}}}{{{T_{{\text{atm}}}}{p_{{\text{nat}}}}}} + {V_{{\text{wh}}\theta }} - 1)。$

(18)

根据有效应力原理，超孔隙压力与沉积物变形有关，

$\begin{aligned} u_{\mathrm{e} i, j} & =-E_{\mathrm{s}} \Delta \varepsilon_{\mathrm{v}}=E_{\mathrm{s}} \frac{\Delta V}{V} \\ & =E_{\mathrm{s}} \phi \Delta S_{\mathrm{h} i, j}\left(\frac{164.6 p_{\text {atm }} T_{\text {nat }}}{T_{\mathrm{atm}} p_{\text {nat }}}+V_{\mathrm{wh}}-1\right), \end{aligned}$

(19)

式中，u_{e i, j}为时刻i时深度j处的超孔隙压力，ε_v为沉积物体应变，E_s为压缩模量，其余参数的物理意义同前。综上，可以得到地层升温后考虑THC耦合的超孔隙压力及其演化特征。

需要指出的是，在超孔压计算中做了一些合理性假设，忽略了一部分气体渗流和其余介质的压缩量，故计算出的超孔压会出现大于实际值的情况。另外，水合物分解产生的孔压会增大地层压力P_nat，进而反向影响水合物的分解，使水合物分解减缓，上述超孔压计算方法为单向耦合过程，即不考虑这种超孔压的反向耦合效应，使得海底斜坡的稳定性评价偏于安全。

1.3 方法验证

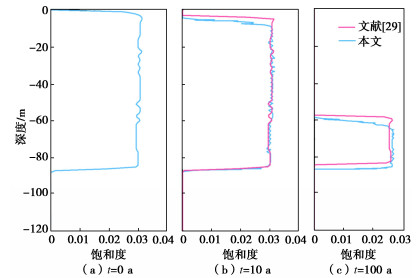
为了检验上述超孔压计算方法的正确性，复刻了Reagan等^[29]基于TOUGH+HYDRATE的模拟案例。TOUGH+HYDRATE为目前关于水合物分解模拟较为普遍的商业软件之一，并得到了广泛应用^[30-31]。此案例描述了浅层水合物赋存的典型场景，其中水深为320 m，海底温度为0.4℃，地温梯度为3℃/100m，模拟了海底水合物层100 a内，以每年0.03℃上升工况下水合物饱和度的动态响应。

对比文献[29]中设定升温工况下的计算结果，可见不同时刻（0，10，100 a）水合物饱和度的演化曲线具有较好的一致性，如图 5所示。根据式（19）可知，超孔压计算结果的合理性取决于水合物饱和度变化量∆S_{hi, j}的正确性，上述饱和度演化曲线的一致性很好的检验了本文提出的超孔压计算方法的正确性。

图 5 水合物饱和度剖面演化曲线对比图

Figure 5. Comparison of evolution curves of hydrate saturation profile

下载: 全尺寸图片幻灯片

2. 海底斜坡动态稳定性评价方法

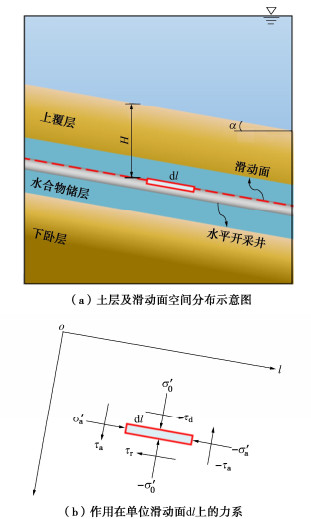
极限平衡方法(LEM)被广泛用于海底斜坡的稳定性评价，尤其对于长度远大于沉积层厚度的无限坡。海洋工程地质调查表明，大多数水合物储层与海底面平行分布，贮藏于一定厚度的不透水覆盖层下方^[10]，因此将海底斜坡概化为由上覆层、水合物储层和下卧层组成的无限斜坡（图 6（a））。注热开采条件下，水平井附近的水合物开始分解，将水合物的分解前缘视为潜在滑动面，并以此对海底斜坡进行稳定性评价，如图 6所示。

图 6 水合物开采影响下典型海底斜坡稳定性评价示意图^[32]

Figure 6. Schematic diagram of stability evaluation of typical submarine slope under influences of hydrate exploitation

下载: 全尺寸图片幻灯片

根据极限平衡方法，海底斜坡的稳定性安全系数等于滑动面上的抗剪强度和剪应力的比值，

${F_{\text{s}}} = \frac{{\int {{{\vec \tau }_{\text{r}}}{\text{d}}l} }}{{\int {{{\vec \tau }_{\text{d}}}{\text{d}}l} }}\text{，}$

(20)

式中， ${\vec \tau _{\text{r}}}$ ， ${\vec \tau _{\text{d}}}$ 分别为滑动面处沉积物的抗剪强度和剪应力，dl为单元滑动面长度，通过建立垂直于l轴的力系平衡，可以导出：

${\vec \tau _{\text{r}}} = c' + {\sigma '_0}\tan \varphi '{\text{ = }}c' + (\sigma - {u_{\text{e}}})\tan \varphi ' \text{，}$

(21)

${\vec \tau _{\text{d}}} = \gamma 'H\sin \alpha \cos \alpha \text{，}$

(22)

式中，φ′为有效内摩擦角， ${\sigma '_0}$ 为上覆有效应力 ${\sigma '_0}$ = $\sigma - {u_{\text{e}}}$ ， $\sigma$ 为总上覆压力 $\sigma$ = $\gamma '$ Hcos² $\alpha$ ， $\gamma '$ 为沉积物有效重度，H为滑面深度，c′为沉积物有效黏聚力。水合物分解会引起沉积物胶结强度弱化，进而导致黏聚力降低^{[31, 33]}，这里假设黏聚力随着水合物的分解呈线性折减：

${c'_i} = - ({c'_1} - {c'_2})\frac{{\Delta {S_{{{\text{h}}^{}}i,j}}}}{{{S_{{{\text{h}}^{}}i,j}}}}{\text{ + }}{c'_1} \text{，}$

(23)

式中， ${c'_i}$ 为i时刻的黏聚力， ${c'_1}$ ， ${c'_2}$ 分别为初始黏聚力和最终黏聚力。

将式（21），（22）代入式（20）中，可得出海底斜坡不同深度、不同时刻的瞬态稳定性安全系数F_{s i, j}为

${F_{{{\text{s}}_{}}i,j}} = \frac{{{{c'}_i}}}{{\gamma 'H\sin \alpha \cos \alpha }} + \left( {1 - \frac{{{u_{{{\text{e}}_{}}i,j}}}}{\sigma }} \right)\frac{{\tan \varphi '}}{{\tan \alpha '}} 。$

(24)

3. 注热开采下海底斜坡稳定性实例分析

3.1 研究区域

选取南海北部陆坡白云凹陷作为研究区，区域整体位于珠江口盆地珠二坳陷内，走向近东西，面积大于2.0×10⁴ km²，是南海北部最大的一个深水凹陷，其北部与番禺低隆起相接，南端是珠江口盆地的南部隆起带^[34]。区域内发育有大量现代海底峡谷（见图 7），沉积物失稳频发。中国地质调查局于2019年10月—2020年4月在此区域进行了第二次天然气水合物试采，实现了连续产气30 d，总产气量86.14×10⁴ m³，大大提高了日产气量和产气总量^[11]。此次试采首次提出了利用水平井开采水合物的工作思路，可有效克服直井开采大压差导致二次水合物和冰生成的风险。由于复杂地质环境影响，开采引起的水合物分解可能在海底斜坡内部产生潜在滑动面，即使在坡度很小的情况下也会引发斜坡破坏。特别是考虑到海底浅表层沉积物强度低^[35-36]，易在外部作用干扰下发生土体失稳，进而可能导致海底滑坡等地质灾害，威胁海洋开采平台、锚固基础和海底管线等水下设施的安全^[37-39]。这里主要探讨水平井注热开采工况下水合物储层的超孔压演化过程及海底斜坡动态稳定性评价。

图 7 研究区位置及区域海底地形条件^{[11, 40]}

Figure 7. Location of study area and topography of regional seabed

下载: 全尺寸图片幻灯片

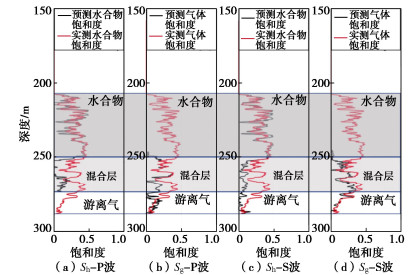
为服务于第二次水合物试采井的轨迹优选，在试采水平井靶点位置附近进行了先导井测试工作，并利用测井得到的P波速度和S波速度预测了水合物饱和度S_h和游离气饱和度S_g分布（图 8）^[41]。分析可见，该区域水合物储层位于海底面以下深度207.8~253.4 m，厚度为45.6 m，平均孔隙度为37.3%，平均水合物饱和度为31.0%^[41]，全井段岩性主要是泥质粉砂，渗透系数较小。另外，海洋地质调查显示此区域水深1000~1500 m，平均地形坡度为3°，海底面温度为3.3~3.7℃，地热梯度为45~67 ℃/km^[9]。基于开采井原位测试数据，构建二维海底斜坡模型，由上覆层、水合物层和下卧层组成，如图 6（a）所示。为达到最大传热效率，将水平井设置在水合物储层中间位置，即H=230.6 m处。设定由于注热影响，地层温度以0.1 K/d的速度匀速增加，总升高温度为10 K，当温度达到设定值后保持不变。模型所用具体参数见表 1。

图 8 先导井测井响应柱状图^[41]

Figure 8. Histogram logging response of pilot well

下载: 全尺寸图片幻灯片

表 1 模型参数^{[9, 11, 26, 41-42]}

Table 1. Model parameters

参数		取值	单位
坡体参数	z (深度)	—	m
	α (坡度)	3	°
	H(水平井位置)	230.6	m
地层参数	T₀(海底温度)	3.5	℃
	G/(地热梯度)	56	K/km
	S_h (初始饱和度)	31	%
	k (渗透率)	2.38	mD
	κ (有效热扩散系数)	4.5×10⁻⁷	m²/s
	λ (有效导热系数)	3.66	W/(m·K)
	c₁′ (初始黏聚力)	800	kPa
	c₂′ (最终黏聚力)	30	kPa
	φ′ (内摩擦角)	8.03	°
	ρ (体密度)	1650	kg/m³
	ϕ (孔隙度)	0.37	m³/m³
通用参数	ρ_l/(液相密度)	1024	kg/m³
	ρ_h (水合物密度)	930	kg/m³
	C_pl (液体比热)	4.18×10³	J/(kg·K)
	C_ph/(水合物比热)	2.16×10³	J/(kg·K)
	μ_l (液体动态黏度)	8.87×10⁻⁴	kg/(m·s)
	S (液体盐度)	3.5	%
	L_h/(水合物潜热)	56552-16.8/T	J/kg

下载: 导出CSV

| 显示表格

3.2 水合物储层动态响应分析

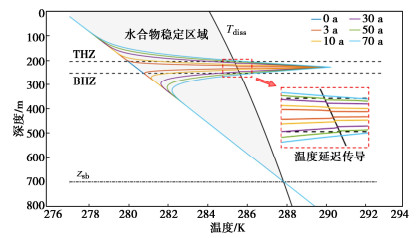
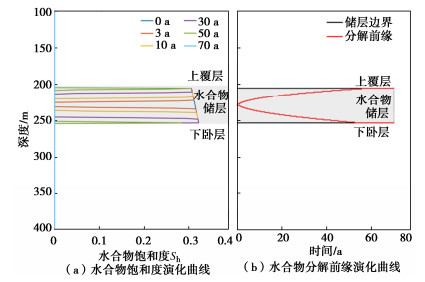
图 9为模拟工况下地层温度剖面的演化曲线，其中THZ和BHZ分别表示水合物储层的上顶面和下底面。初始地温曲线（0 a）和水合物相平衡曲线（T_diss）所围成的阴影部分为水合物的理论稳定区间（下底面为z_sb）。可以看到，由于水平井中热量的注入，水合物储层中部的温度开始升高，并逐渐向上下扩散，一旦温度超过水合物的相平衡温度，水合物开始分解（图 10）。可以观察到，在曲线T_diss附近地层的温度出现局部的降低，这是因为水合物分解是吸热过程，消耗了一定量的潜热，潜热的消耗会造成温度传导的延迟。

图 9 地层温度剖面演化曲线

Figure 9. Evolution curves of stratum temperature profile

下载: 全尺寸图片幻灯片

图 10 升温过程中水合物储层动态响应

Figure 10. Dynamic responses of hydrate reservoir during heating process

下载: 全尺寸图片幻灯片

图 10（a）为水合物饱和度的演化曲线。

可以看到，随着热量的注入储层中部水合物最先开始分解，饱和度逐渐降为0，在地层中形成一条分解带，且随着热量的传递，上下两侧的水合物也开始分解，分解带不断延伸。图 10（b）为水合物分解前缘的演化曲线，可以更加直观地看到水合物的分解及传播过程，其中红色曲线代表水合物分解前缘，黑色曲线为水合物储层的上下界面。可以看到，分解前缘最先产生于储层中部，并不断向两侧移动，直到与水合物储层上下界面重合，意味着水合物全部分解；在储层中部，水合物分解前缘的演化非常迅速，而在储层两侧则相对缓慢。这是因为储层中部靠近水平井热源，此处的水合物分解反应更加剧烈，而如上所述，水合物分解会导致地层中热量的延迟传导，故储层两侧的水合物分解需要更长的时间。

3.3 海底斜坡动态稳定性分析

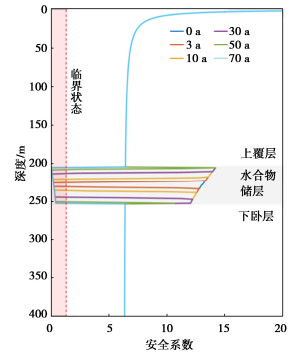
图 11显示海底斜坡安全系数沿深度的变化曲线。可以看到，初始状态下海底斜坡处于稳定状态，且由于水合物的胶结作用，增加了沉积物的强度，使得初始状态下水合物储层处的安全系数明显高于地层其它位置。但随着水合物分解，海底斜坡的安全系数迅速减小，并达到临界状态。一方面是由于胶结作用的丧失，沉积物强度迅速降低，另一方面水合物分解产生的超孔隙压力减小了地层的有效应力，随着水合物分解区域的不断延伸，不稳定区域也不断扩大。

图 11 海底斜坡安全系数沿深度的变化

Figure 11. Variation of safety factor of submarine slope along depth

下载: 全尺寸图片幻灯片

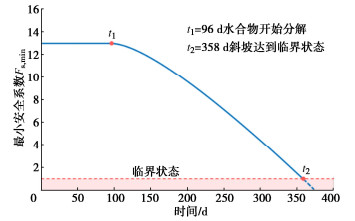
图 12为海底斜坡最小安全系数的演化曲线。可以看到，经过96 d的升温后，地层中的温度达到分解条件，水合物开始分解，此时海底斜坡安全系数开始下降，在开采358 d后安全系数降为1.0，意味着海底斜坡达到临界状态。此时为了后期的持续安全开采，需要调整开采方案。例如：调整施工参数，配合降压法，既可以有效降低地层中的孔隙压力，又可以提高开采效率。

图 12 海底斜坡最小安全系数随时间的变化曲线

Figure 12. Variation of minimum safety factor of submarine slope with time

下载: 全尺寸图片幻灯片

4. 结论

（1）考虑注热开采影响下海底水合物储层的THC耦合作用，推导了水合物分解引起的瞬态超孔隙压力求解格式，并基于极限平衡分析理论建立了海底斜坡动态稳定性简化评价方法。

（2）水平井注热开采影响下，水合物分解前缘最先形成于储层中部，并不断向上、下两侧延伸；由于水合物潜热消耗的影响，导致热量延迟传导，使储层上下两侧的水合物分解需要更长时间。

（3）水合物试采区典型海底斜坡初步分析表明，由于水合物的胶结作用，初始状态下水合物储层处的安全系数偏高；升温96 d后水合物开始分解，海底斜坡安全系数迅速降低，并于358 d后到达临界状态；为保证水合物的持续安全开采，提出调整开采方案。

（4）本文基于无限坡理论分析了水合物注热开采影响下海底斜坡的动态稳定性问题，而实际含水合物层的海底斜坡失稳破坏或滑坡模式，可能表现为弧形、盘式或拉裂刺穿等破坏形式^[13]，未来应加强不同破坏模式的海底斜坡动态稳定性评价方法的深入研究。

图 1 水合物实物与分子结构图^[2]

Figure 1. Physical and molecular structural diagrams of hydrate

下载: 全尺寸图片幻灯片

图 2 水合物沉积物多组分多相孔隙介质示意图

Figure 2. Schematic diagram of multi-component multi-phase porous sediments containing gas hydrate

下载: 全尺寸图片幻灯片

图 3 水合物理论稳定区域与生成区域的空间关系示意图^[26]

Figure 3. Schematic diagram of spatial relationship between hydrate stability zone and hydrate formation zone

下载: 全尺寸图片幻灯片

图 4 注热开采导致的地层温度变化路径示意图

Figure 4. Schematic diagram of change path of stratum temperature caused by hydrate heat injection exploitation

下载: 全尺寸图片幻灯片

图 5 水合物饱和度剖面演化曲线对比图

Figure 5. Comparison of evolution curves of hydrate saturation profile

下载: 全尺寸图片幻灯片

图 6 水合物开采影响下典型海底斜坡稳定性评价示意图^[32]

Figure 6. Schematic diagram of stability evaluation of typical submarine slope under influences of hydrate exploitation

下载: 全尺寸图片幻灯片

图 7 研究区位置及区域海底地形条件^{[11, 40]}

Figure 7. Location of study area and topography of regional seabed

下载: 全尺寸图片幻灯片

图 8 先导井测井响应柱状图^[41]

Figure 8. Histogram logging response of pilot well

下载: 全尺寸图片幻灯片

图 9 地层温度剖面演化曲线

Figure 9. Evolution curves of stratum temperature profile

下载: 全尺寸图片幻灯片

图 10 升温过程中水合物储层动态响应

Figure 10. Dynamic responses of hydrate reservoir during heating process

下载: 全尺寸图片幻灯片

图 11 海底斜坡安全系数沿深度的变化

Figure 11. Variation of safety factor of submarine slope along depth

下载: 全尺寸图片幻灯片

图 12 海底斜坡最小安全系数随时间的变化曲线

Figure 12. Variation of minimum safety factor of submarine slope with time

下载: 全尺寸图片幻灯片

表 1 模型参数^{[9, 11, 26, 41-42]}

Table 1 Model parameters

参数		取值	单位
坡体参数	z (深度)	—	m
	α (坡度)	3	°
	H(水平井位置)	230.6	m
地层参数	T₀(海底温度)	3.5	℃
	G/(地热梯度)	56	K/km
	S_h (初始饱和度)	31	%
	k (渗透率)	2.38	mD
	κ (有效热扩散系数)	4.5×10⁻⁷	m²/s
	λ (有效导热系数)	3.66	W/(m·K)
	c₁′ (初始黏聚力)	800	kPa
	c₂′ (最终黏聚力)	30	kPa
	φ′ (内摩擦角)	8.03	°
	ρ (体密度)	1650	kg/m³
	ϕ (孔隙度)	0.37	m³/m³
通用参数	ρ_l/(液相密度)	1024	kg/m³
	ρ_h (水合物密度)	930	kg/m³
	C_pl (液体比热)	4.18×10³	J/(kg·K)
	C_ph/(水合物比热)	2.16×10³	J/(kg·K)
	μ_l (液体动态黏度)	8.87×10⁻⁴	kg/(m·s)
	S (液体盐度)	3.5	%
	L_h/(水合物潜热)	56552-16.8/T	J/kg

下载: 导出CSV

参考文献(42)

[1]	KVENVOLDEN K A. Gas hydrates-geological perspective and global change[J]. Reviews of Geophysics, 1993, 31(2): 173–187. doi: 10.1029/93RG00268
[2]	SLOAN E D Jr. Fundamental principles and applications of natural gas hydrates[J]. Nature, 2003, 426(6964): 353–363. doi: 10.1038/nature02135
[3]	BOSWELL R, COLLETT T S, FRYE M, et al. Subsurface gas hydrates in the northern Gulf of Mexico[J]. Marine and Petroleum Geology, 2012, 34(1): 4–30. doi: 10.1016/j.marpetgeo.2011.10.003
[4]	FUJII T, SUZUKI K, TAKAYAMA T, et al. Geological setting and characterization of a methane hydrate reservoir distributed at the first offshore production test site on the Daini-Atsumi Knoll in the eastern Nankai Trough, Japan[J]. Marine and Petroleum Geology, 2015, 66: 310–322. doi: 10.1016/j.marpetgeo.2015.02.037
[5]	萧惠中, 张振. 全球主要国家天然气水合物研究进展[J]. 海洋开发与管理, 2021, 38(1): 36–41. doi: 10.3969/j.issn.1005-9857.2021.01.006 XIAO Hui-zhong, ZHANG Zhen. A review on gas hydrates research progress of global main countries[J]. Ocean Development and Management, 2021, 38(1): 36–41. (in Chinese) doi: 10.3969/j.issn.1005-9857.2021.01.006
[6]	王力峰, 付少英, 梁金强, 等. 全球主要国家水合物探采计划与研究进展[J]. 中国地质, 2017, 44(3): 439-448. https://www.cnki.com.cn/Article/CJFDTOTAL-DIZI201703004.htm WANG Li-feng, FU Shao-ying, LIANG Jin-qiang, et al. A review on gas hydrate developments propped by worldwide national projects[J]. Geology in China, 2017, 44(3): 439-448. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DIZI201703004.htm
[7]	袁益龙. 海洋天然气水合物降压开采潜力及力学稳定性数值模拟研究[D]. 长春: 吉林大学, 2019. YUAN Yi-long. Numerical Simulation on Gas Production Potential and the Geo-Mechanical Stability From Marine Natural Gas Hydrate Through Depressurization[D]. Changchun: Jilin University, 2019. (in Chinese)
[8]	宁伏龙, 梁金强, 吴能友, 等. 中国天然气水合物赋存特征[J]. 天然气工业, 2020, 40(8): 1–24, 203. doi: 10.3787/j.issn.1000-0976.2020.08.001 NING Fu-long, LIANG Jin-qiang, WU Neng-you, et al. Reservoir characteristics of natural gas hydrates in China[J]. Natural Gas Industry, 2020, 40(8): 1–24, 203. (in Chinese) doi: 10.3787/j.issn.1000-0976.2020.08.001
[9]	张伟, 梁金强, 陆敬安, 等. 中国南海北部神狐海域高饱和度天然气水合物成藏特征及机制[J]. 石油勘探与开发, 2017, 44(5): 670–680. https://www.cnki.com.cn/Article/CJFDTOTAL-SKYK201705003.htm ZHANG Wei, LIANG Jin-qiang, LU Jin-gan, et al. Accumulation features and mechanisms of high saturation natural gas hydrate in Shenhu Area, northern South China Sea[J]. Petroleum Exploration and Development, 2017, 44(5): 670–680. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKYK201705003.htm
[10]	WANG J L, WU S G, KONG X, et al. Geophysical characterization of a fine-grained gas hydrate reservoir in the Shenhu area, northern South China Sea: integration of seismic data and downhole logs[J]. Marine and Petroleum Geology, 2018, 92: 895–903. doi: 10.1016/j.marpetgeo.2018.03.020
[11]	叶建良, 秦绪文, 谢文卫, 等. 中国南海天然气水合物第二次试采主要进展[J]. 中国地质, 2020, 47(3): 557–568. https://www.cnki.com.cn/Article/CJFDTOTAL-DIZI202003002.htm YE Jian-liang, QIN Xu-wen, XIE Wen-wei, et al. Main progress of the second gas hydrate trial production in the South China Sea[J]. Geology in China, 2020, 47(3): 557–568. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DIZI202003002.htm
[12]	LI A, DAVIES R J, YANG J X. Gas trapped below hydrate as a primer for submarine slope failures[J]. Marine Geology, 2016, 380: 264–271. doi: 10.1016/j.margeo.2016.04.010
[13]	NIAN T K, SONG X L, ZHAO W, et al. Submarine slope failure due to overpressure fluid associated with gas hydrate dissociation[J]. Environmental Geotechnics, 2022, 9(2): 108–123. doi: 10.1680/jenge.19.00070
[14]	JIANG M J, SUN C, CROSTA G B, et al. A study of submarine steep slope failures triggered by thermal dissociation of methane hydrates using a coupled CFD-DEM approach[J]. Engineering Geology, 2015, 190: 1–16. doi: 10.1016/j.enggeo.2015.02.007
[15]	NIXON M F, LH G J. Submarine slope failure due to gas hydrate dissociation: a preliminary quantification[J]. Canadian Geotechnical Journal, 2007, 44(3): 314–325. doi: 10.1139/t06-121
[16]	XIONG Z S, ZHANG J H. Effect of dissociation of gas hydrate on the stability of submarine slope[C]//31st ASME International Conference on Ocean, Offshore and Arctic Engineering. Rio de Janeiro, 2012.
[17]	ZHANG H T, LUO X Q, BI J F, et al. Submarine slope stability analysis during natural gas hydrate dissociation[J]. Marine Georesources & Geotechnology, 2019, 37(4): 467–476.
[18]	CHEN Y M, ZHANG L L, LIAO C C, et al. A two-stage probabilistic approach for the risk assessment of submarine landslides induced by gas hydrate exploitation[J]. Applied Ocean Research, 2020, 99: 102158. doi: 10.1016/j.apor.2020.102158
[19]	刘锋, 吴时国, 孙运宝. 南海北部陆坡水合物分解引起海底不稳定性的定量分析[J]. 地球物理学报, 2010, 53(4): 946–953. doi: 10.3969/j.issn.0001-5733.2010.04.019 LIU Feng, WU Shi-guo, SUN Yun-bao. A quantitative analysis for submarine slope instability of the northern South China Sea due to gas hydrate dissociation[J]. Chinese Journal of Geophysics, 2010, 53(4): 946–953. (in Chinese) doi: 10.3969/j.issn.0001-5733.2010.04.019
[20]	GROZIC J L H. Interplay Between gas hydrates and submarine slope failure[C]// Submarine Mass Movements and Their Consequences-4th International Symposium, Dordrecht, 2010.
[21]	ZHU C Q, JIA Y G. Submarine slope stability analysis during natural gas hydrate dissociation: Discussion[J]. Marine Georesources & Geotechnology, 2020, 38(6): 753–754.
[22]	ARCHER D, BUFFETT B, BROVKIN V. Ocean methane hydrates as a slow tipping point in the global carbon cycle[J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(49): 20596–20601. doi: 10.1073/pnas.0800885105
[23]	XU W Y, RUPPEL C. Predicting the occurrence, distribution, and evolution of methane gas hydrate in porous marine sediments[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B3): 5081–5095. doi: 10.1029/1998JB900092
[24]	SLOAN E D, KOH C A. Clathrate Hydrates of Natural Gases[M]. 3ir ed. New York: Marcel Dekker, 2008.
[25]	DAVIE M K, ZATSEPINA O Y, BUFFETT B A. Methane solubility in marine hydrate environments[J]. Marine Geology, 2004, 203(1/2): 177–184.
[26]	MESTDAGH T, POORT J, DE B M. The sensitivity of gas hydrate reservoirs to climate change: perspectives from a new combined model for permafrost-related and marine settings[J]. Earth-Science Reviews, 2017, 169: 104–131. http://hal.sorbonne-universite.fr/hal-01521071/document
[27]	WAITE W F, STERN L A, KIRBY S H, et al. Simultaneous determination of thermal conductivity, thermal diffusivity and specific heat in SI methane hydrate[J]. Geophysical Journal International, 2007, 169(2): 767–774. doi: 10.1111/j.1365-246X.2007.03382.x
[28]	HU H, ARGYROPOULOS S A. Mathematical modelling of solidification and melting: a review[J]. Modelling and Simulation in Materials Science and Engineering, 1996, 4(4): 371–396. doi: 10.1088/0965-0393/4/4/004
[29]	REAGAN M T, MORIDIS G J. Dynamic response of oceanic hydrate deposits to ocean temperature change[J]. Journal of Geophysical Research Oceans, 2008, 113(C12).
[30]	TAN L, LIU F, HUANG Y, et al. Production-induced instability of a gentle submarine slope: potential impact of gas hydrate exploitation with the huff-puff method[J]. Engineering Geology, 2021, 289: 106174.
[31]	蒋明镜, 陈意茹, 卢国文. 一种实用型深海能源土多场耦合离散元数值方法[J]. 岩土工程学报, 2021, 43(8): 1391–1398. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18686.shtml JIANG Ming-jing, CHEN Yi-ru, LU Guo-wen. A practical multi-field coupling distinct element method for methane hydrate bearing sediments[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(8): 1391–1398. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18686.shtml
[32]	LIU F, TAN L, CROSTA G, et al. Spatiotemporal destabilization modes of upper continental slopes undergoing hydrate dissociation[J]. Engineering Geology, 2020, 264: 105286.
[33]	邹远晶, 韦昌富, 陈合龙, 等. 基于扰动状态概念的含水合物土弹塑性模型[J]. 岩土力学, 2019, 40(7): 2653–2662. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907019.htm ZOU Yuan-jing, WEI Chang-fu, CHEN He-long, et al. Elastic-plastic model for gas-hydrate-bearing soils using disturbed state concept[J]. Rock and Soil Mechanics, 2019, 40(7): 2653–2662. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201907019.htm
[34]	杨胜雄, 梁金强, 陆敬安, 等. 南海北部神狐海域天然气水合物成藏特征及主控因素新认识[J]. 地学前缘, 2017, 24(4): 1–14. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY201704002.htm YANG Sheng-xiong, LIANG Jin-qiang, LU Jin-gan, et al. New understandings on the characteristics and controlling factors of gas hydrate reservoirs in the Shenhu area on the northern slope of the South China Sea[J]. Earth Science Frontiers, 2017, 24(4): 1–14. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY201704002.htm
[35]	年廷凯, 焦厚滨, 范宁, 等. 南海北部陆坡软黏土动力应变-孔压特性试验[J]. 岩土力学, 2018, 39(5): 1564–1572, 1580. NIAN Ting-kai, JIAO Hou-bin, FAN Ning, et al. Experiment on dynamic strain-pore pressure of soft clay in the northern slope of South China Sea[J]. Rock and Soil Mechanics, 2018, 39(5): 1564–1572, 1580. (in Chinese)
[36]	年廷凯, 范宁, 焦厚滨, 等. 南海北部陆坡软黏土全流动强度试验研究[J]. 岩土工程学报, 2018, 40(4): 602–611. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17326.shtml NIAN Ting-kai, FAN Ning, JIAO Hou-bin, et al. Full-flow strength tests on the soft clay in the northern slope of the South China Sea[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 602–611. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17326.shtml
[37]	蒋明镜, 肖俞, 刘芳. 深海能源土开采对海床稳定性的影响研究思路[J]. 岩土工程学报, 2010, 32(9): 1412–1417. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract13601.shtml JIANG Ming-jing, XIAO Yu, LIU Fang. Methodology for assessing seabed instability induced by exploitation of methane hydrate[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1412–1417. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract13601.shtml
[38]	年廷凯, 沈月强, 郑德凤, 等. 海底滑坡链式灾害研究进展[J]. 工程地质学报, 2021, 29(6): 1657–1675. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202106001.htm NIAN Ting-kai, SHEN Yue-qiang, ZHENG De-feng, et al. Research advances on the chain disasters of submarine landslides[J]. Journal of Engineering Geology, 2021, 29(6): 1657–1675. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202106001.htm
[39]	郑德凤, 雷得浴, 闫成林, 等. 基于Web of Science数据库的海底滑坡研究趋势文献计量分析[J]. 工程地质学报, 2021, 29(6): 1805–1814. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202106015.htm ZHENG De-feng, LEI De-yu, YAN Cheng-lin, et al. Global research trends in submarine landslides: a bibliometric analysis based on web of science publications[J]. Journal of Engineering Geology, 2021, 29(6): 1805–1814. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202106015.htm
[40]	吴时国, 董冬冬, 杨胜雄, 等. 南海北部陆坡细粒沉积物天然气水合物系统的形成模式初探[J]. 地球物理学报, 2009, 52(7): 1849–1857. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200907020.htm WU Shi-guo, DONG Dong-dong, YANG Sheng-xiong, et al. Genetic model of the hydrate system in the fine grain sediments in the northern continental slope of South China Sea[J]. Chinese Journal of Geophysics, 2009, 52(7): 1849–1857. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200907020.htm
[41]	QIN X W, LU J A, LU H, et al. Co-existence of gas hydrate, free gas, and water in gas hydrate reservoir system in Shenhu area[J]. China Geology, 2020, 3(2): 210–220.
[42]	石要红, 张旭辉, 鲁晓兵, 等. 南海水合物黏土沉积物力学特性试验模拟研究[J]. 力学学报, 2015, 47(3): 521–528. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201503016.htm SHI Yao-hong, ZHANG Xu-hui, LU Xiao-bing, et al. Experimental study on the static mechanical properties of hydrate-bearing silty-clay in the South China Sea[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(3): 521–528. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201503016.htm

施引文献(2)

期刊类型引用(2)

1.	刘姝，李文杰，李莉佳，罗永江，陶瑞，李晓璇，杨亚会. 天然气水合物开采方法研究现状及展望. 钻探工程. 2024(05): 12-23 . 百度学术
2.	于倩男，唐慧敏，李承龙，梁爽，梁家修，陈志静，张琨. 天然气水合物注热分解渗流特征及数值模拟. 东北石油大学学报. 2023(06): 38-54+127-128 . 百度学术