Coupling model for consolidation and contaminant transport in compactedclay liners under non-isothermal condition
-
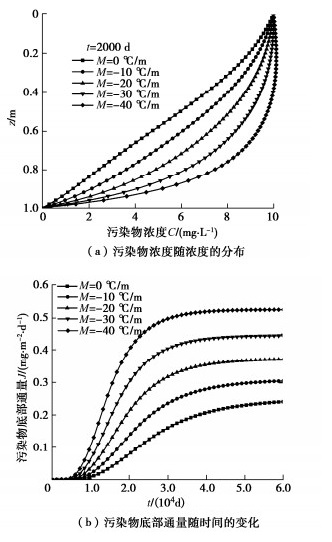
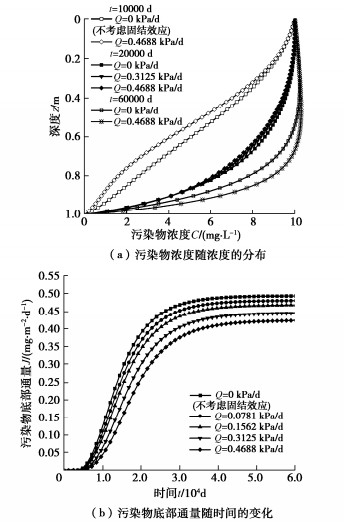
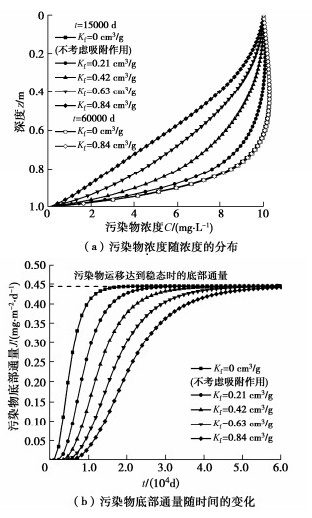
摘要: 考虑到污染场地内部产热会使得压实黏土衬垫处于非等温分布状态，建立了非等温分布条件下压实黏土衬垫中固结与污染物运移的耦合模型，并采用有限差分法对该耦合模型进行了求解。将所建耦合模型的计算结果分别与热扩散试验结果和已有理论模型的计算结果展开对比分析，对耦合模型的正确性进行了验证。基于所建耦合模型，通过某一算例分析了温度梯度M、加荷速率Q和Freundlich吸附系数Kf对污染物运移过程的影响。结果表明：污染物浓度和底部通量会随M绝对值的增大而增大，且一定温度梯度下的底部通量可达不考虑温度梯度时底部通量的2倍以上；Q的增大一方面会减慢污染物运移速率，另一方面会使得运移过程达到稳态时的污染物浓度增大；Kf的增大会减慢污染物运移过程，与不考虑吸附作用相比，考虑吸附作用可使得运移过程达到稳态时所需时间延长3倍及以上。Abstract: Considering that the heat production inside the contaminated site will make the compacted clay liner (CCL) be in a non-isothermal distribution state, a consolidation-contaminant transport coupling model for the CCL subjected to non-isothermal condition is established, and the finite difference method is used to solve the coupling model. The correctness of the established coupling model is verified by comparing the calculated results of the coupling model with the results of the thermal diffusion tests and those of the existing theoretical models, respectively. Based on the established coupling model, the effects of temperature gradient, loading rate and Freundlich adsorption coefficient on the transport process of contaminant are analyzed through an example. The results show that the concentration and bottom flux of contaminants increase with the increase of the absolute value of temperature gradient. Under a certain temperature gradient, the bottom flux of contaminant can be more than twice the bottom flux without considering the temperature gradient. On the one hand, the increase of loading rate will slow down the transport rate of contaminant. On the other hand, it will increase the concentration of contaminant when the transport process reaches a steady state. The increase of Freundlich adsorption coefficient will slow down the transport process of contaminant. The time required for the transport process to reach the steady state can be prolonged by three times or more when the adsorption effect is considered.
-
0. 引言
中国城市轨道交通近年来迅猛发展，已经成为市政基础设施的主要组成之一，随之而来的深基坑工程由于建设条件越来越复杂，常常出现自身安全性与周边环境稳定性的破坏。兰州市东西狭长而南北窄的带状分布严重阻碍了市区交通的运输[1]，为此规划的地铁线网在施工中碰到了西北地区特殊的富水红砂岩层，其工程性质差别很大，压实胶结作用差，揭露后极易发生风化，未扰动前力学性质较好，遇水扰动后强度快速衰退，崩解成流塑形的散沙，从而引发诸多地质工程问题[2-5]，而地铁深基坑支护结构的设计目前仍处在施工探索和实践的阶段。兰州地铁各车站基坑的红砂岩地层岩性差异非常大，若不对红砂岩分类并针对性地进行支护结构设计和地下水处理，将导致基坑被水浸泡、坑壁涌水涌砂等一系列工程问题。定西路站基坑内的红砂岩地层遇水具有典型的崩解特性，与之相应的基坑支护和地下水治理方案的研究刻不容缓。
国内外学者对深基坑支护结构的力学与变形特性已经做了大量的工作[6-10]，但都没有针对兰州地区特殊红砂岩地层的深入研究。本文依托定西路站车站深基坑工程，对开挖过程中的监测数据和Midas GTS的数值模拟结果对比分析，验证支护方案设计的合理性，研究结果可为类似红砂岩分布地区基坑支护结构设计提供技术支持。
1. 工程概况
1.1 车站概况
定西路车站轴线近南北向分布，车站总长185 m，标准段宽约23.3 m，底板埋深24.33~24.73 m，主体基坑施工方式为明挖法。车站两侧密集的建筑物加大了围护结构的受力，对基坑支护产生了不利影响。
1.2 地质及水文条件
场地45.0 m勘探深度范围内各地层的岩性及埋藏条件如表 1。车站地下水为潜水，卵石层为主要含水层，埋深为5.0~11.0 m，其下第三系粉砂岩成岩作用差，岩层内存在与卵石层相通的裂隙水。
表 1 岩土参数Table 1. Geotechnical parameters地层 层厚/m 重度/(kN·m-3) 黏聚力/kPa 内摩擦角/(°) 渗透系数/(m·d-1) 黄土状土 0.7~10.2 18.3 17 20 5.0~8.0 卵石 5.0~11.0 21.0 0 40 25.8~35.3 强风化砂岩 5.7~10.8 20.7 30 33 2.1~2.9 中风化砂岩 未穿透 21.3 40 38 0.5~1.0 1.3 支护结构方案
车站场地砂岩层渗透性较小、流通性差，降水周期短会导致层间滞水，坑壁渗水将引发强风化粉砂岩崩解，给基坑侧壁安全带来极大的风险，场地特有的水文地质条件和岩土工程问题要求车站基坑的支护结构兼具支承及止水能力。
车站结构形式为地下二层单柱双跨箱型框架结构，综合考虑经济性和安全性，该站基坑采用咬合桩加内支撑支护。桩墙由Φ1000@1400 mm的C35钢筋混凝土钻孔灌注桩与Φ800@1400 mm的C15素混凝土旋喷桩咬合而成，咬合深度为200 mm，桩长24.118 m。标准段沿竖向布置三道内支撑，钢筋混凝土撑水平间距约6 m，钢管撑水平间距为3 m，支护结构如图 1所示。
2. 现场测试与分析
2.1 监测方案
根据《城市轨道交通工程监测技术规范》（GB50911—2013）制定监测方案，各监测项目及控制值如表 2，监测点平面布置如图 2。
表 2 基坑监测项目及控制值Table 2. Foundation pit monitoring items and control values监测项目 累计绝对值/mm 累计开挖深度/% 变化速率/(m·d-1) 周边地表沉降 30 0.20 3 建筑物沉降 30 0.20 3 支撑轴力 轴力设计值 2.2 基坑周边地表沉降分析
地表沉降监测点DB10-1、DB10-2和DB10-3随时间的变化关系曲线如图 3。由图 3可得，各监测点的地表累计沉降量随着基坑开挖深度增大上下波动，但总体上都在增大。开挖初期，最大沉降的位置离基坑边缘较近，随着基坑开挖深度增加，距离基坑边缘较远的DB10-3沉降值更大，说明此时坑外土体向内倾斜对地表沉降产生的影响比内支撑的抑制作用大。
随着施工的进行，基坑周边地表起伏变化。基坑开挖是卸荷过程，开挖初期内支撑未支护时，地表沉降。6月17日左右，第一道钢支撑施工完成，支护桩后的土体受到朝基坑外的挤压，地表出现较小的隆起现象。随着开挖深度增大，地表再次沉降，7月15日，第二道钢支撑施工完成，地表再次隆起。DB10-3的最大沉降值为12.28 mm，远小于控制值30 mm，表明基坑支护安全有效，基坑开挖对周边地表的影响在可控范围内。
2.3 基坑周边建筑物沉降分析
某栋楼四角监测点CJ-12、CJ-13、CJ-14和CJ-15的累计沉降值随时间的变化关系曲线如图 4。可知随着基坑开挖建筑物整体上在沉降，5月13日第一道支撑施工完成，建筑物向上隆起，6月17日第二道支撑施工后，建筑物整体发生微小的隆起变形，之后各监测点均表现为沉降，7月15日第三道支撑完成后，建筑物的沉降逐渐趋于平稳。
距离基坑边缘较近的监测点CJ-12和CJ-13，变化曲线基本一致，较远的CJ-14和CJ-15的变化趋势相似，前者的沉降值整体上大于后者，可见基坑开挖对周边建筑物产生的影响随着距离的增加而减小。各测点在监测期得最大沉降量分别为6.29，5.42，4.73，3.72 mm，远小于控制值30 mm，表明内支撑可有效减小基坑周边建筑物沉降。
2.4 内支撑轴力分析
基坑原设计为三道钢支撑，轴力设计值分为721，1847，1616 kN。监测点ZL07的三道内支撑轴力随时间的变化曲线如图 5。随着基坑开挖，三道支撑的轴力变化先上下起伏，在开挖完成后逐渐趋于稳定，可能与开挖深度不相等、内支撑预应力损失、间歇性施工等原因有关。5月13日第一道钢筋混凝土支撑施工完成，由于混凝土的收缩，使之受到943 kN的初始压应力。6月17日第二道支撑完成后，钢筋混凝土支撑的轴力明显下降，这是因为第二道支撑分担了基坑内土层卸荷产生的压力。7月15日第三道支撑完成，第一、二道支撑的轴力明显减小，之后三道支撑承担的围护桩后的土压力随基坑开挖深度增加越来越大，轴力也逐渐增大。
第一道支撑的轴力监测值始终大于设计值，其中最大值为1691 kN，超过设计值的135%，故实际施工中用钢筋混凝土支撑代替了钢支撑。第二道支撑轴力最大值为1367 kN，轴力利用率较高。第三道支撑最大值为598 kN，轴力最大利用率为37%，设计偏保守。开挖过程未出现支撑破坏及基坑变形过大等现象，表明基坑支撑设计还有很大的优化空间，可进一步加强安全与经济的统一性。
3. 数值模拟及对比分析
3.1 模型及边界条件
选取14~20轴之间的基坑标准段建立Midas GTS有限元模型，模型尺寸为100 m×48 m×60 m，网格划分如图 6。将模型涉及的土层简化为4层，岩土体采用修正莫尔-库仑（MMC）模型，支护结构采用弹性本构模型。根据基坑开挖步骤定义施工阶段如表 3。
表 3 开挖工况Table 3. Excavation conditions工况 时间 施工状态 1 开始开挖—2018-05-13 开挖深度2.4 m，第一道钢筋混凝土支撑施工完成 2 2018-05-13—2018-06-17 开挖深度9.7 m，第一道钢支撑施工完成 3 2018-06-17—2018-07-15 开挖深度15.75 m，第二道钢支撑施工完成 4 2018-07-15—2018-07-29 开挖深度20.22 m，防水垫层已浇筑，底板钢筋施工 3.2 基坑周边地表沉降对比分析
对比地表沉降监测点DB10-1的模拟值与监测值，如图 7所示。可知模拟值整体上小于实测值，这是由于模拟计算的条件比较理想，简化了土层，假设开挖在降水完成后进行，且未考虑基坑周围可能出现临时堆载等不确定因素，但两条曲线总体的变化趋势一致，说明模拟计算的各参数选取较为合理。实测最大值为-2.17 mm，模拟最大值为-1.5 mm，均远小于控制值-30 mm，由于咬合桩加内支撑的支护结构刚度大，且同一时间的开挖段较短，对支护墙后的红砂岩地层扰动小，因此基坑周边地表累计沉降值远小于控制值。
3.3 内支撑轴力对比分析
选取建模区域内的支撑轴力监测点ZL07，对比第一道支撑的模拟数据和监测数据如图 8。由图可知，两条曲线的变化趋势基本一致，各工况下轴力的模拟值都小于监测值，可能与建模条件较为理想、忽略了实际施工中基坑周边施工机具堆载等情况有关。由于钢筋混凝土支撑的刚度大，整个开挖过程支撑和基坑都未出现过大的变形。
4. 结论
（1）基坑开挖初期距离基坑边缘较近的位置地表沉降量更大，随着开挖深度增加较远位置的沉降量更大；基坑周边地表竖向位移随施工过程呈现沉降-隆起-沉降的起伏变化；内支撑可有效减小基坑周边建筑物沉降。
（2）第一道支撑的轴力始终大于设计值，第二道的轴力利用率高，第三道设计偏保守，支护结构设计可进一步优化，做到经济性和安全性相统一。
（3）各施工监测项目结果与数值模拟结果随时间的变化趋势一致，表明有限元软件可预测深基坑工程可能存在问题并优化支护方案。
（4）开挖过程未出现支撑破坏及基坑变形过大等现象，说明针对定西路车站红砂岩地层岩性条件下的深基坑支护结构合理有效，设计思路对后续兰州地铁同类型红砂岩基坑支护有指导作用。
-
![]()
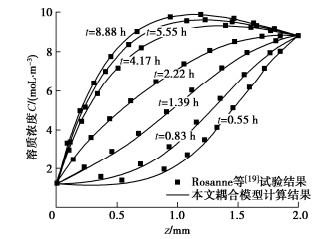
图 2 耦合模型计算结果和Rosanne等[19]热扩散试验结果对比
Figure 2. Comparison between calculated results by proposed coupling model and test results by Rosanne et al.
![]()
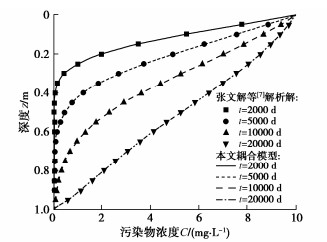
图 3 本文耦合模型与张文杰等[7]解析解计算结果的对比
Figure 3. Comparison between proposed coupling model and analytical solution proposed by Zhang et al.
![]()
图 4 本文耦合模型与Alshawabkeh耦合模型计算结果的对比
Figure 4. Comparison between proposed coupling model and coupling model proposed by Alshawabkeh et al.
![]()
图 5 温度梯度对污染物运移规律的影响
Figure 5. Influence of temperature gradient on law of contaminant transport
![]()
图 6 加荷速率对污染物运移规律的影响
Figure 6. Influences of loading rate on law of contaminant transport
-
[1] 陈云敏. 环境土工基本理论及工程应用[J]. 岩土工程学报, 2014, 36(1): 1–46. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201401003.htm CHEN Yun-min. A fundamental theory of environmental geotechnics and its application[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 1–46. (inChinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201401003.htm
[2] SHACKELFORD C D. The ISSMGE Kerry Rowe Lecture: The role of diffusion in environmental geotechnics 1[J]. Canadian Geotechnical Journal, 2014, 51(11): 1219–1242. doi: 10.1139/cgj-2013-0277
[3] 张春华, 吴家葳, 陈赟, 等. 基于污染物击穿时间的填埋场复合衬垫厚度简化设计方法[J]. 岩土工程学报, 2020, 42(10): 1841 –1848. ZHANG Chun-hua, WU Jia-wei, CHEN Yun, et al. Simplified method for determination of thickness of composite liners based on contaminant breakthrough time[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(10): 1841–1848. (in Chinese)
[4] TOUZE-FOLTZ N, XIE H J, STOLTZ G. Performance issues of barrier systems for landfills: a review[J]. Geotextiles and Geomembranes, 2021, 49(2): 475-488. doi: 10.1016/j.geotexmem.2020.10.016
[5] FOOSE G J. Transit-time design for diffusion through composite liners[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(1): 590–601.
[6] 陈云敏, 谢海建, 柯瀚, 等. 层状土中污染物的一维扩散解析解[J]. 岩土工程学报, 2006, 28(4): 521–524. doi: 10.3321/j.issn:1000-4548.2006.04.018 CHEN Yun-min, XIE Hai-jian, KE Han, et al. Analytical solution of contaminant diffusion through multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(4): 521–524. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.04.018
[7] 张文杰, 黄依艺, 张改革. 填埋场污染物在有限厚度土层中一维对流–扩散–吸附解析解[J]. 岩土工程学报, 2013, 35(7): 1197–1201. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201307004.htm ZHANG Wen-jie, HUANG Yi-yi, ZHANG Gai-ge. Analytical solution for 1D advection-diffusion-adsorption transport of landfill contaminants through a soil layer with finite thickness[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1197–1201. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201307004.htm
[8] FENG S J, PENG M Q, CHEN Z L, et al. Transient analytical solution for one-dimensional transport of organic contaminants through GM/GCL/SL composite liner[J]. Science of the Total Environment, 2019, 650: 479–492. doi: 10.1016/j.scitotenv.2018.08.413
[9] PU H F, QIU J W, ZHANG R J, et al. Analytical solutions for organic contaminant diffusion in triple-layer composite liner system considering the effect of degradation[J]. Acta Geotechnica, 2020, 15(4): 907–921. doi: 10.1007/s11440-019-00783-0
[10] CALDER G V, STARK T D. Aluminum reactions and problems in municipal solid waste landfills[J]. Practice Periodical of Hazardous, Toxic, and Radioactive Waste Management, 2010, 14(4): 258–265. doi: 10.1061/(ASCE)HZ.1944-8376.0000045
[11] JAFARI N H, STARK T D, THALHAMER T. Spatial and temporal characteristics of elevated temperatures in municipal solid waste landfills[J]. Waste Management, 2017, 59: 286–301. doi: 10.1016/j.wasman.2016.10.052
[12] 吴珣, 施建勇, 何俊. 非等温条件下有机污染物在黏土衬垫中的扩散分析[J]. 水文地质工程地质, 2014, 41(3): 120–124. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201403024.htm WU Xun, SHI Jian-yong, HE Jun. An analysis of organic contaminant diffusion through clay liner under the condition of transient temperature[J]. Hydrogeology & Engineering Geology, 2014, 41(3): 120–124. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201403024.htm
[13] XIE H J, ZHANG C H, SEDIGHI M, et al. An analytical model for diffusion of chemicals under thermal effects in semi-infinite porous media[J]. Computers and Geotechnics, 2015, 69: 329–337. doi: 10.1016/j.compgeo.2015.06.012
[14] 张春华. 填埋场复合衬垫污染物热扩散运移规律及其优化设计方法[D]. 杭州: 浙江大学, 2018. ZHANG Chun-hua. Mechanisms for Contaminant Transport in Landfill Composite Liners under Thermal Effect and Its Optimization Design Method[D]. Hangzhou: Zhejiang University, 2018. (in Chinese)
[15] YAN H X, SEDIGHI M, XIE H J. Thermally induced diffusion of chemicals under steady-state heat transfer in saturated porous media[J]. International Journal of Heat and Mass Transfer, 2020, 153: 119664. doi: 10.1016/j.ijheatmasstransfer.2020.119664
[16] PENG M Q, FENG S J, CHEN H X, et al. Analytical model for organic contaminant transport through GMB/CCL composite liner with finite thickness considering adsorption, diffusion and thermodiffusion[J]. Waste Management, 2021, 120(9): 448–458.
[17] PENG M Q, FENG S J, CHEN H X, et al. An analytical solution for organic pollutant diffusion in a triple-layer composite liner considering the coupling influence of thermal diffusion[J]. Computers and Geotechnics, 2021, 137: 104283. doi: 10.1016/j.compgeo.2021.104283
[18] MON E E, HAMAMOTO S, KAWAMOTO K, et al. Temperature effects on solute diffusion and adsorption in differently compacted Kaolin clay[J]. Environmental Earth Sciences, 2016, 75(7): 1–9.
[19] ROSANNE R, PASZKUTA M, TEVISSEN E, et al. Thermodiffusion in compact clays[J]. Journal of Colloid and Interface Science, 2003, 267(1): 194–203. doi: 10.1016/S0021-9797(03)00670-2
[20] ROSANNE M, PASZKUTA M, ADLER P M. Thermodiffusional transport of electrolytes in compact clays[J]. Journal of Colloid and Interface Science, 2006, 299(2): 797–805. doi: 10.1016/j.jcis.2006.03.002
[21] YU Y, ROWE R K. Modelling deformation and strains induced by waste settlement in a centrifuge test[J]. Canadian Geotechnical Journal, 2018, 55(8): 1116–1129. doi: 10.1139/cgj-2017-0558
[22] CHEN Y M, ZHAN T L T, WEI H Y, et al. Aging and compressibility of municipal solid wastes[J]. Waste Management, 2009, 29(1): 86–95. doi: 10.1016/j.wasman.2008.02.024
[23] LIU J Y, XU D M, ZHAO Y C, et al. Long-term monitoring and prediction for settlement and composition of refuse in Shanghai Laogang Municipal Landfill[J]. Environmental Management, 2004, 34(3): 441–448. doi: 10.1007/s00267-004-2762-2
[24] PU H F, FOX P J. Model for coupled large strain consolidation and solute transport in layered soils[J]. International Journal of Geomechanics, 2016, 16(2): 04015064. doi: 10.1061/(ASCE)GM.1943-5622.0000539
[25] YAN H X, WU J W, THOMAS H R, et al. Analytical model for coupled consolidation and diffusion of organic contaminant transport in triple landfill liners[J]. Geotextiles and Geomembranes, 2021, 49(2): 489–499. doi: 10.1016/j.geotexmem.2020.10.019
[26] XIE H, YAN H, FENG S, et al. An analytical model for contaminant transport in landfill composite liners considering coupled effect of consolidation, diffusion, and degradation[J]. Environmental Science & Pollution Research, 2016, 23(19): 1–14.
[27] 田改垒, 张志红. 考虑热效应的污染物在土中扩散、渗透和固结耦合模型[J]. 岩土工程学报, 2022, 44(2): 278–287. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202202009.htm TIAN Gai-lei, ZHANG Zhi-hong. Coupled model for contaminant diffusion, osmosis and consolidation in soil considering thermal effects[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(2): 278–287. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202202009.htm
[28] LEE J, FOX P J, LENHART J J. Investigation of consolidation-induced solute transport. I: Effect of consolidation on transport parameters[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(9): 1228–1238. doi: 10.1061/(ASCE)GT.1943-5606.0000047
[29] 张志红, 许照刚, 杜修力. 吸附模式及固结变形对溶质运移规律的影响研究[J]. 土木工程学报, 2013, 46(1): 104– 111. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301012.htm ZHANG Zhi-hong, XU Zhao-gang, DU Xiu-li. Study on the effects of adsorption modes and consolidation deformation on solute transport[J]. China Civil Engineering Journal, 2013, 46(1): 104–111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301012.htm
[30] PU H, FOX, P J, SHACKELFORD C D, et al. Assessment of consolidation-induced contaminant transport for compacted clay liner systems[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(3): 04015091.
[31] ALSHAWABKEH A N, RAHBAR N. Parametric study of one-dimensional solute transport in deformable porous media[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(8): 1001–1010.
[32] CHO W J, LEE J O, CHUN K S. The temperature effects on hydraulic conductivity of compacted bentonite[J]. Applied Clay Science, 1999, 14(1/2/3): 47-58.
[33] 何俊, 胡晓瑾, 颜兴, 等. 黏土渗透性温度效应试验[J]. 水利水电科技进展, 2017, 37(3): 55–60. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201703009.htm HE Jun, HU Xiao-jin, YAN Xing, et al. Experiments on temperature effect of hydraulic conductivity of compacted clay[J]. Advances in Science and Technology of Water Resources, 2017, 37(3): 55–60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201703009.htm
[34] 张宇宁, 陈宇龙, 李博. 饱和黏土的一维热固结特性试验研究[J]. 东北大学学报(自然科学版), 2016, 37(12): 1794–1799. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201612026.htm ZHANG Yu-ning, CHEN Yu-long, LI Bo. Experimental study of one-dimensional thermal consolidation of saturated clays[J]. Journal of Northeastern University (Natural Science), 2016, 37(12): 1794–1799. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201612026.htm
[35] 费康, 戴迪, 付长郓. 热–力耦合作用下黏性土体积变形特性试验研究[J]. 岩土工程学报, 2019, 41(9): 1752–1758. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909023.htm FEI Kang, DAI Di, FU Chang-yun. Experimental study on volume change behavior of clay subjected to thermo-mechanical loads[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1752–1758. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909023.htm
[36] SMITH D W. One-dimensional contaminant transport through a deforming porous medium: theory and a solution for a quasi-steady-state problem[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(8): 693–722.
[37] 尹铁锋, 刘干斌, 郭桢, 等. 竖井地基热排水固结理论初探[J]. 水文地质工程地质, 2014, 41(3): 41–46. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201403010.htm YIN Tie-feng, LIU Gan-bin, GUO Zhen, et al. A preliminary study of the theory of consolidation by vertical thermal drain[J]. Hydrogeology & Engineering Geology, 2014, 41(3): 41–46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201403010.htm
[38] HARRIS K R, WOOLF L A. Pressure and temperature dependence of the self-diffusion coefficient of water and oxygen-18 water[J]. Journal of the Chemical Society, 1980, 76: 377–385.
[39] ROWE R K. Short- and long-term leakage through composite liners. The 7th Arthur casagrande lecture[J]. Canadian Geotechnical Journal, 2012, 49(2): 141–169.
下载:
计量
- 文章访问数: 138
- HTML全文浏览量: 30
- PDF下载量: 21
