孔隙变化条件下黄土土水特征曲线预测模型

张玉伟; 宋战平; 谢永利

doi:10.11779/CJGE202211007

孔隙变化条件下黄土土水特征曲线预测模型 English Version

张玉伟^{1, 2,},
宋战平^{1, 2},
谢永利³

1.
西安建筑科技大学土木工程学院, 陕西西安 710055
2.
西安建筑科技大学陕西省岩土与地下空间工程重点实验室, 陕西西安 710055
3.
长安大学公路学院, 陕西西安 710064

基金项目:

国家自然科学基金项目 52178393

陕西省科技创新团队项目 2020TD-005

陕西省教育厅专项项目 20JK0709

详细信息

作者简介:
张玉伟(1989—)，男，讲师，博士，主要从事黄土力学与工程方面的研究。E-mail：zhangyuwei@xauat.edu.cn

中图分类号: TU411
计量
- 文章访问数: 251
- HTML全文浏览量: 37
- PDF下载量: 41
出版历程
- 收稿日期: 2021-09-05
- 网络出版日期: 2022-12-08
- 刊出日期: 2022-10-31

Prediction model for soil-water characteristic curve of loess under porosity change

1.
School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China
2.
Shaanxi Key Laboratory of Geotechnical and Underground Space, Xi'an University of Architecture and Technology, Xi'an 710055, China
3.
School of highway, Chang'an University, Xi'an 710064, China

摘要

摘要: 黄土具有明显的大孔隙结构，浸水湿陷过程中内部孔隙不断变化，导致其浸水过程的土水特征曲线也动态变化。为简便预测孔隙变化条件下黄土的土水特征曲线，以孔隙体积函数为切入点，假定浸水引起孔隙变化对孔隙体积函数的影响规律，引入平移因子ξ_1i和压缩因子ξ_2i，通过平均孔隙半径建立平移因子和压缩因子与孔隙指标e之间的关系，基于初始孔隙状态推导得到不同孔隙条件下的孔隙体积函数，以Gardner模型为基础，引入孔隙指标建立考虑浸水孔隙变化的黄土土水特征曲线模型，当不考虑孔隙变化影响时本模型退化为Gardner模型。模型包含6个参数，均可通过试验确定，由初始状态对模型参数进行标定，并预测孔隙变化时黄土的土水特征曲线，研究表明模型预测结果与试验结果吻合较好，运用本模型可准确预测浸水引起的孔隙变化条件下黄土土水特征演化规律，这为建立黄土的本构模型奠定了良好的基础。
- 黄土 /
- 孔隙变化 /
- 土水特征曲线 /
- 预测模型
Abstract: The loess has obvious macropore structure. The internal pores change continuously in the process of water immersion and collapsibility, resulting in the dynamic change of soil-water characteristic curve in the process of water immersion. In order to simply predict the soil-water characteristic curve of loess under different pore conditions, taking the pore volume function as the breakthrough point, assuming the influence law of the change of soaking pore on the pore volume function, and introducing the translation factor ξ_1i and the compression factor ξ_2i, the relationship among the translation factor, the compression factor and the pore index e is established through the average pore radius, and the different pores are derived based on the initial pore state. Based on the Gardner model and introducing the pore index, the model for the soil-water characteristic curve of loess considering the change of soaking pore is established. When the influences of pore change are not considered, the model degenerates to the Gardner model. The model contains six parameters, which can be determined by experiments. The parameters of the model are calibrated by the initial state, and the soil-water characteristic curve of loess with pore change is predicted. The combination shows that the predicted results by the model are in good agreement with the test ones. The evolution law of the soil-water characteristics of loess under different conditions of water soaked pore changes can be accurately predicted by using this model, which may provide preference for establishing the constitutive model for loess.
- loess /
- pore change /
- soil-water characteristic curve /
- prediction model

HTML全文

0. 引言

中国西部地区大多数山坡是由风化岩石、坡积物、残积层等堆积形成的堆积体边坡，其中有很多边坡由于长历时、大强度的降雨入渗形成滑坡，给人民生命财产带来严重损失^[1]，尤其是青藏高原东北边缘。究其原因，强烈的新构造运动使得青藏高原东北边缘地形陡峻、地震频发，构造应力以及地震会使边坡土石的内部结构变形或破坏，从而产生新的构造结构面^[2-3]，受降雨、构造应力等影响逐渐发展为潜在滑裂面，其形态大多为折线型。降雨入渗对滑坡稳定性有着较大影响，降雨诱发的滑坡稳定性定量评价通常是在选取合理的降雨入渗模型后采用合适的稳定性评价方法来计算其稳定性系数。

国内外许多学者开展了丰富的研究，得到了一些分析降雨入渗的经典模型，如Green-Ampt(G-A)模型^[4]、基于G-A假设的Mein-Larson模型^[5]、利用级数表述的Philip模型^[6]，以及Iveson和Baum等发展的Trigrs模型^[7]等。其中G-A模型由于物理意义明确、参数较少，在降雨型滑坡分析中应用较广。Mein等^[8]以G-A模型为基础，将降雨入渗过程分为自由入渗和积水入渗两个阶段，但其并未考虑斜坡效应；为考虑斜坡效应，Chen等^[9]在G-A模型的基础上得到了一个统一的斜坡降雨入渗模型；汪丁建等^[10]、苏永华等^[11]基于G-A模型，建立了适用于有限长坡且能综合考虑湿润层土体含水率分布情况与饱和层内平行于坡面渗流作用的降雨入渗分析（LSGA）模型，然而其忽略了坡体非饱和区的存在。

为进一步考虑非饱和区的影响，Yao等^[12]考虑了饱和区与非饱和区厚度各占湿润锋深度的50%，并将其用于边坡稳定性分析；雷文凯等^[13]将非饱和区土体体积含水率按椭圆形分布考虑，但其假设的非饱和区厚度同样占湿润层厚度的50%；然而实际上随着降雨的持续，饱和层占湿润层的比例会不断变大，而非定值，非渗透系数也会随着降雨的持续而变化。张杰等^[14]研究了适用于斜坡降雨的G-A模型，但其将渗透系数采用饱和渗透系数的一半，未考虑渗透系数随着湿润锋的推进而不断变化的情况。此外针对降雨作用下堆积体滑坡稳定性评价的算法多是在土体条块上假定湿润线，然而在持续降雨作用下，堆积体边坡上的湿润线是动态变化的，导致边坡稳定系数也不断变化。

综上，在前人研究的基础上，首先基于G-A模型，同时考虑坡面倾角、非饱和区及饱和区内渗流的影响，建立持续降雨作用下堆积体边坡的入渗模型，其次结合不平衡推力法，推导折线型滑裂面堆积体边坡在持续降雨作用下稳定性算法，最后通过对比现场入渗试验结果和分析工程案例来验证本文算法的合理性。

1. 持续降雨下堆积体边坡稳定性计算

1.1 边坡降雨入渗公式

为描述堆积体滑坡在持续降雨作用下雨水入渗过程，基于G-A模型同时考虑边坡倾角、饱和区渗流和非饱和区渗透系数变化建立堆积体边坡降雨入渗模型。取堆积体边坡其中一个条块进行降雨入渗分析，如图 1所示，建模分析假定如下：①滑坡基岩上部坡体为均匀堆积体，基岩不透水，且不考虑地下水的影响。②降雨入渗过程分为2个阶段。第1阶段为饱和层形成前，此时土体按体积含水率分为过渡层和未湿润层，如图 1（a）所示；第2阶段为饱和层形成后，此时土体按体积含水率分为饱和层，过渡层和未湿润层，饱和层和过渡层统称为湿润层，如图 1（b）所示，湿润层的厚度为湿润锋至边坡表面的垂直距离。③饱和层和未湿润层土体体积含水率为定值，而过渡层体积含水率分布规律采用椭圆形曲线来描述^[13]，因此可得到持续降雨下边坡土体体积含水率分布规律为

图 1 边坡降雨入渗过程图

Figure 1. Process of rainfall infiltration of slope

下载: 全尺寸图片幻灯片

$\theta (z) = \left\{ \begin{array}{l} {\theta _{\text{s}}}{{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}(0 \leqslant z < {Z_{\text{s}}}){\text{ }} \hfill \\ {\theta _{\text{i}}} + \frac{{{\theta _{\text{s}}} - {\theta _{\text{i}}}}}{{{Z_{\text{w}}}}}\sqrt {Z_{\text{w}}^2 - {{(z - {Z_{\text{s}}})}^2}} {{\;\;\;\;\;\;\;}}({Z_{\text{s}}} \leqslant z < {Z_{\text{f}}}) \hfill \\ {\theta _i}{{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(}}{Z_{\text{f}}} \leqslant z{\text{) }} \hfill \\ \end{array} \right.。$

(1)

式中 ${\theta _{\text{s}}}$ 为土体饱和体积含水率（%）； ${\theta _{\text{i}}}$ 为土体天然体积含水率（%）； ${Z_{\text{s}}}$ 为坡体饱和层厚度（m）； ${Z_{\text{w}}}$ 为坡体过渡层厚度（m）； ${Z_{\text{f}}}$ 为坡体湿润层厚度（m）。

在第1阶段，饱和层尚未出现，湿润层仅包括过渡层，饱和层厚度为0，此时雨水入渗速率等于降雨强度。此阶段的极限状态为饱和层初始出现的时刻，即雨水入渗速率等于第2阶段开始时土体的初始入渗速率，即

$f_1(t)=q \cos \alpha \equiv \bar{k} \frac{Z_{\mathrm{w}} \cos \alpha+s_{\mathrm{f}}}{Z_{\mathrm{w}}}。$

(2)

式中q为降雨强度（m/h）； $\alpha$ 为边坡倾角（°）； ${s_{\text{f}}}$ 为未湿润层相对饱和层的基质势能水头（m），根据文献[]的建议，取土体进气压力值对应水势的一半； $\overline k$ 为非饱和层的等效导水率，取值参考何忠明等^[16]，则有

$\overline k = \frac{{{k_{\text{s}}} - {k_{\text{i}}}}}{{\ln {k_{\text{s}}} - \ln {k_{\text{i}}}}} ,$

(3)

式中， ${k_{\text{s}}}$ 为土体饱和渗透系数（m/s）； ${k_{\text{i}}}$ 为土体干燥层的导水率（m/s）。

根据图 1（a）及式（1），对过渡层体积含水率积分可得到饱和层初始出现的时刻雨水入渗总量为

$I1 = \int {_{Z{\text{s}}}^{Z{\text{s}} + {Z_{\text{w}}}}} \theta (z){\text{d}}z = \frac{{{\text{π }}{Z_{\text{w}}}}}{4}({\theta _{\text{s}}} - {\theta _i}) 。$

(4)

根据质量守恒定律，结合式（2）和式（4），可得第1阶段 ${t_{\text{p}}}$ 时间内降雨入渗量的等价关系式为

${t_{\text{p}}}q\cos \alpha = \frac{{{\text{π }}{Z_{\text{w}}}}}{4}({\theta _{\text{s}}} - {\theta _{\text{i}}}) 。$

(5)

结合式（2）和（5）可得到饱和层初始出现时对应的时刻 ${t_{\text{p}}}$ 和湿润锋厚度 ${Z_{\text{f}}}$ 。

在第2阶段，边坡内饱和层已经形成，此时湿润层包括饱和层和过渡层。渗入坡体的雨水一部分在饱和层平行于坡表向下流动，另一部分将继续渗入下方非饱和层土体，直至土体完全饱和，如图 2（b）所示。根据彭振阳等^[17]成果，随着湿润层厚度不断增大，过渡层体积占湿润层体积的比例沿湿润层厚度线性减小，有

图 2 折线型滑裂面边坡稳定性计算简图

Figure 2. Diagram of slope stability with broken-line slip surface

下载: 全尺寸图片幻灯片

$\frac{{{Z_{\text{w}}}}}{{{Z_{\text{f}}}}} = \alpha {z_{\text{f}}} + b,$

(6)

式中，a，b为经验参数，取值可参考文献[16]。

第2阶段的降雨入渗速率为^[15]

${f_2}(t) = \frac{{{Z_{\text{f}}}\cos \alpha + {s_{\text{f}}}}}{{{Z_{\text{f}}}}} \cdot \frac{{{k_{\text{s}}}}}{{n{Z_{\text{f}}} + m}},$

(7)

式中， $m = \frac{{\ln {k_s} - \ln {k_{\text{i}}}}}{{{k_s} - {k_i}}}b{k_{\text{s}}} + 1 - b$ ， $n = \frac{{\ln {k_{\text{s}}} - \ln {k_{\text{i}}}}}{{{k_{\text{s}}} - {k_{\text{i}}}}} \cdot$ $(a{k_{\text{s}}} - a)$ 。

根据图 1（b），结合式（6）和Darcy定律对式（2）积分可得第2阶段t时刻内土体累计入渗量为

${I_2} = \frac{{{\text{π }}(aZ_{\text{f}}^2 + b{Z_{\text{f}}}) + 4[(1 - b){Z_{\text{f}}} - aZ_{\text{f}}^2]}}{4} \cdot$

$({\theta _{\text{s}}} - {\theta _{\text{i}}}) + {k_{\text{s}}}[(1 - b){Z_{\text{f}}} - aZ_{\text{f}}^{\text{2}}]\sin \alpha 。$

(8)

将式（8）对时间t求导可得降雨入渗速率为

${f_2}(t) = \frac{{{\text{d}}I}}{{{\text{d}}t}} = \left\{ {\frac{{{\text{π }}(2a{Z_{\text{f}}} + b)}}{4} + [({\theta _{\text{s}}} - {\theta _{\text{i}}}) + {k_{\text{s}}}\sin \alpha ]} \right. \cdot$

$(1 - b) - 2a{Z_{\text{f}}}\left. \begin{array}{l} \hfill \\ \hfill \\ \end{array} \right\}\frac{{{\text{d}}{Z_{\text{f}}}}}{{{\text{d}}t}} 。$

(9)

结合式（7）和式（9），可得

$\left[ {\frac{{{\text{π }}(2a{Z_{\text{f}}} + b)}}{4} + [({\theta _{\text{s}}} - {\theta _{\text{i}}}) + {k_{\text{s}}}\sin \alpha ][(1 - b) - 2a{Z_{\text{f}}}]} \right]\frac{{{\text{d}}{Z_{\text{f}}}}}{{{\text{d}}t}} = \frac{{{Z_{\text{f}}}\cos \alpha + {s_{\text{f}}}}}{{{Z_{\text{f}}}}} \cdot \frac{{{k_{\text{s}}}}}{{n{Z_{\text{f}}} + m}}。$

(10)

对式（10）进行数值积分可得到饱和层出现后湿润层厚度 ${Z_{\text{f}}}$ 随降雨时间t的关系式。

结合式（9）~（13），可得到整个降雨入渗过程中堆积体边坡湿润层厚度随降雨时间的变化式为

${Z}_{\text{f}}(t)=\left\{ \begin{array}{l}\frac{4qt\mathrm{cos}\alpha }{\text{π}({\theta }_{\text{s}}-{\theta }_{i})}{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(}0\le t < {t}_{\text{p}}), \\ \left[\frac{\text{π}(2a{Z}_{\text{f}}+b)}{4}+(({\theta }_{\text{s}}-{\theta }_{i})+{k}_{s}\mathrm{sin}\alpha )((1-b)-2a{Z}_{\text{f}}^{})\right]\cdot \\ \frac{\text{d}{Z}_{\text{f}}}{\text{d}t}=\frac{{Z}_{\text{f}}\mathrm{cos}\alpha +{s}_{\text{f}}}{{Z}_{\text{f}}}\cdot \frac{{k}_{\text{s}}}{n{Z}_{\text{f}}+m}{\;\;\;\;\;\;\;\;\;\;\;\;\;(}{t}_{\text{p}}\le t\le {t}_{\text{d}}\text{)}。\end{array} \right.$

(11)

从式（11）可以看出，坡体湿润层厚度的扩展速率与边坡坡面倾角，降雨强度，坡体含水量和渗透系数等有关，湿润层的厚度随降雨的持续而动态变化。值得注意的是，由于堆积体边坡各条块的坡面倾角及条块厚度存在差异，各条块内湿润层厚度的扩展速率及坡体到达完全饱和状态的时间也不一致。

1.2 堆积体滑坡稳定性计算公式

基于不平衡推力法，结合1.1节滑坡降雨入渗公式推导适用于折线型滑裂面堆积体边坡随降雨变化下的稳定性计算公式。忽略各条块饱和层产生的渗流对下一条块的影响，将整个滑坡沿滑面折线段分为n个条块，则每个条块可视为有限坡长滑坡体，折线型滑坡条块计算简图如图 2所示。

取过渡层土体重度为饱和重度和天然重度的均值，得到各层土体的重度计算公式为

${W_{{\text{1}}i}} = {l_i}{Z_{\text{s}}}(t){\gamma _{\text{s}}} ,$

(12a)

${W_{{\text{2}}i}} = \frac{{{l_i}}}{2}({\gamma _{\text{s}}} + {\gamma _{\text{t}}}){Z_{{\text{w}}i}}(t),$

(12b)

${W_{{\text{3}}i}} = {l_i}({h_i} - {Z_{{\text{f}}i}}{\text{(}}t{\text{)}}){\gamma _{\text{t}}}。$

(12c)

式中 ${l_i}$ 为第i个条块的坡长（m）； ${\gamma _{\text{s}}}$ 为土体饱和重度（kN/m³）； ${\gamma _{\text{t}}}$ 为土体天然重度（kN/m³）； ${h_i}$ 为第i个条块两侧厚度的较小值（m）。

由图 2可以得到第i条块的下滑力为

${F_i} = ({W_{{\text{1}}i}} + {W_{{\text{2}}i}} + {W_{{\text{3}}i}})\sin {\alpha _i} + {D_i}\cos ({\alpha _i} - {\beta _i})。$

(13)

结合Mohr-Coulomb准则得第i条块抗滑力为

${R}_{i}={c}_{i}{L}_{i}+[({W}_{1i}+{W}_{2i}+{W}_{3i})\mathrm{cos}{\alpha }_{i}-{D}_{i}\mathrm{sin}({\alpha }_{i}-{\beta }_{i})]\mathrm{tan}{\varphi }_{i}\text{ }。$

(14)

式中 ${\alpha _i}$ 为第i个条块的坡底角度（°）； ${\beta _{\text{i}}}$ 为第i个条块的坡面角度（°）； ${D_i}$ 为第i条块中由于饱和带水体渗流作用，在土条块上产生平行于坡表的渗透力（kN）， ${D_i} = {\gamma _{\text{w}}}{l_i}\sin {\beta _i}{Z_{si}}{\text{(}}t{\text{)}}$ ； ${\varphi _i}$ 为滑带土的内摩擦角（°）； ${c_i}$ 为滑带土的黏聚力（kPa）。

根据超载法可得堆积体滑坡稳定系数为

${F_{\text{s}}} = \frac{{\sum\nolimits_{i = 1}^{n - 1} {({R_i}\prod\nolimits_{j = 1}^{n - 1} {{\psi _j}) + {R_n}} } }}{{\sum\nolimits_{i = 1}^{n - 1} {({F_i}\prod\nolimits_{j = 1}^{n - 1} {{\psi _j}) + {F_n}} } }},$

(15)

式中， ${\psi _j}$ 为第j块段的剩余下滑力传递至i+1块时的传递系数

${\psi _j} = \cos ({\beta _j} - {\beta _{j + 1}}) - \sin ({\beta _j} - {\beta _{j + 1}})\tan {\varphi _j}。$

(16)

2. 模型验证与案例分析

2.1 降雨入渗公式验证

采用雷文凯等^[13]开展的南昆铁路黏土堑坡入渗试验来验证本文方法的合理性。试验坡段宽2.5 m，坡面长度为6 m，坡面角度为30°，试验降雨强度为25 mm/h，喷头均布于坡面，距坡面垂直距离为2 m，降雨持续时间为10 h。该边坡天然体积含水率为0.22，饱和体积含水率为0.45；未湿润层相对饱和层的基质势能水头取1.5 m；坡体天然密度为2.12 g/cm³，饱和渗透系数为3.37×10^-7 m/s，初始渗透系数为0.001 m/d。

图 3为不同降雨入渗模型下湿润层厚度随降雨持续时间变化图。从图 3中可以发现，基于本文模型和分层假定入渗模型计算得到的结果与试验结果比较接近。在入渗开始阶段（0≤t≤57 min），3种模型计算得到的湿润层扩展速率相同；随着降雨的持续（t > 57 min），在同一时刻，本文模型湿润层抵达厚度开始大于传统G-A模型而小于分层假定入渗模型，且彼此间的差值越来越大，这是因为伴随着降雨的持续，坡体内开始出现饱和层，饱和层的出现将导致渗入坡体的一部分雨水在饱和层平行于坡表流出，而分层假定入渗模型未考虑雨水流失这一情况，其是假定雨水全部渗入下方非饱和层，因此本文模型计算得到的湿润层扩展速率要小于分层假定入渗模型。传统G-A模型未考虑土体非饱和区的影响，且其渗透系数为定值，这导致同一时刻下传统G-A模型计算得到的湿润层厚度的扩展速率要低于本文模型和分层假定入渗模型。

图 3 不同入渗模型下湿润层厚度随降雨时间变化图

Figure 3. Variation of thickness of wetting layer with rainfall time under different infiltration models

下载: 全尺寸图片幻灯片

2.2 工程实例分析

甘肃舟曲江顶崖H1滑坡为一堆积层滑坡，目前处于稳定状态，滑体主要由碎石土组成，平均厚度26.5 m，渗透性较好，滑带以黑色含砾黏土为主，滑床为以板岩为主的基岩。滑面形态为折线型，整体上缓下陡，后部、中部较为平缓，坡度13°~15°；下部、前缘较为陡峭，坡度20°~25°，整体平均20°，其中某一主滑剖面图如图 4（a）所示，图 4（b）为主滑剖面中H1滑坡体剖面计算简图。

图 4 江顶崖H1滑坡剖面图

Figure 4. Profile of Jiangdingya H1 landslide

下载: 全尺寸图片幻灯片

据舟曲县气象站和中国气象数据网统计资料得知舟曲多年平均降水量为420.6 mm，24 h最大降水量为63.3 mm，1 h最大降水量为47.0 mm，降水常以连续阴雨形式出现，因此给定降水强度q=35 mm/h。土体基本参数：天然重度为20.5 kN/m³，饱和重度为22.0 kN/m³，天然含水率为13.1%，饱和含水率为43.7%，饱和渗透系数为1×10^-6 m/s，基质势水头为50 cm，黏聚力为6 kPa，内摩擦角为15°。

对江顶崖H1堆积体滑坡进行持续降雨下不同方法的稳定性计算，边坡稳定性系数随降雨持续时间变化规律如图 5所示。

图 5 滑坡稳定系数随降雨持续时间变化规律

Figure 5. Variation laws of stability coefficient of landslide with rainfall duration

下载: 全尺寸图片幻灯片

由图 5可见，随着降雨的持续，两种模型计算得到的滑坡稳定性逐渐下降，降雨初期，滑坡稳定性下降较快，降雨后期，稳定性下降速率逐渐放缓。传统G-A模型计算得到的稳定系数F_s=1的时间为163 h，而本文模型计算得到的稳定系数F_s=1的时间为210 h，比传统G-A模型计算的结果提前47 h。这是因为传统G-A模型未考虑非饱和区以及饱和区内渗流的影响，导致其湿润层厚度的扩展速率小于本文模型，且计算时未考虑饱和层内沿坡表向下的渗透力，造成稳定性系数计算结果偏大。

3. 结论

（1）推导的降水入渗公式同时考虑了边坡倾角、饱和区渗流和非饱和区渗透系数变化的影响，降雨强度、边坡坡面倾角、渗透系数等都影响着饱和层的形成快慢以及湿润层厚度的扩展速度。

（2）本文模型和分层假定入渗模型计算得到的结果较传统G-A模型与试验结果更接近，在降雨入渗开始阶段，三种模型得到的湿润层扩展速率相同；随着降雨的持续，本文模型计算的湿润层扩展速率大于传统G-A模型而小于分层假定入渗模型。

（3）江顶崖折线型滑裂面堆积体边坡的稳定性随着降雨的持续逐渐减小，降雨初期，滑坡稳定性下降较快，降雨后期，稳定性下降速率逐渐放缓；提出的稳定性计算方法得到的边坡滑动时间要早于传统入渗模型下稳定性计算结果。

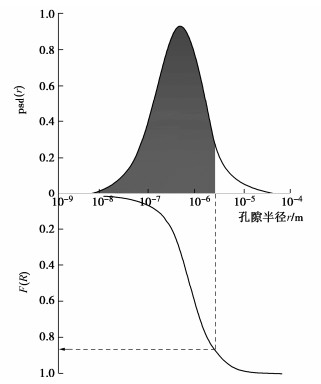
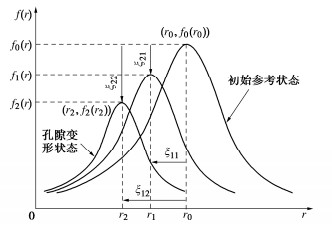
图 1 孔隙分布示意图^[26]

Figure 1. Schematic diagram of pore distribution

下载: 全尺寸图片幻灯片

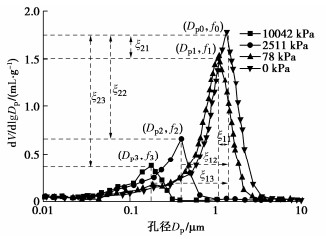
图 2 单孔结构土体压汞实验^[25]

Figure 2. MIP results of dromedary soil

下载: 全尺寸图片幻灯片

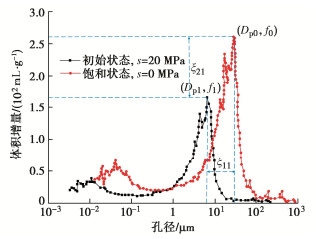
图 3 双孔结构土体压汞实验^[26]

Figure 3. MIP results of bimodal soil

下载: 全尺寸图片幻灯片

图 4 孔隙变形对孔隙分布函数影响

Figure 4. Influences of deformation of pore on its distribution function

下载: 全尺寸图片幻灯片

图 5 模型标定曲线

Figure 5. Calibration curve of model

下载: 全尺寸图片幻灯片

图 6 孔隙比为0.8时结果对比

Figure 6. Comparison of results under pore ratio of 0.8

下载: 全尺寸图片幻灯片

图 7 孔隙比为0.75时结果对比

Figure 7. Comparison of results under pore ratio of 0.75

下载: 全尺寸图片幻灯片

图 8 孔隙比为0.7时结果对比

Figure 8. Comparison of results under pore ratio of 0.7

下载: 全尺寸图片幻灯片

图 9 孔隙比为0.65时结果对比

Figure 9. Comparison of results under pore ratio of 0.65

下载: 全尺寸图片幻灯片

图 10 孔隙比为0.6时结果对比

Figure 10. Comparison of results under pore ratio of 0.6

下载: 全尺寸图片幻灯片

图 11 孔隙变化对土水特征曲线的影响规律

Figure 11. Influences of deformation of pore on SWCC

下载: 全尺寸图片幻灯片

参考文献(31)

[1]	郑方, 邵生俊, 佘芳涛, 等. 重塑黄土在不同基质吸力下的真三轴剪切试验[J]. 岩土力学, 2020, 41(增刊1): 156–162. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2020S1018.htm ZHENG Fang, SHAO Sheng-jun, SHE Fang-tao, et al. True triaxial shear tests of remolded loess under different matrix suctions[J]. Rock and Soil Mechanics, 2020, 41(S1): 156–162. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2020S1018.htm
[2]	占鑫杰, 詹良通, 林伟岸, 等. 一种基于持水曲线的市政污泥水分分布测试方法研究[J]. 岩土工程学报, 2021, 43(11): 2112–2118. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18824.shtml ZHAN Xin-jie, ZHAN Liang-tong, LIN Wei-an, et al. Moisture distribution in sewage sludge based on soil-water characteristic curve[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2112–2118. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18824.shtml
[3]	李达, 汪时机, 李贤, 等. 不同覆土压力下砂质黏性紫色土的土–水特征曲线研究[J]. 岩土工程学报, 2021, 43(10): 1950–1956. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18803.shtml LI Da, WANG Shi-ji, LI Xian, et al. Soil-water characteristic curve of sandy clayey purple soil under different overburden pressures[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(10): 1950–1956. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18803.shtml
[4]	BROOKS R H, COREY A T. Hydraulic Properties of Porous Media[M]. Fort Collins: Colorado State University, 1964.
[5]	NUTH M, LALOUI L. Advances in modelling hysteretic water retention curve in deformable soils[J]. Computers and Geotechnics, 2008, 35(6): 835–844. doi: 10.1016/j.compgeo.2008.08.001
[6]	GARDNER W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science, 1958, 85(4): 228–232. doi: 10.1097/00010694-195804000-00006
[7]	FREDLUND D G, XING A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521–532. doi: 10.1139/t94-061
[8]	费锁柱, 谭晓慧, 董小乐, 等. 基于土体孔径分布的土水特征曲线预测[J]. 岩土工程学报, 2021, 43(9): 1691–1699. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18770.shtml FEI Suo-zhu, TAN Xiao-hui, DONG Xiao-le, et al. Prediction of soil-water characteristic curve based on pore size distribution of soils[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(9): 1691–1699. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18770.shtml
[9]	VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892–898. doi: 10.2136/sssaj1980.03615995004400050002x
[10]	LU N, LIKOS W J. Suction stress characteristic curve for unsaturated soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(2): 131–142. doi: 10.1061/(ASCE)1090-0241(2006)132:2(131)
[11]	SHENG D C. Review of fundamental principles in modelling unsaturated soil behaviour[J]. Computers and Geotechnics, 2011, 38(6): 757–776.
[12]	RUSSELL A R, BUZZI O. A fractal basis for soil-water characteristics curves with hydraulic hysteresis[J]. Géotechnique, 2012, 62(3): 269–274. doi: 10.1680/geot.10.P.119
[13]	孙德安, 张俊然, 吕海波. 全吸力范围南阳膨胀土的土–水特征曲线[J]. 岩土力学, 2013, 34(7): 1839–1846. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307004.htm SUN De-an, ZHANG Jun-ran, LÜ Hai-bo. Soil-water characteristic curve of Nanyang expansive soil in full suction range[J]. Rock and Soil Mechanics, 2013, 34(7): 1839–1846. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307004.htm
[14]	孙德安, 刘文捷, 吕海波. 桂林红黏土的土-水特征曲线[J]. 岩土力学, 2014, 35(12): 3345–3351. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412001.htm SUN De-an, LIU Wen-jie, LÜ Hai-bo. Soil-water characteristic curve of Guilin lateritic clay[J]. Rock and Soil Mechanics, 2014, 35(12): 3345–3351. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412001.htm
[15]	高游, 孙德安, 张俊然, 等. 考虑孔隙比和水力路径影响的非饱和土土水特性研究[J]. 岩土工程学报, 2019, 41(12): 2191–2196. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18065.shtml GAO You, SUN De-an, ZHANG Jun-ran, et al. Soil-water characteristics of unsaturated soils considering initial void ratio and hydraulic path[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(12): 2191–2196. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18065.shtml
[16]	SUN D A, SHENG D C, SLOAN S W. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated soils[J]. Mechanics of Materials, 2007, 39(3): 212–221.
[17]	胡冉, 陈益峰, 周创兵. 基于孔隙分布的变形土土水特征曲线模型[J]. 岩土工程学报, 2013, 35(8): 1451–1462. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15253.shtml HU Ran, CHEN Yi-feng, ZHOU Chuang-bing. A water retention curve model for deformable soils based on pore size distribution[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1451–1462. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15253.shtml
[18]	周葆春, 孔令伟. 考虑体积变化的非饱和膨胀土土水特征[J]. 水利学报, 2011, 42(10): 1152–1160. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201110002.htm ZHOU Bao-chun, KONG Ling-wei. Effect of volume changes on soil-water characteristics of unsaturated expansive soil[J]. Journal of Hydraulic Engineering, 2011, 42(10): 1152–1160. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201110002.htm
[19]	孙德安. 非饱和土的水力和力学特性及其弹塑性描述[J]. 岩土力学, 2009, 30(11): 3217–3231. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911003.htm SUN De-an. Hydro-mechanical behaviours of unsaturated soils and their elastoplastic modelling[J]. Rock and Soil Mechanics, 2009, 30(11): 3217–3231. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911003.htm
[20]	ZHOU A, SHENG D, CARTER J. Modelling the effect of initial density on soil-water characteristic curves[J]. Géotechnique, 2012, 62(8): 669–680.
[21]	SIMMS P H, YANFUL E K. Measurement and estimation of pore shrinkage and pore distribution in a clayey till during soil-water characteristic curve tests[J]. Canadian Geotechnical Journal, 2001, 38(4): 741–754.
[22]	张雪东, 赵成刚, 刘艳, 等. 变形对土水特征曲线影响规律模拟研究[J]. 土木工程学报, 2011, 44(7): 119–126. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201107018.htm ZHANG Xue-dong, ZHAO Cheng-gang, LIU Yan, et al. Modeling study of the relationship between deformation and water retention curve[J]. China Civil Engineering Journal, 2011, 44(7): 119–126. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201107018.htm
[23]	HUANG S Y, BARBOUR S L, FREDLUND D G. Development and verification of a coefficient of permeability function for a deformable unsaturated soil[J]. Canadian Geotechnical Journal, 1998, 35(3): 411–425.
[24]	GALLIPOLI D. A hysteretic soil-water retention model accounting for cyclic variations of suction and void ratio[J]. Géotechnique, 2012, 62(7): 605–616.
[25]	HU R, CHEN Y F, LIU H H, et al. A water retention curve and unsaturated hydraulic conductivity model for deformable soils: consideration of the change in pore-size distribution[J]. Géotechnique, 2013, 63(16): 1389–1405.
[26]	DELLA VECCHIA G, DIEUDONNÉ A C, JOMMI C, et al. Accounting for evolving pore size distribution in water retention models for compacted clays[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(7): 702–723.
[27]	MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976, 12(3): 513–522.
[28]	TANAKA H, SHIWAKOTI D R, OMUKAI N, et al. Pore size distribution of clayey soils measured by mercury intrusion porosimetry and its relation to hydraulic conductivity[J]. Soils and Foundations, 2003, 43(6): 63–73.
[29]	MONROY R, ZDRAVKOVIC L, RIDLEY A. Evolution of microstructure in compacted London clay during wetting and loading[J]. Géotechnique, 2010, 60(2): 105–119.
[30]	LLORET A, ROMERO E, VILLAR M V. FEBEX II project final report on thermo-hydro-mechanical laboratory tests[R]. Madrid: Publication Technical ENRESA 10/2004, 2004.
[31]	张玉伟, 宋战平, 翁效林. Q₃原状黄土与重塑黄土的土水特性研究[J]. 水资源与水工程学报, 2019, 30(3): 224–229. https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201903035.htm ZHANG Yu-wei, SONG Zhan-ping, WENG Xiao-lin. Study on soil water characteristic curve of Q₃ intact and remolded loess[J]. Journal of Water Resources and Water Engineering, 2019, 30(3): 224–229. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201903035.htm