孔隙变化条件下黄土土水特征曲线预测模型

张玉伟; 宋战平; 谢永利

doi:10.11779/CJGE202211007

孔隙变化条件下黄土土水特征曲线预测模型 English Version

张玉伟^{1, 2,},
宋战平^{1, 2},
谢永利³

1.
西安建筑科技大学土木工程学院, 陕西西安 710055
2.
西安建筑科技大学陕西省岩土与地下空间工程重点实验室, 陕西西安 710055
3.
长安大学公路学院, 陕西西安 710064

基金项目:

国家自然科学基金项目 52178393

陕西省科技创新团队项目 2020TD-005

陕西省教育厅专项项目 20JK0709

详细信息

作者简介:
张玉伟(1989—)，男，讲师，博士，主要从事黄土力学与工程方面的研究。E-mail：zhangyuwei@xauat.edu.cn

中图分类号: TU411
计量
- 文章访问数: 250
- HTML全文浏览量: 37
- PDF下载量: 41
出版历程
- 收稿日期: 2021-09-05
- 网络出版日期: 2022-12-08
- 刊出日期: 2022-10-31

Prediction model for soil-water characteristic curve of loess under porosity change

1.
School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China
2.
Shaanxi Key Laboratory of Geotechnical and Underground Space, Xi'an University of Architecture and Technology, Xi'an 710055, China
3.
School of highway, Chang'an University, Xi'an 710064, China

摘要

摘要: 黄土具有明显的大孔隙结构，浸水湿陷过程中内部孔隙不断变化，导致其浸水过程的土水特征曲线也动态变化。为简便预测孔隙变化条件下黄土的土水特征曲线，以孔隙体积函数为切入点，假定浸水引起孔隙变化对孔隙体积函数的影响规律，引入平移因子ξ_1i和压缩因子ξ_2i，通过平均孔隙半径建立平移因子和压缩因子与孔隙指标e之间的关系，基于初始孔隙状态推导得到不同孔隙条件下的孔隙体积函数，以Gardner模型为基础，引入孔隙指标建立考虑浸水孔隙变化的黄土土水特征曲线模型，当不考虑孔隙变化影响时本模型退化为Gardner模型。模型包含6个参数，均可通过试验确定，由初始状态对模型参数进行标定，并预测孔隙变化时黄土的土水特征曲线，研究表明模型预测结果与试验结果吻合较好，运用本模型可准确预测浸水引起的孔隙变化条件下黄土土水特征演化规律，这为建立黄土的本构模型奠定了良好的基础。
- 黄土 /
- 孔隙变化 /
- 土水特征曲线 /
- 预测模型
Abstract: The loess has obvious macropore structure. The internal pores change continuously in the process of water immersion and collapsibility, resulting in the dynamic change of soil-water characteristic curve in the process of water immersion. In order to simply predict the soil-water characteristic curve of loess under different pore conditions, taking the pore volume function as the breakthrough point, assuming the influence law of the change of soaking pore on the pore volume function, and introducing the translation factor ξ_1i and the compression factor ξ_2i, the relationship among the translation factor, the compression factor and the pore index e is established through the average pore radius, and the different pores are derived based on the initial pore state. Based on the Gardner model and introducing the pore index, the model for the soil-water characteristic curve of loess considering the change of soaking pore is established. When the influences of pore change are not considered, the model degenerates to the Gardner model. The model contains six parameters, which can be determined by experiments. The parameters of the model are calibrated by the initial state, and the soil-water characteristic curve of loess with pore change is predicted. The combination shows that the predicted results by the model are in good agreement with the test ones. The evolution law of the soil-water characteristics of loess under different conditions of water soaked pore changes can be accurately predicted by using this model, which may provide preference for establishing the constitutive model for loess.
- loess /
- pore change /
- soil-water characteristic curve /
- prediction model

HTML全文

0. 引言

天然原状黄土具有大孔隙结构，浸水增湿可导致其微观孔隙结构破坏，宏观表现为湿陷现象，浸水增湿过程中孔隙结构变化同时改变了黄土的土水特征曲线SWCC(soil-water characteristic curve)^[1]，准确描述孔隙改变时的土水特性演化规律对建立本构模型具有重要意义^[2-12]。关于土水特征曲线模型已多有研究，对于一般土体，孔隙结构变化不大，土水特征曲线可不考虑孔隙变化影响，预测结果也相对准确^[13-14]，但对于孔隙结构明显的土体，孔隙结构变化将对土水特征曲线造成明显影响，如何预测不同孔隙条件下的土水特征曲线是研究重点。为了反映孔隙对土水特征曲线的影响，一些学者引入孔隙参数来建立土水特征曲线模型^[15-19]，Zhou等^[20]确定了饱和度和初始密度的增量关系，建立了考虑初始密度的土水特征曲线模型；Simmis等^[21]获得了脱湿过程中黏土的孔隙变化规律，引入孔隙参数建立了土水特征曲线模型；张雪东等^[22]引入平均孔隙、孔隙分布指数与孔隙率，基于Brooks & Corey模型建立了变形土的土水特征曲线模型。还有学者通过假定孔隙参数与土水特征曲线模型参数的关系，从而引入孔隙参数建立土水特征曲线模型，Huang等^[23]考虑孔隙改变对进气值、孔隙分布参数的影响，间接引入孔隙参数来反映孔隙改变对土水特征曲线的影响；Gallipoli^[24]定义了进气值与孔隙比的函数关系，在土水特征曲线模型中引入孔隙比反应孔隙变化的影响；Hu等^[25]假定孔隙函数在压缩变形过程中形状保持不变，建立了考虑孔隙变化的土水特征曲线模型。可以看出目前针对黄土浸水孔隙变化引起的土水特征曲线变化研究还比较少见，黄土具有大孔隙性和结构性，浸水引起的孔隙变化对土水特征曲线的影响不可忽略。

本文以大孔隙性黄土为研究对象，考虑黄土浸水孔隙变形特性，以孔隙体积函数为切入点，分析浸水孔隙结构演化特征，假定孔隙变化对孔隙体积函数的影响规律，引入压缩因子和平移因子，建立孔隙变化指标与压缩因子及平移因子之间的关系，推导引入孔隙指标的孔隙体积函数关系，基于经典Gardner模型建立考虑孔隙变化的黄土土水特征曲线模型，当模型不考虑孔隙变化时可退化为经典Gardner模型。最后标定模型参数，采用不同孔隙比黄土土水特征曲线试验结果验证了模型的可靠性，研究结果可为预测不同孔隙黄土的土水特性曲线提供一种新的简化方法。

1. 黄土孔隙变形演化特征描述

1.1 孔隙分布函数

天然原状黄土可认为是由大小不同的孔隙及颗粒组成的多孔介质，假定任意孔隙半径为 ${\xi _{1i}} = \frac{{{r_i}}}{{{r_0}}}$ ， $f{\text{(}}r{\text{)}}$ 为多孔介质的孔隙体积函数，则孔隙半径从 $r$ 到 $r + {\text{d}}r$ 时，这部分孔隙为 $f(r){\text{d}}r$ ，对孔隙半径从0到∞进行积分，则土体的孔隙体积可表述为

$\int_0^\infty {f(r)} {\text{d}}r 。$

(1)

土中孔隙半径全部介于最小半径 ${r_{\min }}$ 和最大半径 ${r_{\max }}$ 之间，另外根据体积含水率的定义以及局部平衡假设，小于某孔隙半径R的孔隙会被水充满^[17]，则体积含水率与孔隙体积函数的关系表述为

$\theta (s) = \int_0^R {f(r)} {\text{d}}r \text{，}$

(2)

式中， $\theta$ 为体积含水率， $s$ 为吸力。

结合比水容量曲线(毛细压力分布函数)定义为^[20]

$g(s) = \frac{{{\text{d}}\theta }}{{{\text{d}}s}} = \frac{{f(r){\text{d}}r}}{{{\text{d}}s}} 。$

(3)

根据Zhou等^[20]研究，土中孔隙水分为两部分：①孔隙自由水，自由水毛细现象明显；②由于化学粘结作用附着于固体颗粒的水，并且认为是恒定的，等于残余饱和度 $S_{\text{r}}^{{\text{res}}}$ ，对应于残余体积含水率 ${\theta _{\text{r}}}$ 。由于土体饱和度看作是微观饱和度 $S_{\text{r}}^{\text{m}}$ 和宏观饱和度 $S_{\text{r}}^{\text{M}}$ 之和： $S = S_{\text{r}}^{\text{m}} + S_{\text{r}}^{\text{M}}$ ，体积含水率也可以看成时残余体积含水率与变化的部分体积含水率组成，因此，体积含水率与孔隙体积函数的的关系满足：

$\theta (s) = \int_{{r_{\min }}}^R {f(r)} {\text{d}}r{\text{ + }}{\theta _{\text{r}}} 。$

(4)

结合式（3）用比水容量曲线函数来表示为

$\theta (s) = \int_{ + \infty }^s {g(s)} {\text{d}}r{\text{ + }}{\theta _{\text{r}}} 。$

(5)

当土体吸力 $s \to + \infty$ 时，土体体积含水率为残余体积含水率， $\theta (s) = {\theta _{\text{r}}}$ ，土体饱和度为残余饱和度， ${S_{\text{r}}} = S_{\text{r}}^{\text{m}} = S_{\text{r}}^{{\text{res}}}$ ，当吸力 $s = 0$ 时，体积含水率为 $\theta (s) =$ $\int_{ + \infty }^0 {g(s)} {\text{d}}s + {\theta _{\text{r}}}$ ，饱和度为1， ${S_{\text{r}}} = S_{\text{r}}^{\text{s}} = 1$ 。

有效饱和度定义为^[15-16]

${S_{\text{e}}} = \frac{{\theta - {\theta _{\text{r}}}}}{{{\theta _{\text{s}}} - {\theta _{\text{r}}}}} 。$

(6)

则以孔隙体积函数表示为

${S_{\text{e}}} = \frac{{\int_{{r_{\min }}}^R {f(x)} {\text{d}}x}}{{\int_{{r_{\min }}}^{{r_{\max }}} {f(x)} {\text{d}}x}} 。$

(7)

以比水容量曲线函数表示为

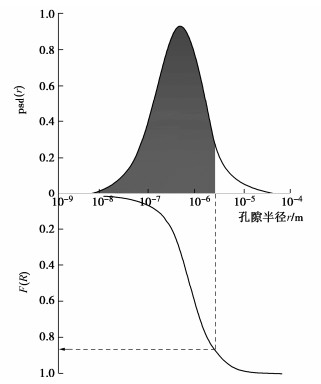
${S_{\text{e}}} = \frac{{\int_{ + \infty }^s {g(x)} {\text{d}}x}}{{\int_{ + \infty }^0 {g(x)} {\text{d}}x}} 。$

(8)

由式（7），（8）可以看出要推导土水特征曲线，首先要知道孔隙体积函数或者比水容量曲线函数，孔隙体积函数又可以通过孔隙密度函数来表达，本文首先采用Della等^[26]的方法推导孔隙密度函数 ${\text{psd(}}r{\text{)}}$ ，记 ${F^{\text{e}}}{\text{(}}R{\text{)}}$ 为孔隙半径小于 ${\xi _{1i}} = \frac{{{r_i}}}{{{r_0}}}$ 的孔隙对总孔隙比的贡献，定义为变量 ${F^{\text{e}}}{\text{(}}R{\text{)}}$ ：

${F^{\text{e}}}(R) = eF(R) = {e_{\text{w}}}(R) \text{，}$

(9)

式中， ${e_{\text{w}}}$ 为水分比，又因为Mualem ^[27]提出的局部平衡假设，土体内部的水将优先从小孔隙开始填充，此时孔隙半径的积分函数 $F{\text{(}}R{\text{)}}$ 就可以与土体的饱和度联系起来：

${S_{\text{r}}}{\text{(}}R{\text{)}} = F{\text{(}}R{\text{)}} 。$

(10)

又定义 ${\text{psd(}}r{\text{)}}$ 为多孔介质的孔隙密度函数(pore size density function)，则孔隙半径从 $r$ 到 $r + {\text{d}}r$ 时，孔隙所占百分比为 ${\text{psd(}}r{\text{)d}}r$ ，有

$\int_0^\infty {{\text{psd(}}r{\text{)}}} {\text{d}}r = 1 。$

(11)

土中孔隙半径全部位于最小半径 ${r_{\min }}$ 和最大半径 ${r_{\max }}$ 之间，则

$\int_{{r_{\min }}}^{{r_{\max }}} {{\text{psd(}}r{\text{)}}} {\text{d}}r = 1 。$

(12)

记 $F{\text{(}}R{\text{)}}$ 为半径小于 $R$ 的孔隙所占的概率，半径小于 $R$ 的孔隙量为

$F(R) = \int_{{r_{\min }}}^R {{\text{psd(}}r{\text{)}}} {\text{d}}r 。$

(13)

孔隙密度分布曲线见所示。对于特定吸力值 $s$ ，对应特定孔隙半径 $r$ ，土体中孔隙半径大于 $r$ 的孔隙全部被空气填满，小于 $r$ 的孔隙全部被水填满。则根据土体饱和度定义，可得饱和度与孔隙分布的关系：

${S_{\text{r}}}(R) = F(R) = \int_{{r_{\min }}}^R {{\text{psd(}}r{\text{)}}} {\text{d}}r 。$

(14)

图 1 孔隙分布示意图^[26]

Figure 1. Schematic diagram of pore distribution

下载: 全尺寸图片幻灯片

则得到水分比：

${e_{\text{w}}}(R) = {F^{\text{e}}}(R) = eF(R) = e{S_{\text{r}}}(R) 。$

(15)

则根据文献[26]的孔隙体积函数定义：

$f{\text{(}}r{\text{)}} = \frac{{{\text{d}}{F^{\text{e}}}{\text{(}}r{\text{)}}}}{{{\text{d}}\ln r}} = \frac{{e{\text{d}}{S_r}R}}{{{\text{d}}\ln r}} 。$

(16)

另外根据Young-laplace方程，孔隙半径与吸力之间的关系为

$s = \frac{{2T\cos \alpha }}{r} \text{，}$

(17)

式中， $s$ 为吸力，T为孔隙水表面张力， $\alpha$ 为孔隙水与颗粒之间的接触角， $r$ 为孔隙半径。对于特定的土体，其矿物组成和孔隙液体组成都是不变的，因此认为 $2T\cos \alpha$ 为常数C。

饱和度与吸力关系函数满足：

${S_{\text{r}}}(R) = \int_{{r_{\min }}}^R {{\text{psd(}}r{\text{)}}} {\text{d}}r = \int_{{r_{\min }}}^R {{\text{psd}}\left( {\frac{{2T\cos \alpha }}{s}} \right)} {\text{d}}r = G(s) 。$

(18)

$G(s)$ 为土水特征曲线模型，即由现有的土水特征曲线模型来推导孔隙体积函数。

选择Gardner模型来推导孔隙体积函数，其土水特征曲线函数为^[6]

${s_r}(s) = \frac{1}{{1 + \alpha {s^\beta }}} = \frac{1}{{1 + \alpha {{\left( {\frac{C}{r}} \right)}^\beta }}} 。$

(19)

则有

${F^{\text{e}}}(R) = e \cdot {S_{\text{r}}}(R) = e\frac{1}{{1 + \alpha {{\left( {\frac{C}{r}} \right)}^\beta }}} 。$

(20)

孔隙密度分布函数为

${\text{ps}}{{\text{d}}^{\text{e}}}{\text{(}}r{\text{)}} = \frac{{{\text{d}}{F^{\text{e}}}(r)}}{{{\text{d}}r}} = \frac{{eabC}}{{{r^2}}}\frac{1}{{{{\left( {1 + \alpha {{\left( {\frac{C}{r}} \right)}^\beta }} \right)}^2}}}{\left( {\frac{C}{r}} \right)^{\beta - 1}} 。$

(21)

孔隙体积函数为

$f(r) = \frac{{{\text{d}}{F^{\text{e}}}(R)}}{{{\text{d}}\ln r}} = {\text{ps}}{{\text{d}}^{\text{e}}}(r) \cdot r = eab\frac{1}{{{{\left( {1 + \alpha {{\left( {\frac{C}{r}} \right)}^\beta }} \right)}^2}}}{\left( {\frac{C}{r}} \right)^\beta } 。$

(22)

式（22）中 $f(r)$ 即为选择Gardner模型时土体孔隙体积分布函数的显示表达式。建立土体孔隙体积函数之后，要描述浸水引起的孔隙变形对土水特征曲线的影响关系，首先要明确土体浸水孔隙变化对孔隙体积函数的影响。

1.2 孔隙变化对孔隙体积函数的影响

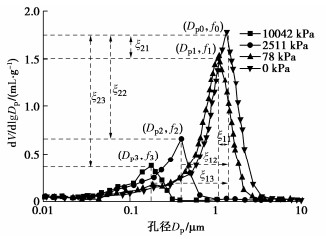
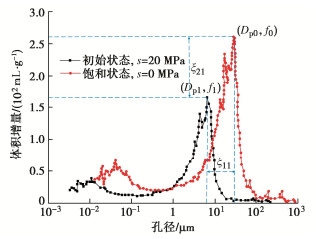
目前针对荷载、增湿、干湿循环等作用引起的土体孔隙结构演化规律已有很多研究，Tanaka等^[28]开展了土样不同压力下的压汞试验（图 2），研究了变形条件下土体孔隙结构的变化，Monroy等^[29]对伦敦黏土进行了增湿和荷载耦合作用下的压汞试验和电镜扫描试验，分析了伦敦黏土的微观结构演化，Lloret^[30]开展了不同压缩饱和状态下粉土的压汞试验（图 3），讨论了压缩变形对微观孔隙的影响规律，Hu^[25]总结各种土样的压汞试验成果，认为孔隙分布的大致形态在压缩过程中不发生显著变形，孔隙结构可通过孔隙半径表征，且孔隙半径与压缩应力在双对数坐标存在比例关系，进一步假定孔隙分布函数在半对数坐标下可通过平移和缩放得到，平移与缩放量与孔隙结构指标相关。考虑到黄土浸水过程中也是大孔隙（集合体间孔隙）先崩塌，小孔隙（集合体内孔隙）相对稳定，浸水孔隙变形也可简化为单峰规律变化，因此本文也采用上述理念建立浸水孔隙变化对孔隙体积函数的影响关系，认为浸水孔隙变化过程孔隙体积函数形状不变，通过引入压缩因子和平移因子来表征浸水对孔隙体积函数的影响。

图 2 单孔结构土体压汞实验^[25]

Figure 2. MIP results of dromedary soil

下载: 全尺寸图片幻灯片

图 3 双孔结构土体压汞实验^[26]

Figure 3. MIP results of bimodal soil

下载: 全尺寸图片幻灯片

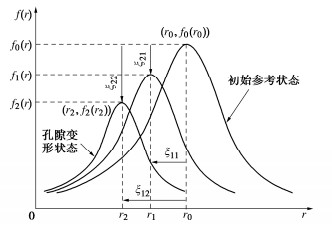
基于上述孔隙变形对对孔隙体积函数影响规律假定，在不考虑集合体内孔隙变化时，可把土体简化看作单孔结构，黄土浸水孔隙变形对孔隙体积函数的影响可由某一初始状态通过平移和缩放得到，即任意孔隙变形状态的孔隙体积函数可以通过初始状态的孔隙体积函数得到，通过引入平移因子 ${\xi _{1i}}$ 和压缩因子 ${\xi _{2i}}$ ，通过平均孔隙半径建立孔隙指标e与平移因子及压缩因子的关键，即可描述任意浸水孔隙变形下的孔隙体积函数，见所示，平移因子 ${\xi _{1i}}$ 和压缩因子 ${\xi _{2i}}$ 可以表示为

${\xi _{1i}} = \frac{{{r_i}}}{{{r_0}}} \text{，}$

(23)

${\xi _{2i}} = {f_i}({r_i})/{f_0}({r_0}) 。$

(24)

图 4 孔隙变形对孔隙分布函数影响

Figure 4. Influences of deformation of pore on its distribution function

下载: 全尺寸图片幻灯片

可以看出只要建立土体孔隙指标（如孔隙比、孔隙率等）与平移因子和压缩因子之间的关系，就可以得到任意孔隙状态的孔隙体积函数，在得到孔隙体积函数的基础上可以通过积分得到任意孔隙状态下的土水特征曲线。

2. 考虑孔隙变化的土水特征曲线模型

以Gardner模型为基础，则有初始状态的孔隙体积分布函数为

${f_0}(r) = \frac{{{\text{d}}{F^{\text{e}}}(R)}}{{{\text{d}}\ln r}} = {\text{ps}}{{\text{d}}^{\text{e}}}(r) \cdot r = {e_0}ab\frac{1}{{{{\left( {1 + \alpha {{\left( {\frac{C}{r}} \right)}^\beta }} \right)}^2}}}{\left( {\frac{C}{r}} \right)^\beta } 。$

(25)

求初始参考状态的峰值 $f({r_0})$ ，则对孔隙体积分布函数求导得

$\begin{aligned} \frac{\partial f_0(r)}{\partial \ln r}&=r \cdot\left[2 \alpha \beta \cdot\left(1+\alpha\left(\frac{C}{r}\right)^\beta\right)^{-3} \cdot\left(\frac{C}{r}\right)^{\beta-1} \cdot\left(\frac{C}{r^2}\right) .\right. \\ &\left.\left(\frac{C}{r}\right)^\beta-\beta\left(1+\alpha\left(\frac{C}{r}\right)^\beta\right)^{-2} \cdot\left(\frac{C}{r}\right)^{\beta-1} \cdot\left(\frac{C}{r^2}\right)\right] 。 \end{aligned}$

(26)

令 $\frac{{\partial {f_0}(r)}}{{\partial \ln r}} = 0$ ，进一步化简则可以得到 ${r_0}$ ：

${r_0} = C{(\alpha )^{\frac{1}{\beta }}} 。$

(27)

将 ${r_0}$ 带入孔隙体积分布函数可得

${f_0}({r_0}) = \frac{{{e_0}ab}}{4} \cdot \frac{1}{a} 。$

(28)

同理可以得到任意状态下的孔隙体积分布函数：

${f_i}({r_i}) = \frac{{{e_i}ab}}{4} \cdot \frac{1}{a} 。$

(29)

由此可得压缩因子 ${\xi _{2i}}$ ：

${\xi _{2i}} = \frac{{{f_i}({r_i})}}{{{f_0}({r_0})}} = \frac{{\frac{{{e_i}ab}}{4} \cdot \frac{1}{a}}}{{\frac{{{e_0}ab}}{4} \cdot \frac{1}{a}}} = \frac{{{e_i}}}{{{e_0}}} 。$

(30)

平移因子又可以表示为

${\xi _{1i}} = \frac{{{{\overline r }_i}}}{{\overline {{r_0}} }} 。$

(31)

可以看出要求得平移因子 ${\xi _{1i}}$ ，首先需要得到土体平均孔隙半径的表达式，由平均孔隙半径可推导得到平移因子 ${\xi _{1i}}$ 与孔隙指标的关系。根据前述孔隙体积分布函数 $f(r)$ 的定义，以孔隙体积占比为权，结合孔隙体积分布函数则可以得到平均孔隙半径的的表达式为

$\overline r = \frac{{\int_{{r_{\min }}}^{{r_{\max }}} {rf(r){\text{d}}r} }}{{\int_{{r_{\min }}}^{{r_{\max }}} {f(r){\text{d}}r} }} 。$

(32)

结合Young-Laplace方程式（17），并带入体积含水率可得

$\overline r = \frac{{{\text{C}}\int_{{\theta _{\text{r}}}}^{{\theta _{\text{s}}}} {\frac{1}{s}{\text{d}}\theta } }}{{\int_{{\theta _{\text{r}}}}^{{\theta _{\text{s}}}} {1{\text{d}}\theta } }} 。$

(33)

为了求解 $\mathop r\limits^ -$ ，只需求得 $1/s$ ，根据关系式(以体积含水率和吸力来表示)^[2]：

$\theta ={\theta }_{\text{r}}+({\theta }_{\text{s}}-{\theta }_{\text{r}})\cdot {\left(\frac{{s}_{\text{a}}}{s}\right)}^{\lambda }（s\ge {s}_{\text{a}}）。$

(34)

换算可得

$\frac{1}{s} = \frac{1}{{{s_{\text{a}}}}}{\left( {\frac{{\theta - {\theta _{\text{r}}}}}{{{\theta _{\text{s}}} - {\theta _{\text{r}}}}}} \right)^{\frac{1}{\lambda }}} 。$

(35)

代入式（33）可得

$\overline r = \int_{{\theta _{\text{r}}}}^{{\theta _{\text{s}}}} {\left[ {\frac{{\text{C}}}{{{s_{\text{a}}}}}{{\left( {\frac{{\theta - {\theta _{\text{r}}}}}{{{\theta _{\text{s}}} - {\theta _{\text{r}}}}}} \right)}^{\frac{{\lambda + 1}}{\lambda }}}\left( {\frac{\lambda }{{\lambda + 1}}} \right)} \right] = \frac{{\text{C}}}{{{s_{\text{a}}}}}\left( {\frac{\lambda }{{\lambda + 1}}} \right) = {\text{C}} \cdot {r_{\text{a}}}} \text{，}$

(36)

式中， ${r_{\text{a}}}$ 为平均孔隙半径指数， ${s_{\text{a}}}$ 为进气吸力， $\lambda$ 为土性参数，张雪东等^[22]给出了平均孔隙半径指数与孔隙率的关系，结合孔隙率与孔隙比的关系式就可以得到平均孔隙半径与孔隙比的关系式：

$n = {\left( {\frac{{{r_{\text{a}}}}}{{a + {r_{\text{a}}}}}} \right)^b} = {\left( {\frac{{\overline {{r_i}} /{\text{C}}}}{{a + \overline {{r_i}} /{\text{C}}}}} \right)^b} = \frac{e}{{1 + e}} 。$

(37)

进一步可得任意状态的评价孔隙半径：

$\overline {{r_i}} = \frac{{a{\text{C}}{{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}}}{{1 - {{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}}} 。$

(38)

代入式（31）可得

$\frac{1}{{{\xi _{1i}}}} = \frac{{\overline {{r_0}} }}{{\overline {{r_i}} }} = \frac{{a{\text{C}}{{\left( {\frac{{{e_0}}}{{1 + {e_0}}}} \right)}^{1/b}}}}{{1 - {{\left( {\frac{{{e_0}}}{{1 + {e_0}}}} \right)}^{1/b}}}} \cdot \frac{{1 - {{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}}}{{a{\text{C}}{{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}}} 。$

(39)

简化为

$\frac{1}{{{\xi _{1i}}}} = \frac{{{{\left( {\frac{{{e_0}}}{{1 + {e_0}}}} \right)}^{1/b}}\left[ {1 - {{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}} \right]}}{{\left[ {1 - {{\left( {\frac{{{e_0}}}{{1 + {e_0}}}} \right)}^{1/b}}} \right]{{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}}} 。$

(40)

由初始参考状态的孔隙体积分布函数 ${f_0}({r_0})$ ，平移因子 ${\xi _{1i}}$ 和压缩因子 ${\xi _{2i}}$ 就可以得到任意状态的孔隙体积分布函数 ${f_i}({r_i})$ ：

${f}_{i}({r}_{i})={\xi }_{2i}{f}_{0}({\xi }_{1i}{r}_{i})={\xi }_{2i}{e}_{0}ab\frac{1}{{\left(1+\alpha {\left(\frac{\text{C}}{{\xi }_{1i}r}\right)}^{\beta }\right)}^{2}}{\left(\frac{\text{C}}{r{\xi }_{1i}}\right)}^{\beta }。$

(41)

则任意孔隙状态的比水容量曲线为

${g_i}(s) = \frac{{{f_i}({r_i}){\text{d}}r}}{{{\text{d}}s}} 。$

(42)

将任意状态的比水容量曲线带入到土水特征曲线积分函数即可得到任意孔隙状态状态下的土水特征曲线：

${S_{\text{e}}} = \frac{{\int_{ + \infty }^s {{g_i}(x){\text{d}}x} }}{{\int_{ + \infty }^0 {{g_i}(x){\text{d}}x} }} = \frac{{\int_{ + \infty }^s {\left[ {{\xi _{2i}}{e_0}ab\frac{1}{{{{\left( {1 + \alpha {{\left( {\frac{s}{{{\xi _{1i}}}}} \right)}^\beta }} \right)}^2}}}{{\left( {\frac{s}{{{\xi _{1i}}}}} \right)}^\beta }} \right]{\text{d}}x} }}{{\int_{ + \infty }^0 {\left[ {{\xi _{2i}}{e_0}ab\frac{1}{{{{\left( {1 + \alpha {{\left( {\frac{s}{{{\xi _{1i}}}}} \right)}^\beta }} \right)}^2}}}{{\left( {\frac{s}{{{\xi _{1i}}}}} \right)}^\beta }} \right]{\text{d}}x} }} 。$

(43)

化简整理得

${S_{\text{e}}} = {\left( {1 + \alpha {{\left( {\frac{s}{{{\xi _{1i}}}}} \right)}^\beta }} \right)^{ - 1}} 。$

(44)

又有 $\frac{1}{{{\xi _{1i}}}} = \frac{{{{\left( {\frac{{{e_0}}}{{1 + {e_0}}}} \right)}^{1/b}}\left[ {1 - {{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}} \right]}}{{\left[ {1 - {{\left( {\frac{{{e_0}}}{{1 + {e_o}}}} \right)}^{1/b}}} \right]{{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}}}$ ，代入式（44）可得

${S_{\text{e}}} = {\left( {1 + \alpha {{\left( {\frac{{{{\left( {\frac{{{e_0}}}{{1 + {e_0}}}} \right)}^{1/b}}\left[ {1 - {{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}} \right]}}{{\left[ {1 - {{\left( {\frac{{{e_0}}}{{1 + {e_o}}}} \right)}^{1/b}}} \right]{{\left( {\frac{{{e_i}}}{{1 + {e_i}}}} \right)}^{1/b}}}}s} \right)}^\beta }} \right)^{ - 1}} 。$

(45)

可以看出任意孔隙状态下的土水特征曲线函数表示为吸力和孔隙比的函数，即土水特征曲线随孔隙比变化而变化，可理解为饱和度为吸力和孔隙比组成的三维空间曲面，当不考虑孔隙变化影响时，即可取初始状态 ${e_i} = {e_0}$ ，此时模型退化为经典Gardner模型，即可认为Gardner模型是本文模型的一种特殊形式。

3. 模型的验证

3.1 参数标定

为验证模型合理性，通过开展不同孔隙比重塑黄土的土水特征曲线试验结果来验证所建立模型的可靠性，所用原状土样为强湿陷性黄土^[31]。要计算不同孔隙比下的土水特征曲线，先以某一孔隙比为初始孔隙比进行参数的标定，本文以 ${e_0} = 0.85$ 作为初始孔隙比进行模型参数标定。由式（6）结合有效饱和度的定义：

$\theta ={\theta }_{\text{r}}+({\theta }_{\text{s}}-{\theta }_{\text{r}})\cdot {\left(1+\alpha {\left(\frac{{\left(\frac{{e}_{0}}{1+{e}_{0}}\right)}^{1/b}\left[1-{\left(\frac{{e}_{i}}{1+{e}_{i}}\right)}^{1/b}\right]}{\left[1-{\left(\frac{{e}_{0}}{1+{e}_{o}}\right)}^{1/b}\right]{\left(\frac{{e}_{i}}{1+{e}_{i}}\right)}^{1/b}}s\right)}^{\beta }\right)}^{-1}。$

(46)

当 ${e_i} = {e_0} = 0.85$ 时， ${\xi _{1i}} = 1$ ，式（46）退化为Gardner模型，根据孔隙比为0.85时的土水特征曲线试验值进行模型参数标定。由式（46）可看出，考虑孔隙比时的土水特征曲线模型包含 ${\theta _{\text{s}}}$ ， ${\theta _{\text{r}}}$ ， $\alpha$ ， $\beta$ ， ${e_0}$ ，b。 ${\theta _{\text{s}}}$ ， ${\theta _{\text{r}}}$ ， $\alpha$ ， $\beta$ 参数标定方法： ${\theta _{\text{s}}}$ 通过初始状态饱和土体的饱和度进行换算得到， ${\theta _{\text{r}}}$ 根据Mualem提出的确定非饱和残余状态体积含水率的方法确定， $\alpha$ ， $\beta$ 通过试验曲线拟合确定。 ${e_0}$ 为某一初始孔隙比，此处取0.85，进而通过孔隙与平均孔隙半径的关系标定 $b$ ，对于不同孔隙比时的土体b也不同，通过拟合得孔隙比0.8时b为0.15，孔隙比0.75时b为0.2，孔隙比0.7时b为0.25，孔隙比0.65时b为0.3，孔隙比0.6时b为0.35，模型参数标定曲线见，最终得到模型参数： ${\theta _{\text{s}}}$ =0.455， ${\theta _{\text{r}}}$ =0.095， $\alpha$ =0.015， $\beta$ =0.98。

图 5 模型标定曲线

Figure 5. Calibration curve of model

下载: 全尺寸图片幻灯片

3.2 模型初步验证

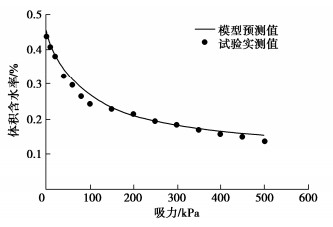
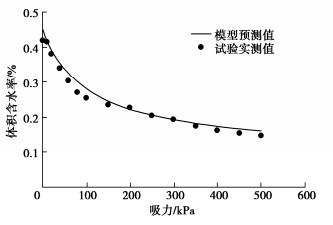
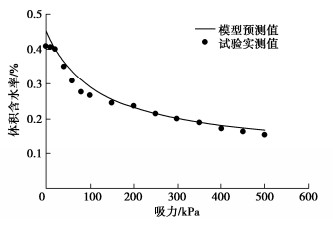
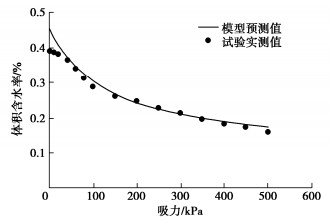
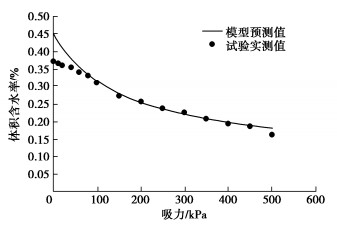
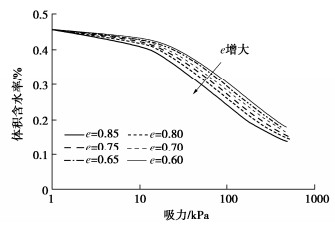
在标定得到模型参数的条件下，根据式（46）即可预测任意孔隙比时的土水特征曲线。图 6~10分别给出了不同孔隙比时的模型预测结果与试验结果的对比情况，可以看出，孔隙比越接近0.85得到的预测结果越准确，随着孔隙比偏离0.85越远，初始吸力段模型预测结果与试验结果逐渐有所偏差，但吸力大于100 kPa时的预测结果与试验结果仍然吻合较好，说明利用本文模型可以较好的预测考虑孔隙变化的非饱和黄土土水特征曲线。同时看出孔隙比远离基准标定孔隙比时，模型预测结果会逐渐出现一定误差，这是因为，模型参数以基准孔隙比进行标定得到，因此孔隙比越接近基准孔隙比模型预测结果越准确，同时需要指出，虽然整体上考虑孔隙变化的土水特征曲线模型能够较好的预测不同孔隙比土体的土水特征变化，但对低吸力段进气吸力以前的曲线部分拟合效果不是很好，尤其是与基本标定孔隙比差距越大，低吸力段预测结果误差越明显，因此在应用本模型时可尽量选择中间孔隙比进行模型参数标定，然后进行两边不同孔隙条件下土水特征曲线预测，另外，后续如果非饱和黄土土水试验数据积累丰富，可利用所有数据标定参数的平均值作为模型参数值，预测同类土不同孔隙变形条件下的土水特征变化。

图 6 孔隙比为0.8时结果对比

Figure 6. Comparison of results under pore ratio of 0.8

下载: 全尺寸图片幻灯片

图 7 孔隙比为0.75时结果对比

Figure 7. Comparison of results under pore ratio of 0.75

下载: 全尺寸图片幻灯片

图 8 孔隙比为0.7时结果对比

Figure 8. Comparison of results under pore ratio of 0.7

下载: 全尺寸图片幻灯片

图 9 孔隙比为0.65时结果对比

Figure 9. Comparison of results under pore ratio of 0.65

下载: 全尺寸图片幻灯片

图 10 孔隙比为0.6时结果对比

Figure 10. Comparison of results under pore ratio of 0.6

下载: 全尺寸图片幻灯片

图 11给出了由计算模型得到的考虑孔隙变化影响的非饱和黄土土水特征曲线。由图可以看出，孔隙比变化对土水特征曲线变化影响明显，随着孔隙比的增加，体积含水率随吸力变化敏感性增加，且吸力超过进气吸力值时表现越明显，说明土体由于荷载和浸水等各种因素导致的孔隙变化对土体的土水特征影响明显，实际中不得不予以考虑。本文模型可以准确描述不同孔隙条件下土水特征曲线变化，实际可认为体积含水率–吸力–孔隙比为三维空间的土水特征曲面，在无试验数据时可开展一组土水特征试验标定参数或根据经验进行参数取值，然后预测三维曲面上不同孔隙条件下的土水特征曲线演化规律；在积累足够试验数据时，可通过参数标定的平均值预测同类土三维曲面上不同孔隙条件下的土水特征曲线演化规律。

图 11 孔隙变化对土水特征曲线的影响规律

Figure 11. Influences of deformation of pore on SWCC

下载: 全尺寸图片幻灯片

4. 结论

（1）假定了黄土浸水增湿过程的孔隙结构演化规律，通过引入压缩因子和平移因子描述黄土浸水孔隙变化导致的孔隙体积函数变化规律，推导了孔隙指标 $e$ 与压缩因子与平移因子的关系。

（2）从孔隙体积函数出发，引入孔隙指标，基于Gardner模型建立了考虑浸水孔隙变化影响的黄土土水特征曲线模型，模型包含6个参数，当不考虑孔隙变化影响时，模型退化为Gardner模型。

（3）开展了不同孔隙条件下黄土的土水特征试验，选取初始状态对模型参数进行标定，并对不同孔隙条件下模型结果进行验证，模型在标定孔隙比附近具有良好的模拟能力，离标定孔隙比较大时低吸力段误差较大，表明本模型能够相对准确预测不同孔隙变形条件下黄土土水特征曲线演化规律。

图 1 孔隙分布示意图^[26]

Figure 1. Schematic diagram of pore distribution

下载: 全尺寸图片幻灯片

图 2 单孔结构土体压汞实验^[25]

Figure 2. MIP results of dromedary soil

下载: 全尺寸图片幻灯片

图 3 双孔结构土体压汞实验^[26]

Figure 3. MIP results of bimodal soil

下载: 全尺寸图片幻灯片

图 4 孔隙变形对孔隙分布函数影响

Figure 4. Influences of deformation of pore on its distribution function

下载: 全尺寸图片幻灯片

图 5 模型标定曲线

Figure 5. Calibration curve of model

下载: 全尺寸图片幻灯片

图 6 孔隙比为0.8时结果对比

Figure 6. Comparison of results under pore ratio of 0.8

下载: 全尺寸图片幻灯片

图 7 孔隙比为0.75时结果对比

Figure 7. Comparison of results under pore ratio of 0.75

下载: 全尺寸图片幻灯片

图 8 孔隙比为0.7时结果对比

Figure 8. Comparison of results under pore ratio of 0.7

下载: 全尺寸图片幻灯片

图 9 孔隙比为0.65时结果对比

Figure 9. Comparison of results under pore ratio of 0.65

下载: 全尺寸图片幻灯片

图 10 孔隙比为0.6时结果对比

Figure 10. Comparison of results under pore ratio of 0.6

下载: 全尺寸图片幻灯片

图 11 孔隙变化对土水特征曲线的影响规律

Figure 11. Influences of deformation of pore on SWCC

下载: 全尺寸图片幻灯片

参考文献(31)

[1]	郑方, 邵生俊, 佘芳涛, 等. 重塑黄土在不同基质吸力下的真三轴剪切试验[J]. 岩土力学, 2020, 41(增刊1): 156–162. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2020S1018.htm ZHENG Fang, SHAO Sheng-jun, SHE Fang-tao, et al. True triaxial shear tests of remolded loess under different matrix suctions[J]. Rock and Soil Mechanics, 2020, 41(S1): 156–162. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2020S1018.htm
[2]	占鑫杰, 詹良通, 林伟岸, 等. 一种基于持水曲线的市政污泥水分分布测试方法研究[J]. 岩土工程学报, 2021, 43(11): 2112–2118. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18824.shtml ZHAN Xin-jie, ZHAN Liang-tong, LIN Wei-an, et al. Moisture distribution in sewage sludge based on soil-water characteristic curve[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2112–2118. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18824.shtml
[3]	李达, 汪时机, 李贤, 等. 不同覆土压力下砂质黏性紫色土的土–水特征曲线研究[J]. 岩土工程学报, 2021, 43(10): 1950–1956. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18803.shtml LI Da, WANG Shi-ji, LI Xian, et al. Soil-water characteristic curve of sandy clayey purple soil under different overburden pressures[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(10): 1950–1956. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18803.shtml
[4]	BROOKS R H, COREY A T. Hydraulic Properties of Porous Media[M]. Fort Collins: Colorado State University, 1964.
[5]	NUTH M, LALOUI L. Advances in modelling hysteretic water retention curve in deformable soils[J]. Computers and Geotechnics, 2008, 35(6): 835–844. doi: 10.1016/j.compgeo.2008.08.001
[6]	GARDNER W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science, 1958, 85(4): 228–232. doi: 10.1097/00010694-195804000-00006
[7]	FREDLUND D G, XING A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521–532. doi: 10.1139/t94-061
[8]	费锁柱, 谭晓慧, 董小乐, 等. 基于土体孔径分布的土水特征曲线预测[J]. 岩土工程学报, 2021, 43(9): 1691–1699. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18770.shtml FEI Suo-zhu, TAN Xiao-hui, DONG Xiao-le, et al. Prediction of soil-water characteristic curve based on pore size distribution of soils[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(9): 1691–1699. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18770.shtml
[9]	VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892–898. doi: 10.2136/sssaj1980.03615995004400050002x
[10]	LU N, LIKOS W J. Suction stress characteristic curve for unsaturated soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(2): 131–142. doi: 10.1061/(ASCE)1090-0241(2006)132:2(131)
[11]	SHENG D C. Review of fundamental principles in modelling unsaturated soil behaviour[J]. Computers and Geotechnics, 2011, 38(6): 757–776.
[12]	RUSSELL A R, BUZZI O. A fractal basis for soil-water characteristics curves with hydraulic hysteresis[J]. Géotechnique, 2012, 62(3): 269–274. doi: 10.1680/geot.10.P.119
[13]	孙德安, 张俊然, 吕海波. 全吸力范围南阳膨胀土的土–水特征曲线[J]. 岩土力学, 2013, 34(7): 1839–1846. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307004.htm SUN De-an, ZHANG Jun-ran, LÜ Hai-bo. Soil-water characteristic curve of Nanyang expansive soil in full suction range[J]. Rock and Soil Mechanics, 2013, 34(7): 1839–1846. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307004.htm
[14]	孙德安, 刘文捷, 吕海波. 桂林红黏土的土-水特征曲线[J]. 岩土力学, 2014, 35(12): 3345–3351. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412001.htm SUN De-an, LIU Wen-jie, LÜ Hai-bo. Soil-water characteristic curve of Guilin lateritic clay[J]. Rock and Soil Mechanics, 2014, 35(12): 3345–3351. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412001.htm
[15]	高游, 孙德安, 张俊然, 等. 考虑孔隙比和水力路径影响的非饱和土土水特性研究[J]. 岩土工程学报, 2019, 41(12): 2191–2196. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18065.shtml GAO You, SUN De-an, ZHANG Jun-ran, et al. Soil-water characteristics of unsaturated soils considering initial void ratio and hydraulic path[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(12): 2191–2196. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18065.shtml
[16]	SUN D A, SHENG D C, SLOAN S W. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated soils[J]. Mechanics of Materials, 2007, 39(3): 212–221.
[17]	胡冉, 陈益峰, 周创兵. 基于孔隙分布的变形土土水特征曲线模型[J]. 岩土工程学报, 2013, 35(8): 1451–1462. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15253.shtml HU Ran, CHEN Yi-feng, ZHOU Chuang-bing. A water retention curve model for deformable soils based on pore size distribution[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1451–1462. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15253.shtml
[18]	周葆春, 孔令伟. 考虑体积变化的非饱和膨胀土土水特征[J]. 水利学报, 2011, 42(10): 1152–1160. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201110002.htm ZHOU Bao-chun, KONG Ling-wei. Effect of volume changes on soil-water characteristics of unsaturated expansive soil[J]. Journal of Hydraulic Engineering, 2011, 42(10): 1152–1160. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201110002.htm
[19]	孙德安. 非饱和土的水力和力学特性及其弹塑性描述[J]. 岩土力学, 2009, 30(11): 3217–3231. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911003.htm SUN De-an. Hydro-mechanical behaviours of unsaturated soils and their elastoplastic modelling[J]. Rock and Soil Mechanics, 2009, 30(11): 3217–3231. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911003.htm
[20]	ZHOU A, SHENG D, CARTER J. Modelling the effect of initial density on soil-water characteristic curves[J]. Géotechnique, 2012, 62(8): 669–680.
[21]	SIMMS P H, YANFUL E K. Measurement and estimation of pore shrinkage and pore distribution in a clayey till during soil-water characteristic curve tests[J]. Canadian Geotechnical Journal, 2001, 38(4): 741–754.
[22]	张雪东, 赵成刚, 刘艳, 等. 变形对土水特征曲线影响规律模拟研究[J]. 土木工程学报, 2011, 44(7): 119–126. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201107018.htm ZHANG Xue-dong, ZHAO Cheng-gang, LIU Yan, et al. Modeling study of the relationship between deformation and water retention curve[J]. China Civil Engineering Journal, 2011, 44(7): 119–126. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201107018.htm
[23]	HUANG S Y, BARBOUR S L, FREDLUND D G. Development and verification of a coefficient of permeability function for a deformable unsaturated soil[J]. Canadian Geotechnical Journal, 1998, 35(3): 411–425.
[24]	GALLIPOLI D. A hysteretic soil-water retention model accounting for cyclic variations of suction and void ratio[J]. Géotechnique, 2012, 62(7): 605–616.
[25]	HU R, CHEN Y F, LIU H H, et al. A water retention curve and unsaturated hydraulic conductivity model for deformable soils: consideration of the change in pore-size distribution[J]. Géotechnique, 2013, 63(16): 1389–1405.
[26]	DELLA VECCHIA G, DIEUDONNÉ A C, JOMMI C, et al. Accounting for evolving pore size distribution in water retention models for compacted clays[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(7): 702–723.
[27]	MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976, 12(3): 513–522.
[28]	TANAKA H, SHIWAKOTI D R, OMUKAI N, et al. Pore size distribution of clayey soils measured by mercury intrusion porosimetry and its relation to hydraulic conductivity[J]. Soils and Foundations, 2003, 43(6): 63–73.
[29]	MONROY R, ZDRAVKOVIC L, RIDLEY A. Evolution of microstructure in compacted London clay during wetting and loading[J]. Géotechnique, 2010, 60(2): 105–119.
[30]	LLORET A, ROMERO E, VILLAR M V. FEBEX II project final report on thermo-hydro-mechanical laboratory tests[R]. Madrid: Publication Technical ENRESA 10/2004, 2004.
[31]	张玉伟, 宋战平, 翁效林. Q₃原状黄土与重塑黄土的土水特性研究[J]. 水资源与水工程学报, 2019, 30(3): 224–229. https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201903035.htm ZHANG Yu-wei, SONG Zhan-ping, WENG Xiao-lin. Study on soil water characteristic curve of Q₃ intact and remolded loess[J]. Journal of Water Resources and Water Engineering, 2019, 30(3): 224–229. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201903035.htm

施引文献(47)

期刊类型引用(19)

1.	杜岩，张洪达，谢谟文，蒋宇静，张明，贾北凝. 矿山采空区边坡动态稳定性评价方法. 工程科学学报. 2025(02): 215-223 . 百度学术
2.	潘网生，马宗源，傅良同. 贵州三叠纪垄头组软岩优势结构面研究意义和进展. 绿色科技. 2024(06): 236-240 . 百度学术
3.	陶通铭. 采动作用下岩质斜坡变形破坏机制研究——以贵州龙场崩塌为例. 中国水运(下半月). 2024(11): 113-114+145 . 百度学术
4.	陶通铭. 采动作用下岩质斜坡变形破坏机制研究——以贵州龙场崩塌为例. 中国水运. 2024(22): 113-114+145 . 百度学术
5.	梁博，杨更社，冯伟，潘振兴，孙杰龙，刘慧，陈奇. 冻融诱发平面滑移型岩质边坡失稳模型试验研究. 西安科技大学学报. 2024(06): 1118-1126 . 百度学术
6.	于群群，孙朝燚. 顺层岩质边坡滑剪破坏规律研究. 河南城建学院学报. 2023(01): 15-21 . 百度学术
7.	杨忠平，向宫固，赵茜，刘新荣，赵亚龙. 水动力-溶蚀作用下灰岩结构面剪切力学特性. 岩土工程学报. 2023(08): 1555-1563 . 本站查看
8.	李华. 基于无人机航摄三维模型的地质信息提取和数值模拟应用. 中国水运(下半月). 2023(09): 31-33 . 百度学术
9.	牛犇，冯春，丛俊余，孙子正，张一鸣. 基于CDEM颗粒流的三维高速远程滑坡成灾范围分析. 岩石力学与工程学报. 2023(S2): 4018-4027 . 百度学术
10.	杨小龙，王刚. 滑坡堆积体反粒序现象的离散元数值分析. 工程地质学报. 2023(06): 1941-1950 . 百度学术
11.	李华. 基于无人机航摄三维模型的地质信息提取和数值模拟应用. 中国水运. 2023(18): 31-33 . 百度学术
12.	穆成林，裴向军，王睿，王超. 基于物理模型试验的含多层软弱夹层顺层开挖高边坡变形破坏特征分析. 中国地质灾害与防治学报. 2022(03): 61-67 . 百度学术
13.	朱彦鹏，杜一博，杨校辉，张卫雄，朱鋆川. 甘肃舟曲河那滑坡变形特征及孕灾机理. 科学技术与工程. 2022(25): 10884-10895 . 百度学术
14.	朱赛楠，殷跃平，王猛，朱茂，王晨辉，王文沛，李俊峰，赵慧. 金沙江结合带高位远程滑坡失稳机理及减灾对策研究——以金沙江色拉滑坡为例. 岩土工程学报. 2021(04): 688-697 . 本站查看
15.	易连兴，李瑜. 岩溶及水动力对鸡尾山滑坡影响作用研究. 工程地质学报. 2021(03): 583-592 . 百度学术
16.	刘宁波，钟立力，龙森. 山区公路单斜坡回头曲线路段滑坡成因及治理方案研究. 路基工程. 2020(03): 190-195 . 百度学术
17.	李巧学，周洪福，冉涛，铁永波. 中倾侧向坡中一种岩体破坏过程的模拟研究. 路基工程. 2020(04): 62-65+72 . 百度学术
18.	崔芳鹏，李滨，杨忠平，吴乐乐，李宁，彭健全. 贵州纳雍普洒滑坡动力触发机制离散元模拟分析. 中国岩溶. 2020(04): 524-534 . 百度学术
19.	何忠明，杨煜，曾新发，刘森峙. 土洞演化过程中路基变形的响应分析. 中南大学学报(自然科学版). 2018(12): 3068-3076 . 百度学术