基于贝叶斯高斯过程回归与模型选择的岩石单轴抗压强度估计方法

宋超; 赵腾远; 许领

doi:10.11779/CJGE20220734

基于贝叶斯高斯过程回归与模型选择的岩石单轴抗压强度估计方法 English Version

西安交通大学人居环境与建筑工程学院, 陕西西安 710049

基金项目:

国家自然科学基金青年基金项目 42107204

中央高校基本科研业务费专项资金项目（西安交通大学）

详细信息

作者简介:
宋超(1993—)，女，博士研究生，主要从事岩土工程数据分析与机器学习建模方向的研究工作。E-mail: song_chao@stu.xjtu.edu.cn

通讯作者:
赵腾远, E-mail: tyzhao@xjtu.edu.cn

中图分类号: TU45
计量
- 文章访问数: 501
- HTML全文浏览量: 84
- PDF下载量: 166
出版历程
- 收稿日期: 2022-06-08
- 网络出版日期: 2023-02-26

Estimation of uniaxial compressive strength based on fully Bayesian Gaussian process regression and model selection

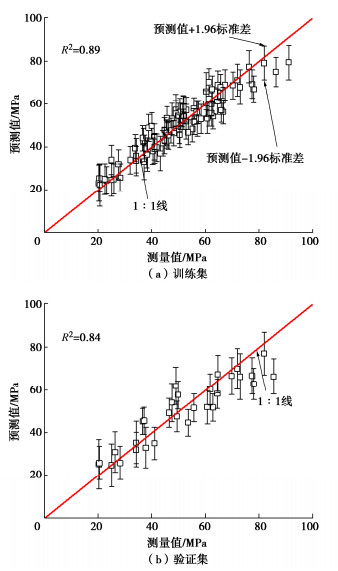
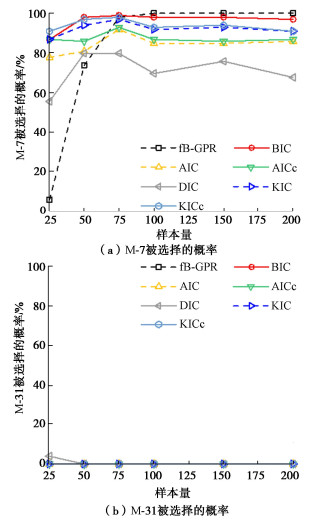
School of Human Settlements and Civil Engineering, Xi'an Jiaotong University, Xi'an 710049, China

摘要

摘要: 为构建间接估计岩石单轴抗压强度（UCS）的最优模型并实现UCS的合理估计，提出了贝叶斯高斯过程回归（fB-GPR）方法。fB-GPR综合了高斯过程回归、贝叶斯理论与马尔科夫链蒙特卡洛模拟。所提方法与其它模型选择方法进行了对比，如赤池信息准则、贝叶斯信息准则、偏差信息准则、Kullback信息准则等。研究结果表明：基于fB-GPR的最优模型选择结果更为准确，预测结果与实际情况吻合度更高；100次随机试验中，fB-GPR方法将M-7选为最优模型的概率达到100%，最优模型选择的准确率远远高于其他模型选择方法；fB-GPR方法在误差值达到UCS标准差的50%时，仍可准确地进行模型选择，说明fB-GPR的准确性和鲁棒性更好，受UCS测量误差影响相对较小。研究成果可为构建岩土工程中关键参数预测的最优模型并实现合理预测提供借鉴与参考。
- 岩土参数刻画 /
- 贝叶斯理论 /
- 数据驱动模型构建 /
- 信息准则 /
- 机器学习方法
Abstract: In order to establish an optimal model for estimating the uniaxial compressive strength (UCS) of rocks as well as its reasonable estimation, a fully Bayesian Gaussian process regression method (fB-GPR) is proposed by combining the Gaussian process regression (GPR), Bayesian framework and Markov Chain Monte Carlo (MCMC) simulation. The proposed fB-GPR approach is compared with different model selection methods, such as the Akaike information criterion (AIC), Bayesian information criterion (BIC), deviation information criterion (DIC), Kullback information criterion (KIC), etc. The results show that the proposed fB-GPR method performs better than other methods. In 100 random trials, the probability of M-7 being selected as the optimal model by fB-GPR method reaches 100%, and the accuracy of selecting the optimal model is far higher than other model selection methods. When the measurement noise reaches 50% of UCS standard deviation, the proposed fB-GPR can still achieve model selection accurately, which shows that the fB-GPR approach is robust and accurate, and is less affected by the measurement noise associated with UCS, comparing with other model selection methods. The proposed fB-GPR therefore provides a new way for establishing the optimal estimation model as well as reasonable estimation for the key geotechnical parameters in practice.
- characterization of geotechnical parameters /
- Bayesian theorem /
- data-driven model development /
- information criterion /
- machine learning method

HTML全文

0. 引言

在水利水电工程当中，快速正确的对岩体完整性以及质量进行分级与评价是岩体开挖和加固支护设计、快速施工必不可少的条件，其作为重要课题一直被科研人员密切关注^[1-5]。岩体质量主要受到岩体内部结构特性的影响，岩体完整性是重要作用的因素之一，在分类时需要考虑参数的不确定性。因此，如何对岩体完整性及岩体质量进行快速有效的划分，是岩土工程领域解决岩体安全稳定的一个重要问题。目前，岩体质量评价的方法主要有T评分^[6]、Q系统^[7]、地质强度指标(GSI)^[8]、岩体地质力学分类(RMR)^[9]等。这些指标结合了岩体本身的性质，在一定程度上反映了岩体的完整性，而这也对岩体质量的优劣起控制性作用。

针对岩体完整性判断问题，李明超等^[10]基于岩体对穿声波波速数据，采用加权随机森林算法，提出了一种新的多尺度岩体完整性评价指标和相应的分析方法，该方法没有考虑节理及岩体岩性等情况。曹瑞琅等^[11]通过提出钻进过程指数DPI，建立了DPI与RQD之间联系，为评价岩体完整性提供一种新指标，但钻孔中会忽略各向异性等问题。李清波等^[12]基于边缘阈值分割钻孔图像的方法，对RQD进行自动分析，与波速测试及钻孔图像对比，提高RQD统计的准确性，但对于图像中反射差异不明显的结构面，还未能进行研究。Guo等^[13]基于高清数字钻孔电视技术，提出了一种新的完整性评价方法，克服了RQD计算过程中岩心脱落和破碎问题的影响，在实际施工过程中，能够对岩体的完整性及裂隙的演化过程进行动态评价，但缺乏对结构面发育情况以及特征的研究。殷明伦等^[14]通过统计调研大量工程数据，研究体积节理数J_v与岩体完整性系数K_v之间的关系，提出了考虑结构面类别的J_v表征K_v的修正方法，但理论上还是根据K_v对岩体完整性进行评价，并且在实际工程中J_v与K_v的关系较差。Song等^[15]根据岩体完整性系数K_v与地质强度指标GSI关系，推导出K_v与RMR评分体系中某些项的关系，用这些指标进行预测K_v有着很高的相关性，其最终只是得到K_v值，是预测获取K_v值的另一途径，不能很好地进行岩体完整性评价。

实际工程中评价岩体质量时，常利用RQD、K_v、J_v中某一定量指标对岩体完整性进行分析，不能综合反映岩体特征，导致结果代表性差，与实际情况不符^[16]。例如，RQD不能与岩块挂钩，具有多解性；K_v主要考虑的是地下水、高地应力、卸荷等影响；J_v仅能反映结构面的几何发育特征。

针对水利工程中岩体完整性评价问题，耦合多源勘察信息，通过采用熵权-云模型对工程中误判数据进行修正，并使用少数类过采样方法对岩体完整性分级中不均衡数据进行预处理，改进数据集结构，利用随机森林算法对岩体完整性进行分类预测；由于影响岩体完整性评价的因素较多（如节理、地质构造、风化程度以及地下水等），为避免单一指标误差大，减少人为判断的主观性，结合影响因素对实际情况进行具体分析，并对所提出的方法进行应用拓展，为工程岩体完整性分析提供新的方法。

1. 岩体完整性指标及多指标的融合

1.1 岩体质量指标RQD

岩体质量指标（rock quality designation，RQD）自Deere^[17]提出后，便成为划分岩体结构特征的基本方法及重要参数。RQD常用岩芯钻探法进行获取，需要严格采用金刚石钻头、双层岩芯管钻进进行实现^[18]。RQD为一定量指标，是某岩组中大于或等于10 cm的柱状岩芯的累计长度与某岩组钻探总进尺之比^[19]，以百分数表示：

${\text{RQD}} = \frac{{{A_1}}}{A} \times 100\% \text{，}$

(1)

式中， ${A_1}$ 为累计大于等于10 cm岩芯长度，A为单位岩芯钻孔总长度。

RQD计算方式便捷，同时作为裂隙间距以及密度的指标，可以很好地反映岩体的连通性、压缩性、渗透性等物理力学性质，能定量反映岩体的完整性。但是，传统的RQD计算方法没有考虑阈值的合理性，不能很好地体现岩体的尺寸效应和各向异性，没有涉及岩体中结构面的发育情况^[20]，难以反映岩体结构本身的复杂性，导致评价结果会与真实情况有一定出入。

1.2 岩体体积节理数J_v

岩体体积节理数J_v是国际岩石力学委员会推荐使用评价岩体完整性和岩体节理化程度的指标，J_v的定义为单位体积内包含节理的数目，工程中常常采用间距法及条数法进行计算，最后取二者均值得出该施工阶段或工程地质勘察阶段的情况。间距法公式为

${J_{\text{v}}} = \left( {\frac{1}{{{S_1}}} + \frac{1}{{{S_2}}} + \cdot \cdot \cdot + \frac{1}{{{S_n}}}} \right){\text{ }}(i = 1,2,3, \cdot \cdot \cdot ,n) \text{，}$

(2)

式中，S_i为各组裂隙平均间距，i为裂隙数。

条数法计算方法如下：

${J_{\text{v}}} = \frac{{\sum\limits_{i = 1}^N {{n_i}} }}{N} \times (1.3\text{~}1.5){\text{ }}(i = 1,2,3, \cdot \cdot \cdot ,n) \text{，}$

(3)

式中，n_i为第i个单位测量面积内的节理条数，N为同级别岩体中的样本数，一般不少于10个。

获取 ${J_{\text{v}}}$ 的方法简单快捷，并且该指标能很好反映结构面的组数、迹长、间距等岩体结构面的几何发育特征，可以定量评价岩体的完整性，然而其不能够反映结构面的结合程度，评价的结果依赖于专家的个人经验与能力，会产生一定的误差。

1.3 岩体完整性系数K_v

岩体完整性系数可以定量表达岩体的完整程度，K_v定义为岩体中纵波的传播速度与岩石中的传播速度的比值的平方，即

${K_{\text{V}}} = {\left( {\frac{{{v_{{\text{pm}}}}}}{{{v_{{\text{pr}}}}}}} \right)^2} 。$

(4)

式中： ${v_{{\text{pm}}}}$ 为岩体当中的纵波波速，纵波波速通常采用弹性波勘探技术进行收集； ${v_{{\text{pr}}}}$ 为岩石当中的纵波波速。

岩体完整性系数K_v的大小反映了岩体相对于岩石的完整或破坏程度，常作为各种评价指标中的一项重要参数，通常K_v值小于1；当所测岩体处于高地应力^[21]、试验测试方向以及岩体含水状态等^[22]情况时，会出现K_v值大于1；当岩块从原有岩层取出时，产生卸荷效应，使波速发生变化，导致结果不准^[23]。

1.4 多源数据耦合方法

目前，用于表征岩体完整性的指标较多^[24]，常用指标为岩体质量指标RQD、岩体完整性系数K_v以及岩体体积节理数 ${J_{\text{v}}}$ 。GB50487—2008^[6]及GB50287—2016^[24]根据结构面组数及结构面间距确定，但只用K_v对岩体完整性进行定量评价；GB50287—2016^[24]中可使用 ${J_{\text{v}}}$ 及K_v作为岩体完整性的定量指标；3个规范对于K_v的评分范围皆是相同的， ${J_{\text{v}}}$ 采用GB/T50218—2014^[25]中评分，具体见表 1；鲁布革、二滩水电站、《中小型水利水电工程地质勘察规范：SL55—93》^[26]采用RQD对岩体完整性程度进行分析，但RQD评分范围不同，学者常用表 1中的数据进行研究^[27]。

表 1 岩体完整性评价标准

Table 1. Evaluation standards for rock mass integrity

完整程度	完整	较完整	完整性差	较破碎	破碎
RQD/%	90~100	75~90	50~75	25~50	0~25
J_v/ (条·m^-3)	0~3	3~10	10~20	20~35	＞35
K_v	0.75~1	0.55~0.75	0.35~0.55	0.15~0.35	0~0.15

下载: 导出CSV

| 显示表格

因此，根据相关工程经验以及各种评价方法，将岩体按照完整程度划分为完整、较完整、完整性差、较破碎和破碎5个等级。相关岩体完整性评价标准如表 1所示。

工程数据中存在工程师误判的情况，因此利用熵权-云模型对数据进行修正，具体步骤如下：

（1）整理确定岩体完整性评价指标，并依据规范确定各级分类标准见表 1。

（2）将各指标进行归一化处理，并根据下式利用熵权法确定指标权重：

${H_j} = \frac{{ - \sum\limits_{i = 1}^m {{k_{ij}}\ln {k_{ij}}} }}{{\ln m}} \text{，}$

(5)

$W = \frac{{1 - {H_j}}}{{\sum\limits_{j = 1}^n {(1 - {H_j})} }} 。$

(6)

式中：H_j为信息熵；k_ij为无量纲化后的评价指标值；m为待评对象数量；n为每个待评对象包含的评价指标；W为个指标权重。

（3）通过各个指标的上下限，根据下式确定云模型的数字特征：

$\left. {\begin{array}{*{20}{l}}{E}_{\text{x}}=({C}_{\mathrm{min}}+{C}_{\mathrm{max}})/2\text{ }\text{，}\\ {E}_{\text{n}}=({C}_{\mathrm{max}}-{C}_{\mathrm{min}})/6\text{ }\text{，}\\ {H}_{\text{e}}=k\text{ }。\end{array}} \right\}$

(7)

式中，C_min与C_max为某一岩体完整性等级范围的最小值与最大值， ${E_{\text{x}}}$ 为该范围内期望， ${E_{\text{n}}}$ 为该范围内熵， ${H_{\text{e}}}$ 为该范围内超熵，k为常数，取0.002。

（4）采用正向发生器生成不同指标对应的云模型，根据

$Y = \sum\limits_{i = 1}^n {{\mu _i}{W_i}}$

(8)

计算综合确定度Y，最后依据最大综合确定度原则，修正岩体完整性等级。

经过熵权-云模型预处理后，得到的数据评价结果与真实情况更加符合。该处理可以修正工程中判断误差较大部分，对于相邻评价等级则以工程师评价为准。

2. 岩体完整性智能评价方法

2.1 总体流程

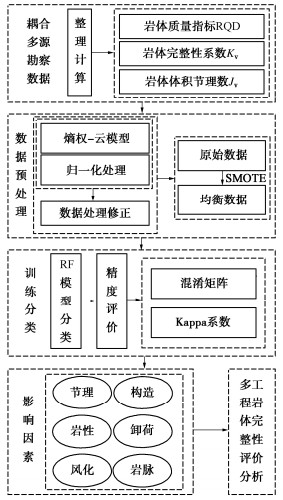
针对单一指标评价岩体完整性的局限性，本文将耦合工程中常用评价3个指标RQD、Jv、K_v，综合评价岩体完整性，增加准确率。图 1为主要研究路线，主要包括：①计算工程中3个评价岩体完整性指标，利用熵权-云模型对工程数据修正；②利用SMOTE算法对少数类样本中数据进行均衡；③使用随机森林分别对原始样本数据及均衡后数据进行训练分类；④计算Kappa系数及绘制混淆矩阵，结合影响岩体完整性因子，对多工程进行评价分析。

图 1 方法总体结构

Figure 1. Overall framework

下载: 全尺寸图片幻灯片

2.2 SMOTE算法

合成少数类过采样技术(synthetic minority oversampling technique，SMOTE)^[28]通常用于处理不平衡数据集。分类模型处理不平衡数据集时对少数类样本的分类效果通常较差，且当少数类样本远小于多数类样本时，预测精度易出现虚高现象。利用SMOTE方法对实际工程数据进行预处理，可使样本集达到均衡，进而优化评价结果。SMOTE算法的具体思路如下：

（1）假设某一少数类样本集为S={s₁, s₂, …, s_a}，a为少数类岩体完整性样本数量。对于少数类中每一个样本s，采用欧氏距离计算它到少数类样本集中所有样本的距离，得到其k近邻。

（2）根据样本不平衡比例，确定生成的样本数量占原少数类样本的百分比N%，对于每一个样本s_i(i=1, 2, …, a)从k近邻中随机选取b个样本数据，放入sample={ ${s'_1}$ , ${s'_2}$ , …, ${s'_b}$ }集合当中，每个数据记为 ${s'_i}$ ，其中， $0 \leqslant b \leqslant a$ ， $1 \leqslant l \leqslant b$ 。

（3）记采样倍数c=int(N/100)，取(0，1)随机数r=rand(0，1)，依据式（9）生成新的样本。

${S_j} = {s_i} + r({s'_i} - {s_i}){\text{ }}(j = 1,2,3, \cdot \cdot \cdot ,c) 。$

(9)

（4）重复（1）~（3）步骤合成其他少数类样本。

2.3 随机森林算法

随机森林算法(random forest，RF)是由Breiman^[29]提出的一种分类算法，其有着简单、抗噪能力强、性能稳定等优点，被广泛地运用于各种领域数据处理中。RF模型算法的思路如下：

（1）设总集合为W，采用Bootstrap自助法随机有放回的选取训练样本，形成k个子训练集{N_i}(i=1, 2, 3, …, k)，每一个训练样本为一棵CART决策树。

（2）k棵CART树组成了随机森林，每棵分类树的子节点进行分裂时，会从M个特征变量中随机选取m个变量(0＜m≤M)，作为每棵CART训练模型的指标。

（3）重复步骤（2），构建出随机森林中所有子树。

（4）将训练集导入构建好的RF模型当中，利用投票选举的方式进行统计，将票数最多的一类作为最终的预测结果。

RF算法在使用时通过Gini值作为切分节点的标准，Gini值反映了每个特征在每个CART树上做了多大的贡献，最后取均值，得出每个特征的贡献大小。RF预测模型的准确率跟CART树的数量以及最大深度有关，合理控制RF模型的参数可以使模型达到最优。

2.4 分类模型评价指标

岩体完整性预测模型通常为多分类模型可利用敏感性（sensitivity）、F1指标（F1-measure）等指标进行分析，但其步骤繁琐，因此本文采用混淆矩阵以及Kappa系数进行分析。混淆矩阵是一种图像精度评价，将实际值与预测值显示在同一个n行n列的矩阵中，效果直观简单。Kappa系数是基于混淆矩阵的一种统计学评估方法，实际工程中取值为[0，1]，Kappa系数越高，代表模型分类准确度越高，

${P_{\text{e}}} = \frac{{\sum\limits_{i = 1}^k {{m_i}{n_i}} }}{{\sum\limits_{i = 1}^k {{m_i}} }}{\text{ }}(i = 1,2,3, \cdot \cdot \cdot ,k) \text{，}$

(10)

$K = \frac{{{P_0} - {P_{\text{e}}}}}{{1 - {P_{\text{e}}}}} 。$

(11)

式中：k为类别总数；m_i为第i类真实样本数；n_i为第i类预测出来的样本数； ${P_0}$ 为总体分类精度。

一致等级情况如表 2所示。

表 2 Kappa系数一致等级表

Table 2. Scales of Kappa coefficient

系数	0~0.2	0.2~0.4	0.4~0.6	0.6~0.8	0.8~1.0
一致等级	极低	一般	中等	高度	几乎完全一致

下载: 导出CSV

| 显示表格

3. 工程应用

3.1 平硐勘查数据预处理与模型训练

为了验证模型的有效性，先依据某水电站坝址平硐勘探数据（记为工程1），分析模型在岩体完整性评价中的适用情况，再利用另一水利工程坝址勘探平硐数据（记为工程2）进行有效性验证，两工程数据均使用1.4节中熵权-云模型流程进行修正。工程1河谷狭窄，两岸陡峻，坡顶行对高差最多可达1000~1700 m，坡度可达30°~90°。其中数据包括9个勘探线，27个平硐，共被划分为118个平硐岩体完整性分段，岩体岩性以大理岩、粉砂质板岩为主。

采用RQD， ${J_{\text{v}}}$ ，K_v 3个常用评价岩体完整性指标进行模型训练及验证。 ${J_{\text{v}}}$ 在计算时，式（3）中系数为1.3~1.5，因此取二者系数均值1.4，在与式（2）计算结果取均值；K_v计算时岩体中纵波波速选用对穿声波波速，少数缺省值利用插值进行计算。表 3列举出部分典型的实际勘探数据。

表 3 工程岩体多源勘察数据

Table 3. Multi-source survey data of engineering rock mass

序号	平硐	桩号	RQD/%	J_v/(条·m^-3)	K_v	应力分带	岩体结构类型	岩体嵌合程度	完整性
1	PD01	220—250	99	6.0	0.85	集中带	块状结构	紧密	完整(1)
2	PD04	130—175	63	12.9	0.37	过渡带	次块状结构	较紧密	完整性差(3)
3	PD05	146.7—188	55	7.3	0.87	平稳带	镶嵌碎裂结构	较紧密	较完整(2)
4	PD07	70—160	80	5.5	0.88	过渡带	中厚层状结构	较紧密	较完整(2)
5	PD12	37—75	29	21.0	0.17	弱卸荷带	层状破碎结构	松弛	较破碎(4)
6	PD30	17—65	51	16.8	0.53	释放带	破碎结构	较松驰	完整性差(3)

下载: 导出CSV

| 显示表格

工程1包含完整分段数据9个，较完整分段数据45个，完整性差分段数据54个，较破碎分段数据10个，采用的训练集与测试集比例为7∶3。由于4个分段数据比例不均衡，先利用SMOTE算法对完整数据与较破碎进行扩充，使得4个分段数据基本上相等，再使用RF算法对预处理后的数据进行调参训练，得到最优时最大树深为7，决策树数目为50，其余参数为默认值。同时，将未采用SMOTE算法处理的数据也进行训练，作为对比。

3.2 完整性评价与分析

如表 4所示，可以看出完整、较破碎两个少数类样本经过均衡调节处理后，准确率有所上升，分析数据可知，仅利用RF模型会将完整性岩体分类成较完整岩体，将较破碎岩体分类成较破碎岩体，使得与实际情况更加不符。而提前用SMOTE算法处理后再进行分类，整体准确率从83.3%提升到94.4%，提升明显。

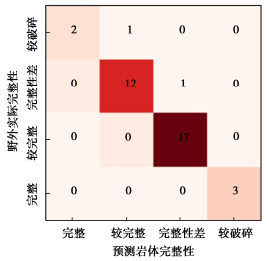
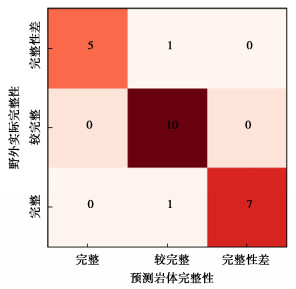
表 4 两种模型输出结果与岩体完整性对应关系

Table 4. Correspondence between output results of two models and rock mass integrity

岩体完整性	两种机器学习模型测试准确率/%
岩体完整性	RF模型	SMOTE-RF模型
完整	33.3	66.7
较完整	92.3	92.3
完整性差	88.2	100.0
较破碎	66.7	100.0
总准确率	83.3	94.4

下载: 导出CSV

| 显示表格

SMOTE-RF模型与RF模型K值分别为0.91，0.73，两者混淆矩阵如图 2，3所示。说明经过预处理后的数据，预测模型更加可靠，且少数类样本预测概率有所提升。

图 2 SMOTE-RF模型混淆矩阵

Figure 2. Confusion matrix of SMOTE-RF model

下载: 全尺寸图片幻灯片

图 3 RF模型混淆矩阵

Figure 3. Confusion matrix of RF model

下载: 全尺寸图片幻灯片

如表 5所示，为SMOTE-RF模型训练结果与实际情况不符分段。根据影响岩体完整性节理、岩性、卸荷、构造、风化、岩脉等因素对不符合分段进行简要分析。

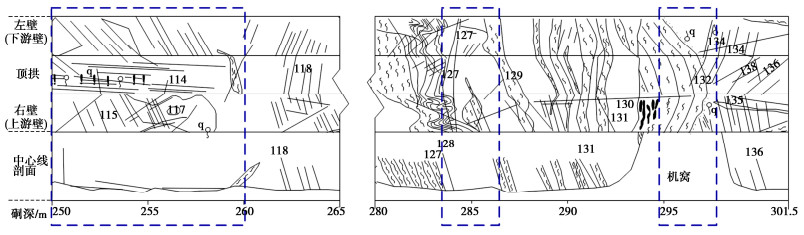
表 5 工程岩体分段评价结果

Table 5. Sectional evaluation results of engineering rock mass

序号	平硐	桩号	野外勘探岩体完整性评价	SMOTE-RF模型岩体完整性评价
1	PD01	250—301.5	完整(1)	较完整(2)
2	PD46	190—215	较完整(2)	完整性差(3)

下载: 导出CSV

| 显示表格

PD01位于Ⅰ线右岸抗力体，硐深301.5 m，硐口高程1656.09 m。RQD、J_v、K_v值为96.3，9.25，0.96。岩体结构类型为镶嵌碎裂结构，以厚层角砾状大理岩为主，局部夹绿片岩透镜体，岩体整体处于微风化，局部弱风化，沿NWW向溶蚀裂隙发育，间距0.2~0.5 m，沿^#114、^#117溶蚀张开1~3 cm。250~301.5 m之间有4组规则裂隙，裂隙发育特征如表 6所示，说明该分段岩体裂隙发育，而RQD值没有考虑裂隙的发育情况，导致数值过高，与真实情况存在一定出入。

表 6 裂隙发育特征

Table 6. Characteristics of fracture development

组别	规则裂隙产状	裂隙线平均间距统计（5 m×2 m）	规则裂隙延伸长度	张开度/mm	粗糙度	充填物类型	主要结构面类型	地下水
1	N40-60°E/SE∠65-80°	一般 > 1，个别0.1~0.5	一般1~3	0~2	平糙	少许钙膜	节理裂隙	干燥
2	N30-50°E/NW∠25-35°	薄—中层	> 2	0~2	起滑	绿泥石膜	节理裂隙	湿润
3	N5-20°W/SW∠50-70°	零星	1~3	0~5	起糙	不连续泥膜、岩屑	结构面	湿润
4	N30-50°W/NE∠25-30°	零星	> 1	0~2	起糙	不连续泥膜、岩屑	结构面	湿润

下载: 导出CSV

| 显示表格

另外，岩块嵌合较紧密，应力分带为集中-平稳带，存在地下水，如图 4中蓝色虚线框所示，在250~260 m，局部张开0.5~2 cm线状水，259 m附近处有滴水存在；285 m附近岩体湿润；296 m处为绿片岩与大理岩接触面，有连续滴水-流水，层面起伏，这些会导致测得的纵波波速偏高^[30]，从而导致K_v值变高。

图 4 PD01局部展开图

Figure 4. PD01 partial expansion diagram

下载: 全尺寸图片幻灯片

表 7 该岩体分段三组构造带基本情况与特征

Table 7. Basic situations and characteristics of three groups of structural zones in rock mass

编号	构造类型	产状	起伏情况	充填物	力学性质	其他特征
f46-1	切层错动带	N25E/SE∠80	起伏	灰黄色压碎岩	压性	上游壁与顶拱接触处见一长25 cm，宽 6 cm，深60 cm的溶洞
f46-3	切层错动带	N75E/NW∠70	起伏	黑色压碎岩	压性	含土白色方解石粉沫，局部软化夹泥；上游壁见宽40~80 cm影响带，逆断层
f46-4	切层错动带	N20E/SE∠25	微起伏	灰黑色角砾岩及压碎岩	压扭性	局部软化，泥化；下盘见宽1.2 m破碎岩，破碎结构，上盘湿润

下载: 导出CSV

| 显示表格

因此，虽然该分段的RQD与K_v值较高，但J_v值处于较完整分段，并且接近于完整性差分段，岩体完整性有待商榷。

PD46位于Ⅵ线左岸抗力体下游部位，硐口高程为1818.1 m，硐深250.3 m。RQD，J_v，K_v值为74.6，9.13，0.56。如表 7所示，该段受f46-1、f46-3、f46-4三组构造带影响，断层两侧同倾向裂隙发育，岩体较松弛、完整性差，在顶拱213.2 m处存在一平硐层间挤压带，风化较强烈，裂隙主要发育3组，裂面普遍中锈，充填不连续钙膜，岩块嵌合较松弛。虽然整体野外评价为较完整，但是此分段存在各种不良地质体，且三者值处于较完整与完整性差边界处，因此需要酌情考虑此处岩体完整性，避免施工造成损失。

3.3 SMOTE-RF模型工程应用拓展

为进一步验证方法模型的有效性及适用性，利用工程2中的数据对工程1所训练的模型进行研究。工程2距离区域性断裂较近，区域内岩体主要由燕山早期侵入岩-花岗闪长岩组成，地质构造相对简单。其中数据包括7个勘探线，16个平硐，共被划分为87个平硐岩体完整性分段，岩性以花岗岩为主，存在砂岩；包含完整，较完整、完整性差和较破碎分段数据分别为20，34，25，2个，由于较破碎岩体分段数据较少，因此选择前3个分段进行验证，训练集与测试集比例为7∶3，保持两种模型的各项参数，得出模型分类的准确率如表 8所示，可以看出分类为完整以及完整性差的岩体准确率有所上升，说明SMOTE-RF模型更优，更加符合实际情况。

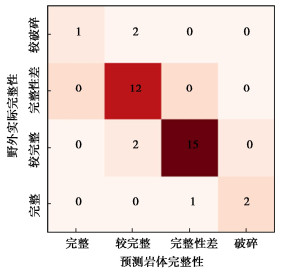
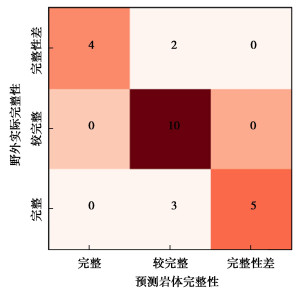
表 8 两种模型输出结果与岩体完整性对应关系

Table 8. Correspondence between output results of two models and rock mass integrity

岩体完整性	两种机器学习模型测试准确率/%
岩体完整性	RF模型	SMOTE-RF模型
完整	66.7	83.3
较完整	100.0	100.0
完整性差	62.5	87.5
总准确率	79.2	91.7

下载: 导出CSV

| 显示表格

两种模型的K值分别为0.87，0.67，二者混淆矩阵如图 5，6所示。可以看出，完整与完整性差少数类分段在SMOTE数据处理过后，预测效果更好，可以进一步扩充该类中的关键特征。

图 5 SMOTE-RF模型混淆矩阵

Figure 5. Confusion matrix of SMOTE-RF model

下载: 全尺寸图片幻灯片

图 6 RF模型混淆矩阵

Figure 6. Confusion matrix of RF model

下载: 全尺寸图片幻灯片

SMOTE-RF模型评价与实际不符情况如表 9所示。包括PD102与PD107中两个分段，将完整以及完整性差岩体均预测成了较完整岩体，先对这两分段进行分析。

表 9 工程岩体分段评价结果

Table 9. Sectional evaluation results of engineering rock mass

序号	平硐	桩号	野外勘探岩体完整性评价	SMOTE-RF模型岩体完整性评价
1	PD102	64—85	完整(1)	较完整(2)
2	PD107	25—38	完整性差(3)	较完整(2)

下载: 导出CSV

| 显示表格

PD102位于Ⅲ勘探线线左岸下坝址，硐深152 m，硐口高程2263 m，RQD，J_v，K_v分别为94，3.7和0.74。该段岩性为花岗闪长岩，有2组裂隙发育，间距20~30 cm，中度发育，岩体新鲜，较紧密，次块-镶嵌结构，岩体无卸荷，存在两条岩脉，弱风化，较坚硬，与围岩焊熔接触，湿润，岩脉其它特征描述表如表 10所示，两组岩脉如图 7所示，因此该段为较完整岩体更合适。

表 10 工程岩体岩脉特征描述表

Table 10. Description of dike characteristics of engineering rock mass

编号	桩号	产状	宽度/cm	颜色	特征	完整性	蚀变程度
Ym102~5	左72顶72.8右75	N60°E/NW∠80°	30~60	浅黄色	发育断层f102~5及宽 2~4 cm的石英脉，石英脉局部宽9 cm	完整性差	蚀变不明显
Ym102~6	左78.3~79.4顶78.5~79.1右81~81.6	N60°E/NW∠60°	60~110	灰白—浅黄色	宽2~3 cm的石英脉，断续延伸	较完整	上盘局部蚀变3~5 cm

下载: 导出CSV

| 显示表格

图 7 PD102岩脉照片

Figure 7. PD102 rock vein photograph

下载: 全尺寸图片幻灯片

PD107位于下横Ⅳ线左岸，硐深151 m，硐口高程为2263 m。RQD，J_v，K_v分别为86，9.85，0.32。该段岩体为花岗闪长岩，裂隙发育2组，间距30~50 cm，中度发育；该分段岩体质量等级为Ⅲ₂，弱风化，弱卸荷，较紧密，次块-块状结构，但此处岩体干燥，岩体含水率低，导致对穿声波波速值较小，因此将此处岩体完整性评定为较完整更加合理，但具体施工时还需要依据现场情况采取相应措施。

3.4 讨论

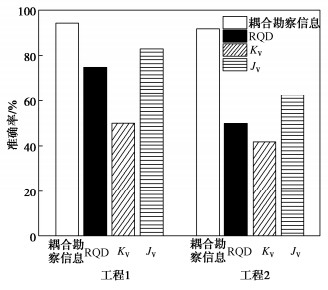
依据表 1利用常用传统指标RQD，K_v，J_v对两个工程测试集中数据分别进行岩体完整性评价，三者评价及耦合勘探信息情况如图 8所示。利用单一指标对岩体分段进行评价时，工程1与工程2中的依据单指标RQD，K_v，J_v评价准确率分别为75%，50%，83.3%以及50%，41.7%，62.5%，而经过少数类样本生成后，利用RF进行预测的准确率分别为94.4%，91.7%。

图 8 各方法评价情况

Figure 8. Evaluation of various methods

下载: 全尺寸图片幻灯片

可以看出，单一指标评价方法只能从部分角度反映岩体的完整程度，较为片面。耦合多源勘察信息指标可以减少因单一指标的造成的误差，增加岩体完整性评价的准确率，有助于工程师在进行野外勘探时判断岩体的分类情况。

4. 结论

针对传统工程岩体完整性评价时仅利用单一指标导致的评价精度差、准确率低等问题，提出了耦合多源勘察数据的SMOTE-RF模型，对具体工程岩体完整性数据不均衡分段进行定量评价分析，得到以下3点结论。

（1）运用熵权-云模型方法对数据进行预处理，可以检测出工程中误判数据。通过耦合多源勘探信息方法以及对比传统的方法，不难看出利用该方法得出来的效果比传统方法好，可以减少因单一指标反映岩体情况不周导致的效果差、准确率较低等问题，可以有效减少主观评价时存在的问题。

（2）对于工程中原始岩体完整性分段数据比例不均衡问题，利用SMOTE算法对少数类样本进行过采样处理，使训练集数据分布均衡，改善数据结构，进而采用RF机器学习模型对工程岩体完整性分段数据进行分类预测与验证，准确率得到较大提升。对其他工程进行了应用拓展，进一步说明了SMOTE-RF模型的有效性，且相较RF模型岩体完整性预测结果与实际情况更加符合，证明了该模型的有效性和普适性。

（3）预测结果问题分析：①样本数据量一直都是影响分类算法中的重要因素，少数类样本特征信息包含不全面，导致将少数类分类为多数类中；②当数据处于边界位置时，例如PD46中RQD，J_v，K_v值为74.6，9.13，0.56，依据表 1分类为较完整岩体，但分类为完整性差岩体；③当勘探参数跨度较大时，例如PD107中RQD，J_v，K_v值分别为86，9.85，0.32，跨度较大原因为各参数考虑因素不同，因此可能导致分类不准。

针对上述存在预测结果的问题，尚需进一步深入研究：结合其他工程数据，增加数据量，以减少单工程中分段特征相似情况，对于边界数据能更好考虑；将机器学习算法与评价标准进一步融合，提升模型方法的准确率。

图 1 岩性参数各变量相关关系图

Figure 1. Pearson correlation coefficient among rock indices

下载: 全尺寸图片幻灯片

图 2 测量值与预测值分布散点图及fB-GPR预测的不确定性

Figure 2. Scatter plot between measured and predicted UCS and uncertainty of UCS prediction by fB-GPR

下载: 全尺寸图片幻灯片

图 3 验证集中决定系数R²分布的箱形图

Figure 3. Box plot of R² for testing database

下载: 全尺寸图片幻灯片

图 4 各模型选择方法选出的次数最多的模型所对应的R²在验证集中的统计特征

Figure 4. Statistical characteristics of R² in testing dataset corresponding to model selected most frequently by each method

下载: 全尺寸图片幻灯片

图 5 误差值对模型选择结果的影响

Figure 5. Influences of measurement noise on model selection

下载: 全尺寸图片幻灯片

图 6 样本量对模型选择结果的影响

Figure 6. Influences of sample size on model selection

下载: 全尺寸图片幻灯片

表 1 岩性参数数据集的基本统计特征

Table 1 Basic descriptive statistics of rock index database

参数	UCS/ MPa	I_s50/ MPa	R_L	v_p/(m·s^-1)	η_e/%	G_s
最小值	20.30	1.08	16.80	1160.00	0.64	2.42
平均值	49.65	4.47	42.30	4145.69	2.27	2.57
最大值	91.00	8.19	56.50	5661.00	7.23	2.66
标准值	15.65	1.63	7.51	841.73	1.53	0.05

下载: 导出CSV

表 2 模型编号及其对应的岩性参数指标

Table 2 Candidate models for model selection and corresponding rock indices

模型编号	I_s50/MPa	R_L	v_p/(m·s^-1)	η_e/%	G_s	“模型证据” 的对数值	概率	R²
模型编号	I_s50/MPa	R_L	v_p/(m·s^-1)	η_e/%	G_s	“模型证据” 的对数值	概率	训练集	验证集
M-1	▲					-450.66	3.27×10^-14	0.72	0.60
M-2		▲				-468.83	4.19×10^-22	0.52	0.49
M-3			▲			-451.09	2.13×10^-14	0.69	0.69
M-4				▲		-479.57	9.14×10^-27	0.38	0.33
M-5					▲	-486.61	7.94×10^-30	0.22	0.19
M-6	▲	▲				-450.14	5.51×10^-14	0.75	0.63
M-7	▲		▲			-419.98	0.688	0.89	0.84
M-8	▲			▲		-447.66	6.54×10^-13	0.77	0.67
M-9	▲				▲	-450.96	2.42×10^-14	0.74	0.62
M-10		▲	▲			-437.88	1.15×10^-8	0.80	0.79
M-11		▲		▲		-470.91	5.27×10^-23	0.53	0.49
M-12		▲			▲	-471.13	4.21×10^-23	0.53	0.49
M-13			▲	▲		-444.98	9.58×10^-12	0.82	0.79
M-14			▲		▲	-451.24	1.84×10^-14	0.72	0.71
M-15				▲	▲	-481.87	9.14×10^-28	0.38	0.34
M-16	▲	▲	▲			-421.69	0.125	0.89	0.84
M-17	▲	▲		▲		-449.34	1.23×10^-13	0.78	0.67
M-18	▲	▲			▲	-451.48	1.45×10^-14	0.75	0.64
M-19	▲		▲	▲		-421.99	9.21×10^-2	0.89	0.84
M-20	▲		▲		▲	-422.43	5.96×10^-2	0.89	0.84
M-21	▲			▲	▲	-449.80	7.74×10^-14	0.77	0.67
M-22		▲	▲	▲		-440.12	1.24×10^-9	0.80	0.79
M-23		▲	▲		▲	-440.40	9.37×10^-10	0.80	0.79
M-24		▲		▲	▲	-473.20	5.32×10^-24	0.53	0.49
M-25			▲	▲	▲	-447.12	1.13×10^-12	0.82	0.80
M-26	▲	▲	▲	▲		-423.83	1.47×10^-2	0.89	0.84
M-27	▲	▲	▲		▲	-424.15	1.06×10^-2	0.89	0.84
M-28	▲	▲		▲	▲	-451.70	1.16×10^-14	0.77	0.67
M-29	▲		▲	▲	▲	-424.35	8.70×10^-3	0.89	0.84
M-30		▲	▲	▲	▲	-442.47	1.17×10^-10	0.80	0.79
M-31	▲	▲	▲	▲	▲	-426.30	1.23×10^-3	0.89	0.84

下载: 导出CSV

表 3 不同方法的模型选择结果对比

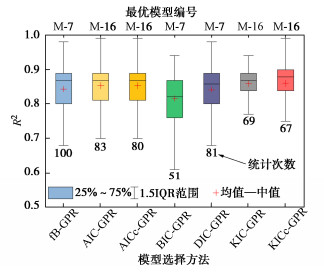
Table 3 Comparison of model selection results by different methods

方法	I_s50/MPa	R_L	v_p/(m·s^-1)	η_e/%	G_s	R²
文献[11]	▲		▲			0.83
fB-GPR	▲		▲			0.89
BIC-GPR	▲	▲	▲			0.89
AIC-GPR	▲	▲	▲			0.89
AICc-GPR	▲	▲	▲			0.89
DIC-GPR	▲		▲	▲		0.89
KIC-GPR	▲	▲	▲			0.89
KICc-GPR	▲	▲	▲			0.89

下载: 导出CSV

表 4 各模型选择方法选出的最优模型编号及其被选为最优模型的次数统计

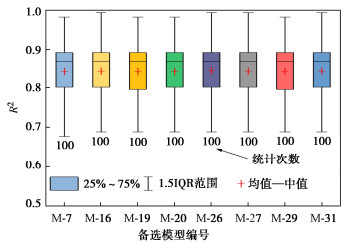
Table 4 Number of optimal models selected by each method and number of times selected as the optimal model

模型	fB-GPR	AIC -GPR	AICc -GPR	BIC -GPR	DIC -GPR	KIC -GPR	KICc -GPR
M-7	100	14	18	51	81	29	31
M-16	0	83	80	47	14	69	67
M-19	0	3	2	2	5	2	2

下载: 导出CSV

参考文献(25)

[1]	李文, 谭卓英. 基于P波模量的岩石单轴抗压强度预测[J]. 岩土力学, 2016, 37(增刊2): 381-387. doi: 10.16285/j.rsm.2016.S2.049 LI Wen, TAN Zhuoying. Prediction of uniaxial compressive strength of rock based on P-wave modulus[J]. Rock and Soil Mechanics, 2016, 37(S2): 381-387. (in Chinese) doi: 10.16285/j.rsm.2016.S2.049
[2]	孙欢, 刘晓丽, 王恩志, 等. 基于X射线断层扫描预测岩石单轴抗压强度[J]. 岩石力学与工程学报, 2019, 38(增刊2): 3575-3582. doi: 10.13722/j.cnki.jrme.2019.0614 SUN Huan, LIU Xiaoli, WANG Enzhi, et al. Prediction on uniaxial compression strength of rocks with X-ray computed tomography[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S2): 3575-3582. (in Chinese) doi: 10.13722/j.cnki.jrme.2019.0614
[3]	沙鹏, 张庆同, 林军, 等. 基于点荷载强度的火成岩单轴抗压强度原位估算[J]. 岩土力学, 2020, 41(增刊2): 1-10. doi: 10.16285/j.rsm.2020.0371 SHA Peng, ZHANG Qingtong, LIN Jun, et al. In-situ estimation of uniaxial compressive strength of igneous rock based on point load strength[J]. Rock and Soil Mechanics, 2020, 41(S2): 1-10. (in Chinese) doi: 10.16285/j.rsm.2020.0371
[4]	ÇELIK S B. Prediction of uniaxial compressive strength of carbonate rocks from nondestructive tests using multivariate regression and LS-SVM methods[J]. Arabian Journal of Geosciences, 2019, 12(6): 1-17.
[5]	LIU D S, LIU H L, WU Y, et al. Characterization of geo-material parameters: gene concept and big data approach in geotechnical engineering[J]. Geosystems and Geoenvironment, 2022, 1(1): 100003. doi: 10.1016/j.geogeo.2021.09.003
[6]	HAN L, WANG L, DING X M, et al. Similarity quantification of soil parametric data and sites using confidence ellipses[J]. Geoscience Frontiers, 2022, 13(1): 101280. doi: 10.1016/j.gsf.2021.101280
[7]	MATIN S S, FARAHZADI L, MAKAREMI S, et al. Variable selection and prediction of uniaxial compressive strength and modulus of elasticity by random forest[J]. Applied Soft Computing, 2018, 70: 980-987. doi: 10.1016/j.asoc.2017.06.030
[8]	FATTAHI H. Applying soft computing methods to predict the uniaxial compressive strength of rocks from Schmidt hammer rebound values[J]. Computational Geosciences, 2017, 21(4): 665-681. doi: 10.1007/s10596-017-9642-3
[9]	FENG X, JIMENEZ R. Estimation of deformation modulus of rock masses based on Bayesian model selection and Bayesian updating approach[J]. Engineering Geology, 2015, 199: 19–27. doi: 10.1016/j.enggeo.2015.10.002
[10]	WU Z X, JI H, YU C, et al. EPR-RCGA-based modelling of compression index and RMSE-AIC-BIC-based model selection for Chinese marine clays and their engineering application[J]. Journal of Zhejiang University-SCIENCE A, 2018, 19(3): 211-224. [LinkOut] doi: 10.1631/jzus.A1700089
[11]	NG I T, YUEN K V, LAU C H. Predictive model for uniaxial compressive strength for Grade Ⅲ granitic rocks from Macao[J]. Engineering Geology, 2015, 199: 28–37. doi: 10.1016/j.enggeo.2015.10.008
[12]	RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Cambridge Mass: MIT Press, 2006.
[13]	苏国韶, 肖义龙. 边坡可靠度分析的高斯过程方法[J]. 岩土工程学报, 2011, 33(6): 916-920. http://www.cgejournal.com/cn/article/id/14030 SU Guoshao, XIAO Yilong. Gaussian process method for slope reliability analysis[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 916-920. (in Chinese) http://www.cgejournal.com/cn/article/id/14030
[14]	赵腾远, 宋超, 何欢. 小样本条件下江苏软土路基回弹模量的贝叶斯估计——基于静力触探数据与高斯过程回归的建模分析[J]. 岩土工程学报, 2021, 43(增刊2): 137–141. doi: 10.11779/CJGE2021S2033 ZHAO Tengyuan, SONG Chao, HE Huan. Bayesian estimation of resilient modulus of Jiangsu soft soils from sparse data—Gaussian process regression and cone penetration test data-based modelling and analysis[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S2): 137–141. (in Chinese) doi: 10.11779/CJGE2021S2033
[15]	蒋水华, 刘源, 张小波, 等. 有限数据条件下空间变异岩土力学参数随机反演分析及比较[J]. 岩石力学与工程学报, 2020, 39(6): 1265–1276. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202006017.htm JIANG Shuihua, LIU Yuan, ZHANG Xiaobo, et al. Stochastic back analysis and comparison of spatially varying geotechnical mechanical parameters based on limited data[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(6): 1265–1276. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202006017.htm
[16]	VANHATALO J, RIIHIMÄKI J, HARTIKAINEN J, et al. GPstuff: Bayesian modeling with Gaussian processes[J]. Journal of Machine Learning Research, 2013, 14(1): 1175-1179.
[17]	仉文岗, 顾鑫, 刘汉龙, 等. 基于贝叶斯更新的非饱和土坡参数概率反演及变形预测[J]. 岩土力学, 2022, 43(4): 1112–1122. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202204024.htm ZHANG Wengang, GU Xin, LIU Hanlong, et al. Probabilistic back analysis of soil parameters and displacement prediction of unsaturated slopes using Bayesian updating[J]. Rock and Soil Mechanics, 2022, 43(4): 1112-1122. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202204024.htm
[18]	ZHAO T Y, SONG C, LU S F, et al. Prediction of uniaxial compressive strength using fully Bayesian Gaussian process regression (fB-GPR) with model class selection[J]. Rock Mechanics and Rock Engineering, 2022, 55(10): 6301-6319.
[19]	CZADO C. Analyzing dependent data with vine copulas[J]. Lecture Notes in Statistics, Springer, 2019.
[20]	付代光, 刘江平, 周黎明, 等. 基于贝叶斯理论的软夹层多模式瑞雷波频散曲线反演研究[J]. 岩土工程学报, 2015, 37(2): 321-329. doi: 10.11779/CJGE201502016 FU Daiguang, LIU Jiangping, ZHOU Liming, et al. Inversion of multimode Rayleigh-wave dispersion curves of soft interlayer based on Bayesian theory[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 321-329. (in Chinese) doi: 10.11779/CJGE201502016
[21]	唐小松, 李典庆, 周创兵, 等. 基于Bootstrap方法的岩土体参数联合分布模型识别[J]. 岩土力学, 2015, 36(4): 913-922. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201504001.htm TANG Xiaosong, LI Dianqing, ZHOU Chuangbing, et al. Bootstrap method for joint probability distribution identification of correlated geotechnical parameters[J]. Rock and Soil Mechanics, 2015, 36(4): 913-922. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201504001.htm
[22]	HURVICH C M, TSAI C L. Regression and time series model selection in small samples[J]. Biometrika, 1989, 76(2): 297-307.
[23]	SPIEGELHALTER D J, BEST N G, CARLIN B P, et al. Bayesian measures of model complexity and fit[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2002, 64(4): 583-639.
[24]	CAVANAUGH J E. A large-sample model selection criterion based on Kullback's symmetric divergence[J]. Statistics & Probability Letters, 1999, 42(4): 333-343.
[25]	SEGHOUANE A K. Multivariate regression model selection from small samples using Kullback's symmetric divergence[J]. Signal Processing, 2006, 86(8): 2074-2084.