考虑松动区渐进破坏的隧道松动土压力研究

耿哲; 袁大军; 金大龙; 舒计城; 娄瑞

doi:10.11779/CJGE20220684

考虑松动区渐进破坏的隧道松动土压力研究 English Version

耿哲^{1, 2,},
袁大军^{1, 2},
金大龙^{1, 2, ,},
舒计城³,
娄瑞³

1.
北京交通大学城市地下工程教育部重点实验室, 北京 100044
2.
北京交通大学土木建筑工程学院, 北京 100044
3.
中铁十四局集团大盾构工程有限公司, 江苏南京 211800

基金项目:

国家自然科学基金“联合基金项目” U1834208

详细信息

作者简介:
耿哲(1994—)，男，博士研究生，主要从事盾构隧道方面的科研工作。E-mail: gz1013307644@163.com

通讯作者:
金大龙, E-mail: jindalong@163.com

中图分类号: TU432
计量
- 文章访问数: 320
- HTML全文浏览量: 81
- PDF下载量: 120
出版历程
- 收稿日期: 2022-05-26
- 网络出版日期: 2023-02-23

Loose earth pressure of tunnels considering progressive failure of loosen zone

GENG Zhe^{1, 2,},
YUAN Dajun^{1, 2},
JIN Dalong^{1, 2, ,},
SHU Jicheng³,
LOU Rui³

1.
Key Laboratory of Urban Underground Engineering, Ministry of Education, Beijing Jiaotong University, Beijing 100044, China
2.
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
3.
China Railway 14th Bureau Group Shield Engineering Co., Ltd., Nanjing 211800, China

摘要

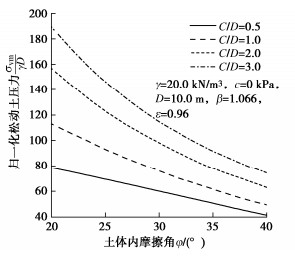
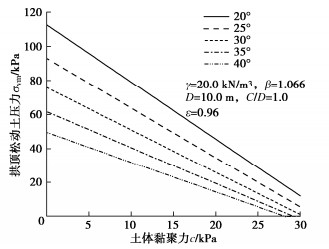
摘要: 浅埋盾构隧道所受松动土压力与松动区的渐进破坏和土拱效应密切相关，基于椭球体理论建立了椭圆形松动区模型，提出了土体损失量与松动区高度之间的关系，探明了松动区渐进破坏的演化过程和极限状态。考虑土体黏聚力和松弛区椭圆形状，基于大主应力迹线法给出了滑移面任意倾角下的侧向土压力系数，推导并验证了隧道拱顶松动土压力的迭代计算方法，针对极限状态和非极限状态展开参数分析，研究结果表明：①拱顶松动土压力随土体内摩擦角和黏聚力的增加而减小；②随松动区高度的增加，拱顶松动土压力先急剧减小，然后逐渐增加，最终趋于稳定。
- 盾构隧道 /
- 渐进破坏 /
- 松动土压力 /
- 非极限状态
Abstract: The loose earth pressure of shallow shield tunnel is closely related to the soil arch effect and the progressive failure of the loosen zone. Based on the ellipsoidal theory, the elliptic loosen zone model is established, and the relationship between the ground loss and the loosen zone height is proposed. The process of progressive failure and the limit state are defined. Considering the soil cohesion and the ellipse shape of the loosen zone, the lateral earth pressure coefficient under arbitrary dip angle of slip surface is obtained by means of the large principal stress trace method. The formula for calculating the loose earth pressure at tunnel top is derived and verified. The parameter analysis is carried out for the limit state and non-limit state, and the research results show that: (1) The loose soil pressure at tunnel top decreases with the increase of the internal friction angle and cohesion. (2) With the increase of the loosen zone height, the loose earth pressure at tunnel top decreases sharply first, then increases gradually, and finally tends to be stable.
- shield tunnel /
- progressive failure /
- loose earth pressure /
- non-limit state

HTML全文

0. 引言

近年来，中国地下综合管廊快速发展，地下管廊抗震分析受到了人们的重视，学者们通过振动台模型试验或数值模拟等方法对地下管廊的抗震性能进行了大量研究。李杰等^[1]根据振动台试验中地基土的实际边界条件，提出一种变刚度方法模拟层状剪切土箱，并验证了模拟方法的可靠性。汤爱平等^[2]通过振动台试验，讨论了管廊体系及其周围土体的地震反应，结果表明管体与其内部管线的动力响应存在显著不同。郭恩栋等^[3]通过数值模拟方法研究了地下管廊体系的横断面地震响应，提出与管廊内部管线相比，应重点关注管廊自身的抗震设计。由于地下管廊多被设计为浅埋结构，需穿越不同类别场地，因此一些学者研究了面波作用下或不同类型场地中管廊的地震响应。施有志等^[4]讨论了Rayleigh波作用下，地下管廊的动力特征。蒋录珍等^[5]研究了饱和土体内地下管廊的动力响应，讨论了不同地震动峰值、地震波入射角度及土体孔隙率等因素的影响。李金奎等^[6]通过等价线性本构模拟地基土的动力非线性特性，给出了地震作用下，管廊自身的薄弱位置。阮滨等^[7]研究了可液化场地中地下管廊结构的变形响应，结果表明管廊接头张开量在液化区显著增大。此外，由于装配式管廊的预应力承插式接头与盾构隧道结构多采用的拼装式螺栓接头在力学性能上有很大不同，谷音等^[8]、梁建文等^[9]研究了管廊预制接头的建模及接头预应力的实现方法，讨论了预制接头对地下管廊自身抗震性能的影响。

值得注意的是，与地铁隧道等地下交通结构不同，地下管廊相互交叉，形成大量十字或T型交叉节点；由于交叉管廊在两个主轴方向上的抗侧移刚度相差较大，交叉节点的地震内力非常复杂，成为地下管廊抗震性能的薄弱点。然而，目前中国还没有专门的地下管廊抗震设计规范，而《地下结构抗震设计标准》等现行标准^[10-11](以下简称《标准》)也仅给出了直线型地下(隧道)结构纵向抗震设计方法。

关于交叉管廊的抗震分析，近期有一些初步研究。赵丹阳^[12]计算了某十字交叉管廊的动力响应，讨论了单向及双向地震作用下交叉节点的破坏模式。梁建文等^[13-14]基于拟静力方法和动力时程方法，计算了某T型交叉管廊的地震反应，给出了地震作用下，T型交叉节点的内力放大系数及影响范围。由于交叉管廊体系中两个主轴结构的计算长度一般较大，由地震作用引起的两个主轴结构的拉压及挠曲等纵向地震反应对交叉节点的影响不可忽略，然而上述研究^[12-14]均是横向抗震分析，研究交叉管廊交叉节点处顶板和底板之间相对变形，受限于地震动输入机制，这些研究均没有涉及交叉管廊的纵向抗震设计。

为此，本文提出地下交叉管廊纵向抗震设计的一个反应位移法，并以预制装配式T型交叉管廊为例，进行了算例分析。研究可为交叉管廊的纵向抗震设计提供一定参考。

1. T型交叉管廊纵向反应位移法

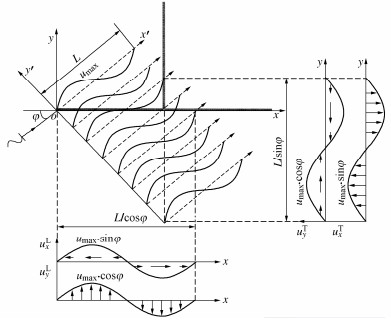
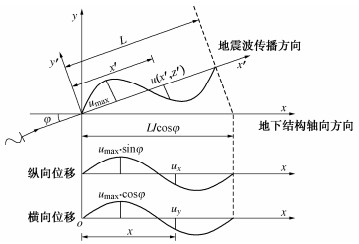
现行《标准》中规定，地震作用下，地层沿结构轴线方向的纵向位移u_x及与结构轴线垂直方向的横向位移u_y可采用正弦规律分布，如图 1所示，场地的位移分布函数u(x', z')为

图 1 《标准》中纵向反应位移法计算模型

Figure 1. Computational model for longitudinal response deformation method in Chinese standard

下载: 全尺寸图片幻灯片

$u(x',z') = {u_{\max }}(z')\sin \left( {\frac{{2{\text{π }}}}{L}x'} \right) 。$

(1)

式中：φ为地震波传播方向与地下结构轴向的夹角；u_max为地震作用下场地深度z(z=z')处的水平位移峰值；L为地层变形波长。

可以看到，纵向反应位移法基本假定下，当给定φ和u_max两个参数后，观测场地同一深度z处沿纵向将呈现出正弦模式下的单一地层变形，仅一次计算即可获得结构的地震响应峰值。值得注意的是，该方法仅适用于单线地下结构，当研究对象为交叉管廊时，上述单一地层变形思想将不再适用。

鉴于此，本文基于反应位移法基本原理，提出一种适用于交叉管廊纵向抗震设计的反应位移法。以某T型管廊为例，假定某一地层变形状态下，管廊所在场地的地层变形形式如所示。图中， $u_x^{\text{L}}$ ， $u_x^{\text{T}}$ 表示管廊结构所在位置地基土的纵向(x向)变形， $u_y^{\text{L}}$ ， $u_y^{\text{T}}$ 表示结构所在地基土的横向(y向)变形，上标L和T分别表示x向结构和y向结构。o-x'-y'-z'为入射波坐标系，o-x-y-z为场地坐标系。

图 2 T型交叉管廊地层位移分解模型

Figure 2. Decomposition of stratum deformation for T-type utility tunnels

下载: 全尺寸图片幻灯片

定义o-x'-y'-z'坐标系中任意一点( ${x'_i}$ , ${y'_j}$ , ${z'_k}$ )，经坐标变换后，其与场地坐标系o-x-y-z的关系为

$\left\{ \begin{gathered} {{x'}_i} \hfill \\ {{y'}_j} \hfill \\ {{z'}_k} \hfill \\ \end{gathered}\right\} = \left[ {\begin{array}{*{20}{c}} {\cos \varphi }&{\sin \varphi }&0 \\ { - \sin \varphi }&{\cos \varphi }&0 \\ 0&0&1 \end{array}} \right]\left\{ \begin{gathered} {x_i} \hfill \\ {y_j} \hfill \\ {z_k} \hfill \\ \end{gathered}\right\} 。$

(2)

点( ${x'_i}$ , ${y'_j}$ , ${z'_k}$ )的位移u( ${x'_i}$ , ${y'_j}$ , ${z'_k}$ )与其在o-x-y-z坐标系内的分量u_x，u_y和u_z的关系可为

$\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol u_x}({x_i},{y_j},{z_k})} \\ {{\boldsymbol u_y}({x_i},{y_j},{z_k})} \\ {{\boldsymbol u_z}({x_i},{y_j},{z_k})} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} { - \sin \varphi } \\ {\cos \varphi } \\ 1 \end{array}} \right\}\boldsymbol u({x'_i},{y'_j},{z'_k}) \text{，}$

(3)

式中， ${z'_k}$ = ${z_k}$ 。

将式(2)，(3)代入式(1)，可得u(x', y', z')在场地坐标系o-x-y-z下的分布函数，其沿x向和y向的位移函数形式如式分别为

$u_x(x, y, z)=-u_{\max }(z) \sin \varphi \sin \left[\frac{2 \pi}{L}(y \sin \varphi+x \cos \varphi)\right]，$

(4)

$u_y(x, y, z)=u_{\max }(z) \cos \varphi \sin \left[\frac{2 \pi}{L}(y \sin \varphi+x \cos \varphi)\right] 。$

(5)

值得注意的是，式(4)，(5)仅为图 2示意单一状态下场地的x向及y向地层变形分布，不足以反映整个地层变形周期内T型交叉管廊结构的全部地震响应。

与单线地下结构相比，交叉型地下结构纵向抗震设计的一个显著区别在于，一次分析计算无法反映整个地层变形周期内结构的变形历程。由于交叉节点的存在，交叉型地下结构在处于同一周期内不同状态下的地层变形分布时，结构峰值响应可能会有很大区别。因此，明确交叉型地下结构两个主轴方向各自的地层变形计算方法，设计可反映其周期内变形历程的计算模型十分必要。

为体现出一个地层变形周期内结构的变形历程，本文引入计算步长i，通过改变位移函数相位来实现场地地层变形的周期性运动，分n步逐次令场地运动一个地层变形周期，这里约定图 2示意为整个地层变形周期的初始状态(i=0)，那么整个周期内所有状态下场地的地层变形分布为

${u}_{x}(x,y,z)=-{u}_{\mathrm{max}}\text{(}z\text{)sin}\varphi \mathrm{sin}\left[\frac{2\text{π}}{L}(y\mathrm{sin}\varphi +x\mathrm{cos}\varphi -\frac{i}{n}L)\right]\text{，}$

(6)

${u}_{y}(x,y,z)={u}_{\mathrm{max}}\text{(}z\text{)cos}\varphi \mathrm{sin}\left[\frac{2\text{π}}{L}\left(y\mathrm{sin}\varphi +x\mathrm{cos}\varphi -\frac{i}{n}L\right)\right]。$

(7)

式中，i=0, 1, 2, ..., n，n为计算步长总数。

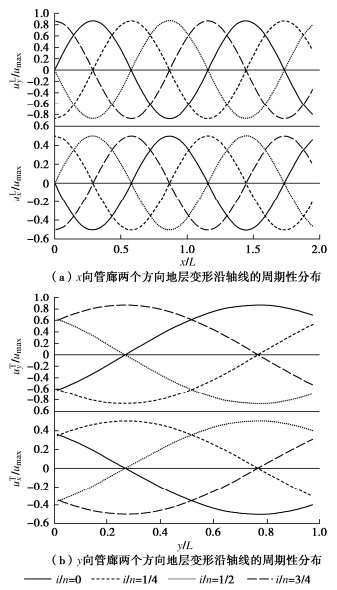
可以看到，i=0时，由式(6)，(7)计算得到的地层变形分布即为图 2示意的初始地层变形模式；随着计算步长i的增加，两个主轴方向管廊轴线处的地层变形在一个地层变形周期内逐渐偏移，直至i=n时完成一整个周期的运动历程。图 3展示了由式(6)，(7)计算得到的场地周期性变形。图 3中，φ取30°，T型交叉管廊x向及y向尺寸分别取为2L和L，以i/n=0，1/4，1/2，3/4四个周期状态为例。

图 3 T管廊所在位置地层变形的周期性分布

Figure 3. Periodic distribution of stratum deformation at location of T-type utility tunnels

下载: 全尺寸图片幻灯片

可以看到，本文方法可以反映场地在一个地层变形周期内的运动历程。因此，仅需确定适宜的计算步长总数n的取值，便可保证获取足够丰富的场地变形细节，关于n的取值问题将在下文详细讨论。

结合上文计算方法，本文于ABAQUS有限元平台编制了用于交叉管廊抗震设计的Python程序，实现了从模型建立→地基弹簧及接头弹簧添加→周期性地层变形赋予等全流程作业，从建模到输出结果自动运行，无需外部干预。

2. T型交叉管廊纵向抗震分析

2.1 算例

以某拟建的T型交叉综合管廊为例，该T型管廊两个主轴方向横截面均为双舱形式，总宽度11000mm，高5750 mm，底板厚600 mm，顶板和侧板厚500 mm，中隔板厚300 mm。管廊混凝土强度等级为C60，密度2650 kg/m³，弹性模量35.5 GPa。管廊纵向接头通过承插口连接，预制管廊段长1.5 m，腋角处共配置6条钢绞线，有效截面积140 mm²，弹性模量195000 MPa，屈服强度1628 MPa。管廊处于弹性基岩上的软土场地，计算埋深3 m，场地总厚度为80 m，共包含4类土，具体土层参数信息及土体非线性特性参数见文献[15]。

2.2 计算模型

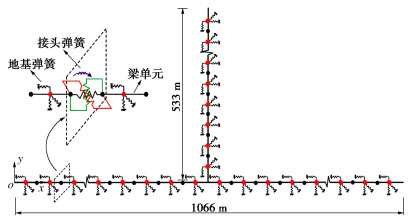
采用三维线性B31梁单元模拟管廊结构，单元尺寸0.75 m。结合《标准》中相关规定，模型纵向(x向)计算长度取2个地层变形波长(2L=1066 m)，横向(y向)计算长度取一个地层变形长(L=533 m)，模型中T型节点为整体现浇式，其余部分为预制装配式。

于管节间承插式接头处将梁单元断开，采用非线性弹簧单元模拟接头力学行为，其中3个方向平动弹簧用于模拟预制接头的轴向及横向行为，两个方向转动弹簧用于模拟接头弯曲行为，忽略接头扭转行为。地基土采用沿地下结构轴向均匀布置的纵向弹簧和横向弹簧模拟，如图 4所示。

图 4 计算模型示意

Figure 4. Computational model

下载: 全尺寸图片幻灯片

考虑到承插式接头构造，假定由管廊腋角6根钢绞线承担全部拉力，止水橡胶圈及接头混凝土协同承担压力和剪力，接头弹簧刚度系数由K_i=E_iA/l计算，其中K_i为弹簧不同阶段的刚度系数，E_i为接头处混凝土或止水橡胶或钢绞线的弹性模量，A为钢绞线截面积或混凝土承压面积，l为钢绞线有效长度。接头转动时，假定断面受拉区由钢绞线承担拉力，受压区由橡胶混凝土协同承担压力，结构始终处于弹性状态，采用静力有限元法^[16]计算两个方向转动弹簧刚度。接头弹簧参数具体计算方法见文献[9]。

2.3 场地地震动反应及模型地震动参数

入射波选用El Centro波，其加速度峰值调幅为0.20g，本文采用一维地震分析程序EERA^[17]计算场地地震反应，计算得到的模型地震动参数如表 1所示。

表 1 计算模型地震动参数

Table 1. Parameters of model ground motion

u_max/m	G_d/MPa	k_t/(kN·m^-1)	k_l/(kN·m^-1)
0.0934	7.3723	190758.52	370458.58

下载: 导出CSV

| 显示表格

采用本文方法于地基弹簧远端逐次输入地层位移，直至完成一个周期的地层变形，计算地震波传播方向与x向管廊轴线夹角φ=0°，30°，45°，60°四种情况下的结构响应。

2.4 计算步长总数的确定

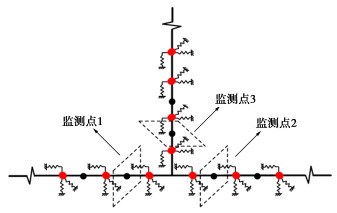
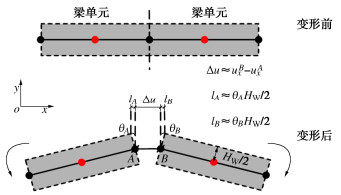
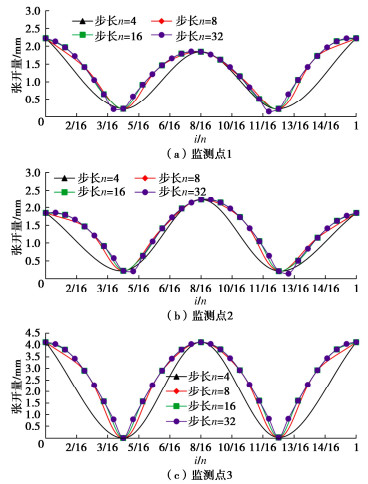
本文通过改变位移函数的方式分步逐次令场地运动一个地层变形周期，为了确定适宜的计算步长总数n，保证获取足够丰富的结构变形细节且兼顾计算机时，计算了步长总数n=4，8，16，32四类情况(以入射角φ=0°为例)的T型交叉管廊地震反应。以T型交叉节点处的接头变形为观测对象，提取了图 5所示3个监测点的接头张开量，其中每个监测点接头张开量取为接头相邻节点的位移差Δu与节点转动弧长l(l_A+l_B)之和，具体计算方法如图 6所示。图 6中，u_x为节点位移，上标A和B为接头处梁单元节点；θ_A和θ_B分别为节点A和节点B相对初始位置的转角；H_W为管廊顶、底板宽度。

图 5 交叉节点处监测点示意

Figure 5. Selection of monitoring points at T-type cross

下载: 全尺寸图片幻灯片

图 6 接头挠曲变形示意及张开量计算方法

Figure 6. Schematic diagram of joint deflection and method for joint opening

下载: 全尺寸图片幻灯片

图 7给出了各监测点张开量在一个地层变形周期内的变化如所示。可以看到，3个监测点的张开量在不同周期状态(i/n)下存在显著差异。随着计算步长总数n的增加，各监测点的周期内变形响应逐渐趋同。当步长数n≥8后，各张开量曲线已基本重合，足以捕捉变形响应峰值，且满足计算精度要求。因此，为兼顾计算机时，本文将计算步长总数取n为8。

图 7 不同工况下各监测点的周期内变形

Figure 7. Periodic deformations of monitoring points

下载: 全尺寸图片幻灯片

3. 计算结果

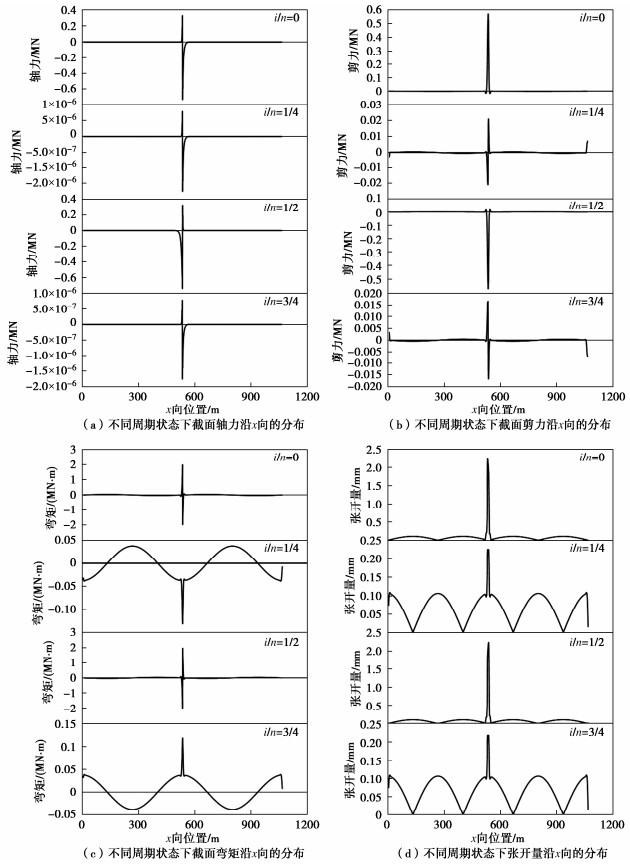
一个地层变形周期内T型交叉管廊的接头变形及结构内力响应沿管廊轴线的分布(以x向管廊为例，限于篇幅，仅展示了φ=0°时，i/n=0，1/4，1/2，3/4等4个状态下的结构地震响应分布)，如图 8所示。

图 8 T型交叉管廊内力和变形沿管廊轴线的分布

Figure 8. Distribution of internal forces and deformations along axis of T-type cross utility tunnels

下载: 全尺寸图片幻灯片

可以看到，T型节点处因存在截面突变，整个地层变形周期内均表现出显著的变形及内力集中，T型交叉节点的影响范围约为20 m。地震波传播方向与x向管廊轴线夹角φ=0°时，x向管廊虽仅承担弯曲变形，但图 8中，T型交叉节点处在初始状态(i/n=0)及1/2周期状态(i/n=1/2)下仍表现出较大的轴力，其它地震响应也均出现不同程度的放大现象，体现出交叉节点的影响。随着地层变形的周期内推移，T型节点处的地震响应不断变化且不同周期状态i/n下的幅值差距较大，表明周期内不同的地层变形分布形式对交叉型地下结构的地震响应影响显著，因此确定交叉节点处结构响应达到最不利状态时的地层变形十分必要。

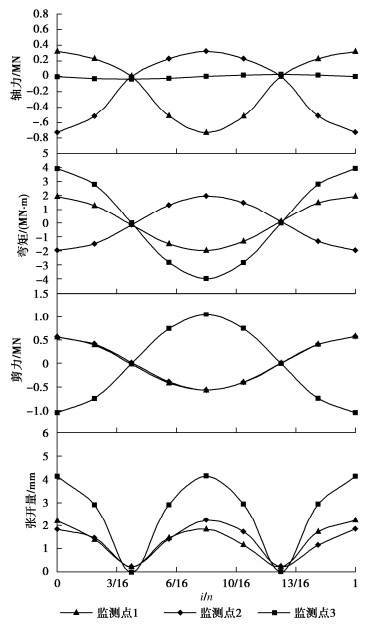
为获取地震作用下，由本文方法计算得到的T型交叉管廊的响应峰值及其对应的结构最不利模式，根据图 8所示T型交叉节点的变形及受力特征，提取了不同地震波入射角度φ下，T型交叉节点处的接头的变形响应以及结构的内力响应，各类响应峰值在一个地层变形周期内的变化如图 9所示(以φ=0°为例，监测点选取与图 5相同)。

图 9 T型交叉节点处内力和变形的周期内变化

Figure 9. Periodic variation of internal forces and deformations

下载: 全尺寸图片幻灯片

可以看到，在一个地层位移周期内，不同阶段、不同变形模式下T型交叉节点处的变形及内力响应存在显著不同。地震波入射角度φ=0°时，管廊的内力响应峰值均出现在初始周期状态(i/n=0)，而变形响应则在初始周期状态(i/n=0)及1/2周期状态(i/n=1/2)均表现出较大值，监测点3峰值张开量达到4.1 mm，已超出《城市综合管廊工程技术规范：GB50838— 2015》^[18]规定的限值2 mm。

不同地震波入射角度φ下，各监测点的地震响应峰值及其对应周期状态(i/n)如表 2所示。出于简便，这里定义轴力最不利状态对应步长i_f，剪力最不利状态对应步长i_s，弯矩最不利状态对应步长i_m；接头变形的不利状态对应步长i_d。

表 2 T型交叉节点最不利状态下的峰值响应

Table 2. Peak responses of T-type cross under most unfavorable state

φ/(°)	峰值轴力/MN	i_f/n	峰值剪力/MN	i_s/n	峰值弯矩/(MN·m)	i_m/n	峰值张开量/mm	i_d/n
0	-0.72(监测点2)	0	1.05(监测点3)	0	3.96(监测点3)	0	4.13(监测点3，超限)	0
30	-5.59(监测点2)	7/8	1.33(监测点1)	3/8	3.28(监测点1)	3/8	3.66(监测点1，超限)	7/8
45	-5.94(监测点2)	3/4	1.20(监测点2)	1/4	2.64(监测点2)	1/4	3.31(监测点2，超限)	1/4
60	-5.61(监测点1)	1/2	1.33(监测点2)	0	3.27(监测点2)	0	3.67(监测点2，超限)	1/2

下载: 导出CSV

| 显示表格

现有研究^[19]表明，采用纵向反应位移法进行线长形地下结构的地震反应计算时，随着入射角度φ的增大，结构的弯矩、剪力逐渐减小，轴力及张开量先增大后减小。但从表 2中可以看出，T型交叉管廊的地震响应与上述规律存在显著区别。可以看到，地震波入射角度φ=0°时，x向管廊主要承担弯曲变形，而y向管廊表现为整体平动，当两者变形耦合在一起后，主要体现为整体平动的y向管廊出现了较大的接头张开，这是由于两个主轴方向管廊结构的抗侧向刚度及结构周围地基弹簧的约束能力相差较大，x向管廊在周期内弯曲过程中，y向交叉节点出现较大接头转动导致。

随着入射角度的增大，管廊的接头变形峰值和截面弯矩峰值有所减小，而轴力和剪力峰值有所增大。其中，截面轴力峰值的变化最为显著，φ=45°时监测点2处轴力达到峰值5940 kN，表明双向地层变形的耦联运动对T型交叉节点处轴力有不利影响。

4. 敏感性分析

4.1 正交试验方案设计

为了进一步研究地震作用下，T型交叉管廊的变形及受力机理，明确不同地层条件、地震动参数等因素对本文方法计算结果及T型管廊最不利模式的影响，获取一定普适性结论，拟通过正交试验对本文方法进行敏感性分析，考虑了包括场地剪切波速v_s、入射角度φ、地震峰值加速度a_max以及管廊计算埋深h在内的4个因素的交互影响，每个因素设计为3个水平。

由于城市综合管廊处地层的等效剪切波速v_s通常小于500 m/s，且多为浅埋结构，故选取剪切波速v_s为200~400 m/s的场地进行分析，设计结构埋深h为2~4 m。同时，仅讨论入射角φ > 0°的情况，地震动峰值调幅为0.10g~0.20g。综上，设计了L9(3⁴)正交表，如表 3所示。假定场地覆土深度H为80 m，质量密度ρ为2000 kg/m³，场地地层变形波长L为400 m，暂不考虑地基土的非线性影响，各工况模型参数计算方法与上文相同。

表 3 正交试验方案

Table 3. Scheme of orthogonal experiments

工况	v_s/(m·s^-1)	φ/(°)	a_max/g	h/m
1	200	30	0.10	2
2	200	45	0.15	3
3	200	60	0.20	4
4	300	30	0.15	4
5	300	45	0.20	2
6	300	60	0.10	3
7	400	30	0.20	3
8	400	45	0.10	4
9	400	60	0.15	2

下载: 导出CSV

| 显示表格

4.2 正交试验计算结果

计算了各正交试验工况，得到的各工况下T型交叉管廊的内力和变形峰值响应及其对应周期状态(i/n)如表 4所示。

表 4 正交模型结果汇总

Table 4. Results of orthogonal model

工况	峰值轴力/MN	i_f/n	峰值剪力/MN	i_s/n	峰值弯矩/(MN·m)	i_m/n	峰值张开量/mm	i_d/n
1	-6.85(监测点2)	7/8	2.20(监测点1)	3/8	3.76(监测点1)	3/8	2.22(监测点3)	7/8
2	-10.25(监测点2)	3/4	2.42(监测点2)	1/4	3.52(监测点2)	1/4	2.10(监测点2)	1/4
3	-13.69(监测点1)	1/2	4.40(监测点2)	0	7.53(监测点2)	0	4.43(监测点3)	1/2
4	-11.72(监测点2)	7/8	3.92(监测点1)	3/8	6.02(监测点1)	3/8	2.41(监测点1)	7/8
5	-15.48(监测点2)	3/4	3.69(监测点2)	1/4	4.78(监测点2)	1/4	1.85(监测点2)	1/4
6	-7.85(监测点1)	1/2	2.63(监测点2)	0	4.03(监测点2)	0	1.61(监测点3)	1/2
7	-18.44(监测点2)	7/8	6.20(监测点1)	3/8	8.87(监测点1)	3/8	2.55(监测点3)	7/8
8	-9.05(监测点2)	3/4	2.14(监测点2)	1/4	2.58(监测点2)	1/4	0.70(监测点2)	1/4
9	-13.87(监测点2)	1/2	4.66(监测点2)	0	3.88(监测点2)	0	6.68(监测点2)	1/2

下载: 导出CSV

| 显示表格

可以看到，四类因素交互作用下，入射角φ相同时，T型交叉节点处内力和变形峰值的最不利模式一致，即同一地震波入射角度φ下，改变其它因素不会影响内力和变形出现峰值时所对应的周期状态(i/n)，表明线弹性假定下，地震波入射角度φ对T型管廊的最不利模式起控制作用。利用本文方法进行T型交叉管廊纵向抗震计算时，需着重验算表 5中最不利变形下的地震响应。

表 5 交叉节点处截面轴力峰值极差分析

Table 5. Range analysis of axial force at cross section

水平	因子
水平	v_s/(m·s^-1)	φ/(°)	a_max/g	h/m
1	10.263	12.337	7.917	12.067
2	11.683	11.593	11.947	12.180
3	13.787	11.803	15.870	11.487
极差	3.523	0.743	7.953	0.693
影响度排序	2	3	1	4

下载: 导出CSV

| 显示表格

根据正交试验结果，计算得到的每个因素在不同水平情况下各个指标的平均值及极差如表 5~8所示。可以看到，加速度峰值对T型交叉管廊的内力和变形均影响显著；入射角度是影响T型交叉管廊挠曲及接头变形的主要因素，但对交叉节点处轴力峰值的影响较小；埋深及剪切波速对交叉节点处内力和变形的影响不明显。因此，对交叉型管廊进行纵向地震反应计算时，需着重验算不同入射角φ下交叉管廊的内力和变形。

表 6 交叉节点处截面剪力峰值极差分析

Table 6. Range analysis of shear force at cross section

水平	因子
水平	v_s/(m·s^-1)	φ/(°)	a_max/g	h/m
1	3.007	4.107	2.323	3.517
2	3.413	2.750	3.667	3.750
3	4.333	3.897	4.763	3.487
极差	1.327	1.357	2.440	0.263
影响度排序	3	2	1	4

下载: 导出CSV

| 显示表格

表 7 交叉节点处截面弯矩峰值极差分析

Table 7. Range analysis of bending moment at cross section

水平	因子
水平	v_s/(m·s^-1)	φ/(°)	a_max/g	h/m
1	4.937	6.217	3.457	4.140
2	4.943	3.627	4.473	5.473
3	5.110	5.147	7.060	5.377
极差	0.173	2.590	3.603	1.333
影响度排序	4	2	1	3

下载: 导出CSV

| 显示表格

表 8 交叉节点处接头张开量峰值极差分析

Table 8. Range analysis of joint opening at cross section

水平	因子
水平	v_s/(m·s^-1)	φ/(°)	a_max/g	h/m
1	2.917	2.393	1.510	3.583
2	1.957	1.550	3.730	2.087
3	3.310	4.240	2.943	2.513
极差	1.353	2.690	2.220	1.497
影响度排序	4	1	2	3

下载: 导出CSV

| 显示表格

5. 结论

基于纵向反应位移法基本思想，提出了一种适用于T型交叉管廊纵向抗震设计方法。通过赋予地基弹簧周期性地层变形的方式，研究了T型交叉管廊的周期内变形历程，并据此讨论了交叉节点处变形和内力的最不利模式，以及计算参数对计算结果的敏感性，得到以下3点结论。

(1) 本文通过改变位移函数的方式，分为n步逐次令场地运动一个地层变形周期，可捕捉交叉型地下结构的峰值地震响应。讨论了计算步长n对计算结果精度的影响，建议计算步长n不宜小于8步。

(2) 在一个地层位移周期内，不同阶段、不同模式下T型管廊交叉节点处的变形及内力响应存在显著不同，即不同物理量的最不利模式不同。讨论了不同地震波入射角度下，T型交叉管廊的地震峰值响应。结果表明入射角对交叉节点处的轴力存在显著不利影响，随着入射角度的增大，结构的挠曲变形有所减小。给出了线弹性假定下，不同地震波入射角度时，各类最不利工况对应周期状态及地层变形，可为相关地下结构抗震设计提供参考。

(3) 考虑到场地剪切波速、入射角度、地震峰值加速度以及管廊计算埋深等四个因素的交互影响，设计了相应正交试验方案，讨论了不同参数对T型交叉管廊最不利模式的敏感性。结果表明，同一入射角度下，T型交叉节点处各类峰值响应的最不利模式一致，改变其它因素不会影响各类物理量出现峰值时所对应的周期状态，地震波入射角度对T型管廊的最不利模式起控制作用。

需要指出的是，本文计算方法并不局限于“T型”交叉管廊的地震反应计算，该计算思想经过一定拓展，也可应用于“十字型”、“L型”等交叉管廊结构，乃至地下管廊网络的抗震分析中，具体将另文讨论。

图 1 松动区横向影响范围

Figure 1. Transverse influence range of loosen zone

下载: 全尺寸图片幻灯片

图 2 松动区几何模型

Figure 2. Geometric model for loosen zone

下载: 全尺寸图片幻灯片

图 3 松动区演化

Figure 3. Evolution of loosen zone

下载: 全尺寸图片幻灯片

图 4 竖直滑移面下微分土条应力分布

Figure 4. Stress distribution of differential soil strip under vertical slip plane

下载: 全尺寸图片幻灯片

图 5 任意倾角滑移面下微分土条应力分布

Figure 5. Stress distribution of differential soil strip under arbitrary dip slip plane

下载: 全尺寸图片幻灯片

图 6 滑移面倾角α与侧向土压力系数K的关系曲线

Figure 6. Relationship between slip plane dip angle α and lateral earth pressure coefficient K

下载: 全尺寸图片幻灯片

图 7 松动区水平梯形土条应力图

Figure 7. Stress balance of horizontal trapezoidal soil strip in loosen zone

下载: 全尺寸图片幻灯片

图 8 离散块数与拱顶松动土压力的关系

Figure 8. Relationship between number of discrete blocks and loose earth pressure at tunnel top

下载: 全尺寸图片幻灯片

图 9 不同土体损失比下理论计算与模型试验1对比

Figure 9. Comparison between theoretical calculation and model test 1 under different ground loss ratios

下载: 全尺寸图片幻灯片

图 10 不同土体损失比下理论计算与模型试验2对比

Figure 10. Comparisons between theoretical calculation and model test 2 under different ground loss ratios

下载: 全尺寸图片幻灯片

土体内摩擦角φ与拱顶松动土压力 ${\sigma _{{\text{vm}}}}$ 的关系曲线

Relationship between internal friction angle φ and loose earth pressure at tunnel top ${\sigma _{{\text{vm}}}}$

下载: 全尺寸图片幻灯片

土体黏聚力c与拱顶松动土压力 ${\sigma _{{\text{vm}}}}$ 的关系曲线

Relationship between cohesion c and loose earth pressure at tunnel top ${\sigma _{{\text{vm}}}}$

下载: 全尺寸图片幻灯片

图 13 土跨覆比C/D与拱顶松动土压力 ${\sigma _{{\text{vm}}}}$ 的关系曲线

Figure 13. Relationship between cover-to-diameter ratio C/D and loose earth pressure at tunnel top ${\sigma _{{\text{vm}}}}$

下载: 全尺寸图片幻灯片

拱顶松动土压力 ${\sigma _{{\text{vm}}}}$ 随松动区高度H的演化曲线

Evolution curves of loose earth pressure at tunnel top ${\sigma _{{\text{vm}}}}$ with height of loosen zone

下载: 全尺寸图片幻灯片

参考文献(23)

[1]	陈湘生, 徐志豪, 包小华, 等. 中国隧道建设面临的若干挑战与技术突破[J]. 中国公路学报, 2020, 33(12): 1-14. doi: 10.3969/j.issn.1001-7372.2020.12.001 CHEN Xiangsheng, XU Zhihao, BAO Xiaohua, et al. Challenges and technological breakthroughs in tunnel construction in China[J]. China Journal of Highway and Transport, 2020, 33(12): 1-14. (in Chinese) doi: 10.3969/j.issn.1001-7372.2020.12.001
[2]	KOYAMA Y, KONISHI S, OKANO N. In-situ measurement and consideration on shield tunnel[J]. Quarterly Report of RTRI, 2001, 42(3): 125-129. doi: 10.2219/rtriqr.42.125
[3]	KOYAMA Y. Present status and technology of shield tunneling method in Japan[J]. Tunnelling and Underground Space Technology, 2003, 18(2/3): 145-159.
[4]	袁大军, 吴俊, 沈翔, 等. 超高水压越江海长大盾构隧道工程安全[J]. 中国公路学报, 2020, 33(12): 26-45. doi: 10.3969/j.issn.1001-7372.2020.12.003 YUAN Dajun, WU Jun, SHEN Xiang, et al. Engineering safety of cross-river or cross-sea long-distance large-diameter shield tunneling under superhigh water pressure[J]. China Journal of Highway and Transport, 2020, 33(12): 26-45. (in Chinese) doi: 10.3969/j.issn.1001-7372.2020.12.003
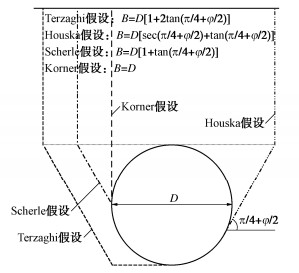
[5]	TERZAGHI K. Stress distribution in dry and in saturated sand above a yielding trap-door[C]// Proceedings of First International Conference on Soil Mechanics and Foundation Engineering. Cambridge, 1936.
[6]	TERZAGHI K, PECK R, MESRI G. Soil Mechanics in Engineering Practice[M]. New York: Hohn Wiley and Sons, Inc, 1948.
[7]	HANDY R L. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302-318. doi: 10.1061/(ASCE)0733-9410(1985)111:3(302)
[8]	HARROP-WILLIAMS K. Arch in soil arching[J]. Journal of Geotechnical Engineering, 1989, 115(3): 415-419. doi: 10.1061/(ASCE)0733-9410(1989)115:3(415)
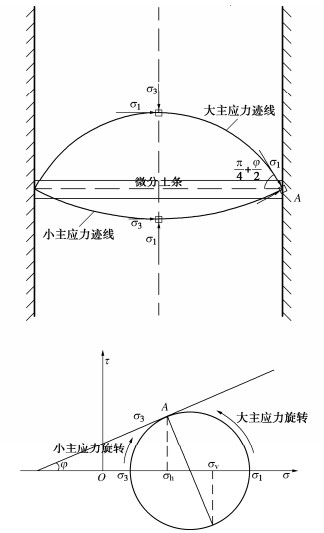
[9]	陈若曦, 朱斌, 陈云敏, 等. 基于主应力轴旋转理论的修正Terzaghi松动土压力[J]. 岩土力学, 2010, 31(5): 1402-1406. doi: 10.3969/j.issn.1000-7598.2010.05.009 CHEN Ruoxi, ZHU Bin, CHEN Yunmin, et al. Modified Terzaghi loozening earth pressure based on theory of main stress axes rotation[J]. Rock and Soil Mechanics, 2010, 31(5): 1402-1406. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.05.009
[10]	陈国舟, 周国庆. 考虑土拱效应的滑移面间竖向应力研究[J]. 中国矿业大学学报, 2014, 43(3): 374-379. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201403002.htm CHEN Guozhou, ZHOU Guoqing. Study of vertical stress between slip planes considering soil arching effect[J]. Journal of China University of Mining & Technology, 2014, 43(3): 374-379. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201403002.htm
[11]	陈国舟, 周国庆. 考虑土拱效应的倾斜滑移面间竖向应力研究[J]. 岩土力学, 2013, 34(9): 2643-2648. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201407050.htm CHEN Guozhou, ZHOU Guoqing. Study of vertical stress within inclined slip surfaces considering soil arching[J]. Rock and Soil Mechanics, 2013, 34(9): 2643-2648. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201407050.htm
[12]	徐长节, 梁禄钜, 陈其志, 等. 考虑松动区内应力分布形式的松动土压力研究[J]. 岩土力学, 2018, 39(6): 1927-1934. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806002.htm XU Changjie, LIANG Luju, CHEN Qizhi, et al. Research on loosening earth pressure considering the patterns of stress distribution in loosening zone[J]. Rock and Soil Mechanics, 2018, 39(6): 1927-1934. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806002.htm
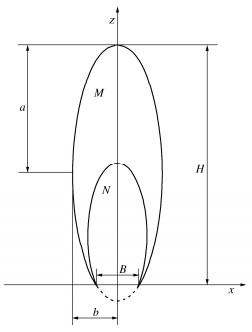
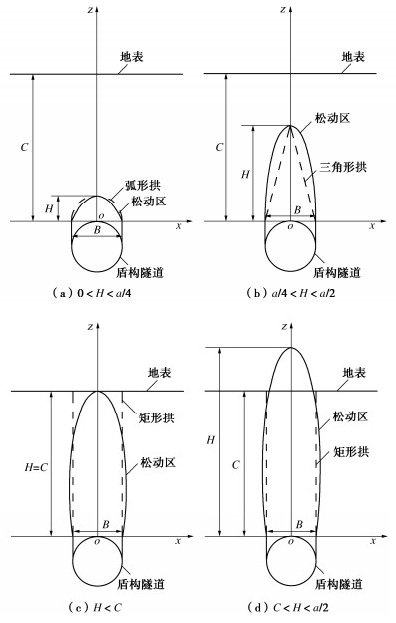
[13]	宫全美, 张润来, 周顺华, 等. 基于颗粒椭球体理论的隧道松动土压力计算方法[J]. 岩土工程学报, 2017, 39(1): 99-105. doi: 10.11779/CJGE201701008 GONG Quanmei, ZHANG Runlai, ZHOU Shunhua, et al. Method for calculating loosening earth pressure around tunnels based on ellipsoid theory of particle flows[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(1): 99-105. (in Chinese) doi: 10.11779/CJGE201701008
[14]	汪大海, 贺少辉, 刘夏冰, 等. 基于主应力旋转特征的浅埋隧道上覆土压力计算及不完全拱效应分析[J]. 岩石力学与工程学报, 2019, 38(6): 1284-1296. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201906019.htm WANG Dahai, HE Shaohui, LIU Xiabing, et al. A modified method for determining the overburden pressure above shallow tunnels considering the distribution of the principal stress rotation and the partially mobilized arching effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(6): 1284-1296. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201906019.htm
[15]	汪大海, 贺少辉, 刘夏冰, 等. 地层渐进成拱对浅埋隧道上覆土压力影响研究[J]. 岩土力学, 2019, 40(6): 2311-2322. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906031.htm WANG Dahai, HE Shaohui, LIU Xiabing, et al. Study on the influence of gradual arching of strata on the earth pressure on shallow tunnel[J]. Rock and Soil Mechanics, 2019, 40(6): 2311-2322. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906031.htm
[16]	IGLESIA G R. Trapdoor Experiments on the Centrifuge, A Study of Arching in Geomaterials and Similitude in Geotechnical Models[D]. Boston: Dept of Civil Engineering, MIT, 1991.
[17]	IGLESIA G R, EINSTEIN H H, WHITMAN R V. Validation of centrifuge model scaling for soil systems via trapdoor tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(11): 1075-1089.
[18]	IGLESIA G R, EINSTEIN H H, WHITMAN R V. Investigation of soil arching with centrifuge tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(2): 04013005.
[19]	JACOBSZ S. Trapdoor Experiments Studying Cavity Propagation[M]// Proceedings of the First Southern African Geotechnical Conference. Los Angeles: CRC Press, 2016: 159-165.
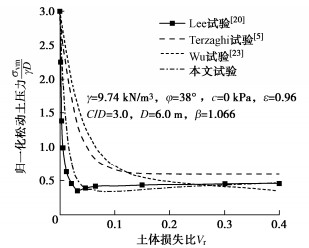
[20]	LEE C, CHEN H, LIN W, et al. Evolution of Arching Effect during Tunneling in Sandy Soil[M]// Physical Modelling in Geotechnics. New York: Taylor & Francis, 2006.
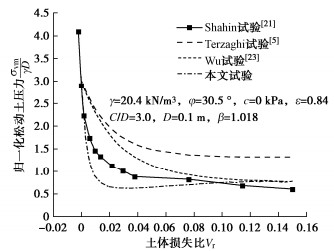
[21]	SHAHIN H M, NAKAI T, ZHANG F, et al. Model tests and numerical simulations on shallow circular tunneling-Ground movement and earth pressure due to circular tunneling[C]// Proc. of the 6th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, Shanghai, China. 2008: 709-715.
[22]	JANELID I, KVAPIL R. Sublevel caving[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 1966, 3(2): 129-132.
[23]	WU J, LIAO S M, LIU M B. An analytical solution for the arching effect induced by ground loss of tunneling in sand[J]. Tunnelling and Underground Space Technology, 2019, 83: 175-186.

施引文献(3)

期刊类型引用(2)

1.	李东桥，严晓威，梁建文，赵华. 丁字及十字交叉管廊纵向地震响应分析. 天津大学学报(自然科学与工程技术版). 2024(01): 21-30 . 百度学术
2.	梁建文，陈慧芳，李东桥，巴振宁. 地下管廊抗震研究现状综述. 天津大学学报(自然科学与工程技术版). 2024(02): 209-222 . 百度学术