土水特征曲线试验单阶段贝叶斯优化设计方法

李典庆; 丁少林; 曹子君; 陶睿

doi:10.11779/CJGE20220263

土水特征曲线试验单阶段贝叶斯优化设计方法 English Version

李典庆^{1, 2,},
丁少林^{1, 2},
曹子君^{1, 2, ,},
陶睿³

1.
武汉大学水资源与水电工程科学国家重点实验室, 湖北武汉 430072
2.
武汉大学工程风险与防灾研究所, 湖北武汉 430072
3.
挪威科技大学土木与环境工程学院, 特隆赫姆 7047

基金项目:

国家自然科学基金重点项目 U2240211

国家自然科学基金面上项目 51879205

详细信息

作者简介:
李典庆(1975—)，男，博士，教授，主要从事岩土工程可靠度与风险控制方面的研究工作。E-mail: dianqing@whu.edu.cn

通讯作者:
曹子君, E-mail: zijuncao@whu.edu.cn

中图分类号: TU411
计量
- 文章访问数: 299
- HTML全文浏览量: 51
- PDF下载量: 99
出版历程
- 收稿日期: 2022-03-10
- 网络出版日期: 2023-02-15
- 刊出日期: 2023-05-31

One-stage Bayesian experimental design optimization for measuring soil-water characteristic curve

LI Dianqing^{1, 2,},
DING Shaolin^{1, 2},
CAO Zijun^{1, 2, ,},
TAO Rui³

1.
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
2.
Institute of Engineering Risk and Disaster Prevention, Wuhan University, Wuhan 430072, China
3.
Department of Civil and Environmental Engineering, Norwegian University of Science and Technology, Trondheim 7047, Norway

摘要

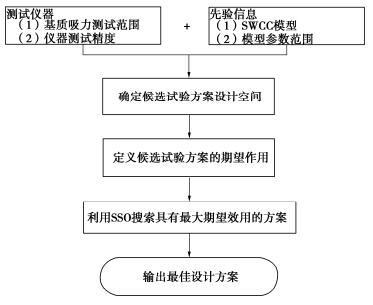
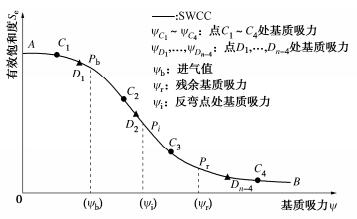
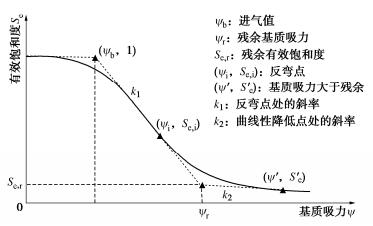
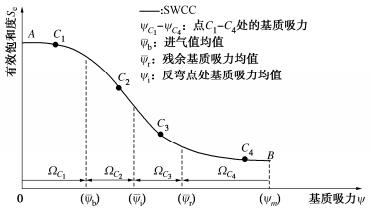
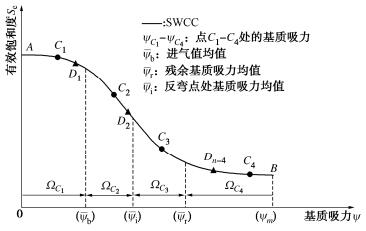
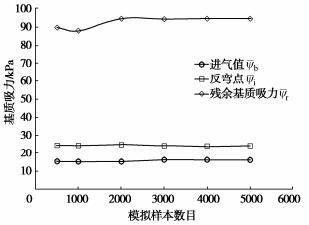
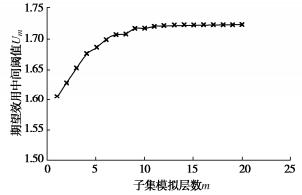
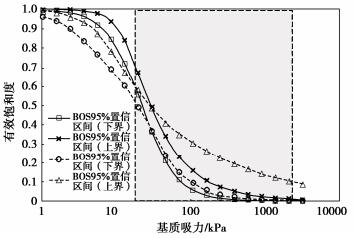
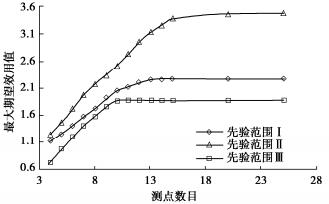
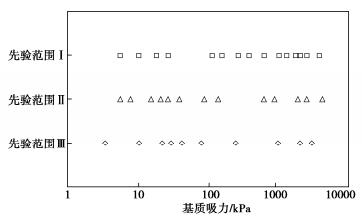
摘要: 直接测量土水特征曲线（SWCC）十分耗时。因此，SWCC试验通常只能获得有限的试验数据，基于有限数据估计SWCC不可避免地存在不确定性。因此，合理地确定试验方案（即指定SWCC测点控制变量的值），以提高试验数据的价值，减少所估计SWCC的不确定性十分重要。基于SWCC模型参数先验信息和试验仪器信息，提出了一种SWCC试验单阶段贝叶斯优化设计（OBEDO）方法。首先，所提方法通过离散试验控制变量（比如基质吸力）生成试验方案设计空间；设计空间中的候选试验方案由控制点及附加点构成，其作用分别为控制SWCC的主要趋势和降低SWCC的不确定性。然后，采用期望效用量化候选试验方案对应数据的价值，并利用子集模拟优化（SSO）方法搜索具有最大期望效用的候选试验方案。最后选取具有最大期望效用的候选试验方案为最优试验设计方案。通过一个SWCC试验设计实例说明了所提方法的有效性。结果表明，所提方法可为考虑不确定性条件下的SWCC试验设计提供一个合理的工具。
- 贝叶斯方法 /
- 子集模拟 /
- 试验设计 /
- 信息价值 /
- 土水特征曲线
Abstract: The direct measurements of soil-water characteristic curve (SWCC) are often costly and time-consuming. Therefore, only a limited number of test data can be obtained from a single SWCC test, based on which the estimated SWCC inevitably produces uncertainty. It is reasonable to select the experimental scheme (i.e., specify the values of the control variables at measuring points) in order to improve the expected value of information of the measurement data for reducing the uncertainty in the estimated SWCC. A one-stage Bayesian experimental design optimization (OBEDO) approach is developed for SWCC testing exploiting prior knowledge and information of testing apparatus. Discretization of control variables (e.g., matric suction) is used to generate the design space of the candidate experimental scheme, which is specified by the initial measuring points and the additional measuring points to control the general trajectory of SWCC and further reduce the uncertainty in SWCC, respectively. The value of data corresponding to the experimental scheme is quantified by the expected utility. The candidate experimental scheme with the maximum expected utility is identified using the subset simulation optimization (SSO) and treated as the optimal experimental design scheme. The proposed approach is illustrated using an experimental design example. The results show that it provides a rational tool to determine the optimal experiment scheme for SWCC testing considering the uncertainty of soil.
- Bayesian method /
- subset simulation /
- experimental design /
- value of information /
- soil-water characteristic curve

HTML全文

0. 引言

锚杆荷载试验时要根据荷载-位移-时间三者关系来判取锚固体抗拔承载力（以下简称抗拔力），核心问题就是判定锚头位移稳定与否（简称判稳）。国内各标准中与抗拔力相关的锚杆荷载试验方法共有4种，但判稳方法高达六七十种，同一个试验结果采用不同判稳方法判取的抗拔力有时相差较大。而抗拔桩的抗拔力判取就简单得多，各标准提供的方法几乎相同。

问题来了：①各种判稳方法除了经验，是否还基于内在机理？②如果基于机理，是基于多种机理、同一机理还是各种荷载试验基于各自机理？③锚杆与抗拔桩的判稳机理是否相同？如果是，为什么抗拔桩的判稳方法几乎相同，而锚杆的则五花八门，都合理可行吗？遗憾的是，对这些问题的研究成果——试验的或理论的，极少，尤其是关于各方法所遵循的机理、方法之间的差异等内容，各标准未作说明，几乎见不到公开文献。这给工程技术人员带来了极大的困惑。

本文以注浆黏结锚杆为对象，带着上述疑惑，以深坪锚杆试验^[1]成果为主要试验依据，对锚杆荷载试验如何判稳问题进行较为全面的研究探讨。

1. 蠕变曲线与机理

先从抗拔桩说起。静载荷试验判取桩极限抗拔力的方法可归纳为：①没发生破坏时取最大试验荷载；②缓变破坏型取位移-时间曲线尾部显著弯曲的前一级荷载；③陡变破坏型取荷载-位移（P-s）相应于陡变段起点的荷载。这3种情况的位移-时间（s-t）曲线分别如图 1曲线1，2，3所示。

图 1 3种蠕变曲线

Figure 1. Three kinds of creep curves

下载: 全尺寸图片幻灯片

尽管极少有资料提及，但该3条曲线显然可以看作分别对应着3种蠕变形态的材料通用蠕变曲线，只是岩石等材料的蠕变曲线通常采用应变作为纵坐标，而桩因为使用性能需求采用了位移（桩顶位移）。从蠕变机理角度理解：①曲线2为一条蠕变过程齐全清晰的蠕变曲线，可分为Ⅰ、Ⅱ、Ⅲ 3个阶段，第Ⅰ阶段为初始蠕变阶段，位移快速增加但速率逐渐趋缓；第Ⅱ阶段为持续蠕变阶段，位移持续增加但速率基本稳定；第Ⅲ阶段为加速蠕变阶段，位移再次快速增加且速率加大；曲线1可分为Ⅰ、Ⅱ阶段，其中第Ⅱ阶段位移缓慢增加或停止增加；曲线3可分为Ⅰ、Ⅲ阶段，第Ⅱ阶段持续时间极短甚至没有。②曲线1对应着稳定蠕变（或称衰减蠕变、收敛蠕变等），而曲线2，3对应着蠕变破坏（或称非衰减蠕变、不收敛蠕变、不稳定蠕变等），其中曲线2对应着缓变型破坏、曲线3对应着突变型破坏。③荷载较小时发生曲线1所示稳定蠕变，即位移稳定；随着荷载不断增加，最终将发生曲线2，3所示蠕变破坏，蠕变从稳定状态转变为破坏状态的临界荷载对应着极限抗拔力。④桩的抗拔力源自桩侧与地层界面摩阻力，桩顶位移主要源自界面剪切变形，判稳就是要通过桩顶位移判断界面剪切变形是否趋于稳定从而判断是否达到了临界荷载。

锚杆抗拔力源自锚固体与地层界面（以下简称界面）黏结力，与桩的摩阻力本质相同只是术语不同，判稳时判断的同样是界面变形是否趋于稳定，图 1所示蠕变曲线及其所揭示的蠕变过程与机理对于锚杆以及岩^[2]、土^[3]同样适用，锚杆荷载试验主要就是测试界面蠕变特性。

尽管蠕变机理及判稳机理相同，但锚杆判稳具体方法与抗拔桩确实应有所不同。抗拔桩荷载试验时，每级荷载的位移观测时间最少1 h，多则十几小时甚至几十小时，蠕变全过程通常可在试验中直接测得，曲线1，2，3清晰可见，故判稳较为简单，方法也基本统一。而锚杆不同，工程中锚杆试验数量远大于桩，个体承载力及单价远低于桩，基于工期及造价考虑，每条锚杆的试验时间不可能太长, 如果足够长、可以测得完整的蠕变曲线，则采用与抗拔桩相同的判稳方法就可以了，大量的抗浮锚杆及基础锚杆成果均可证实。锚杆的试验时间较短，曲线1，3情况简单还容易判稳，但对于曲线2，观测到的蠕变曲线通常并不是完整过程的，往往只试验到蠕变Ⅰ、Ⅱ阶段，之后是发生稳定蠕变形成曲线1还是发生蠕变破坏形成曲线2，需要进一步分析预测，而这就是锚杆试验判稳的主要任务。同时，锚杆种类较多，预应力锚杆等的传力机理也更复杂，蠕变曲线形态比图 1所示也要多，这使得判稳愈发困难、复杂，故业界基于不同经验及对蠕变与判稳机理的不同理解产生了几十种判稳方法，但只要以图 1所示蠕变曲线及机理为基本理论，理解、评估这些判稳方法及制订新方法会更容易且更准确。

2. 现场试验

关于锚杆蠕变曲线，仅见少量全黏结锚杆模型试验成果^[4-5]，关于足尺锚杆及预应力锚杆的^[6]极少。深圳市《锚杆试验技术标准》编制组在深圳坪山第四系中粒花岗岩残积砂（砾）质黏性土层中制作了182条注浆黏结足尺试验锚杆进行了专项试验，取得了近500组数据^{[1, 7]}，本文将展示并分析拉力型预应力锚杆及全黏结锚杆与蠕变性能相关的部分试验成果。文中锚杆编号以B18a为例，含义如下：B表示锚杆类型（A为全黏结型，B为一次注浆拉力型，C为二次注浆拉力型），18表示锚杆全长18 m（长度分为6，9，12，15，18 m），a表示锚杆序号（每组锚杆有a，b，c，d计4根）；B、C型锚筋自由段长度均为3 m。

（1）试验表明，锚固体拔出破坏、亦即界面剪切破坏可分为突变型及缓变型两种形式，其中突变型比例约2/3，试验用时较短，缓变型约1/3，试验用时较长。分析认为两种破坏形式产生原因主要与荷载增量有关：分级荷载较大时（试验中为0.1倍最大试验荷载）更容易发生突变破坏，较小时（试验中为0.05倍最大试验荷载）时更容易发生缓变破坏；是否还有其它原因尚不清楚。突变型及缓变型典型P-s曲线分别如图 2，3所示。

图 2 锚杆C12a的P-s曲线（突变型）

Figure 2. P-s curves of anchor C12c(mutant type)

下载: 全尺寸图片幻灯片

图 3 锚杆C18c的P-s曲线（缓变型）

Figure 3. P-s curves of anchor C18c(slow type)

下载: 全尺寸图片幻灯片

（2）位移增量-时间（Δs-t）曲线形态可细分为5种，如图 4所示：①曲线1表示稳定蠕变，Δs随着时间增加但最终收敛到某一数值，蠕变过程可分为图 1所示初始及持续两个阶段。②曲线2可分为初始、持续及加速3个蠕变阶段，典型如B18a；曲线2a及2b可视为曲线2的异形，曲线2a和曲线2相比没有明显的加速阶段，典型如C18c；曲线2b和曲线2相比持续蠕变阶段较短，典型如C9c。③曲线3所示蠕变过程可分为初始及加速两个阶段，典型如C12a。④曲线3主要对应着突变型破坏，曲线2，2a主要对应着缓变型破坏，典型2b则介于两者之间但更偏于缓变型破坏。这几类曲线是判稳的基础理论依据。在蠕变前期阶段，曲线2系与曲线1形态相似，容易混淆，导致了很多判稳方法将稳定蠕变误判为蠕变破坏或正好相反，此时往往需要蠕变率-时间曲线等进一步判断。

图 4 锚杆Δs-t曲线

Figure 4. Δs-t curves for anchors

下载: 全尺寸图片幻灯片

（3）蠕变第Ⅰ阶段为初始阶段，多数锚杆持续时间为1~3 min，少数为4~5 min，总体来看荷载水平越高持续时间越长，最长不超过5 min。需要指出，这个新现象的发现有赖于新设备-试验采用了编制组新研制的自动化设备，自动加卸载、补压及以1次/min的高频记录数据。推测可能业界以往锚杆试验普遍采用人工记录，各判稳方法没有要求加载完成后即按较高频率测读位移，故这个重要现象一直未被发现。以C18c为例，各级荷载的位移数据、曲线、荷载P为1100 kN时前15 min位移数据及曲线分别如表 1，2和图 5，6所示，其中P为300~1100 kN时发生稳定蠕变，为1200 kN时发生缓变型破坏，为1250 kN时发生突变型破坏。

表 1 锚杆C18c在各级荷载下变形量

Table 1. Displacements under various loads of anchor C18c

P/kN	S₀/mm	S_f/mm	Δs₅/mm	Δs/mm	α/mm
300	9.06	9.14	0.06	0.08	0.04
500	17.29	17.31	0.01	0.02	0.02
600	21.18	21.38	0.18	0.20	0.04
700	25.43	25.83	0.34	0.40	0.11
800	31.00	31.86	0.68	0.86	0.38
900	38.76	39.66	0.74	0.90	0.34
1000	48.62	49.86	0.98	1.24	0.55
1100	59.12	61.40	1.88	2.28	0.84
1200	76.22	86.32	2.36	> 10	> 5.29
注：表中S₀表示各级荷载初始位移读数，S_f表示该级最终位移读数，Δs₅表示该级前5 min的位移增量，Δs表示该级总的位移增量。下同。

下载: 导出CSV

| 显示表格

表 2 锚杆C18c在1100 kN时前15 min的位移

Table 2. Displacements of anchor C18c in first 15 min at 1100 kN

t/min	S₀/mm	Δs_n/mm	Δs/mm	t/min	S₀/mm	Δs_n/mm	Δs/mm
0	59.12	—	—	8	61.16	-0.01	2.04
1	60.39	1.27	1.27	9	61.31	0.15	2.19
2	60.63	0.24	1.51	10	61.31	0	2.19
3	60.85	0.22	1.73	11	61.31	0	2.19
4	60.86	0.01	1.74	12	61.31	0	2.19
5	61.00	0.14	1.88	13	61.40	0.09	2.28
6	61.16	0.16	2.04	14	61.40	0	2.28
7	61.17	0.01	2.05	15	61.40	0	2.28
注：表中Δs_n表示单元时长位移增量，即某一时刻位移读数减去与其相邻的前一时刻位移读数。下同。

下载: 导出CSV

| 显示表格

图 5 锚杆C18c在1100 kN时前15 min的Δs-t曲线

Figure 5. Δs-t curves of anchor C18c in first 15 min at 1100 kN

下载: 全尺寸图片幻灯片

图 6 锚杆C18c蠕变曲线

Figure 6. Creep curves for anchor C18c

下载: 全尺寸图片幻灯片

3. 判稳参数及方法分析

判稳要实现判定破坏与否及判取极限抗拔力两个功能，根据试验目的而定。①破坏判定，过程为：荷载施加后锚杆产生位移，持荷，测读并记录锚头位移，通过分析位移与时间关系判断界面蠕变是否稳定；稳定时试验结束，不稳定时延长观测时间，取得更多数据后再次判稳，如此反复直至试验结束，进而判定最大试验荷载下是否破坏。②判取极限抗拔力，过程为：荷载分级施加，荷载水平较低时发生稳定蠕变，持续时间通常数十分钟；前一级位移稳定后再施加后一级荷载，随着荷载增加，蠕变量越来越大，蠕变稳定用时越来越长，稳定与破坏之间必然存在着临界荷载，荷载水平达到临界荷载附近时，稳定时间可长达数小时甚至不收敛，进而判取临界荷载及极限抗拔力。判稳时荷载已经明确，可变因素主要有位移与时间，这两项变化及变化组合很多，如何选择决定了判稳方法的优劣。

3.1 位移参数

（1）位移增量。桩抗拔试验时位移计安装于桩顶，桩顶位移即桩侧与地层界面的剪切变形，为某级荷载持荷过程中某时刻的位移读数与初始荷载下的位移读数之差，直接用于判稳。而锚杆试验时位移计通常安装在锚头附近的锚筋上，锚头位移除了锚固体与地层界面的剪切变形外，还包括了锚筋受力伸长量、锚筋与锚固体相对滑移量等，均需在判稳时扣除，故锚杆不能采用绝对位移而应采用相对位移，即移增量作为判稳参数。故某些判稳方法要求锚头总位移量不应超过设计允许值^[8-11]显然不妥。位移增量也称蠕变量，指某级荷载持荷过程中某时刻的位移读数与该级荷载加载完成后即测读的初始位移读数之差，也指某时刻的位移读数与前面相邻时刻位移读数之差（本文采用“单元时长位移增量”一词加以区分），如果仅有一级荷载，则位移增量与绝对位移是相等的。

有些判稳方法直接采用位移增量Δs作为判稳参数、没有考虑其与时间的关系，以其增加幅度判稳，典型如：后一级荷载产生的位移增量超过前一级荷载产生的位移增量的2倍^{[8-9, 11]}或5倍^[12-13]时判为破坏。这种方法来源于桩，试验表明不适用于锚。以C18c为例，各级荷载下Δs如表 1及图 6所示：600 kN时Δs为0.2 mm，是500 kN时（0.02 mm）的10倍，但显然600 kN时应判定为稳定；800 kN时类似，为700 kN时Δs的2.15倍，但800 kN时亦应判定为稳定。锚杆位移受干扰因素较多，除了筋体变形及滑移外，位移突增现象还可能由某种异常原因引发，例如有浆液渗入到锚筋自由段的护管内或有石子落入孔内，可能使锚筋恰好被卡住，某级荷载把它拉松动了，看起来是该级位移突增，实际可能是前一级异常减少所致；还有可能是地层性状不均匀、浅部存在较硬夹层、导致前一级位移较小所致；还可能与加载设备与反力装置的稳定性相关。这种位移突增现象对锚杆来说较为常见，不应作为判定依据，否则可能会极大低估抗拔力、产生误判。以位移突增作为依据的判稳方法原本是针对突变型破坏的，本以为发生位移突增即可表明发生了图 1曲线3所示蠕变破坏，实际上却容易造成误判断。

另外，试验表明位移增量与加载速率无关。试验中采用了5种不同加压原理的液压泵，加卸载速率为1~10 kN/s，未发现位移增量（包括初始阶段的）与液压泵类型及工作方式、加卸载速率等有关。分析认为：位移随荷载增加，两者呈一一对应关系，不管荷载增加速度是快是慢，加到某荷载就会产生相应位移，没有加到该荷载就不会产生那么大位移，即加载速率与位移量及位移增量无关。国内判稳方法一般要求加载速率不超过1~2 kN/s，国际锚杆标准^[14-16]则建议为1~10 kN/s，远快于国内，所以只要不因加载过快产生冲击荷载就不需慢速加载，意义不大，实际上，美国标准^[15]鼓励快速加载以便更准确地读取各级初始位移。

（2）位移增量阈值。该阈值指判稳时用于数据对比的最小位移增量，各判稳方法普遍采用0.01~2.0 mm/单位时长。试验表明阈值不应低于0.1 mm，宜为0.2 mm，否则很难实施并容易产生误判。以锚杆C12a为例，720 kN时的持荷时间为1 h，每5 min位移增量如表 3所示，如果阈值采用0.1 mm，第25~30 min的Δs_n为0.1 mm，结合前30 min数据可判定为位移稳定，但第30~35 min的Δs_n为0.16 mm，因位移增量大于前一单元时长的，则要判定为不稳定。这个结论显然不妥。表 2第10 min的数据说明了同样问题。试验表明，采用0.1 mm作为指标时有70%以上试验第3级荷载都会判定为不稳定，不足0.1 mm时比例更大。如前所述，锚头位移增量中除了界面剪切变形外还包括其它因素产生的变形，干扰因素较多，阈值越大容错能力越强，越小则受干扰因素产生的误差的影响程度越大，故阈值不应太小。假如干扰因素产生的位移为0.01 mm，如果阈值为0.1 mm，则误差占到阈值的比例为10%，不可忽视；但如果阈值为0.5 mm，误差所占比例下降到2%，可以忽略不计。非科研性质的工程锚杆荷载试验是件“粗活”，作为数据对比所采用的位移阈值很难达到0.1 mm这种精度并且也不需达到，国际锚杆试验标准^[14]中为0.2~0.25 mm，可以借鉴。

表 3 锚杆C12a在720 kN时的位移

Table 3. Displacements of anchor C12a at 720 kN

t/min	S/mm	Δs_n/mm	Δs/mm	α/mm
0	33.35	—	—	—
5	34.67	1.32	1.32	—
10	35.42	0.75	2.07	2.49
15	35.72	0.30	2.37	2.20
20	35.88	0.16	2.53	1.28
25	36.04	0.16	2.69	1.44
30	36.14	0.10	2.79	1.40
35	36.30	0.16	2.95	1.58
40	36.34	0.04	2.99	1.46
45	36.44	0.10	3.09	1.51
50	36.54	0.10	3.19	1.57
55	36.58	0.04	3.23	1.52
60	36.64	0.06	3.29	1.53

下载: 导出CSV

| 显示表格

很多判稳方法中阈值不高于0.1 mm的原因为：①来自传统锚杆经验。设备加载完成后少则数十秒多则数分钟压力就会慢慢损失、即发生掉压现象，掉压到一定程度后会导致位移读数减小，要通过补压来控制压力衰减幅度。传统设备靠人工监视压力变化及手动补压，准确度差且响应滞后，常常晚补、漏补或过补，误差较大。本试验按1次/min高频自动记录到的数据表明，位移增量主要在加载过程中及加载之后数十秒内产生，在保压及掉压过程中通常不会产生，除非锚杆已经蠕变不稳定。以往业界加压过程中并不测读位移，而保压及掉压过程中位移基本不增加、位移计读数不变，于是便认为位移增量为0、即位移稳定，可采用0.1 mm作为阈值。②来自于桩的经验。基桩静载试验普遍采用自动加卸载、补压及记录设备，采用0.1 mm作为阈值，例如采用1 h位移量不大于0.1 mm作为判稳指标。但桩与锚情况不同，一则桩的位移几乎不受其它因素干扰，二则桩的试验荷载通常远大于锚，掉压后补压时压力波动幅度在试验荷载中所占比例通常不足1%，因此产生的位移变化很小，位移基本稳定、波动幅度很小，故可以采用0.1 mm作为阈值。

3.2 时间参数

（1）单元时长。判稳时需要把位移数据按时间段划分成单元，各单元数据直接对比或组合后对比，各判稳方法常用的单元时长有5，10，15，20，30，60 min等几种。试验表明，为满足各单元位移增量不小于0.1 mm的阈值需求，单元时长至少应为10 min，总持荷时长超过1 h后不宜少于30 min；但单元时长不应为5 min，5 min时间太短、产生的位移增量过小、通常不够用。例如有些判稳方法规定以下情况可判为稳定：①每5 min读数一次，后5 min位移增量小于前5 min^[13]；②后5 min位移增量小于前5 min，连续出现两次^[10]。位移增量不断减速表明了数据在收敛，蠕变将趋于稳定，看起来符合图 1曲线1所示蠕变机理，但5 min时间太短了，收集到的位移增量不足够大。以C18c为例，1200 kN时各单元时长位移读数S如表 4所示：第5~10分钟及第10~15分钟的Δs_n均小于前一单元时长的，按上述判稳方法1200 kN时应判定为稳定；但把持荷时间加长后发现，第2小时的位移增量已达到2.39 mm且位移及蠕变率均不收敛，可清晰判定蠕变不稳定。这种误判现象比较普遍。故后文中不再评价与阈值小于0.1 mm及单元时长小于10 min有关的判稳方法^[8-13]。

表 4 锚杆C18c在1200 kN时的位移

Table 4. Displacements of anchor C18c at 1200 kN

t/min	S/mm	Δs_n/mm	Δs/mm	α/mm
0	76.22	—	—	—
5	78.58	2.36	2.36	—
10	79.42	0.84	3.20	2.79
15	80.05	0.63	3.83	2.84
60	82.31	2.26	6.09	3.75
120	84.70	2.39	8.48	5.15

下载: 导出CSV

| 显示表格

（2）首次时长。首次判稳及所需的持荷观测时长很重要，时长太短则数据量值太小不容易判定甚至误判，太长则浪费时间。蠕变初始阶段的数据不能用于判稳，首次时长应超出初始阶段至少一个单元时长，试验表明以15 min为宜，利用第5~15分钟（从测读完初始位移后开始计时，下同）这10 min的数据判稳，不用前5 min初始阶段数据。对于曲线3，首次时长15 min完全能够成功判稳，对于主要利用蠕变持续阶段数据进行判稳的曲线1及曲线2，这15 min能够解决绝大部分判稳问题，效率很高。ISO及欧盟锚杆试验专项标准^[14]中，无黏性土及岩层首次时长取5 min，利用第2~5分钟数据判稳，而黏性土取15 min，利用第5~15分钟数据判稳。

试验表明，土层锚杆初始蠕变阶段位移增量通常较大，5 min内超过1.0 mm的机率很大，尤其是荷载水平达到最大试验荷载的一半以后，如表 2~4所示，故那些判稳时间中没有剔除初始阶段数据且判稳阈值不超过1.0 mm的判稳方法均容易产生误判、低估抗拔力，这些方法如：①第1~10分钟位移增量不大于1.0 mm^{[8, 10-11]}。②如果第1~10分钟的位移增量大于1.0 mm，则1 h内位移增量不大于2.0 mm^{[8, 12, 17]}。试验表明，如果初始阶段位移增量大于1.0 mm，则1 h内大于2.0 mm是大概率事件，案例如表 3所示。③如果第1~10分钟的位移增量大于1.0 mm，则2 h内位移增量不大于2.0 mm^{[9, 11]}。时间越长位移增量越大，故本法比“1 h内不大于2.0 mm”更难实现。④1 h内位移增量不大于1.0 mm^[10]。⑤1 h内位移增量不大于0.5 mm^[17]。⑥黏性土10 min内位移增量不大于2.0 mm^[11]。这3个指标看起来比较宽松，但因为包括了蠕变初始阶段数据，仍难以实现或导致抗拔力判取值偏低，案例如表 2~4所示。

（3）最大时长。首次不稳定通常意味着情况比较复杂需要延时，各判稳方法中延时1~6 h不等。试验表明：每级荷载最大持荷时间不应小于4 h，宜为5 h，短于4 h容易发生误判。例如某判稳方法^[13]规定：每1 h内位移增量不大于1.0 mm，观测时间不超过3 h。以锚杆B18a为例，其1000 kN时的数据如表 5所示，按该方法，第3小时的位移增量Δs_n为0.64 mm，小于1.0 mm，应判为稳定。但第4小时蠕变率并没有收敛，反而在加大，最终判为蠕变不稳定。最大时长亦无需超过5 h，试验中十几组长达十几个小时的观测结果表明，5 h内如果蠕变稳定，之后亦稳定。以锚杆B18b为例，750 kN时（极限抗拔力为800 kN）持荷观测18 h的结果如表 6所示。

表 5 锚杆B18a在1000 kN时的位移

Table 5. Displacements of anchor B18a at 1000 kN

T	t/h	S₀/mm	Δs_n/mm	Δs/mm	α/mm
10:49	0	54.46	—	—	—
11:49	1	59.34	4.88	4.88	2.06
12:49	2	61.40	1.06	5.94	3.52
13:49	3	61.04	0.64	6.58	3.69
14:49	4	61.66	0.62	7.20	4.96

下载: 导出CSV

| 显示表格

表 6 锚杆B18b在750 kN时的位移

Table 6. Displacements of anchor B18b at 750 kN

t/min	S₀/mm	Δs_n/mm	Δs/mm	α/mm
0	30.39	—	—	—
5	32.79	2.40	2.40	—
60（1 h）	33.65	0.86	3.26	0.80
300（5 h）	34.66	1.01	4.27	1.44
1080（18 h）	35.46	0.80	5.07	1.44

下载: 导出CSV

| 显示表格

3.3 基于位移与时间的判稳参数及方法

显然，位移与时间两个因素结合起来才能准确判稳，即判稳参数应具有位移与时间双重属性，但如何结合众说纷纭，生成了多种判稳方法。

（1）蠕变率及蠕变曲线。表明，持荷过程中位移增量可能增加或不增加，增加速率可能是减速、匀速或加速，匀速且速率较小或减速时应判定为稳定蠕变，匀速但速率较大或加速时则判定为蠕变破坏。位移增量增加速率称为蠕变率（ $\alpha$ ），采用时间对数表示，计算公式如下所示：

。

$\alpha =({S}_{\text{b}}-{S}_{\text{a}})/(\mathrm{lg}{t}_{\text{b}}-\mathrm{lg}{t}_{\text{a}})\text{ }。$

(1)

式中： ${t_{\text{b}}}$ ， ${t_{{\text{ao}}}}$ 为计算时间对数周期终、始时刻（min）；S_b，S_a为t₂，t₁时刻的锚头位移读数（mm）。

式中S_b与S_a之差即为单元时长位移增量Δs_n，当S_a为某级荷载的初始位移读数，即S₀时，两者之差为位移增量Δs，当S_b为最终位移读数S_f且S_a为S₀时，两者之差为该级荷载总的位移增量。经验表明，持荷时长超过1 h时t_b宜大于t_a至少30 min以利于判稳准确。~计算 $\alpha$ 时S_a主要采用第15分钟的位移增量以便于判断蠕变稳定，~计算 $\alpha$ 时主要采用Δs_n以便于判断蠕变不稳定。蠕变稳定时Δs-t曲线及蠕变率-时间（α-lgt）曲线分别如图 4曲线1及曲线A所示， $\alpha$ 形状为单调下降，数值连续减少，最终稳定在较低水平波动；反之，正如试验实测曲线表明的，如果Δs不收敛，Δs-t曲线将如曲线2~3所示， $\alpha$ -lgt曲线会出现图 7曲线B~G所示各种形态，最终将发生蠕变破坏。

表 7 锚杆B18a在1050 kN时的位移

Table 7. Displacements of anchor B18a at 1050 kN

t/min	S/mm	Δs_n/mm	Δs/mm	α/mm
0	66.92	—	—	—
5	70.52	3.60	3.60	—
15 min	72.92	2.40	6.00	5.03
60（1 h）	77.04	4.12	10.12	6.84
120（2 h）	79.72	2.68	12.80	8.90
180（3 h）	80.76	1.04	13.84	5.91
240（4 h）	81.80	1.04	14.88	8.32
300（5 h）	82.38	0.58	15.46	5.98
360（6 h）	83.02	0.64	16.10	8.08

下载: 导出CSV

| 显示表格

表 8 锚杆A15b在990 kN时的位移

Table 8. Displacements of anchor A15b at 990 kN

t/min	S₀/mm	Δs_n/mm	Δs/mm	α/mm
0	61.74	—	—	—
5	64.22	2.48	2.48	—
15	65.55	1.33	3.81	2.79
60（1 h）	68.02	2.47	6.28	4.10
120（2 h）	69.42	1.40	7.68	4.65
180（3 h）	70.35	0.93	8.61	5.28
240（4 h）	71.08	0.73	9.34	5.84
300（5 h）	71.66	0.58	9.92	5.98
360（6 h）	72.36	0.70	10.62	8.84

下载: 导出CSV

| 显示表格

图 7 锚杆α-lgt曲线

Figure 7. α-t curves of anchors

下载: 全尺寸图片幻灯片

（2）定性判稳与定量判稳。所有判稳方法都应该遵循蠕变与判稳机理，从定性及定量两方面入手：①定性判断蠕变率变化趋势，稳定蠕变总体上蠕变率应随时间递减，如图 7中曲线A所示。②要有定量指标，如图 7中的蠕变率2.0 mm，低于该指标最终将位移收敛，蠕变稳定。试验表明，加载量超过第二级以后，蠕变总会或多或少产生，很难达到长时间一丝不动地稳定；总会存在着某个临界值，蠕变达到该值就认为达到极限抗拔力，否则就认为蠕变稳定，该临界值就是定量指标。有的判稳方法仅采用定性方法，将后一单元时长位移增量小于前一单元时长时判为稳定^{[10, 13]}，显然不妥。以锚杆B18a为例，1050 kN时位移数据见表 7，第2小时，第3小时位移均较前一单元时长收敛，但曲线并没有稳定，第4小时以后蠕变率加大，最终蠕变破坏。实际上，B18a在1000 kN时就已经蠕变破坏了，如表 5所示。

（3）蠕变率2.0 mm。α取2.0 mm不是理论分析或试验统计结果而是经验值，如同桩的承载力安全系数为2。坪山试验近千个结果试验表明，对于预应力锚杆及全黏结锚杆^[7]等所有注浆黏结锚杆， $\alpha$ =2.0 mm都是个适合定量判稳依据：①任何情况下 $\alpha$ =2.0 mm都是安全指标。十几组长达十几个小时的持荷观测结果表明， $\alpha$ ≤2.0 mm时无论持荷多久均不会发生蠕变破坏；图 7中α > 2.0 mm时，形态不管如何变化，一旦小于2.0 mm就预示着蠕变将趋于稳定，最终会发展成为曲线A所示的稳定蠕变。② $\alpha$ =2.0 mm又是个经济判据。对于突变型破坏，一旦 $\alpha$ > 2.0 mm即可随时判定；对于缓变型破坏，如果 $\alpha$ > 2.0 mm，即使该级荷载可不判定破坏则后一级也会判定，即 $\alpha$ =2.0 mm可判得较高的极限承载力而不会产生误判断。实际上，蠕变率2.0 mm一直是国际标准^{[14-16, 18]}中最主要的判稳依据，没有之一。可见，蠕变率2.0 mm既是判稳定量指标又是定性指标，但因在现场应用不便，美国锚杆标准^[15]将之具体量化为：如果1~10 min的位移增量大于1.0 mm，则延长观测50 min，第6~60分钟区间内蠕变量不大于2.0 mm。1~10 min的蠕变量不大于1.0 mm即意味 $\alpha$ 不大于1.0 mm，如能满足锚杆必然蠕变稳定，故为缩短试验时间先用该量化指标进行初判，如不稳定再采用第6~60分钟内蠕变量2.0 mm（即 $\alpha$ 为2.0 mm）这个量化指标再判。其它国际标准^{[14, 16, 18]}方法类似。

采用蠕变率法时，为消除试验误差，常常采用蠕变率拟合曲线。①锚杆试验一般分为5~8级加载，级数越多试验结果准确程度越高但时间也越长。国内通常取破坏荷载的前一级荷载为抗拔力，以C18c为例，1200 kN时首次时长 $\alpha$ =3.08 mm，可判定为破坏，抗拔力取上一级荷载则为1100 kN。按蠕变率2.0 mm方法，计算各级荷载 $\alpha$ （结果见），因蠕变率随分级荷载的增加而单调增加，两级荷载之间的 $\alpha$ 可采用内插法获得，绘制蠕变率-荷载（ $\alpha$ -P）曲线如所示，取 $\alpha$ =2.0 mm对应的荷载作为抗拔力则为1160 kN，比1100 kN增大了60 kN（5.5%），基本上消除了这种因荷载分级后不连续而产生的试验误差。②在用式（1）计算 $\alpha$ 时，同一结果通常会因t₁及t₂取值不同而产生多个 $\alpha$ ，有些会存在较大偏差，例如C18c在1100 kN时 $\alpha$ 为0.84，如所示，如果按所示拟合曲线取值则 $\alpha$ 为1.03，存在着0.19 mm的负偏差，而 $\alpha$ 为1.03更合理一些。 $\alpha$ 随着荷载增加而增加是蠕变特性，如果哪级荷载的 $\alpha$ 不符合拟合曲线，偏大或者偏小，都说明了该 $\alpha$ 值的偏差较大，如所示800 kN时的 $\alpha$ 即明显偏大。这种偏差可能是地质条件的变异性造成的固有偏差，也可能是因掉压补压、反力装置沉降、测量仪表读数等原因造成的测试误差，判稳时长越小其影响越大，通常难以辨别也无需辨别，但有时有些关键数据（如不同判稳方法确定量化指标时选用的第5，6，15，60分钟等时刻的位移读数）误差较大会影响到稳定与否的判断，此时可将 $\alpha$ 计算结果拟合为图 8所示曲线或拟合方程后加以校核。

图 8 锚杆C18c按α-P曲线计取抗拔力方法

Figure 8. Method for calculating anchor resistance according to α-P curve of anchor C18c

下载: 全尺寸图片幻灯片

试验还发现： $\alpha$ ≤2.0 mm时蠕变稳定， $\alpha$ > 5.0 mm时蠕变不稳定，2.0 mm < $\alpha$ ≤5.0 mm位移可能会收敛，即临界荷载对应着这个区间，故在蠕变较大情况判取极限承载力时 $\alpha$ 也可位于2.0~5.0 mm。

（4）单元时长位移增量。判稳时各单元时长显然应该相等，不同时长的数据进行比较没有意义，但遗憾的是有不少判稳方法忽略了这一点。利用单元时长位移增量判稳的典型方法如：每1 h蠕变量不大于1.0 mm，共不超过3 h^[13]。按该方法绘制3 h的蠕变曲线，如图 9所示，进入第3小时后蠕变率并未减小反而在加大，不符合稳定蠕变机理，故容易产生误判，案例如表 7所示。按蠕变机理，单元时长越往后判稳量化指标应该越小，这样蠕变曲线才能越来越缓直至收敛，该方法中第3小时以0.70 mm作为判稳指标才能与第2小时的1.0 mm大致匹配。另外，该方法由于没有剔除蠕变初始阶段的数据，故第1小时观测期通常会判断为不稳定，要进入第2小时甚至第3小时观测期，耗时较长。尽管如此，由于避开了0.1 mm阈值、5 min单元时长、初始蠕变值等缺陷，该方法成为了国内判稳准确率最高的方法之一。

图 9 按某判稳方法绘制的锚杆蠕变曲线

Figure 9. Creep curves for anchor according to a method

下载: 全尺寸图片幻灯片

采用单元时长位移增量的典型方法还有：①某方法规定，每5 min读数一次，第5，10分钟测读的位移增量之和不大于1.0 mm^[10]；②持荷时间内观测不少于3次，取平均值作为该级位移量^{[9, 11-12]}，有的方法要求初始位移也测读3次^[12]。不管是取和还是取平均值，这些判稳方法都将蠕变随时间变化这一动态特性人为静态化了，显然不妥。

（5）各参数对比。蠕变是时间的函数，同一位移增量在蠕变曲线不同时段的意义不同，作为判稳的定量指标最好恒定、不随时长及时段位置而改变，故位移增量作为定量指标时宜将时间无量纲化以消除对时段及时长的依赖性，即应采用对数时间，而这么做形成的就是蠕变率2.0 mm指标及方法。单元时长位移增量法采用的是原始时间，而蠕变率法采用的是对数时间，采用蠕变率描述蠕变机理显然更直观、更敏感、更准确及更具通用性。以锚杆A15b为例，在990 kN时的持荷观测时间为6 h，蠕变数据及曲线如表 8及图 10所示：位移增量Δs前期不稳定、但第4小时~第6小时大致匀速发展，蠕变特性相当于图 1曲线2的第Ⅰ、Ⅱ阶段；单元时长位移增量Δs_n前期不稳定，但第4小时~第6小时基本稳定；而 $\alpha$ 前1 h内不稳定、之后2~3 h基本稳定，但到了第4小时后再次增加，第6小时快速发散至8.86 mm，故990 kN时宜判定为蠕变不稳定。可见，用 $\alpha$ 可容易地判断出蠕变稳定情况，而Δs及单元时长位移增量Δs_n均很难判准。

图 10 锚杆A15b在990 kN时的蠕变曲线

Figure 10. Creep curves of anchor A15b at 990 kN

下载: 全尺寸图片幻灯片

还需指出，国内有标准^{[11, 13]}认为蠕变率能够表征锚杆的长期工作性能，认为最大试验荷载下蠕变率为2.0 mm/对数周期，意味着在30 min至50 a内蠕变量不超过12 mm。也就是说，蠕变率是界面固有特性，具备时间属性，从最少只持续十几分钟的短期试验到持续两三年（临时锚杆）甚至可能几十年（长期锚杆）的长期使用，贯穿锚杆寿命周期，而其它指标均不具备这个能够把锚杆短期试验结果与长期工作性能联系在一起的功能。另外试验发现，界面的蠕变特性与锚杆长度无关，说明蠕变曲线纵坐标采用位移（增量）是适合的，不需采用应变。

4. 本文判稳方法及说明

4.1 判稳方法及特点

参考国内外标准及经试验验证，本文推荐的判稳方法为：①持荷观测15 min，第5分钟~第15分钟蠕变量不大于1.0 mm判定为位移稳定；②否则延长持荷时间45 min，第15分钟~第60分钟蠕变量不大于1.2 mm判定为稳定；③再次判稳时如不稳定，验收试验可中止试验，极限试验、适应试验及蠕变试验宜再次延长持荷时间4 h，取不同时间段计算蠕变率 $\alpha$ ，可判断出 $\alpha$ 不大于2.0 mm时或 $\alpha$ 大于5.0 mm时即可进入下一循环试验，否则宜试验至持荷时间结束。

本方法特点为：①首次判稳采用了单元时长10 min且避开了初始蠕变阶段，能解决90%以上的判稳问题；第三次判稳最大时长5 h以最终解决准确率问题，两者之间增加时长45 min进行再次判稳以提高判稳效率。②采用蠕变率2.0 mm作为唯一定量指标并进行了具体量化。③最大时长5 h相当于蠕变试验时长，无需再进行专项蠕变试验。④前15 min按1次/1 min、之后45 min按1次/5 min、再之后按1次/10 min测读并记录锚头位移，记录频率高于常规判稳所需以获取更多数据，目的在于除了便于计算 $\alpha$ 外，还可通过观察数据系列从宏观上感知位移读数的有效性及甄别误差。

4.2 相关说明

（1）本文判稳方法，不管对于极限试验、适应试验、蠕变试验或验收试验等不同类型的试验，对于基坑、基础、抗浮、边坡、地下空洞、挡墙加固等不同场合的锚杆，还是拉力型、压力型、扩体型或全黏结型（也称为土钉）等不同类型的锚杆，只要是黏性土层的注浆黏结锚杆，就都适用。

国内与锚杆抗拔力相关的荷载试验分为极限试验、适应试验、验收试验及蠕变试验4类：①极限试验加载至破坏以测取极限抗拔力；②适应试验也称基本试验，主要目的是验证设计参数及施工工艺对场地的适应能力，一般加载至2倍设计抗拔力即终止加载；③验收试验一般加载至1.2~2.0倍设计抗拔力即可；④蠕变试验。美国标准^[15]建议只在某些易于蠕变的地层进行，时长5 h，称为延长蠕变试验，而持荷时长在60 min以内的试验均称为短时蠕变试验；其它国际标准^{[14, 16, 18]}认为所有地层都产生蠕变，同样认为锚杆荷载试验无论时间长短本质上都是蠕变试验，但没有专项蠕变试验，只是持荷观测时间普遍较长，尤其是黏性土层。国际标准中普遍采用蠕变率2.0 mm原则，目的是为了判稳，不仅预应力锚杆，注浆黏结的土钉及微型桩等细长抗拔构件的极限试验、适应试验、验收试验、蠕变试验等各种荷载试验均采用该指标判稳，但均不用于预测锚杆长时间蠕变等变形特性，研究长期性能的锚杆试验持荷期一般为3~10 d^{[16, 18]}。国内蠕变试验为专项试验，作法与美国标准延长蠕变试验类似。本文亦认为，不管是用作锚固类的锚杆还是改良类的土钉，不管用于基坑、抗浮等什么场所，也不管用于极限试验、验收试验等什么类型的试验，判稳对象都是锚固体与地层界面的剪切变形，遵循的都是同一蠕变机理，而蠕变机理是界面的固有特性，并不会随着锚杆应用场所、试验类型及用途等而改变，所以判稳方法必然应该相同。

（2）锚杆试验主要有3种加卸载方法，典型程序如图 11所示：①分级递增多循环法，简称多循环法；②慢速加载单循环法，也称分级维荷法；③快速加载单循环法，简称快速法。本文建议极限试验采用多循环法，适应试验及蠕变试验采用多循环法或分级维荷法，验收试验主要采用快速法，也可采用多循环法或分级维荷法。本文判稳方法对于这些加载形式都是适用的，也是统一的。

图 11 锚杆试验加载方式

Figure 11. Loading methods for anchor tests

下载: 全尺寸图片幻灯片

各种荷载试验中：①均应读取各级卸载位移，目的是为了计算锚杆的弹性位移及塑性位移，从而获取锚杆的变形特性。各判稳方法中分级卸载时长各不相同，一般1~15 min，卸载过程中不会再补压，位移不会增加且可能会在持荷保压时间较长后因掉压而减小，故每级荷载停留1 min能够测读一次位移读数即可，无需再长，多次测读以提高准确性的说法并不成立；②极限试验是探究性质的，事先不知道试验荷载会不会超过极限承载力，故应采用多循环法，如果采用分级维荷法，可能因加载过程中极限破坏而测不到卸载位移数据；③适应试验、蠕变试验的性质以验证为主、探究为辅，事先是知道最大试验荷载小于极限抗拔力的，故采用多循环法或分级维荷法均可，习惯上支护类锚杆多采用多循环法，基础类锚杆多采用分级维荷法，荷载级数可比极限试验的少1~2级以节省试验时间；④快速法仅用于验收试验。验收试验只有验证性质、不具有探究功能，能够得出试验结果合格与否的结论即可；只要在最大试验荷载下蠕变稳定，过程荷载下自然稳定，故加载过程中每级荷载停留1 min、能够测读位移即可，测读目的是记录数据以备用，无需停留过长时间以观测是否稳定。这与适应试验等需求不同，适应试验还兼具探究功能，如果加载过程中发生破坏，还需知道破坏荷载以获取极限承载力。实际上，快速加载对于多循环法也适用，有的判稳方法规定加载时过程荷载停留2~5 min，实际上没必要，1 min即可，时间长了还可能会掉压，美国标准规定不得超过1 min。和多循环法或分级维荷法分级加载到最大试验荷载后持荷15 min相比，快速法并不会影响判稳结果，这与桩的情况不同。桩静载试验中，快速法每级荷载持荷时长低限为1 h，慢速法为2 h，桩采用桩顶绝对位移作为判稳指标，通常位移越小判取的承载力越大，1 h位移显然小于2 h，故快速法判取的承载力可能会高于慢速法。但锚杆采用相对位移作为判稳指标，判稳结果基本不受位移绝对值大小影响，判稳准确程度客观上主要是由初始蠕变阶段以后的持荷观测时长决定的，观测时间越长准确程度越高，但越高并不是因为绝对位移越大，而是因为相对位移越大、干扰因素产生的误差在其中的影响程度越小，与加载到最大试验荷载之前是否分级加载、分多少级、各级持荷时长以及加载速率大小等因素均无关。对于验收试验，国内几乎所有判稳方法都规定最大试验荷载的判稳时长为5~10 min，而快速法为15 min，判稳的准确性更高。实际上，快速法也是ISO与欧盟锚杆试验专项标准^[14]中用于验收试验的几乎唯一方法。

（3）和黏性土层相比，在砂性土层及岩层中的锚杆蠕变稳定时间通常会短一些，初始阶段位移增量会小一些，国内外判稳方法通常不加区分或在砂性土层及岩层中判稳时间略短，如前所述；尽管本文现场试验基于黏性土层，但判稳所依据的蠕变机理、需遵循的主要原则及判稳具体方法同样适用于砂性土层及岩层，并且因判稳时间比较保守，结果更加安全可靠。

（4）笔者曾指出水泥净浆、水泥砂浆、混凝土、水泥基灌浆材料等所有水泥系黏结材料对界面的影响几无差别并解释了原因^[19]，本试验采用水泥净浆的判稳方法适用于所有水泥系黏结材料；美标^[15]中基于水泥系与基于树脂系黏结材料的判稳采用同样方法及指标，但尚未见到国内相关研究成果。

5. 几种典型判稳方法对比

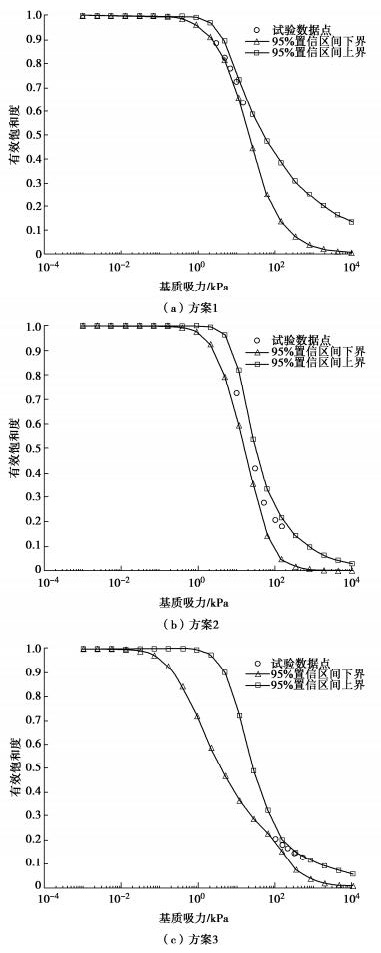
在各种判稳方法中，选取判稳准确程度最高的3种与本文方法进行比较。①方法1：持荷观测10 min，如果位移增量小于1.0 mm则判为稳定，否则继续观测50 min，1 h内位移增量不大于2.0 mm^{[8, 12, 17]}则判为稳定。②方法2：持荷观测30 min，每5 min测读一次，相邻两次位移增量小于0.1 mm时则判为稳定，否则应延时观测，之后每1 h内位移增量不大于1.0 mm则判为稳定，总观测时间不超过3 h^[13]。③方法3为前述美国标准^[15]方法。④本文方法，为了对比，按本方法判稳但按方法3绘制 $\alpha$ -P曲线及判取极限抗拔力。

对A、B、C型锚杆判稳结果表明，和本文方法相比：①方法1用时较少，误判较多，判取的极限抗拔力明显偏低；②方法2用时较长，有时会高判抗拔力；③方法3用时稍长，有时会低判承载力。试验发现，各方法对于突变型破坏判稳结果几乎相同，对缓变型破坏判稳结果有时相差较大。另外，采用 $\alpha {\text{ - }}P$ 曲线按 $\alpha$ =2.0 mm判取极限承载力稍显复杂，与采用分级荷载法判取结果总体而言相差无几，故从工程简化及实用角度，可按分级荷载法判取。

6. 结论

通过理论研究、深坪锚杆试验专项测试及工程经验验证，对注浆黏结锚杆各种荷载试验的位移稳定判定方法，主要得到以下8点结论。

（1）锚杆荷载试验时依据位移是否稳定来判取抗拔力，本质上判定位移是否稳定（简称判稳）判定的就是锚固体与地层界面剪切变形，即蠕变是否稳定，荷载试验就是测试界面蠕变特性的试验。

（2）各种荷载试验时界面蠕变都遵循同一蠕变机理，即荷载较小时发生稳定蠕变，超过临界荷载后发生蠕变破坏，稳定蠕变过程可分为初始及持续两个阶段，蠕变破坏则多了加速阶段。

（3）判稳的主要任务即根据蠕变持续阶段的蠕变特性来判断是否发生加速蠕变，而初始阶段时长最长宜取5 min、位移数据不能用于判稳。

（4）蠕变破坏形状约2/3锚杆为突变型，约1/3为缓变型，两类破坏对应着3类蠕变曲线形态。

（5）位移增量不能直接用作判稳参数，用于判稳的位移阈值不应小于0.1 mm、单元时长不应短于10 min，持荷观测的最大时长宜为5 h。

（6）判稳应从定性与定量两方面着手，即定性判断蠕变速率总体上在减速，确定定量指标使蠕变速率维持在较低水平从而使位移收敛。

（7）试验时荷载已明确，主要应依据具有位移与时间双重属性的参数判稳，单元时长位移增量作为指标的判稳方法准确度较高，而蠕变率2.0 mm指标任何情况下都准确、安全、经济且省时。

（8）判稳方法以国际标准中普遍采用的蠕变率2.0 mm指标为内在原则并进行了具体化，适用于各种应用场合及各种类型的注浆黏结锚杆，适用于各种荷载试验及快速法等各种加卸载方式。

图 1 试验方案对SWCC置信区间的影响

Figure 1. Effects of experimental schemes on CIs of SWCC

下载: 全尺寸图片幻灯片

图 2 SWCC试验单阶段贝叶斯优化设计（OBEDO）框架

Figure 2. One-stage Bayesian experimental design optimization (OBEDO) framework for SWCC tests

下载: 全尺寸图片幻灯片

图 3 附加点D₁，D₂，…，D_n-4分布

Figure 3. Positions of additional points D₁, D₂, …, D_n-4

下载: 全尺寸图片幻灯片

图 4 典型土水特征曲线

Figure 4. Typical SWCC

下载: 全尺寸图片幻灯片

基于 ${\bar \psi _{\text{b}}}$ ， ${\bar \psi _{\text{i}}}$ 和 ${\bar \psi _{\text{r}}}$ 的SWCC分区

Figure 5. Partition of SWCC

下载: 全尺寸图片幻灯片

图 6 控制点和附加点分布

Figure 6. Positions of control points and additional point

下载: 全尺寸图片幻灯片

利用先验信息确定 ${\bar \psi _{\text{b}}}$ ， ${\bar \psi _{\text{i}}}$ 和 ${\bar \psi _{\text{r}}}$

Determination of ${\bar \psi _{\text{b}}}$ , ${\bar \psi _{\text{i}}}$ and ${\bar \psi _{\text{r}}}$ based on prior knowledge

下载: 全尺寸图片幻灯片

图 8 SSO过程中期望效用中间阈值的变化

Figure 8. Evolution of intermediate threshold value of expected utility during SSO

下载: 全尺寸图片幻灯片

图 9 测点数目n对应的期望效用中间阈值U_m的变化

Figure 9. Evolution of intermediate threshold value of expected utility U_m for different measuring points n

下载: 全尺寸图片幻灯片

图 10 不同测点数目n时的最大期望效用

Figure 10. Expected utilities of optimal experimental schemes with different numbers of measuring points n

下载: 全尺寸图片幻灯片

图 11 SWCC实测数据

Figure 11. Measured data of SWCC

下载: 全尺寸图片幻灯片

图 12 随机试验方案的效用

Figure 12. Utilities of random experimental schemes

下载: 全尺寸图片幻灯片

图 13 基于BOS模拟数据和ROS实测数据获得的SWCC置信区间对比

Figure 13. CIs of SWCC with simulated data of BOS and measuring data of ROS

下载: 全尺寸图片幻灯片

图 14 不同先验信息条件下测点数目n对应的最大期望效用值

Figure 14. Maximum expected utilities using different prior knowledge

下载: 全尺寸图片幻灯片

图 15 不同先验范围对应的最优设计方案BOS

Figure 15. Optimal design scheme BOS using different prior knowledge

下载: 全尺寸图片幻灯片

参考文献(23)

[1]	LU N, LIKOS W J. Unsaturated Soil Mechanics[M]. New Jersey: Wiley, 2004: 40-42.
[2]	NAM S, GUTIERREZ M, DIPLAS P, et al. Comparison of testing techniques and models for establishing the SWCC of riverbank soils[J]. Engineering Geology, 2010, 110(1/2): 1-10. http://www.researchgate.net/profile/Panayiotis_Diplas/publication/222581777_Comparison_of_testing_techniques_and_models_for_establishing_the_SWCC_of_riverbank_soils/links/02bfe50dda8e569bcd000000
[3]	邢旭光, 赵文刚, 马孝义, 等. 土壤水分特征曲线测定过程中土壤收缩特性研究[J]. 水利学报, 2015, 46(10): 1181-1188. doi: 10.13243/j.cnki.slxb.20150632 XING Xuguang, ZHAO Wengang, MA Xiaoyi, et al. Study on soil shrinkage characteristics during soil water characteristic curve measurement[J]. Journal of Hydraulic Engineering, 2015, 46(10): 1181-1188. (in Chinese) doi: 10.13243/j.cnki.slxb.20150632
[4]	GATABIN C, TALANDIER J, COLLIN F, et al. Competing effects of volume change and water uptake on the water retention behaviour of a compacted MX-80 bentonite/sand mixture[J]. Applied Clay Science, 2016, 121/122: 57-62. doi: 10.1016/j.clay.2015.12.019
[5]	VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. doi: 10.2136/sssaj1980.03615995004400050002x
[6]	FREDLUND D G, XING A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521-532. doi: 10.1139/t94-061
[7]	陶睿, 李典庆, 曹子君, 等. 含砂黄土土水特征曲线试验研究与参数识别[J]. 武汉大学学报(工学版), 2021, 54(7): 579-587. doi: 10.14188/j.1671-8844.2021-07-001 (TAO Rui, LI Dianqing, CAO Zijun, et al. Experimental study and parameter identification of soil water characteristic curve of sandy loess[J]. Engineering Journal of Wuhan University, 2021, 54(7): 579-587. doi: 10.14188/j.1671-8844.2021-07-001
[8]	WANG L, CAO Z J, LI D Q, et al. Determination of site-specific soil-water characteristic curve from a limited number of test data–A Bayesian perspective[J]. Geoscience Frontiers, 2018, 9(6): 1665-1677. doi: 10.1016/j.gsf.2017.10.014
[9]	王林, 李典庆, 曹子君, 等. 基于贝叶斯理论的土水特征曲线模型选择与参数识别方法[J]. 应用基础与工程科学学报, 2019, 27(6): 1269-1284. https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201906008.htm WANG Lin, LI Dianqing, CAO Zijun, et al. Bayesian approaches for model selection and parameter identification of soil-water characteristic curve[J]. Journal of Basic Science and Engineering, 2019, 27(6): 1269-1284. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201906008.htm
[10]	SIVIA D, SKILLING J. Data Analysis: A Bayesian Tutorial[M]. Oxford: OUP Oxford, 2006.
[11]	张万涛, 余宏明. 正交试验设计方法在库岸滑坡敏感性分析中的应用[J]. 安全与环境工程, 2009, 16(5): 13-16. doi: 10.3969/j.issn.1671-1556.2009.05.004 ZHANG Wantao, YU Hongming. Applications of orthogonal experiment design to sensitivity analysis of bank landslide[J]. Safety and Environmental Engineering, 2009, 16(5): 13-16. (in Chinese) doi: 10.3969/j.issn.1671-1556.2009.05.004
[12]	STRAUB D. Value of information analysis with structural reliability methods[J]. Structural Safety, 2014, 49: 75-85. doi: 10.1016/j.strusafe.2013.08.006
[13]	SCHWECKENDIEK T, VROUWENVELDER A C W M. Reliability updating and decision analysis for head monitoring of levees[J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2013, 7(2): 110-121. doi: 10.1080/17499518.2013.791034
[14]	LI X Y, ZHANG L M, JIANG S H, et al. Assessment of slope stability in the monitoring parameter space[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(7): 04016029. doi: 10.1061/(ASCE)GT.1943-5606.0001490
[15]	LI H S. Subset simulation for unconstrained global optimization[J]. Applied Mathematical Modelling, 2011, 35(10): 5108-5120. doi: 10.1016/j.apm.2011.04.023
[16]	ZHAI Q, RAHARDJO H. Determination of soil-water characteristic curve variables[J]. Computers and Geotechnics, 2012, 42: 37-43. doi: 10.1016/j.compgeo.2011.11.010
[17]	ZHAI Q, RAHARDJO H, SATYANAGA A. Effects of residual suction and residual water content on the estimation of permeability function[J]. Geoderma, 2017, 303: 165-177. doi: 10.1016/j.geoderma.2017.05.019
[18]	丁少林. 考虑不确定性的土水特征曲线室内试验设计与含气土现场勘探优化方法[D]. 武汉: 武汉大学, 2022. DING Shaolin. Laboratory experimental design of soil-water characteristic curve and site investigation optimization of gassy soils considering uncertainty[D]. Wuhan: Wuhan University, 2022. (in Chinese)
[19]	HUAN X, MARZOUK Y M. Simulation-based optimal Bayesian experimental design for nonlinear systems[J]. Journal of Computational Physics, 2013, 232(1): 288-317. doi: 10.1016/j.jcp.2012.08.013
[20]	CHIU C F, YAN W M, YUEN K V. Reliability analysis of soil–water characteristics curve and its application to slope stability analysis[J]. Engineering Geology, 2012, 135/136: 83-91. doi: 10.1016/j.enggeo.2012.03.004
[21]	BISHOP C M. Pattern Recognition and Machine Learning[M]. New York: Springer, 2006.
[22]	ZHOU Y F, THAM L G, YAN R W M, et al. The mechanism of soil failures along cracks subjected to water infiltration[J]. Computers and Geotechnics, 2014, 55: 330-341. doi: 10.1016/j.compgeo.2013.09.009
[23]	LI X P, WANG C H, XU J. Surficial stability analysis of unsaturated loess slopes subjected to rainfall infiltration effects[J]. Wuhan University Journal of Natural Sciences, 2006, 11(4): 825-828. http://www.cqvip.com/QK/85480X/200604/22434488.html

施引文献(2)

期刊类型引用(2)

1.	张子洋，汪波，刘锦超，刘金炜，杨凯. 后注浆预应力树脂锚杆应力损失后注浆段效用分析. 铁道科学与工程学报. 2025(02): 783-794 . 百度学术
2.	谈博海，姚囝，杜键，孙明伟，刘海，关文超. 膨胀型浆体注浆锚杆拉拔力学特性及损伤失效机制研究. 岩石力学与工程学报. 2024(12): 3058-3069 . 百度学术