砂土中锚板上拔三维物质点法模拟研究

高宇新; 朱鸿鹄; 张春新; 刘威; 王静; 张巍

doi:10.11779/CJGE202202011

砂土中锚板上拔三维物质点法模拟研究 English Version

南京大学地球科学与工程学院, 江苏南京 210023

基金项目:

国家自然科学基金项目 42077235

国家自然科学基金项目 41722209

国家重点研发计划课题 2018YFC1505104

详细信息

作者简介:
高宇新(1998—)，女，博士研究生，主要从事地质与岩土工程监测评价方面的科研工作。E-mail: gaoyx@smail.nju.edu.cn

通讯作者:
朱鸿鹄，E-mail: zhh@nju.edu.cn

中图分类号: TU441
计量
- 文章访问数: 270
- HTML全文浏览量: 29
- PDF下载量: 111
出版历程
- 收稿日期: 2021-05-11
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-01-31

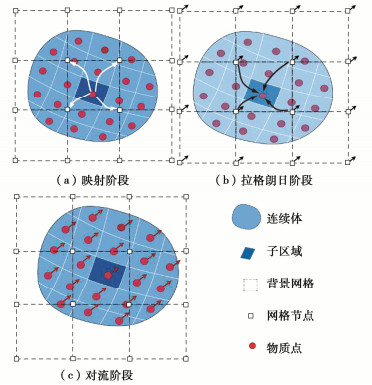
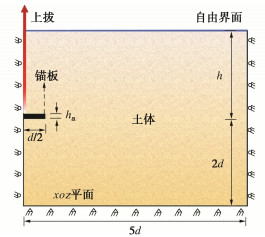
Three-dimensional uplift simulation of anchor plates in sand using material point method

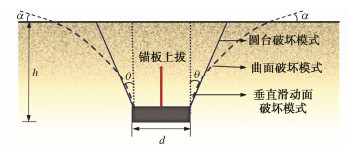
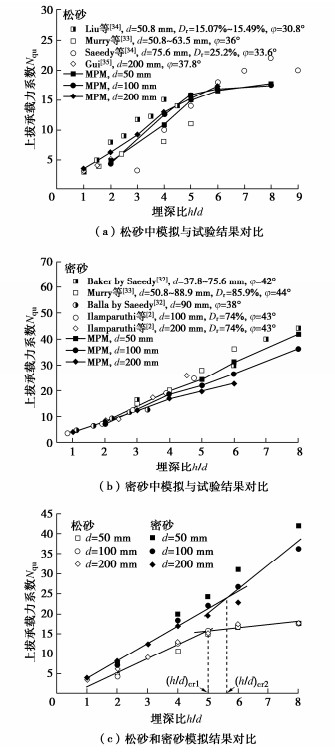
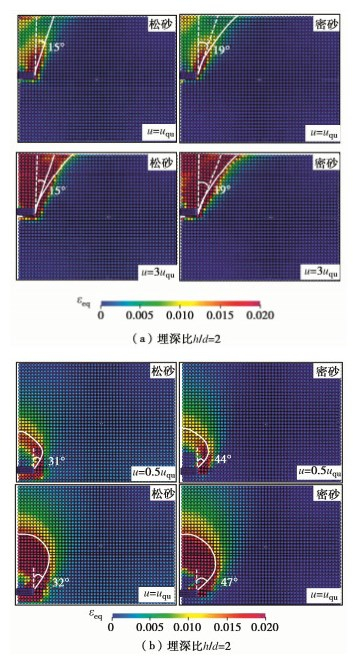
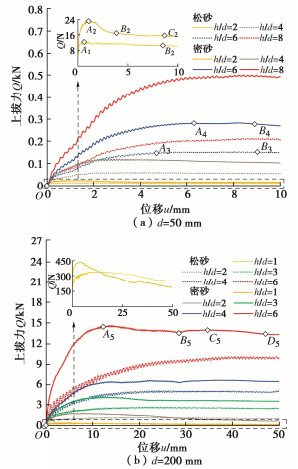
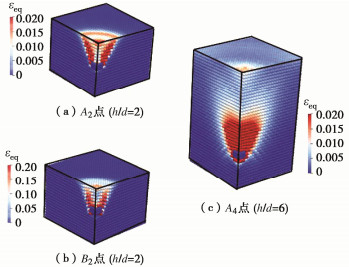
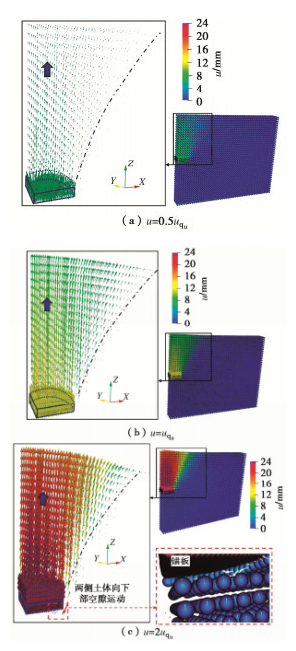
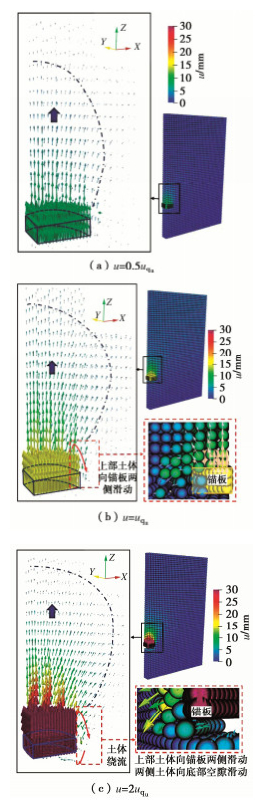
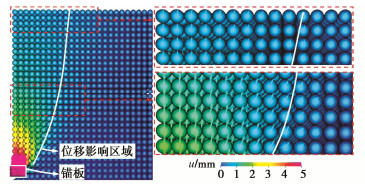
School of Earth Science and Engineering, Nanjing University, Nanjing 210023, China

摘要

摘要: 土体中锚板的上拔过程存在复杂的锚土相互作用，掌握其变形及破坏机制对于确定锚板的极限承载力和优化设计具有重要的意义。采用三维物质点法（MPM）模拟了砂土中圆形锚板的上拔过程，探究了不同埋深条件下土体的位移场分布及锚板的上拔破坏机制，并结合极限平衡法研究了砂土密实度、锚板尺寸和埋深等因素对其极限承载力的影响。结果表明，临界埋深比主要受土体性质影响，受锚板直径的影响较小。当埋深比小于临界埋深比时，土体表现为浅埋破坏，破坏面延伸至地表，其形状在松砂中为圆台状，在密砂中为曲面状；当埋深比大于临界埋深比时，土体中的破坏面呈灯泡状，且不延展至地表。当上拔位移较大时，锚板上方出现土体绕流现象。保持埋深比不变，锚板直径越大，则极限承载力越大，上拔承载力系数越小。砂土密实度对锚板上拔力–位移曲线有较大的影响，密砂中的极限承载力明显大于松砂，且两者的差值随埋深比的增加而增大。
- 物质点法 /
- 锚板 /
- 破坏面 /
- 极限承载力 /
- 相互作用
Abstract: There are complex anchor-soil interactions in the uplift process of the anchor plate, and it is of great significance to master the deformation mechanism and displacement distribution of the soil to predict the uplift bearing capacity and optimize the design. Based on the three-dimensional material point method (MPM) to simulate the uplift of the anchor plate, the uplift failure mechanism under different embedment depth ratios is explored, and the influences of soil compactness, diameter and embedment depth ratio of the anchor plate on the peak bearing capacity are analyzed using limit equilibrium method. The results show that the limit embedment depth ratio is mainly affected by the nature of the soil, but less affected by the diameter. When the embedment depth ratio is less than the critical one, the soil exhibits shallow embedment failure, and the failure surface extends to the surface. Its shape is truncated cone-shaped in loose sand and curved in dense sand. When the embedment depth ratio is greater than the critical one, the damage surface in the soil is bulb-shaped and does not extend to the surface. When the uplift displacement is large, the soil above the anchor plate appears to flow around. When the embedment depth ratio remains unchanged, the larger the plate diameter, the greater the ultimate bearing capacity, and the smaller the uplift bearing capacity coefficient. Considering the softening effects, the load-displacement response in the uplift process of loose sand and dense sand is different. The ultimate bearing capacity of the dense sand is greater than that of the loose sand, and the difference between them increases with the increase of the embedment depth ratio.
- material point method /
- anchor plate /
- failure plane /
- ultimate bearing capacity /
- interaction

HTML全文

0. 引言

盐渍土具有溶陷、冻胀及腐蚀等特殊工程性质，盐渍土地区修建道路在工程上常采用换填土层处理。黑龙江省处于季冻区，路基土受到交通动荷载、冬季低温及冻融循环综合作用，路基土的力学性能和动力特性因此发生改变，主要体现在土体动剪切模量和阻尼比的变化^[1]。目前对于盐渍土的研究主要包括温度变化下水盐迁移运动研究^[2-3]，通过室内试验结果，分析水盐运动主要影响因素，建立温度梯度下盐渍土水–热–盐多场耦合模型，揭示水盐运动规律；土体冻胀和溶陷特性研究，将湿陷和溶陷加以区分，提出峰值溶陷系数以描述不同含盐量对压缩、湿陷和溶陷的影响。考虑冻胀和盐胀综合作用，分析冻胀影响因素^[4-6]；盐渍土改性剂种类和掺量以及改良盐渍土的静力性质研究，采用不同改性剂对盐渍土进行改良，并对改良盐渍土抗剪强度及破坏强度进行测定，根据试验结果，建立考虑多重因素的改良盐渍土破坏强度及抗剪强度预测模型^[7-8]。以上研究多针对未处理盐渍土，或主要考虑改良盐渍土静力性质。若通过石灰改良含盐量较低的盐渍土，使其满足路基力学性能的要求，可以降低成本并节约土壤资源。综上，目前对于季冻区低温及冻融循环作用下的石灰改良盐渍土动力特性研究偏少但其影响不容忽视。

本文以黑龙江省哈肇公路沿线盐渍土为研究对象，经石灰改良后进行循环三轴试验，研究其在不同动荷载频率、围压、温度以及冻融循环作用下的动剪切模量及阻尼比变化规律。并基于Hardin双曲线模型进行曲线拟合，分析石灰改良盐渍土动力参数在不同因素下的响应规律，为工程设计提供动力参数，并为进一步研究不同改性剂种类及不同盐分种类的改良盐渍土动力特性提供理论基础。

1. 试验材料与试验方案

1.1 试验材料

试验土样取自黑龙江省哈肇公路沿线，依据《公路土工试验规程：JTG E40-2007》，测得土样基本物理参数：天然含水率为6.85%，液限为21.2%，塑限为14.2%，最大干密度为1.79 g/cm³，最佳含水率为16%。土样的颗粒级配曲线如图 1所示，由试验结果可知该土样属于低液限黏土，土样中各离子种类及含量如表 1所示。由试验结果可知此土样总含盐量为0.5047%，其中CO₃^2-离子含量最高达0.2205%，夹杂有含量0.1086%的HCO₃^-离子和0.1134%的Cl^-离子，由此判定此土样为含有少量Cl^-的碳酸盐渍土且含盐量较低。

图 1 试验用土颗粒级配曲线

Figure 1. Grain-size distribution curves of test specimens

下载: 全尺寸图片幻灯片

表 1 盐渍土离子含量测定值

Table 1. Measured values of ion content of saline soil (%)

阳离子					阴离子
K⁺	Na⁺	Ca²⁺	Mg²⁺	总量	CO₃^2-	HCO₃^-	SO₄^2-	Cl^-	总量
0.21	0.2173	0.0244	0.0357	0.4870	0.2205	0.1086	0.0622	0.1134	0.5047

下载: 导出CSV

| 显示表格

1.2 试样制备

依据《公路路基设计规范：JTG D30—2015》选择压实度为96%，并查阅相关文献及结合工程实际，确定石灰掺量为6%^[9]。

试样制备采用击实法，烘干土样经0.25 mm土工标准筛筛分，并与蒸馏水充分混合后装入塑料袋中后闷料24 h。按照石灰掺量称取一定质量的石灰均匀拌入盐渍土中，称取所需质量的土样，分3层制成直径39.1 mm，高80 mm的圆柱试样，将其密封后进行恒温恒湿养护28 d。

1.3 试验仪器

试验采用英国GDS公司的动态三轴试验系统（GDSTAS），仪器可以施加最大荷载为10 kN，荷载频率范围为1~5 Hz，最大围压为200 MPa，温度调节范围为-20℃~20℃。冻融循环过程采用DP.CDR-2型快速冻融试验设备。

1.4 试验条件和方案

试验主要控制条件为温度和冻融循环次数。根据相关文献及该地区路基冬季低温温度范围^[10-11]，低温试验温度设置为20℃，0℃，-2℃，-4℃，-6℃，-8℃，-10℃，-16℃共8个温度变化梯度，养护后的试样在设定温度下冻结24 h后，进行温度控制的循环加载试验。冻融循环次数为0，1，3，5，7，9次，冻融循环试验的冻结温度为-16℃，融化温度为20℃。

研究动荷载频率及围压对动力特性影响时采用未冻融试样，试验温度为20℃。荷载参数^[12-14]参考公路交通荷载设置频率为1，3，5 Hz，围压为50，100，150 kPa。试验方案见表 2。

表 2 试验方案

Table 2. Test plan

试验编号	试验温度 /℃	频率/Hz	有效围压 /kPa	冻融循环次数
S1	20	1	100	0
S2~S3	20	3，5	100	0
S4~S6	20	1	50，100，150	0
S7~S13	0，-2，-4，-6， -8，-10，-16	1	100	0
S14~S18	20	1	100	1，3，5，7，9

下载: 导出CSV

| 显示表格

养护完成的试样进行试验前，需在动三轴仪器上进行CO₂排气，水头差饱和、多级反压饱和，当B值大于0.95时结束饱和。试样等压固结后，施加分级正弦波荷载，固结过程及动荷载加载过程见图 2。进行低温加载试验时，养护后的试样经饱和后需按照设定温度冻结24 h，并预先将试验仪器温度控制在设定温度后再进行试验。终止加载条件为轴向变形达到5%或破坏。

图 2 正弦形式轴向动荷载示意图

Figure 2. Schematic diagram of sinusoidal axial dynamic load

下载: 全尺寸图片幻灯片

2. 试验结果与分析

2.1 不同频率下动力参数的变化

未冻融，围压100 kPa，温度20℃，不同频率石灰改良盐渍土动剪切模量变化如图 3（a）所示。3种频率下，随着剪应变的增大，动剪切模量呈衰减趋势，曲线形式为上凸形。剪应变较小时，动剪切模量衰减速度较慢。剪应变较大时，动剪切模量衰减速度加快。在动剪切模量–剪应变曲线变化过程中存在转折点，Lin等^[15]认为转折点动剪切模量可以评价不同因素对于动剪切模量的影响。动荷载频率由1 Hz增加到5 Hz，转折点动剪切模量增加168%。

图 3 不同频率下动剪切模量及阻尼比拟合曲线

Figure 3. Fitting curves of dynamic shear modulus and damping ratio at different frequencies

下载: 全尺寸图片幻灯片

不同频率下阻尼比变化情况如图 3（b）所示，3种频率下，随着剪应变的增大，阻尼比逐渐增加，较低剪应变水平时阻尼比增长缓慢，较高剪应变水平时阻尼比迅速增长，频率增大引起阻尼比降低。以剪应变最小时对应的阻尼比为最小阻尼比，当动荷载频率由1 Hz增长到5 Hz，最小阻尼比下降0.06。

对不同频率下的动剪切模量–剪应变，阻尼比–剪应变曲线按照Hardin等^[16-17]的双曲线模型进行拟合，拟合公式为

${\tau _{\text{d}}} = \frac{{{\gamma _{\text{d}}}}}{{{a} + b{\gamma _{\rm{d}}}}} \text{，}$

(1)

${{G} _{\text{d}}}{\text{ = }}\frac{{{\tau _{\text{d}}}}}{{{\gamma _{\rm{d}}}}}{\text{ = }}\frac{1}{{{a} + b{\gamma _{\rm{d}}}}} \text{，}$

(2)

$\lambda = {\lambda _{\rm{max}}}{\left( {1 - \frac{{G} }{{{{G} _{\rm{max}}}}}} \right)^{n} } = {\lambda _{\rm{max}}}{\left( {1 - \frac{1}{{1 + \frac{{{\gamma _{\text{d}}}}}{c}}}} \right)^n} 。$

(3)

式中 ${\tau _{\text{d}}}$ 为动应力； ${\lambda _{\rm{max}}}$ 为最大阻尼比；a，b，c，n为拟合参数，拟合参数如表 3所示，拟合曲线如图 3所示。

表 3 不同频率及围压下动剪切模量及阻尼比的拟合参数

Table 3. Fitting parameters of dynamic shear modulus and damping ratio under different frequencies and confining pressures

频率/Hz	动剪切模量G_d			阻尼比 $\lambda$
频率/Hz	a	b	R²	${\lambda _{\max }}$	c	n	R²
1	0.0101	4.7873	0.9865	0.46	0.0025	0.6845	0.9183
3	0.0076	3.4389	0.9886	0.39	0.0096	0.3665	0.9893
5	0.0056	3.3365	0.9887	0.36	0.0169	0.3469	0.9950

围压/kPa	动剪切模量G_d			阻尼比λ
围压/kPa	a	b	R²	λ_max	c	n	R²
50	0.0145	4.7686	0.9942	0.55	0.0036	0.4693	0.9940
100	0.0101	4.7873	0.9865	0.46	0.0025	0.6845	0.9183
150	0.0080	3.4256	0.9941	0.43	0.1306	0.2455	0.9802

下载: 导出CSV

| 显示表格

当式（2）中 ${\gamma _{\text{d}}}$ →0时

${{G} _{{\text{dmax}}}} = \frac{1}{{a} } \text{；}$

(4)

当式（2）中 ${\gamma _{\text{d}}}$ →+∞时，得到

${\tau _{{\text{dult}}}} = \frac{1}{{b} } 。$

(5)

式中，G_dmax为最大动剪切模量， ${\tau _{{\text{dult}}}}$ 为最终动应力幅值。由式（3）可以得到 ${\lambda _{\rm{max}}}$ ，由式（4）可以得出不同温度下的G_dmax。不同频率下G_dmax及 ${\lambda _{\rm{max}}}$ 如表 4所示。

表 4 不同频率及围压下最大动剪切模量及阻尼比

Table 4. Maximum dynamic shear modulus and damping ratios under different frequencies and confining pressures

参数	频率/Hz			围压/kPa
参数	1	3	5	50	100	150
G_dmax/MPa	98.81	130.89	177.31	69.11	98.81	125.31
λ_max	0.46	0.39	0.36	0.55	0.46	0.42

下载: 导出CSV

| 显示表格

曲线变化的原因与试样中土粒重新排列有关，较低剪应变水平时，石灰与土体形成稳定结构使得土体变形较小，动剪切模量和阻尼比变化缓慢。较高剪应变水平时，石灰与土体形成的稳定结构逐渐破坏，土粒重新排列，黏滞性水膜在荷载作用下发生流动，产生较大变形，动剪切模量和阻尼比迅速变化。对于不同频率而言，频率增大使得加载速率提高，相同加载周次中塑性变形积累速度变慢，达到同样塑性变形所需动应力增加。同时，试样中黏滞性水膜流动和重新排列效应减弱，土粒重组时间减少，塑性变形相应减弱，塑性变形耗能降低，表现出动剪切模量增加，阻尼比降低的特性。

2.2 不同围压下动力参数的变化

未冻融，20℃，1Hz加载的石灰改良盐渍土动剪切模量在不同围压下的变化情况如图 4（a）所示，不同围压曲线变化趋势与频率相同，围压增加，转折点动剪切模量增加，阻尼比下降。转折点动剪切模量增加84%，最小阻尼比降低0.05。围压增加，试样中土颗粒发生位移，孔隙得到填充，土体结构性得到增强，强度得到提升。不同围压下拟合曲线如图 4所示，拟合参数如表 3所示，不同围压下G_dmax及 ${\lambda _{\rm{max}}}$ 如表 4所示。

图 4 不同围压下动剪切模量及阻尼比拟合曲线

Figure 4. Fitting curves of dynamic shear modulus and damping ratio under different confining pressures

下载: 全尺寸图片幻灯片

由不同频率及围压下石灰改良盐渍土动剪切模量和阻尼比的拟合参数 ${\lambda _{\rm{max}}}$ ，得到最大阻尼比，并通过式（4）计算不同频率及围压下石灰改良盐渍土最大动剪切模量，如表 4所示。

2.3 温度对动力参数影响及温度修正系数

不同温度下的动剪切模量–剪应变，阻尼比–剪应变曲线同样按照式（1）~（3）进行拟合，拟合参数如表 5所示，拟合曲线见图 5。

表 5 不同温度下动剪切模量及阻尼比的拟合参数

Table 5. Fitting parameters of dynamic shear modulus and damping ratio under different temperatures

温度/℃	动剪切模量G_d			阻尼比 $\lambda$
温度/℃	a	b	R²	${\lambda _{\max }}$	c	n	R²
20	0.0101	4.7873	0.9865	0.4546	0.0025	0.6845	0.9183
0	0.0073	4.1682	0.9965	0.3928	0.0018	0.5971	0.9384
-2	0.0041	3.2572	0.9728	0.3718	0.0016	0.6851	0.9707
-4	0.0031	2.7513	0.9908	0.2818	0.0015	0.6153	0.9330
-6	0.0028	2.5054	0.9989	0.2170	0.0013	0.5750	0.9742
-8	0.0024	2.5351	0.9966	0.1915	0.0010	0.6831	0.9409
-10	0.0024	2.1925	0.9811	0.1441	0.0008	0.5857	0.9024
-16	0.0024	1.7242	0.9247	0.0700	0.0006	0.4172	0.9567

下载: 导出CSV

| 显示表格

图 5 不同温度下动剪切模量及阻尼比拟合曲线

Figure 5. Fitting curves of dynamic shear modulus and damping ratio under different temperatures

下载: 全尺寸图片幻灯片

由不同温度下石灰改良盐渍土动剪切模量和阻尼比的拟合参数 ${\lambda _{\rm{max}}}$ 得到最大阻尼比，并通过式（4）计算不同温度下石灰改良盐渍土最大动剪切模量，如表 6所示。

表 6 不同温度下最大动剪切模量及阻尼比

Table 6. Maximum dynamic shear modulus and damping ratios under different temperatures

温度/℃	G_dmax/MPa	${\lambda _{\rm{max}}}$
20	98.81	0.46
0	137.17	0.39
-2	242.13	0.37
-4	320.51	0.28
-6	357.14	0.22
-8	413.22	0.19
-10	414.94	0.14
-16	423.73	0.07

下载: 导出CSV

| 显示表格

随着温度的降低，动剪切模量增加，阻尼比降低。温度由20℃降低至-16℃，转折点动剪切模量增加263 MPa（75→338 MPa），阻尼比减小0.10。随着温度降低，土中水分不断结冰，土体结构更加致密使黏结力增大。抗动荷载能力及抗变形能力增加，动剪切模量增大，达到相同动应力幅值所需能量降低，阻尼比减小。

根据不同温度下动力参数试验结果，提出温度修正系数：

${G'_{\rm{dmax}}} = {\alpha _{\rm{G}}}{{G} _{\rm{dmax}}} \text{，}$

(6)

${\lambda '_{\rm{dmax}}} = {\alpha _\lambda }{\lambda _{\rm{max}}} 。$

(7)

式中， ${\alpha _{\rm{G}}}$ 为动剪切模量的温度修正系数， ${\alpha _\lambda }$ 为阻尼比的温度修正系数。基于孙锐等^[18]对于负温下的黏土动力参数预测公式，对 ${\alpha _G}$ 和 ${\alpha _\lambda }$ 进行拟合分析：

${\alpha _G} = {\alpha _1}\left( {\frac{{{{A} _1} - {{A} _2}}}{{1 + {{\text{e}}^{(T - {T_{\text{0}}})/{r_1}}}}} + {{A} _2}} \right) + {\alpha _2}({{y} _0} + {{A} _0}{e^{{{ - {T} } \mathord{\left/ {\vphantom {{ - {T} } {{{r} _2}}}} \right. } {{{r} _2}}}}}) \text{，}$

(8)

${\alpha _\lambda } = {y_0} + {A'_0}{{\text{e}}^{{T \mathord{\left/ {\vphantom {T {{{r'}_2}}}} \right. } {{{r'}_2}}}}} 。$

(9)

拟合参数如表 7所示，拟合曲线如图 6所示。得到温度修正系数表达式为

$\begin{array}{c} {\alpha _G} = 0.53\left( {\frac{{2.76 + 0.29}}{{1 + {{\text{e}}^{{{\left( {T + 0.76} \right)} \mathord{\left/ {\vphantom {{\left( {T + 0.76} \right)} {2.26}}} \right. } {2.26}}}}}} - 0.29} \right) + \\ 0.66(4.48-3.12{\text{e}}^{-T/-4.32})\text{ }\text{，} \end{array}$

(10)

${\alpha _\lambda } = - 0.019 + 0.91{{\text{e}}^{{T \mathord{\left/ {\vphantom {T {11.42}}} \right. } {11.42}}}} 。$

(11)

表 7 温度修正系数的拟合参数

Table 7. Fitting parameters of temperature correction coefficient

A₁	A₂	T₀	r₁	A₀	y₀	r₂
2.76	-0.29	-0.76	2.26	-4.32	4.48	-3.12

${\alpha _1}$	${\alpha _2}$	R²	${y'_0}$	${A'_0}$	${r'_2}$	R²
0.53	0.66	0.991	-0.019	0.91	11.42	0.990

下载: 导出CSV

| 显示表格

图 6 动剪切模量和阻尼比温度修正系数拟合曲线

Figure 6. Fitting curves of temperature correction coefficient for dynamic shear modulus and damping ratio

下载: 全尺寸图片幻灯片

由图 6可知，温度修正系数转折点位于-6℃附近，T < -6℃时，温度修正系数下降缓慢；T > -6℃时，温度修正系数迅速下降。

2.4 冻融循环作用对动力参数影响及冻融修正系数

在不同冻融循环次数下，动剪切模量–剪应变、阻尼比–剪应变曲线按式（1）~（3）拟合，a₂，b₂，c₂，n₂为拟合参数，拟合参数如表 8所示，拟合曲线如图 7所示。

表 8 不同冻融循环次数动剪切模量及阻尼比的拟合参数

Table 8. Fitting parameters of dynamic shear modulus and damping ratio under different freeze-thaw cycles

冻融循环次数	动剪切模量G_d			阻尼比λ
冻融循环次数	a₂	b₂	R²	${\lambda _{\rm{max}}}$	c₂	n₂	R²
0	0.0102	4.7873	0.9865	0.4649	0.0025	0.6972	0.8884
1	0.0145	6.1150	0.9960	0.5675	0.0040	0.7006	0.9551
3	0.0214	6.1155	0.9984	0.6641	0.0049	0.6692	0.9631
5	0.0227	6.9325	0.9951	0.6827	0.0061	0.7094	0.9558
7	0.0262	7.8786	0.9953	0.7022	0.0075	0.7610	0.9514
9	0.0283	7.6030	0.9983	0.7124	0.0085	1.0048	0.9741

下载: 导出CSV

| 显示表格

图 7 不同冻融循环次数下动剪切模量及阻尼比拟合曲线

Figure 7. Fitting curves of dynamic shear modulus and damping ratio under different freeze-thaw cycles

下载: 全尺寸图片幻灯片

由不同冻融循环次数下石灰改良盐渍土动剪切模量和阻尼比的拟合参数 ${\lambda _{\rm{max}}}$ ，得到最大阻尼比，并通过式（4）计算不同冻融循环次数下石灰改良盐渍土最大动剪切模量，如表 9所示。

表 9 不同冻融循环次数下最大动剪切模量及阻尼比

Table 9. Maximum dynamic shear modulus and damping ratios under different freeze-thaw cycles

冻融循环次数	G_dmax/MPa	${\lambda _{\rm{max}}}$

0	98.81	0.47
1	70.08	0.57
3	46.53	0.66
5	43.80	0.68
7	39.26	0.70
9	35.65	0.71

下载: 导出CSV

| 显示表格

由图 7（a）可知，动剪切模量在冻融循环作用后显著下降，尤其是第3次冻融后，动剪切模量下降40 MPa（75→35 MPa），降幅约为47%。当冻融循环次数超过3次后，动剪切模量衰减趋于稳定。第9次冻融循环作用后，较高剪应变水平时，试件的动剪切模量衰减至较低数值，强度几乎损失殆尽。随着冻融循环作用次数的增加，阻尼比不断增大，3次冻融循环作用后，阻尼比变化不明显。

土体冻结伴随着盐胀作用，土体中孔隙增加。融化后土体中的孔隙仍然存在，石灰胶结土体的稳定结构受到一定程度的破坏，导致土体结构较冻融前更加松散。在动荷载作用下土体塑性变形增加，动剪切模量大幅降低。达到同样动应力幅值需要的能量增加使得阻尼比提升。随着冻融循环作用次数的增加，特别是冻融循环次数超过3次后，试样土体结构中孔隙大幅增加，石灰胶结土体的稳定结构遭到破坏。同时试样土体内的楔形力不断增长，内部的应力累计超过土体自身黏结力导致土体结构破坏，但由于没有来自外界的水分补充，这种破坏效应逐渐停止，动剪切模量降低到较低状态后趋于稳定。

根据不同冻融循环次数下动力参数试验结果，提出冻融修正系数：

${G'_{\rm{dmax}}} = {\beta _G}{{G} _{\rm{dmax}}} \text{，}$

(12)

${\lambda '_{\max }} = {\beta _\lambda }{\lambda _{\max }} \text{，}$

(13)

式中， ${\beta _{\rm{G}}}$ 为动模量的冻融修正系数， ${\beta _\lambda }$ 为阻尼比的冻融修正系数。

根据严晗等^[19]、张向东等^[20]提出的冻融修正系数公式，对本试验的冻融修正系数进行拟合分析，拟合公式为

${\beta _G} = {{a} _3}{{b} _3}{{\text{e}}^{\frac{{ - N}}{{{c_3}}}}} \text{，}$

(14)

${\beta _\lambda } = {{a} _4} - {{b} _4}{e^{{c_4}N}} 。$

(15)

拟合参数如表 10所示，拟合曲线如图 8所示。

表 10 冻融循环修正系数的拟合参数

Table 10. Fitting parameters of freeze-thaw cycle correction coefficient

${a_3}$	${b_3}$	${c_3}$	${R^2}$
0.56	1.87	0.38	0.991

${a_4}$	${b_4}$	${c_4}$	${R^2}$
1.53	-0.50	0.65	0.980

下载: 导出CSV

| 显示表格

图 8 动剪切模量和阻尼比冻融修正系数拟合曲线

Figure 8. Fitting curves of freeze-thaw correction coefficient for dynamic shear modulus and damping ratio

下载: 全尺寸图片幻灯片

得到冻融修正系数：

${\beta _G} = 0.56 - 1.87{{\text{e}}^{\frac{{ - N}}{{0.38}}}} \text{，}$

(16)

${\beta _\lambda } = 1.53 - 0.50{{\text{e}}^{0.65N}} 。$

(17)

由图 8可知，冻融转折点为第3次冻融循环，第3次冻融循环之前，曲线变化急促，当冻融循环次数大于3时，冻融修正系数曲线趋于平缓。这也同样印证冻融循环作用使得土体内水分冻结，融化后对土体产生不可逆破坏，土体动剪切模量大幅下降。由于缺少外界水分的补充，在冻融循环3次之后，动剪切模量修正系数的衰减趋于停止。

3. 结论

针对季冻区低温冻融环境下，采用GDS冻土动三轴试验系统，对不同试验温度、不同冻融循环次数下的石灰改良盐渍土的动力参数进行研究，并提出两种修正系数，根据建立的动力参数的预测模型，为工程设计中提供所需的动力参数，同时对长期冻融循环劣化作用后石灰改良盐渍土路基稳定性分析提供参考。

（1）随剪应变的增加石灰改良盐渍土的动剪切模量不断衰减，存在动剪切模量转折点，经过转折点后动剪切模量衰减速度加快；阻尼比随剪应变的增加而增加。动荷载频率及围压增加，石灰改良盐渍土的动剪切模量增加，阻尼比降低。

（2）温度降低，石灰改良盐渍土动剪切模量转折点不断提高，阻尼比下降。提出温度修正系数，对不同温度下动剪切模量和阻尼比进行修正，并对温度修正系数进行曲线拟合，基于此提出温度修正系数公式，该系数在-6℃存在转折点，转折点后低温影响逐渐减弱。

（3）冻融1次后，动剪切模量转折点大幅降低，冻融3次后，动剪切模量转折点进一步降低并趋于稳定，随着冻融循环次数增加阻尼比小幅上升。提出冻融修正系数，对不同冻融循环次数下动剪切模量和阻尼比进行修正，并对冻融修正系数进行曲线拟合，拟合曲线在3次冻融循环处存在转折点，冻融循环的劣化作用存在极限，转折点后影响变小直至忽略不计。提出冻融循环修正系数，基于未冻融动力参数对不同冻融次数下动力参数进行预测。

图 1 MPM求解算法

Figure 1. Discrete schematic diagram of material point method

下载: 全尺寸图片幻灯片

图 2 锚板上拔数值模型（xoz平面）

Figure 2. Numerical model for uplift of anchor plate (in xoz plane)

下载: 全尺寸图片幻灯片

图 3 锚板破坏模式

Figure 3. Failure modes of anchor plate

下载: 全尺寸图片幻灯片

图 4 锚板上拔承载力系数–埋深比关系曲线

Figure 4. Curves of uplift factor-embedment depth ratio of anchor plates

下载: 全尺寸图片幻灯片

图 5 xoz平面不同埋深比条件下等效塑性应变云图(d=100 mm)

Figure 5. Contours of equivalent plastic strain under different embedment depth ratios in xoz plane

下载: 全尺寸图片幻灯片

图 6 上拔力–位移曲线

Figure 6. Uplift force-displacement curves

下载: 全尺寸图片幻灯片

图 7 三维等效塑性应变云图(d=50 mm)

Figure 7. Contours of three-dimensional equivalent plastic strain

下载: 全尺寸图片幻灯片

图 8 切片示意图(d=200 mm)

Figure 8. Schematic diagram of slice

下载: 全尺寸图片幻灯片

图 9 不同上拔阶段位移矢量场(d=200 mm，h/d=2)

Figure 9. Displacement vector fields at different uplift stages

下载: 全尺寸图片幻灯片

图 10 不同上拔阶段位移矢量场(d=200 mm，h/d=6)

Figure 10. Displacement vector fields at different uplift stages

下载: 全尺寸图片幻灯片

图 11 密砂中峰值位移时土体位移矢量图(d=50 m，h/d=6)

Figure 11. Vector diagram of soil displacement at peak displacement in dense sand

下载: 全尺寸图片幻灯片

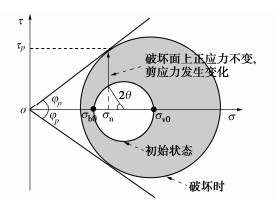
图 12 初始状态和破坏时的莫尔应力圆^[39]

Figure 12. Mohr's circles in situ and at failure

下载: 全尺寸图片幻灯片

表 1 砂土的物理力学参数

Table 1 Physical and mechanical parameters of soil

砂土	重度 $\gamma$ /(kN∙m^-3)	相对密实度D_r/%	内摩擦角φ/(°)	剪胀角ψ/(°)	变形模量E/(kN∙m^-2)	黏聚力c/kPa	泊松比 $\nu$
松砂	15.5	28.8	31.8	4	25000	0.5	0.2
密砂	17.5	76.2	—	—	30000	0.5	0.3

下载: 导出CSV

表 2 MC软化模型的计算参数

Table 2 Computational parameters of MC softening model

锚板直径d/mm	埋深比h/d	峰值内摩擦角φ_p/(°)	峰值剪胀角ψ_p/(°)
50	2	51.46	24.57
	4	49.79	22.49
	5	49.36	21.95
	6	48.82	21.28
	8	48.13	20.41
100	2	49.79	22.49
	4	48.13	20.41
	5	47.77	19.97
	6	47.16	19.20
	8	46.47	18.33
200	1	49.79	22.49
	2	48.13	20.41
	3	47.16	19.20
	4	46.47	18.33
	5	46.19	17.99
	6	45.49	17.12

下载: 导出CSV

表 3 计算参数

Table 3 Computational parameters

锚板直径 d/mm	上拔速度v/(mm·s^-1)	时间步长 Δt/s	总上拔位移u₀/mm
50	1	1.0	10
100	2	0.5	30
200	5	0.5	50

下载: 导出CSV

参考文献(39)

[1]	ADAMS J I, HAYES D C. The uplift capacity of shallow foundations[J]. Ontario Hydro Research Quarterly, 1967, 19: 1.
[2]	ILAMPARUTHI K, DICKIN E A, MUTHUKRISNAIAH K. Experimental investigation of the uplift behaviour of circular plate anchors embedded in sand[J]. Canadian Geotechnical Journal, 2002, 39(3): 648–664. doi: 10.1139/t02-005
[3]	胡伟, 刘顺凯, 邹贵华, 等. 竖向条形锚定板水平拉拔极限承载力统一理论解研究[J]. 岩土工程学报, 2018, 40(2): 296–304. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802012.htm HU Wei, LIU Shun-kai, ZOU Gui-hua, et al. Unified theoretical solution for ultimate bearing capacity of vertical strip anchor[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 296–304. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802012.htm
[4]	黄茂松, 余生兵. 基于块体集上限法的砂土中条形锚板抗拔承载力分析[J]. 岩土工程学报, 2013, 35(2): 201–207. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201302003.htm HUANG Mao-song, YU Sheng-bing. Pull-out capacity of strip anchor plate in sand based on block set mechanism[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 201–207. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201302003.htm
[5]	郝冬雪, 符胜男, 陈榕, 等. 砂土中锚板拉拔模型试验及其抗拔力计算[J]. 岩土工程学报, 2015, 37(11): 2101–2106. doi: 10.11779/CJGE201511023 HAO Dong-xue, FU Sheng-nan, CHEN Rong, et al. Experimental investigation of uplift behavior of anchors and estimation of uplift capacity in sands[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(11): 2101–2106. (in Chinese) doi: 10.11779/CJGE201511023
[6]	SAKAI T, TANAKA T. Experimental and numerical study of uplift behavior of shallow circular anchor in two-layered sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(4): 469–477. doi: 10.1061/(ASCE)1090-0241(2007)133:4(469)
[7]	PÉREZ Z A, SCHIAVON J A, DE HOLLANDA CAVALCANTI TSUHA C, et al. Numerical and experimental study on influence of installation effects on behaviour of helical anchors in very dense sand[J]. Canadian Geotechnical Journal, 2018, 55(8): 1067–1080. doi: 10.1139/cgj-2017-0137
[8]	KANITZ M, HAGER A, GRABE J, et al. Numerical and experimental analysis of the extraction mechanism of an anchor plate embedded in saturated sand[J]. Computers and Geotechnics, 2019, 111: 191–201. doi: 10.1016/j.compgeo.2019.03.014
[9]	EVANS T M, ZHANG N. Three-dimensional simulations of plate anchor pullout in granular materials[J]. International Journal of Geomechanics, ASCE, 2019, 19(4): 04019004. doi: 10.1061/(ASCE)GM.1943-5622.0001367
[10]	LIANG W J, ZHAO J D, SOGA K. Multiscale modeling of anchor pull-out in sand[M]//Challenges and Innovations in Geomechanics. Cham: Springer International Publishing, 2021: 787–793.
[11]	ZHANG X, CHEN Z, LIU Y. The material point method[M]// The Material Point Method. Amsterdam: Elsevier, 2017: 37–101.
[12]	FERN J, ROHE A, SOGA K, et al. The material point method for geotechnical engineering: a practical guide[M]// The Material Point Method for Geotechnical Engineering. Boca Raton: CRC Press, 2019: 3–22.
[13]	刘春, 乐天呈, 施斌, 等. 颗粒离散元法工程应用的三大问题探讨[J]. 岩石力学与工程学报, 2020, 39(6): 1142–1152. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202006006.htm LIU Chun, LE Tian-cheng, SHI Bin, et al. Discussion on three major problems of engineering application of the particle discrete element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(6): 1142–1152. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202006006.htm
[14]	SULSKY D, CHEN Z, SCHREYER H L. A particle method for history-dependent materials[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 118(1/2): 179–196.
[15]	SULSKY D, ZHOU S J, SCHREYER H L. Application of a particle-in-cell method to solid mechanics[J]. Computer Physics Communications, 1995, 87(1/2): 236–252.
[16]	BEUTH L, BENZ T, VERMEER P A. Large deformation analysis using a quasi-static material point method[J]. Journal of Theoretical and Applied Mechanics, 2008, 38(1/2): 45–60.
[17]	史卜涛, 张云, 张巍. 边坡稳定性分析的物质点强度折减法[J]. 岩土工程学报, 2015, 38(9): 1678–1684. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201609018.htm SHI Bo-tao, ZHANG Yun, ZHANG Wei. Strength reduction material point method for slope stability[J]. Chinese Journal of Geotechnical Engineering, 2015, 38(9): 1678–1648. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201609018.htm
[18]	孙玉进, 宋二祥. "12·20"深圳滑坡动态模拟[J]. 岩土工程学报, 2018, 40(3): 441–448. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201803009.htm SUN Yu-jin, SONG Er-xiang. Dynamic simulation of "12·20" Shenzhen landslide[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 441–448. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201803009.htm
[19]	张春新, 朱鸿鹄, 李豪杰, 等. 支护压力控制下隧道周围砂土变形破坏物质点法模拟[J]. 浙江大学学报(工学版), 2021, 55(7): 1317–1326. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202107011.htm ZHANG Chun-xin, ZHU Hong-hu, LI Hao-jie, et al. Material point method simulations of sand deformation and failure around tunnel controlled by support pressure[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(7): 1317–1326. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202107011.htm
[20]	张芮瑜, 孙玉进, 宋二祥. 强夯的物质点法模拟及其能量转化规律分析[J]. 岩土工程学报, 2019, 41(7): 1208–1216. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201907005.htm ZHANG Rui-yu, SUN Yu-jin, SONG Er-xiang. Simulation of dynamic compaction using material point method and analysis of its energy conversion law[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1208–1216. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201907005.htm
[21]	张春新, 朱鸿鹄, 周谷宇, 等. 落球检测技术的三维物质点法模拟研究[J]. 防灾减灾工程学报, 2021, 41(2): 311–320. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202102014.htm ZHANG Chun-xin, ZHU Hong-hu, ZHOU Gu-yu, et al. Simulation of falling ball test using three-dimensional material point method[J]. Journal of Disaster Prevention and Mitigation Engineering, 2021, 41(2): 311–320. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202102014.htm
[22]	COETZEE C J, VERMEER P A, BASSON A H. The modelling of anchors using the material point method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2005, 29(9): 879–895. doi: 10.1002/nag.439
[23]	CECCATO F, BISSON A, COLA S. Large displacement numerical study of 3D plate anchors[J]. European Journal of Environmental and Civil Engineering, 2020, 24(4): 520–538. doi: 10.1080/19648189.2017.1408498
[24]	陈榕, 符胜男, 郝冬雪, 等. 密砂中圆形锚上拔承载力尺寸效应分析[J]. 岩土工程学报, 2019, 41(1): 78–85. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201901012.htm CHEN Rong, FU Sheng-nan, HAO Dong-xue, et al. Scale effects of uplift capacity of circular anchors in dense sand[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 78–85. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201901012.htm
[25]	FERN E J, DE LANGE D A, ZWANENBURG C, et al. Experimental and numerical investigations of dyke failures involving soft materials[J]. Engineering Geology, 2017, 219: 130–139. doi: 10.1016/j.enggeo.2016.07.006
[26]	FERN E J, SOGA K. The role of constitutive models in MPM simulations of granular column collapses[J]. Acta Geotechnica, 2016, 11 (3): 659–678. doi: 10.1007/s11440-016-0436-x
[27]	蔡正银. 砂土的渐进破坏及其数值模拟[J]. 岩土力学, 2008, 29(3): 580–585. doi: 10.3969/j.issn.1000-7598.2008.03.002 CAI Zheng-yin. Progressive failure of sand and its numerical simulation[J]. Rock and Soil Mechanics, 2008, 29(3): 580–585. (in Chinese) doi: 10.3969/j.issn.1000-7598.2008.03.002
[28]	BOLTON M D. The strength and dilatancy of sands[J]. Géotechnique, 1986, 36(1): 65–78. doi: 10.1680/geot.1986.36.1.65
[29]	朱泳, 朱鸿鹄, 李飞, 等. 砂土中水平锚板抗拔特性试验研究[J]. 中南大学学报(自然科学版), 2018, 49(7): 1768–1774. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201807025.htm ZHU Yong, ZHU Hong-hu, LI Fei, et al. Experimental study on uplift behavior of anchor plate in sand[J]. Journal of Central South University (Science and Technology), 2018, 49(7): 1768–1774. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201807025.htm
[30]	张昕, 乐金朝, 刘明亮, 等. 砂土中锚板的抗拔机理与承载力计算模型研究[J]. 岩土工程学报, 2012, 34(9): 1734–1739. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201209032.htm ZHANG Xin, YUE Jin-chao, LIU Ming-liang, et al. Uplifting behavior and bearing capacity of plate anchors in sand[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9): 1734–1739. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201209032.htm
[31]	郝冬雪, 岳冲, 陈榕, 等. 常压至高压下中砂剪切特性及应力–剪胀关系[J]. 岩土工程学报, 2020, 42(4): 765–772. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004027.htm HAO Dong-xue, YUE Chong, CHEN Rong, et al. Shear characteristics and stress-dilation relation of medium sand under normal to high pressures[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(4): 765–772. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004027.htm
[32]	SAEEDY H S. Stability of circular vertical earth anchors[J]. Canadian Geotechnical Journal, 1987, 24(3): 452–456. doi: 10.1139/t87-056
[33]	MURRAY E J, GEDDES J D. Uplift of anchor plates in sand[J]. Journal of Geotechnical Engineering, 1987, 113(3): 202–215. doi: 10.1061/(ASCE)0733-9410(1987)113:3(202)
[34]	LIU J Y, LIU M L, ZHU Z D. Sand deformation around an uplift plate anchor[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(6): 728–737. doi: 10.1061/(ASCE)GT.1943-5606.0000633
[35]	桂美兵. 砂土中锚板抗拔承载力室内试验研究[D]. 合肥: 合肥工业大学, 2020. GUI Mei-bing. Pullout Capacity of Plate Anchor in Sand by Laboratory Test[D]. Hefei: Hefei University of Technology, 2020. (in Chinese)
[36]	SAKAI T, TANAKA T. Scale effect of a shallow circular anchor in dense sand[J]. Soils and Foundations, 1998, 38(2): 93–99. doi: 10.3208/sandf.38.2_93
[37]	史旦达, 毛逸瑶, 杨勇, 等. 基于DIC技术的砂土中圆形锚板上拔土体变形特性试验研究[J]. 岩土力学, 2020, 41(10): 3201–3213. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202010005.htm SHI Dan-da, MAO Yi-yao, YANG Yong, et al. Experimental study on the deformation characteristics of soils around uplift circular plate anchors using digital image correlation technology[J]. Rock and Soil Mechanics, 2020, 41(10): 3201–3213. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202010005.htm
[38]	倪钰菲, 乔仲发, 朱泳, 等. 基于粒子图像测速的锚板抗拔破坏机理试验研究[J]. 土木与环境工程学报(中英文), 2020, 42(1): 24–30. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN202001004.htm NI Yu-fei, QIAO Zhong-fa, ZHU Yong, et al. Experimental study on uplift failure of anchor plate based on PIV technology[J]. Journal of Civil and Environmental Engineering, 2020, 42(1): 24–30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN202001004.htm
[39]	WHITE D J, CHEUK C Y, BOLTON M D. The uplift resistance of pipes and plate anchors buried in sand[J]. Géotechnique, 2008, 58(10): 771–779. doi: 10.1680/geot.2008.3692

施引文献(10)

期刊类型引用(8)

1.	王炜，窦锦钟，袁青云，韩磊，孙旻. 抽水蓄能电站绿色施工技术. 施工技术(中英文). 2024(18): 129-133+153 . 百度学术
2.	张昕阳，申玉生，常铭宇，王浩鱇，潘笑海，王岩岩. 基于GA-BP神经网络的隧道围岩相似材料配合比设计. 现代隧道技术. 2024(06): 82-91 . 百度学术
3.	廖光明. 胶凝砂砾石坝抗滑稳定可靠度分析方法研究. 湖南水利水电. 2023(02): 22-25 . 百度学术
4.	丁泽霖，王肖楠，张宏洋，王婧，包闯. 复杂地基重力坝与胶凝砂砾石坝变形破坏对比分析. 工程科学与技术. 2023(04): 197-206 . 百度学术
5.	杨锐婷，万露. 折线形胶凝砂砾石坝三维静力有限元分析. 吉林水利. 2023(07): 14-20 . 百度学术
6.	丁泽霖，徐良杰，王肖楠. 基于多元优化的百米级胶凝砂砾石坝设计方法. 水力发电学报. 2023(12): 119-131 . 百度学术
7.	杨玉坚，刘艳华，陈雪冬. 胶凝砂砾石坝导流设计方法研究. 水利建设与管理. 2023(S1): 35-39 . 百度学术
8.	刘欢. 基于AutoBANK的流固耦合场沙田水库坝体渗流变形特征研究. 水利科学与寒区工程. 2022(08): 26-30 . 百度学术