Analytical solution for longitudinal equivalent bending stiffness of quasi-rectangular shield tunnels
-
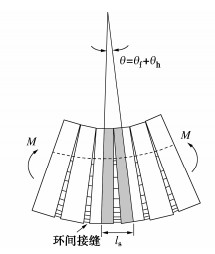
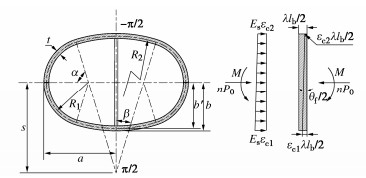
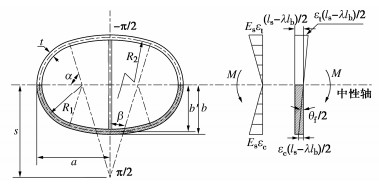
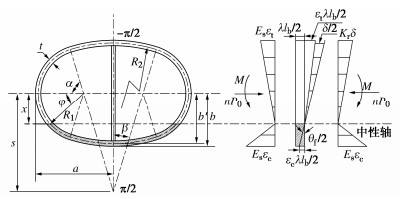
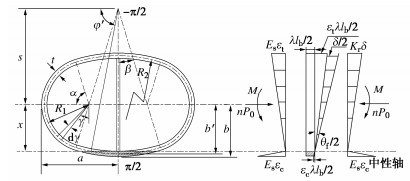
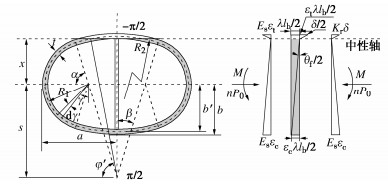
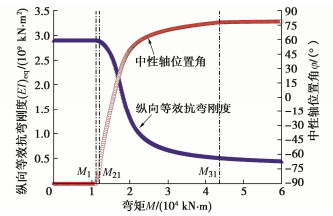
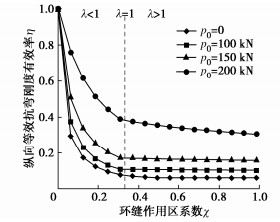
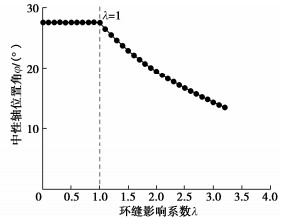
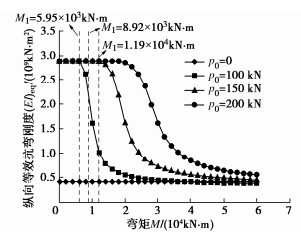
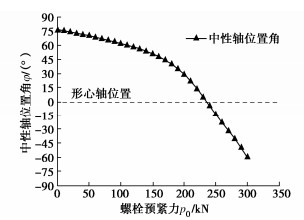
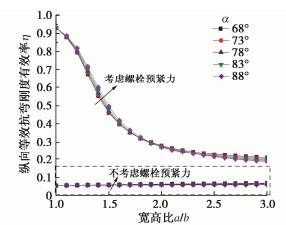
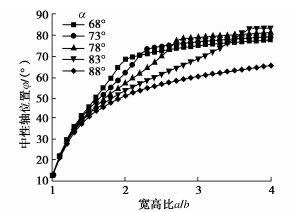
摘要: 结合类矩形盾构隧道截面特点,分别对中性轴位于截面上部边缘(环缝完全闭合)、截面上拱部、截面腰部和截面下拱部4种情况进行分析,并进一步考虑螺栓预紧力和环缝影响范围,推导得到类矩形盾构隧道的纵向等效抗弯刚度解析解,并对影响纵向等效刚度的相关因素进行探究。研究表明:当施加弯矩小于环缝启动弯矩时,环缝全部闭合,等效纵向抗弯刚度有效率为1,中性轴位于截面上部外缘;随着弯矩进一步增加,环缝逐渐张开,同时中性轴位置逐步下移,等效纵向抗弯刚度减小;纵向等效抗弯刚度有效率随环缝作用区系数增大呈现先迅速下降而后缓慢减小的趋势;螺栓预紧力越大,纵向等效刚度越大,中性轴位置随之上移;随宽高比增大,等效纵向抗弯刚度有效率逐渐下降,中性轴位置随之下移,并在中性轴位置角与小圆弧圆心角相等时出现转折点。Abstract: According to the sectional characteristics of quasi-rectangular shield tunnels, the neutral axes located at four different positions, the upper section edge (the ring joint is completely closed), the section vault, the section waist and the section invert, are analyzed, respectively. The analytical solution for the equivalent longitudinal bending stiffness of quasi-rectangular shield tunnels is then derived by further considering the pretightening force of bolts and the influence range of circumferential joints. The relative influencing factors on the longitudinal equivalent stiffness are also investigated. It is shown that when the applied bending moment is smaller than the activating one, the circumferential joint is completely closed, the effective efficiency of equivalent bending stiffness is 1, and the neutral axis is located at the upper edge of the section. By further increasing the applied bending moment, the circumferential joint starts to partially separate. Simultaneously, the position of the neutral axis moves down gradually. The equivalent longitudinal bending stiffness decreases with the increase of the applied bending moment. The effective efficiency of the equivalent longitudinal bending stiffness decreases first rapidly and then slowly with the increase of the coefficient of circumferential seam action zone. The greater the pretightening force of bolts is, the larger the equivalent longitudinal bending stiffness is. Subsequently, the position of the neutral axis moves up. With the increase of width-height ratio, the effective efficiency of the equivalent bending stiffness decreases gradually, the position of the neutral axis moves down subsequently, and a turning point appears when the position angle of the neutral axis is equal to the center angle of small arc.
-
0. 引言
管棚超前预支护技术能在一定范围内较大幅度提高天然土体强度、刚度,有效减小地表沉降、拱顶沉降,确保隧道掘进支护安全,且因具有施工简便、经济、支护距离长和安全效益高的特点而成为经常采用的超前预支护方法。
目前国内外学者关于管棚预支护技术的作用机理和加固效果开展了大量研究。Hisatake等[1]、Juneja等[2]通过离心机模型试验,考虑了开挖效果的影响,研究了管棚支护的作用效果。郭璇等[3]采用设计正交模型试验的方法,研究了管棚预支护的作用效果以及管棚对土压力分布的影响。周顺华等[4]在原位观测和室内模型离心模型试验的基础上,提出了管棚作用的棚架原理。董新平[5]则基于棚架体系建立了管棚的空间分析模型,研究了管棚支护作用的主要特征。Chungsik等[6]、Ali等[7]通过建立三维数值模型研究了管棚的受力和变形特征以及预支护效果。在理论分析方面,由于基于弹性地基梁理论的管棚分析模型具有简单实用的特点,故而具有很高的进一步研究完善的价值。李忠凯[8]通过建立基于Winkler地基模型的管棚分析模型,推导出一个开挖循环过程中管棚内力和变形的计算表达式。郑俊杰等[9]考虑了开挖对基床系数的影响,提出了变基床系数下管棚的地基梁模型。丁祖德等[10]则对弹性地基梁模型中基床系数的取值展开详细研究。王炳智等[11]通过改进弹性地基约束形式,采用Pasternak弹性地基理论建立管棚的分析模型并进行了求解。王道远等[12]通过对比两个地基模型的计算结果与现场试验值的比较,得到基于Pasternak弹性地基理论的管棚模型更具合理性,并通过讨论地层反力系数以及管棚直径对管棚作用效果的影响,得出通过调整注浆改善地层反力系数或直径的方法来控制管棚变形效果甚微的结论。武松等[13]根据弹性理论的刚度等效法,将管棚的一维弹性地基梁模型拓展至二维弹性地基各向异性板模型,并采用有限元法对模型进行了求解。
综上所述,针对基于弹性地基梁理论的管棚分析模型的研究已较为成熟,但在模型的建立过程中,对荷载的分布范围和管棚约束形式的认识上还存在矛盾,并且通过对模型的求解,并没有得到关于管棚设计和施工参数对管棚支护效果影响的一般性结论。预支护区段开挖支护完成后管棚全长范围内力和变形的最终分布并不明确。本文结合管棚超前预支护技术在实际运用过程中的问题以及国内外学者对管棚预支护技术研究的基础上,考虑掌子面失稳段对管棚约束的弱化以及隧道开挖支护动态施工过程,通过建立基于Pasternak弹性地基梁理论的管棚分析模型,采用理论推导的方法研究管棚预支护技术的支护效果以及受力特点,并系统地研究各设计施工参数对管棚力学响应的影响,从而为管棚的设计施工提供参考和借鉴。
1. 管棚分析模型的建立
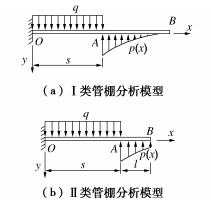
根据管棚作用下隧道开挖过程的施工经验以及管棚既有设计方法,可采用Euler-Bernoulli梁来对管棚的受力和变形进行分析计算。根据管棚的受力特点,可将管棚沿纵向分为初期支护段、开挖段和未开挖段3部分来进行分析(见图 1)。位于洞口的导向墙由于具有独立的基础和仅承受管棚作用的特点,可认为导向墙对管棚的约束形式为固定端约束,且无初始位移。在隧道开挖过程中,开挖段在围岩压力的作用下将力传递给导向墙或初期支护以及掌子面前方围岩,管棚发生变形。将该开挖段支护后,管棚则以该变形状态固结在初期支护中,初期支护前端对管棚的约束可认为具有初始位移和初始转角的固定端约束,而此处管棚的变形值即为下个循环开挖分析时管棚起固定端处的初始变形值。在掌子面前方,可认为由于隧道的开挖,掌子面在地应力作用下发生失稳,则该段围岩将无法承受管棚变形引起的附加应力,则可认为掌子面失稳段与开挖段具有相同的性质。失稳段前方围岩承受因管棚变形而产生的附加力,该段管棚受围岩的弹性地基约束。
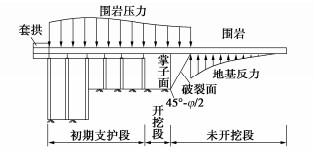
在单个循环进尺的分析中,以初期支护前端作为分析模型的起点,为具有初始竖向位移ω0和初始转角θ0的固定端。管棚承受开挖段及掌子面失稳段上方的围岩压力。根据莫尔–库仑强度准则,可假设掌子面沿开挖方向失稳的破裂面与铅垂线的夹角为45° −φ/2,若单个循环开挖进尺长度为a,则围岩压力作用范围为s=a+Htan(45∘−φ/2),其中H为上台阶高度。由于一个循环开挖进尺长度较短,可认为作用于管棚上的围岩压力值在该分析段保持不变。而围岩压力在纵向方向上的连续变化可离散为每个开挖区段上的常围岩压力。破裂面前方围岩以弹性地基约束形式作用于管棚,从而建立单个循环进尺的管棚分析模型(见图 2)。在管棚超前支护作用下隧道的循环开挖,其力学行为等价于单个循环进尺的管棚分析模型的不断移动,通过迭代计算可得到管棚全长范围最终的内力和变形分布。
通过对管棚受力过程的分析,针对管棚的分析模型提出以下假设:①导向墙或初期支护对管棚的约束假设为固定端约束;②导向墙处管棚无初始挠度和转角;③假设掌子面前方失稳段围岩对管棚不具有约束作用;④掌子面前方岩体对管棚的约束反力采用Pasternak弹性地基理论来确定。
围岩对管棚的弹性地基约束根据管棚长度可分为两种类型。类型Ⅰ,埋入围岩中的管棚长度足够长,该条件下可认为管棚B端的边界条件为:当x→∞时,ω(x)=0,θ(x)=0,分析图示如图 2(a)所示。类型Ⅱ,以类型Ⅰ为基本分析模型,随着在管棚预支护范围内开挖的不断推进,在对预支护段的最后一个循环进尺进行分析时,B端将发生变形。此时B端的边界条件为:当x=s+l时,M(x)=0,Q(x)=0,其中l为搭接长度,分析如图 2(b)所示。
管棚作为松散破碎地层中开挖隧道所采用的预支护技术,其预支护地层往往是破碎的散体介质,因此在进行管棚结构的分析计算时,采用松散围岩压力计算方法确定作用于管棚结构上的荷载比较符合实际情况。本模型浅埋隧道围岩压力的计算采用全土柱理论,深埋隧道围岩压力的计算采用普氏理论,则围岩压力可表示为统一的表达式:
q∗=γ⋅h。 (1) 式中γ为围岩重度(kN/m3);h为上覆松动围岩的高度(m),浅埋隧道为取隧道埋深,深埋隧道取压力拱高度。
Pasternak弹性地基模型是在Winkler弹性地基模型的基础上假定弹簧之间存在剪切作用,引入地基剪切模量Gp,则弹性地基作用于梁上的约束反力为
p(x)=kb∗ω(x)−Gpb∗d2ω(x)dx2。 (2) 式中k为地基基床系数(kN/m3);ω(x)为x点处梁的挠度(m);Gp为地基剪切模量(kN/m);b∗为地基剪切层的等效宽度(m),满足b∗=b[1+√Gp/k/b],b为管棚钢管的管径。Pasternak弹性地基模型相比Winkler地基模型通过引入地基剪切模量,弥补了Winkler模型地基不连续的缺陷,因此更符合实际情况,并且相比弹性半空间模型,Pasternak模型大大降低了计算复杂度。
2. 管棚分析模型的求解
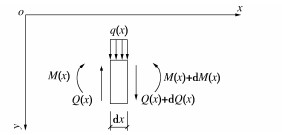
分析Euler-Bernoulli梁在受外荷载作用发生变形时,在梁上任选微段作为分析单元,其中,剪力、弯矩及荷载的正方向均如图 3所示。
根据平衡条件可得
dQ(x)dx=−q(x), (3) dM(x)dx=Q(x)。 (4) 再根据梁的挠曲线近似微分方程:
EIdω2(x)dx2=−M(x)。 (5) 将式(4),(5)代入式(3),即可得到分布荷载作用下,梁的变形控制微分方程为
EId4ω(x)dx4=q(x)。 (6) 单个循环进尺的管棚分析模型如图 2所示,根据荷载和约束的分布形式,可分段建立管棚的控制微分方程并求解,得到OA段控制微分方程:
EId4ω(x)dx4=q, (7) 式中,q=jq∗,j为管棚环向间距(m),即作用于单根梁上围岩压力的宽度。其通解为
ω1(x)=q24EIx4+B1x3+B2x2+B3x+B4。 (8) 根据式(5)~(7)表示的梁的弯矩、剪力和荷载与梁挠度之间的微分关系,将挠度表达式进行求导运算,即可得到管棚转角、弯矩和剪力的分段表达式。其中OA段转角、弯矩和剪力的解析表达式分别为
θ1(x)=q6EIx3+3B1x2+2B2x+B3, (9) M1(x)=−EI(q2EIx2+6B1x+2B2), (10) Q1(x)=−EI(qEIx+6B1)。 (11) 根据AB段的荷载分布形式,建立控制微分方程:
EId4ω(x)dx4−Gpb∗d2ω(x)dx2+kb∗ω(x)=0, (12) 令λ4 = kb∗4EI,α=√1+Gpλ2k,β=√1−Gpλ2k,求得其通解为
ω2(x)=e−αλx(B5cosβλx+B6sinβλx)+eαλx(B7cosβλx+B8sinβλx)。 (13) 同理求得AB段转角、弯矩和剪力的解析表达式分别为
θ2(x)=−B5e−αλx(βλsinβλx+αλcosβλx)+B6e−αλx(βλcosβλx−αλsinβλx)+B7eαλx(αλcosβλx−βλsinβλx)+B8eαλx(βλcosβλx+αλsinβλx), (14) M2(x)=−EI{B5e−αλx[(α2−β2)λ2cosβλx+2αβλ2sinβλx]+B6e−αλx[(α2−β2)λ2sinβλx−2αβλ2cosβλx]+B7eαλx[(α2−β2)λ2cosβλx−2αβλ2sinβλx]+B8eαλx[(α2−β2)λ2sinβλx+2αβλ2cosβλx]}, (15) Q2(x)=−EI{B5e−αλx[(3αβ2−α3)λ3cosβλx+(β3−3α2β)λ3⋅sinβλx]+B6e−αλx[(3αβ2−α3)λ3sinβλx−(β3−3α2β)λ3⋅cosβλx]+B7eαλx[(α3−3αβ2)λ3cosβλx+(β3−3α2β)λ3⋅sinβλx]+B8eαλx[(α3−3αβ2)λ3sinβλx+(3α2β−β3)λ3⋅cosβλx]}, (16) 式中,B1,B2,B3,B4,B5,B6,B7,B8均为待求积分常数。
2.1 Ⅰ类管棚分析模型的求解
类型Ⅰ的模型示意图如图 2(a)所示,对于AB段梁,由于B端满足ω2(x)|x→∞=0,θ2(x)|x→∞=0的边界条件,则代入式(13)可求得B7 = B8 = 0。由边界条件ω1(x)|x=0=ω0,θ1(x)|x=0=θ0,ω1(x)|x=s=ω2(x)|x=s,θ1(x)|x=s=θ2(x)|x=s,M1(x)|x=s=M2(x)|x=s,Q1(x)|x=s= Q2(x)|x=s,得方程组:
[000100001000s3s2s1φ35φ363s22s10φ45φ466s200φ55φ566000φ65φ57][B1B2B3B4B5B6]=[ω0θ0ψ3ψ4ψ5ψ6], (17) 式中,φ35=−e−αλscosβλs,φ36=−e−αλssinβλs,φ45= e−αλs(βλsinβλs+αλcosβλs),ϕ46=−e−αλs(βλcosβλs−αλsinβλs),ϕ55=−e−αλs[2αβλ2sinβλs+(α2−β2)λ2⋅ cosβλs],ϕ56=−e−αλs[−2αβλ2cosβλs+(α2−β2)λ2⋅ sinβλs],ϕ65=−e−αλs[(β3−3α2β)λ3sinβλs−(α3−3αβ2)⋅λ3cosβλs],ϕ66=e−αλs[(β3−3α2β)λ3cosβλs+(α3−3αβ2)λ3sinβλs],ψ3=−qs4/(24EI),ψ4=−qs3/(6EI),ψ5=−qs2/(2EI),ψ6=−qs/(EI)。
通过式(17)即可求得积分常数B1,B2,B3,B4,B5,B6,将其回代到挠度、转角、弯矩和剪力表达式中,即可求得满足类型Ⅰ分析模型边界条件下管棚的变形和受力分布。
2.2 Ⅱ类管棚分析模型的求解
类型Ⅱ的模型示意图如图 3(b)所示,由边界条件ω1(x)|x=0=ω0,θ1(x)|x=0=θ0,ω1(x)|x=s=ω2(x)|x=s,θ1(x)|x=s=θ2(x)|x=s,M1(x)|x=s=M2(x)|x=s,Q1(x)|x=s= Q2(x)|x=s,M2(x)|x=s+l=0,Q2(x)|x=s+l=0,得方程组:
[0001000000100000s3s2s1φ35φ36φ37φ383s22s10φ45φ46φ47φ486s200φ55φ56φ57φ586000φ65φ66φ67φ680000φ75φ76φ77φ780000φ85φ86φ87φ88][B1B2B3B4B5B6B7B8]=[ω0θ0ψ3ψ4ψ5ψ600], (18) 式中,φ35=−e−αλscosβλs,ϕ36=−e−αλssinβλs,ϕ37=−eαλscosβλs,ϕ38=−eαλssinβλs,ϕ45=e−αλs(βλsinβ⋅ λs+αλcosβλs),φ46=−e−αλs(βλcosβλs−αλsinβλs),φ47=−eαλs(αλcosβλs−βλsinβλs),φ48=−eαλs⋅(βλ cosβλs+αλsinβλs),ϕ55=−e−αλs[2αβλ2sinβλs+(α2−β2)λ2cosβλs],ϕ56=−e−αλs[−2αβλ2cosβλs+(α2−β2)λ2sinβλs],φ57=−eαλs[−2αβλ2sinβλs+(α2−β2)λ2 cosβλs],φ58=−eαλs[2αβλ2cosβλs+(α2−β2)λ2⋅sinβλs],ϕ65=−e−αλs[(β3−3α2β)λ3sinβλs−(α3−3αβ2)⋅λ3cosβλs],ϕ66=e−αλs[(β3−3α2β)λ3cosβλs+(α3−3αβ2)⋅λ3sinβλs],ϕ67=−eαλs[(α3−3αβ2)λ3cosβλs+(β3−3α2β)⋅λ3sinβλs],ϕ68=−eαλs[(α3−3αβ2)λ3sinβλs−(β3−3α2β)⋅λ3cosβλs],φ75=e−αλ(s+l)[2αβλ2sinβλ(s+l)+(α2−β2)λ2cosβλ(s+l)],φ76=e−αλ(s+l)[−2αβλ2cosβλ(s+ l)+(α2−β2)λ2sinβλ(s+l)],ϕ77=eαλ(s+l)[−2αβλ2⋅sinβλ(s+l)+(α2−β2)λ2cosβλ(s+l)],φ78=eαλ(s+l)⋅[2αβλ2cosβλ(s+l)+(α2−β2)λ2sinβλ(s+l)],ϕ85=e−αλ(s+l)⋅[(β3−3α2β)λ3sinβλ(s+l)−(α3−3αβ2)⋅λ3cosβλ(s+l)],ϕ86=e−αλ(s+l)[(3α2β−β3)λ3cosβλ(s+l)−(α3−3αβ2)⋅λ3sinβλ(s+l)],ϕ87=eαλ(s+l)[(β3−3α2β)⋅λ3sinβλ(s+l)+(α3−3αβ2)λ3cosβλ(s+l)],ϕ88=eαλ(s+l)⋅[(3α2β−β3)λ3cosβλ(s+l)+(α3−3αβ2)λ3sinβλ(s+l)],ψ3=−qs4/(24EI),ψ4=−qs3/(6EI),ψ5=−qs2/(2EI),ψ6=−qs/(EI)。
同理,通过式(18)即可求得积分常数B1,B2,B3,B4,B5,B6,B7,B8,将其回代到挠度、转角、弯矩和剪力表达式中,即可求得满足类型Ⅱ分析模型边界条件下管棚的变形和受力分布。
3. 案例计算
南宁至崇左铁路引入机场隧道起讫里程DK25+615—DK28+935,全长3320 m。其中DK25+940—DK27+234段长度1294 m为暗挖区间,埋深3.4~15.2 m,施工工法为CRD法(350 m)和三台阶临时仰拱(944 m);该隧道暗挖区间存在浅埋、开挖下穿既有道路、临近既有构(建)筑物。隧址内岩层上部为杂填土,下部为粉质黏土、泥质砂岩夹砂质泥岩、砾岩,弱风化至全风化,岩溶发育,层面起伏变化大。本隧道进口明暗分界处拱部设置一环35 m长Φ108 mm×6 mm管棚加强支护,管棚环向间距40 cm,具体参数见表 1。
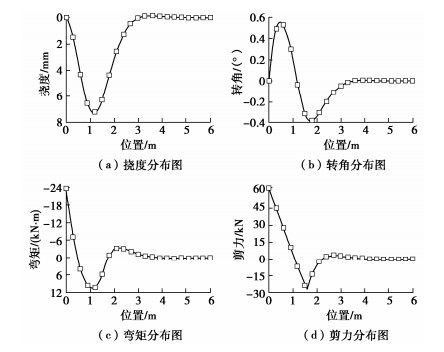
表 1 设计参数取值Table 1. Values of design parameters基床系数/(kN·m-3) 地基剪切模量/(kN·m-1) 隧道埋深/m 内摩擦角/(°) 围岩重度/(kN·m-3) 等效惯性矩/m4 等效弹性模量/kPa 开挖高度/m 管棚间距/m 进尺深度/m 30000 2800 6 45.6 24 6.68×10-6 7.89×107 2.4 0.4 0.6 本文以隧道进口明暗分界处拱顶单根钢管为研究对象,则该钢管的挠曲变形与隧道因开挖引起的拱顶沉降值相同。对管棚分析模型中的参数分别确定取值,并利用MATLAB编程进行应用分析。第一个循环进尺下管棚挠度、转角、弯矩和剪力在开挖方向上的分布曲线如图 4所示。
图 4表明,管棚挠度在OA段逐渐增大,且在A点处达到最大值7.2 mm。AB段挠度逐渐减小,当计算深度为4 m时,该循环开挖对该处管棚的变形无影响。随计算深度的加深,弯矩呈震荡形式趋近于零,其中最大值位于固定端处为-23.5 kN·m。剪力的分布同样随计算深度的增大而收敛于零,最大值同样位于固定端处,大小为62.6 kN。当计算深度达到4 m时,管棚的弯矩和剪力将趋近于零,由此可得一个循环开挖区段对管棚的影响范围长度为4 m。
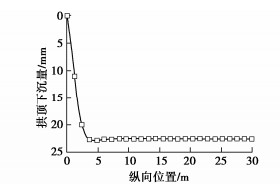
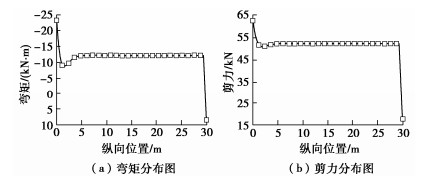
通过以上单个开挖区段的分析,得到管棚在该分析区段的变形和受力特征。该区段前0.6 m的变形与受力将随初期支护的完成而与初期支护固结在一起,0.6 m处的变形值将成为下一个分析区段的位移初值。通过迭代计算,可得到管棚预支护范围内30 m全部开挖支护完成后隧道拱顶下沉分布如图 5所示,管棚全长范围内内力的分布情况如图 6所示。
图 5表明,管棚的挠曲变形随掌子面的不断推进而逐渐增大。当拱顶沉降达到22.8 mm时,随掌子面的进一步推进,拱顶沉降将基本保持不变。
王道远等[12]通过现场试验得出,管棚的变形整体呈凹形分布,在开挖初期,管棚的变形速率较快。而图中管棚变形分布特征符合这一规律,且管棚变形的数量级基本一致,从而证明了该分析模型的合理性和实用性。
图 6表明,管棚的弯矩和剪力的最不利截面均发生在导向墙的约束处,其中弯矩最大值为23.5 kN·m,剪力最大值为62.6 kN。管棚全长范围内弯矩基本保持在12 kN·m,剪力基本保持在52 kN。
综上所述,利用该分析模型可以系统地对管棚的支护效果和受力特征进行预测。通过对算例的数值计算,得到管棚预结构的受力和变形分布特征,从而体现了管棚预支护体系的主要特征。
4. 参数分析
本节在前述理论研究的基础上,通过调整管棚的环向间距、管径、开挖进尺长度以及搭接长度的设计参数,研究各设计参数对管棚受力和变形的影响形式和程度,从而指导管棚的设计和施工。
4.1 环向间距对管棚受力和变形的影响分析
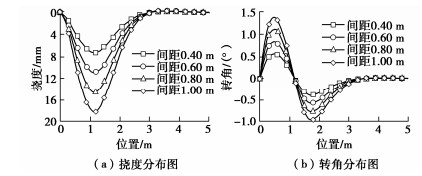
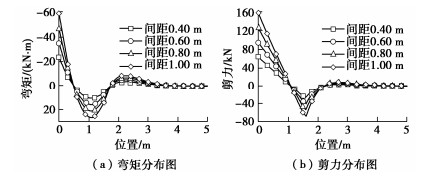
取其他参数不变,当管棚环向间距j为0.40,0.60,0.80,1.00 m时,分别计算并绘出管棚的变形分布曲线(见图 7)和内力分布曲线(见图 8),研究环向间距对管棚变形和受力的影响。
图 7表明,管棚环向间距的变化不改变其变形分布形式,最大挠度ωmax(mm)和最大转角θmax(°)发生的位置不变,其中最大挠度和最大转角均与环向间距之间满足线性增长关系,关系式分别为
ωmax=18.159j ,θmax=1.3863j 。} (19) 图 8表明,管棚环向间距同样不改变管棚的内力分布形式,最不利截面不随环向间距的变化而变化,管棚的最大弯矩Mmax(kN⋅m)和最大剪力Qmax(kN)均与环向间距之间满足线性增长关系,关系式分别为
Mmax=58.657j ,Qmax=156.61j 。} (20) 4.2 管径对管棚受力和变形的影响分析
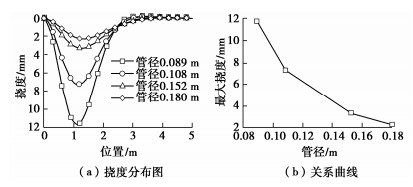
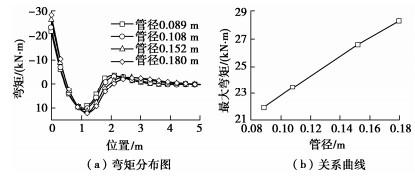
取其他参数不变,当管径b分别为0.089,0.108,0.152,0.180 m时,分别计算并绘制出管棚的挠度分布曲线(见图 9)和弯矩分布曲线(见图 10),研究管径对管棚变形和受力的影响。当管棚的管径发生变化时,管棚的等效截面惯性矩和等效弹性模量均发生变化,根据刚度等效法[14]求得不同管径下的等效截面惯性矩和等效弹性模量见表 2。
表 2 不同管径的截面计算参数Table 2. Cross section calculation parameters of different pipe diameters管径/m 等效惯性矩/(10-6 m4) 等效弹性模量/(107 kPa) 0.089 3.08 9.24 0.108 6.68 7.89 0.152 26.00 5.89 0.180 51.50 5.07 从图 9可以看出,管径越粗,管棚的挠曲变形越平缓,随着管径的增大,最大挠度ωmax逐渐减小,并且随着管径的不断增大对管棚挠曲变形的影响将越来越小。最大挠度ωmax与管径b(m)之间满足
ωmax=0.0397b−2.346。 (21) 从图 10可以看出,随着管径的增大,弯矩的危险截面位置不变,管棚所受的最大弯矩Mmax(kN·m)也随着增大。最大弯矩与管径之间满足
Mmax=−115.67b2+100.87b+13.917。 (22) 4.3 开挖进尺长度对管棚受力和变形的影响分析
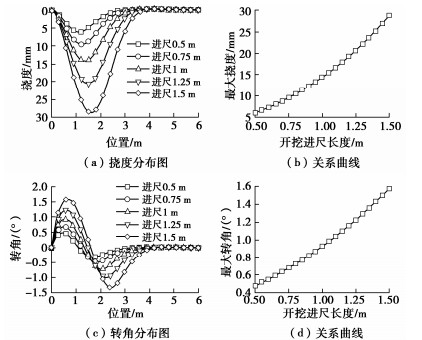
取其他参数不变,当开挖进尺长度a分别为0.5,0.75,1,1.25,1.5 m时,分别绘制出管棚变形分布曲线(图 11)和内力分布曲线(图 12),研究开挖进尺长度对管棚变形和受力的影响。
图 11表明,随着开挖进尺长度的增大,管棚最大变形位置不断前移,且最大值不断增大。通过开挖进尺长度与最大变形关系曲线图可得到,开挖进尺长度与最大挠度ωmax和最大转角θmax之间呈非线性增长关系,进尺越长,变形增长速度越快,关系式分别为
ωmax=9.6241a2+1.9131a+2.6503 ,θmax=0.2622a2+0.487a+0.1679 。} (23) 说明开挖进尺长度是控制管棚变形的关键施工技术指标。
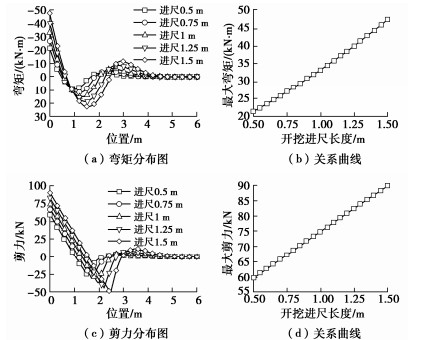
图 12表明,开挖进尺长度的增大同样会使管棚的内力分布前移,但最不利截面总位于固定端处。最大弯矩Mmax与开挖进尺长度之间满足非线性关系式:
Mmax=4.5114a2+17.093a+11.583, (24) 式中,开挖进尺长度a(m),Mmax最大弯矩(kN·m)。而最大剪力Qmax(kN)与开挖进尺长度之间满足线性关系式:
Qmax=30.841x+44.13。 (25) 4.4 搭接长度对管棚受力和变形的影响分析
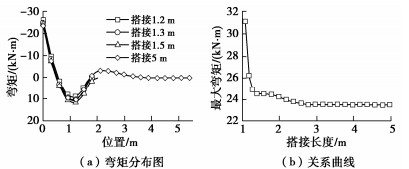
由类型Ⅱ分析模型可计算管棚搭接长度对管棚作用效果的影响,搭接长度D=Htan(45∘−φ/2)+l,分别取搭接长度为1.1,1.3,1.5,5 m,分别绘制出管棚挠度分布曲线以及搭接长度与最大挠度关系曲线(图 13)和弯矩分布曲线以及搭接长度与最大弯矩关系曲线(图 14),研究搭接长度对管棚变形和受力的影响。
图 13表明,随着搭接长度的增大,管棚发生最大挠度的位置和挠度分布形式基本不变。当搭接长度大于2.5 m时,最大挠度将趋近于7.3 mm而保持不变。
图 14表明,随着搭接长度的增大,管棚的最不利截面位置和弯矩的分布形式基本不变。当搭接长度大于2.5 m时,最大弯矩将趋近于23.5 kN·m而保持不变。综上所述,在该工程条件下,当管棚搭接长度大于2.5 m时,搭接长度的变化将对管棚的变形和受力基本没有影响。
5. 结论
(1)通过建立和求解基于Pasternak弹性地基理论的单个循环进尺下管棚分析模型可得管棚的受力和变形的分布特征。考虑隧道开挖支护动态施工过程,通过迭代计算可有效预测管棚预支护段开挖支护完成后管棚整体的受力和变形分布,且其理论值与已有文献实测结果具有相同的分布特征,从而证明了模型的合理性。
(2)管棚环向间距的变化不改变管棚内力和变形的分布形式,且最不利截面位置保持不变,管棚的受力和变形与环向间距之间呈线性增长关系,随环向间距的增大而增大。
(3)选用的管径越粗,管棚的挠曲变形越平缓,挠曲变形越小,并且随着管径的不断增大,管径对管棚挠曲变形的影响将越来越小。随着管径的增大,弯矩的危险截面位置不变,管棚的最大弯矩与管径之间呈非线性增长关系。
(4)随着开挖进尺长度的增大,管棚最大变形位置不断前移,最大变形值与开挖进尺长度之间呈非线性增长关系,开挖进尺越长,变形增长速度越快。说明开挖进尺长度是控制管棚变形的关键施工技术指标。开挖进尺长度越大,最大弯矩和最大剪力越大。
(5)管棚的最大内力及变形随搭接长度的增长而迅速趋于收敛。在本文案例工况下,当管棚搭接长度大于2.5 m时,搭接长度的变化将对管棚的变形和受力基本没有影响。
-
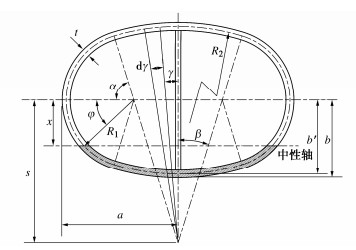
表 1 类矩形盾构隧道衬砌主要设计参数
Table 1 Design parameters for linings of quasi-rectangular shield tunnel
隧道宽度2a/m 隧道高度2b/m 半径R1/m 半径R2/m 偏移s/m 角α/(°) 角β/(°) 环宽ls/m 管片厚度t/m 弹性模量Es/MPa 11.50 6.937 2.975 15.225 11.98 78 12 1.2 0.45 3.45×104 表 2 类矩形隧道纵向接头主要参数
Table 2 Parameters for longitudinal joint of quasi-rectangular shield tunnel
纵向螺栓数量n/个 直径/mm 长度lb/mm 弹性模量Eb/MPa 抗拉刚度/(kN·m-1) 30 30 370 2.06×105 3.12×105 -
[1] 朱瑶宏, 朱雁飞, 黄德中, 等. 类矩形盾构法隧道关键技术研究与应用[J]. 隧道建设, 2017, 37(9): 1055–1062. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201709001.htm ZHU Yao-hong, ZHU Yan-fei, HUANG De-zhong, et al. Development and application of key technologies to quasi-rectangular shield tunneling[J]. Tunnel Construction, 2017, 37(9): 1055–1062. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201709001.htm
[2] 小泉淳, 村上博智, 西野健三. ツールドトネルの轴方向特性のモデルイヒにつぃて[C]// 土木学会论文集. 1988: 79–88. KOIZUMI A, MURAKAMI H, NISHINO K. A Model of the Directional Properties of Tool de Tonel[C]// Journal of the Japan Society of Civil Engineers, 1988: 79–88. (in Japanese)
[3] 志波由纪夫, 川岛一彦, 大日方尚己, 等. 应答变位法にょるツ—ルドトンネルの地震时断面力の算定法[C]// 土木学会论文集, 1989: 385–394. SHIWA Y, KAWASHIMA K, ODATEKA N, et al. A method for calculating the seismic cross-sectional force of a tunnel with a negative response method[C]// Journal of the Japan Society of Civil Engineers, 1989: 385–394. (in Japanese)
[4] 林永国. 地铁隧道纵向变形结构性能研究[D]. 上海: 同济大学, 2001. LIN Yong-guo. Study on the Performance of Longitudinal Deformation Structure of Metro Tunnel[D]. Shanghai: Tongji University, 2001. (in Chinese)
[5] 廖少明. 圆形隧道纵向剪切传递效应研究[D]. 上海: 同济大学, 2002. LIAO Shao-ming. Study on Longitudinal Shear Transfer Effect of Circular Tunnel[D]. Shanghai: Tongji University, 2002. (in Chinese)
[6] WU H N, SHEN S L, LIAO S M, et al. Longitudinal structural modelling of shield tunnels considering shearing dislocation between segmental rings[J]. Tunnelling and Underground Space Technology, 2015, 50: 317–323. doi: 10.1016/j.tust.2015.08.001
[7] 张文杰, 徐旭, 李向红, 等. 广义的盾构隧道纵向等效连续化模型研究[J]. 岩石力学与工程学报, 2009, 28(增刊2): 3938–3944. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2009S2098.htm ZHANG Wen-jie, XU Xu, LI Xiang-hong, et al. Research on generalized longitudinal equivalent continuous model of shield tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2): 3938–3944. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2009S2098.htm
[8] 叶飞, 何川, 朱合华, 等. 考虑横向性能的盾构隧道纵向等效刚度分析[J]. 岩土工程学报, 2011, 33(12): 1870–1876. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201112010.htm YE Fei, HE Chuan, ZHU He-hua, et al. Longitudinal equivalent rigidity analysis of shield tunnel considering transverse characteristics[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1870–1876. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201112010.htm
[9] 李翔宇, 刘国彬, 杨潇, 等. 基于修正纵向等效连续化模型的隧道变形受力研究[J]. 岩土工程学报, 2014, 36(4): 662–670. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201404012.htm LI Xiang-yu, LIU Guo-bin, YANG Xiao, et al. Deformation and stress of tunnel structures based on modified longitudinal equivalent continuous model[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 662–670. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201404012.htm
[10] 耿萍, 陈枰良, 张景, 等. 轴力和弯矩共同作用下盾构隧道纵向非线性等效抗弯刚度研究[J]. 岩石力学与工程学报, 2017, 36(10): 2522–2534. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201710021.htm GENG Ping, CHEN Ping-liang, ZHANG Jing, et al. Nonlinear longitudinal equivalent bending stiffness of shield tunnel under the combined effect of axial force and bending moment[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(10): 2522–2534. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201710021.htm
[11] 徐凌. 软土盾构隧道纵向沉降研究[D]. 上海: 同济大学, 2005. XU Ling. Study on Longitudinal Settlement of Soft Soil Shield Tunnel[D]. Shanghai: Tongji University, 2005. (in Chinese)
[12] 梁荣柱, 夏唐代, 胡军华, 等. 新建隧道近距离上穿对既有地铁隧道纵向变形影响分析[J]. 岩土力学, 2016, 37(增刊1): 391–399. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1051.htm LIANG Rong-zhu, XIA Tang-dai, HU Jun-hua, et al. Analysis of longitudinal displacement of existing metro tunnel due to construction of above-crossing new tunnel in close distance[J]. Rock and Soil Mechanics, 2016, 37(S1): 391–399. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1051.htm
[13] 许有俊, 陶连金, 文中坤, 等. 新建地铁隧道上穿既有隧道引起的结构隆起变形[J]. 中国铁道科学, 2014, 35(6): 48–54. doi: 10.3969/j.issn.1001-4632.2014.06.08 XU You-jun, TAO Lian-jin, WEN Zhong-kun, et al. Upheaval deformation induced by newly-built metro tunnel upcrossing existing tunnel[J]. China Railway Science, 2014, 35(6): 48–54. (in Chinese) doi: 10.3969/j.issn.1001-4632.2014.06.08
[14] LIANG R Z, XIA T D, HONG Y, et al. Effects of above-crossing tunnelling on the existing shield tunnels[J]. Tunnelling and Underground Space Technology, 2016, 58(9): 159–176.
[15] 康成, 叶超, 梁荣柱, 等. 基坑开挖诱发下卧盾构隧道纵向非线性变形研究[J]. 岩石力学与工程学报, 2020, 39(11): 2341–2350. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202011017.htm KANG Cheng, YE Chao, LIANG Rong-zhu, et al. Nonlinear longitudinal deformation of underlying shield tunnels induced by foundation excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(11): 2341–2350. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202011017.htm
[16] 张子新, 朱叶艇, 朱雁飞, 等. 大断面异形盾构衬砌结构纵向力学性能[J]. 同济大学学报(自然科学版), 2017, 45(5): 684–691. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201705010.htm ZHANG Zi-xin, ZHU Ye-ting, ZHU Yan-fei, et al. Study on the longitudinal mechanical behavior of large shield lining structure with a specialshaped cross-section[J]. Journal of Tongji University (Natural Science), 2017, 45(5): 684–691. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201705010.htm
[17] 黄亮, 梁荣柱, 吴小建, 等. 类矩形盾构隧道纵向抗弯刚度分析[J]. 岩土工程学报, 2019, 41(11): 2094–2102. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201911017.htm HUANG Liang, LIANG Rong-zhu, WU Xiao-jian, et al. Longitudinal bending stiffness of quasi-rectangular shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(11): 2094–2102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201911017.htm
[18] 鲁志鹏. 基于静态量测数据的盾构法地铁隧道建设和运营安全评价研究[D]. 上海: 同济大学, 2008. LU Zhi-peng. Study on the Safety Evaluation of Tunnel Construction and Operation Based on Static Measurement Data[D]. Shanghai: Tongji University, 2008. (in Chinese)
-
期刊类型引用(8)
1. 邹增富,唐世禄,廖云朋,代荣,谢昌志. 直墙拱型引水隧洞洞口段管棚预加固技术分析. 四川建筑. 2024(02): 132-134+138 .  百度学术
百度学术
2. 张小波,荣耀,张雕,孙洋. 考虑初支滞后性的软弱地层隧道进洞段管棚注浆加固效果研究. 公路. 2024(08): 425-433 .  百度学术
百度学术
3. 王晓东. 基于最大开挖进尺的管棚设计参数研究. 铁道建筑技术. 2023(03): 40-43 .  百度学术
百度学术
4. 张小波,张雕,姚池,杨建华,蒋水华,荣耀. 考虑微拱效应的隧道洞口段管棚合理间距确定方法及参数分析. 岩土力学. 2023(06): 1625-1635 .  百度学术
百度学术
5. 姬云鹏,房灵国,唐昊天,张兴丽,王祥金,白云天,李健,赵红华. 隧道开挖全过程管棚支护受力研究. 现代隧道技术. 2023(03): 123-138 .  百度学术
百度学术
6. 石钰锋,张涛,曹成威,阳军生,陈祥胜. 基于双参数地基的隧道预支护拱棚壳体力学模型. 工程科学与技术. 2023(04): 142-152 .  百度学术
百度学术
7. 李奎双,王峥,尹学鑫,程星源. 浅埋软弱地层中超大跨度地铁隧道管棚支护效果研究. 四川建筑. 2023(04): 133-137 .  百度学术
百度学术
8. 施英,罗春. 隧道管棚超前支护作用机理及其影响因素研究. 人民长江. 2022(11): 130-135 .  百度学术
百度学术
其他类型引用(12)



 下载:
下载: