地基承载力机理及新计算方法

宋二祥; 付浩; 李贤杰

doi:10.11779/CJGE202201002

地基承载力机理及新计算方法 English Version

清华大学土木工程系, 北京 100084

基金项目:

国家重点研发计划（“973”计划）课题 2014CB047003

国家自然科学基金项目 51778339

详细信息

作者简介:
宋二祥(1957—)，男，博士，教授，主要从事岩土力学及工程方面的教学及科研工作。E-mail: songex@tsinghua.edu.cn

中图分类号: TU470
计量
- 文章访问数: 441
- HTML全文浏览量: 62
- PDF下载量: 451
出版历程
- 收稿日期: 2021-06-23
- 网络出版日期: 2022-09-22
- 刊出日期: 2021-12-31

Mechanism and new calculation method for bearing capacity of foundations

Department of Civil Engineering, Tsinghua University, Beijing 100084, China

摘要

摘要: 地基承载力计算是土力学中的基本课题，但地基土自重对承载力的贡献一直未能较准确地予以计算，究其原因在于此部分的计算不是孤立的。为深入探讨地基承载力的机理及计算理论，首先，证明基础埋深相应超载及地基土重度对承载力的作用可分别转换为等效黏聚力及黏聚力随深度的增长率。随后，针对承受非偏心竖向荷载的条形基础下地基的整体剪切破坏，提出一种全新的地基极限承载力计算方法，特别是构造了一个可以综合考虑地基土强度、基础埋深超载及地基土重度影响的无量纲参数，进而给出统一考虑各有关因素的地基承载力计算公式，并对地基局部剪切破坏、非条形基础、倾斜荷载等复杂情况下利用本文公式进行地基承载力的计算给出建议。通过与精细数值方法计算比较，对所提出的计算方法进行了严格的检验，表明其正确性和高精度，同时也表明本文思路及所构造无量纲参数的合理性和正确性。此外，还与目前常用的太沙基解、Hansen解进行了比较讨论，表明所提出计算公式较现用公式有显著改进。
- 地基承载力 /
- 统一计算公式 /
- 太沙基解 /
- Hansen解
Abstract: The calculation of bearing capacity of foundations is a fundamental topic in soil mechanics. However, the contribution of the unit weight of the foundation soil to the bearing capacity cannot yet be satisfactorily calculated. The fundamental reason is that this part of bearing capacity is actually not independent, and consequently cannot be calculated separately. In order to study the mechanism of foundation bearing capacity and the relevant theory thoroughly, it is first revealed that the surcharge load corresponding to footing embedment and the unit weight of the foundation soil, multiplied by the soil strength parameter $\tan \varphi$ , can be treated respectively as the equivalent cohesion and the rate of cohesion increase along depth. Then a new method is developed for the general failure mode of strip footing under non-eccentric vertical loads. In this new method a non-dimensional parameter is defined to well reflect the influences of the soil strength and soil weight on the bearing capacity, and based on which a unified formula for the calculation of bearing capacity is established, in which the soil strength, the embedment depth of the footing and the soil weight are all considered as closely related elements. For the bearing capacity of foundation under other more complicated conditions, such as failure in local mode, different footing shapes, inclined loads etc., the available methods of treatment can be still applied in combination with the newly developed formula. Careful comparison with the refined numerical calculations proves the reliability and high accuracy of the proposed formula, and at the same time it proves the rationality and correctness of the whole idea as well as the constructed non-dimensional parameter. Besides, comparisons are also made with the formulas by Terzaghi and Hansen to show the significant improvement of the proposed method over the formers.
- bearing capacity of foundation /
- unified formula /
- Terzaghi formula /
- Hansen formula

HTML全文

0. 引言

浅基础地基承载力计算是土力学中的一个基本课题，几乎所有土力学教科书中均对有关理论和方法有专章予以介绍。业内不少人士得到的印象是，地基承载力的理论及计算方法已经难以再行改进，而实际并非如此。

目前，针对非偏心竖向荷载下条形基础广泛采用的地基承载力计算公式有3项：cN_c，qN_q和0.5 $\gamma$ BN_γ，分别对应于黏聚力c、埋深相应的基础周围超载q以及地基土重度 $\gamma$ 或基础宽度对承载力的贡献，N_c，N_q及N_γ是仅与土的摩擦角φ有关的承载力系数^[1-3]，对其他基础形状、倾斜荷载等情况，再对上述每一项乘以相应的修正系数^[2]。在不计地基土重度的情况下，前两个承载力系数N_c，N_q分别由Prandtl和Reissner给出，且在理论上是精确的^[1-3]，而当考虑地基土重度的影响时问题便复杂得多。

太沙基于1943年最早考虑地基土重度进行条形基础下地基承载力的计算^[1]，他认为此时基底与土之间存在的摩擦及黏着作用将在基底下方产生一个三角形弹性核，进而通过分析给出地基承载力的3项，其中的3个承载力系数仍然只是内摩擦角的函数，但前2个系数参考Prandtl和Reissner所给相应土压力的解给出了计算式，第3个系数N_γ只能给出数值解，所以太沙基解一般是以图表形式给出。因问题复杂，太沙基解的一个重要近似处理是，在求解第3项时采用了与前两项不同的破坏滑移面，这就决定了这解答是有误差的，且有些情况下误差可达30%（见本文第3节）。

因此，在太沙基之后很多研究者对地基承载力的计算进行研究，给出各不相同的承载力系数N_γ。较著名的解有Meyerhof给出的N_γ为(N_q-1)tan(1.4φ)^[3]；Vesic^[4]在Caquot和Kerisel工作基础上给出的2(N_q+ 1)tanφ；Hansen^[5]则给出1.8(N_q-1)tanφ，后又将系数由1.8改为1.5，而Verruijt则认为这系数取2.0在总体上更精确些^[6]。对前两个承载力系数多数研究者采用Prandtl和Reissner针对无刚性核情况下提出的解。由这些解相互之间的显著差异可见，地基承载力的计算还很值得研究。所以，直至目前仍有不少研究者讨论地基承载力第3项的承载力系数计算，Diaz-Segura^[7]曾比较了60篇文献给出的各不相同但均与上述类似的承载力系数N_γ，发现差异明显。

由上述分析可见，目前地基承载力不能准确计算的根本原因，是对极限荷载计算这一塑性力学问题采用了叠加计算，亦即对于地基承载力计算式中本非相互独立的三部分按相互独立进行计算。近年来一些研究者注意到这一点，采用不同的思路研究系数N_γ的计算，考虑多个参数对N_γ的影响。文献[8]较早进行了这方面的研究，文献[9]则在综述前人研究的基础上，采用数值滑移线法进行计算拟合给出N_γ的近似计算式。

本文摒弃叠加思路，统一考虑地基及基础的有关参数，力求给出综合考虑各参数影响的高精度计算公式。为此，首先深入分析地基承载力的内在机理，揭示了与埋深相应的超载q可以等效转换为黏聚力来考虑其对地基承载力的贡献，而地基土的重度可等效转换为随深度线性增大的黏聚力，进而利用本课题组此前针对饱和黏性土地基承载力的计算，考虑其不固结不排水强度随深度线性增大的情况所提出的计算方法^[10-11]。针对承受非偏心竖向荷载的条形基础下地基发生整体剪切破坏时的承载力问题，构建了一个将经典公式的三项统一为一个整体的计算公式，克服了以往计算公式的理论缺陷，显著改进了地基承载力的计算精度。

对于地基土相对较软或基础埋深相对较大情况下地基的局部剪切破坏，对于其他形状的基础、倾斜荷载等情况，也建议了利用本文公式进行计算的方法。

本文除给出地基承载力计算的较为完善的公式之外，重要的是深入阐释了地基承载的机理，提出一种全新的计算思路，这对有关研究同样有重要参考价值。

1. 地基土重度与地基承载力的内在联系

本节深入分析地基承载力的机理，揭示埋深相应超载q与地基土重度作用的实质。

首先，考察埋深相应的基础周围超载q的作用与黏聚力c的联系。实际上，由于Prandtl与Reissner给出的解是精确的，q与c的关系自然应含于他们所给计算式之中。由Reissner所给地基承载力系数N_q与Prandtl地基承载力系数N_c的关系有

$q{N_q} = q({N_c}\tan \varphi + 1) = q\tan \varphi {N_c} + q 。$

(1)

考察式（1）不难得出以下认识：q对承载力的贡献首先是使地基承载力提高一倍q值，进而在φ > 0的情况下又使地基承载力提高qtan φ N_c。这意味着qtanφ在承载力的计算中可以与同值的黏聚力等效，而超载q使地基承载力即便在φ=0时也会提高一倍q值。其力学机理按笔者的理解是，基础周围的地面超载与基底压力中等于q的部分共同构成满布于地基顶面的均布荷载，这均布荷载显然不会使地基破坏，而在φ > 0时，又进一步按黏聚力等同于qtanφ提高地基承载力。由于Prandtl和Reissner给出的承载力系数N_c和N_q在理论上是精确的，又按太沙基所给N_c和N_q的关系，同样可以得出式（1），所以上述推理的结论是肯定的，同时也回答了为什么N_q的下限为1。

在理解了q的上述本质作用之后，进一步深入分析则不难理解土体重度 $\gamma$ 的作用与黏聚力的等效作用。从基底往下任一深度z，其下土层所受到的满布压力在超载q之外又增加 $\gamma z$ ，按上段的论证可理解这相当于等效黏聚力增大 $\gamma z\tan \varphi$ ，这样 $\gamma \tan \varphi$ 则等同于黏聚力随深度的增大率。这一理解在地基承载力计算中的合理性和正确性，将由下面给出的计算对比进一步予以证实。

为验证土体重度 $\gamma$ 与黏聚力随深度增大率的等效性，这里采用基于极限分析上、下限定理的有限元极限分析这一精细数值方法^[12-13]进行如下两种计算对比：一计算中照常输入地基土强度指标c、φ及重度 $\gamma$ 进行地基承载力计算，而在另一计算中将土体重度 $\gamma$ 设为0，同时取地基土的黏聚力为c+ $\gamma z\tan \varphi$ ，亦即黏聚力从基底往下随深度的增长率为 $\gamma \tan \varphi$ 。所完成的大量计算表明，两套输入参数下的有限元极限分析结果完全相同。计算中分别按基底光滑和粗糙进行计算，也就是假定基底与其下土体间可以相对滑动和不可相互滑动来进行计算。为节省篇幅，表 1仅列出基底粗糙情况下部分计算给出的破坏滑移面深度及地基承载力值，可见两种参数下的计算结果几乎没有差异，这就又从数值计算方面证实了两者的精确等价。

表 1 基底粗糙时土体重度γ与黏聚力随深度增大率的等效性验证

Table 1. Verification of equivalence between γ and the rate of cohesion increase with depth under rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	滑移面深度/m		地基承载力/kPa
算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	原模型	重度等效模型	原模型	重度等效模型
1	5	10	20	3	0	1.91	1.94	77.4	77.3
2	5	10	20	6	0	3.32	3.32	87.2	87.2
3	10	10	10	6	20	4.22	4.22	167.7	167.8
4	20	5	20	6	0	3.77	3.77	309.0	309.0
5	30	0	20	6	20	5.82	5.82	1509.2	1509.5
6	40	0	20	6	0	7.76	7.76	5107.1	5104.9

下载: 导出CSV

| 显示表格

2. 地基承载力计算的统一公式

2.1 总体思路

这里首先考虑非偏心竖向荷载下条形基础的地基承载力问题。由第1节的分析可知，与基础埋深对应的基础周边超载q的作用，除首先将地基承载力提高1倍q外，在土的内摩擦角大于零时另有与 $q\tan \varphi$ 等值的黏聚力作用，而地基土重度 $\gamma$ 的作用则等价于黏聚力随深度的增长率 $\gamma \tan \varphi$ 。这样，借鉴此前针对饱和黏性土地基在不排水强度随深度线性增大情况下承载力计算方法的思路，此时的地基承载力同样可取一半滑移面深度处的黏聚力乘以与黏聚力对应的承载力系数N_c，并考虑滑移面形状变化引入一修正系数进行计算，亦即可给出如下形式的计算公式：

${p_{\text{u}}} = {\text{(}}c{\text{ + }}q\tan \varphi {\text{ + }}0.5\beta \gamma \tan \varphi {Z_{\max }}){N_c}{\text{ + }}q \text{，}$

(2)

式中，Z_max为滑移面最大深度， $\beta$ 为考虑滑移面形状变化对地基承载力系数影响的修正系数。这样式（2）右端的前一项近似是滑移面平均深度处的等效黏聚力与Prandtl地基承载力系数N_c的乘积，后一项为单独列出的基础周围超载q对地基承载力的最低贡献。

式（2）是统一考虑基础宽度B、地基土强度指标c与φ、基础埋深对应的基础周围超载q以及地基土重度γ作用的地基承载力计算公式。它没有叠加计算的理论缺陷，如能较好确定其滑移面的最大深度Z_max及滑移面形状修正系数β，则可得到计算精度显著改善的计算结果。随后的计算对比可以证实这理论的正确。

2.2 表征等效黏聚力深度增长率的无量纲参数

显然，按式（2）计算地基承载力的关键之一是确定地基破坏时的滑移面深度Z_max。据力学基本原理，对于诸如地基承载力之类的极限荷载问题，极限荷载的大小及相应的滑移面深度等与材料的刚度参数无关，而只与材料的强度及地基基础的几何参数等有关。将这里所考虑的地基在强度特性本质方面与Prandtl- Reissner地基比较可见，这里地基的不同点仅仅是“黏聚力”随深度线性增大，因为地基土重度的作用可等效视为黏聚力的深度增长率。而对于Prandtl和Reissner所考虑的地基，由其所给滑移线形状不难得到滑移面最大深度的计算式。所以这里确定滑移面深度的思路是在Prandtl-Reissner滑移面深度的基础上考虑黏聚力随深度增大予以修正。而黏聚力随深度增大这一特性应可以也应该采用一个无量纲的相对增长率来表征，也就是应采用等效黏聚力在一定深度上的增加值与其稳定值的比来表征。根据所有这些深度理论思考，建议取下式定义的无量纲参数：

$k{\text{ = }}\frac{{B\gamma \tan \varphi }}{{c + q\tan \varphi }} 。$

(3)

式（3）中，分子是从基底往下一倍基础宽度的深度处等效黏聚力的增加值，而分母是等效黏聚力的稳定值。对此无量纲参数的正确性，由上述的严格论证可以理解是肯定的。但这里仍进一步通过大量有限元极限分析计算对其予以检验。计算结果表明，对任意可能的给定φ值，可以在可能的取值范围内任意变化B，c，q和 $\gamma$ ，但只要按式（3）计算的k值相同，实际滑移面深度与Prandtl-Reissner滑移面深度的比值是恒定的。将这一比值记为深度修正系数 $\alpha$ ，表 2，3分别列出基底粗糙和光滑时不同参数时的计算情况。

表 2 基底粗糙时无量纲参数k确定滑移面深度的检验

Table 2. Validation of dimensionless parameter k to determine depth of slip plane for rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	深度/m	深度修正系数α
1	10	10	20	3	0.0	1.06	1.95	0.73
2	10	0	20	3	56.7	1.06	1.95	0.73
3	10	10	10	6	0.0	1.06	3.91	0.73
4	10	10	20	6	56.7	1.06	3.91	0.73
5	20	20	10	6	0.0	1.09	5.51	0.79
6	20	0	10	6	54.9	1.09	5.51	0.79
7	20	10	20	6	0.0	4.37	4.36	0.63
8	20	0	20	6	27.5	4.37	4.36	0.63
9	20	5	20	6	0.0	8.74	3.77	0.54
10	20	10	20	12	0.0	8.74	7.54	0.54
11	30	5	10	6	0.0	6.93	5.95	0.63
12	30	5	20	6	8.7	6.93	5.95	0.63
13	30	0	20	6	0.0	无穷	4.66	0.49
14	30	0	20	12	0.0	无穷	9.33	0.49

下载: 导出CSV

| 显示表格

表 3 基底光滑时无量纲参数k确定滑移面深度的检验

Table 3. Validation of dimensionless parameter k to determine depth of slip plane for smooth footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	深度/m	深度修正系数α
1	10	10	20	3	0.0	1.06	1.15	0.43
2	10	0	20	3	56.7	1.06	1.15	0.43
3	10	10	10	6	0.0	1.06	2.31	0.43
4	10	10	20	6	56.7	1.06	2.31	0.43
5	20	20	10	6	0.0	1.09	3.04	0.44
6	20	0	10	6	54.9	1.09	3.04	0.44
7	20	10	20	6	0.0	4.37	2.30	0.33
8	20	0	20	6	27.5	4.37	2.30	0.33
9	20	5	20	6	0.0	8.74	2.13	0.31
10	20	10	20	12	0.0	8.74	4.27	0.31
11	30	5	10	6	0.0	6.93	3.18	0.33
12	30	5	20	6	8.7	6.93	3.18	0.33
13	30	0	20	6	0.0	无穷	2.36	0.25
14	30	0	20	12	0.0	无穷	4.72	0.25

下载: 导出CSV

| 显示表格

如无机理分析，仅看计算数值的变化趋势，就很可能会给出一个式（3）的分子中没有 $\tan \varphi$ 也无实际物理意义的无量纲参数，将增加后续拟合高精度计算式的难度。

2.3 滑移面深度及形状修正系数的确定

为由式（2）计算地基承载力，需首先确定地基失稳破坏时的滑移面深度Z_max与考虑滑移面形状变化使承载力系数变化的修正系数β。

首先看滑移面深度。当不考虑地基土重度时，对于地基典型的整体剪切破坏形式，由Prandtl-Reissner滑移面形状得出其滑移面最大深度为

${Z_{{\text{PR}}}}{\text{ = }}{{\text{e}}^{\left( {\frac{{\text{π }}}{4} + \frac{\varphi }{2}} \right)\tan \varphi }}\sin \left( {\frac{{\text{π }}}{4} + \frac{\varphi }{2}} \right)B \text{，}$

(4)

滑移面最大深度是基础宽度B的倍数，而这倍数只与内摩擦角φ有关。当地基土的重度对地基承载力有贡献时（亦即φ > 0时），与Prandtl-Reissner地基的唯一本质差别是等效“黏聚力”随深度增长，而反映这增长的无量纲参数是式（3）定义的k，所以此时的滑移面最大深度应为

${Z_{\max }}{\text{ = }}\alpha (\varphi , k){Z_{{\text{PR}}}} \text{，}$

(5)

亦即由Prandtl滑移面深度乘以修正系数α给出实际滑移面的最大深度Z_max，修正系数α是无量纲参数k和内摩擦角φ的函数。

修正系数α可通过拟合精细数值计算的结果来确定。本文拟合给出修正系数 $\alpha$ 的计算式为

$\alpha (\varphi , k) = 1 - {{\text{e}}^{ - M{k^{ - 0.5}} - N}} \text{，}$

(6)

其中，基底粗糙的情况下：

$M{\text{ = }}1.0 \text{，}\ \ N{\text{ = }}0.8\sin 2\varphi \text{；}$

(7)

而在基底光滑的情况下：

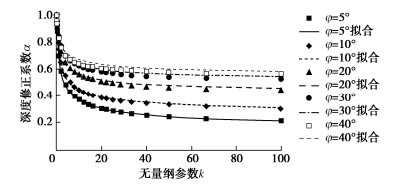
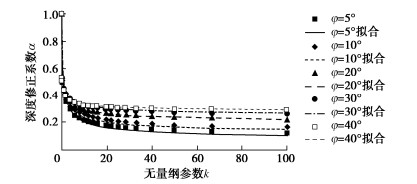
$M = 0.6 - 0.4\tan \varphi \text{，}\ \ N{\text{ = }}0.33\sin 2\varphi 。$

(8)

图 1，2分别为基底粗糙和光滑情况下，对不同φ值，相应修正系数α随无量纲参数k变化的情况，其中实线为按式（6）拟合的结果，离散点为精细数值计算的结果，可见拟合情况良好。同时由图 1，2可见，滑移面最大深度随φ和k的增大而减小，但减小的速率递减。此外，基底粗糙时的滑移面深度较大。

图 1 基底粗糙时滑移面深度修正系数的拟合

Figure 1. Fitting of slip surface depth correction coefficient for rough footings

下载: 全尺寸图片幻灯片

图 2 基底光滑时滑移面深度修正系数的拟合

Figure 2. Fitting of slip surface depth correction coefficient for smooth footings

下载: 全尺寸图片幻灯片

现在看滑移面形状修正系数 $\beta$ 。这系数实际是考虑滑移面形状与Prandtl滑移面不同时，承载力系数N_c的改变，只用于与地基土重度 $\gamma$ 有关的部分。计算表明，对常见情况这系数 $\beta$ 可取1.0，也就是不需修正。但是，当k值很大，也就是与土重度 $\gamma$ 对应的等效黏聚力随深度相对增长率很大，且内摩擦角很小的情况下，滑移面深度很小，其形状极为扁平，此时的承载力系数N_c要显著增大，也就是β需取较大值。

修正系数的取值可通过拟合精细数值计算的地基承载力结果来确定。本文结合以上类似的定性规律分析，通过大量计算拟合给出修正系数β的计算式。对于基底粗糙的情况，

$\beta {\text{ = 1 + }}\frac{1}{{\sqrt 2 {N_c}({k^{ - 0.5}} + 1.5\tan \varphi )}} \text{，}$

(9)

而当基底光滑时，

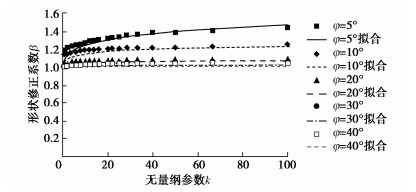
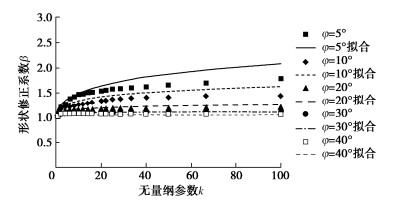
$\beta = {\text{1 + }}\frac{1}{{\sqrt 2 (0.6 - 0.4\tan \varphi ){N_c}({k^{ - 0.5}} + 0.9\tan \varphi )}} 。$

(10)

图 3，4分别为基底粗糙和光滑情况下，对不同φ值，相应修正系数β随无量纲参数k变化的情况，其中实线为按式（9）或式（10）拟合的结果，离散点为精细数值计算的结果。由图可见，拟合情况总体良好，但当摩擦角小且基底光滑时的拟合误差稍大。不过，此时地基土重度对整个地基承载力的贡献所占比例较小，故所计算地基承载力的误差会远小于 $\beta$ 的误差。

图 3 基底粗糙时滑移面形状修正系数的拟合

Figure 3. Fitting of slip surface shape correction coefficient for rough footings

下载: 全尺寸图片幻灯片

图 4 基底光滑时滑移面形状修正系数的拟合

Figure 4. Fitting of slip surface shape correction coefficient for smooth footings

下载: 全尺寸图片幻灯片

2.4 其他复杂情况下的承载力计算

至此，针对承受非偏心竖向荷载条形基础下地基的整体剪切破坏，本文提出了统一考虑各有关因素的地基承载力计算公式。但实际工程中有多种复杂情况，这里简要说明其他情况下利用本文公式的计算方法。当地基土相对较软或埋深相对较大情况下，地基可能发生局部剪切破坏而非前述的整体剪切破坏，此时建议仍按太沙基的做法，采用折减的强度指标进行计算，亦即将土的强度指标折减后再如上进行计算。

对于其他形状的基础、荷载倾斜、地面倾斜等情况，建议仍采用Hansen等给出的修正系数^{[2, 5]}。此时需明确，本文的计算公式仍可如经典公式一样写成3项，即式（2）可改写为

${p_{\text{u}}} = c{N_c}{\text{ + (}}{N_c}\tan \varphi + 1)q{\text{ + }}0.5\beta \gamma \tan \varphi {Z_{\max }}{N_c} 。$

(11)

式（11）右端3项与经典公式的3项逐一对应，只是改进了第3项的计算。当计算诸如矩形基础的地基极限承载力时，可先按宽度等于矩形宽度的条形基础如上计算式（11）右端的3项，再分别乘以Hansen所给基础形状系数s_c，s_q和s_γ。可以理解，这样计算的精度不会较原公式有任何降低。限于篇幅，这里不再展示相应的算例。

此外，对式（11）的最后一项还可以整理为经典公式中第3项的样式，从而可以清楚而肯定地认识到N_γ到底与哪些参数或参数的组合式有关。

2.5 计算方法的检验

为检验上述整个计算方法的正确性及计算精度，针对承受非偏心竖向荷载的条形基础取多种不同的基础宽度B、土体强度指标c、φ及重度 $\gamma$ ，以及基础埋深对应的超载q，分别按上述计算公式和有限元极限分析方法计算相应滑移面深度Z_max及地基极限承载力p_u，结果表明所提出的计算方法的计算精度很高，相对误差一般不大于5%。表 4，5分别给出基底粗糙和基底光滑情况下的部分计算对比。对比两表计算结果还可以看出，基底粗糙时的地基承载力明显大于基底光滑时的值，特别是在内摩擦角和土体重度大的情况下。

表 4 基底粗糙时计算方法的检验

Table 4. Verification of calculation method for rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	极限分析			公式计算		承载力相对误差/%
算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	Z_max/m	Α	p_u/kPa	α	p_u/kPa	承载力相对误差/%
1	5	20	10	3	0	0.13	2.24	0.94	136.8	0.94	136.4	-0.3
2	5	5	20	3	0	1.05	1.58	0.66	43.6	0.67	42.4	-2.8
3	5	0	20	3	0	无穷	0.40	0.17	3.4	0.13	3.2	-5.3
4	10	10	20	3	0	1.06	1.86	0.69	116.8	0.71	113.5	-2.9
5	10	0	20	6	40	3.00	3.11	0.58	153.4	0.57	148.6	-3.1
6	10	0	20	6	0	无穷	1.50	0.28	26.0	0.24	24.9	-4.2
7	20	20	10	6	0	1.09	5.40	0.77	458.3	0.77	446.3	-2.6
8	20	5	20	6	0	8.74	3.89	0.56	308.9	0.57	301.7	-2.3
9	20	0	20	6	0	无穷	2.81	0.40	169.9	0.40	164.5	-3.2
10	30	20	20	6	0	3.46	6.40	0.67	1823.2	0.71	1793.8	-1.6
11	30	5	20	6	0	13.86	5.42	0.57	1195.4	0.62	1194.2	-0.1
12	30	0	20	6	0	无穷	4.66	0.49	884.6	0.50	849.7	-3.9
13	40	20	20	6	0	5.03	8.80	0.62	7737.9	0.71	7850.8	1.5
14	40	0	20	6	0	无穷	7.55	0.54	5113.0	0.55	4889.8	-4.4

下载: 导出CSV

| 显示表格

表 5 基底光滑时计算方法的检验

Table 5. Verification of calculation method for smooth footings

模型编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	极限分析			公式计算		承载力相对误差/%
模型编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	Z_max/m	α	P_u/kPa	α	P_u/kPa	承载力相对误差/%
1	5	20	10	3	0	0.13	1.42	0.60	133.4	0.80	135.6	1.7
2	5	5	20	3	0	1.05	1.03	0.43	38.7	0.46	39.7	2.6
3	5	0	20	3	0	无穷	0.28	0.12	2.6	0.06	2.6	0.5
4	10	10	20	3	0	1.06	1.15	0.43	101.9	0.47	104.4	2.5
5	10	0	20	6	40	3.00	1.80	0.34	130.8	0.34	131.7	0.7
6	10	0	20	6	0	无穷	0.84	0.16	16.9	0.11	16.9	0.1
7	20	20	10	6	0	1.09	3.04	0.44	384.2	0.48	393.7	2.5
8	20	5	20	6	0	8.74	2.21	0.32	207.8	0.31	207.7	-0.1
9	20	0	20	6	0	无穷	1.49	0.21	94.6	0.19	95.0	0.4
10	30	20	20	6	0	3.46	3.58	0.38	1269.0	0.38	1276.1	0.6
11	30	5	20	6	0	13.86	2.98	0.31	716.1	0.32	722.2	0.8
12	30	0	20	6	0	无穷	2.36	0.25	457.9	0.25	461.8	0.8
13	40	20	20	6	0	5.03	4.80	0.34	4835.7	0.36	4785.6	-1.0
14	40	0	20	6	0	无穷	3.84	0.27	2571.0	0.28	2586.4	0.6

下载: 导出CSV

| 显示表格

3. 与现有主流计算公式的对比

3.1 与太沙基解的比较

本节将本文公式与太沙基解进行比较。太沙基解是假定基底粗糙给出地基承载力的3个系数，其中前两个系数 ${N_c}$ 与 ${N_q}$ 较Prandtl-Reissner给出的要大。因其第3个承载力系数 ${N_\gamma }$ 仅能给出数值解，故其承载力系数在多数土力学教科书中是以曲线形式给出，但文献[14]列表给出了太沙基承载力系数值，这里在按太沙基公式计算时采用文献[14]给出的系数值。

表 6列出不同土体强度参数取值时太沙基公式、本文式（2）与有限元极限分析计算结果的对比。这里取基础宽度B=6 m，周边超载q=0，地基土重度γ=20 kN/m³。按太沙基的假定，认为基底粗糙，故这里的有限元极限分析和本文计算公式均按基底粗糙来考虑。由表 6可见，太沙基公式误差最高可达30%。且在φ=0时，太沙基公式仍是不准确的，这说明太沙基公式中的系数N_c存在误差。实际上φ=0时即使假定基底粗糙，还是Prandtl-Reissner解精确。

表 6 与太沙基公式的比较

Table 6. Comparisons with Terzaghi formula

算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	太沙基公式/kPa	太沙基公式相对误差/%	本文公式/kPa	本文公式相对误差/%
1	0	5	25.7	28.5	10.9	25.7	0.0
2	5	5	51.7	66.5	28.7	49.7	-3.9
3	10	5	92.3	120.0	30.0	88.4	-4.2
4	20	5	308.9	388.5	25.8	301.7	-2.3
5	30	5	1195.5	1368.0	14.4	1194.2	-0.1
6	40	5	5968.4	6502.5	8.9	6074.9	1.8
7	44	5	12705.0	16359.5	28.7	13033.0	2.6
8	0	50	257.1	285.0	10.9	257.1	0.0
9	5	50	351.7	395.0	12.3	349.9	-0.5
10	10	50	492.6	552.0	12.1	486.3	-1.3
11	20	50	1074.6	1185.0	10.3	1049.7	-2.3
12	30	50	2880.0	3042.0	5.6	2825.9	-1.9
13	40	50	10609.0	10809.0	1.9	10700.1	0.9
14	44	50	20430.0	23195.0	13.5	20938.2	2.5

下载: 导出CSV

| 显示表格

3.2 与Hansen解的比较

Hansen解是为改进太沙基解的计算精度而提出的，其前两个地基承载力系数与Prandtl-Reissner的相同，而第3个系数 ${N_\gamma }$ 的计算式为

${N_\gamma } = 1.8({N_q} - 1)\tan \varphi 。$

(12)

式（12）中的系数1.8是Hansen最初建议的^[5]，后来改为1.5^[2]，而Verruijt认为这系数理论上取2.0更准确些^[6]。

这里同样取基础宽度B=6 m，基础周边超载q=0，地基土重度 $\gamma$ =20 kN/m³。有限元极限分析和本文计算公式均按基底粗糙进行计算。表 5列出与Hansen公式计算结果的比较，其中对Hansen所给式（12）中的系数分别取3种不同的值。可见系数取1.5时承载力普遍偏小，相对误差绝对值接近30%，而取2.0时确实总体误差绝对值减小，但φ较大且c较小时出现正的误差，亦即结果偏大。

表 7 与Hansen公式的比较

Table 7. Comparisons with Hansen formula

算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	系数1.5		系数1.8		系数2.0		本文公式/kPa	本文公式相对误差/%
算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	Hansen解/kPa	相对误差/%	Hansen解/kPa	相对误差/%	Hansen解/kPa	相对误差/%	本文公式/kPa	本文公式相对误差/%
1	0	5	25.7	25.7	0.0	25.7	0.0	25.7	0.0	25.7	0.0
2	5	5	51.7	36.9	-28.6	37.8	-26.9	38.4	-25.7	49.7	-3.9
3	10	5	92.3	65.1	-29.5	69.7	-24.4	72.9	-21.1	88.4	-4.2
4	20	5	308.9	251.0	-18.7	286.4	-7.3	310.0	0.4	301.7	-2.3
5	30	5	1195.5	1054.9	-11.8	1235.7	3.4	1356.3	13.4	1194.2	-0.1
6	40	5	5968.4	5149.0	-13.7	6103.5	2.3	6739.8	12.9	6074.9	1.8
7	0	50	257.1	257.1	0.0	257.1	0.0	257.1	0	257.1	0.0
8	5	50	351.7	328.9	-6.5	329.8	-6.2	330.4	-6.1	349.9	-0.5
9	10	50	492.6	440.6	-10.6	445.3	-9.6	448.4	-9.0	486.3	-1.3
10	20	50	1074.6	918.6	-14.5	954.0	-11.2	977.6	-9.0	1049.7	-2.3
11	30	50	2880.0	2411.2	-16.3	2592.0	-10.0	2712.6	-5.8	2825.9	-1.9
12	40	50	10609.0	8538.1	-19.5	9492.6	-10.5	10128.9	-4.5	10700.1	0.9

下载: 导出CSV

| 显示表格

尽管Hansen解在计算N_γ时，其计算式中的系数用1.5普遍偏保守，但笔者的观点是，在可能条件还是尽量准确计算，之后再考虑参数的可能误差及工程之重要性来决定安全系数的大小。否则，决策是盲目的，对复杂工程未必安全。

此外，如将Hansen解与基底光滑情况下的有限元极限分析结果比较，即使取其中的系数为1.5，Hansen解也多给出偏大的结果，且正误差最大超过50%，限于篇幅这里不再列出详细结果。

4. 结论

本文针对目前一般地基承载力计算中存在的问题，在深入分析地基承载力机理的基础上，提出一种新的改进计算方法。

（1）现有计算公式在理论上存在的突出问题是对极限荷载问题采用了叠加计算的思路，故难以达到较好的计算精度。太沙基解的误差可达30%，Hansen解的误差稍小，但最大也接近30%。

（2）本文深入分析了地基承载的机理，揭示了基础埋深对应的基础周围超载和地基土自重在地基承载力的计算中可分别等价为黏聚力和黏聚力随深度增长率，从而可采用统一的方法予以考虑。

（3）采用理论分析确定公式形式、数值计算拟合确定修正系数的方法，针对非偏心竖向荷载下的条形基础给出了综合考虑地基土强度、基础埋深和地基土重度的无量纲参数以及相应的地基承载力统一计算式，分别考虑了基底粗糙和光滑两种情况，与精细数值计算结果的对比表明所提出无量纲参数及地基承载力计算公式的合理性、正确性及高精度。

（4）与目前已有太沙基解、Hansen解的计算对比，表明本文所提方法的计算精度显著提高。

（5）对于其他形状的基础、倾斜荷载等情况，利用本文公式计算时仍可采用已有的修正系数。

图 1 基底粗糙时滑移面深度修正系数的拟合

Figure 1. Fitting of slip surface depth correction coefficient for rough footings

下载: 全尺寸图片幻灯片

图 2 基底光滑时滑移面深度修正系数的拟合

Figure 2. Fitting of slip surface depth correction coefficient for smooth footings

下载: 全尺寸图片幻灯片

图 3 基底粗糙时滑移面形状修正系数的拟合

Figure 3. Fitting of slip surface shape correction coefficient for rough footings

下载: 全尺寸图片幻灯片

图 4 基底光滑时滑移面形状修正系数的拟合

Figure 4. Fitting of slip surface shape correction coefficient for smooth footings

下载: 全尺寸图片幻灯片

表 1 基底粗糙时土体重度γ与黏聚力随深度增大率的等效性验证

Table 1 Verification of equivalence between γ and the rate of cohesion increase with depth under rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	滑移面深度/m		地基承载力/kPa
算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	原模型	重度等效模型	原模型	重度等效模型
1	5	10	20	3	0	1.91	1.94	77.4	77.3
2	5	10	20	6	0	3.32	3.32	87.2	87.2
3	10	10	10	6	20	4.22	4.22	167.7	167.8
4	20	5	20	6	0	3.77	3.77	309.0	309.0
5	30	0	20	6	20	5.82	5.82	1509.2	1509.5
6	40	0	20	6	0	7.76	7.76	5107.1	5104.9

下载: 导出CSV

表 2 基底粗糙时无量纲参数k确定滑移面深度的检验

Table 2 Validation of dimensionless parameter k to determine depth of slip plane for rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	深度/m	深度修正系数α
1	10	10	20	3	0.0	1.06	1.95	0.73
2	10	0	20	3	56.7	1.06	1.95	0.73
3	10	10	10	6	0.0	1.06	3.91	0.73
4	10	10	20	6	56.7	1.06	3.91	0.73
5	20	20	10	6	0.0	1.09	5.51	0.79
6	20	0	10	6	54.9	1.09	5.51	0.79
7	20	10	20	6	0.0	4.37	4.36	0.63
8	20	0	20	6	27.5	4.37	4.36	0.63
9	20	5	20	6	0.0	8.74	3.77	0.54
10	20	10	20	12	0.0	8.74	7.54	0.54
11	30	5	10	6	0.0	6.93	5.95	0.63
12	30	5	20	6	8.7	6.93	5.95	0.63
13	30	0	20	6	0.0	无穷	4.66	0.49
14	30	0	20	12	0.0	无穷	9.33	0.49

下载: 导出CSV

表 3 基底光滑时无量纲参数k确定滑移面深度的检验

Table 3 Validation of dimensionless parameter k to determine depth of slip plane for smooth footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	深度/m	深度修正系数α
1	10	10	20	3	0.0	1.06	1.15	0.43
2	10	0	20	3	56.7	1.06	1.15	0.43
3	10	10	10	6	0.0	1.06	2.31	0.43
4	10	10	20	6	56.7	1.06	2.31	0.43
5	20	20	10	6	0.0	1.09	3.04	0.44
6	20	0	10	6	54.9	1.09	3.04	0.44
7	20	10	20	6	0.0	4.37	2.30	0.33
8	20	0	20	6	27.5	4.37	2.30	0.33
9	20	5	20	6	0.0	8.74	2.13	0.31
10	20	10	20	12	0.0	8.74	4.27	0.31
11	30	5	10	6	0.0	6.93	3.18	0.33
12	30	5	20	6	8.7	6.93	3.18	0.33
13	30	0	20	6	0.0	无穷	2.36	0.25
14	30	0	20	12	0.0	无穷	4.72	0.25

下载: 导出CSV

表 4 基底粗糙时计算方法的检验

Table 4 Verification of calculation method for rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	极限分析			公式计算		承载力相对误差/%
算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	Z_max/m	Α	p_u/kPa	α	p_u/kPa	承载力相对误差/%
1	5	20	10	3	0	0.13	2.24	0.94	136.8	0.94	136.4	-0.3
2	5	5	20	3	0	1.05	1.58	0.66	43.6	0.67	42.4	-2.8
3	5	0	20	3	0	无穷	0.40	0.17	3.4	0.13	3.2	-5.3
4	10	10	20	3	0	1.06	1.86	0.69	116.8	0.71	113.5	-2.9
5	10	0	20	6	40	3.00	3.11	0.58	153.4	0.57	148.6	-3.1
6	10	0	20	6	0	无穷	1.50	0.28	26.0	0.24	24.9	-4.2
7	20	20	10	6	0	1.09	5.40	0.77	458.3	0.77	446.3	-2.6
8	20	5	20	6	0	8.74	3.89	0.56	308.9	0.57	301.7	-2.3
9	20	0	20	6	0	无穷	2.81	0.40	169.9	0.40	164.5	-3.2
10	30	20	20	6	0	3.46	6.40	0.67	1823.2	0.71	1793.8	-1.6
11	30	5	20	6	0	13.86	5.42	0.57	1195.4	0.62	1194.2	-0.1
12	30	0	20	6	0	无穷	4.66	0.49	884.6	0.50	849.7	-3.9
13	40	20	20	6	0	5.03	8.80	0.62	7737.9	0.71	7850.8	1.5
14	40	0	20	6	0	无穷	7.55	0.54	5113.0	0.55	4889.8	-4.4

下载: 导出CSV

表 5 基底光滑时计算方法的检验

Table 5 Verification of calculation method for smooth footings

模型编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	极限分析			公式计算		承载力相对误差/%
模型编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	Z_max/m	α	P_u/kPa	α	P_u/kPa	承载力相对误差/%
1	5	20	10	3	0	0.13	1.42	0.60	133.4	0.80	135.6	1.7
2	5	5	20	3	0	1.05	1.03	0.43	38.7	0.46	39.7	2.6
3	5	0	20	3	0	无穷	0.28	0.12	2.6	0.06	2.6	0.5
4	10	10	20	3	0	1.06	1.15	0.43	101.9	0.47	104.4	2.5
5	10	0	20	6	40	3.00	1.80	0.34	130.8	0.34	131.7	0.7
6	10	0	20	6	0	无穷	0.84	0.16	16.9	0.11	16.9	0.1
7	20	20	10	6	0	1.09	3.04	0.44	384.2	0.48	393.7	2.5
8	20	5	20	6	0	8.74	2.21	0.32	207.8	0.31	207.7	-0.1
9	20	0	20	6	0	无穷	1.49	0.21	94.6	0.19	95.0	0.4
10	30	20	20	6	0	3.46	3.58	0.38	1269.0	0.38	1276.1	0.6
11	30	5	20	6	0	13.86	2.98	0.31	716.1	0.32	722.2	0.8
12	30	0	20	6	0	无穷	2.36	0.25	457.9	0.25	461.8	0.8
13	40	20	20	6	0	5.03	4.80	0.34	4835.7	0.36	4785.6	-1.0
14	40	0	20	6	0	无穷	3.84	0.27	2571.0	0.28	2586.4	0.6

下载: 导出CSV

表 6 与太沙基公式的比较

Table 6 Comparisons with Terzaghi formula

算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	太沙基公式/kPa	太沙基公式相对误差/%	本文公式/kPa	本文公式相对误差/%
1	0	5	25.7	28.5	10.9	25.7	0.0
2	5	5	51.7	66.5	28.7	49.7	-3.9
3	10	5	92.3	120.0	30.0	88.4	-4.2
4	20	5	308.9	388.5	25.8	301.7	-2.3
5	30	5	1195.5	1368.0	14.4	1194.2	-0.1
6	40	5	5968.4	6502.5	8.9	6074.9	1.8
7	44	5	12705.0	16359.5	28.7	13033.0	2.6
8	0	50	257.1	285.0	10.9	257.1	0.0
9	5	50	351.7	395.0	12.3	349.9	-0.5
10	10	50	492.6	552.0	12.1	486.3	-1.3
11	20	50	1074.6	1185.0	10.3	1049.7	-2.3
12	30	50	2880.0	3042.0	5.6	2825.9	-1.9
13	40	50	10609.0	10809.0	1.9	10700.1	0.9
14	44	50	20430.0	23195.0	13.5	20938.2	2.5

下载: 导出CSV

表 7 与Hansen公式的比较

Table 7 Comparisons with Hansen formula

算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	系数1.5		系数1.8		系数2.0		本文公式/kPa	本文公式相对误差/%
算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	Hansen解/kPa	相对误差/%	Hansen解/kPa	相对误差/%	Hansen解/kPa	相对误差/%	本文公式/kPa	本文公式相对误差/%
1	0	5	25.7	25.7	0.0	25.7	0.0	25.7	0.0	25.7	0.0
2	5	5	51.7	36.9	-28.6	37.8	-26.9	38.4	-25.7	49.7	-3.9
3	10	5	92.3	65.1	-29.5	69.7	-24.4	72.9	-21.1	88.4	-4.2
4	20	5	308.9	251.0	-18.7	286.4	-7.3	310.0	0.4	301.7	-2.3
5	30	5	1195.5	1054.9	-11.8	1235.7	3.4	1356.3	13.4	1194.2	-0.1
6	40	5	5968.4	5149.0	-13.7	6103.5	2.3	6739.8	12.9	6074.9	1.8
7	0	50	257.1	257.1	0.0	257.1	0.0	257.1	0	257.1	0.0
8	5	50	351.7	328.9	-6.5	329.8	-6.2	330.4	-6.1	349.9	-0.5
9	10	50	492.6	440.6	-10.6	445.3	-9.6	448.4	-9.0	486.3	-1.3
10	20	50	1074.6	918.6	-14.5	954.0	-11.2	977.6	-9.0	1049.7	-2.3
11	30	50	2880.0	2411.2	-16.3	2592.0	-10.0	2712.6	-5.8	2825.9	-1.9
12	40	50	10609.0	8538.1	-19.5	9492.6	-10.5	10128.9	-4.5	10700.1	0.9

下载: 导出CSV

参考文献(14)

[1]	TERZAGHI K. Theoretical Soil Mechanics[M]. Hoboken: John Wiley and Sons, 1943.
[2]	LI Guang-xin, ZHANG Bing-yin, YU Yu-zhen. Soil Mechanics[M]. Beijing: Tsinghua University Press, 2013. (in Chinese)
[3]	CRAIG R F. Soil Mechanics[M]. Boston: Springer, 1983.
[4]	VESIĆ A S. Analysis of ultimate loads of shallow foundations[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 99(1): 45–73. doi: 10.1061/JSFEAQ.0001846
[5]	HANSEN J B. A general formula for bearing capacity[J]. Danish Geotechnical Institute, 1961(11): 38–46.
[6]	VERRUIJT A. Soil Mechanics[D]. Delft: Delft University of Technology, 2012.
[7]	DIAZ-SEGURA E G. Assessment of the range of variation of N_γ from 60 estimation methods for footings on sand[J]. Canadian Geotechnical Journal, 2013, 50(7): 793–800. doi: 10.1139/cgj-2012-0426
[8]	肖大平, 朱维一, 陈环. 滑移线法求解极限承载力问题的一些进展[J]. 岩土工程学报, 1998, 20(4): 25–29. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC804.005.htm XIAO Da-ping, ZHU Wei-yi, CHEN Huan. Progress in slip lines method to solve the bearing capacity problem[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(4): 25–29. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC804.005.htm
[9]	韩冬冬, 谢新宇, 王忠瑾, 等. 条形粗糙基础极限承载力求解与误差分析[J]. 岩土工程学报, 2016, 38(10): 1789–1796. doi: 10.11779/CJGE201610007 HAN Dong-dong, XIE Xin-yu, WANG Zhong-jin, et al. Solution and error evaluation for bearing capacity of rough strip footings[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(10): 1789–1796. (in Chinese) doi: 10.11779/CJGE201610007
[10]	李贤杰. 深基坑坑底抗隆起验算方法及圆形基坑分析方法研究[D]. 北京: 清华大学, 2020. LI Xian-jie, Calculation Method for Basal Stability of Deep Excavation and Analysis of Circular Foundation Pit[D]. Beijing: Tsinghua University, 2020. (in Chinese)
[11]	SONG Er-xiang, FU Hao, LI Xian-jie, A calculation method for the bearing capacity of saturated soil under undrained conditions[J]. Rock and Soil Mechanics, 2021, 42(11): 2919–2924, 2952. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103024.htm
[12]	KRABBENHOFT K. OPTUM G2: Theory[M]. Copenhagen: Optum Computational Engineering, 2019.
[13]	宋二祥, 孔郁斐, 杨军. 土工结构安全系数定义及相应计算方法讨论[J]. 工程力学, 2016, 33(11): 1–10. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201611001.htm SONG Er-xiang, KONG Yu-fei, YANG Jun. Discussion of safety factor definitions and computation methods for geotechnical structures[J]. Engineering Mechanics, 2016, 33(11): 1–10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201611001.htm
[14]	SU Dong. Soil Mechanics[M]. Beijing: Tsinghua University Press, 2015. (in Chinese)

施引文献(15)

期刊类型引用(8)

1.	宋二祥. 饱和土不排水计算理论与方法探究. 岩土工程学报. 2025(01): 1-29 . 本站查看
2.	史元祺，曹振中，景立平，莫红艳. 基于剪切破坏面修正的地基极限承载力计算方法. 地下空间与工程学报. 2025(01): 31-41 . 百度学术
3.	杨峰，慈新航，高益康，赵炼恒. 底部刚性层限制条件下条形基础地基承载力系数N_c与破坏模式. 岩石力学与工程学报. 2023(04): 1031-1040 . 百度学术
4.	曹振中，卢秀莲，莫红艳，秦志光，史元祺. 高内摩擦角下珊瑚礁砂地基极限承载力初步分析. 岩石力学与工程学报. 2023(S1): 3609-3617 . 百度学术
5.	谢得峰，张文，杨晓林，范延彬，张秉来，王新红，袁媛，韩磊磊. 倾斜荷载盐渍土地基承载力数值计算与试验研究. 科学技术与工程. 2023(16): 7033-7043 . 百度学术
6.	刘润，宋毅然，练继建，林毅峰，汪嘉钰. 成层土中海上风电筒型基础竖向承载影响深度研究. 河北工程大学学报(自然科学版). 2023(04): 1-8+24 . 百度学术
7.	宋二祥，陈星屹，林世杰. 关于偏心荷载下地基承载力的验算方法. 岩土力学. 2022(07): 1925-1932 . 百度学术
8.	王艳坤，刘杰，宋玲，张兴疆，高斌. 土工格室加固风积沙地基模型试验研究. 公路交通科技. 2022(07): 40-48 . 百度学术