Mechanism and new calculation method for bearing capacity of foundations
-
摘要: 地基承载力计算是土力学中的基本课题,但地基土自重对承载力的贡献一直未能较准确地予以计算,究其原因在于此部分的计算不是孤立的。为深入探讨地基承载力的机理及计算理论,首先,证明基础埋深相应超载及地基土重度对承载力的作用可分别转换为等效黏聚力及黏聚力随深度的增长率。随后,针对承受非偏心竖向荷载的条形基础下地基的整体剪切破坏,提出一种全新的地基极限承载力计算方法,特别是构造了一个可以综合考虑地基土强度、基础埋深超载及地基土重度影响的无量纲参数,进而给出统一考虑各有关因素的地基承载力计算公式,并对地基局部剪切破坏、非条形基础、倾斜荷载等复杂情况下利用本文公式进行地基承载力的计算给出建议。通过与精细数值方法计算比较,对所提出的计算方法进行了严格的检验,表明其正确性和高精度,同时也表明本文思路及所构造无量纲参数的合理性和正确性。此外,还与目前常用的太沙基解、Hansen解进行了比较讨论,表明所提出计算公式较现用公式有显著改进。Abstract: The calculation of bearing capacity of foundations is a fundamental topic in soil mechanics. However, the contribution of the unit weight of the foundation soil to the bearing capacity cannot yet be satisfactorily calculated. The fundamental reason is that this part of bearing capacity is actually not independent, and consequently cannot be calculated separately. In order to study the mechanism of foundation bearing capacity and the relevant theory thoroughly, it is first revealed that the surcharge load corresponding to footing embedment and the unit weight of the foundation soil, multiplied by the soil strength parametertanφ, can be treated respectively as the equivalent cohesion and the rate of cohesion increase along depth. Then a new method is developed for the general failure mode of strip footing under non-eccentric vertical loads. In this new method a non-dimensional parameter is defined to well reflect the influences of the soil strength and soil weight on the bearing capacity, and based on which a unified formula for the calculation of bearing capacity is established, in which the soil strength, the embedment depth of the footing and the soil weight are all considered as closely related elements. For the bearing capacity of foundation under other more complicated conditions, such as failure in local mode, different footing shapes, inclined loads etc., the available methods of treatment can be still applied in combination with the newly developed formula. Careful comparison with the refined numerical calculations proves the reliability and high accuracy of the proposed formula, and at the same time it proves the rationality and correctness of the whole idea as well as the constructed non-dimensional parameter. Besides, comparisons are also made with the formulas by Terzaghi and Hansen to show the significant improvement of the proposed method over the formers.
-
Keywords:
- bearing capacity of foundation /
- unified formula /
- Terzaghi formula /
- Hansen formula
-
0. 引言
土与结构接触面在土木、建筑、水利、市政、交通等实际工程中广泛存在,如建筑基础与地基间、桩与桩周土体间、面板堆石坝混凝土面板与垫层料间、地下隧道衬砌与土体间等均存在土与结构接触面。接触面是结构与土之间应力、变形传递的重要媒介,其特有的力学特性对土体、结构物的受力变形及其相互作用会产生重要影响,是结构物系统稳定的薄弱环节乃至关键部位。大量学者对其抗剪强度[1-12]、切向应力位移关系[2, 4-11, 13-17]、剪切体变[4, 6-8, 16, 18]等力学特性进行了深入研究,同时对土体性质[2, 4, 15, 17]、面板粗糙度[1-3, 5, 8-9, 11-12, 16]、剪切路径[4, 7, 10, 15]、法向应力[1, 5, 16]、法向边界条件[4, 7, 19]等影响因素进行了分析探讨。
实际工程中,土与结构接触面主要受到三维加载作用,呈现显著的三维力学特性。例如桩与桩周土接触面受到周围土体的法向约束、上部结构自重产生的竖向剪切以及风或波浪产生的水平剪切等三维荷载作用。蓄水条件下紫坪铺面板堆石坝面板在“5·12”汶川地震中产生的局部破坏亦表现出显著的三维作用和三维特性。因此,深入研究三维加载条件下土与结构接触面的力学规律,建立能够真实反应接触面三维力学特性的本构模型是进行土与结构相互作用系统设计、保证结构物安全稳定的基础。但以往研究主要集中于土与结构接触面二维力学特性的研究,仅有少数学者[4, 7, 10, 19]对接触面三维力学特性进行了探讨。
同时,土与结构接触面在地震等极限荷载作用下可能会产生大剪切变形导致破坏;但实际工程中接触面在正常工作状态下的剪切变形较破坏时小得多,此时用切向应力控制条件模拟接触面受力变形特性将更为科学有效[20]。以往学者为了分析接触面破坏及抗剪强度,主要采用切向位移控制条件来全面研究其静动力学特性[1-17],只有少数学者采用切向应力控制条件来探究接触面力学特性。Dejong等[18, 20]对切向应力控制条件下砂土与结构接触面的力学特性进行了少量研究,但主要局限于二维加载条件。冯大阔等[21]对切向应力控制条件粗粒土与结构接触面三维循环特性进行了研究,但未深入分析切向应力幅值对接触面切向位移、非共轴特性及剪切体变等三维力学特性的影响。
本文运用自主研制的80 t大型三维多功能土工试验机,进行了不同应力幅值往返圆形剪切路径下粗粒土与结构接触面大型三维循环直剪试验,深入分析和总结了切向应力幅值对接触面x向和y向位移及偏移、非共轴角、剪切柔度等接触面切向变形特性参数及其关系的影响规律,发现了接触面非共轴角稳定值和剪切柔度初始峰值间的对立统一关系以及两者与切向应力幅值间的良好关系,并构建了计算公式,为接触面三维本构模型的建立奠定了基础。
1. 试验条件
接触面试验采用自主研制的80 t大型三维多功能土工试验机(3DMAS)进行[22]。该接触面试验机具有三维化、大尺寸、高加载、多功能、自动化等特点。可施加800 kN的竖向力(施加在500 mm直径圆形容器上的法向应力为4.0 MPa)和400 kN的水平力(施加在500 mm直径圆形容器上的切向应力为2.0 MPa)。法向可实现常应力、常刚度和常位移3种边界条件,切向可自动施加应力控制、位移控制和复合控制等方式。80 t大型三维多功能土工试验机详见文献[22]。
试验接触面由粗粒土和三维钢板构成。粗粒土为北京麦子峪石场开采的不良级配(Cu =1.8,Cc = 0.9)粗粒土,表面有一定的尖角锐缘。粒径范围5~16 mm,平均粒径9.0 mm;试验时在圆形直剪容器中将其分5层击实。粗粒土试样直径500 mm,高度225 mm,干密度1.78 g/cm3。三维钢板为人造钢板,面积800 mm × 800 mm,略大于直剪容器直径,可保证接触面面积在剪切过程中保持不变。与粗粒土接触的钢板表面均布底边长5 mm、顶边长1 mm、高2 mm的正四棱台;用正四棱台的高度定义三维钢板表面的粗糙度,则其粗糙度为R=2 mm。钢板表面正四棱台经过特殊加工,保证其在剪切过程中不被磨损,故结构面粗糙度在剪切过程中始终保持不变。接触面单调剪切结果表明,该粗粒土与结构接触面抗剪强度约为τf=280 kPa。
剪切路径采用切向应力控制往返圆形路径(图 1)。试验时,法向应力施加到400 kPa并保持不变(常应力法向边界条件);待法向位移稳定后,先沿直线路径①剪切到指定的切向应力幅值(如图 1中τm所示),然后沿圆形路径②—③—④—⑤—⑥—⑦—⑧—⑨—……进行顺时针和逆时针往返循环剪切,并规定②—③—④—⑤—⑥—⑦—⑧—⑨为一个完整循环周次N。为便于试验结果分析,将接触面每个循环周次中沿顺时针方向的剪切过程②—③—④—⑤称为正向剪切,沿逆时针方向的剪切过程⑥—⑦—⑧—⑨称为反向剪切。试验时,可通过改变切向应力幅值τm来研究其对接触面三维循环力学特性的影响。本文主要进行了切向应力幅值τm为50,100,150,200,220,230,240,250 kPa时接触面三维剪切试验。
2. 切向位移及关系
图 2给出应力控制往返圆形剪切路径(切向应力幅值τm=230 kPa)下接触面法向位移v–y向位移uy–x向位移ux三维关系图(v–uy–ux曲线)。可以看出,应力控制往返圆形剪切路径下,接触面产生了明显的切向位移(uy,ux)和法向位移v。本文主要研究三维加载条件下接触面切向变形特性,故后续不再给出和讨论接触面法向位移。
为更清晰地分析切向位移的数值和发展趋势,图 2亦给出相应的x向和y向位移随循环周次的时程曲线。图 3给出了应力控制单向往返剪切路径(二维剪切路径,τm=230 kPa)下接触面x向、y向位移时程曲线及y向应力位移关系曲线,以对比分析接触面二维和三维力学特性的异同。可以看出,在应力控制往返圆形剪切路径下,x向和y向位移幅值均随循环剪切的进行逐渐减小,初始几个循环周次内减小速率较大,而后基本趋于稳定。同时,x向和y向位移均向其负向偏移,且初始几个循环周次内偏移较快,而后亦基本趋于稳定。而在单向往返剪切路径下,接触面仅在剪切方向(y向)产生了切向位移;在其正交切向(x向)由于未进行剪切,不产生切向应力和切向位移,故图 3未给出x向应力位移关系曲线。y向位移幅值随循环剪切的进行亦逐渐减小而后趋于基本稳定,这与往返圆形剪切路径较为类似。不同的是,单向往返剪切路径下,接触面y向位移幅值稳定值较往返圆形剪切路径稍小,且向其正向稍有偏移,这主要是由剪切定向效应以及正交切向没有剪切作用所致。同时,往返圆形剪切路径下,接触面切向位移时程曲线在其幅值处呈平滑转变,单向往返剪切路径下则有明显的突变,不再呈平滑过渡。这说明接触面在三维加载条件下呈现出明显的三维力学响应,且与二维力学特性有显著不同,需要进行深入分析和研究。
图 4给出不同切向应力幅值(τm为50,100,150,200,220,240 kPa)往返圆形剪切路径下接触面x向位移ux随循环周次N的时程曲线。结合图 2可以看出,切向应力幅值主要影响切向位移幅值大小及其偏移程度。切向应力幅值越大,其更接近接触面抗剪强度,x向位移幅值越大,向其负向偏移的程度也越大。当切向应力幅值τm=240 kPa时,第15循环周次(N=15)的x向位移已达到约-40 mm,接近切向位移传感器LVDT的量程(50 mm),故其时程曲线只给到第15循环周次。接触面切向位移的偏移由接触面异向性(土体异向性和结构面异向性)和切向应力不等幅两个因素共同作用引起,前者是切向位移产生偏移的内因,后者是外因。切向位移的偏移可能会产生切向应力幅值未达到抗剪强度但切向位移却很大的现象(如τm= 240 kPa),这种情况会导致实际工程中接触面的大剪切变形和剪切破坏,需要在工程设计时予以重点关注。
切向应力幅值对x向位移随循环周次的时程变化形式影响不大。当切向应力幅值不大时(如τm≤230 kPa),x向位移幅值均随循环剪切的进行而逐渐减小;但当切向应力幅值增大到一定程度时(如τm=240 kPa),x向位移幅值随循环剪切的进行基本保持不变,甚至有所增大。将接触面切向位移幅值随循环周次保持不变时对应的切向应力幅值定义为临界应力幅值τmcr,相应的应力水平为临界应力幅值水平(SLmcr= τmcr/τf);因此该粗粒土与结构接触面的临界应力幅值约为τmcr≈240 kPa,临界应力幅值水平约为SLmcr≈ 0.857。当切向应力幅值超过240 kPa时,接触面切向位移幅值随循环剪切的进行则逐渐增大。如切向应力幅值τm=250 kPa时,第1循环周次(N=1)接触面切向位移已超过-20 mm,第2循环周次(N=2)时已接近-40 mm;故图 4未给出切向应力幅值τm=250 kPa时的接触面试验结果,仅在后续某些图中给出。y向位移随循环周次的时程变化形式与切向应力幅值τm=230 kPa时的基本一致,限于篇幅这里不再给出。
图 5给出特定循环周次(N为1,10)不同切向应力幅值下接触面x向和y向位移间的关系图(uy-ux曲线)。由于切向应力幅值τm=240 kPa时接触面切向位移在第10循环周次(N=10)偏移过大(约-20 mm),为更清晰显示接触面力学特性,故在图 5(b)中未给出。可以看出,应力控制往返圆形剪切路径下,接触面切向位移关系曲线呈两个开口的椭圆形;开口的存在,说明在切向应力路径旋转360°时,切向位移未旋转360°;切向位移和切向应力的变化不同步,两者之间存在一定的相位差。随切向应力幅值的增大,椭圆长短轴及开口程度增大,进一步证明了切向位移幅值随切向应力幅值的增加而增大。切向应力幅值对接触面x向和y向位移关系曲线形式基本没有影响,这也进一步证实了不同切向应力幅值下y向位移随循环周次的时程变化曲线形式的相似性。
3. 切向应力位移关系
图 6给出特定循环周次不同切向应力幅值下接触面切向应力位移关系图,包括x向应力位移关系(τx–ux曲线)、y向应力位移关系(τy–uy曲线)以及正交切向应力位移关系(τy–ux曲线、τx–uy曲线)。可以看出,与直线型剪切路径(如十字剪切路径[21]、单向往返剪切路径)下接触面切向应力位移关系曲线呈双曲线形式(图 3)不同,往返圆形路径下该曲线类似椭圆形,说明接触面产生了明显的剪切耦合效应。剪切耦合效应是指一个切向的剪切作用对其正交切向的影响作用,从正交切向应力位移曲线(图 6中τy–ux曲线、τx–uy曲线)可以更清楚地证明三维加载条件下接触面的剪切耦合效应。而在单向往返剪切路径下,接触面仅在y向进行剪切,不存在剪切耦合效应。
切线应力幅值对接触面切向应力位移关系曲线形式影响不大,这亦可从其对接触面切向位移随循环周次的时程曲线形式影响不大得到验证。一个循环周次内,接触面开始剪切时,x向位移随x向应力的增加而逐渐增大,x向位移幅值并未在x向应力幅值处达到,而是在x向应力达到幅值后由于正交切向(y向)的剪切耦合效应仍有所增加,在x向应力减小到一定程度时才达到幅值,并随x向应力的持续减小而逐渐减小;后续变化重复前面的特性,并在剪切方向反向时其数值由减小变为增大。y向位移在开始剪切时稍有增加便达到幅值,而后随y向应力的减小而逐渐减小,在y向应力达到负向幅值后由于x向的剪切耦合效应其数值仍在增加,逐步达到幅值后才随y向应力的持续减小而逐渐减小。这与直线型剪切路径下接触面切向位移幅值在切向应力幅值处达到的现象(图 3)有明显区别。上述现象也进一步证明,切向位移和切向应力变化的不同步性,存在相位差。
4. 非共轴角
为进一步分析接触面切向位移和切向应力变化的相位差,图 7给出了切向应力幅值τm=230 kPa时特定循环周次接触面正向和反向剪切时单位应力切向位移增量υ分布图。
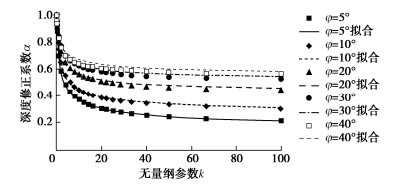
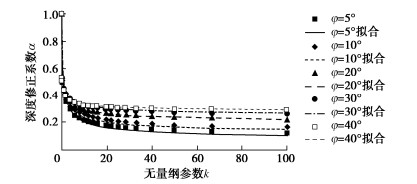
单位应力切向位移增量是指由单位切向应力所产生的切向位移增量(即υ=du/|dτ |),其为向量,既有大小,亦有方向。确定了单位应力切向位移增量的大小和方向,即可确定切向位移增量及其发展变化。单位应力切向位移增量的大小用剪切柔度(υ= |υ|)来衡量,方向用非共轴角α(图 1)来度量。
由图 7可以看出,单位应力切向位移增量方向与当前切向应力方向不同,亦与切向应力增量方向不同,处于两者之间,接触面产生了显著的非共轴特性。接触面非共轴特性是指单位应力切向位移增量方向或切向位移增量方向与当前切向应力方向不一致的现象,两者之间的夹角定义为接触面非共轴角α,其可从切向应力角ατ(图 1)与切向位移增量角αdu(图 1)的差值得到(α=αdu-ατ),取值范围为[-180°,180°]。
图 8给出了切向应力幅值τm=230 kPa时接触面切向应力角ατ、单位应力切向位移增量角αdu以及非共轴角α随循环周次N的时程曲线。可以看出,切向应力角、单位应力切向位移增量角随循环周次均呈现出有规律地变化,两者的变化形式基本一致但并不同步,存在一定的相位差,即存在非共轴角。这种有规律的变化使得接触面非共轴角也呈现有规律变化,这从图 7的单位应力切向位移增量随切向应力路径的有序变化亦可得到印证。
每个循环周次开始时,接触面进行正向剪切(图 7(a),7(c)),非共轴角均从一定数值开始迅速减小,而后基本趋于稳定,稳定值约为αr=38°,进一步说明接触面单位应力切向位移增量介于当前切向应力及其增量之间。当y向应力达到正向幅值接触面开始反向剪切时(图 7(b),7(d)),非共轴角迅速变为负值,且从一定数值迅速减小,而后基本稳定在约αr= -38°。应力控制往返圆形剪切路径下,当剪切方向反向时,结构面附近土颗粒要大幅调整,由原来的定向排列转向其相反方向;此时,切向位移增量与切向应力增量方向比较接近,非共轴角突然增大。当剪切到一定程度,土颗粒再次基本完成定向排列后,剪切时土颗粒只需局部调整,接触面非共轴角就基本达到稳定值。接触面正向剪切和反向剪切时非共轴角稳定值基本相等,且不同循环周次亦保持恒定。
图 9给出了第1循环周次(N=1)不同切向应力幅值下接触面单位应力切向位移增量分布图,图 10相应给出了接触面非共轴角α随循环周次N的时程曲线。结合图 7,8可以看出,不同切向应力幅值下接触面单位应力切向位移增量随切向应力路径均呈现出有规律地变化,切向应力幅值对单位应力切向位移增量分布形式影响不大,对非共轴角随循环周次的时程变化形式影响也很小。不同切向应力幅值下,每个循环周次接触面非共轴角均从一定数值逐渐减小,而后基本趋于稳定;并在半个循环周次接触面剪切方向反向时,非共轴角变为负值,但数值及发展趋势基本相同。接触面正向和反向剪切时非共轴角稳定值相等,且随循环剪切的进行基本保持不变。
不同切向应力幅值下,非共轴角稳定值不同;切向应力幅值对接触面非共轴角稳定值有显著影响。图 11给出接触面非共轴角稳定值αr及其变化率kαr随切向应力幅值的发展变化曲线;非共轴角稳定值变化率定义为其随切向应力幅值变化曲线的斜率(即kαr= dαr/dτm)。可以看出,随切向应力幅值的增加,接触面非共轴角稳定值逐渐减小,而减小速率则在逐渐增大;当切向应力幅值增大到一定程度时,非共轴角稳定值变化率迅速增大。也就是说,切向应力幅值越大,接触面非共轴角越小,其稳定值减小的越快;单位应力切向位移增量越向当前切向应力靠近,塑性剪应变的产生越趋向于当前切向应力,即接触面产生非共轴特性的能力越弱。可以推断,当切向应力幅值达到抗剪强度时(即τm=τf),塑性剪应变主要沿切向应力方向产生;接触面基本不会产生非共轴现象,非共轴角接近于零。接触面非共轴角稳定值αr与切向应力幅值τm呈现良好的关系:
αr=arccos(τmτf)。 (1) 式(1)满足当τm=τf时,非共轴角为零的条件。图 11也给出了式(1)的模拟结果,可以看出,模拟结果与试验结果吻合度良好。对式(1)进行求导,可以得到接触面非共轴角稳定值变化率kαr的计算式:
kα r=dαrdτm=−1τf√1−(τm/τmτfτf)2。 (2) 图 11也给出了非共轴角稳定值变化率曲线,可以看出,当切向应力幅值τm≥240 kPa,接触面非共轴角稳定值迅速减小,变化率迅速增大。
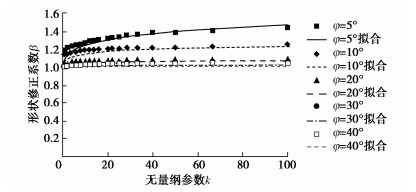
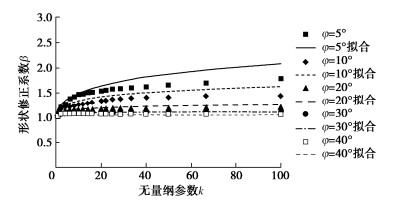
5. 剪切柔度
由图 7,9可以看出,单位应力切向位移增量不仅方向随剪切的进行发生有规律地变化,其大小也随剪切的进行有规律地增大和减小。定义单位应力所产生的切向位移增量的大小为接触面剪切柔度υ,其取值为单位应力切向位移增量的模(即υ=|υ|)。图 12给出了不同切向应力幅值下接触面剪切柔度υ随循环周次N的时程曲线。可以看出,不同切向应力幅值下,接触面剪切柔度随循环周次的变化形式较为类似,每个循环周次均从零开始增加,达到峰值后稍有减小。当切向应力幅值较小时(如τm≤230 kPa),接触面剪切柔度峰值随循环剪切的进行逐渐减小,而后总体上趋于稳定,呈现出明显的演化特性。当切向应力幅值较大时(如τm=240 kPa),接触面剪切柔度峰值随循环周次基本保持不变,与切向位移幅值随循环周次基本不变的规律一致。这说明切向应力幅值对接触面剪切柔度随循环周次的变化形式影响较小,主要影响接触面剪切柔度的大小及其随循环剪切的演化。切向应力幅值越大,同一循环周次接触面剪切柔度及其峰值越大,且增加程度非常明显。
图 13给出初始剪切时接触面剪切柔度首次达到的峰值(称为接触面剪切柔度初始峰值υp)及其变化率kυp与切向应力幅值τm的关系图;剪切柔度变化率定义为其初始峰值随切向应力幅值变化曲线的斜率(即kυp=dυp/dτm)。应力控制条件初始剪切时接触面物态演化程度很小,接触面剪切柔度可以进行比较;而当循环剪切到一定程度时,同一循环周次接触面物态演化程度不同,相应的剪切柔度很难进行比较。由图 13可以看出,接触面剪切柔度初始峰值随切向应力幅值的增加而显著增大;尤其是当切向应力幅值增加到一定程度时(如τm≥240 kPa),剪切柔度初始峰值迅速增加,其变化率迅速增大。接触面剪切柔度初始峰值υp与切向应力幅值τm间具有良好的关系,可用下式进行描述:
υp=a(1−τm/τf)2。 (3) 当τm=τf时,接触面剪切柔度初始峰值无限大,即切向位移将无限增加。由图 13给出的模拟结果和试验结果可以看出,该式的模拟效果良好。同样,对式(3)进行求导,可以得到接触面剪切柔度初始峰值变化率kνp的计算式:
kνp=dvpdτm=2aτf(1−τm/τf)3。 (4) 图 13也给出了剪切柔度初始峰值变化率曲线,可以看出,当切向应力幅值τm≥240 kPa,接触面剪切柔度初始峰值迅速增加,变化率迅速增大。
由图 11,13可以看出,接触面非共轴角稳定值αr、剪切柔度初始峰值υp随切向应力幅值τm的变化趋势完全相反。切向应力幅值越大,非共轴角及其稳定值越小,剪切柔度及其初始峰值则越大;这说明接触面非共轴角稳定值和剪切柔度初始峰值呈现对立统一的关系。将不同切向应力幅值下接触面剪切柔度初始峰值υp和非共轴角稳定值αr的关系绘制于图 14中,可以更清晰地看出两者的对立统一特性。接触面非共轴角和剪切柔度是单位应力切向位移增量的两个度量指标,随剪切的进行同时产生和发展,不可能单独存在;但两者的发展趋势则完全相反。非共轴角稳定值越大,其对剪切柔度产生和发展的阻碍作用越大,剪切柔度峰值越小。特别地,在每个循环周次开始剪切时,接触面在y向应力正向幅值处剪切方向反向,切向应力及其增量间夹角约为90°,非共轴角突然增大而后逐渐减小(图 10),此时剪切柔度则从较小值(接近于零)逐渐增大(图 12)。反之,接触面剪切柔度峰值越大,剪切柔度及切向变形发展越快,非共轴角则来不及发展,从而使非共轴角发展程度越低、稳定值越小;特别地,当切向应力幅值接近接触面抗剪强度时,剪切柔度增长极快、数值非常大(图 13),此时接触面非共轴角基本上没有发展,接近于零(图 11)。而当剪切柔度较小时,接触面非共轴角则有充分的时间和能力去发展,从而稳定值变大。由式(1),(3)可以推导出接触面剪切柔度初始峰值υp与非共轴角稳定值αr的关系式:
υp=a(1−cosαr)2。 (5) 可以更清楚地看出两者的反比关系及对立统一关系。图 14也给出了式(5)的模拟结果,可以看出与试验结果吻合度较好。
6. 结论
(1)应力控制往返圆形剪切路径下,接触面产生了明显的x向和y向位移,并均向负向偏移;显现出显著的三维特性和剪切耦合效应。切向应力幅值越大,x向和y向位移幅值越大,向负向偏移程度越大。当切向应力幅值小于临界应力幅值时,切向位移幅值随循环周次逐渐减小而后趋于稳定。当切向应力幅值等于临界应力幅值时,切向位移幅值则保持基本不变
(2)应力控制往返圆形路径下,接触面呈现出显著的非共轴特性,可用非共轴角和剪切柔度定量描述。每个循环周次接触面非共轴角均从一定数值逐渐减小,而后趋于稳定;该稳定值随循环剪切保持基本不变。切向应力幅值越大,非共轴角稳定值越小,切向位移增量越向当前切向应力靠近。非共轴角稳定值和切向应力幅值间存在良好的关系,可以用式αr=arccos(τm/τf)进行描述。
(3)每个循环周次,接触面剪切柔度均从较小值(接近零)开始增加,达到峰值后稍有减小。当切向应力幅值小于临界应力幅值时,剪切柔度峰值随循环剪切逐渐减小而后趋于稳定;当切向应力幅值达到临界应力幅值时,剪切柔度峰值随循环剪切基本不变。切向应力幅值越大,剪切柔度峰值越大。接触面剪切柔度初始峰值与切向应力幅值呈现良好的关系,可用式υp=a/(1−τm/τf)2进行描述。
(4)接触面剪切柔度初始峰值、非共轴角稳定值随切向应力幅值的变化趋势完全相反,两者呈对立统一的关系;在应力控制往返圆形剪切路径下可用式υp=a/(1−cosαr)2进行描述。接触面剪切柔度峰值越大,切向变形发展越快,非共轴角则来不及发展,发展程度越低、稳定值越小;反之亦然。
(5)切向应力幅值主要影响x向和y向位移幅值及其偏移程度、非共轴角和剪切柔度等接触面切向变形特性参数的数值,对切向位移间关系、切向应力位移关系及切向位移、非共轴角和剪切柔度随循环周次的时程变化等曲线形式影响较小。
-
表 1 基底粗糙时土体重度γ与黏聚力随深度增大率的等效性验证
Table 1 Verification of equivalence between γ and the rate of cohesion increase with depth under rough footings
算例编号 φ/(°) c/kPa γ/(kN·m-3) B/m q/kPa 滑移面深度/m 地基承载力/kPa 原模型 重度等效模型 原模型 重度等效模型 1 5 10 20 3 0 1.91 1.94 77.4 77.3 2 5 10 20 6 0 3.32 3.32 87.2 87.2 3 10 10 10 6 20 4.22 4.22 167.7 167.8 4 20 5 20 6 0 3.77 3.77 309.0 309.0 5 30 0 20 6 20 5.82 5.82 1509.2 1509.5 6 40 0 20 6 0 7.76 7.76 5107.1 5104.9 表 2 基底粗糙时无量纲参数k确定滑移面深度的检验
Table 2 Validation of dimensionless parameter k to determine depth of slip plane for rough footings
算例编号 φ/(°) c/kPa γ/(kN·m-3) B/m q/kPa 无量纲参数k 深度/m 深度修正系数α 1 10 10 20 3 0.0 1.06 1.95 0.73 2 10 0 20 3 56.7 1.06 1.95 0.73 3 10 10 10 6 0.0 1.06 3.91 0.73 4 10 10 20 6 56.7 1.06 3.91 0.73 5 20 20 10 6 0.0 1.09 5.51 0.79 6 20 0 10 6 54.9 1.09 5.51 0.79 7 20 10 20 6 0.0 4.37 4.36 0.63 8 20 0 20 6 27.5 4.37 4.36 0.63 9 20 5 20 6 0.0 8.74 3.77 0.54 10 20 10 20 12 0.0 8.74 7.54 0.54 11 30 5 10 6 0.0 6.93 5.95 0.63 12 30 5 20 6 8.7 6.93 5.95 0.63 13 30 0 20 6 0.0 无穷 4.66 0.49 14 30 0 20 12 0.0 无穷 9.33 0.49 表 3 基底光滑时无量纲参数k确定滑移面深度的检验
Table 3 Validation of dimensionless parameter k to determine depth of slip plane for smooth footings
算例编号 φ/(°) c/kPa γ/(kN·m-3) B/m q/kPa 无量纲参数k 深度/m 深度修正系数α 1 10 10 20 3 0.0 1.06 1.15 0.43 2 10 0 20 3 56.7 1.06 1.15 0.43 3 10 10 10 6 0.0 1.06 2.31 0.43 4 10 10 20 6 56.7 1.06 2.31 0.43 5 20 20 10 6 0.0 1.09 3.04 0.44 6 20 0 10 6 54.9 1.09 3.04 0.44 7 20 10 20 6 0.0 4.37 2.30 0.33 8 20 0 20 6 27.5 4.37 2.30 0.33 9 20 5 20 6 0.0 8.74 2.13 0.31 10 20 10 20 12 0.0 8.74 4.27 0.31 11 30 5 10 6 0.0 6.93 3.18 0.33 12 30 5 20 6 8.7 6.93 3.18 0.33 13 30 0 20 6 0.0 无穷 2.36 0.25 14 30 0 20 12 0.0 无穷 4.72 0.25 表 4 基底粗糙时计算方法的检验
Table 4 Verification of calculation method for rough footings
算例编号 φ/(°) c/kPa γ/(kN·m-3) B/m q/kPa 无量纲参数k 极限分析 公式计算 承载力相对误差/% Zmax/m Α pu/kPa α pu/kPa 1 5 20 10 3 0 0.13 2.24 0.94 136.8 0.94 136.4 -0.3 2 5 5 20 3 0 1.05 1.58 0.66 43.6 0.67 42.4 -2.8 3 5 0 20 3 0 无穷 0.40 0.17 3.4 0.13 3.2 -5.3 4 10 10 20 3 0 1.06 1.86 0.69 116.8 0.71 113.5 -2.9 5 10 0 20 6 40 3.00 3.11 0.58 153.4 0.57 148.6 -3.1 6 10 0 20 6 0 无穷 1.50 0.28 26.0 0.24 24.9 -4.2 7 20 20 10 6 0 1.09 5.40 0.77 458.3 0.77 446.3 -2.6 8 20 5 20 6 0 8.74 3.89 0.56 308.9 0.57 301.7 -2.3 9 20 0 20 6 0 无穷 2.81 0.40 169.9 0.40 164.5 -3.2 10 30 20 20 6 0 3.46 6.40 0.67 1823.2 0.71 1793.8 -1.6 11 30 5 20 6 0 13.86 5.42 0.57 1195.4 0.62 1194.2 -0.1 12 30 0 20 6 0 无穷 4.66 0.49 884.6 0.50 849.7 -3.9 13 40 20 20 6 0 5.03 8.80 0.62 7737.9 0.71 7850.8 1.5 14 40 0 20 6 0 无穷 7.55 0.54 5113.0 0.55 4889.8 -4.4 表 5 基底光滑时计算方法的检验
Table 5 Verification of calculation method for smooth footings
模型编号 φ/(°) c/kPa γ/(kN·m-3) B/m q/kPa 无量纲参数k 极限分析 公式计算 承载力相对误差/% Zmax/m α Pu/kPa α Pu/kPa 1 5 20 10 3 0 0.13 1.42 0.60 133.4 0.80 135.6 1.7 2 5 5 20 3 0 1.05 1.03 0.43 38.7 0.46 39.7 2.6 3 5 0 20 3 0 无穷 0.28 0.12 2.6 0.06 2.6 0.5 4 10 10 20 3 0 1.06 1.15 0.43 101.9 0.47 104.4 2.5 5 10 0 20 6 40 3.00 1.80 0.34 130.8 0.34 131.7 0.7 6 10 0 20 6 0 无穷 0.84 0.16 16.9 0.11 16.9 0.1 7 20 20 10 6 0 1.09 3.04 0.44 384.2 0.48 393.7 2.5 8 20 5 20 6 0 8.74 2.21 0.32 207.8 0.31 207.7 -0.1 9 20 0 20 6 0 无穷 1.49 0.21 94.6 0.19 95.0 0.4 10 30 20 20 6 0 3.46 3.58 0.38 1269.0 0.38 1276.1 0.6 11 30 5 20 6 0 13.86 2.98 0.31 716.1 0.32 722.2 0.8 12 30 0 20 6 0 无穷 2.36 0.25 457.9 0.25 461.8 0.8 13 40 20 20 6 0 5.03 4.80 0.34 4835.7 0.36 4785.6 -1.0 14 40 0 20 6 0 无穷 3.84 0.27 2571.0 0.28 2586.4 0.6 表 6 与太沙基公式的比较
Table 6 Comparisons with Terzaghi formula
算例编号 φ/(°) c/kPa 极限分析承载力/kPa 太沙基公式/kPa 太沙基公式相对误差/% 本文公式/kPa 本文公式相对误差/% 1 0 5 25.7 28.5 10.9 25.7 0.0 2 5 5 51.7 66.5 28.7 49.7 -3.9 3 10 5 92.3 120.0 30.0 88.4 -4.2 4 20 5 308.9 388.5 25.8 301.7 -2.3 5 30 5 1195.5 1368.0 14.4 1194.2 -0.1 6 40 5 5968.4 6502.5 8.9 6074.9 1.8 7 44 5 12705.0 16359.5 28.7 13033.0 2.6 8 0 50 257.1 285.0 10.9 257.1 0.0 9 5 50 351.7 395.0 12.3 349.9 -0.5 10 10 50 492.6 552.0 12.1 486.3 -1.3 11 20 50 1074.6 1185.0 10.3 1049.7 -2.3 12 30 50 2880.0 3042.0 5.6 2825.9 -1.9 13 40 50 10609.0 10809.0 1.9 10700.1 0.9 14 44 50 20430.0 23195.0 13.5 20938.2 2.5 表 7 与Hansen公式的比较
Table 7 Comparisons with Hansen formula
算例编号 φ/(°) c/kPa 极限分析承载力/kPa 系数1.5 系数1.8 系数2.0 本文公式/kPa 本文公式相对误差/% Hansen解/kPa 相对误差/% Hansen解/kPa 相对误差/% Hansen解/kPa 相对误差/% 1 0 5 25.7 25.7 0.0 25.7 0.0 25.7 0.0 25.7 0.0 2 5 5 51.7 36.9 -28.6 37.8 -26.9 38.4 -25.7 49.7 -3.9 3 10 5 92.3 65.1 -29.5 69.7 -24.4 72.9 -21.1 88.4 -4.2 4 20 5 308.9 251.0 -18.7 286.4 -7.3 310.0 0.4 301.7 -2.3 5 30 5 1195.5 1054.9 -11.8 1235.7 3.4 1356.3 13.4 1194.2 -0.1 6 40 5 5968.4 5149.0 -13.7 6103.5 2.3 6739.8 12.9 6074.9 1.8 7 0 50 257.1 257.1 0.0 257.1 0.0 257.1 0 257.1 0.0 8 5 50 351.7 328.9 -6.5 329.8 -6.2 330.4 -6.1 349.9 -0.5 9 10 50 492.6 440.6 -10.6 445.3 -9.6 448.4 -9.0 486.3 -1.3 10 20 50 1074.6 918.6 -14.5 954.0 -11.2 977.6 -9.0 1049.7 -2.3 11 30 50 2880.0 2411.2 -16.3 2592.0 -10.0 2712.6 -5.8 2825.9 -1.9 12 40 50 10609.0 8538.1 -19.5 9492.6 -10.5 10128.9 -4.5 10700.1 0.9 -
[1] TERZAGHI K. Theoretical Soil Mechanics[M]. Hoboken: John Wiley and Sons, 1943.
[2] LI Guang-xin, ZHANG Bing-yin, YU Yu-zhen. Soil Mechanics[M]. Beijing: Tsinghua University Press, 2013. (in Chinese) [3] CRAIG R F. Soil Mechanics[M]. Boston: Springer, 1983.
[4] VESIĆ A S. Analysis of ultimate loads of shallow foundations[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 99(1): 45–73. doi: 10.1061/JSFEAQ.0001846
[5] HANSEN J B. A general formula for bearing capacity[J]. Danish Geotechnical Institute, 1961(11): 38–46.
[6] VERRUIJT A. Soil Mechanics[D]. Delft: Delft University of Technology, 2012.
[7] DIAZ-SEGURA E G. Assessment of the range of variation of Nγ from 60 estimation methods for footings on sand[J]. Canadian Geotechnical Journal, 2013, 50(7): 793–800. doi: 10.1139/cgj-2012-0426
[8] 肖大平, 朱维一, 陈环. 滑移线法求解极限承载力问题的一些进展[J]. 岩土工程学报, 1998, 20(4): 25–29. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC804.005.htm XIAO Da-ping, ZHU Wei-yi, CHEN Huan. Progress in slip lines method to solve the bearing capacity problem[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(4): 25–29. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC804.005.htm
[9] 韩冬冬, 谢新宇, 王忠瑾, 等. 条形粗糙基础极限承载力求解与误差分析[J]. 岩土工程学报, 2016, 38(10): 1789–1796. doi: 10.11779/CJGE201610007 HAN Dong-dong, XIE Xin-yu, WANG Zhong-jin, et al. Solution and error evaluation for bearing capacity of rough strip footings[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(10): 1789–1796. (in Chinese) doi: 10.11779/CJGE201610007
[10] 李贤杰. 深基坑坑底抗隆起验算方法及圆形基坑分析方法研究[D]. 北京: 清华大学, 2020. LI Xian-jie, Calculation Method for Basal Stability of Deep Excavation and Analysis of Circular Foundation Pit[D]. Beijing: Tsinghua University, 2020. (in Chinese)
[11] SONG Er-xiang, FU Hao, LI Xian-jie, A calculation method for the bearing capacity of saturated soil under undrained conditions[J]. Rock and Soil Mechanics, 2021, 42(11): 2919–2924, 2952. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103024.htm [12] KRABBENHOFT K. OPTUM G2: Theory[M]. Copenhagen: Optum Computational Engineering, 2019.
[13] 宋二祥, 孔郁斐, 杨军. 土工结构安全系数定义及相应计算方法讨论[J]. 工程力学, 2016, 33(11): 1–10. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201611001.htm SONG Er-xiang, KONG Yu-fei, YANG Jun. Discussion of safety factor definitions and computation methods for geotechnical structures[J]. Engineering Mechanics, 2016, 33(11): 1–10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201611001.htm
[14] SU Dong. Soil Mechanics[M]. Beijing: Tsinghua University Press, 2015. (in Chinese) -
期刊类型引用(13)
1. 赵晶,陈诚,杜棣宾,文桃,简涛,应赛,周继强. 基于NMR的饱和土渗透系数预测方法. 山东大学学报(工学版). 2025(01): 108-116 .  百度学术
百度学术
2. 李鸿玮,马丽娜,张彦辉,李柏生. 干湿循环下基于Wiener退化的水泥基复合加芯墙板寿命预测. 兰州理工大学学报. 2023(01): 22-29 .  百度学术
百度学术
3. 韩立炜,姬伟斌. 降雨对膨胀土孔隙结构的影响研究. 人民黄河. 2023(05): 143-147+162 .  百度学术
百度学术
4. 包义勇,程学磊,李文东,方大转,李顺群,赵磊. 膨胀土地基海绵化改造技术分析. 安徽建筑. 2023(06): 97-98 .  百度学术
百度学术
5. 吴广水,田慧会,郝丰富,王书齐,杨文洲,祝婷梅. 基于核磁共振T_2时间分布快速预测不同干密度土体的渗透系数. 岩土力学. 2023(S1): 513-520 .  百度学术
百度学术
6. 吴广水,王书齐,祝婷梅,杨文洲,施航向,赵延平. 初始含水率和干密度对膨胀土膨胀力影响的试验研究. 河南工程学院学报(自然科学版). 2023(04): 29-32+50 .  百度学术
百度学术
7. 雷胜友,袁文治,翟志刚,田刚,陈雨菲,李思雨,芦地,柳明宇. 盐溶液质量分数对非饱和膨胀土抗剪强度的影响. 河南理工大学学报(自然科学版). 2022(02): 178-184 .  百度学术
百度学术
8. 李宝平,支枭雄,张玉,平高权. NaCl溶液改良膨胀土滞回曲线形态特征. 科学技术与工程. 2022(13): 5322-5330 .  百度学术
百度学术
9. 李宝平,支枭雄,张玉,平高权,杨倩. NaCl溶液改良膨胀土动力特性试验. 中国科技论文. 2022(07): 780-788 .  百度学术
百度学术
10. 雷胜友,田刚,陈雨菲,袁文治,翟志刚. 考虑盐溶液渗入影响的膨胀土边坡稳定性分析. 中国科技论文. 2021(02): 150-157 .  百度学术
百度学术
11. 陈君廉,李辉,谈云志. 盐溶液浸润下团粒膨润土的膨胀与渗透性能研究. 三峡大学学报(自然科学版). 2021(02): 80-85 .  百度学术
百度学术
12. 邱翱博,王欢,张旭,曹义康,杨惠如. 粉砂土改良膨胀土渗透性与孔隙特性研究. 河南大学学报(自然科学版). 2021(05): 614-623 .  百度学术
百度学术
13. 田芳. 冻融循环作用下膨胀土的力学与孔隙分布特点. 山东农业大学学报(自然科学版). 2020(02): 365-369 .  百度学术
百度学术
其他类型引用(15)




 下载:
下载: