双层均质边坡临界高度研究及其稳定性分析

田泽润; 张彦洪; 周茂定; 郭亚峰; 豆换换

doi:10.11779/CJGE20211365

双层均质边坡临界高度研究及其稳定性分析 English Version

甘肃农业大学水利水电工程学院, 甘肃兰州 730070

基金项目:

甘肃省科技重点研发计划项目 20YF3FA036

甘肃省高等学校创新基金项目 2020A-048

甘肃农业大学水利水电工程学院青年教师科技创新基金项目 SLSDXY-QN2019-06

详细信息

作者简介:
田泽润(1989—)，男，硕士，讲师，主要从事岩土数值模拟的教学和科研工作。E-mail: tianzerun1989@163.com

通讯作者:
张彦洪, E-mail: zhyh9606@163.com

中图分类号: TU457
计量
- 文章访问数: 219
- HTML全文浏览量: 44
- PDF下载量: 105
出版历程
- 收稿日期: 2021-11-17
- 网络出版日期: 2023-02-23
- 刊出日期: 2023-01-31

Critical height and stability of two-layered homogeneous slopes

Gansu Agricultural University, College of Water Conservancy and Hydropower Engineering, Lanzhou 730070, China

摘要

摘要: 基于边坡塑性极限理论，假定组合对数螺旋线破坏机构，直接推导出双层均质边坡的临界高度方程。通过强度折减法使边坡逐步处于极限平衡状态，进而获得边坡的稳定性安全系数。该方法直接进行外功率积分，无需采用数值方法解决外功率积分困难，并且显式表达边坡临界高度。针对强度折减过程中优化计算对初值的依赖性问题，基于均质边坡上限法的对数螺旋线优化参数，提出了层状边坡初值估算方法，通过重点空间重点搜索，使得边坡稳定性分析过程更加高效。通过算例的验证与对比分析，表明该方法具有较高的计算精度和稳定性，指出上限法在层状边坡局部稳定性分析中存在的问题，并重新构造出可以兼容整体与局部破坏模式的目标函数，解决该问题。最后，以兰州市某黄土边坡为工程背景，采用多种方法进行了稳定性分析，验证了所提方法的可靠以及初值的低依赖性, 可快速有效的应用于工程实践。
- 层状均质边坡 /
- 上限分析法 /
- 局部稳定性 /
- 初值估计 /
- 黄土边坡
Abstract: Based on the plastic limit theory of slopes, the critical height equation for a two-layered homogeneous slope is derived directly by using the sectioned logarithmic spiral failure mechanism. Through the strength reduction method, the slope is gradually placed in the limit equilibrium state, and then the factor of safety of slope stability is obtained. This method integrates the external power directly without using numerical methods, and displays the critical height of the slope. In view of the dependence of the initial values on the optimal calculation in the process of strength reduction, using the logarithmic spiral parameters of the upper bound limit analysis of the homogeneous slope, an estimation method for the initial values is proposed to make the slope stability analysis more efficient through the focus search in key optimization space. By vertifying and comparing the results of examples, the computational accuracy and stability are demonstrated, the problem of the upper bound method in local stability analysis of layered slopes is pointed out, and the objective function which can be used for various failure modes is derived. Finally, taking a loess slope in Lanzhou as the background, the stability of the slope is analyzed by using several methods. The results show that the proposed method is stable and reliable, with little dependence on the initial values, and can be applied to projects quickly and effectively.
- layered slope /
- upper bound limit analysis /
- local stability /
- initial estimation /
- loess slope

HTML全文

0. 引言

作为岩土力学的核心问题之一，边坡稳定性分析存在多种分析方法，总体来说可分为：刚体极限平衡法、有限元法、塑性极限分析法。其中，刚体极限平衡法由瑞典学者Fellenius^[1]于1927年首次提出，即瑞典圆弧法，随后诸多学者在此基础上先后提出简化Bishop法^[2]、Morgenstern-perice法^[3]、Spencer法^[4]、Janbu法^[5]等。刚体极限平衡方法假定边坡滑动区域为刚体，并认为边坡在极限滑移状态必然处于静力平衡状态，该法由于计算简单、适用性强，故而在工程实践中获到普遍应用，但根据塑性极限理论，极限平衡法的解答并非真实解的上、下限。有限元法认为边坡的失效是由于岩土体内产生等效塑性应变、位移、剪应变, 并持续发展导致，该方法也具备一定的适用性，但关于边坡发生极限滑移的判断标准并不统一，而且具有本构关系的不确定性^[6-7]，更多用于其他方法的验证对比。而塑性极限分析上限法由于忽略材料本构关系，其计算效率和精度较高，已被诸多学者逐渐接受。Chen^[8]首次将塑性上限分析法用于岩土工程问题，并推导出了边坡临界高度的显示表达式。随后Karal^[9]在前人基础上改进塑性极限上限法，推导出边坡安全系数表达式。Michalowski^[10]垂直划分边坡滑块，基于非关联流动法则, 给出平动运动场安全系数上限解法。Donald等^[11]基于变形协调，斜条划分边坡滑体, 并建立机动许可速度场，提出平动速度场的极限分析上限法。杨峰等^[12]基于非线性规划模型，提出一种刚体平动单元上限有限元法获得较高计算精度。刘锋涛等^[13]提出了基于滑动面摄动的刚体有限元上限法，并验证了考虑刚体滑动的必要性。

目前关于边坡稳定分析的极限上限法的众多研究主要针对于均质边坡，而对于层状边坡研究较少。王珍等^[14]虽然通过对数螺旋线的多项式拟合, 解决了层状边坡的积分问题，提高了边坡塑性上限法的适用性。但是仍然存在需要改善的方面：①层状边坡分界处滑移面连续性条件不一定严格满足，即使拟合精度较高；②针对滑移面通过坡趾下方的情况，拟合过程不一定满足必要的数学条件；③未能显式表达边坡临界高度，未能通用于局部边坡稳定性分析，并且拟合计算量较大。基于以上不足，本文采用塑性极限分析上限法的基本原理直接推导出双层均质边坡的临界高度公式，一定程度上否定了层状边坡的外功率积分的困难性，并提出了一种基于均质边坡优化参数和多项式拟合的初值估计方法，缩小了优化搜索范围，尽可能地兼顾了全局最优性和优化效率；尝试将基于对数螺旋线破坏机构的上限法通用于层状边坡的局部稳定性分析，指出了该上限法的局限性，并推导出可以同时兼容边坡整体和局部稳定性分析的目标函数，解决了该问题。

1. 层状边坡稳定性分析

1.1 层状边坡破坏模式及特征

根据已有研究成果^[15-17]，层状土坡的临界破坏机构可假设为组合对数螺旋线，其主要破坏特征为：①组合对数螺旋线的交点处的速度必然存在唯一性，例如图 1中B点。考虑到滑动土体的刚性体特征，每段对数螺旋线的角速度和旋转中心相同。②层状边坡滑移面可能通过坡趾、坡趾下方、坡趾上方。这取决于边坡的坡比和内摩擦角的相对大小，以及边坡层高比例。边坡最终破坏模式取决于以上稳定性最差的模式，故而需要同时分析尽可能多的失效模式。基于整体失效模式建立的边坡稳定分析上限法原理是否可直接适用于所有情况，值得商榷。

图 1 双层边坡破坏机构示意图

Figure 1. Illustration of failure mechanism of two-layered slope

下载: 全尺寸图片幻灯片

图 1中参数m，1-m为层高比例系数，即每层边坡高度与水平总高度H之比。两段对数螺旋线方程可用式（1）表示，为推导公式的方便，将两个方程中的指数部分分别用g₁和G₁代替表示，如式（2）所示。

$\left. {\begin{array}{*{20}{l}}r={r}_{0}\mathrm{exp}[(\theta -{\theta }_{0})\mathrm{tan}{\varphi }_{1}]\text{ }\text{，}\\ r={r}_{\text{m}}\mathrm{exp}[(\theta -{\theta }_{\text{m}})\mathrm{tan}{\varphi }_{2}]\text{ }\text{，}\end{array}} \right\}$

(1)

式中， ${r_{\text{m}}}$ ， ${r_{\text{h}}}$ 可以表示为式（2），并为方便公式推导，将其指数部分表示为g₁，G₁。

$\left. {\begin{array}{*{20}{l}}{r}_{\text{m}}={r}_{0}\mathrm{exp}[({\theta }_{\text{m}}-{\theta }_{0})\mathrm{tan}{\varphi }_{1}]={r}_{0}{g}_{1}\text{ }\text{，}\\ {r}_{\text{h}}={r}_{\text{m}}\mathrm{exp}[({\theta }_{\text{h}}-{\theta }_{\text{m}})\mathrm{tan}{\varphi }_{2}]={r}_{0}{g}_{1}{G}_{1}\text{ }。\end{array}} \right\}$

(2)

由图 1中的几何关系式可知H/r₀，L₁/ r₀，L₂/ r₀，L₂/ r_m等的表达式为

$\frac{H}{{{r_0}}} = \frac{{\sin \beta '}}{{\sin (\beta ' - {\alpha _1})}}\left\{ {{g_1}{G_1}\sin ({\theta _{\text{h}}} + {\alpha _1}) - \sin ({\theta _0} + {\alpha _1})\begin{array}{*{20}{c}} {} \\ {} \end{array}} \right\}\text{，}$

(3)

$\frac{{{L_1}}}{{{r_0}}} = \frac{1}{{\cos {\alpha _1}}}\left\{ {\cos {\theta _0} - {g_1}{G_1}\cos {\theta _{\text{h}}} - \frac{H}{{{r_0}}}\cot \beta '} \right\} \text{，}$

(4)

$\frac{{{L_2}}}{{{r_0}}} = \frac{1}{{\cos {a_2}}}\left\{ {{g_1}\cos {\theta _{\text{m}}} - {g_1}{G_1}\cos {\theta _{\text{h}}} - (1 - m')\frac{H}{{{r_0}}}\cot \beta '} \right\},$

(5)

$m' = m[1 + \frac{{\sin {a_2}\sin \beta '}}{{\sin (\beta ' - {a_2})}}(\cot \beta ' - \cot \beta )] \text{，}$

(6)

$\frac{{{L_2}}}{{{r_m}}} = \frac{{{L_2}}}{{{r_0}{g_1}}} 。$

(7)

式中：L₁，L₂分别为中的AE、BG段长度； $m'$ 为虚层高比例系数，其物理含义为虚坡面CE上的比例系数，当 ${a_2} = 0$ 时， $m' = m$ 。

1.2 边坡塑性极限上限法

极限分析上限法又称极限分析能量法，认为对于某种机动许可速度场与变形场，根据外力功率等于速度间断面处内部能量耗散率确定的极限荷载一定是真实解的上限。该法应用于土质边坡需满足假设条件：①将土体视为理想塑性材料，破坏时服从线性莫尔库仑破坏准则；②土体服从相关流动法则。

（1）重力功率计算

由图 1可知，极限平衡状态下的边坡重力功率W可以表示为

$W = ({W_{AENB}} + {W_{MNB}}) + {W_{MBC}} - {W_{EMG}} - {W_{MGDC}} \text{，}$

(8)

式中，W_AENB，W_MNB，W_MBC，W_EMG，W_MGDC分别为图 1中四边形AENB、∆MNB、∆MBC、∆EMG以及四边形MGDC的重力功率（kW）。

a）滑块AENB的重力功率

${W_{AENB}} = {\text{ }}{W_{OAB}} - {\text{ }}{W_{OAE}} - {W_{ONE}} \\ \ \ \ \ \ \ \ \ \ \ = {\gamma _1}r_0^3\omega ({f_{OAB}} - {f_{OAE}} - {f_{ONE}}) \text{，}$

(9)

式中， $\omega$ 为角速度（rad/s）， ${\gamma _1}$ 为重度（kN/m³）， ${f_{OAB}}$ ， ${f_{OAE}}$ ， ${f_{ONE}}$ 可以表示为

${f_{OAB}} = \frac{1}{{3{\text{(1}} + {\text{9ta}}{{\text{n}}^2}{\varphi _1}{\text{)}}}}\left\{ {(3\tan {\varphi _1}\cos {\theta _m} + \sin {\theta _m})} \right.g_1^3 - \\ \ \ \ \ \ \ \ \ \ \ \left. {(3\tan {\varphi _1}\cos {\theta _0} + \sin {\theta _0})} \right\}\text{，}$

(10)

${f_{OAE}}{\text{ = }}\frac{1}{6}\frac{{{L_1}}}{{{r_0}}}(2\cos {\theta _0} - \frac{{{L_1}}}{{{r_0}}}\cos {\alpha _1})\sin ({\theta _0} + {\alpha _1})\text{，}$

(11)

$\begin{array}{l} {f_{ONE}} = \frac{1}{6}\sin ({\theta _m} + \beta ')\left( {{g_1} - \frac{{{L_2}}}{{{r_0}}}\frac{{\sin \beta '}}{{\sin ({\theta _{\text{m}}} + \beta ')}}} \right) \cdot \hfill \\ \left( {\frac{{m'}}{{\sin \beta '}}\frac{H}{{{r_0}}} - \frac{{\sin {\theta _{\text{m}}}}}{{\sin ({\theta _{\text{m}}} + \beta ')}}\frac{{{L_2}}}{{{r_0}}}} \right)({g_1}{G_1}\cos {\theta _{\text{h}}} + \hfill \\ \ \ \frac{H}{{{r_0}}}\cot \beta ' + {g_1}\cos {\theta _m} - \frac{{{L_2}}}{{{r_0}}}\frac{{\sin \beta '\cos {\theta _m}}}{{\sin ({\theta _m} + \beta ')}}) \text{，} \end{array}$

(12)

式中， $\beta '$ 为中角度 $\angle ECD$ 。

b）滑块MNB的重力功率

${W_{MNB}} = {\text{ }}{\gamma _1}r_0^3\omega {f_{MNB}}\text{，}$

(13)

式中， ${f_{MNB}}$ 可以表示为

${f_{MNB}} = \frac{1}{6}\frac{{\sin \beta '\sin {\theta _{\text{m}}}}}{{\sin ({\theta _{\text{m}}} + \beta ')}}{\left( {\frac{{{L_2}}}{{{r_0}}}} \right)^2}\left\{ \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right.{g_1}{G_1}\cos {\theta _h} + (1 - m') \cdot \\ \ \ \ \ \ \ \ \ \ \left. {\frac{H}{{{r_0}}}\cot \beta ' + 2{g_1}{\text{cos}}{\theta _{\text{m}}} - \frac{{{L_2}}}{{{r_0}}}\frac{{sin\beta '\cos {\theta _{\text{m}}}}}{{\sin ({\theta _{\text{m}}} + \beta ')}}} \right\}。$

(14)

c）滑块MBC的重力功率

${W_{MBC}} = {\text{ }}{W_{OBC}} - {\text{ }}{W_{OMB}} - {W_{OMC}} \\ \ \ \ \ \ \ \ \ \ \ = {\gamma _2}r_0^3\omega ({f_{OBC}} - {f_{OMB}} - {f_{OMC}})\text{，}$

(15)

式中， ${\gamma _2}$ 为下层材料的重度， ${f_{OBC}}$ ， ${f_{OMB}}$ ， ${f_{OMC}}$ 可以表示为

${f}_{OBC}=\frac{1}{3（\text{1}+{\text{9tan}}^{2}{\varphi }_{2}）}\{(3\mathrm{tan}{\varphi }_{2}\mathrm{cos}{\theta }_{\text{h}}+\mathrm{sin}{\theta }_{\text{h}}){G}_{1}^{3}- \\ \ \ \ \ \ \ \ \ \ \ \left. {(3\tan {\varphi _2}\cos {\theta _{\text{m}}} + \sin {\theta _{\text{m}}})} \right\}g_1^3\text{，}$

(16)

${f}_{OMB}\text{=}\frac{1}{6}\frac{{L}_{2}}{{r}_{\text{m}}}\left(2\mathrm{cos}{\theta }_{\text{m}}-\frac{{L}_{2}}{{r}_{\text{m}}}\mathrm{cos}{\alpha }_{2}\right)\mathrm{sin}（{\theta }_{\text{m}}\text{+}{\alpha }_{2}）{g}_{1}^{3} \text{，}$

(17)

${f_{OMC}}{\text{ = }}\frac{1}{6}{G_{\text{1}}}\left\{ {\sin ({\theta _{\text{h}}} - {\theta _{\text{m}}}) - \frac{{{L_2}}}{{{r_{\text{m}}}}}{\text{sin}}({\theta _{\text{h}}}{\text{ + }}{\alpha _2})} \right\} \\ \ \ \ \ \ \ \ \ \ \left\{ {{\text{cos}}{\theta _{\text{m}}} - \frac{{{L_2}}}{{{r_{\text{m}}}}}{\text{cos}}{\alpha _2}{\text{ + cos}}{\theta _{\text{h}}}{G_1}} \right\}g_1^3\text{，}$

(18)

d）滑块EMG的重力功率

${W_{EMG}} = {\text{ }}{\gamma _1}r_0^3\omega {f_{EMG}}\text{，}$

(19)

式中， ${f_{EMG}}$ 可以表示为

${f_{EMG}} = \frac{{{{m'}^2}}}{6}{\left( {\frac{H}{{{r_0}}}} \right)^2}(\cot \beta ' - \cot \beta )[3{g_1}{G_1}\cos {\theta _{\text{h}}} + \\ \ \ \ \ \ \ \ \ 3\frac{H}{{{r_0}}}\cot \beta ' - m'\frac{H}{{{r_0}}}(\cot \beta ' + \cos \beta )] 。$

(20)

e）滑块MGDC的重力功率

${W_{MGDC}} = {\text{ }}{\gamma _2}r_{\text{m}}^3\omega {f_{MGDC}}\text{，}$

(21)

式中， ${f_{MGDC}}$ 可以表示为

$\begin{array}{l} {f_{MGDC}} = \frac{{(1 - m')(\cot \beta ' - \cot \beta )}}{6}{\left( {\frac{H}{{{r_{.0}}}}} \right)^2}\left[ \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right.3{g_1}{G_1}\cos {\theta _{\text{h}}} + \hfill \\ \left. {\frac{H}{{{r_{.0}}}}\cot \beta '(2 - m') - \frac{H}{{{r_{.0}}}}\cot \beta } \right] + \frac{{(1 - m)(\cot \beta ' - \cot \beta )}}{6} \hfill \\ {\left( {\frac{H}{{{r_{.0}}}}} \right)^2}\left\{ {3{g_1}{G_1}\cos {\theta _h} + \frac{H}{{{r_{.0}}}}\left[ {\cot \beta '(3 - m') - (1 + m)\cot \beta } \right]} \right\} \cdot \hfill \\ \ \ \frac{{m\sin \beta '\sin (\beta - {a_2})}}{{\sin (\beta ' - {a_2})\sin \beta }} 。 \end{array}$

(22)

（2）内部耗散率计算

对岩土体的塑性上限法来说，将滑移面视作速度间断面，其内过渡层的变形模式由平行于滑裂面的剪流与垂直于该层的拉伸效应组合而成^[8]。故而发生在速度间断面处的能量耗损只包含黏聚力项。

对于双层边坡，存在两个对数双螺旋速度间断面，故而边坡极限状态的内能耗散等于两个速度间断面内能耗散的总和：

$D = \int_{{\theta _0}}^{{\theta _{\text{m}}}} {{c_1}({V_1}\cos {\varphi _1})\frac{{{R_1}{\text{d}}\theta }}{{\cos {\varphi _1}}}} + \int_{{\theta _{\text{m}}}}^{{\theta _{\text{h}}}} {{c_2}(V} \cos {\varphi _2})\frac{{{R_2}{\text{d}}\theta }}{{\cos {\varphi _2}}} \\ \ \ \ \ \ \ = \frac{{{c_1}r_0^2\omega }}{{2\tan {\varphi _1}}}(g_1^2 - 1) + \frac{{{c_2}r_0^2\omega }}{{2\tan {\varphi _2}}}(G_1^2 - 1)g_1^2 。$

(23)

式中：D为内能耗散率；V₁，V₂，c₁，c₂，R₁，R₂分别为上、下层微元滑块对数螺旋线切线方向的线速度（m/s），黏聚力（kPa），以及对数螺旋线半径。

（3）边坡临界高度

由岩土体的塑性上限方法可知，处于极限平衡状态的边坡，外力功率等于内部能量耗散率，由此可以得出非均质边坡临界高度表达式：

${H_{{\text{cr}}}} = \left[ {\frac{{{c_1}}}{{{\gamma _1}}}{\text{ }}\frac{{{c_2}}}{{{\gamma _2}}}} \right]{\left[ \begin{gathered} {f_{11}}({\theta _{\text{h}}}, {\theta _0}, \beta ') \hfill \\ {f_{22}}({\theta _{\text{h}}}, {\theta _0}, \beta ') \hfill \\ \end{gathered} \right]_{}}\text{，}$

(24)

式中， ${f_{11}}$ ， ${f_{22}}$ 可以表示为

${f_{11}}\sin ({\theta _{\text{h}}}, {\theta _{\text{0}}}, \beta ') = \frac{{g_{\text{1}}^2 - 1}}{{2\tan {\varphi _1}FF({\theta _{\text{h}}}, {\theta _{\text{0}}}, \beta ')}}\left( {\frac{H}{{{r_0}}}{\gamma _1}} \right)\text{，}$

(25)

${f_{22}}\sin ({\theta _{\text{h}}}, {\theta _{\text{0}}}, \beta ') = \frac{{g_{\text{1}}^2G_{\text{1}}^2 - 1}}{{2\tan {\varphi _2}FF({\theta _{\text{h}}}, {\theta _{\text{0}}}, \beta ')}}\left( {\frac{H}{{{r_0}}}{\gamma _2}} \right)\text{，}$

(26)

其中，g₁，G₁为对数螺旋线半径表达式的指数部分，如式（8）所示。 $FF({\theta _{\text{h}}}, {\theta _0}, \beta ')$ 可表示

$FF({\theta _{\text{h}}}, {\theta _0}, \beta ') = ({f_{OAB}} + {f_{MNB}} - {f_{ONE}} - {f_{OAE}} - \\ \ \ \ \ \ \ \ \ {f_{EMG}}){\gamma _1} + ({f_{OBC}} - {f_{OBM}} - {f_{OMC}} - {f_{MGDC}}){\gamma _2} 。$

(27)

由此可见，对于层状边坡来说，无量纲系数N_cr不再是一个单一边坡稳定系数，而是一个元素相互关联的列向量。当临界高度等于边坡实际高度时候，该稳定系数列向量就是一个上限解答。

式（24）中的待优化参数为 ${\theta _0}$ ， ${\theta _{\text{h}}}$ ， $\beta '$ ，不含 ${\theta _{\text{m}}}$ ，因为 ${\theta _{\text{m}}}$ 与 ${\theta _0}$ 以及 ${\theta _{\text{h}}}$ 之间存在隐式关系，如等式（28）所示，通过采用MATLAB中的vpasolve函数求解 ${\theta _{\text{m}}}$ ，需注意初值必须选在 ${\theta _0}$ 与 ${\theta _{\text{h}}}$ 之间。

$m'\left( {{g_1}{G_1}\sin {\theta _{\text{h}}} - {g_1}\sin {\theta _{\text{m}}} - \frac{{{L_2}}}{{{r_o}}}\sin {\alpha _2}} \right) - (1 - m') \cdot \\ \ \ \ \ \ \ \ \ \ \ \left( {{g_1}\sin {\theta _{\text{m}}} - \sin {\theta _0} - \frac{{{L_1}}}{{{r_o}}}\sin {\alpha _1} + \frac{{{L_2}}}{{{r_o}}}\sin {\alpha _2}} \right) = 0 。$

(28)

基于强度折减法，将每次强度折减后的参数代入式（29）进行优化计算，直到边坡临界高度等于边坡实际高度，则此时的折减系数就是边坡的稳定性安全系数。

可以直接将H_cr（或F_s隐函数）看作目标函数则边坡稳定分析的数学规划表达式为

$\min {\text{ }}{H_{cr}} = \frac{{{c_1}{f_{11}}({\theta _h}, {\theta _0}, \beta ')}}{{{\gamma _1}}} + \frac{{{c_2}{f_{22}}({\theta _h}, {\theta _0}, \beta ')}}{{{\gamma _2}}}\text{，}$

(29)

${\text{s}}{\text{.t}}{\text{. }}\left\{ \begin{array}{l} {\theta _0} < {\theta _{\text{h}}} < {\text{π }} \hfill \\ 0 < {\theta _0} \leqslant \frac{{\text{π }}}{2} \hfill \\ 0 < \beta ' < \beta \hfill \\ \end{array} \right.。$

(30)

对于采用了对数螺旋线破坏机构的上限法来说，式（29）或其他外功率与内能耗散率平衡的表述，并不完全适用于层状边坡的局部稳定分析（后续算例说明），因此重新构造目标函数：

$\bar{\text{ H}} = {H_{{\text{cr}}}}\left\{ {{\text{sin}}\left( {\frac{{\text{π }}}{2}{\text{ + }}{\varphi _1}} \right){\text{exp}}\left[ {\left( {\frac{{\text{π }}}{2}{\text{ + }}{\varphi _1} - {\theta _0}} \right){\text{tan}}{\varphi _1}} \right]} \right. - \\ \ \ \ \ \ \ \ \left. {{\text{sin}}{\theta _0} - \frac{{mH}}{{{r_0}}}} \right\} \text{，}$

(31)

即

$\min {\text{ }}\bar H = \bar H({\theta _0}, {\theta _{\text{h}}}, \beta ')\text{，}$

(32)

(33)

目标函数（31）物理含义明确，等式右侧第一项为边坡临界高度表达式即式（29）；右侧第二项大括号内的表达式是上层边坡滑移面侵入下层深度的度量；该目标函数将搜索所有满足H_cr≤H，并且侵入量最小的滑移面，可根据工程实际需要将零或某个可接受的极小正值作为最优目标函数值。若令式（31）中m=1，并且满足约束条件（33），则与式（29）等效，因此该重构函数可方便地应用于边坡整体及局部稳定性分析，具有较好的兼容性。

优化过程中，优化结果对于初值的依赖性问题是一个亟待解决的问题，本文探索性地提出了一种初值估算方法，并通过工程实例进行了研究分析。

2. 优化过程初值估计

对于边坡的塑性极限上限法来说，独立优化参数只有3个，即 ${\theta _0}$ ， ${\theta _{\text{h}}}$ ， $\beta '$ 。考虑到同一边坡模型上双层材料的整体抗剪效果应该介于两种均质材料之间。因此非均质边坡的最终优化参数值应该是两种不同材料优化参数估计值的某种组合，考虑到每层层高对优化参数的影响，提出以下初值估算公式：

$\left. {\begin{array}{*{20}{l}}{\theta }_{\text{H}}=m({\theta }_{\text{h1}}\text{+}{\alpha }_{1})+(1-m)({\theta }_{\text{h2}}\text{+}{\alpha }_{2})\text{ }\text{，}\\ {\theta }_{0}=m{\theta }_{01}({\theta }_{\text{h1}}\text{+}{\alpha }_{1})+(1-m){\theta }_{02}({\theta }_{\text{h2}}\text{+}{\alpha }_{2})\text{ }。\end{array}} \right\}$

(34)

式中：θ₀₁和θ_h1、θ₀₂和θ_h2为上、下层边坡材料所对应的优化参数估计值，可将其转化为约束条件，以缩小优化搜索空间；θ_H， ${\theta _0}$ 为层状边坡初始估计值。对于参数 $\beta '$ ，通常直接取坡趾角度β作为初始估计值。只要获得均质边坡的优化参数估计值，则可由式（34）获得层状边坡的优化参数的估计值。

分别取β=[15°，20°，25°， $\cdots$ ，90°]，取φ=[1° 2° $\cdots$ 50°]，进行边坡稳定系数优化计算，并根据最终优化结果，进行数据拟合，获得以下表达式。

（1） ${\theta _0}$ 的拟合表达式（拟合确定性系数0.9994）

${\theta _0} = {\text{0}}{\text{.792}} - {\text{1}}{\text{.825}}\beta + {\text{3}}{\text{.506}}\varphi + {\text{1}}{\text{.967}}{\beta ^2} - {\text{0}}{\text{.6}}{\beta ^3} - \\ \ \ \ \ \ \ \ {\text{5}}{\text{.011}}\beta \varphi + {\text{1}}{\text{.401}}{\varphi ^2} + {\text{2}}{\text{.02}}{\beta ^2}\varphi - {\text{0}}{\text{.862}}\beta {\varphi ^2}。$

(35)

（2） ${\theta _{\text{h}}}$ 的拟合表达式（拟合确定性系数0.9992）

当折减后的内摩擦角φ满足以下不等式：

$\varphi \leqslant {\text{2}}{\text{.429}}{\beta ^3} - {\text{3}}{\text{.497}}{\beta ^2} + {\text{1}}{\text{.242}}\beta + {\text{0}}{\text{.046}}\text{，}$

(36)

则可通过下式估算 ${\theta _{\text{h}}}$ （拟合确定性系数为0.9957）：

${\theta _{\text{h}}} = {\text{2}}{\text{.735}} - {\text{0}}{\text{.988}}\beta - {\text{8}}{\text{.239}}\varphi + {\text{1}}{\text{.743}}{\beta ^2} + {\text{10}}{\text{.6}}{\varphi ^2} + \\ \ \ \ \ \ \ \ {\text{22}}{\text{.197}}\beta \varphi - {\text{1}}{\text{.062}}{\beta ^3} - {\text{33}}{\text{.065}}{\beta ^2}\varphi - {\text{1}}{\text{.145}}\beta {\varphi ^2}。$

(37)

当折减后的内摩擦角φ满足

$\varphi \geqslant {\text{2}}{\text{.429}}{\beta ^3} - {\text{3}}{\text{.497}}{\beta ^2} + {\text{1}}{\text{.242}}\beta + {\text{0}}{\text{.046}}\text{，}$

(38)

则可通过下式估算 ${\theta _{\text{h}}}$ （拟合确定性系数为0.9997）：

$\begin{array}{l} {\theta _{\text{h}}} = 1.11{\beta ^5} - 3.91{\beta ^4}\varphi - 5.185{\beta ^4} + 6.377{\beta ^3}{\varphi ^2} + \hfill \\ 14.364{\beta ^3}\varphi + 9.417{\beta ^3} - 4.952{\beta ^2}{\varphi ^3} - 17.808{\beta ^2}{\varphi ^2} - \hfill \\ 19.269{\beta ^2}\varphi - 8.399{\beta ^2} + 1.533\beta {\varphi ^4} + 10.538\beta {\varphi ^3} + \hfill \\ 14.465\beta {\varphi ^2} + 12.385\beta \varphi + 2.676\beta - 0.29{\varphi ^5} - \hfill \\ \ \ 1.217{\varphi ^4} - 6.169{\varphi ^3} - 2.168{\varphi ^2} - 3.86\varphi + 2.012{\text{ }} 。 \end{array}$

(39)

根据以上拟合关系式结合式（34）可求出层状边坡初始估计值，进而允许局部优化算法在兼顾全局最优性和优化效率的前提下，在重点优化空间内的关键点附近快速完成优化计算过程。

3. 算例分析

层状边坡稳定失效模式不唯一，目前基于对数螺旋线破坏机构的上限法研究成果多针对于整体破坏模式，而整体稳定分析程序在局部稳定性分析上的通用性问题并未获得重视，因此本节首先通过已有算例进行程序验证，然后基于该算例指出对数螺旋线破坏机构在边坡局部稳定中存在的局限性，并给出相关建议。

3.1 计算程序验证分析（整体+局部）

（1）算例1：采用已有案例^[18]进行稳定性分析验证，边坡模型坡高8 m，坡比1∶1.3，层高比例系数为0.5，其材料参数如表 1中整体失效模式所示，分别采用Morgenstern-Price法、本文上限法以及刚体单元上限法（OPTUM-G2）进行稳定性分析，其结果如图 2和表 2所示。

表 1 双层边坡材料组合

Table 1. Material combination of two-layered slope

失效模式	位置	黏聚力c/kPa	内摩擦φ/(°)	重度γ/(kN·m^-3)
整体^[21]	上层	5.3	23	19.5
整体^[21]	下层	7.2	20	19.5
局部1	上层	4	20	19.5
局部1	下层	7.2	27	19.5
局部2 β=30°, m=5/8	上层	12	14	19.5
局部2 β=30°, m=5/8	下层	20	23	19.5

下载: 导出CSV

| 显示表格

图 2 算例1:边坡稳定性分析(整体失效模式)

Figure 2. Stability analysis of slope (global failure mode)

下载: 全尺寸图片幻灯片

表 2 边坡稳定安全系数验证对比(算例1)

Table 2. Verification and comparison of factors of safety (slope example 1)

计算方法	安全系数F_s
瑞典条分法^[18]	0.96
Bishop法^[18]	1.00
Janbu法^[18]	1.00
刚体单元上限法	1.02
刚体单元下限法^[18]	0.98
Morgenstern-Price法	1.004
本文方法	1.007

下载: 导出CSV

| 显示表格

结合图 2和表 2可知，本文方法与Bishop法、Janbu法以及刚体单元上限法最为接近，说明了该方法的准确性。

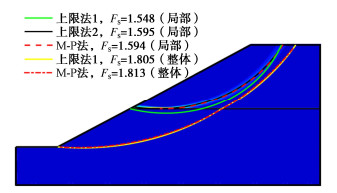
（2）算例2，3：分别采用表 1中局部失效模式1、2，并且前者采用式（29），后者采用式（31）进行边坡稳定性分析，并将其分别记为“上限法1”，“上限法2”，结果如图 3，4所示。其中刚体单元上限法安全系数表示在括号内。

图 3 算例2:边坡稳定性分析(局部1，F_s=1.076)

Figure 3. Exmple 2: stability analysis of slope (local model 1, F_s=1.076)

下载: 全尺寸图片幻灯片

图 4 算例3:边坡稳定性分析(局部2，F_s=1.614)

Figure 4. Exmple 3: stability analysis of slope (local model 2, F_s=1.614)

下载: 全尺寸图片幻灯片

分析图 3与表 1可知，当坡度较大、内摩擦角相差不大时，令m=1，可准确实现局部稳定分析。

分析图 4可知，当坡度减小为30°，并且内摩擦角相差较大时，令m=1，即简单的视作均质边坡进行稳定性分析，求出滑移面（图 4中上限法1）存在明显的错误下侵，并不合理，这就说明边坡整体失效的计算理论或程序并不具有通用性, 究其原因，是由于对数螺旋线的曲率半径递增特性。为了解决该问题，采用重构目标函数的方法（上限法2）进行稳定性分析，虽然H_cr≠H，但安全系数以及滑移面都与Morgenstern-Price法非常接近，说明重构目标函数比目标函数（29）更加有效。

3.2 工程应用（算例4，5）

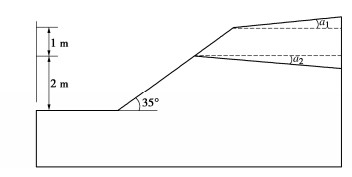
兰州市黄河北岸某天然植被边坡，坡度35°，由坡顶1m厚的植被黄土层和植被层以下2 m厚的素黄土层构成，坡面上没有植物。植被主要是小型灌木和旱生草本为主，上坡角 ${\alpha _1} =$ 6°，分界面夹角 ${\alpha _2} =$ -5°。植被黄土层的土重度为 ${\gamma _1} =$ 14.5 kN/m³，黏聚力 ${c_1} =$ 22 kPa，内摩擦角 ${\varphi _1} =$ 32°，素黄土层重度为 ${\gamma _2} =$ 15.8 kN/m³，黏聚力18 kPa，内摩擦角 ${\varphi _2} =$ 24°。为验证滑移面通过坡趾下方的情况，可取 ${\varphi '_1} =$ 18°， ${\varphi '_2} =$ 16°，边坡几何模型如图 5所示。

图 5 兰州市黄河北岸某植被边坡

Figure 5. Vegetated slope on north bank of Yellow River in Lanzhou

下载: 全尺寸图片幻灯片

选用兰州市南山植被边坡岩土体参数，基于每次强度折减获得的强度参数和所示几何模型，利用拟合关系式可以获得两组材料分别对应的优化参数估计值（ ${\theta _{01}}$ ， ${\theta _{{\text{h1}}}}$ ， ${\theta _{02}}$ ， ${\theta _{{\text{h2}}}}$ ），然后利用式（34）计算出非均质边坡的优化参数估计值（ ${\theta _0}$ ， ${\theta _{\text{H}}}$ ），如表 3所示。

表 3 双层边坡优化参数估计（植被边坡）

Table 3. Parameter estimation for optimization of two-layered slope(vegetated slope)

折减系数	均质边坡优化参数初始估计值				非均质边坡参数初始估计值		优化参数实际值		临界高度
F_s	θ₀₁	θ_h1	θ₀₂	θ_h2	θ₀	θ_H	Θ₀	Θ_H	H_cr /m
1.000	1.322	1.857	0.843	1.758	1.026	1.814	0.972	1.837	60.768
2.000	0.822	1.996	0.491	1.832	0.625	1.910	0.582	1.913	8.767
2.500	0.725	2.015	0.425	1.848	0.549	1.927	0.513	1.932	5.826
3.700	0.618	2.039	0.353	1.869	0.464	1.949	0.439	1.958	3.408
3.818	0.596	2.045	0.338	1.873	0.447	1.954	0.424	1.965	3.000

下载: 导出CSV

| 显示表格

由可知：①优化参数实际值（ ${\Theta _0}$ ， ${\Theta _H}$ ）全部介于均质边坡参数初始估计值之间，说明可以限定重点区域，②层状边坡的优化参数实际值与估计值（ ${\theta _0}$ ， ${\theta _{\text{H}}}$ ）之间最大误差只有6%，说明全局最优值处在估计初值附近。由此可见，该初值估计方法能够限定搜索重点优化空间内的关键区域，进而快速可靠的完成边坡稳定性分析。

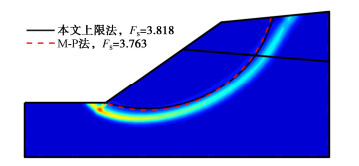
分别采用Morgenstern-Price法、本文上限法以及刚体单元上限法进行工程案例稳定性分析，计算结果如图 6，7所示。

图 6 算例4: 边坡稳定分析结果（过坡趾，F_s=3.770）

Figure 6. Example 4: results of slope stability analysis(F_s=3.770)

下载: 全尺寸图片幻灯片

图 7 算例5:边坡稳定分析结果（过坡趾下方，F_s=3.285）

Figure 7. Eaxmple 5: results of slope stability analysis(F_s=3.285)

下载: 全尺寸图片幻灯片

结合算例1~5可知，比较本文上限法与刚体单元上限法分析结果可知：①以上两种上限法与Morgenstern-Price法相比较，计算精度都较高（不超过1.5%），但本文方法求出的滑移面相较于前者，更接近Morgenstern-Price法；②两种上限法的计算精度与层状边坡抗剪参数的差异性存在关联性。

采用多项式拟合对数螺旋线，可规避外功率积分困难性，但本质上来说是拟合对数螺旋线在笛卡尔直角坐标系下的反函数，因此必须满足反函数存在的数学条件，当层状边坡形状复杂或滑移面通过坡趾下方或上方的时候，将面临挑战。本文方法直接实现外功率积分，未采用任何数值方法，不必满足拟合对数螺旋线法相关的数学条件，因此具有较好的适用性和研究前景。

4. 结论

（1）基于极限理论以及组合螺旋线破坏机构，推导出能够显式表达的双层边坡临界高度计算公式，一定程度否定了外力功率积分的困难性，为复杂边坡上限法研究提供了新思路。

（2）提出的局部优化初值估计方法，使优化搜索仅限制在重点优化空间内的关键点附近，兼顾了全局最优性以及优化效率，保证了边坡稳定分析高效性。

（3）通过多个算例，验证了本文方法的准确性、稳定性以及适用性，并且指出了采用对数螺旋线破坏机构进行边坡局部稳定分析时存在的局限性，并重新构造了待优化目标函数，提高了程序通用性，获得了比较符合实际情况的分析结果。

图 1 双层边坡破坏机构示意图

Figure 1. Illustration of failure mechanism of two-layered slope

下载: 全尺寸图片幻灯片

图 2 算例1:边坡稳定性分析(整体失效模式)

Figure 2. Stability analysis of slope (global failure mode)

下载: 全尺寸图片幻灯片

图 3 算例2:边坡稳定性分析(局部1，F_s=1.076)

Figure 3. Exmple 2: stability analysis of slope (local model 1, F_s=1.076)

下载: 全尺寸图片幻灯片

图 4 算例3:边坡稳定性分析(局部2，F_s=1.614)

Figure 4. Exmple 3: stability analysis of slope (local model 2, F_s=1.614)

下载: 全尺寸图片幻灯片

图 5 兰州市黄河北岸某植被边坡

Figure 5. Vegetated slope on north bank of Yellow River in Lanzhou

下载: 全尺寸图片幻灯片

图 6 算例4: 边坡稳定分析结果（过坡趾，F_s=3.770）

Figure 6. Example 4: results of slope stability analysis(F_s=3.770)

下载: 全尺寸图片幻灯片

图 7 算例5:边坡稳定分析结果（过坡趾下方，F_s=3.285）

Figure 7. Eaxmple 5: results of slope stability analysis(F_s=3.285)

下载: 全尺寸图片幻灯片

表 1 双层边坡材料组合

Table 1 Material combination of two-layered slope

失效模式	位置	黏聚力c/kPa	内摩擦φ/(°)	重度γ/(kN·m^-3)
整体^[21]	上层	5.3	23	19.5
整体^[21]	下层	7.2	20	19.5
局部1	上层	4	20	19.5
局部1	下层	7.2	27	19.5
局部2 β=30°, m=5/8	上层	12	14	19.5
局部2 β=30°, m=5/8	下层	20	23	19.5

下载: 导出CSV

表 2 边坡稳定安全系数验证对比(算例1)

Table 2 Verification and comparison of factors of safety (slope example 1)

计算方法	安全系数F_s
瑞典条分法^[18]	0.96
Bishop法^[18]	1.00
Janbu法^[18]	1.00
刚体单元上限法	1.02
刚体单元下限法^[18]	0.98
Morgenstern-Price法	1.004
本文方法	1.007

下载: 导出CSV

表 3 双层边坡优化参数估计（植被边坡）

Table 3 Parameter estimation for optimization of two-layered slope(vegetated slope)

折减系数	均质边坡优化参数初始估计值				非均质边坡参数初始估计值		优化参数实际值		临界高度
F_s	θ₀₁	θ_h1	θ₀₂	θ_h2	θ₀	θ_H	Θ₀	Θ_H	H_cr /m
1.000	1.322	1.857	0.843	1.758	1.026	1.814	0.972	1.837	60.768
2.000	0.822	1.996	0.491	1.832	0.625	1.910	0.582	1.913	8.767
2.500	0.725	2.015	0.425	1.848	0.549	1.927	0.513	1.932	5.826
3.700	0.618	2.039	0.353	1.869	0.464	1.949	0.439	1.958	3.408
3.818	0.596	2.045	0.338	1.873	0.447	1.954	0.424	1.965	3.000

下载: 导出CSV

参考文献(18)

[1]	FELLENIUS W. Earth Stability Calculations Assuming Friction and Cohesion on Circular Slip Surfaces[M]. Berlin: Wilhelm Ernst, 1927.
[2]	BISHOP A W. The use of the slip circle in the stability analysis of slopes[J]. Géotechnique, 1955, 5(1): 7-17. doi: 10.1680/geot.1955.5.1.7
[3]	MORGENSTER N R, PRICE V E. The analysis of the stability of general slip circles[J]. Géotechnique, 1955, 15(1): 79-93.
[4]	SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique, 1967, 17(1): 11-26. doi: 10.1680/geot.1967.17.1.11
[5]	JANBU N. Slope Stability Computations Embankment Dam Engineering[M]. New York: Wiley, 1973.
[6]	郑惠峰, 陈胜宏, 吴关叶. 岩石边坡稳定的块体单元极限分析上限法[J]. 岩土力学, 2008, 29(增刊1): 323-327. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2008S1065.htm ZHENG Huifeng, CHEN Shenghong, WU Guanye. Upper bound limit method for stability analysis of rock slopes by block element method[J]. Rock and Soil Mechanics, 2008, 29(S1): 323-327. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2008S1065.htm
[7]	唐高朋, 赵炼恒, 李亮, 等. 基于MATLAB的边坡稳定性极限上限分析程序开发[J]. 岩土力学, 2013, 34(7): 2091-2098. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307040.htm TANG Gaopeng, ZHAO Lianheng, LI Liang, et al. Program development for slope stability using MATLAB software and upper bound limit analysis[J]. Rock and Soil Mechanics, 2013, 34(7): 2091-2098. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307040.htm
[8]	CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam: Elsevier Scientific Pub Co, 1975.
[9]	KARAL K. Application of energy method[J]. Journal of the Geotechnical Engineering Division, 1977, 103(5): 381-397. doi: 10.1061/AJGEB6.0000419
[10]	MICHALOWSKI R L. Slope stability analysis: a kinematical approach[J]. Géotechnique, 1995, 45(2): 283-293. doi: 10.1680/geot.1995.45.2.283
[11]	DONALD I B, CHEN Z Y. Slope stability analysis by the upper bound approach: fundamentals and methods[J]. Canadian Geotechnical Journal, 1997, 34(6): 853-862. doi: 10.1139/t97-061
[12]	杨峰, 赵炼恒, 张箭, 等. 基于刚体平动运动单元的上限有限元研究[J]. 岩土力学, 2014, 35(6): 1782-1786, 1808. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201406042.htm YANG Feng, ZHAO Lianheng, ZHANG Jian, et al. Investigation on finite element upper bound solution based on rigid translatory moving element[J]. Rock and Soil Mechanics, 2014, 35(6): 1782-1786, 1808. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201406042.htm
[13]	刘锋涛, 张绍发, 戴北冰, 等. 边坡稳定分析刚体有限元上限法的锥规划模型[J]. 岩土力学, 2019, 40(10): 4084-4091, 4100. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201910044.htm LIU Fengtao, ZHANG Shaofa, DAI Beibing, et al. Upper bound limit analysis of soil slopes based on rigid finite element method and second-order cone programming[J]. Rock and Soil Mechanics, 2019, 40(10): 4084-4091, 4100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201910044.htm
[14]	王珍, 曹兰柱, 王东. 非均质边坡稳定性上限分析评价研究[J]. 岩土力学, 2019, 40(2): 737-742. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902037.htm WANG Zhen, CAO Lanzhu, WANG Dong. Evaluation on upper limit of heterogeneous slope stability[J]. Rock and Soil Mechanics, 2019, 40(2): 737-742. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902037.htm
[15]	年廷凯, 刘凯, 黄润秋, 等. 多阶多层复杂边坡稳定性的通用上限方法[J]. 岩土力学, 2016, 37(3): 842-849. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201603030.htm NIAN Tingkai, LIU Kai, HUANG Runqiu, et al. A generalized upper-bound limit analysis approach for stability analysis of complex multistep and multilayer slopes[J]. Rock and Soil Mechanics, 2016, 37(3): 842-849. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201603030.htm
[16]	KUMAR J, SAMUI P. Stability determination for layered soil slopes using the upper bound limit analysis[J]. Geotechnical & Geological Engineering, 2006, 24(6): 1803-1819.
[17]	栾茂田, 金崇磐, 林皋, 等. 层状非均质土坡抗震稳定性的变分解法[J]. 地震工程与工程振动, 1993, 13(4): 73-80. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199304007.htm LUAN Maotian, JIN Chongpan, LIN Gao, et al. Variational procedure for aseismic stability of layered soil slopes[J]. Earthquake Engineering and Engineering Vibration, 1993, 13(4): 73-80. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199304007.htm
[18]	王根龙, 伍法权, 张军慧. 非均质土坡稳定性分析评价的刚体单元上限法[J]. 岩石力学与工程学报, 2008, 27(增刊2): 3425-3430. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2008S2022.htm WANG Genlong, WU Faquan, ZHANG Junhui. Upper bound approach of rigid elements for inhomogeneous soil slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S2): 3425-3430. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2008S2022.htm

施引文献(7)

期刊类型引用(3)

1.	祝方才，周俊杰，赖国森，晏仁，刘海媚. 破碎岩体隧道洞口开挖诱导滑坡与古滑坡耦合分析. 湖南工业大学学报. 2024(03): 1-8 . 百度学术
2.	刘杰，杨轶博，郭督，马志宏. 地震作用下双层土质边坡稳定性上限分析. 沈阳大学学报(自然科学版). 2024(03): 237-245 . 百度学术
3.	唐先习，李昊杰，李明泽，王之鲁. 地聚物固化黄土力学性能及边坡稳定性研究. 湖南大学学报(自然科学版). 2024(09): 133-144 . 百度学术