Seismic fragility analysis of pile-supported wharf in nearshore liquefiable ground
-
摘要: 地震易损性分析已成为结构工程和桥梁工程界的研究热点。然而,近岸液化场地高桩码头地震易损性研究相对较少。鉴于此,依托典型工程实例,建立了近岸液化场地全直桩高桩码头地震反应分析数值模型,针对弯曲失效和弯剪失效两种失效模式,通过模态分析和Pushover分析,识别了高桩码头损伤演化过程,提出了各损伤阶段定量化判别准则。然后,以PGA为地震动强度指标,选取14组典型地震动并分别缩小至8个不同强度等级,通过增量动力分析,给出了近岸液化场地高桩码头IM-EDP曲线。最后,基于提出的高桩码头损伤判别标准,推导了高桩码头地震易损性曲线,采用对数正态分布累积分布函数对易损性曲线进行拟合,确定了便于实际应用、简化的高桩码头地震易损性曲线。研究工作可为近岸液化场地高桩码头的抗震加固提供重要的理论基础。
-
关键词:
- 液化场地 /
- 高桩码头 /
- 易损性分析 /
- 增量动力分析 /
- Pushover分析
Abstract: The seismic fragility analysis has become a research hotspot in structural engineering and bridge engineering, but there are few studies in the field of pile-supported wharf in nearshore liquefiable ground. Based on the typical engineering examples, a numerical model for seismic response analysis of all-straight pile and pile-supported wharf in nearshore liquefiable ground is established. In view of bending failure and bending shear failure, through the modal analysis and pushover analysis, the damage evolution process of pile-supported wharf and the quantitative discrimination criteria for each damage stage are proposed. With PGA as the ground motion intensity index, 14 groups of typical ground motions are selected and scaled to 8 different intensity levels. With the aid of the incremental dynamic analysis, the IM-EDP curve of the pile-supported wharf in nearshore liquefiable ground is proposed. Based on the proposed criterion for determining the damage of pile-supported wharf, the seismic fragility curve of pile-supported wharf is derived. The cumulative distribution function of log-normal distribution is used to fit the seismic fragility curve, and a simplified seismic fragility curve of pile-supported wharf is proposed for practical application. This work may provide important theoretical basis for the seismic reinforcement of pile-supported wharf in nearshore liquefiable ground. -
0. 引言
地震易损性曲线能够给出结构在指定强度地震作用下达到或超过某种损伤状态的条件概率,是一种从概率角度评价结构抗震性能的方法,更是一种能够将结构损伤与经济损失相关联的有效手段[1-2]。关于地震易损性研究多集中在结构工程和桥梁工程领域且研究成果丰富。随着“一带一路”倡议的提出,中国在海上丝绸之路沿线建设了大批高桩码头工程,广泛分布于断裂带和可液化土层上,地震风险十分严重且基于高桩码头地震易损性的研究较少。因此开展可液化场地高桩码头地震易损性的研究工作极具工程价值。
目前,国内外针对码头结构地震易损性研究相对较少。Ichii[3]针对重力式码头的岸壁结构,基于简化有限元动力模型,建立了理论易损性曲线。Chiou等[4]针对台湾典型高桩码头结构,建立了三维数值模型,采用地震峰值加速度PGA作为地震动强度指标,码头甲板位移作为码头性能指标,建立了高桩码头结构地震易损性曲线。Heidary-Torkamani等[5]围绕典型含叉桩桩支码头体系,研究了8条地震动作用下桩基非线性时程响应,提出了一种综合考虑位移延性系数、面板与回填土间差异沉降、归一化残余水平位移等3项工程需求参数在内的极限状态指标,并基于增量动力分析方法,采用数值模型获得了含叉桩桩支码头体系的地震易损性曲线。Su等[6-7]初步发展了考虑桩-土相互作用的易损性曲线,进一步探究了渗透系数的影响。Mirzaeefard等[8]研究了腐蚀对高桩码头结构地震易损性曲线的影响。综上,震害突出的近岸液化场地高桩码头结构体系抗震的研究尚较少,而且尚无合理的近岸液化场地高桩码头地震易损性曲线。
为此,本文依托典型工程实例,建立了近岸液化场地全直桩高桩码头地震反应分析数值模型,揭示弯曲失效和弯剪失效两种失效模式下高桩码头结构的损伤演化规律,确定不同失效模式下高桩码头达到不同损伤阶段的定量判别标准,给出高桩码头地震易损性曲线,得到便于应用推广的简化高桩码头地震易损性曲线。
1. 工程背景
1.1 工程概况
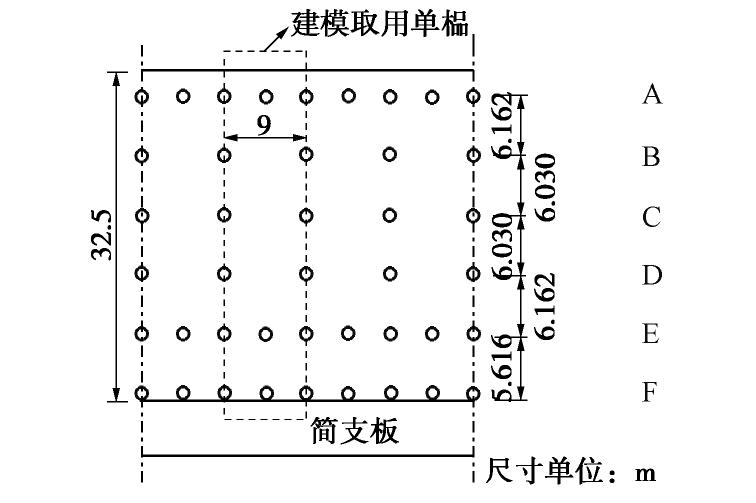
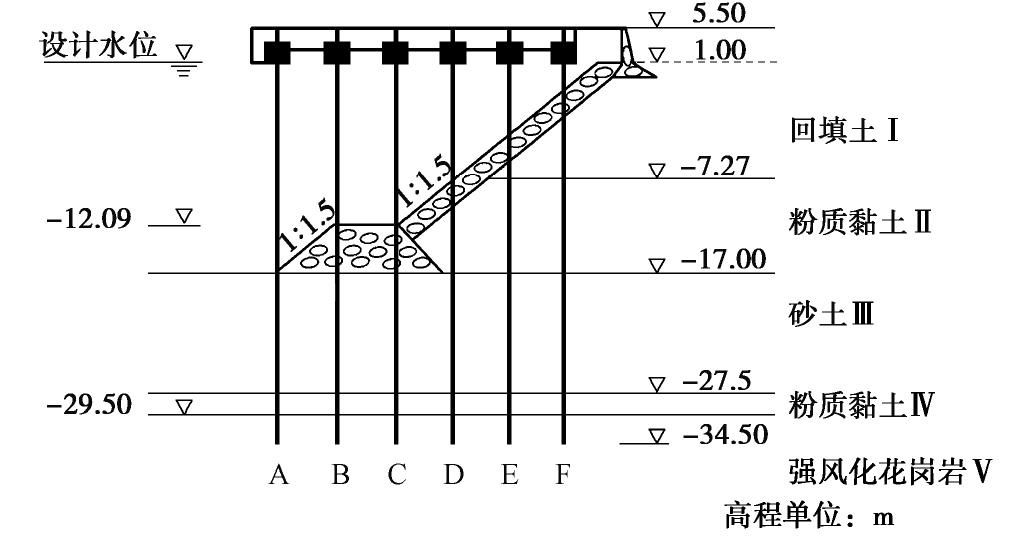
某港区有一设计船型为十万吨级集装箱货船,并兼顾十五万吨级集装箱货船的高桩码头工程,结构断面图见图1[9]。码头采用梁板式全直桩结构,地震设防烈度为7度,设计高水位2.91 m,低水位0.41 m。
1.2 高桩码头结构
码头沿海岸线纵向长度为324 m,桩台宽度为32.5 m。码头排架间距为9 m,每榀排架内部平均布置9根大直径PHC管桩,平面布置见图2,其中在轨距为24.384 m的装卸桥前、后轨道梁下,以及轨距为30 m的装卸桥后轨道梁下各设置2根管桩,其余节点均为单根管桩。桩台面板厚度为430 mm,路面及磨耗层厚度为70 mm,平均密度为2550 kg/m3。桩台与接岸结构之间采用简支板过渡。所有桩基选型均为AB桩,长度为40 m,桩端打入强风化花岗岩层。管桩直径为1200 mm,壁厚150 mm。为了方便叙述,统一将桩基编号为A—F。
1.3 工程地质条件
根据工程地质资料,结合区域地质特征及土体的物理力学性质,场区内土层自上而下为回填土、粉质黏土、砂土、粉质黏土和花岗岩强风化层。回填土主要由中粗砂组成,属中等压缩性土,一般地段均有一定埋深,经长期碾压已完全固结；粉质黏土色杂,可塑状,有一定埋深,厚度变化不大,属中等压缩性土,性质较好；砂土呈灰色/黄色,饱和,标准贯入锤击数16～27击,平均值22击,属中等压缩性土,性质良好；粉质黏土湿,硬塑状,厚度较薄,属中等压缩性土；花岗岩强风化层标准贯入锤击数51～75击,为本工程桩基础的持力层。参考OpenSees命令手册[10]和《工程地质手册》[11],确定各类土体的物理力学参数,详见表1。
表 1 土体的计算参数Table 1. Model parameters of soils土层编号 饱和密度/(kg·m-3) 剪切模量/kPa 体积模量/kPa 黏聚力/kPa 摩擦角/(°) 峰值剪应变 参考围压p/kPa 相位转换角/(°) Ⅰ 1700 55 150 0 29 0.1 80 29 Ⅱ 1950 60 300 30 18 0.1 80 — Ⅲ 2000 100 300 0 37 0.1 80 27 Ⅳ 1900 150 750 25 19 0.1 80 — Ⅴ 2790 280 1300 0 40 0.1 80 — Ⅵ 2240 140 1300 15 45 0.1 80 27 2. 高桩码头地震反应分析数值方法
计算平台OpenSees由加州大学伯克利分校主导研发,具有很强的非线性分析能力,广泛用于岩土地震工程方面分析的有限元模拟[12]。本文基于OpenSees计算平台,构建近岸液化场地全直桩高桩码头地震反应分析数值模型,其中数数值建模技术途径的可靠性已得到系统验证,详见参考文献[13～17]。
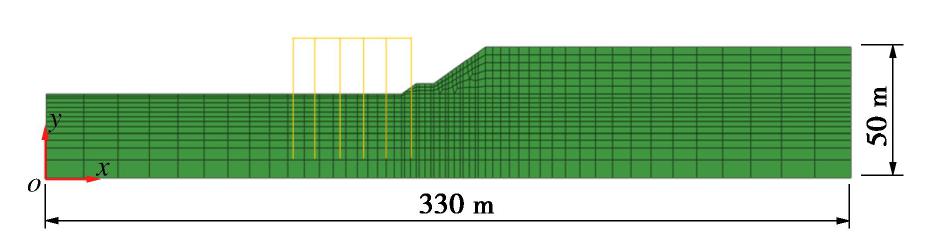
实际工程中,桩台与接岸结构采用简支板过渡,约束较弱。数值模型中,忽略桩台与岸坡之间的连接作用。为了减弱边界效应对桩的内力、变形等不利影响,模型宽度和高度分别设为330,50 m。有限元网格见图3。数值分析时,除了考虑水压力、重力及地震动外,还考虑了30 kN/m2的桩台面堆货荷载。此外,模型沿x方向边界条件为自由场边界,模型底部y方向为固定边界,模型顶部y方向为自由边界[17]。
通过在桩节点两侧添加梁-柱单元与零长度单元模拟桩-土相互作用,其中通过赋予梁-柱单元极大的刚度（桩单元刚度的10000倍）实现刚性连接[16-17],并使刚性连接单元长度等于桩半径,进而模拟桩基尺寸效应的影响。通过为各零长度单元,赋予不同类型的单轴材料,模拟桩与土之间的各类接触效应[17]。
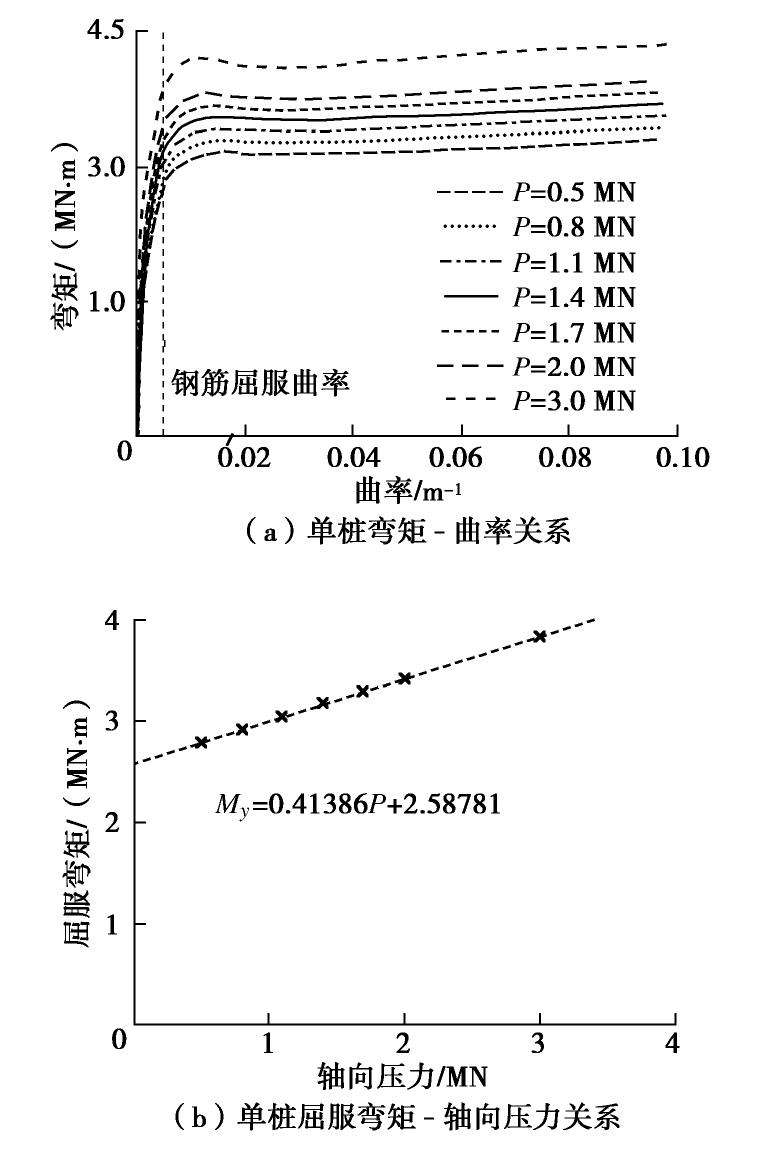
由于地震动下高桩码头工程受力属平面应变问题,因此采用二维模型进行地震响应分析。同时,忽略桩的扭转力学特性。PHC管桩材料参数如表2所示。图4给出了PHC管桩单桩弯矩-曲率关系和屈服弯矩-轴向压力关系。
参数类别 混凝土抗压强度fc/MPa 混凝土抗压强度应变εc 混凝土压碎强度fcu/MPa 混凝土压碎强度应变εcu 钢筋屈服强度Fy/MPa 钢筋初始抗拉刚度Es/MPa 钢筋张拉应力Epre/MPa PHC管桩整体抗剪刚度G/MPa 桩B/C/D -80 -0.00215 -50.2 -0.003 1570 200000 994 16282.051 桩A/E/F -160 -0.00215 -100.4 -0.003 3140 400000 1988 32564.102 ![]()
图 4 数值计算得到的PHC管桩单桩力学性能Figure 4. Mechanical properties of PHC piles from numerical analysis数值模型中﹐为了模拟地震过程中饱和土体剪切变形的累积液化特性,采用多屈服面塑性本构模型(Pressure Dependent Multi Yield,简称PDMY)模拟饱和土体的动力响应[18-19]。通过在土-水交界面处的土节点附加流体质量来模拟海测饱和土表面上方的自由水体。土体采用四节点双向线性等参元quadUP进行剖分。
采用非线性纤维梁柱单元模拟在地震荷载作用下管桩的非线性力学特性。非线性纤维梁柱单元中,采用基于加载/卸载刚度线性衰减的单轴材料（Kent-Scott-Park本构模型）Concrete01模型模拟C80混凝土,并根据文献[20]和等刚度准则确定其计算参数。采用等向应变硬化单轴钢筋材料（Giuffre-Menegotto- Pinto本构模型）模拟预应力钢筋,同时,参考标准GB/T 5223.3—2017《预应力混凝土用钢棒》[21]及等刚度准则确定其计算。将线弹性单轴材料赋给纤维截面中,模拟PHC管桩整体的剪切力学特性,并依据参考文献[22]及等刚度准则确定其计算参数。
3. 高桩码头损伤状态分析
首先,针对高桩码头结构进行模态分析,确定其基本周期约为0.55 s,基本振型见图5。可见,高桩码头在地震作用下主要表现为甲板整体向海侧运动,各桩在岸坡以上附近区域向陆侧产生较小幅度运动。
其次,针对高桩码头开展Pushover分析[23],将高桩码头受到的总侧向力,按比例施加于各标高处桩的节点上,计算方法为[24]
Fi=(wiϕi/n∑i=1wiϕi)×V, (1) 式中,
Fi 为桩节点i受到的侧向力,V 为高桩码头受到的总侧向力,wi 为桩节点i分担的结构重力,ϕi 为桩节点i处对应于基本阵型的振幅,n 为高桩码头模型中桩的总节点数。最后,在竖向荷载作用的基础上,按照上述侧向力加载模式,将水平荷载单调递增方式,施加于各个桩节点处,计算出码头结构的内力和变形,得到码头结构的侧向承载力曲线。
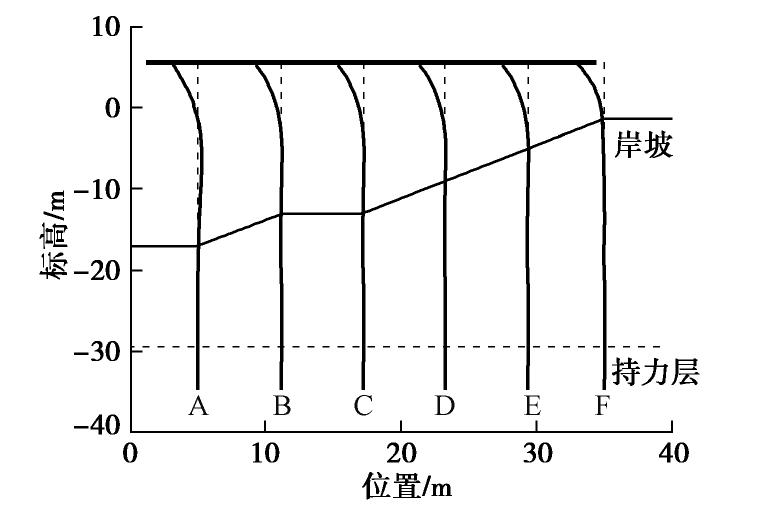
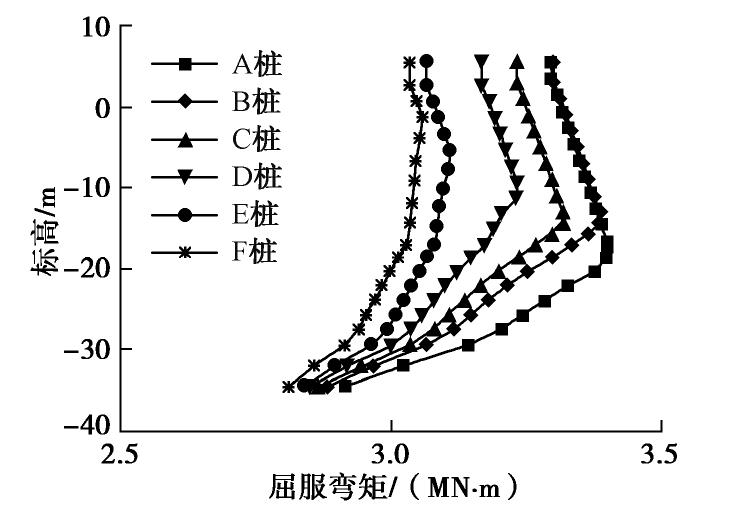
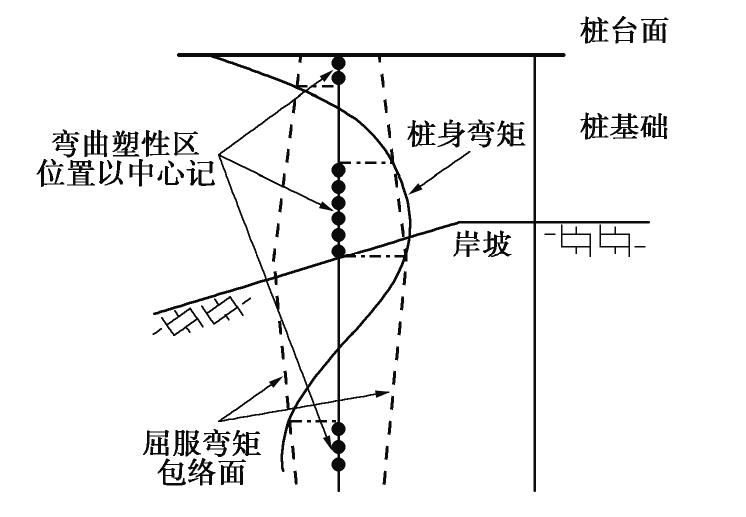
根据图4中PHC管桩力学性能及桩身初始轴力,可以得到高桩码头桩身屈服弯矩分布见图6。通过Pushover分析中获取的桩身内力和对应位置处的屈服弯矩进行对比,可以确定桩身塑性区的发展位置,见图7。须指出,该方法同样能够用于桩身弯曲开裂位置和剪切破坏位置的确定。
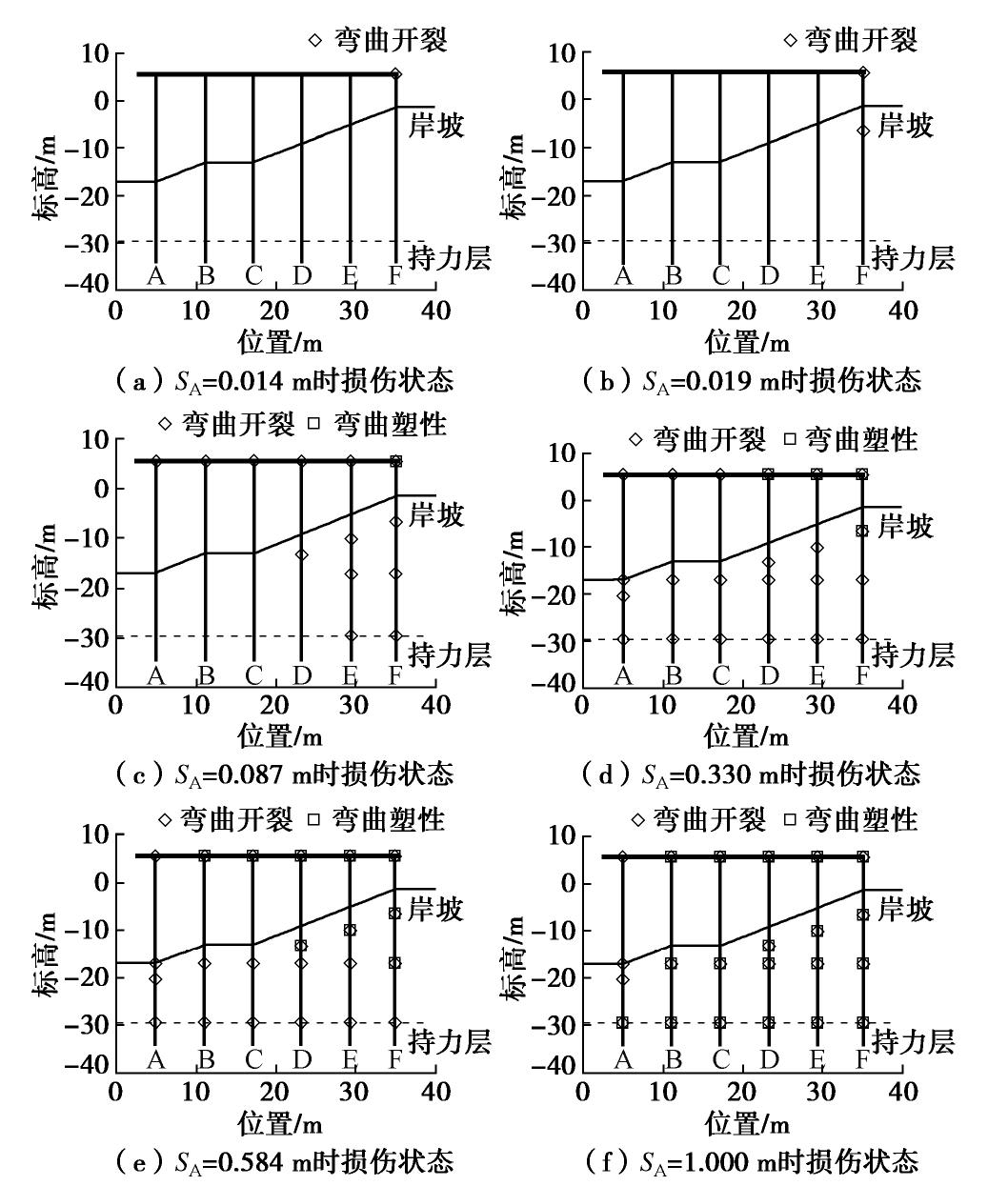
由文献[25]可知,管桩的抗裂弯矩为1469 kN·m,抗裂剪力为1056 kN。以A桩顶部向海侧位移SA为监测指标,根据上述损伤定位方法,结合Pushover分析得到的结果,获得弯曲失效模式下高桩码头损伤演化过程,见图8。
![]()
图 8 弯曲失效模式下高桩码头损伤演化过程Figure 8. Damage evolution of pile-supported wharf under bending failure mode随着SA的不断增加,高桩码头弯曲损伤不断从陆侧的桩向海侧的桩发展,并持续从桩顶向持力层扩展。桩身弯曲损伤分布并不连续,主要集中在桩顶处、岸坡以下一定深度处、砂层与上覆土层交界处,以及持力层处等较敏感位置。其中,当SA=0.014 m时,高桩码头出现首次开裂,开裂位置为F桩桩顶处；当SA=0.019 m时,高桩码头首次在土体内出现开裂,开裂位置为F桩在岸坡以下一定深度处；当SA=0.087 m时,高桩码头出现首个塑性铰,发生为F桩桩顶处。此时,E桩和F桩在各个敏感位置处已完全开裂,开裂不断由陆侧向海侧发展；当SA=0.33 m时,高桩码头在土体内出现第1个塑性铰,土体内塑性铰的位置为F桩在岸坡以下一定深度处。此时,各桩在各个敏感位置处均已完全开裂,塑性铰不断由陆侧的桩向海侧的桩发展；当SA=0.584 m时,高桩码头在土体内首次出现2个塑性铰,且均出现在F桩上,因此导致F桩的承载力急剧下降。此时,塑性铰进入快速发展阶段；当SA=1.0 m时,B,C,D,E,F桩在各敏感位置处已完全进入塑性阶段,而A桩仅在持力层处进入塑性阶段。总体上,高桩码头结构已完全丧失侧向的承载性能。
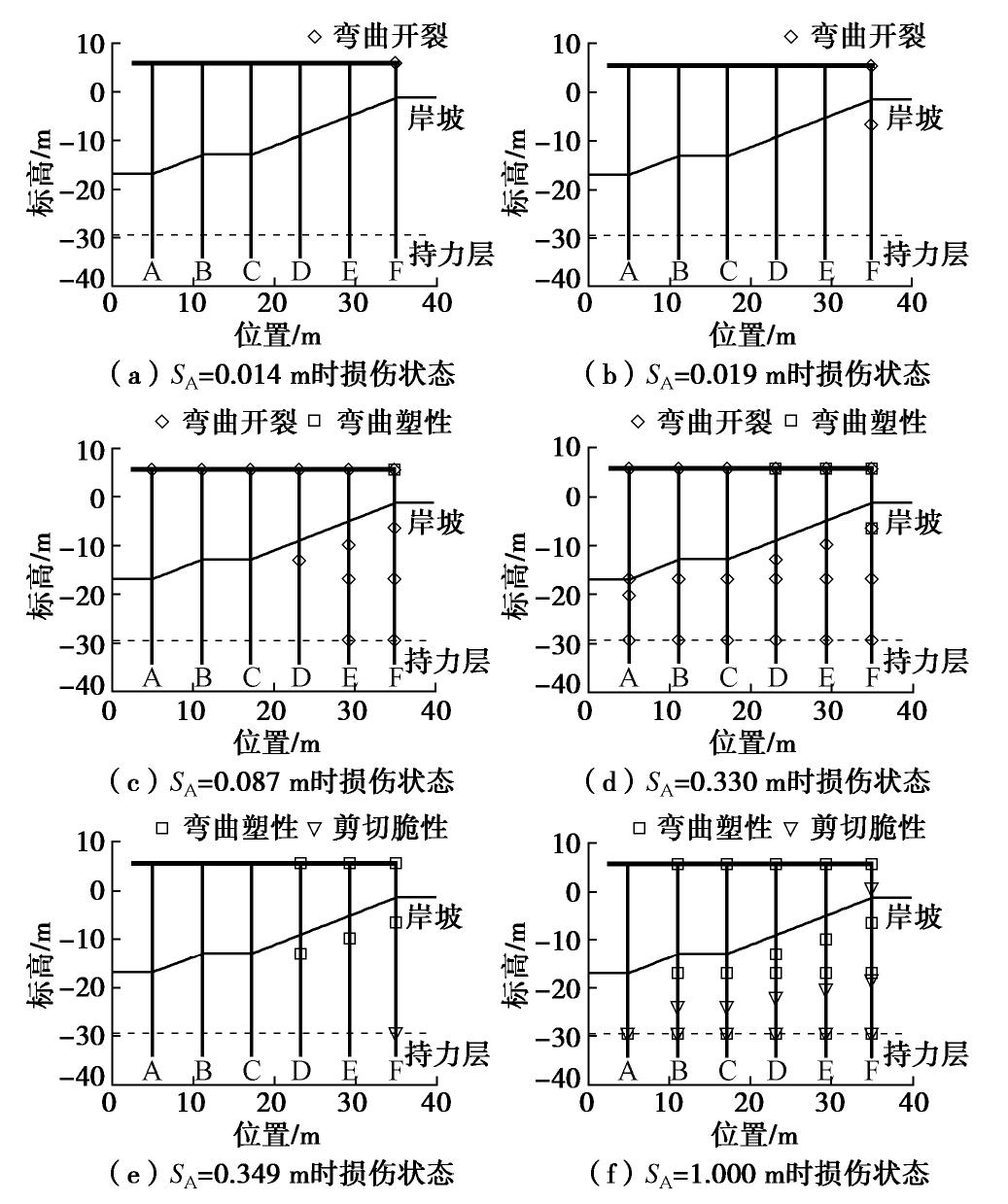
采用与弯曲失效模式同样的方法,得到弯剪失效模式下高桩码头损伤演化过程,见图9。随着A桩顶部向海侧的位移不断增加,高桩码头剪切损伤不断从陆侧的桩向海侧的桩发展,并持续从持力层向岸坡扩展。桩身剪切损伤的分布不连续,主要集中在持力层处、岸坡以下约8倍桩径处,以及岸坡附近处等较敏感的位置。当SA<0.330 m时,弯剪失效模式与弯曲失效模式下高桩码头损伤演化过程完全一致。当SA=0.349 m时,高桩码头首次出现剪切开裂,开裂位置位于F桩的持力层处。考虑到剪切破坏的脆性特征及F桩上已在土体中产生了一个塑性铰的情况,基于保守设计理念,可判定高桩码头不再具备正常工作能力；当SA=1.0 m时,B,C,D,E,F桩在各个敏感位置处,已完全进入塑性并发生了较严重的剪切破裂,而A桩仅在持力层处进入塑性并发生剪切开裂。整体上,高桩码头结构也已完全丧失的侧向承载性能。
![]()
图 9 弯剪失效模式下高桩码头损伤演化过程Figure 9. Damage evolution process of pile-supported wharf under bending shear failure mode国际航行协会提出了港口工程4阶段损伤概念,见表3[26],给出了各损伤阶段的定性描述,但并没有明确给出定量的判据。为了将上述概念更好用于实际工程中,结合得到的弯曲失效模式下高桩码头损伤演化过程,以SA为指标,确定了各阶段的损伤判别标准,具体位移限值与标准如下：
表 3 港口工程4阶段损伤概念Table 3. Concept of four-stage damage in port engineering损伤阶段 Ⅰ Ⅱ Ⅲ Ⅳ 概括描述 基本完好 可控损伤 广泛损伤 完全崩塌 具体描述 结构处于完好状态或产生轻微损伤 结构在可修复条件下产生有限有限的损伤,并直至发生一定的延性响应 结构产生广泛的损伤直至接近崩塌的延性响应 结构崩塌并丧失承载性能 （1）界限1（阶段Ⅰ与阶段Ⅱ的界限,即对应s1=0.087 m）
当SA<0.087 m时,高桩码头仅在某些位置产生一定程度的开裂,未影响到高桩码头的承载性能,高桩码头基本处于完好状态。当SA=0.087 m时,由于F桩桩顶处出现塑性铰,高桩码头承载性能将有一定程度降低下降,且位于桩顶处的塑性铰在震后可进行维修加固,属于可修复范畴。
（2）界限2（阶段Ⅱ与阶段Ⅲ的界限,即对应s2=0.330 m）
当SA=0.330 m时,F桩在岸坡以下一定深度处产生了新的塑性铰,高桩码头的承载性能将进一步下降,且位于土内的塑性铰不便在震后进行维修加固,属于不可修复范畴。基于塑性铰自身的有限承载能力及震后F桩桩顶处塑性铰得到及时修复的可能性,F桩依旧属于单铰结构范畴,判定此时高桩基码头并未丧失承载性能。
（3）界限3（阶段Ⅲ与阶段Ⅳ的界限,即对应s3=0.584 m）
当SA=0.584 m时,F桩在持力层处又产生了新的塑性铰,同样属于不可修复范畴。此时,F桩即使经过震后维修,也属于双铰结构范畴。此时,判定F桩已丧失承载性能,且D桩和E桩也有塑性铰的显著发展,由此判定高桩码头整体已丧失承载性能。
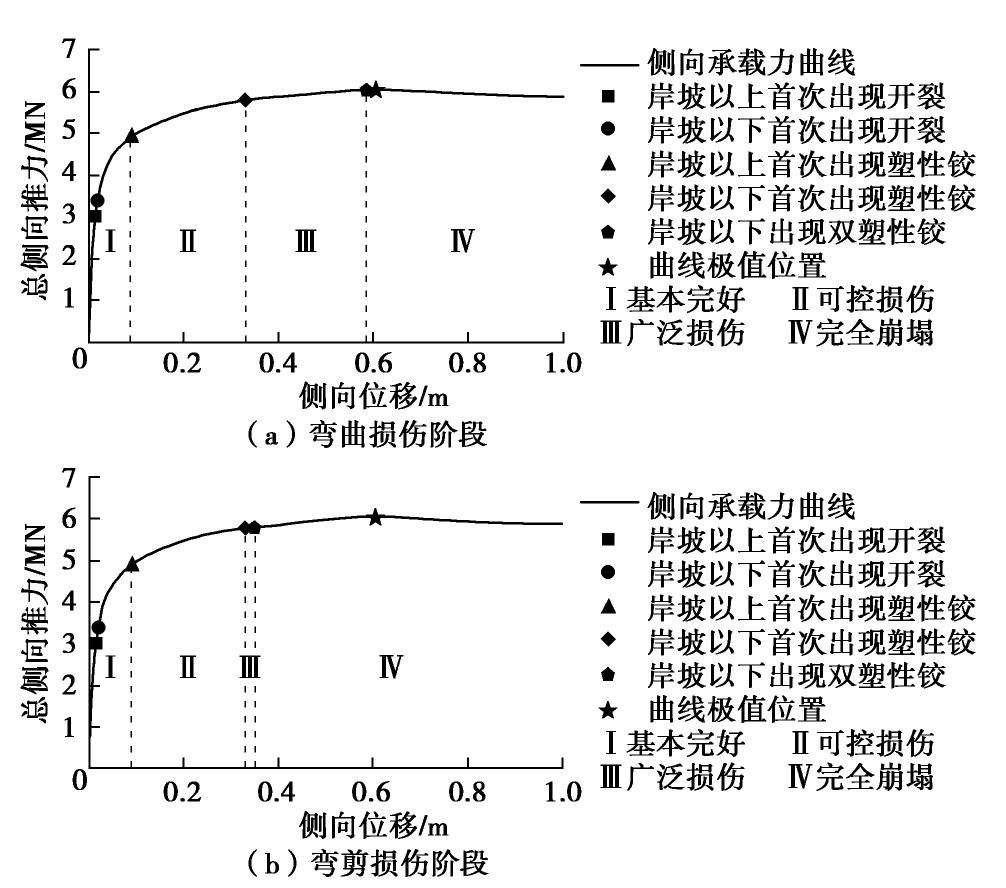
同理,采用与弯曲失效模式相同的损伤判别标准,确定弯剪失效各损伤阶段的位移限值如下：①界限1对应s1=0.087 m；②界限2对应s2=0.087 m；③界限3对应s3=0.349 m。为了对上述位移限值与损伤判别标准的合理性进行检验,将其与Pushover分析得到的侧向承载力曲线进行对比,见图10。
![]()
图 10 高桩码头侧向承载性能及损伤阶段图Figure 10. Lateral loading performances and damage stages of pile-supported wharf由图10（a）得到,弯曲失效模式下,通过上述标准确定的界限1位移限值,位于侧向承载力曲线的直线段附近,高桩码头侧向承载性能基本完整。界限2位移限值处,高桩码头侧向承载性能已发生较大程度衰减。界限3位移限值位于侧向承载力曲线极值位置附近,高桩码头侧向承载性能基本丧失。由图10（b）可以得到,弯剪失效模式下,高桩码头结构在进入可控损伤阶段后迅速达到完全失效阶段。此时,高桩码头整体抗弯性能并未得到充分发挥,反映了该损伤评价模式相对弯曲失效模式更为保守。
4. 高桩码头增量动力分析
为了能够系统地反映峰值、持时、频谱等地震动特性对高桩码头地震响应的影响,从PEER地震动数据库选取了14组较为典型的真实地震动记录,见表4。
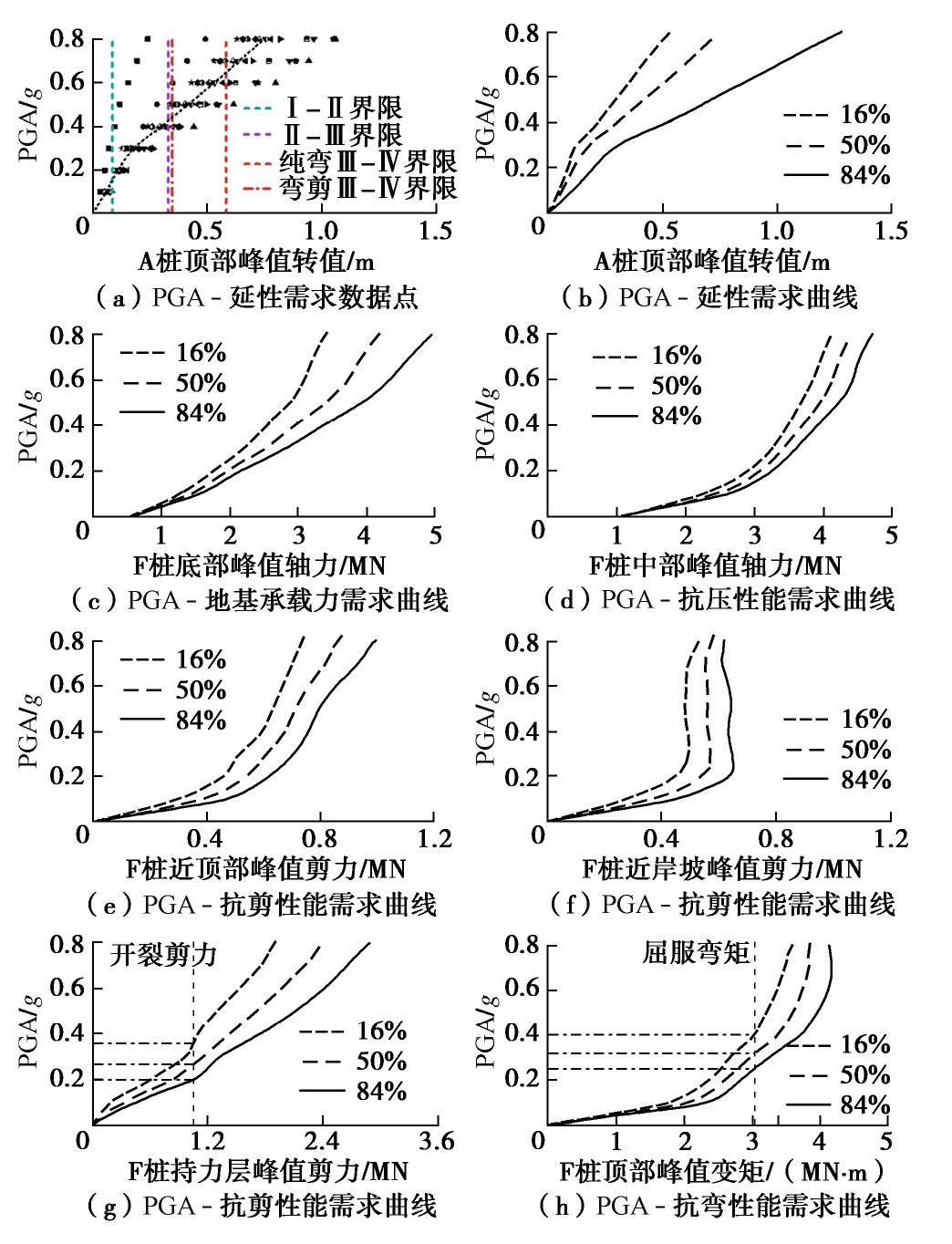
表 4 选取的地震动记录Table 4. Selected ground motion records序号 名称 台站 年份 PGA/g Tp/s Tm/s D5-95/s 1 Morgan hill Capitola 1984年 0.14 0.20 0.31 15.30 2 Livermore San Ramon-Eastman Kodak 1980年 0.15 0.62 1.00 14.20 3 Trinidad 090 CDMG Station 1498 1983年 0.19 0.32 0.38 12.18 4 Hollister USGS Station 1028 1961年 0.20 0.48 0.63 16.48 5 Imperial Valley Chihuahua 1979年 0.27 0.26 0.58 24.00 6 Imperial Valley USGS Station 5115 1979年 0.32 0.36 0.44 11.04 7 San Fernando Santa Felita Dam (Outlet) 1971年 0.34 0.10 0.46 23.60 8 Kobe Kakogawa 1995年 0.35 0.16 0.48 13.20 9 Kocaeli Yarimca 1999年 0.35 0.52 1.24 15.11 10 Friuli Tolmezzo 1976年 0.35 0.26 0.40 4.90 11 Chi-Chi TCU045 1999年 0.36 0.44 0.47 11.34 12 Loma Prieta 090 CDMG Station 47381 1989年 0.37 0.40 0.37 5.00 13 Northridge 090 CDMG Station 24278 1994年 0.57 0.52 0.79 6.80 14 Landers 000 SCE Station 24 1992年 0.78 0.32 0.75 21.34 根据文献[27],针对某一地震动强度,当施加在结构体系的地震激励条数超过7组时,能够采用平均响应结果代替最不利响应结果,以更加科学、客观地表述结构体系的抗震性能需求。鉴于《中国地震动参数区划图》中已提供详细的地震动峰值加速度区划,并将其与地震烈度很好关联起来[28],本节以地震动峰值加速度PGA作为地震动强度指标(IM),分别选取A桩顶部峰值位移,F桩底部峰值轴力,F桩中部峰值轴力,F桩近岸坡处、岸坡以下约8倍桩径处、持力层处峰值剪力,以及F桩顶部峰值弯矩,作为刻画高桩码头整体延性、地基承载力、抗压性能、抗剪性能和抗弯性能的需求参数（EDP）。
以0.1g为增量将各组地震动分别调幅至0.1g～0.8g等8个不同的强度等级,通过计算112组动力非线性分析数值模型,完成高桩码头地震响应的分析,得到保证率在16%,50%和84% 3个不同等级下的高桩码头IM-EDP曲线,见图11。
5. 高桩码头地震易损性分析
5.1 地震易损性曲线
通过对两种失效模式下高桩码头各损伤阶段位移限值和增量动力分析得到的高桩码头A桩顶部峰值位移矩阵,进行统计学分析,得到高桩码头地震易损性曲线。
首先,将112个位移数据按照地震动强度等级进行分组。根据Chiou等研究成果[4],每个强度等级地震动作用下得到14个位移数据样本,假定其服从对数正态分布。据此,以高桩码头A桩顶部峰值位移为变量,其概率密度函数可表述为
fXj(x)=1√2πςjxexp[−12(lnx−λjςj)] (0≤Xj<∞), (2) ςj=√ln[1+(σjμj)2], (3) λj=lnμj−12(ςj)2。 (4) 式中
Xj 为地震动强度为j时高桩码头A桩顶部峰值位移的随机变量；x为区间点坐标；ςj 为地震动强度为j时位移样本对数标准差；λj 为地震动强度为j时位移样本对数均值；σj 为地震动强度为j时位移样本标准差；μj 为地震动强度为j时位移样本均值。根据对数正态分布与标准正态分布之间的关系,以弯剪和弯曲失效模式下各损伤阶段位移限值为区间点坐标,可以得到高桩码头在不同损伤状态下的条件概率：
P(SA>si|PGA=j)=P(Xj>xi|PGA=j)=1−Φ[lnxi−λjςj], (5) 式中,xi为等值于界限i位移限值的区间点坐标,
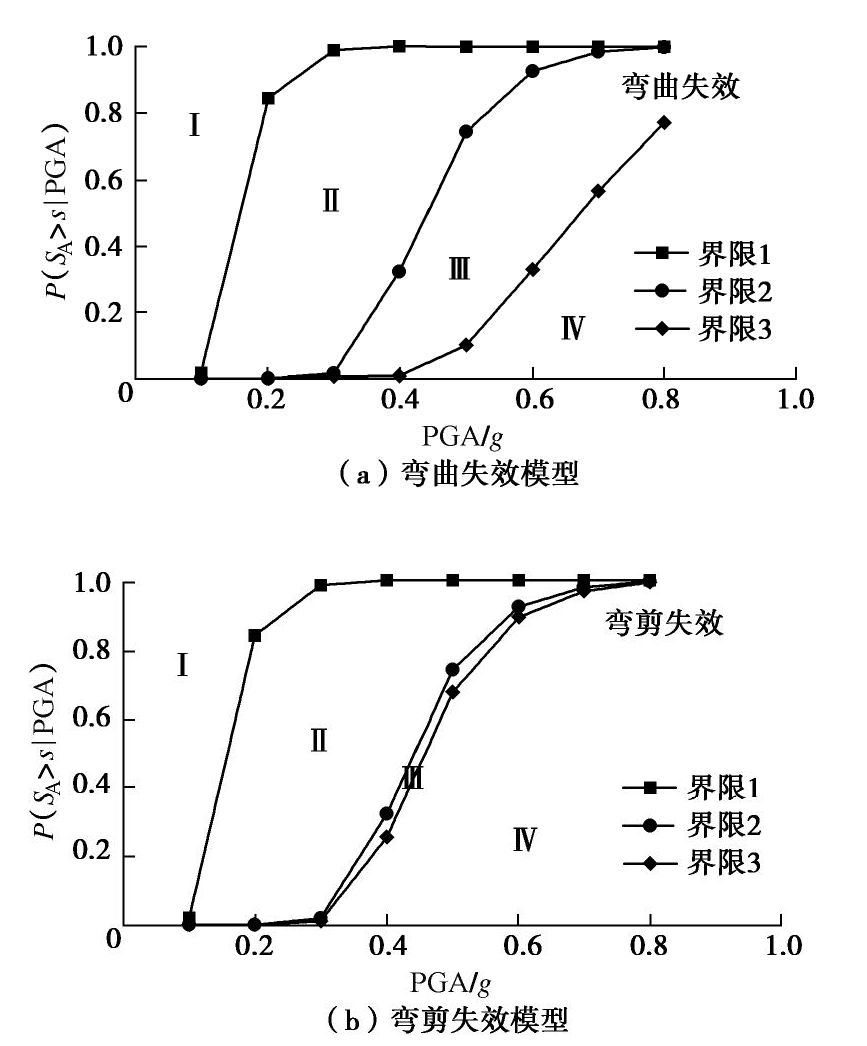
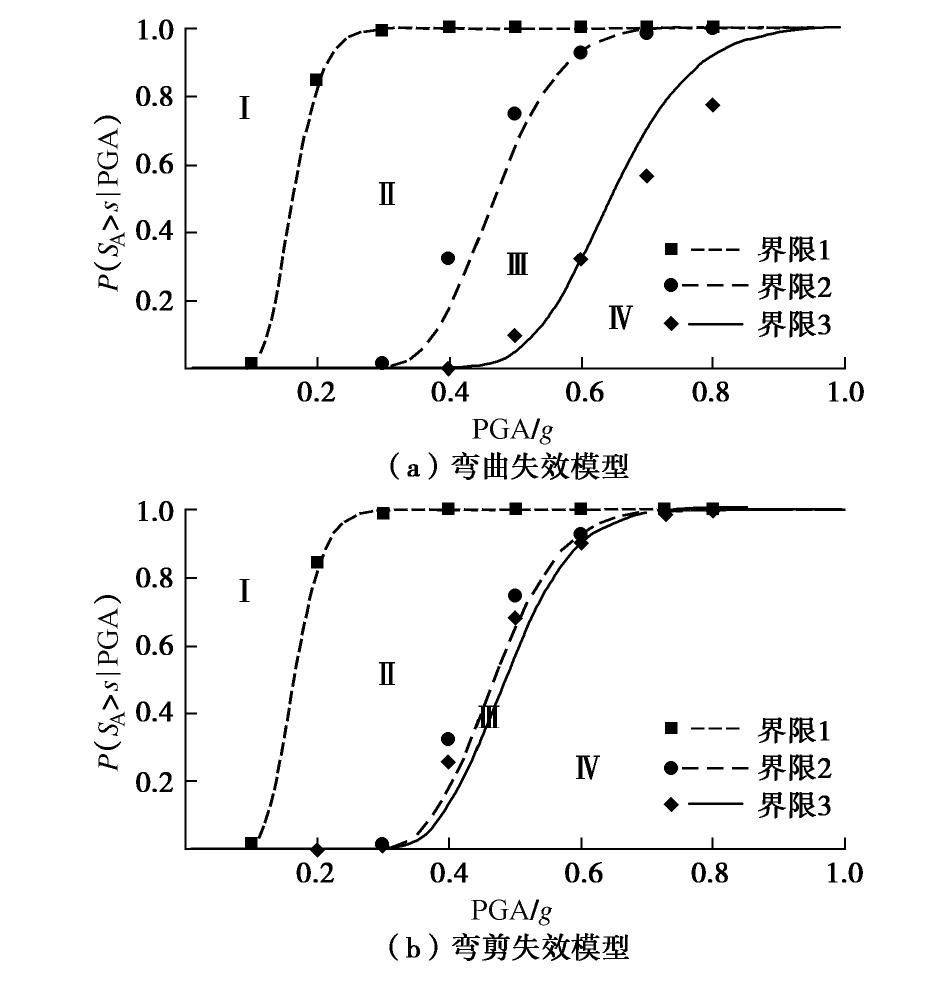
Φ 为标准正态分布的累积分布函数。整理上述统计结果,得到不同损伤模式下的高桩码头地震易损性曲线,见图12。根据地震易损性曲线,容易得到在一定强度等级地震作用下高桩码头达到某一具体损伤阶段的概率。当地震作用PGA=0.4g时,高桩码头以弯曲失效模式达到广泛损伤阶段的概率为32.15%。由图12（a）可知,弯曲失效模式下,当PGA= 0.4g时高桩码头可能发生广泛损伤,当PGA=0.5g时高桩码头可能发生完全崩塌。由图12（b）可知,弯剪失效模式下,当PGA=0.4g时高桩码头可能发生广泛损伤,甚至完全崩塌。此外,由图12（a）,12（b）对比可知,在弯剪失效模式下,高桩码头出现完全崩塌的可能性也明显提高。
5.2 简化的地震易损性曲线
为了更好地将性能化这一概念落实到高桩码头设计中,并预测地震过程中高桩码头发生破坏的概率,本节基于概率论及统计学知识,对高桩码头进行了地震易损性分析。
基于大量震后的破坏数据,早期专家学者们研究得到的易损性曲线的图形形式与对数正态分布形式相差不大,并且在传统可靠度理论下推导的易损性曲线也服从对数正态分布。因此,大多数学者采用对数正态分布的累积分布函数对高桩码头地震易损性曲线进行分析[29-31]。Singhal等[32]基于贝叶斯理论,分析了结构震害的损伤数据,指出结构损伤指标的随机性能够采用均值未知、对数标准差已知的对数正态分布表示。据此推导得到高桩码头的地震易损性曲线,并按照对数正态分布的累积分布函数进行拟合。这样,简化的地震易损性曲线可由包含参数
γ1 ,γ2 确定：P(SA>si|PGA=j)=∫j01√2πγ1×PGA⋅exp{−12[ln(PGA)−γ2γ1]2}dPGA。 (6) 根据对数分布正态与标准正态分布之间的数学关系,引入中间变量Z对式（6）进行简化得到：
P(SA>si|PGA=j)=Φ(Z), (7) Z=ln(PGA)−γ2γ1=Φ−1[P(SA>si|PGA=j)], (8) 式中,Φ-1为标准正态分布的累积分布函数的反函数。
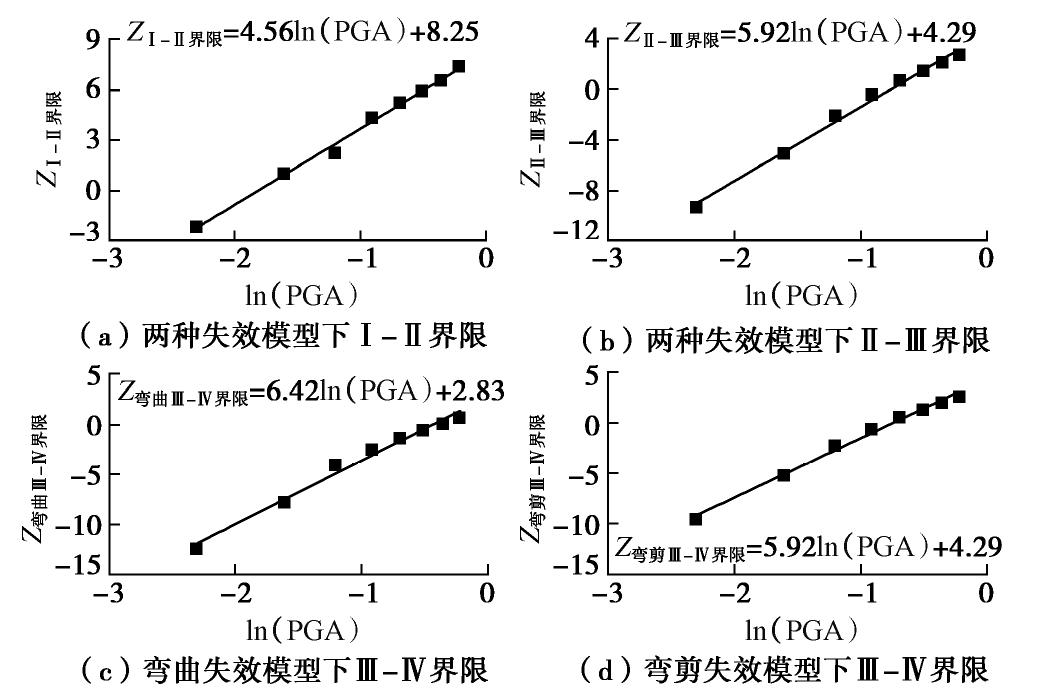
通过对高桩码头地震易损性曲线的数学拟合,见图13,并将各拟合直线的截距和斜率反算求得与各曲线对应的参数
γ1 ,γ2 ,见表5。![]()
图 13 高桩码头地震易损性曲线具体拟合过程Figure 13. Fitting of seismic fragility curve of pile-supported wharf表 5 高桩码头地震易损性曲线拟合参数表Table 5. Fitting parameters of seismic fragility curve of pile-supported wharf失效模式 弯曲失效 弯剪失效 γ1 γ2 γ1 γ2 界限1 0.2195 -1.8113 0.2195 -1.8113 界限2 0.1706 -0.7598 0.1706 -0.7598 界限3 0.1557 -0.4404 0.1691 -0.7258 根据拟合结果,计算得到简化的高桩码头地震易损性曲线,见图14。简化的高桩码头地震易损性曲线能够很好地对高桩码头各损伤阶段的超越概率进行捕捉,从而为高桩码头的震后损伤评估、经济损失分析提供必要的技术支持,具有很好的工程价值。
![]()
图 14 简化的高桩码头地震易损性曲线Figure 14. Simplified seismic fragility curves of pile-supported wharf6. 结论
针对近岸液化场地高桩码头实际工程,建立了液化场地全直桩高桩码头地震反应分析数值模型,综合运用模态分析、Pushover分析、增量动力分析和易损性分析等方法,从概率角度深入研究了高桩码头抗震性能,得到4点结论。
（1）针对弯曲失效和弯剪失效两种失效模式,分别提出可用于量化描述高桩码头破坏的损伤指标。发现高桩码头在弯剪失效模式下的整体抗弯性能并未完全发挥。因此,应注意高桩码头剪力集中区域的抗震设防。
（2）基于IDA分析方法分析了地震过程中高桩码头抗震性能,获得了其在不同强度地震作用下的动力响应结果,确定了弯曲和弯剪两种失效模式下高桩码头的需求参数。
（3）借助概率论及统计学知识,建立了高桩码头地震易损性模型,分别预测了不同地震强度下高桩码头在弯曲和弯剪两种失效模式下的损伤程度及所达到的性能水准。本文建立高桩码头地震易损性曲线的技术途径可为类似工程提供技术参考。
（4）鉴于高桩码头地震易损性曲线的影响因素众多,包括桩的计算参数、布桩形式、土层条件等,将在今后研究工作中给予进一步考虑与探讨。
-
![]()
图 4 数值计算得到的PHC管桩单桩力学性能
Figure 4. Mechanical properties of PHC piles from numerical analysis
![]()
图 8 弯曲失效模式下高桩码头损伤演化过程
Figure 8. Damage evolution of pile-supported wharf under bending failure mode
![]()
图 9 弯剪失效模式下高桩码头损伤演化过程
Figure 9. Damage evolution process of pile-supported wharf under bending shear failure mode
![]()
图 10 高桩码头侧向承载性能及损伤阶段图
Figure 10. Lateral loading performances and damage stages of pile-supported wharf
![]()
图 13 高桩码头地震易损性曲线具体拟合过程
Figure 13. Fitting of seismic fragility curve of pile-supported wharf
![]()
图 14 简化的高桩码头地震易损性曲线
Figure 14. Simplified seismic fragility curves of pile-supported wharf
表 1 土体的计算参数
Table 1 Model parameters of soils
土层编号 饱和密度/(kg·m-3) 剪切模量/kPa 体积模量/kPa 黏聚力/kPa 摩擦角/(°) 峰值剪应变 参考围压p/kPa 相位转换角/(°) Ⅰ 1700 55 150 0 29 0.1 80 29 Ⅱ 1950 60 300 30 18 0.1 80 — Ⅲ 2000 100 300 0 37 0.1 80 27 Ⅳ 1900 150 750 25 19 0.1 80 — Ⅴ 2790 280 1300 0 40 0.1 80 — Ⅵ 2240 140 1300 15 45 0.1 80 27 
下载: 导出CSV
参数类别 混凝土抗压强度fc/MPa 混凝土抗压强度应变εc 混凝土压碎强度fcu/MPa 混凝土压碎强度应变εcu 钢筋屈服强度Fy/MPa 钢筋初始抗拉刚度Es/MPa 钢筋张拉应力Epre/MPa PHC管桩整体抗剪刚度G/MPa 桩B/C/D -80 -0.00215 -50.2 -0.003 1570 200000 994 16282.051 桩A/E/F -160 -0.00215 -100.4 -0.003 3140 400000 1988 32564.102
下载: 导出CSV
表 3 港口工程4阶段损伤概念
Table 3 Concept of four-stage damage in port engineering
损伤阶段 Ⅰ Ⅱ Ⅲ Ⅳ 概括描述 基本完好 可控损伤 广泛损伤 完全崩塌 具体描述 结构处于完好状态或产生轻微损伤 结构在可修复条件下产生有限有限的损伤,并直至发生一定的延性响应 结构产生广泛的损伤直至接近崩塌的延性响应 结构崩塌并丧失承载性能
下载: 导出CSV
表 4 选取的地震动记录
Table 4 Selected ground motion records
序号 名称 台站 年份 PGA/g Tp/s Tm/s D5-95/s 1 Morgan hill Capitola 1984年 0.14 0.20 0.31 15.30 2 Livermore San Ramon-Eastman Kodak 1980年 0.15 0.62 1.00 14.20 3 Trinidad 090 CDMG Station 1498 1983年 0.19 0.32 0.38 12.18 4 Hollister USGS Station 1028 1961年 0.20 0.48 0.63 16.48 5 Imperial Valley Chihuahua 1979年 0.27 0.26 0.58 24.00 6 Imperial Valley USGS Station 5115 1979年 0.32 0.36 0.44 11.04 7 San Fernando Santa Felita Dam (Outlet) 1971年 0.34 0.10 0.46 23.60 8 Kobe Kakogawa 1995年 0.35 0.16 0.48 13.20 9 Kocaeli Yarimca 1999年 0.35 0.52 1.24 15.11 10 Friuli Tolmezzo 1976年 0.35 0.26 0.40 4.90 11 Chi-Chi TCU045 1999年 0.36 0.44 0.47 11.34 12 Loma Prieta 090 CDMG Station 47381 1989年 0.37 0.40 0.37 5.00 13 Northridge 090 CDMG Station 24278 1994年 0.57 0.52 0.79 6.80 14 Landers 000 SCE Station 24 1992年 0.78 0.32 0.75 21.34
下载: 导出CSV
表 5 高桩码头地震易损性曲线拟合参数表
Table 5 Fitting parameters of seismic fragility curve of pile-supported wharf
失效模式 弯曲失效 弯剪失效 γ1 γ2 γ1 γ2 界限1 0.2195 -1.8113 0.2195 -1.8113 界限2 0.1706 -0.7598 0.1706 -0.7598 界限3 0.1557 -0.4404 0.1691 -0.7258
下载: 导出CSV
-
[1] BRADLEY B A, CUBRINOVSKI M, DHAKAL R P, et al. Probabilistic seismic performance and loss assessment of a bridge-foundation-soil system[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(5): 395-411. doi: 10.1016/j.soildyn.2009.12.012
[2] GOULET C A, HASELTON C B, MITRANI-REISER J, et al. Evaluation of the seismic performance of a code-conforming reinforced-concrete frame building—from seismic hazard to collapse safety and economic losses[J]. Earthquake Engineering & Structural Dynamics, 2007, 36(13): 1973-1997.
[3] ICHII K. Fragility curves for gravity-type quay walls based on effective stress analyses[C]//13th WCEE. 2004, Vancouver.
[4] CHIOU J S, CHIANG C H, YANG H H, et al. Developing fragility curves for a pile-supported wharf[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(5/6): 830-840.
[5] HEIDARY-TORKAMANI H, BARGI K, AMIRABADI R, et al. Fragility estimation and sensitivity analysis of an idealized pile-supported wharf with batter piles[J]. Soil Dynamics and Earthquake Engineering, 2014, 61/62: 92-106. doi: 10.1016/j.soildyn.2014.01.024
[6] SU L, WAN H P, DONG Y, et al. Seismic fragility assessment of large-scale pile-supported wharf structures considering soil-pile interaction[J]. Engineering Structures, 2019, 186: 270-281. doi: 10.1016/j.engstruct.2019.02.022
[7] SU L, WAN H P, BI K M, et al. Seismic fragility analysis of pile-supported wharves with the influence of soil permeability[J]. Soil Dynamics and Earthquake Engineering, 2019, 122: 211-227. doi: 10.1016/j.soildyn.2019.04.003
[8] MIRZAEEFARD H, HARIRI-ARDEBILI M A, MIRTAHERI M. Time-dependent seismic fragility analysis of corroded pile-supported wharves with updating limit states[J]. Soil Dynamics and Earthquake Engineering, 2021, 142: 106551. doi: 10.1016/j.soildyn.2020.106551
[9] 王炳煌. 高桩码头工程[M]. 北京: 人民交通出版社, 2010. WANG Bing-huang. Pile Wharf Engineering[M]. Beijing: China Communications Press, 2010. (in Chinese)
[10] MCKENNA F. OpenSees: a framework for earthquake engineering simulation[J]. Computing in Science & Engineering, 2011, 13(4): 58-66.
[11] 常士骠, 张苏民. 工程地质手册[M]. 北京: 中国建筑工业出版社, 2007. CHANG Shi-piao, ZHANG Su-min. Geological Engineering Handbook[M]. Beijing: China Architecture and Building Press, 2007. (in Chinese)
[12] 唐亮, 凌贤长, 徐鹏举, 等. 液化场地桩-土地震相互作用振动台试验数值模拟[J]. 土木工程学报, 2012, 45(增刊1): . https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2012S1060.htm TANG Liang, LING Xian-zhang, XU Peng-ju, et al. Numerical simulation of shaking table test for seismic soil-pile interaction in liquefying ground[J]. Chinese Civil Engineering Journal, 2012, 45(S1): . (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2012S1060.htm
[13] HUI S Q, TANG L, ZHANG X Y, et al. An investigation of the influence of near-fault ground motion parameters on the pile's response in liquefiable soil[J]. Earthquake Engineering and Engineering Vibration, 2018, 17(4): 729-745. doi: 10.1007/s11803-018-0472-7
[14] CONG S Y, TANG L, LING X Z, et al. Numerical analysis of liquefaction-induced differential settlement of shallow foundations on an island slope[J]. Soil Dynamics and Earthquake Engineering, 2021, 140: 106453. doi: 10.1016/j.soildyn.2020.106453
[15] 孟畅. 液化场地高桩码头地震易损性分析[D]. 哈尔滨: 哈尔滨工业大学, 2020. MENG Chang. Seismic Fragility Analysis of the Pile-supported Wharf in Liquefiable Soils[D]. Harbin: Harbin Institute of Technology, 2020. (in Chinese)
[16] 苏雷. 液化侧向扩展场地桩-土体系地震模拟反应分析[D]. 哈尔滨: 哈尔滨工业大学, 2016. SU Lei. Earthquake Simulation Response of Soil-pile System in Liquefaction-induced Lateral Spreading Ground[D]. Harbin: Harbin Institute of Technology, 2016. (in Chinese)
[17] 惠舒清. 液化场地简支桥梁体系地震反应与抗震性态分析[D]. 哈尔滨: 哈尔滨工业大学, 2018. HUI Shu-qing. Seismic Response and Performance Analysis of Soil-pile Group-multi-span Simply Supported Bridge System in Liquefiable Ground[D]. Harbin: Harbin Institute of Technology, 2018. (in Chinese)
[18] YANG Z. Numerical Modeling of Earthquake Site Response Including Dilation and Liquefaction[D]. NewYork: Columbia University, 2000.
[19] YANG Z, LU J, ELGAMAL A. OpenSees Soil Models and Solid-fluid Fully Coupled Elements Wser Manual[Z]. San Diego: University of California, 2008.
[20] 梁兴文, 王社良, 李晓文. 混凝土结构设计原理[M]. 北京: 科学出版社, 2003. LIANG Xing-wen, WANG She-liang, LI Xiao-wen. Design Theory for Concrete Structure[M]. Beijing: Science Press, 2003. (in Chinese)
[21] 预应力混凝土用钢棒：GB/T 5223.3—2017[S]. 2017. Steel Bars for the Prestressing of Concrete: GB/T 5223.3— 2017[S]. Beijing: Standards Press of China, 2017. (in Chinese)
[22] 张楠. 考虑结构—桩—土相互作用的PHC管桩抗震性能研究[D]. 天津: 天津大学, 2014. ZHANG Nan. Study on Seismic Performance of Pipe Piles Considering Soil-Pile-Superstructure Interaction[D]. Tianjin: Tianjin University, 2014. (in Chinese)
[23] ZACCHEI E, LYRA P H C, STUCCHI F R. Pushover analysis for flexible and semi-flexible pile-supported wharf structures accounting the dynamic magnification factors due to torsional effects[J]. Structural Concrete, 2020, 21(6): 2669-2688. doi: 10.1002/suco.202000137
[24] JOHNSON G S, ARULMOLI A K, ASAVAREUNGCHAI S. Seismic Design of Piers and Wharves[M]. ASCE, 2014.
[25] 阮起楠. 预应力混凝土管桩[M]. 中国建材工业出版社, 2000. RUAN Qi-nan. Prestressed Concrete Pipe Pile[M]. Beijing: China Building Material Industry Publishing House, 2000. (in Chinese)
[26] BOULANGER R W. Seismic design guidelines for port structures[J]. Earthquake Spectra, 2002, 18(3): 579-580. doi: 10.1193/1.1510751
[27] Design of Structures for Earthquake Resistance; General Rules, Seismic Actions, Design Rules for Buildings, Foundations and Retaining Structures: Designer's Guide To EN 1998-1 and en 1998-5 Eurocode 8[S]. 2005.
[28] 中国地震动参数区划图：GB 18306—2015[S]. 2015. Seismic Ground Motion Parameters Zonation Map of China: GB 18306—2015[S]. 2015. (in Chinese)
[29] CIMELLARO G P, REINHORN A M. Multidimensional performance limit state for hazard fragility functions[J]. Journal of Engineering Mechanics, 2011, 137(1): 47-60. doi: 10.1061/(ASCE)EM.1943-7889.0000201
[30] LU D G, YU X H, PAN F, et al. Probabilistic seismic demand analysis considering random system properties by an improved cloud method[C]//The 14th World Conference on Earthquake Engineering, 2008, Beijing.
[31] DE RISI R, GODA K, TESFAMARIAM S. Multi- dimensional damage measure for seismic reliability analysis[J]. Structural Safety, 2019, 78: 1-11. doi: 10.1016/j.strusafe.2018.12.002
[32] SINGHAL A, KIREMIDJIAN A S. Bayesian updating of fragilities with application to RC frames[J]. Journal of Structural Engineering, 1998, 124(8): 922-929. doi: 10.1061/(ASCE)0733-9445(1998)124:8(922)
-
期刊类型引用(4)
1. 宋鹏彦，王晨，赵仰康. 考虑主余震强度比和主震损伤状态的RC框架结构易损性分析. 世界地震工程. 2024(02): 14-25 . 
百度学术
2. 周峰，汪振，戴启权，聂智超. 堆场堆载作用下岸坡及高桩码头响应特性研究. 水道港口. 2024(05): 739-746 . 百度学术
3. 吴九江，胡浩东，李艳. 可液化场地桥梁桩基震害及抗液化研究进展. 工业建筑. 2023(10): 169-178+118 . 百度学术
4. 陶连金，文虎，贾志波，边金，张海祥. 基于性能的组合边坡加固设计方法研究. 工程地质学报. 2022(05): 1620-1628 . 百度学术
其他类型引用(5)
计量
- 文章访问数: 244
- HTML全文浏览量: 40
- PDF下载量: 130
- 被引次数: 9
