考虑约束的贝叶斯概率反演方法

陶袁钦; 孙宏磊; 蔡袁强

doi:10.11779/CJGE202110014

考虑约束的贝叶斯概率反演方法 English Version

陶袁钦^1,,
孙宏磊^2, ,,
蔡袁强^{1, 2}

1.
浙江大学建筑工程学院,浙江　杭州　310058
2.
浙江工业大学土木工程学院,浙江　杭州　310014

基金项目:

国家重点研发计划项目 2017YFE0119500

国家重点研发计划项目 2016YFC0800200

国家自然科学基金项目 52078464

国家自然科学基金项目 U2006225

国家自然科学基金项目 51620105008

详细信息

作者简介:
陶袁钦(1995— ),女,博士研究生,主要从事岩土工程中的数据融合等方面的研究。E-mail：taoyuanqin@zju.edu.cn

通讯作者:
孙宏磊, E-mail：sunhonglei@zju.edu.cn

中图分类号: TU431
计量
- 文章访问数: 369
- HTML全文浏览量: 53
- PDF下载量: 169
出版历程
- 收稿日期: 2021-01-13
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-09-30

Bayesian back analysis considering constraints

1.
College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
2.
College of Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, China

摘要

摘要: 土体参数对岩土工程计算模型的预测效果至关重要。在土体参数识别问题中,基于MCMC抽样的贝叶斯方法是一种反演土体参数概率分布的常见方法。然而该方法通常仅考虑土体参数的先验分布、预测与观测间的差异,不考虑其他已知信息如土体参数间的经验性相互关系等,当采用数值模拟作为计算模型时,该方法计算负担大,限制了其运用。为此,提出了一种考虑附加约束信息的近似贝叶斯方法REnKF-MDA,并将其与无约束MCMC、考虑约束的MCMC、正则化集合卡尔曼滤波REnKF进行对比,采用简单多项式算例和地基沉降案例说明该方法的有效性。结果表明：融合附加约束信息有助于提高反演参数的合理性和可信度,约束强弱由约束协方差决定。以考虑约束的MCMC为参考,REnKF可准确估计均值但显著低估了参数后验分布的不确定性,REnKF-MDA可同时合理地估计均值和不确定性。
- 贝叶斯方法 /
- 参数估计 /
- 集合卡尔曼滤波 /
- 约束信息 /
- 数据融合
Abstract: Soil parameters significantly affect the prediction performance of geotechnical models. In the field of parameter identification, the MCMC-based Bayesian method is an effective way to infer the probability distribution of soil parameters. However, this method only considers the prior distribution of soil parameters and the difference between predictions and observations, without considering other additional information such as empirical correlations between soil parameters. In addition, the MCMC method leads to high computational cost if the numerical methods are used as the model, which limits its application. In this study, a new approximate Bayesian method considering the additional constraints is proposed, named REnKF-MDA. The proposed method is compared with the MCMC-based Bayesian method, MCMC-based Bayesian method with constraints, and REnKF. The effectiveness of the proposed REnKF-MDA method is illustrated by a simple polynomial case and a foundation settlement project. The results indicate that assimilating the additional constraint informations is helpful to improve the rationality and confidence of the inferred parameters. The confidence of the constraint is determined by the covariance of the constraint information. Taking the MCMC-based Bayesian method with constraints as a reference, the REnKF provides an accurate evaluation of the mean value, but significantly underestimates the uncertainty of the posterior distributions. In contrast, the REnKF-MDA estimates both the mean and uncertainty well.
- Bayesian method /
- parameter identification /
- ensemble Kalman filter /
- constraint information /
- data assimilation

HTML全文

0. 引言

随着工业化和城市化的加速发展，人们对化石能源的消耗和全球变暖趋势加剧，对新能源的开发和利用变得日益重要^[1]。准确测定岩土材料的导热系数是岩土工程温度场分析和能源桩设计的重要内容，土体导热系数是一个复杂的性质，主要取决于土体的类型、饱和度、粒径分布和颗粒堆积密度等因素^[2]。导热系数是土体热力学特性的重要指标之一，能够直接反映热能在土体介质中的传递特性^[3]。

近年来，很多学者对土体热传导特性进行大量研究，并提出大量的预测模型。Kersten等^[4]采用单根线柱热源径向加热的热传导测试方法对19种不同类型土体的导热系数进行测试，分析了含水率和干密度对导热系数的影响，得出了基于含水率和干密度预测土体导热系数的经验公式；Cote等^[5]和Johansen^[6]对650多个土样的导热系数测试结果进行分析，并在Johansen^[4]提出的归一化模型的基础上建立了广义的归一化模型；Erzin等^[7]基于人工神经网络模型建立了预测土体导热系数的单个预测模型和广义预测模型，得出人工神经网络模型在预测土体导热系数方面的有效性。综上所述，预测土体导热系数的主要是通过经验关系模型、理论计算模型和人工神经网络模型，经验关系模型由于考虑的因素较少，计算精度较低。理论计算模型在计算土体导热系数时，所涉及的参数较多，计算过程复杂，难以在实际工程中应用。人工神经网络模型可以考虑的影响因素较多，在预测土体导热系数时精度较高。

为建立预测土体导热系数预测模型，首先对土体导热系数的主要影响因素进行分析，然后利用人工智能算法对土体导热系数进行预测，对预测结果进行检验，并与传统经验关系模型进行对比，验证人工智能算法的有效性和稳健性。

1. 土体导热特性

土体导热系数是表征土体热物理性质的重要指标，与众多因素密切相关，如土颗粒矿物成分、饱和度、粒径分布和孔隙率等，其中矿物成分是决定土颗粒导热性能的关键因素^[8]。导热系数能够直接反映热能在土体介质中的传递特性。因此，为了研究土体的传热机理，本文主要介绍土体饱和度、矿物成分、颗粒分布和温度等参数对热传导的影响。

为研究饱和度对土体导热系数的影响，根据Tarnawski等^[9-11]对40种土体导热系数实测数据，选择黏土、粉土和粉砂的测试结果来研究饱和度对导热系数的影响，如图 1所示。从图 1可以看出，当土体饱和度增加时，导热系数也随之增加，饱和度增加会提高土体中的含水率，含水率的增加会使土颗粒表面形成水膜，颗粒之间形成水桥，而空气的占比会减小，由于水的导热系数明显大于空气的导热系数，热量通过颗粒表面水膜及其水桥传递增加，使土体导热系数增加^[12]。土体饱和度的增加会提高颗粒间的接触面积，热量通过颗粒与颗粒间的传递增加，使土体的导热系数增大。

图 1 饱和度对导热系数的影响

Figure 1. Influences of degree of saturation on thermal conductivity

下载: 全尺寸图片幻灯片

在影响土体导热系数的因素中，固相的矿物组成成分对固体颗粒导热系数的影响非常重要^[13]，土体的固体颗粒主要由原生矿物和次生矿物组成，而这些矿物的导热系数不同，固体颗粒矿物的组成成分不同会影响土体的导热系数。在土体的矿物组成中，石英的导热系数为7.69 (W·m^-1·K^-1)，而其他矿物的导热系数通常在1.25~4.00 (W·m^-1·K^-1)，石英的导热系数明显高于其他矿物，石英含量高的土体其导热系数也较大^[14]。从图 1可以看出，粉砂的导热系数明显高于黏土的导热系数，因为粉砂的石英含量高于黏土的石英含量，所以石英含量高的土体导热系数较大。因此，土体固体颗粒的导热系数取决于矿物的类型和比例，尤其是石英的含量。

对土体导热系数的影响还包括颗粒分布、颗粒粒径大小、颗粒形状、各向异性和温度等因素。颗粒分布会影响土体的级配，级配的变化会影响颗粒与颗粒间的接触面积，从而影响土体的导热系数。在相同干密度下，颗粒粒径越小，颗粒间的接触点越多，而热量通过固体颗粒内部传递热量要快于颗粒间的传播，在相同情况下，颗粒粒径越小，导热系数越低，从图 1可以看出黏土的颗粒粒径最小，在相同情况下其导热系数最小；颗粒形状会影响颗粒与颗粒间接触的面积，从而影响热量的传播。Macaulay等^[15]对澳大利亚粉砂岩导热系数测试，得出导热系数随层理方向角增加而增加，但层理方向角增加到40°后，其导热系随层理方向角的增加而数趋于平稳。温度的变化会影响分子的热运动，Xu等^[16]得出膨润土的导热系数随温度升高而增大，当温度为90℃时，其导热系数为5℃时的（1.2~1.5）倍；当温度为5~60℃时，导热系数随温度的变化相对较小；当温度高于60℃时，导热系数显著增加。

2. 土体导热系数数据库

本文使用的数据来源于40种加拿大田间土^[9-11]。其中22种为细粒土（含砂量 < 40%），18种为粗粒土（含砂量 > 40%）。根据前述土体导热系数影响因素的分析，选择干密度、饱和度、黏粒含量、粉粒含量和砂粒含量作为预测模型的输入参数，土体导热系数作为模型的输出参数。表 1列出了预测模型输入参数和输出参数的边界值。

表 1 预测模型输入参数的输出参数的边界值

Table 1. Boundary values of input parameters and output parameters of prediction model

类型	参数项	最小值	最大值
输入参数	干密度ρ_d/(g·cm^-3)	0.999	1.728
	饱和度S_r/%	0	100
	黏粒含量c/%	0	42
	粉粒含量s_i/%	0	83.4
	砂粒含量s_a/%	0	100
输出参数	导热系数λ/(W·m^-1·K^-1)	0.1	3.2

下载: 导出CSV

| 显示表格

3. 计算模型

随着人工智能算法在岩土工程领域快速发展，使用这些算法对岩土工程参数进行计算，将节约工程造价及时间。基于这一目的，通过人工神经网络模型（ANN模型）、基于自适应神经网络的模糊推理系统（ANFIS模型）和支持向量机模型（SVM模型）对土体的导热系数λ进行计算。

3.1 人工神经网络模型

人工神经网络模型是基于模仿人类大脑的结构和功能的信息处理系统^[17]。目前已经开发出很多神经网络算法，如Levenberg-Marqurdt算法、共轭梯度算法、贝叶斯正则化算法^[17-19]。神经网络模型由输入层、隐藏层和输出层组成，层与层之间通过激活函数 $f(x)$ 进行转换，激活函数 $f(x)$ 通常为Sigmoid函数、双曲线正切函数（Tanh）和校正线性函数（Relu）。图 2是一个典型的神经网络结构，其中N₁，N₂和N_i是输入参数，Y是输出参数。使用下列过程对人工神经网络建模：

图 2 人工神经网络模型结构

Figure 2. Structure of artificial neural network model

下载: 全尺寸图片幻灯片

将输入数据和输出数据在0到1之间进行归一化。归一化计算式为^[7]

${x_{{\text{norm}}}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} \text{，}$

(1)

式中，x_norm为标准化值，x为实际值，x_max为最大值，x_min为最小值。输入参数N_i在隐藏层的Sigmoid激活函数的计算式为

${S_{\text{k}}} = {\text{sigmoid}}\left( {\sum\limits_{i = 1}^N {{w_x}{N_i} + {b_x}} } \right) \text{，}$

(2)

${\text{sigmoid}} = \left( {\frac{1}{{1 + {{\text{e}}^{ - x}}}}} \right) \text{，}$

(3)

式中，S_k，w_x和b_x分别为隐藏层节点的计算值、权重参数和偏差因子。输出层节点的计算式为

${Y_n} = \sum\limits_{j = 1}^M {{w_y}{S_{\text{k}}} + {b_y}} \text{，}$

(4)

式中，w_y为权重参数，b_x为输出层偏差因子。输出层数据的反归一化：

$Y = {Y_n}[{x_{\max }} - {x_{\min }}] + {x_{\min }} 。$

(5)

本文使用的神经网络模型是基于贝叶斯正则化算法建立的预测模型，贝叶斯正则化算法使用岭回归将非线性回归转换为统计问题^[19]。这种方法的优点是在验证过程中不需要使用交叉验证技术，这可以简化模型训练，节约模型的计算时间。

3.2 基于自适应神经网络的模糊推理系统

基于自适应神经网络的模糊推理系统（ANFIS）是将模糊系统和神经网络相结合而构成的网络，采用BP算法和最小二乘估计法的混合算法进行学习，考虑了基于一阶Sugeno模型的两种模糊If-then后置规则。

规则一，如果x=A₁和y=B₁，则

${f_1} = {p_1}x + {q_1}y + {r_1} 。$

(6)

规则二，如果x=A₂和y=B₂，则

${f_2} = {p_2}x + {q_2}y + {r_2} 。$

(7)

式中x和y为输入参数；A_i和B_i为模糊集；f_i为模糊规则指定的模糊区域内的输出值；p_i，q_i和r_i为训练过程中确定的参数。本文使用减法聚类算法训练ANFIS模型，这种算法可以自动估计聚类数目及其位置^[20]。

3.3 支持向量机模型

支持向量机模型（SVM）是一种机械学习方法，其理论是建立一个最优分类超平面，将线性不可分问题转换成线性可分问题^[21]。训练样本为{ ${x_i}$ ， ${y_i}$ }，i=1到m，其中 ${x_i}$ ∈R， ${y_i}$ ∈R，R为实数域。以 $\varphi$ ( ${x_i}$ )表示映射到高维空间中的样本，构造得到的函数表达式为

${y_i} = W\varphi ({x_i}) + b \text{，}$

(8)

式中，W为可调权值向量，b为偏置值。

寻找最优的分类超平面亦即寻找最优的W和b。引入松弛变量 $\xi$ 和 $\xi _{}^*$ ，依据结构风险最小化准则，采用 $\varepsilon$ -SVR模型建立带有约束条件的模型优化函数：

${f_{{\text{optimization}}}} = \mathop {\min }\limits_{{\text{W}},{\text{b}},{\xi _i},\xi _i^*} \left[ {\frac{1}{2}{W^{\text{T}}}W + C\sum\limits_{i = 1}^m {({\xi _i} + \xi _i^*)} } \right] \text{，}$

(9)

约束条件为

$\left.\begin{array}{l} y_i-W^{\mathrm{T}} \varphi\left(x_i\right)+b \leqslant \varepsilon+\xi_i^* ,\\ W^{\mathrm{T}} \varphi\left(x_i\right)+b-y_i \leqslant \varepsilon+\xi_i ,\\ \xi_i, \xi_i^* \geqslant 0 \quad(i=1, \cdots, m), \end{array}\right\}$

(10)

式中，C为惩罚函数， $\varepsilon$ 为损失函数。

使用二次规划优化算法SMO（sequential minimal optimization）构造得到关于x的预测函数 $f(x)$ ：

$f(x) = \sum\limits_{i = 1}^m {(a_i^* - {a_i})} \varphi {({x_i})^{\text{T}}}\varphi ({x_i}) + b \text{，}$

(11)

式中， $f(x)$ 为代表土体导热系数， $a_i^*$ 为 ${a_i}$ 的伴随矩阵，m为样本数目。

3.4 蒙特卡罗模拟

在复杂的岩土工程中使用人工智能算法时，蒙特卡罗方法常用于分析计算模型输入参数存在可变性时的鲁棒性^[22]。图 3显示了蒙特卡罗方法的基本原理。它的原理是随机输入参数来多次重现输出结果^[23]。输入参数的随机波动可以在输出解上传播，这意味着输出的概率密度函数是由所有输入参数的统计信息构成的。输出的概率分布定量分析对于表征模型的稳健性是非常有效的。在本文中，使用蒙特卡罗方法分析预测模型的稳健性，并对结果进行统计分析。

图 3 蒙特卡罗方法原理示意图

Figure 3. Schematic diagram of principle of Monte Carlo method

下载: 全尺寸图片幻灯片

4. 预测模型的建立与性能检验

4.1 预测模型的建立

使用了人工智能算法建立预测土体导热系数的预测模型。根据第一节对土体导热系数影响因素的分析，所有计算模型的输入参数为干密度、饱和度、黏粒含量、粉粒含量和砂粒含量，输出参数为土体的导热系数。将数据分为两个部分，训练部分使用70%的数据，测试部分使用30%的数据。人工神经网络模型隐藏层神经元的数量从1开始增加，通过训练得出最佳隐藏层和隐藏层神经元数。SVM模型是由三次多项式核函数构建的，选择盒约束的正则化常数c为0.112，SVM模型的ε参数为0.0111。预测模型（训练集）对土体导热系数λ的计算结果与实测结果如图 4所示。

图 4 预测模型训练数据集预测值与实测值比较

Figure 4. Comparison between predicted and measured values in training data set of prediction model

下载: 全尺寸图片幻灯片

从图 4可以看出，每个智能计算模型在训练数据集中都准确的计算出土体的导热系数，为了得到预测结果与实测结果的相关性，对预测值与实测值进行线性拟合，拟合结果如图 4所示。预测模型训练效果最好的是ANN模型，相关系数R²=0.9784；然后是SVM模型的训练效果较好，相关系数R²=0.9747；训练效果最差的是ANFIS模型，相关系数R²=0.9361。线性拟合结果表明ANN模型和SVM模型的线性拟合最靠近Y=X等值线，也说明ANN模型和SVM模型的预测精度高。

4.2 预测模型的性能检验

为了量化计算模型的质量，采用了相关系数R²、均方根误差RMSE、平均绝对误差MAE和方差比VAF来检验计算模型的性能^{[17, 24]}。均方根误差RMSE、平均绝对误差MAE和方差比VAF的计算公式如下所示：

${\text{RMSE}} = \sqrt {\frac{1}{{N - M}}\sum\limits_1^N {{{({y_0} - {y_{\text{p}}})}^2}} } \text{，}$

(12)

${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{y_0} - {y_{\text{p}}}} \right|} \text{，}$

(13)

${\text{VAF}} = \left[ {1 - \frac{{{var} ({y_0} - {y_{\text{p}}})}}{{{var} ({y_0})}}} \right] \times 100 \text{，}$

(14)

式中， ${y_0}$ 为实测值， ${y_{\text{p}}}$ 为预测值，N为样本的编号，M为回归过程的评估参数，var为方差。如果VAF为100%且RMSE为0，则该模型被视为优秀。表 2给出了各预测模型的性能指标值。预测模型对土体导热系数λ的预测值与实测值对比如图 5所示。

表 2 预测模型性能指标

Table 2. Performance indexes of prediction models

模型代号	数据集	R²	RMSE /(W·m^-1·K^-1)	MAE /(W·m^-1·K^-1)	VAF /%
ANN	训练数据集	0.9784	0.0874	0.0673	97.84
ANN	测试集	0.9746	0.0985	0.0701	97.45
ANFIS	训练数据集	0.9361	0.1391	0.1096	94.50
ANFIS	测试集	0.9078	0.1958	0.1262	90.17
SVM	训练数据集	0.9747	0.0941	0.0725	97.47
SVM	测试集	0.9649	0.1147	0.0767	96.48

下载: 导出CSV

| 显示表格

图 5 预测模型测试数据集预测值与实测值比较

Figure 5. Comparison between predicted and measured values of test data set of prediction model

下载: 全尺寸图片幻灯片

从和可以看出，每个预测模型对土体导热系数 $\lambda$ 的预测精度都很高。预测模型预测精度最高的是ANN模型，SVM模型的预测精度略低于ANN模型；预测精度最低的是ANFIS模型，从图 5（b）中可以看出，预测值与实测值偏差较大，数据较离散。线性拟合方程结果表明ANN模型和SVM模型的预测精度高。为了分析计算模型预测值与实测值之间的误差，预测模型的误差分布如图 6所示。

图 6 预测值与实测值误差分布

Figure 6. Error distribution between predicted and measured values

下载: 全尺寸图片幻灯片

从图 6可以看出，在训练数据集和测试数据集，每个智能计算模型的误差分布主要集中在-0.3~0.3 (W·m^-1·K^-1)，每个智能计算模型的计算误差都很小；ANN模型误差分布达到最高峰值，并靠近零；其次分别是SVM模型和ANFIS模型。然而，从表 2可以看出，在测试测试数据集，ANN模型在均方根误差RMSE方面表现最好，均方根误差RMSE=0.0985 (W·m^-1·K^-1)，而SVM模型和ANFIS模型的均方根误差RMSE分别为0.1958 (W·m^-1·K^-1)和0.1147 (W·m^-1·K^-1)；上述分析结果表明，ANN模型在预测土体的导热系数 $\lambda$ 方面的性能最好，ANN模型的权重和偏差基于贝叶斯正则化优化使模型的性能更好，ANFIS模型和SVM模型也很好的预测了土体的导热系数 $\lambda$ 。

4.3 预测模型的稳健性分析

为了评估智能计算模型的稳健性，将用于训练的70%的数据进行随机组合，作为新的输入数据集，生成了300个蒙特卡罗模拟。统计每个预测模型计算值与实测值之间的偏差，每个预测模型获得了300个相关系数R²、均方根误差RMSE和绝对平均误差MAE，计算了关系数R²和均方根误差RMSE的概率分布，以得出智能计算模型在可变输入参数下的性能。蒙特卡罗模拟的相关系数R²、均方根误差RMSE和绝对平均误差MAE概率分布如图 7所示。模拟结果统计如表 3所示。

图 7 蒙特卡罗模拟检验参数概率分布

Figure 7. Probability distribution of parameters by Monte Carlo simulation tests

下载: 全尺寸图片幻灯片

表 3 蒙特卡罗模拟结果统计

Table 3. Statistics of simulated results by Monte Carlo method

检验参数	预测模型	D25	D50	D75	平均值
R²	ANN	0.8926	0.9512	0.9723	0.9132
	ANFIS	0.8731	0.8951	0.9056	0.8761
	SVM	0.9362	0.9459	0.9552	0.9449
RMSE	ANN	0.0838	0.1338	0.2518	0.1898
	ANFIS	0.1935	0.2105	0.2405	0.2285
	SVM	0.1093	0.1333	0.1623	0.1373
MAE	ANN	0.0432	0.0952	0.1832	0.1322
	ANFIS	0.1234	0.1394	0.1614	0.1464
	SVM	0.0839	0.0959	0.1109	0.0989

下载: 导出CSV

| 显示表格

从图 7（a）和表 3可以看出，在相关系数R²概率分布图中可以看出，ANN模型的相关系数R²分布最靠近1，其次分别是SVM模型和ANFIS模型，其中SVM模型的相关系数R²主要分布在0.9至0.97范围内。从图 7（b）和表 3可以看出，在均方根误差RMSE的概率分布图中ANN模型的概率分布最靠近0，其次是SVM模型和ANFIS模型，分布结果跟相关系数R²的概率分布结果相同。从图 7（c）和表 3可以看出，在绝对平均误差MAE的概率分布图中SVM模型的概率分布最靠近0，其次是ANN模型和ANFIS模型。ANN模型、ANFIS模型和SVM模型相关系数R²和均方根误差RMSE的分位数值和平均值如表 3所示。在300次蒙特卡罗模拟中，对相关系数R²、均方根误差RMSE和绝对平均误差MAE的统计研究表明，SVM模型的稳健性最好，其次分别是ANN模型和ANFIS模型。

5. 预测模型性能评价

目前，计算土体导热系数主要是理论计算模型和经验关系模型，理论计算模型计算土体导热系数时，涉及的参数及要求较多，难以有效计算土体导热系数；经验关系模型计算土体导热系数时，具有计算过程简单、易操作等优点，在工程设计中普遍使用此方法。为了评价智能计算模型预测土体导热系数的性能，本文选取Johansen^[6]模型、Cote^[5]模型和Lu^[25]模型计算土体的导热系数。

Johansen模型是Johansen^[6]基于归一化热传导系数概念提出的经验关系模型，该模型能对冻结和未冻结土的导热系数进行计算，经验关系式为

$\lambda = ({\lambda _{{\text{sat}}}} - {\lambda _{{\text{dry}}}}){K_{\text{e}}} + {\lambda _{{\text{dry}}}} \text{，}$

(15)

式中， ${\lambda _{{\text{sat}}}}$ 为饱和土体热导率， ${\lambda _{{\text{dry}}}}$ 为干土热导率，K_e为土体的归一化热导率，当 ${S_{\text{r}}}$ > 0.05时，K_e对于粗土的计算式为

${K_{\text{e}}} = 0.7\log {S_{\text{r}}} + 1 \text{，}$

(16)

式中， ${S_{\text{r}}}$ 为饱和度。当 ${S_{\text{r}}}$ > 0.1时，K_e对于粗土的计算式为

${K_{\text{e}}} = \log {S_{\text{r}}} + 1 \text{，}$

(17)

Johansen通过改进De Vries^[26]热导系数计算模型，提出了干土的导热系数计算公式：

${\lambda _{{\text{dry}}}} = \frac{{0.137{\rho _{\text{d}}} + 64.7}}{{2650 - 0.947{\rho _{\text{d}}}}} \text{，}$

(18)

式中， ${\rho _{\text{d}}}$ 为干密度。在饱和土导热系数计算方面，Sass等^[27]提出的公式被普遍运用，其计算式为

${\lambda _{{\text{sat}}}} = \lambda _{{\text{water}}}^n\lambda _{{\text{solid}}}^{1 - n} \text{，}$

(19)

式中， $\lambda _{{\text{water}}}^{}$ ， $\lambda _{{\text{solid}}}^{}$ 分别为水和土固体颗粒的导热系数，n为孔隙率。

Cote模型是Cote等^[5]根据Johansen^[6]提出的归一化热导系数计算模型的基础上，建立了广义的归一化预测模型：

$\lambda = ({\lambda _{{\text{sat}}}} - {\lambda _{{\text{dry}}}}){K_{\text{e}}} + {\lambda _{{\text{dry}}}} \text{，}$

(20)

式中，K_e为土体的归一化热导率。但K_e和 ${\lambda _{{\text{dry}}}}$ 的计算公式已经被修改，

${K_{\text{e}}}{\text{ = }}\frac{{\kappa {S_{\text{r}}}}}{{1 + (\kappa - 1){S_{\text{r}}}}} \text{，}$

(21)

${\lambda _{{\text{dry}}}} = \chi ({10^{ - \eta n}}) \text{，}$

(22)

式中，κ为经验参数，用于表达土体种类和冻结或未冻结对K_e的影响，χ和η为考虑土的种类和颗粒形状对干土热导系数影响的参数。

Lu模型是Lu等^[25]对12种不同土性的天然土在各种含水率条件进行了大量导热系数测试，通过试验数据拟合，得到了更为简单的干土导热系数和孔隙率的线性关系，并在Johansen提出的归一化热导系数计算模型的基础上，提出了如下经验公式：

$\lambda {\text{ = }}\left[ {\lambda _{{\text{water}}}^n\lambda _{{\text{solid}}}^{1 - n} - (b - an)} \right]\exp [\alpha (1 - S_{\text{r}}^{\alpha - 1.33})] + (b - an) \text{，}$

(23)

式中，a和b为确定干土热传导系数的参数，建议分别取a=0.56和b=0.51，α反映土种类对Kersten变量的影响，针对粗粒土和细粒土分别取0.96和0.27。

智能计算模型对土体预测所得结果λ与通过使用Johansen模型、Cote模型和Lu模型预测得到的λ值进行比较如图 8所示，智能计算模型和经验关系模型的性能检测如表 4所示。

图 8 预测模型与经验关系模型对比

Figure 8. Comparison between prediction model and empirical relationship model

下载: 全尺寸图片幻灯片

表 4 预测模型的性能指标对比

Table 4. Comparison among performance indexes of prediction models

预测模型	R²	RMSE /(W·m^-1·K^-1)	MAE /(W·m^-1·K^-1)	VAF /%
ANN	0.9746	0.0985	0.0701	97.45
ANFIS	0.9078	0.1958	0.1262	90.17
SVM	0.9649	0.1147	0.0767	96.48
Johansen model	0.6464	0.4251	0.3631	75.05
Cote model	0.7744	0.3841	0.2805	78.34
Lu model	0.6432	0.4075	0.3335	71.49

下载: 导出CSV

| 显示表格

从图 8可以看出，ANN模型、ANFIS模型和SVM模型都准确的预测了土体的导热系数，其预测值与实测值偏差较小；Johansen模型、Cote模型和Lu模型都明显低估了土体的导热系数，当λ < 1 (W·m^-1·K^-1)时，Cote模型和Lu模型的预测结果与实际值偏差较小，Johansen模型的预测结果比实测值偏小，但偏离值较小；当λ > 1 (W·m^-1·K^-1)时，Johansen模型、Cote模型和Lu模型的预测值明显低于实测值，且预测数据较离散，预测精度较低。

从表 4可以看出，ANN模型、ANFIS模型和SVM模型的相关系数R² > 0.9，RMSE < 0.2 (W·m^-1·K^-1)，MAE < 0.13 (W·m^-1·K^-1)，VAF > 90%；Johansen模型、Cote模型和Lu模型的相关系数R² < 0.78，RMSE > 0.38 (W·m^-1·K^-1)，MAE > 0.28 (W·m^-1·K^-1)，VAF < 79%；经验关系模型的性能明显低于ANN模型、ANFIS模型和SVM模型。

上述结果分析表明，预测模型对土体进行预测时，预测精度最高的是ANN模型和SVM模型，其次是ANFIS模型，预测精度最低的是经验关系模型。对于土体导热系数进行计算，建议选择ANN模型或SVM模型进行估算。

6. 结论

基于ANN模型、ANFIS模型和SVM模型对土体的导热系数进行计算研究，对预测模型的误差和稳健性进行分析，主要得出以下结论：

（1）对土体导热系数的影响因素进行分析，确定干密度、饱和度、黏粒含量、粉粒含量和砂粒含量作为预测模型的输入参数。

（2）建立预测土体导热系数的ANN模型、ANFIS模型和SVM模型，模型的计算结果表明，3个预测模型的预测结果精度较高。其中ANN模型的预测精度最高，SVM模型的预测精度略低于ANN模型，ANFIS模型的预测精度最低。基于蒙特卡洛模拟对预测模型的稳健性进行分析，预测模型稳健性最好的是SVM模型。

（3）将ANN模型、ANFIS模型和SVM模型的预测结果和传统经验关系模型的预测结果进行对比，ANN模型、ANFIS模型和SVM模型的预测精度明显高于传统经验关系模型；传统经验关系模型仅以含水率、干密度和土体类别作为计算依据，其预测结果与实际值偏差较大，难以满足工程设计要求。

图 1 无约束时基于MCMC抽样获得的目标参数后验分布

Figure 1. Posterior distribution of target parameters obtained by unconstraint MCMC sampling

下载: 全尺寸图片幻灯片

图 2 考虑约束时3种反演方法获得的目标参数后验分布（P₀=[1, 0; 0, 1], C_c=1）

Figure 2. Posterior distribution of target parameters obtained by three inverse methods considering constraint with C_c=1

下载: 全尺寸图片幻灯片

图 3 考虑约束时3种反演方法获得的目标参数后验分布（P₀=[1, 0; 0, 1],C_c=0.1）

Figure 3. Posterior distribution of target parameters obtained by three inverse methods considering constraints with C_c=0.1

下载: 全尺寸图片幻灯片

图 4 MCMC和REnKF-MDA的参数边际概率密度函数曲线（C_c=0.1）

Figure 4. Marginal PDF of target parameters obtained by MCMC and REnKF-MDA considering constraints with C_c=0.1

下载: 全尺寸图片幻灯片

图 5 地基沉降计算示意图

Figure 5. Schematic diagram of foundation settlement

下载: 全尺寸图片幻灯片

图 6 无约束和考虑约束条件下参数后验分布的比较

Figure 6. Comparison of posterior distributions under unconstrained and constrained conditions

下载: 全尺寸图片幻灯片

表 1 4种反演方法获得的参数后验统计值和相对误差

Table 1 Posterior statistics and relative errors obtained by four back analysis methods

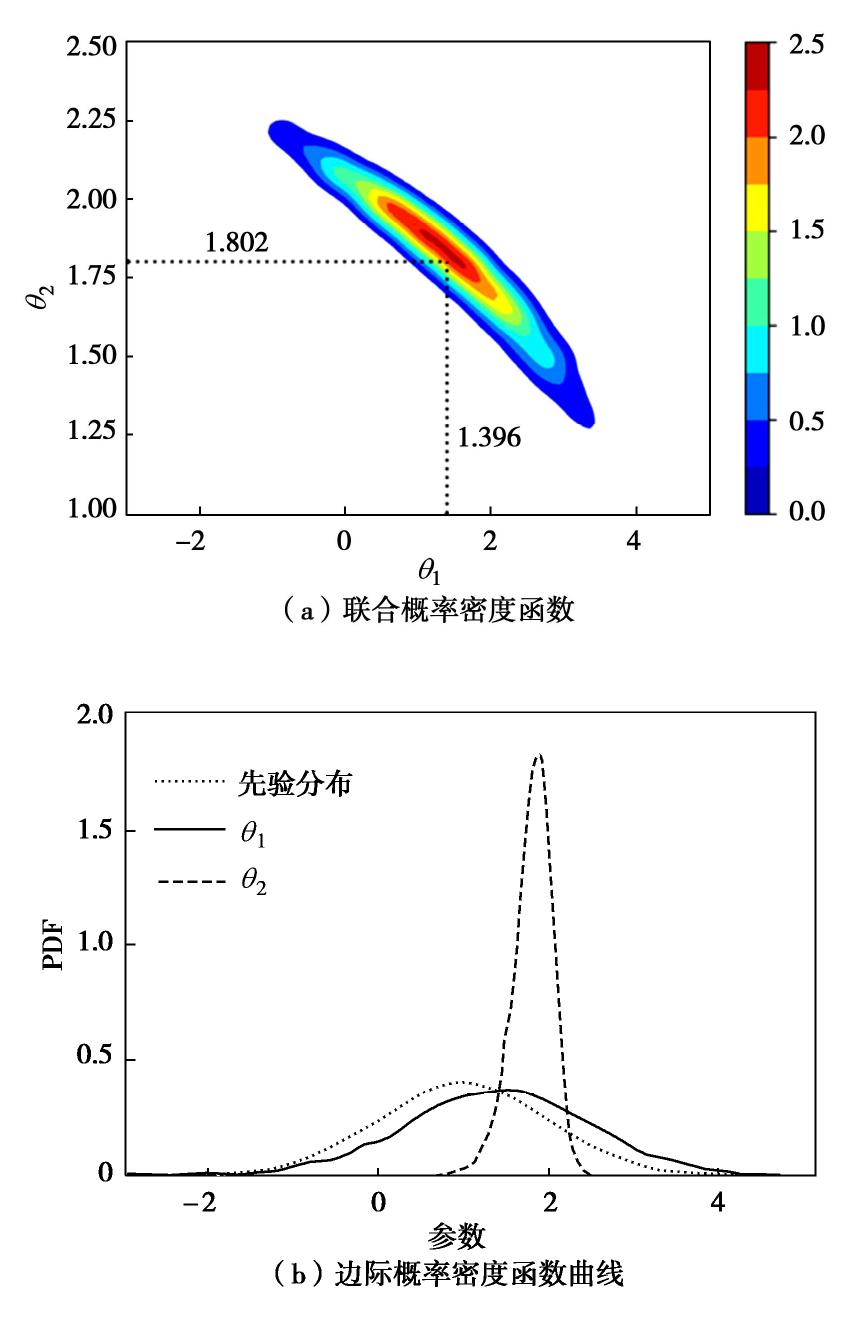
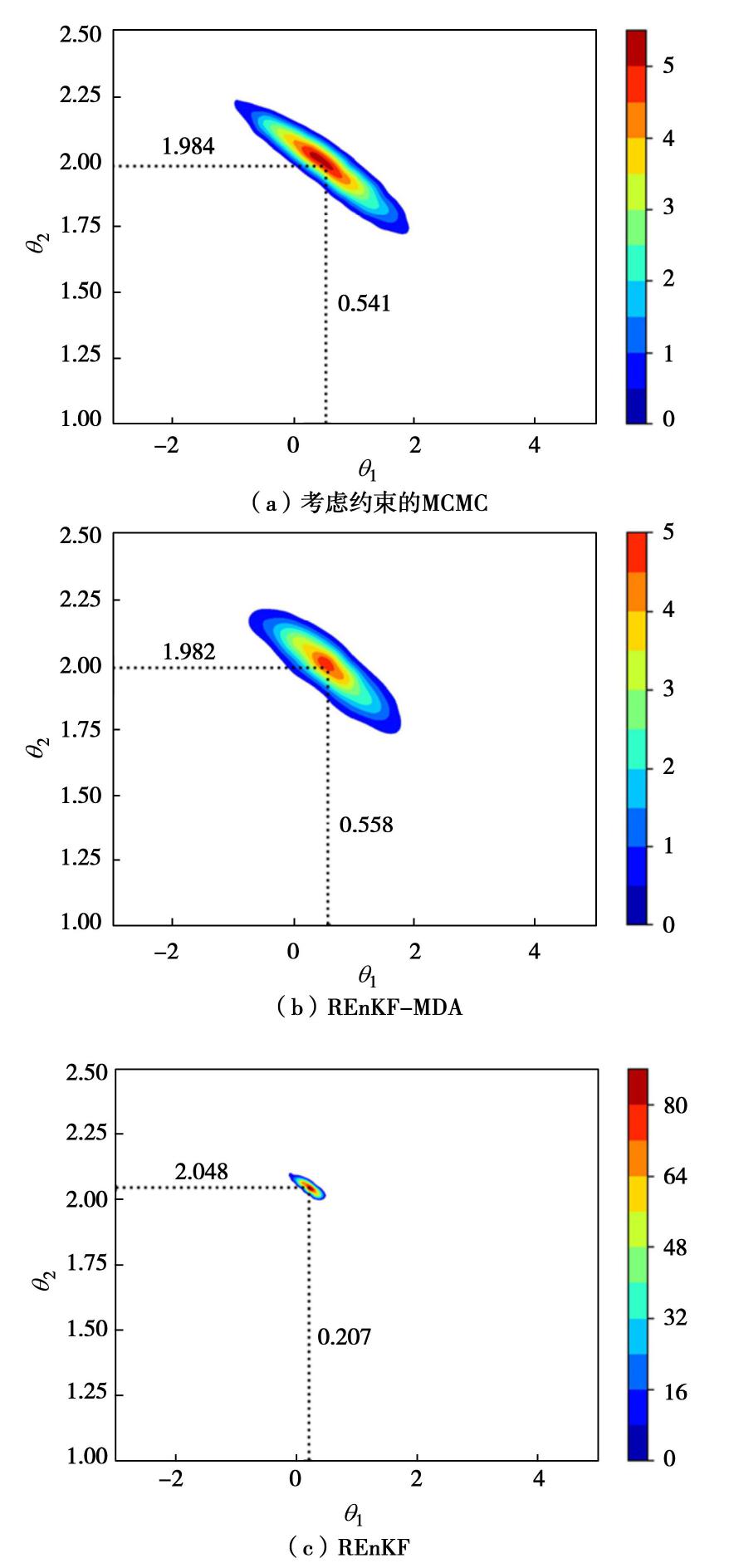
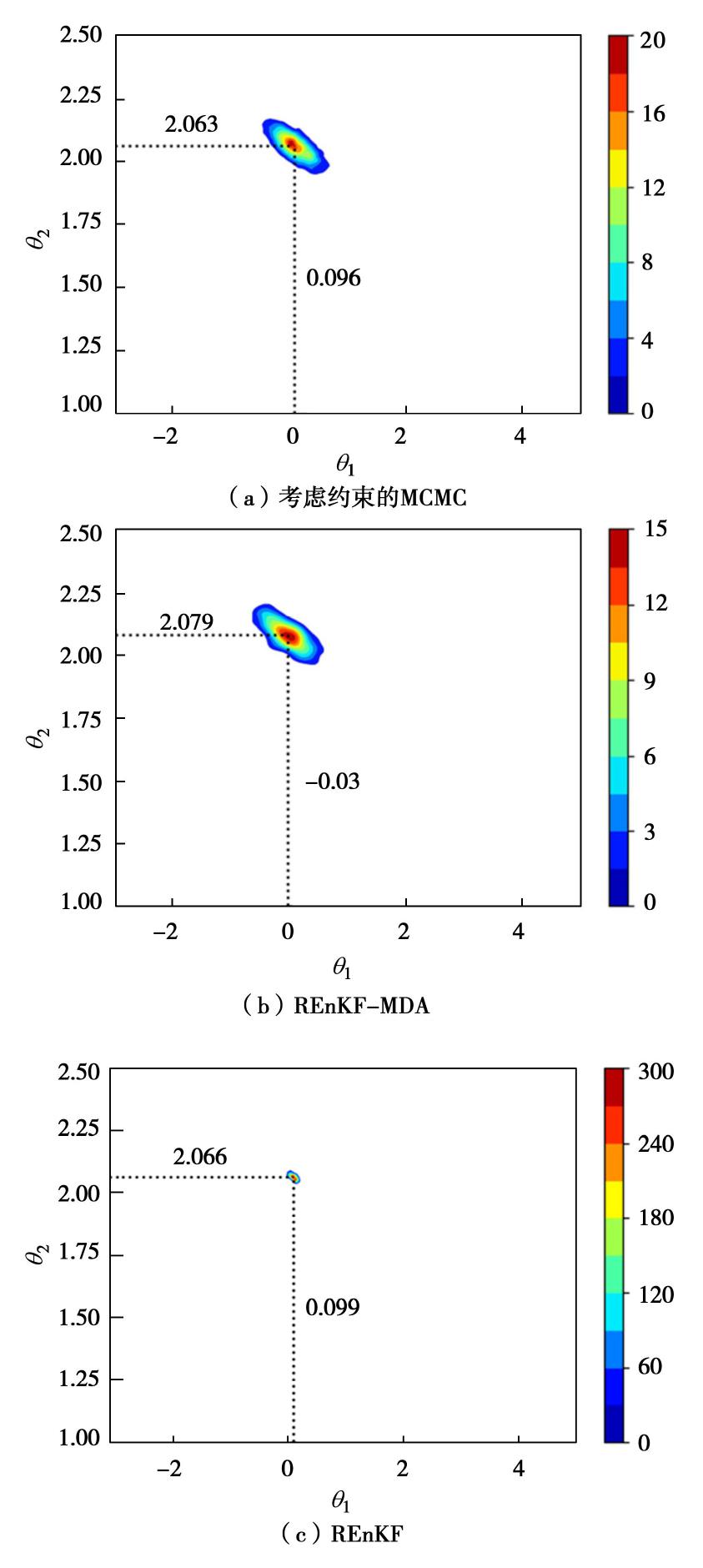
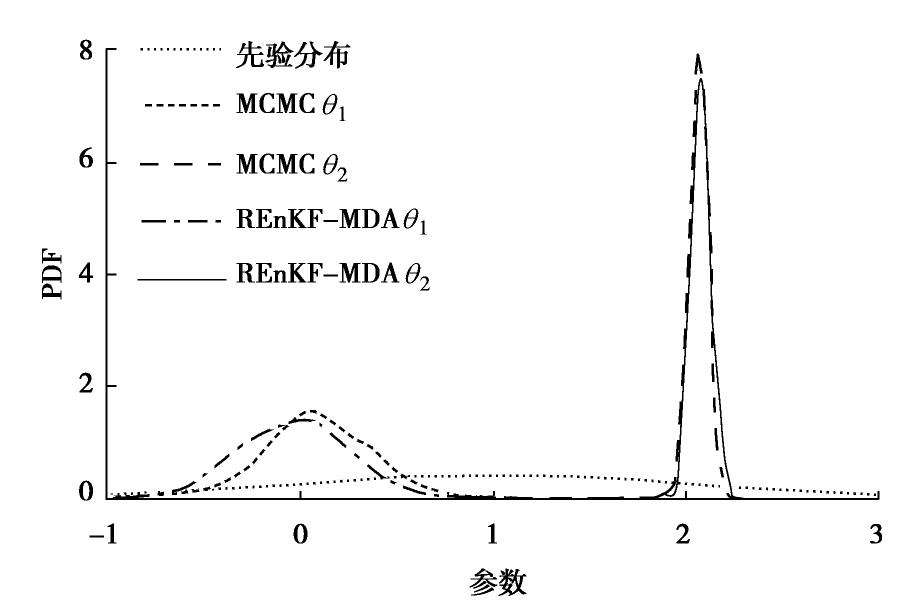
类型	θ ₁			θ₂
类型	均值	标准差	相对误差/%	均值	标准差	相对误差/%
真实值	0.000	—	—	$\sqrt[3]{9}$ （2.080）	—	—
无约束MCMC	1.396	1.068	139.6	1.802	0.2410	13.4
考虑约束MCMC	0.096	0.268	9.6	2.063	0.0511	0.8
REnKF-MDA	-0.030	0.267	3.0	2.079	0.0512	0.1
REnKF	0.099	0.053	9.9	2.066	0.0110	0.7

下载: 导出CSV

表 2 无约束和考虑约束条件下的参数后验统计值

Table 2 Posterior statistics under unconstrained and constrained conditions

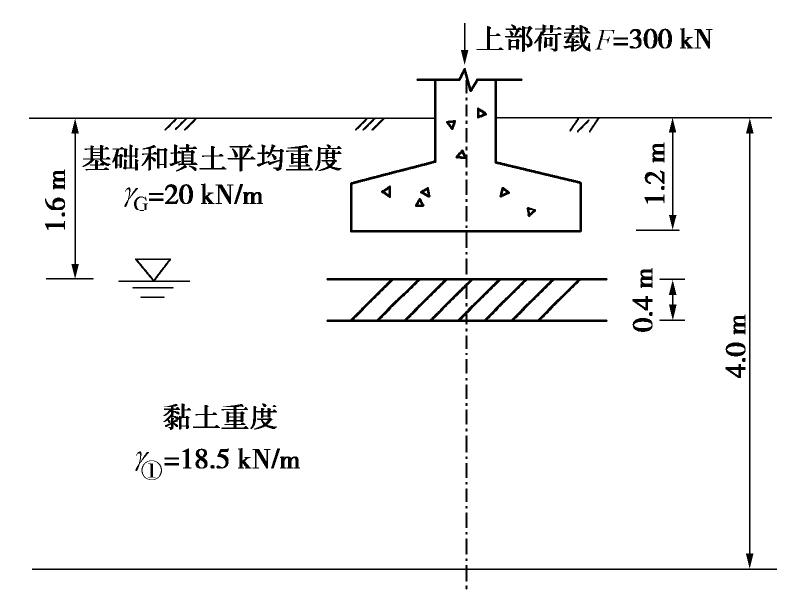
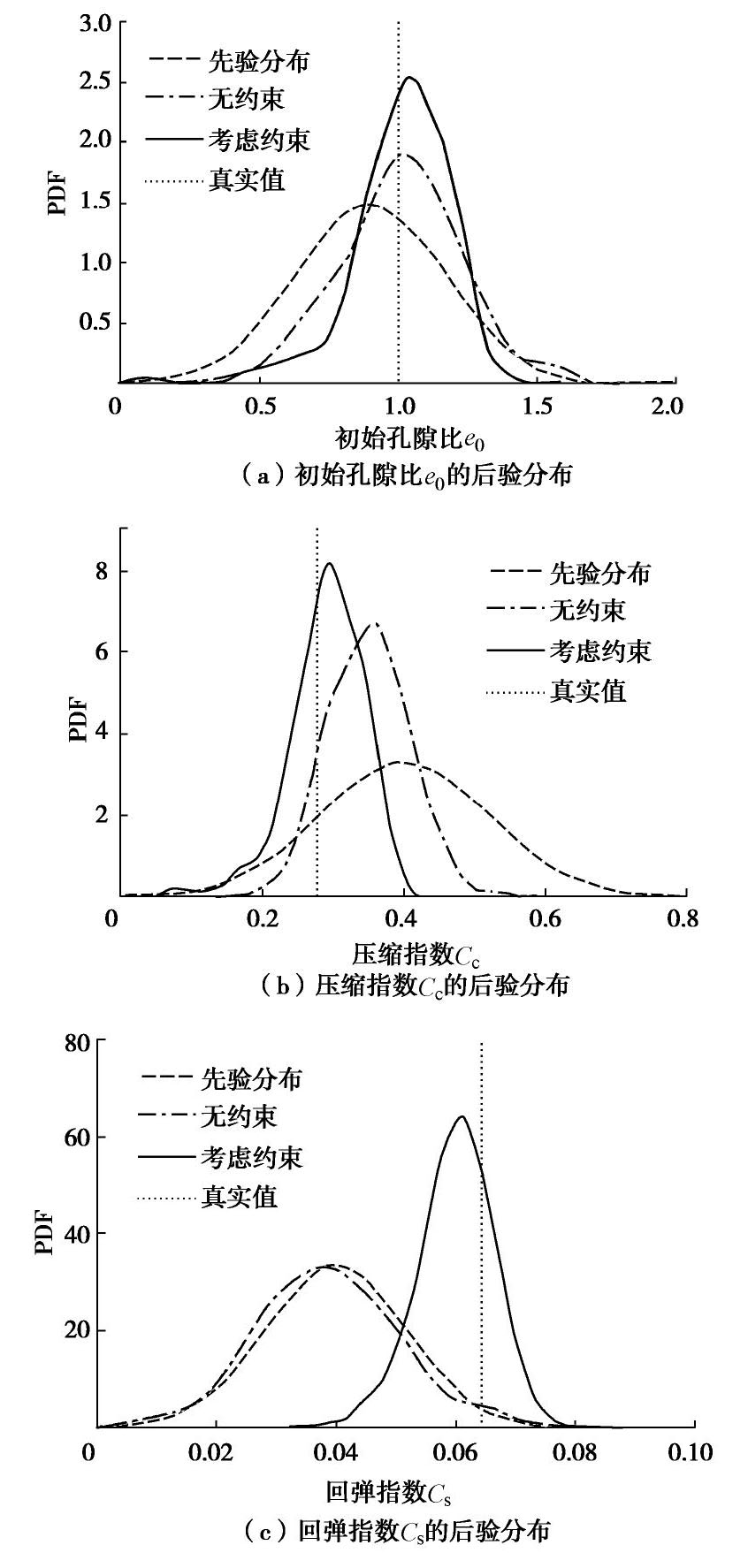
类型	e ₀			C _c			C _s			地基沉降/mm
类型	均值	标准差	相对误差/%	均值	标准差	相对误差/%	均值	标准差	相对误差/%	地基沉降/mm
真实值	1.00	—	—	0.277	—	—	0.064	—	—	25.5
EnKF-MDA	1.01	0.22	1.0	0.350	0.056	26.4	0.039	0.012	39.1	25.6
REnKF-MDA	1.01	0.19	1.0	0.290	0.052	4.7	0.060	0.006	6.3	25.4

下载: 导出CSV

参考文献(30)

[1]	WANG L, HWANG J H, LUO Z, et al. Probabilistic back analysis of slope failure -a case study in taiwan[J]. Computers and Geotechnics, 2013, 51: 12-23. doi: 10.1016/j.compgeo.2013.01.008
[2]	蒋水华, 刘贤, 尧睿智, 等. 基于贝叶斯更新和信息量分析的边坡钻孔布置方案优化设计方法[J]. 岩土工程学报, 2018, 40(10): 1871-1879. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201810016.htm JIANG Shui-hua, LIU Xian, YAO Rui-zhi, et al. Optimization design approach for layout scheme of slope boreholes based on Bayesian updating and value of information analysis[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(10): 1871-1879. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201810016.htm
[3]	郑栋, 黄劲松, 李典庆. 基于多源信息融合的路堤沉降预测方法[J]. 岩土力学, 2019, 40(2): 709-727. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902034.htm ZHENG Dong, HUANG Jin-song, LI Dian-qing. An approach for predicting embankment settlement by integrating multi-source information[J]. Rock and Soil Mechanics, 2019, 40(2): 709-727. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902034.htm
[4]	LO M K, LEUNG Y F. Bayesian updating of subsurface spatial variability for improved prediction of braced excavation response[J]. Canadian Geotechnical Journal, 2019, 56(8): 1169-1183. doi: 10.1139/cgj-2018-0409
[5]	CAO Z J, WANG Y. Bayesian approach for probabilistic site characterization using cone penetration tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(2): 267-276. doi: 10.1061/(ASCE)GT.1943-5606.0000765
[6]	CAI Y, LI J, LI X, et al. Estimating soil resistance at unsampled locations based on limited CPT data[J]. Bulletin of Engineering Geology and the Environment, 2018, 78(5): 3637-3648.
[7]	HASHASH Y M A, LEVASSEUR S, OSOULI A, et al. Comparison of two inverse analysis techniques for learning deep excavation response[J]. Computers and Geotechnics, 2010, 37(3): 323-333. doi: 10.1016/j.compgeo.2009.11.005
[8]	YIN Z Y, JIN Y F, SHEN J S, et al. Optimization techniques for identifying soil parameters in geotechnical engineering: Comparative study and enhancement[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2018, 42(1): 70-94. doi: 10.1002/nag.2714
[9]	ZHAO B D, ZHANG L L, JENG D S, et al. Inverse analysis of deep excavation using differential evolution algorithm[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(2): 115-134. doi: 10.1002/nag.2287
[10]	蒋水华, 刘源, 张小波, 等. 有限数据条件下空间变异岩土力学参数随机反演分析及比较[J]. 岩石力学与工程学报, 2020, 39(6): 190-201. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202006017.htm JIANG Shui-hua, LIU Yuan, ZHANG Xiao-bo, et al. Stochastic back analysis and comparison of spatially varying geotechnical mechanical parameters based on limited data[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(6): 190-201. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202006017.htm
[11]	田密, 李典庆, 曹子君, 等. 基于贝叶斯理论的土性参数空间变异性量化方法[J]. 岩土力学, 2017, 38(11): 3355-3362. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711036.htm TIAN Mi, LI Dian-qing, CAO Zi-jun, et al. Quantification of spatial variability of soil parameters using Bayesian approaches[J]. Rock and Soil Mechanics, 2017, 38(11): 3355-3362. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711036.htm
[12]	QI X H, ZHOU W H. An efficient probabilistic back-analysis method for braced excavations using wall deflection data at multiple points[J]. Computers and Geotechnics, 2017, 85: 186-198. doi: 10.1016/j.compgeo.2016.12.032
[13]	LI X Y, ZHANG L M, JIANG S H. Updating performance of high rock slopes by combining incremental time-series monitoring data and three-dimensional numerical analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 83: 252-261. doi: 10.1016/j.ijrmms.2014.09.011
[14]	SUN Y, HUANG J, JIN W, SLOAN S W, JIANG Q. Bayesian updating for progressive excavation of high rock slopes using multi-type monitoring data[J]. Engineering Geology, 2019, 252: 1-13. doi: 10.1016/j.enggeo.2019.02.013
[15]	XIAO H, CINNELLA P. Quantification of model uncertainty in RANS simulations: a review[J]. Progress in Aerospace Sciences, 2019, 108: 1-31. doi: 10.1016/j.paerosci.2018.10.001
[16]	IGLESIAS M A, LAW K J H, STUART A M. Ensemble Kalman methods for inverse problems[J]. Inverse Probl, 2013, 29(4): 045001. doi: 10.1088/0266-5611/29/4/045001
[17]	EVENSEN G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research, 1994, 99(C5): 10143-10162. doi: 10.1029/94JC00572
[18]	HOMMELS A, MURAKAMI A, NISHIMURA S I. Comparison of the Ensemble Kalman Filter with the Unscented Kalman Filter: Application to the Construction of A Road Embankment[M]. 19th European Young Geotechnical Engineers Conference, 2008, Gyor.
[19]	LIU K, VARDON P J, HICKS M A. Sequential reduction of slope stability uncertainty based on temporal hydraulic measurements via the ensemble Kalman filter[J]. Computers and Geotechnics, 2018, 95: 147-161. doi: 10.1016/j.compgeo.2017.09.019
[20]	TAO Y, SUN H, CAI Y. Predicting soil settlement with quantified uncertainties by using ensemble Kalman filtering[J]. Engineering Geology, 2020, 276: 105753. doi: 10.1016/j.enggeo.2020.105753
[21]	EMERICK A A, REYNOLDS A C. History matching time-lapse seismic data using the ensemble Kalman filter with multiple data assimilations[J]. Computational Geosciences, 2012, 16(3): 639-659.
[22]	ZHANG X, XIAO H, GOMEZ T, COUTIER-DELGOSHA O. Evaluation of ensemble methods for quantifying uncertainties in steady-state CFD applications with small ensemble sizes[J]. Computers & Fluids, 2020, 203: 104530.
[23]	WANG D, CHEN Y, CAI X. State and parameter estimation of hydrologic models using the constrained ensemble Kalman filter[J]. Water Resources Research, 2009, 45: 10.1029.
[24]	ZHANG X L, MICHEL N, STR FER C, XIAO H. Regularized ensemble Kalman methods for inverse problems[J]. Journal of Computational Physics, 2020, 416: 109517.
[25]	WU J, WANG J X, SHADDEN S C. Adding constraints to bayesian inverse problems[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33: 1666-1673.
[26]	VRUGT J A. Markov chain Monte Carlo simulation using the DREAM software package: theory, concepts, and MATLAB implementation[J]. Environmental Modelling & Software, 2016, 75: 273-316.
[27]	李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004: 253-254. LI Guang-xin. Advanced Soil Mechanics[M]. Beijing: Tsinghua University Press, 2004: 253-254. (in Chinese)
[28]	AZZOUZ A S, KRIZEK R J, COROTIS R B. Regression analysis of soil compressibility[J]. Soils & Foundations, 1976, 16(2): 19-29.
[29]	何平, 王卫东, 徐中华. 上海黏土压缩指数和回弹指数经验关系[J]. 岩土力学, 2018, 39(10): 275-84. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810035.htm HE Ping, WANG Wei-dong, XU Zhong-hua. Empirical correlations of compression index and swelling index for Shanghai clay[J]. Rock and Soil Mechanics, 2018, 39(10): 275-284. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810035.htm
[30]	武朝军. 上海浅部土层沉积环境及其物理力学性质[D]. 上海: 上海交通大学, 2016. WU Chao-jun. Depositional Environment and Geotechnical Properties for the Upper Shanghai Clays[D]. Shanghai: Shanghai Jiao Tong University, 2016. (in Chinese)

施引文献(12)

期刊类型引用(11)

1.	崔纪飞，柏林，饶平平，康陈俊杰，张锟. 基于人工智能算法的氯盐侵蚀混凝土预测模型. 硅酸盐通报. 2024(02): 439-447 . 百度学术
2.	段文魁，王来发，晁华俊，明锋. 冻结过程中土体导热系数预测模型. 中国农村水利水电. 2024(05): 47-52 . 百度学术
3.	唐少容，殷磊，杨强，柯德秀. 微胶囊相变材料改良粉砂土的导热系数及预测模型. 中国粉体技术. 2024(03): 112-123 . 百度学术
4.	姚兆明，王洵，齐健. 土体导热系数智能方法预测及影响因素敏感性分析. 工程热物理学报. 2024(05): 1440-1449 . 百度学术
5.	邓志兴，谢康，李泰灃，王武斌，郝哲睿，李佳珅. 基于粗颗粒嵌锁点高铁级配碎石振动压实质量控制新方法. 岩土力学. 2024(06): 1835-1849 . 百度学术
6.	李林，左林龙，胡涛涛，宋博恺. 基于孔压静力触探试验测试数据的原位固结系数物理信息神经网络反演方法. 岩土力学. 2024(10): 2889-2899 . 百度学术
7.	王红旗，李栋伟，钟石明，贾志文，王泽成，陈鑫，秦子鹏. 石灰改良红黏土导热系数影响因素及模型预测. 科学技术与工程. 2023(05): 2084-2092 . 百度学术
8.	王才进，武猛，蔡国军，赵泽宁，刘松玉. 基于多元分布模型预测土体热阻系数. 岩石力学与工程学报. 2023(S1): 3674-3686 . 百度学术
9.	王健翔，任瑞琪. 电学等效的稳态平板导热系数测试实验装置. 电子制作. 2023(11): 105-109 . 百度学术
10.	王才进，武猛，杨洋，蔡国军，刘松玉，何欢，常建新. 基于生物地理优化的人工神经网络模型预测软土的固结系数. 岩土力学. 2023(10): 3022-3030 . 百度学术
11.	徐明，康雅晶，马斯斯，张鹤. 基于贝叶斯优化的XGBoost模型预测路基回弹模量. 公路交通科技. 2023(11): 51-60 . 百度学术