一个基于微观力学分析的散粒体应力-剪胀关系

刘洋; 于鹏强; 张铎; 王肖肖

doi:10.11779/CJGE202110007

一个基于微观力学分析的散粒体应力-剪胀关系 English Version

1.
北京科技大学土木工程系,北京　100083
2.
中南建筑设计院地下空间工程技术中心,湖北　武汉　430071

基金项目:

国家自然科学基金项目 51178044

详细信息

作者简介:
刘洋(1979— ),男,江苏徐州人,博士,教授,主要从事土细观力学和砂土液化等方面的科研和教学工作。E-mail：yangliu@ustb.edu.cn

中图分类号: TU431
计量
- 文章访问数: 295
- HTML全文浏览量: 28
- PDF下载量: 195
出版历程
- 收稿日期: 2020-09-07
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-09-30

Micromechanics-based stress-dilatancy relationship for granular materials

1.
Department of Civil Engineering, University of Science and Technology Beijing, Beijing100083, China
2.
Underground Space Engineering Technology Center, Central South Architectural Design Institute Co., Ltd., Wuhan 430071, China

摘要

摘要: 从微观力学角度出发,基于真应力张量推导了散体中平均接触力与平均接触位移的计算公式,并通过宏-微观能量守恒得到了考虑散体各向异性组构及其演化的应力-剪胀关系；详细分析了剪胀参数的物理意义及对剪胀性的影响,并与经典的剑桥流动法则、Rowe剪胀方程以及室内试验结果进行了比较分析。研究结果表明,提出的应力-剪胀关系宏微观物理意义明确,考虑了材料密实状态和微观各向异性组构及其演化对应力-剪胀关系的影响,可以很好地模拟散粒体的初始剪胀（缩）行为,并可反映峰值应力比滞后于最大剪胀比的现象。同时提出的应力-剪胀方程还可以描述材料在相变点处应力比不等于临界应力比的现象,与已有室内试验结果一致,能够较好地预测散体材料三轴条件下的各向异性应力-剪胀关系。
- 应力-剪胀关系 /
- 微观力学 /
- 组构演化 /
- 能量守恒
Abstract: From the perspective of micromechanics, the formulas for the average contact force and contact displacement in the granular are derived based on the true stress tensor, then the stress-shear dilatancy relationship considering the fabric anisotropy and its evolution is obtained through the macro-micro energy conservation. In addition, the physical meaning of dilatancy parameters and their influence on dilatancy are analyzed. Finally, the proposed formulation is compared with the classical Cambridge flow law, Rowe dilatancy equation and test results to calibrate its reasonableness and applicability. The proposed stress-dilatancy relationship with clear physical meaning can describe the initial dilatancy (contraction) behavior for granular materials, considering the anisotropic evolution of fabric and the influence of the density on the dilatancy. Moreover, the proposed stress-dilatancy equation can reflect that the stress ratio at the phase transition point is less than the critical stress ratio and the peak stress ratio emerges behind the maximum dilatancy ratio. It is in good agreement with the test results and can better predict the anisotropic stress-dilatancy relationship of granular materials.
- stress-dilatancy relationship /
- micromechanics /
- fabric evolution /
- energy conservation

HTML全文

0. 引言

散体材料的剪胀是其在受剪过程中体积发生变化的现象,是散体颗粒间相互运动与约束的宏观表现,是颗粒间三维孔隙相互优化调整的结果,也是在研究散体材料强度与变形中所必须解决的关键性课题。

Schofield等^[1]根据三轴压缩试验结果,基于能量平衡方程得到了黏土的应力-剪胀方程,即剑桥剪胀方程；之后Nova等^[2]、Lagioia等^[3]通过引入材料参数对剑桥剪胀方程进行了修正,使得其具有更强的适用性。

Rowe^[4]进行了颗粒体的三轴压缩实验,从理论上推导了材料颗粒在最密排列、面心排列以及菱形排列等不同排列方式下的流动法则,认为外界对材料做功与材料对外界做功之比应满足最小能量比,最终提出了著名的Rowe剪胀法则；Guo等^[5]则在Rowe剪胀法则的基础上,通过引入一个能量张量,采用能量张量的不变量将Rowe剪胀法则扩展到了三维状态。

上述剪胀方程只与材料的应力状态有关,没有考虑材料本身的状态。对于散体材料而言,剪胀受到密实度的影响,因此有学者在传统剪胀理论中引入孔隙比来提高模型精度^[6]。Wan等^[7]将状态孔隙指数引入Rowe剪胀方程建立了基于当前状态的砂土本构模型；Li等^[8-9]考虑密实度对剪胀的影响,根据剑桥剪胀方程结合状态参数提出了新的砂土剪胀方程。Manzari等^[10],Gajo等^[11]的本构模型中所采用的剪胀方程也是通过在剪胀方程中引入能够反映密实度的状态参数来实现考虑密实度的影响。

在散体材料中,材料颗粒限制了相邻颗粒的运动方向,因此散体材料的接触方向分布决定了颗粒运动方向分布。组构不仅对试样强度有影响,同时也控制着试样变形,这一性质在密砂中体现更为明显：密砂试样孔隙比较低,咬合作用更加明显,接触法向上颗粒难以发生相对位移,故颗粒主要沿接触面切向发生相对滑动,这是密砂发生体胀的根本原因。如Wang等^[12]通过离散元研究表明剪胀性受组构各向异性及其演化的影响很大。为研究土体变形的微观机理,建立考虑试样组构发展的流动法则是十分重要的。

Tobita^[13]基于双剪切面理论,研究了应力主轴旋转条件下的试样体胀；Zhao等^[14]考虑孔隙比等因素影响,提出了能够考虑组构发展的剪胀方程；此外,Yin等^[15]、Liu等^[16]基于微观力学思想从颗粒相对运动的角度考虑材料的剪胀行为。Xiao等^[17]系统地研究了颗粒形状对材料剪胀的影响；Liang等^[18]、Tsegaye等^[19]考虑非共轴的影响建立了更为一般的应力-剪胀关系；杨骏堂等^[20]则基于大数据深度挖掘算法构建了可考虑应变及其增量的剪胀模型。

本文从颗粒运动角度出发,基于微观力学理论以及能量守恒的思想,认为外界对试样所做的功在试样颗粒相对位移中完全消耗,即试样所有接触力的总功与外力总功相等,建立了一个考虑组构发展的流动法则,并将其与室内试验结果进行了对比分析。

1. 平均接触力与平均相对位移

在外界对散体材料做功的同时,材料内部接触发生破坏,颗粒发生相对位移,接触数发生变化,从而产生能量消散。对试样整体而言,根据能量守恒可知试样内部所有接触消散的能量之和应与外界对试样做功相等。由于试样接触多而杂,因此在计算能量耗散中采用颗粒平均接触力、平均相对位移等效替代。

1.1 平均接触力计算

（1）法向平均接触力

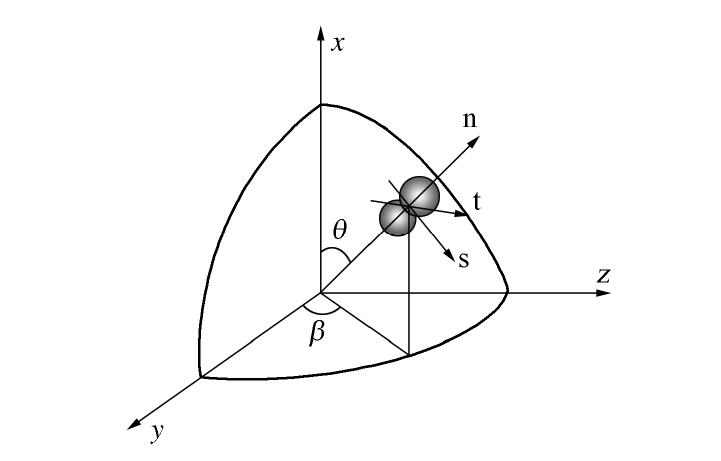
根据Liao等^[21]的静力假设可得试样接触力为

f_{i} = σ_{i j} A_{j n} l_{n} = σ_{i j} {(\frac{1}{V} \sum l_{j} l_{n})}^{- 1} l_{n}

(1)

式中, $σ_{i j}$ 为应力, $l_{i}$ 为枝矢量,V为代表单元体体积。

根据真应力张量定义^[22] $T_{i j} = σ_{i k} {(\frac{1}{V} \sum l_{k} l_{j})}^{- 1}$ ,其在枝向量上的投影为该方向接触力,因此真应力张量反映了宏-微观力学量之间的联系,在散体介质力学研究中具有重要意义。Cauchy应力张量可表示为真应力张量和组构张量的乘积,两者分别体现了颗粒摩擦及微观结构对散体力学性质的影响。

根据上述定义,接触力可表示为

f_{i} = T_{i j} l_{j}

(2)

因此试样中法向接触力为

f_{n} = f_{i} n_{i} = 2 \bar{r} T_{i j} n_{i} n_{j}

(3)

式中, $n_{i}$ 为接触法向分量（见图1）, $\bar{r}$ 为颗粒平均半径。

图 1 全局和局部坐标系统

Figure 1. Global and local coordinate system

下载: 全尺寸图片幻灯片

则散体材料中试样平均法向接触力 $\bar{f_{n}}$ 可记为

\bar{f_{n}} = \frac{1}{N} \sum_{c = 1}^{N} f_{n}^{c}

(4)

式中,N为代表单元体内的接触数。

上式用积分形式可表示为

\bar{f_{n}} = \frac{1}{N} \iint_{Ω} f_{n}^{c} p (θ, β) d Ω ，

(5)

式中, $p (θ, β)$ 为接触分布函数,一般可用二阶球谐级数表示,用笛卡尔坐标系下的张量形式可表示为

p (\vec{n}) = \frac{N}{4 π} D_{i j} n_{i} n_{j}

(6)

式中, $D_{i j}$ 为接触分布张量。

将式（6）代入式（5）可得

{\bar{f}}_{n} = \frac{\bar{r}}{2 π} T_{i j} D_{k l} M_{i j k l}

(7)

式中, $M_{i j k l}$ 的计算可见附录。

将式（7）代入附录式A（2）可化简为

{\bar{f}}_{n} = \frac{6 \bar{r} p_{T}}{5} (1 + \frac{T_{i j} (D_{i j} + D_{j i})}{9 p_{T}})

(8)

式中, $p_{T}$ 为平均真应力。

（2）切向平均接触力

每个接触上的切向接触力为

f_{s}^{c} = \sqrt{f_{i}^{c} \cdot f_{i}^{c} - f_{n}^{c} \cdot f_{n}^{c}} = 2 \bar{r} \sqrt{T_{i j} T_{i l} n_{j}^{c} n_{l}^{c} - T_{i j} T_{k l} n_{i}^{c} n_{j}^{c} n_{k}^{c} n_{l}^{c}}

。

(9)

定义切向平均接触力为

{\bar{f}}_{s} = \sqrt{\iint_{Ω} {(f_{s}^{c})}^{2} p (\vec{n}) d Ω}

。

(10)

则有

{\bar{f}}_{s}^{2} = \frac{{\bar{r}}^{2}}{π} (T_{i j} T_{i l} D_{m n} M_{j l m n} - T_{i j} T_{k l} D_{m n} M_{i j k l m n})

(11)

式中, $M_{i j k l m n}$ 的计算可见附录。

将附录式A（2）代入式（11）后可得

\begin{array}{l} {\bar{f}}_{s}^{2} = \frac{4 {\bar{r}}^{2}}{15} (T_{i l} T_{i l} D_{m m} + 2 T_{i j} T_{i l} D_{j l}) - \\ \frac{4 {\bar{r}}^{2}}{105} (T_{i i} T_{k k} D_{m m} + 4 T_{i i} T_{k l} D_{k l} + 2 T_{k l} T_{l k} D_{m m} + 8 T_{i j} T_{j l} D_{i l}) \end{array}

。

(12)

由于 $T_{i j} T_{i j} = {T^{'}}_{i j} {T^{'}}_{i j} + \frac{T_{k k} T_{m m}}{3}$ ,其中 ${T^{'}}_{i j}$ 为偏真应力张量,则式（12）可改写为

{\bar{f}}_{s}^{2} = \frac{4 {\bar{r}}^{2} {T^{'}}_{k l} {T^{'}}_{k l}}{5} [1 + \frac{(4 T_{i i} T_{k l} - 6 T_{i j} T_{j k}) (δ_{k l} - D_{k l})}{21 {T^{'}}_{k l} {T^{'}}_{k l}}]

(13)

式中, $δ_{k l}$ 为克罗内克尔算子。

综上,三维条件下散体的法向平均接触力、切向平均接触力分别为

\begin{array}{l} {\bar{f}}_{n} = \frac{6 \bar{r} p_{T}}{5} (1 + \frac{T_{i j} (D_{i j} + D_{j i})}{9 p_{T}}) ， \\ {\bar{f}}_{s} = \sqrt{\frac{4 {\bar{r}}^{2} {T^{'}}_{k l} {T^{'}}_{k l}}{5} (1 + \frac{(4 T_{i i} T_{k l} - 6 T_{i j} T_{j k}) (δ_{k l} - D_{k l})}{21 {T^{'}}_{k l} {T^{'}}_{k l}})} 。 \end{array}}

(14)

1.2 平均位移计算

在散体材料中,由于位移场存在不均匀性,颗粒的平动与转动都将导致相邻颗粒发生相对位移。考虑相邻颗粒的相对运动,假设 $u^{1}$ 与 $ω_{}^{1}$ 分别为颗粒1圆心的位移与转动角,则颗粒2的位移与转角分别为

\begin{array}{l} u_{i}^{2} = u_{i}^{1} + \frac{\partial u_{i}}{\partial x_{j}} 2 \bar{r} \cdot n_{j} ， \\ ω_{i}^{2} = ω_{i}^{1} + \frac{\partial ω_{i}}{\partial x_{j}} 2 \bar{r} \cdot n_{j} = ω_{i}^{1} + 2 \bar{r} \cdot K_{i j} n_{j} ， \end{array}}

(15)

式中, $K_{i j}$ 为颗粒转动梯度。

设 $u^{(1)}$ , $u^{(2)}$ 分别为两颗粒接触点处的位移,则：

u_{i}^{(1)} = u_{i}^{1} + \bar{r} ω_{i j}^{1} n_{j} ， u_{i}^{(2)} = u_{i}^{2} - \bar{r} ω_{i j}^{2} n_{j}

(16)

式中, $ω_{i j}$ 为转动张量, $ω_{i j} = - e_{i j k} ω_{k}$ 。

则接触处的相对位移为

Δ u_{i}^{c} = u_{i}^{(2)} - u_{i}^{(1)} = u_{i}^{2} - u_{i}^{1} - \bar{r} n_{j} (ω_{i j}^{2} + ω_{i j}^{1})

。

(17)

将式（15）代入式（17）可得

Δ u_{i}^{c} = 2 \bar{r} (\frac{\partial u_{i}}{\partial x_{j}} - ω^{1}_{i j} + \bar{r} e_{i l j} K_{l k} n_{k}) n_{j}

。

(18)

由于颗粒转动不引起法向位移,故接触法向相对位移仅与颗粒平动相关,即

\begin{array}{l} Δ u_{n} = Δ u_{i}^{c} n_{i} = 2 \bar{r} \frac{\partial u_{i}}{\partial x_{j}} n_{i} n_{j} = 2 \bar{r} ε_{i j} n_{i} n_{j} ， \\ Δ u_{n k} = Δ u_{n} n_{k} = 2 \bar{r} ε_{i j} n_{i} n_{j} n_{k} ， \end{array}}

(19)

式中, $ε_{i j}$ 为应变张量。

（1）法向平均相对位移

散体材料中,法向平均相对位移可通过下式计算：

\bar{Δ u_{n}^{c}} = \frac{1}{N} \sum_{c = 1}^{N_{s}} Δ u_{n}^{c}

(20)

式中, $N_{s}$ 为发生滑动的接触数。

其积分形式可写为

\bar{Δ u_{n}^{c}} = \frac{N_{s}}{N} \iint_{Ω} Δ u_{n}^{c} p_{s} (\vec{n}) d Ω

(21)

式中, $p_{s} (\vec{n})$ 为发生滑动的接触分布密度函数,为某方向上滑动的接触占所有滑动接触之比,可表示为

p_{s} (\vec{n}) = \frac{1}{4 π} Ψ_{i j} n_{i} n_{j}

。

(22)

式中, $Ψ_{i j}$ 为滑动接触分布张量。

将式（22）代入式（21）可得法向平均相对位移：

\bar{Δ u_{n}^{c}} = \frac{\bar{r}}{2 π} \frac{N_{s}}{N} ε_{i j} Ψ_{k l} M_{i j k l}

。

(23)

与式（7）类似,故上式可化简为

\bar{Δ u_{n}^{c}} = \frac{2 \bar{r} ε_{i i}}{5} (\frac{N_{s}}{N}) [1 + \frac{ε_{i j} (Ψ_{i j} + Ψ_{j i})}{3 ε_{i i}}]

。

(24)

（2）切向平均相对位移

接触切向平均相对位移可定义如下：

{\bar{u}}_{s} = \frac{N_{s}}{N} \sqrt{\int_{Γ} {(u_{s}^{c})}^{2} p_{s} (\vec{n}) d Ω}

。

(25)

因此有

\begin{matrix} {({\bar{u}}_{s})}^{2} = {(\frac{N_{s}}{N})}^{2} \int_{Ω} (u_{i}^{c} u_{i}^{c} - u_{n}^{c} u_{n}^{c}) p_{s} (\vec{n}) d Ω \\ = {(\frac{N_{s}}{N})}^{2} [\int_{Ω} u_{i}^{c} u_{i}^{c} p_{s} (\vec{n}) d Ω - \int_{Ω} u_{n}^{c} u_{n}^{c} p_{s} (\vec{n}) d Ω] \end{matrix}

(26)

式中,

\int_{Ω} u_{i}^{2} p_{s} d Ω = 4 {\bar{r}}^{2} \int_{Ω} {(\frac{\partial u_{i}}{\partial x_{j}} n_{j} - ω_{i j} n_{j} + \bar{r} e_{i l j} K_{l k} n_{k} n_{j})}^{2} p_{s} d Ω 。

(27)

由于 $\int_{Ω} n_{i 1} n_{i 2} \dots n_{i m} d Ω = 0$ （m为奇数）,式（27）可化为

\begin{array}{l} \int_{Ω} u_{i} u_{i} p_{s} (\vec{n}) d Ω = 4 {\bar{r}}^{2} \int_{Ω} (ε_{i j} n_{j} ε_{m n} n_{n} + ω_{i j} n_{j} ω_{m n} n_{n} + \\ {\bar{r}}^{2} e_{i j k} e_{m n o} K_{k l} K_{o p} n_{l} n_{j} n_{p} n_{n} - 2 ε_{i j} n_{j} ω_{m n} n_{n}) p_{s} (\vec{n}) d Ω 。 \end{array}

(28)

将式（28）代入式（26）可得

\begin{array}{l} {\bar{u_{s}}}^{2} = \frac{{\bar{r}}^{2}}{π} (ε_{i j} ε_{k l} Ψ_{m n} M_{j l m n} + {\bar{r}}^{2} e_{i j k} e_{m n o} K_{k l} K_{o p} Ψ_{r s} M_{l j p n r s} - \\ 2 ε_{i j} ω_{k l} Ψ_{m n} M_{j l m n} - ε_{i j} ε_{k l} Ψ_{m n} M_{i j k l m n} + ω_{i j} ω_{k l} Ψ_{m n} M_{j l m n}) \end{array}

。

(29)

从上式可以看出,由于考虑了颗粒转动,切向位移计算式比较复杂,括号中可分为如下3个部分：

a） $ε_{i j} ε_{i l} Ψ_{m n} M_{j l m n} - ε_{i j} ε_{k l} Ψ_{m n} M_{i j k l m n}$

这部分仅存在应变张量,反映了颗粒平动对颗粒接触切向位移的影响。

b） $ω_{i j} ω_{i l} Ψ_{m n} M_{j l m n} - 2 ε_{i j} ω_{i l} Ψ_{m n} M_{j l m n}$

这部分同时存在应变张量与颗粒转动张量,反映了均匀的颗粒转动场与颗粒平动对接触切向位移的共同影响。

c） ${\bar{r}}^{2} e_{i j k} e_{i n o} Κ_{k l} Κ_{o p} Ψ_{r s} M_{l j p n r s}$

这部分仅存在颗粒转动梯度张量,反映了颗粒转动场的不均匀性对接触切向位移的影响。

将附录式A（2）代入式（29）化简后可得

(30)

若不考虑颗粒旋转,则切向位移可进一步改写为

\begin{matrix} {\bar{Δ u_{s}}}^{2} = \frac{4}{5} {(\frac{N_{s}}{N})}^{2} {\bar{r}}^{2} {ε^{'}}_{i j} {ε^{'}}_{i j} \cdot \\ [(1 + \frac{(6 ε_{i k} ε_{i l} - 4 ε_{i i} ε_{k l}) (Ψ_{k l} - δ_{k l})}{21 {ε^{'}}_{i j} {ε^{'}}_{i j}})] \end{matrix}

。

(31)

2. 宏微观能量守恒与应力-剪胀关系

2.1 宏微观能量守恒

定义“广义偏真应力 $q_{T}$ ”：

q_{T} = \sqrt{\frac{3}{2} {T^{'}}_{i j} {T^{'}}_{i j}} = \sqrt{3 J_{2 T}}

(32)

式中, $J_{2 T}$ 为真应力张量第二偏不变量。

将式（32）代入式（14）的第二式可得

\begin{matrix} {\bar{f}}_{s} = \sqrt{\frac{8 {\bar{r}}^{2}}{15} \frac{3}{2} {T^{'}}_{k l} {T^{'}}_{k l} (1 + \frac{(4 T_{i i} T_{k l} - 6 T_{i j} T_{j k}) (δ_{k l} - D_{k l})}{21 {T^{'}}_{k l} {T^{'}}_{k l}})} \\ = q_{T} \sqrt{\frac{8 {\bar{r}}^{2}}{15} (1 + \frac{(4 T_{i i} T_{k l} - 6 T_{i j} T_{j k}) (δ_{k l} - D_{k l})}{21 {T^{'}}_{k l} {T^{'}}_{k l}})} \end{matrix}

。

(33)

类似地,定义广义偏应变为

γ = \sqrt{\frac{3}{2} {ε^{'}}_{i j} {ε^{'}}_{i j}} = \sqrt{3 J_{2 ε}}

。

(34)

将式（34）代入式（31）,可得平均切向位移为

Δ {\bar{u}}_{s} = γ \sqrt{\frac{8}{15} {(\frac{N_{s}}{N})}^{2} {\bar{r}}^{2} [(1 + \frac{(6 ε_{i k} ε_{i l} - 4 ε_{i i} ε_{k l}) (Ψ_{k l} - δ_{k l})}{21 {ε^{'}}_{i j} {ε^{'}}_{i j}})]} 。

(35)

对于散体材料,外部能量输入可由下式进行计算：

\begin{matrix} d W = σ_{i j} d ε_{i j} = (σ_{m} δ_{i j} + s_{i j})(d ε_{m} δ_{i j} + d {ε^{'}}_{i j}) \\ = p d ε_{v} + \sqrt{s_{i j} s_{i j}} \sqrt{d {ε^{'}}_{i j} d {ε^{'}}_{i j}} \cos 〈 s_{i j}, d {ε^{'}}_{i j} 〉 \end{matrix}

(36)

式中,p为平均应力, $s_{i j}$ 为偏应力张量, $ε_{m}$ 为平均应变, $ε_{v}$ 为体应变。

若偏应力 $s_{i j}$ 、偏应变增量 $d {ε^{'}}_{i j}$ 共轴,则上式可化为

d W = p d ε_{v} + \sqrt{s_{i j} s_{i j}} \sqrt{d {ε^{'}}_{i j} d {ε^{'}}_{i j}} = p d ε_{v} + \frac{2}{3} q d γ 。

(37)

假定散粒体通过颗粒相对运动消散的能量为

{\bar{f}}_{s} \cdot d Δ {\bar{u}}_{s} = A q_{T} d γ

(38)

式中, $A = \frac{8 {\bar{r}}^{2}}{15} (\frac{N_{s}}{N}) \sqrt{[1 + \frac{(4 T_{i i} T_{k l} - 6 T_{i j} T_{j k}) (δ_{k l} - D_{k l})}{21 {T^{'}}_{k l} {T^{'}}_{k l}}]}$

\sqrt{[1 + \frac{(4 ε_{i i} ε_{k l} - 6 ε_{i k} ε_{i l}) (δ_{k l} - Ψ_{k l})}{21 {ε^{'}}_{i j} {ε^{'}}_{i j}}]}

。

(39)

同时假定单位时间内外界对试样做功通过颗粒间摩擦和接触的生成（消失）完全消散,则有

(p d ε_{v} + \frac{2}{3} q d γ) = \frac{N}{V} A q_{T} d γ + {\dot{N}}_{v} w

(40)

式中, ${\dot{N}}_{v}$ 为单位体积内接触数的变化率,w为单个接触处的平均能量。

2.2 应力-剪胀关系的一般表达式

由能量守恒式（40）很容易得应力-剪胀关系如下：

D = \frac{d ε_{v}}{d γ} = \frac{N}{V} A \frac{q_{T}}{p} - \frac{2}{3} \frac{q}{p} + \frac{{\dot{N}}_{v} w}{p d γ}

。

(41)

将式（39）代入式（41）可得

\begin{matrix} D = \frac{d ε_{v}}{d γ} = \frac{N}{V} \frac{8 {\bar{r}}^{2}}{15} (\frac{N_{s}}{N}) \sqrt{N_{T} N_{\dot{ε}}} \frac{q_{T}}{p} - \frac{2}{3} \frac{q}{p} + \frac{{\dot{N}}_{v} w}{p d γ} \\ = C \frac{q_{T}}{p} - \frac{2}{3} \frac{q}{p} + \frac{{\dot{N}}_{v} w}{p d γ} \end{matrix}

(42)

式中, $C = \frac{8 {\bar{r}}^{2}}{15} \frac{N_{S}}{V} \sqrt{N_{T} N_{\dot{ε}}}$ , $N_{T} = 1 + [(4 T_{i i} T_{k l} - 6 T_{i j} T_{j k}) \cdot$ $(δ_{k l} - D_{k l})] / 21 {T^{'}}_{k l} {T^{'}}_{k l}$ , $N_{\dot{ε}} = 1 + [(4 {\dot{ε}}_{i i} {\dot{ε}}_{k l} - 6 {\dot{ε}}_{i k} {\dot{ε}}_{i l}) \cdot (δ_{k l} -$ $Ψ_{k l})] / 21 {\dot{ε}}^{'}_{i j} {\dot{ε}}^{'}_{i j}$ 。

2.3 应力-剪胀关系的简化表达

上述应力-剪胀关系的一般表达式中, $N_{s} / V$ 能够反映孔隙比对剪胀的影响, $N_{T}$ 表示当前应力及组构对剪胀的影响, $N_{\dot{ε}}$ 反映了塑性应变及组构对剪胀的影响,因此本文提出的应力-剪胀方程能够综合考虑密实度、组构各向异性、应力比、塑性应变、接触变化等因素对材料剪胀的影响。式中C和 ${\dot{N}}_{v}$ 的确定非常关键,但较复杂,为了方便应用,下面根据其物理意义给出一个简化的应力-剪胀关系。

（1）在加载过程中,接触数的变化率 ${\dot{N}}_{v}$ 与剪应变增量 $d γ$ 的变化有关, $d γ$ 的增大意味着试样剪应变速率加快,应变发生较大,颗粒间的相对位移增大,从而导致接触的生成或消失的可能性增大,因此接触数的变化率 ${\dot{N}}_{v}$ 变大；同时平均应力p与接触能量相关,p越大,颗粒越不容易发生滑动,接触处的能量越大,因此w越大；因此可知 ${\dot{N}}_{v} w$ 与 $p d γ$ 呈正相关关系,由于在加载过程中 $d γ$ , $\dot{N}$ 的变化不易确定,本文假定 ${\dot{N}}_{v} w$ 与 $p d γ$ 的比值 $D_{0}$ 在加载过程中保持不变,其物理是等平均应力剪切中单位剪应变增量所消耗的接触能量不变,即

D_{0} = \frac{{\dot{N}}_{v} w}{p d γ}

。

(43)

（2）临界状态下,试样塑性体应变不再增加,剪胀比D为0,因此代入式（42）有

C_{cr} = \frac{2}{3} {(\frac{q}{q_{T}})}_{cr} - {(\frac{p}{q_{T}})}_{cr} D_{0}

。

(44)

（3）函数C中包含滑动接触数 $N_{s}$ 和试样体积V,滑动接触数 $N_{s}$ 与试样密实度和配位数相关,研究表明试样配位数与孔隙比e有关^[23],因此可认为C为临界应力、临界组构以及孔隙比的函数,并假设其关系为

C = C_{cr} {(\frac{e}{e_{cr}})}^{α}

(45)

式中, $α$ 是材料常数。

将式（43）,（44）和式（45）代入式（42）有

D = \frac{2}{3} [{(\frac{q}{q_{T}})}_{cr} {(\frac{e}{e_{c}})}^{α} \frac{q_{T}}{p} - \frac{q}{p}] + [1 - {(\frac{e}{e_{c}})}^{α} {(\frac{p}{q_{T}})}_{cr} \frac{q_{T}}{p}] D_{0} 。

(46)

需要指出的是,式（46）中 $q_{T}$ 与组构张量 $F_{i j}$ 相关,因此本文提出的剪胀方程考虑了组构演化对应力-剪胀关系的影响。

2.4 应力-组构演化关系

上述应力-剪胀关系的一般表达式中包含了偏真应力 $q_{T}$ ,因此需要确定加载过程中的组构发展规律。Oda等^[24-25]的室内试验结果显示组构的发展主要受应力控制,当初始组构与应力共轴时,加载过程中组构张量旋转很小；当二者非共轴时,组构主轴向应力主轴方向旋转,直至与其共轴。因此可以假设组构增量与应力增量共轴^[26],同时,由于颗粒相对运动产生的组构演化与材料的密实度相关,孔隙比越小,颗粒间咬合作用越明显,越不容易发生相对运动,组构变化较小；因此本文采用如下的组构-应力演化关系：

{\dot{F}}_{i j} = β {(\frac{e}{e_{cr}})}^{α} {\dot{η}}_{i j}

(47)

式中,e为孔隙比, $e_{cr}$ 为临界孔隙比, $α$ 和 $β$ 为材料参数,其中 $α$ 反映密实度的影响程度, $β$ 反映材料摩擦性质的影响程度； $η_{i j}$ 为偏应力比张量, $η_{i j} = \frac{s_{i j}}{p}$ 。

积分上式可得

F_{i j} = {(\frac{e}{e_{cr}})}^{α} β (\frac{σ_{i j}}{p} - 1) + F_{i j} |_{0}

(48)

式中, $F_{i j} |_{0}$ 为初始组构。

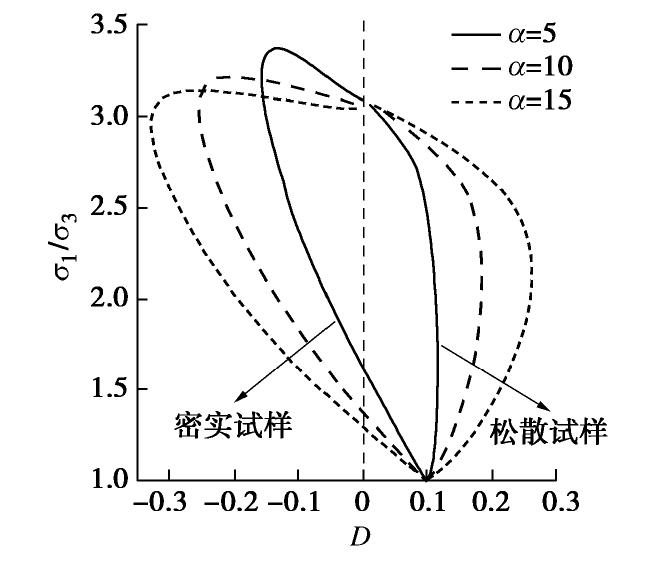
2.5 $α$ 对剪胀的影响

参数 $α$ 表征的是密实状态对材料剪胀性的影响程度。图2为不同 $α$ 条件下由剪胀方程式（46）得到的应力比-剪胀比关系图。

图 2

α

对试样应力比-剪胀比的影响

Figure 2. Effect of

α

on stress-dilatancy relationship

下载: 全尺寸图片幻灯片

从图2中可以看出,随着 $α$ 的增大,密砂的剪胀性越强,而松砂的剪缩性越强,意味着散体材料剪胀（剪缩）性对孔隙比的变化越敏感； $α$ 的变化不会影响材料的临界应力比,但 $α$ 的增大会导致密实材料峰值强度有所减小；即对于同一材料而言,材料的剪胀一定程度上削弱了其强度的发挥。同时从图2中可以看出,峰值应力比要稍微滞后于最大剪胀比,这与一般试验结果相符。

2.6 初始剪胀参数D₀

（1）D₀确定方法

从式（46）中可以看出,D₀与试样各向异性组构共同决定了试样在加载初期的剪胀（剪缩）行为,D₀的具体确定方法如下：

a）确定试样组构及其发展规律；

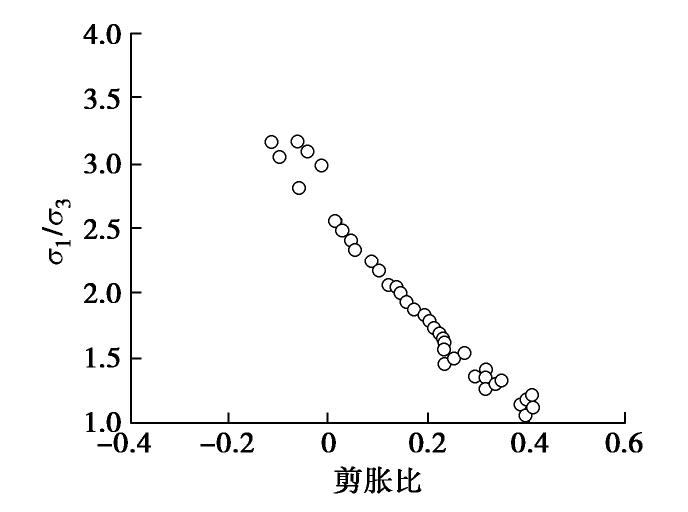
b）绘制应力比-剪胀比曲线,确定初始剪胀比D_ini；D_ini为试样应力比-剪胀比曲线与横轴交点的值。如图3所示,D_ini=0.4；

图 3 应力比-剪胀比关系示意图

Figure 3. Variation of dilatancy with stress ratio

下载: 全尺寸图片幻灯片

c）计算 $\frac{q_{T}}{q}$ , ${(\frac{e}{e_{c}})}^{α}$ 以及临界状态下的 ${(\frac{p}{q_{T}})}_{cr}$ ；

d）初始时q=0,将上述值代入式（46）中可确定D₀。

特别地,当试样为初始各向同性时, $q_{T} = 0$ ,则D₀=D_ini,因此,D₀可称为各向同性初始剪胀比。

（2）D₀对剪胀的影响

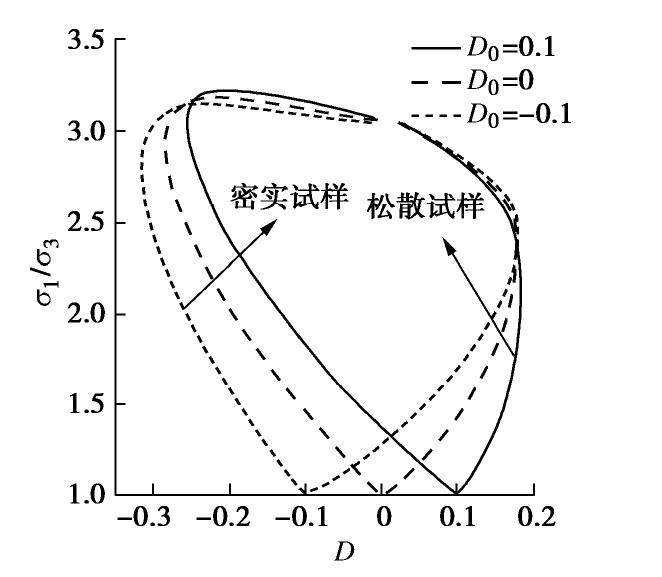
应力-剪胀关系式（46）中,D₀值的大小反映了试样的初始剪胀（缩）行为。图4为初始各向同性松散与密实试样的D₀对应力比-剪胀比关系的影响。

图 4 D₀对试样应力比-剪胀关系的影响

Figure 4. Effect of D₀ on stress-dilatancy relationship

下载: 全尺寸图片幻灯片

从图4中可以看出,对于初始各向同性试样,D₀即为试样应力比-剪胀比图像与横轴的交点坐标,为初始剪胀比。当D₀发生变化时,试样的初始剪胀性也随即改变：D₀=0时,即不考虑接触数变化对材料剪胀性的影响,此时无论松散或密实试样,其初始剪胀比均为0,这与实际不符,因此考虑接触数变化对剪胀的影响很有必要。

当D₀>0时,不管是密实试样还是松散试验,初始剪切阶段均发生剪缩,随后密实试样剪胀比逐渐降低至相变点（D=0）并发生剪胀,直到临界状态；而松散试样持续剪缩至临界状态；这与常见的试验结果相吻合。此外,一些室内试验结果^[27]显示散体材料在初始剪切时会出现剪胀行为,本文提出的流动法则也可以模拟这一情况,即D₀<0。

无论D₀如何变化,随着加载进行,松散和密实试样都趋近于同样的临界应力比；然而,较大的峰值剪胀比获得了较小的峰值强度,这与上文分析一致。

3. 与经典流动法则的比较

本节将提出的应力-剪胀关系简化表达式（46）与经典的剑桥流动法则、Rowe 剪胀方程进行比较。为了比较方便,将式（46）改写为如下形式：

D = \frac{2}{3} [(B_{1} \frac{q_{T}}{p} + \frac{3}{2} B_{2} D_{0}) - η]

(49)

式中, $B_{1} = {(\frac{q}{q_{T}})}_{cr} {(\frac{e}{e_{c}})}^{α} ， B_{2} = 1 - {(\frac{e}{e_{c}})}^{α} {(\frac{p}{q_{T}})}_{cr} (\frac{q_{T}}{p})$ 。

剑桥流动方程和三轴压缩下的Rowe剪胀方程如式（50）,（51）所示：

D = \frac{1}{ξ} (M - η)

(50)

D = \frac{9 (M - η)}{9 + 3 M - 2 M η}

(51)

式中,M为临界应力比, $η = \frac{q}{p}$ 为应力比。

可以看出,本文提出的应力-剪胀方程与剑桥流动方程形式一致。不同的是,剑桥流动法则中,在加载初始,试样应力比为0,初始剪胀比为 $\frac{M}{ξ}$ ,因此剑桥流动法只能模拟初始剪缩行为,而本文的流动法则可模拟材料的初始剪胀性。在临界状态下,式（49）中的 $B_{1} \frac{q_{T}}{p} + \frac{3}{2} B_{2} D_{0}$ 退化为M,与剑桥流动法则一致,且满足剪胀比为0的条件。

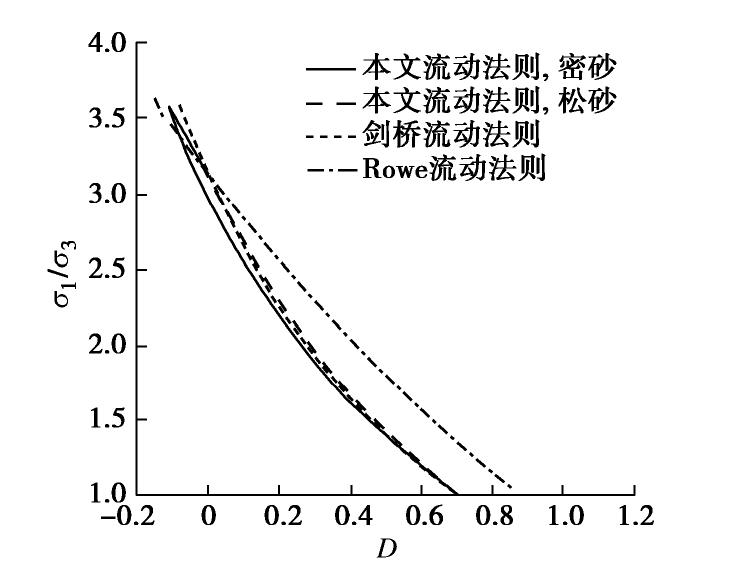
对于三轴压缩条件下的Rowe剪胀方程,初始剪胀比为 $D_{ini} = \frac{9 M}{9 + 3 M}$ ,只与临界状态应力比有关,不能考虑孔隙比,组构各向异性等因素的影响；而本文的流动法则考虑了临界摩擦角、孔隙比、组构演化等因素的影响,可反映摩擦角相同而初始剪胀比不同的材料特性,可以预测更为复杂的应力-剪胀关系。

图5为由上述3种流动法则计算得到的应力比-剪胀比关系对比图。图中试样临界摩擦角为31°,D₀取0.7, $ξ$ 为1.78。

图 5 不同流动法则下应力比-剪胀比关系对比图

Figure 5. Comparison of different stress-dilatancy relationships

下载: 全尺寸图片幻灯片

从图5中可以看出,在该参数条件下,Rowe剪胀方程初始剪胀比D_ini=0.880；而剑桥流动法则与本文应力-剪胀关系得到的初始剪胀比相同,且小于Rowe剪胀方程的结果。对于密实试样而言,随着加载的进行,三者剪胀比都逐渐减小,当剪胀比为0时,剑桥流动法则与Rowe剪胀方程相交应力比等于临界应力比,而本文应力比略小于临界应力比,这与试验及模拟结果一致^{[12, 28]}；此后三者都由剪缩转为剪胀,Rowe剪胀方程的剪胀最大,本文次之,剑桥流动法则得到的剪胀最小；在达到峰值应力比之后都向临界状态发展；到达临界状态时,三者的临界应力比相同；对于松散试样,随着加载的进行,三者得到的剪胀比都逐渐减小,试样持续剪缩,本文结果与剑桥流动法则基本一致,Rowe剪胀方程剪缩较大,但最后都达到与密实试样同样的临界状态。

此外,剑桥流动法则与Rowe剪胀方程在达到峰值强度之后均沿原路线趋向临界状态,且松散和密实试样为同一条曲线,剪胀比只与应力比有关,而本文的流动法则则不按原路线减小,且松散和密实试样为两条曲线,能够反映剪胀比受孔隙比、组构各向异性等的影响,与实际较符。

4. 与室内试验结果的对比

为验证本文应力-剪胀方程的合理性与适用性,本节将得到的应力-剪胀关系对室内试验结果进行预测。

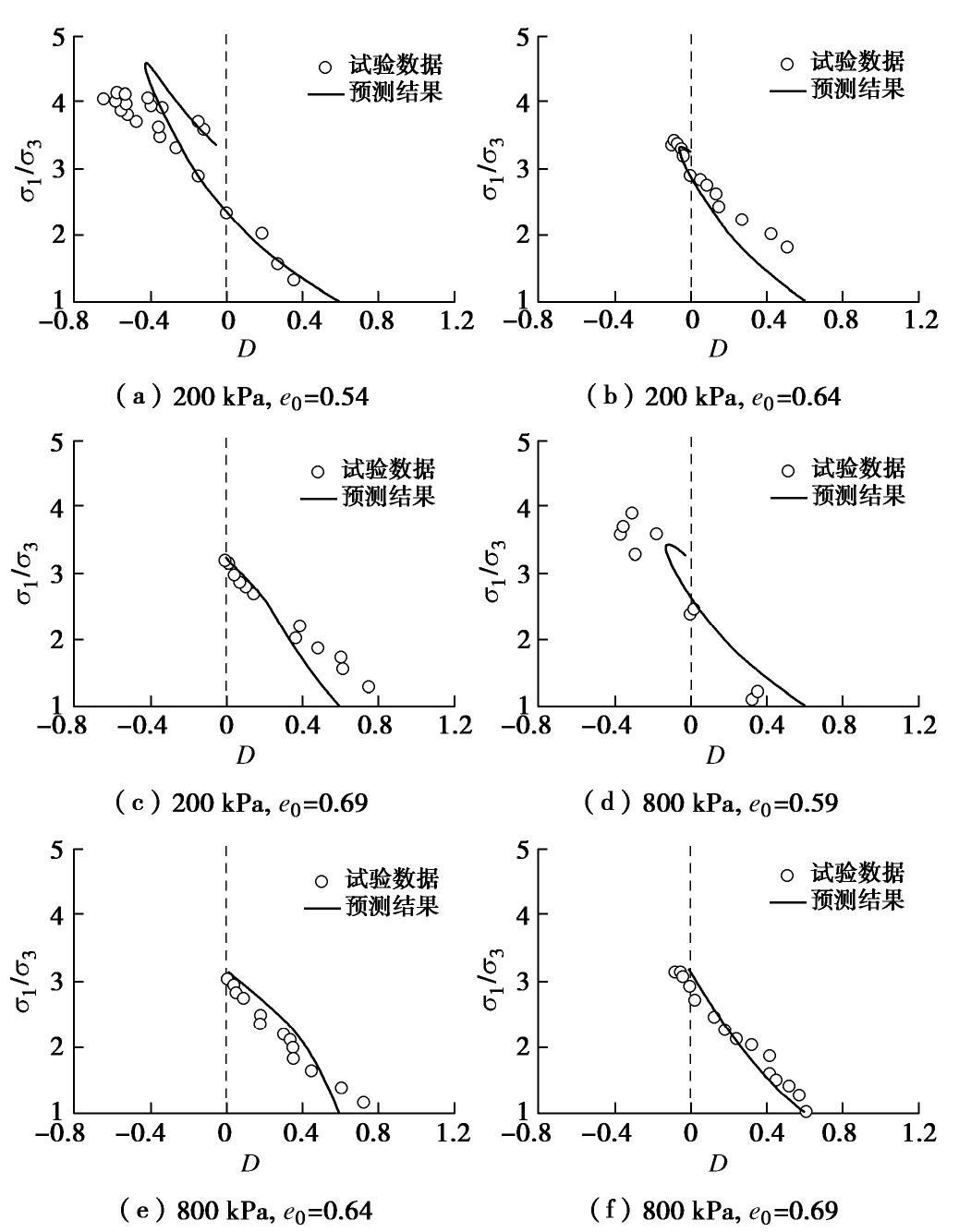
4.1 Ottawa砂

Regier^[29]在1997年进行了一系列不同围压下的初始孔隙比不同的Ottawa砂三轴试验。试样制备采用湿捣法,达到预定孔隙比后对试样进行饱和,接着固结剪切。采用本文的应力-剪胀方程对200,800 kPa固结围压下的松砂（ $e_{0}$ =0.69）、中密砂（ $e_{0}$ =0.64）及密砂（200 kPa时, $e_{0}$ =0.54；800 kPa时, $e_{0}$ =0.59）的试验结果进行预测。Ottawa砂颗粒表面较圆润,形状相对规则,一般认为其在各向同性固结下为初始各向同性,图6为Ottawa砂试验结果与预测结果对比图（剪胀参数 $D_{0} = 0.6$ , $α = 10$ , $β = 0.2$ ）。

图 6 Ottawa砂应力-剪胀关系的试验结果与预测结果对比图

Figure 6. Comparison of predicted and test results for Ottawa sand

下载: 全尺寸图片幻灯片

由图6中可以看出,随着孔隙比的增加,试样的剪胀性降低；随着围压的增大,试验的剪胀性也降低。本文应力-剪胀关系能够很好地反映Ottawa砂在三轴压缩试验下峰值剪胀比及应力比随试样初始密实度降低而降低的现象。

从图6中还可以看出,800 kPa围压下的松砂试样峰值应力比、剪胀比预测偏低,主要是因为在较高围压作用下,部分砂土颗粒发生破碎,破碎形成的细颗粒填充孔隙,材料密实度增大,同时新的接触和咬合产生,从而使得材料的强度增大,剪胀性也相应增强,但本文建立的应力-剪胀方程未考虑这一因素的影响。其他围压条件下峰值状态与临界状态的预测值与室内试验吻合较好。

4.2 Toyoura砂

Pradhan等^[30]在1989年进行了一系列Toyoura砂的循环加载试验,并分析了循环荷载下试样的应力比-剪胀比关系。试验采用砂雨法,Toyoura砂颗粒呈角状,由于颗粒的定向排列,砂雨法制样会使其呈现稍弱的横观各向同性；为避免多次加载对试样初始各向异性及应力比-剪胀比关系造成的影响,本文将其在第一次加载中的应力比-剪胀比关系与得到的应力-剪胀方程进行对比,结果如图7所示。（组构分量 $F_{1} = 0.36$ , $F_{3} = F_{2} = 0.32$ ,剪胀参数D₀=0.45, $α = 2$ , $β = 0.2$ 。）

图 7 Toyoura砂应力-剪胀关系的试验与预测结果对比图

Figure 7. Comparison of predicted and test results for Toyoura sand

下载: 全尺寸图片幻灯片

从图7中可以看出,由于围压相对较小,试样均先发生剪缩,然后表现出明显的剪胀性。随着试样初始孔隙比的增加,试样峰值应力比及剪胀性均有所降低。本文应力-剪胀关系能很好预测Toyoura砂的应力比-剪胀比发展趋势。

5. 结论

从微观力学角度出发,基于真应力张量推导了散体中平均接触力与平均接触位移的计算公式；并在宏-微观能量守恒的基础上,建立了一个简化的散粒体应力-剪胀关系,研究得到的主要结论如下：

（1）本文建立的应力-剪胀方程,宏微观物理意义明确,同时考虑了材料密实状态和微观组构发展对应力-剪胀关系的影响。

（2）在应力-剪胀方程中,参数 $α$ 反映的是密实状态对组构演化以及剪胀（缩）特性的影响。 $α$ 越大,密砂的剪胀性越强,松砂的剪缩性越强,但 $α$ 的变化不影响材料的临界状态强度；参数 $β$ 反映了组构发展快慢及对应力-剪胀发展的影响,而材料的初始剪胀比受参数D₀的影响,D₀与散体中接触数的变化率有关。

（3）本文的应力-剪胀方程可以较好地模拟材料的初始剪缩（胀）行为,并可反映峰值应力比滞后于最大剪胀比的现象。同时提出的应力-剪胀方程还可以描述材料在相变点处应力比不等于临界应力比的特性,可较好地预测散体材料的应力-剪胀关系。

需要指出的是,本文在应力-剪胀关系的分析中,假定由接触变化引起的能量耗散随剪应变均匀变化,鉴于剪切过程中颗粒接触生成/分离变化的复杂性,这个问题尚待进一步深入研究。此外,文中对有代表性的砂土三轴试验结果进行了验证分析,进一步的工作将开展其它应力路径下的砂土剪切试验,并与提出的应力-剪胀关系进行比较分析。

附录：

为简化计算,在文中定义了3个方向张量,

\begin{array}{l} M_{i j} = \iint_{Ω} n_{i} n_{j} d Ω \\ M_{i j k l} = \iint_{Ω} n_{i} n_{j} n_{k} n_{l} d Ω \\ M_{i j k l m n} = \iint_{Ω} n_{i} n_{j} n_{k} n_{l} n_{m} n_{n} d Ω \end{array}}

。

(A(1))

上述3个张量通过积分可得

M_{i j} = \frac{4}{3} π δ_{i j}

(A(2.1))

M_{i j k l} = \frac{4 π}{15} (δ_{i j} δ_{k l} + δ_{i k} δ_{j l} + δ_{i l} δ_{j k})

(A(2.2))

\begin{matrix} M_{i j k l m n} = \frac{4 π}{105} (δ_{i j} δ_{k l} δ_{m n} + δ_{i j} δ_{k m} δ_{l n} + δ_{i j} δ_{k n} δ_{l m} + δ_{i k} δ_{j l} δ_{m n} + \\ δ_{i k} δ_{j m} δ_{l n} + δ_{i k} δ_{j n} δ_{l m} + δ_{i l} δ_{j k} δ_{m n} + δ_{i l} δ_{j m} δ_{k n} + \\ δ_{i l} δ_{j n} δ_{k m} + δ_{i m} δ_{j k} δ_{l n} + δ_{i m} δ_{j l} δ_{k n} + δ_{i m} δ_{j n} δ_{k l} + \\ δ_{i n} δ_{j k} δ_{l m} + δ_{i n} δ_{j l} δ_{k m} + δ_{i n} δ_{j m} δ_{k l}) \end{matrix}

(A(2.3))

式中, $δ_{i j}$ 为克罗内克尔算子。

图 1 全局和局部坐标系统

Figure 1. Global and local coordinate system

下载: 全尺寸图片幻灯片

图 2 $α$ 对试样应力比-剪胀比的影响

Figure 2. Effect of $α$ on stress-dilatancy relationship

下载: 全尺寸图片幻灯片

图 3 应力比-剪胀比关系示意图

Figure 3. Variation of dilatancy with stress ratio

下载: 全尺寸图片幻灯片

图 4 D₀对试样应力比-剪胀关系的影响

Figure 4. Effect of D₀ on stress-dilatancy relationship

下载: 全尺寸图片幻灯片

图 5 不同流动法则下应力比-剪胀比关系对比图

Figure 5. Comparison of different stress-dilatancy relationships

下载: 全尺寸图片幻灯片

图 6 Ottawa砂应力-剪胀关系的试验结果与预测结果对比图

Figure 6. Comparison of predicted and test results for Ottawa sand

下载: 全尺寸图片幻灯片

图 7 Toyoura砂应力-剪胀关系的试验与预测结果对比图

Figure 7. Comparison of predicted and test results for Toyoura sand

下载: 全尺寸图片幻灯片

参考文献(30)

[1]	SCHOFIELD A, WROTH P. Critical State Soil Mechanics[M]. London: McGraw-Hill, 1968.
[2]	NOVA R, WOOD D M. A constitutive model for sand in triaxial compression[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1979, 3(3): 255-278. doi: 10.1002/nag.1610030305
[3]	LAGIOIA R, PUZRIN A M, POTTS D M. A new versatile expression for yield and plastic potential surfaces[J]. Computers & Geotechnics, 1996, 19(3): 171-191.
[4]	ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[J]. Proceedings of the Royal Society of London, Series A. Mathematical and Physical Sciences, 1962, 269(1339): 500-527.
[5]	GUO P J, STOLLE D F. The extension of Rowe’s stress-dilatancy model to general stress condition[J]. Soils and Foundations, 2004, 44(4): 1-10. doi: 10.3208/sandf.44.4_1
[6]	蔡正银, 李相菘. 砂土的剪胀理论及其本构模型的发展[J]. 岩土工程学报, 2007, 29(8): 1122-1128. doi: 10.3321/j.issn:1000-4548.2007.08.002 CAI Zheng-yin, LI Xiang-song. Development of dilatancy theory and constitutive model of sand[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1122-1128. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.08.002
[7]	WAN R, GUO P. A pressure and density dependent dilatancy model for granular materials[J]. Soils and Foundations, 1999, 39(6): 1-11. doi: 10.3208/sandf.39.6_1
[8]	LI X S, DAFALIAS Y F. Constitutive modeling of inherently anisotropic sand behavior[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(10): 868-880. doi: 10.1061/(ASCE)1090-0241(2002)128:10(868)
[9]	LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449-460. doi: 10.1680/geot.2000.50.4.449
[10]	MANZARI M T, DAFALIAS Y F. A critical state two-surface plasticity model for sands[J]. Géotechnique, 1997, 47(2): 255-272. doi: 10.1680/geot.1997.47.2.255
[11]	GAJO A, MUIR WOOD D. Severn-Trent sand: a kinematic-hardening constitutive model: the qp formulation[J]. Géotechnique, 1999, 49(5): 595-614. doi: 10.1680/geot.1999.49.5.595
[12]	WANG R, DAFALIAS Y F, FU P, et al. Fabric evolution and dilatancy within anisotropic critical state theory guided and validated by DEM[J]. International Journal of Solids and Structures, 2019, 188-189(3): 210-222.
[13]	TOBITA Y. Fabric tensors in constitutive equations for granular materials[J]. Soils and Foundations, 1989, 29(4): 91-104. doi: 10.3208/sandf1972.29.4_91
[14]	ZHAO J, GUO N. Unique critical state characteristics in granular media considering fabric anisotropy[J]. Géotechnique, 2013, 63(8): 695-704. doi: 10.1680/geot.12.P.040
[15]	YIN Z Y, CHANG C S. Stress-dilatancy behavior for sand under loading and unloading conditions[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2013, 37(8): 855-870.
[16]	LIU Y, CHANG C S. Relationship between element-level and contact-level parameters of micromechanical and upscaled plasticity models for granular soils[J]. Acta Geotechnica, 2020, 15(7): 1779-1798. doi: 10.1007/s11440-019-00895-7
[17]	XIAO Y, ASCE M, LONG L, et al. Effect of particle shape on stress-dilatancy responses of medium-dense sands[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2018, 145(2): 04018105.
[18]	LIANG J, LU D, DU X, et al. A 3D non-orthogonal elastoplastic constitutive model for transversely isotropic soil[J]. Acta Geotechnica, 2021, in press.
[19]	TSEGAYE A B, BENZ T, NORDAL S. Formulation of non-coaxial plastic dissipation and stress-dilatancy relations for geomaterials[J]. Acta Geotechnica, 2020, 15(10): 2727-2739. doi: 10.1007/s11440-020-00968-y
[20]	杨骏堂, 刘元雪, 郑颖人, 等. 剪胀型土剪胀特性的大数据深度挖掘与模型研究[J]. 岩土工程学报, 2020, 42(3): 513-522. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003018.htm YANG Jun-tang, LIU Yuan-xue, ZHENG Ying-ren et al. Deep mining of big data and model tests on dilatancy characteristics of dilatant soils[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 513-522. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003018.htm
[21]	LIAO C L, CHANG T P, YOUNG D H, et al. Stress-strain relationship for granular materials based on the hypothesis of best fit[J]. International Journal of Solids and Structures, 1997, 34(31/32): 4087-4100.
[22]	刘洋, CHANG C S, 张铎, 等. 散粒介质三维应力-组构解析与破坏分析[J]. 岩土工程学报, 2014, 36(3): 401-408. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403002.htm LIU Yang, CHANG C S, ZHANG Duo, et al. Analytical solution of stress-fabric relationship and failure of granularmaterials in three dimensions[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 401-408. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403002.htm
[23]	CHANG C S, MISRA A. Packing structure and mechanical properties of granulates[J]. Journal of Engineering Mechanics, 1990, 116(5): 1077-1093. doi: 10.1061/(ASCE)0733-9399(1990)116:5(1077)
[24]	ODA M, KONISHI J, NEMAT-NASSER S. Some experimentally based fundamental results on the mechanical behaviour of granular materials[J]. Géotechnique, 1980, 30(4): 479-495. doi: 10.1680/geot.1980.30.4.479
[25]	ODA M, NEMAT-NASSER S, KONISHI J. Stress-induced anisotropy in granular masses[J]. Soils and Foundations, 1985, 25(3): 85-97. doi: 10.3208/sandf1972.25.3_85
[26]	WAN R G, GUO P J. Stress dilatancy and fabric dependencies on sand behavior[J]. Journal of Engineering Mechanics, 2004, 130(6): 635-645. doi: 10.1061/(ASCE)0733-9399(2004)130:6(635)
[27]	BEEN K, JEFFERIES M. Stress dilatancy in very loose sand[J]. Canadian Geotechnical Journal, 2004, 41(5): 972-989. doi: 10.1139/t04-038
[28]	LIU D Y, LOURENÇO S D N. Stress-dilatancy behaviour of a polymer-coated sand[J]. Acta Geotechnica, 2021, 16(2): 647-652. doi: 10.1007/s11440-020-01022-7
[29]	REGIER K. The stress-dilatancy behaviour of sands: pressure and density dependencies in both monotonic and cyclic loading regimes[M]. Calgary: University of Calgary, 1997.
[30]	PRADHAN T B, TATSUOKA F, SATO Y. Experimental stress-dilatancy relations of sand subjected to cyclic loading[J]. Soils and Foundations, 1989, 29(1): 45-64. doi: 10.3208/sandf1972.29.45

施引文献

资源附件(0)

图(7)

计量

文章访问数: 295
HTML全文浏览量: 28
PDF下载量: 195
被引次数: 0

0. 引言
1. 平均接触力与平均相对位移
1.1 平均接触力计算
1.2 平均位移计算
2. 宏微观能量守恒与应力-剪胀关系
2.1 宏微观能量守恒
2.2 应力-剪胀关系的一般表达式
2.3 应力-剪胀关系的简化表达
2.4 应力-组构演化关系
2.5 α对剪胀的影响
2.6 初始剪胀参数D0
3. 与经典流动法则的比较
4. 与室内试验结果的对比
4.1 Ottawa砂
4.2 Toyoura砂
5. 结论
附录：

0. 引言
1. 平均接触力与平均相对位移
1.1 平均接触力计算
1.2 平均位移计算
2. 宏微观能量守恒与应力-剪胀关系
2.1 宏微观能量守恒
2.2 应力-剪胀关系的一般表达式
2.3 应力-剪胀关系的简化表达
2.4 应力-组构演化关系
2.5 $α$ 对剪胀的影响
2.6 初始剪胀参数D₀
3. 与经典流动法则的比较
4. 与室内试验结果的对比
4.1 Ottawa砂
4.2 Toyoura砂
5. 结论
附录：

参考文献(30)

施引文献

资源附件(0)

一个基于微观力学分析的散粒体应力-剪胀关系 English Version

作者简介: 刘洋(1979— ),男,江苏徐州人,博士,教授,主要从事土细观力学和砂土液化等方面的科研和教学工作。E-mail：yangliu@ustb.edu.cn

计量

出版历程

Micromechanics-based stress-dilatancy relationship for granular materials

0. 引言

1. 平均接触力与平均相对位移

1.1 平均接触力计算

1.2 平均位移计算

2. 宏微观能量守恒与应力-剪胀关系

2.1 宏微观能量守恒

2.2 应力-剪胀关系的一般表达式

2.3 应力-剪胀关系的简化表达

2.4 应力-组构演化关系

2.5 α对剪胀的影响

2.6 初始剪胀参数D0

3. 与经典流动法则的比较

4. 与室内试验结果的对比

4.1 Ottawa砂

4.2 Toyoura砂

5. 结论

附录：

计量

出版历程

目录

0. 引言

1. 平均接触力与平均相对位移

1.1 平均接触力计算

1.2 平均位移计算

2. 宏微观能量守恒与应力-剪胀关系

2.1 宏微观能量守恒

2.2 应力-剪胀关系的一般表达式

2.3 应力-剪胀关系的简化表达

2.4 应力-组构演化关系

2.5 α对剪胀的影响

2.6 初始剪胀参数D0

3. 与经典流动法则的比较

4. 与室内试验结果的对比

4.1 Ottawa砂

4.2 Toyoura砂

5. 结论

附录：

作者简介:
刘洋(1979— ),男,江苏徐州人,博士,教授,主要从事土细观力学和砂土液化等方面的科研和教学工作。E-mail：yangliu@ustb.edu.cn

2.5 $α$ 对剪胀的影响

2.6 初始剪胀参数D₀

2.5 $α$ 对剪胀的影响

2.6 初始剪胀参数D₀