基于谱方法的层状竖井地基非线性固结计算模型

许滨华; 何宁; 周彦章; 张中流

doi:10.11779/CJGE202110003

基于谱方法的层状竖井地基非线性固结计算模型 English Version

许滨华^{1, 2,},
何宁^{1, 3, ,},
周彦章¹,
张中流¹

1.
南京水利科学研究院岩土工程研究所,江苏　南京　210024
2.
河海大学土木与交通学院,江苏　南京　210098
3.
水利部水库大坝安全重点实验室,江苏　南京　210029

基金项目:

国家重点研发计划项目 2018YFC1508505

国家自然科学基金面上项目 51379131

详细信息

作者简介:
许滨华(1991— ),男,博士研究生,主要从事软土地基处理和固结计算方面的研究。E-mail：317413076@qq.com

通讯作者:
何宁, E-mail：nhe@nhri.com

中图分类号: TU431
计量
- 文章访问数: 246
- HTML全文浏览量: 43
- PDF下载量: 250
出版历程
- 收稿日期: 2021-02-09
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-09-30

Nonlinear consolidation model for stratified soils with vertical drains based on spectral method

XU Bin-hua^{1, 2,},
HE Ning^{1, 3, ,},
ZHOU Yan-zhang¹,
ZHANG Zhong-liu¹

1.
Department of Geotechnical Engineering, Nanjing Hydraulic Research Institute, Nanjing 210024, China
2.
College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China
3.
Key Laboratory of Reservoir and Dam Safety, Ministry of Water Resources, Nanjing 210029, China

摘要

摘要: 针对实际工程中很多竖井地基呈现层状,且在固结过程中渗透系数和压缩模量呈非线性变化等特性,基于对数模型（e-lgσ'和e-lgk）的非线性压缩渗透本构关系,建立了能同时考虑竖向和径向排水的非线性固结模型,并采用谱方法得到了层状竖井地基的非线性固结计算模型。通过退化研究与已有的非线性固结解析解和室内试验进行对比计算分析,结果显示本模型计算值与解析解和实测值的平均相对误差分别低于0.7%和2.0%,验证了本模型的合理性。最后对某一实际工程案例进行了应用计算分析,结果显示不同深度处的沉降和孔压计算值与实测数据吻合程度较好,能够反映在固结过程中不同土层中沉降和孔压的发展变化过程,进一步说明了本模型在层状竖井地基固结计算的可行性和工程适用性。
- 层状地基 /
- 竖井 /
- 非线性固结 /
- 谱方法
Abstract: Many soft soil foundations with vertical drains are stratified, and the permeability and compressibility of soils change nonlinearly during the consolidation process. A nonlinear consolidation model that can consider both vertical and radial drainage is proposed based on the void-ratio dependent compressibility and permeability (e-lgσ' and e-lgk), and a nonlinear consolidation model for the stratified soils with vertical drains is obtained based on the spectral method. The validation of the solution is verified by the degradation study and the comparative analysis with the existing nonlinear consolidation analytical solutions and laboratory tests. The results show that the average relative error between the calculated value and the analytical solution and the measured value is lower than 0.7% and 2.0%, respectively. A field case is also studied and analyzed. The results show that the calculated values of settlement and pore pressure at different depths are in good agreement with the measured data, which can predict the development of settlement and the dissipation of pore pressure in different soil layers during the consolidation process. The case study further illustrates the feasibility and applicability of the proposed model in the consolidation calculation of stratified soils with vertical drains.
- stratified soil /
- vertical drain /
- nonlinear consolidation /
- spectral method

HTML全文

0. 引言

排水固结法是一种常见的软土地基处理方式,其通过设置竖向排水通道（塑料排水板、袋装砂井、普通砂井、碎石桩、透水软管等）缩短排水通道,具有经济合理、高效率而且施工方便等优点,因此在交通工程、港口工程及码头堤防工程中得到了广泛应用^[1]。

在竖井地基的固结问题方面,已有许多学者开展了相关理论和试验研究。Barron^[2]最早提出了分别基于等应变假设和自由应变假设的理想竖井地基径向固结解析解。Yoshikuni等^[3]在Barron固结解的基础上进行了扩展,给出了能考虑井阻效应的的固结解析解。Hansbo^[4]在Barron固结理论的基础上,同时考虑涂抹效应和井阻效应的影响,给出了基于等应变假设的径向固结解。基于Barron等提出的径向固结理论,竖井固结理论不断完善,例如能够考虑不同模式的涂抹效应（沿径向水平渗透系数呈分段、线性、分段线性、抛物线等模式变化）,不同形式的加载方式（瞬间加载,分段线性加载）,井阻非线性（随空间和时间变化）等^[5-13]。

研究表明,对数形式的非线性压缩渗透模型（e- lgσ'和e-lgk）能普遍适用于常见软黏土。基于此,Lekha等^[14]得到了一种可考虑逐级加载下竖井地基径向固结的简化解。Indraratna等^[8]在考虑竖井地基的涂抹效应的同时,通过将非线性径向固结微分方程进行线性简化,求得了竖井地基非线性径向固结的解析解。卢萌盟等^[15]推导得出碎石桩复合地基的非线性径向固结简化解。郭霄等^[16]推导得到了直排式真空预压法下竖井地基径向固结的通用解。Walker等^[17]得到了基于非达西流的非线性径向固结解析解。Lu等^[18]得到了任意加载条件下竖井地基非线性径向固结的通解。田乙等^[19]基于椭圆柱效应建立了非线性径向固结理论。江文豪等^[20]得到了考虑井阻随时间变化的竖井非线性径向固结解。此外有很多学者关于非线性径向固结问题展开研究^[21-25],以上非线性固结模型由于只能考虑径向排水的非线性特性,当需要考虑竖向固结排水时（例如竖井或排水板打设不深）,需要采用Carrillo定理,且不能考虑竖向渗流的非线性。Tang等^[6]研究了Carrillo定理的可行性,结果表明该定理在变荷载作用下是不成立的。Zhang等^[26]研究表明当使用Carrillo定理时,由于计算竖向固结度和径向固结度时荷载是分别作用于竖向排水和径向排水,与荷载同时作用于竖向和径向排水固结事实相悖,因而使用Carrillo定理会高估固结速率。因此,为了能够更真实准确地计算竖井地基的固结,固结计算模型的建立需要同时考虑竖向和径向排水。

Lu等^[27]建立了考虑井阻效应并同时考虑竖向和径向排水的非线性固结模型。Liu等^[28]建立了真空荷载随时间和空间变化的非线性固结模型。Wang等^[29]和黄鹏华等^[30]得到了考虑电渗和真空联合作用的非线性固结模型。诸多研究关于能同时考虑竖向和径向排水的非线性固结模型,以上非线性固结模型虽然能同时考虑竖向和径向排水的作用,并能结合实际的工程特性,但是都是基于单层土这一假设建立的计算模型,不能应用于层状竖井地基的固结计算。

由于沉积历史和应力条件不同,在实际工程中,很多软土地基并不是均质的,而是呈现层状特性,因此相关学者在竖井层状地基的固结问题上开展了解析方法研究,例如Tang等^[31-32]提出了双层和三层竖井固结理论解析解；Nogami等^[33],Zhou等^[34]以及Liu等^[35]分别采用传递矩阵法,分离变量法和拉普拉斯变换得到了层状竖井地基的解法。还有一些学者针对软土压缩和渗流非线性的问题开展了数值计算研究^[36-38],并能考虑层状甚至大变形等工程特性,但是采用的是常用的有限差分或者有限元等数值方法,其属于局部近似的数值分析方法,其精度和计算时间与网格划分的精细程度有关。谱方法相比于常用局部近似的数值分析方法（例如：有限差分和有限元法）,其选取的是高次多项式（或三角多项式）作为全局基函数,因此当问题的计算域规则且光滑时,具有计算精度高,效率快和稳定性好等优点^[39-40]。Walker等^[41-43]使用谱方法计算了同时考虑水平和竖向排水的层状竖井地基的固结解；Xu等^[13]在Walker等^[43]的固结模型基础上建立了考虑井阻随时间和空间变化的层状竖井固结模型。但是以上研究均是线性固结模型,即假定土体渗透系数和压缩模量在固结过程中保持不变,未考虑土体的非线性固结特性。

基于目前的研究现状,本文首先结合对数模型（e-lgσ'和e-lgk）的非线性压缩渗透本构关系,建立了能同时考虑竖向和径向排水的非线性固结模型,并采用谱方法得到了层状竖井地基的非线性固结计算模型。然后通过对本文计算模型的退化研究,与已有的解析解和室内试验进行了模型验证对比。最后应用该模型对某一实际工程案例进行了计算分析。

1. 固结控制方程

1.1 基本假设

本文在推导和求解过程中,基于以下假设：

（1）土体为饱和土,孔隙水同时在竖向和径向渗流,且满足Darcy定律。

（2）土体的变形只发生在竖向,没有侧向变形,且满足等应变条件。

（3）根据Das等^[44]和Tavenas等^[45]的研究,对数模式的非线性压缩渗透模型（e-lgσ'和e-lgk）能普遍适用于常见软黏土,因此本文假设土体的压缩特性和渗透特性与孔隙比的关系满足式（1）,（2）和（3）的对数关系。

（4）在同一深度处,除了涂抹区内外的初始水平渗透系数不一致,其他土性参数,初始应力和附加应力在同一土层相同。

$\bar{e} = {\bar{e}}_{0} - C_{c} \lg (\frac{\bar{σ^{'}}}{\bar{{σ^{'}}_{0}}})$ ,

(1)

$\bar{e} = {\bar{e}}_{0} + C_{kh} \lg (\frac{k_{h}}{k_{h0}})$ ,

(2)

$\bar{e} = {\bar{e}}_{0} + C_{kv} \lg (\frac{k_{v}}{k_{v0}})$ 。

(3)

式中 $\bar{e}$ , $\bar{σ^{'}}$ , $k_{h}$ 和 $k_{v}$ 分别为某一时刻土体的平均孔隙比,平均有效应力,水平渗透系数和竖向渗透系数； ${\bar{e}}_{0}$ , $\bar{{σ^{'}}_{0}}$ , $k_{h0}$ 和 $k_{v0}$ 分别为初始平均孔隙比,初始平均有效应力,初始水平渗透系数和初始竖向渗透系数； $C_{c}$ , $C_{kh}$ 和 $C_{kv}$ 分别为压缩指数,水平向渗透指数和竖向渗透指数。

1.2 控制方程的建立

基于以上假设,可得到竖井地基的固结方程,方程整体形式与Walker等^[41-43]建立的固结方程类似,区别是渗透系数和压缩系数不是固定值,如下式：

$\bar{u} = \frac{γ_{w} r_{e}^{2} μ}{2 k_{h}} [\frac{1}{γ_{w} H^{2}} \frac{\partial}{\partial Z} (k_{v} \frac{\partial \bar{u}}{\partial Z}) + \frac{\partial ε_{v}}{\partial t}]$ 。

(4)

式中 $\bar{u}$ , $γ_{w}$ , $r_{e}$ , $H$ 和 $ε_{v}$ 分别为平均超静孔隙水压力,水的重度,竖井影响半径,处理地基总深度和平均体积应变； $μ$ 为与涂抹效应和井阻效应相关的参数,具体取值根据涂抹区类型（水平渗透系数呈固定分段、线性、分段线性、抛物线等模式分布）,是否考虑井阻等因素有关,可参考文献[10,17]进行计算。 $Z$ 在本文中是一个归一化的深度,其为 $Z = z / H$ , $z$ 为实际空间深度。

基于假设（2）,可以得到

$\frac{\partial ε_{v}}{\partial t} = - \frac{1}{(1 + e_{0})} \frac{\partial \bar{e}}{\partial t} = m_{v0} \frac{\bar{{σ^{'}}_{0}}}{\bar{σ^{'}}} \frac{\partial \bar{σ^{'}}}{\partial t}$ ,

(5)

式中, $m_{v0}$ 为初始压缩系数, $m_{v0} =$ $\frac{C_{c}}{(1 + e_{0}) \ln 10 \bar{{σ^{'}}_{0}}}$ 。

结合有效应力原理和对数模型的非线性压缩渗透本构关系,控制方程变为

$\begin{array}{l} \frac{2 k_{h0}}{r_{e}^{2} γ_{w} m_{v0} μ} {(1 + \frac{q (t) - \bar{u}}{\bar{{σ^{'}}_{0}}})}^{- \frac{C_{c}}{C_{kh}} + 1} \bar{u} = (\frac{\partial q (t)}{\partial t} - \frac{\partial \bar{u}}{\partial t}) + \\ \frac{k_{v0}}{γ_{w} m_{v0} H^{2}} (1 + \frac{q (t) - \bar{u}}{\bar{{σ^{'}}_{0}}}) \frac{\partial}{\partial Z} [{(1 + \frac{q (t) - \bar{u}}{\bar{{σ^{'}}_{0}}})}^{- \frac{C_{c}}{C_{kv}}} \frac{\partial \bar{u}}{\partial Z}] \end{array}$ ,

(6)

式中, $q (t)$ 为在t时刻的荷载施加值。

2. 谱方法求解控制方程

基于谱方法,超静孔隙水压力可以表示为N级截断级数形式：

$\bar{u} (Z, t) \approx \sum_{j = 1}^{N} Φ_{j} (Z) A_{j} (t) = Φ A$ ,

(7)

对于基函数 $Φ_{j} (Z)$ 的选择需要满足边界条件,（a）当顶部底部两面排水时,边界条件为： $\bar{u} (0, t) = 0$ , $\bar{u} (1, t) = 0$ ；（b）当顶部排水,底部不排水时,边界条件为： $\bar{u} (0, t) = 0$ , $\partial \bar{u} (1, t) / \partial Z = 0$ 。因此基函数可选为 $Φ_{j} (Z) = s i n (M_{j} Z)$ 。其中：

$M_{j} = {\begin{array}{r} j π 双面排水 \\ \frac{π}{2} (2 j - 1) 单面排水 \end{array}$ 。

(8)

通过Galerkin-谱方法,其试函数与基函数一样,因此,控制方程式（6）变成矩阵的形式表达：

$Γ \frac{\partial A}{\partial t} + ΨA = θ$ 。

(9)

式中矩阵 $Γ$ 为单位对角矩阵；矩阵 $Ψ$ 与各个土层土性参数有关,其包含式（6）中的非线性参数；矩阵 $θ$ 是与各个土层附加应力分布和加载过程有关。为简化方程（9）并求得其近似解析解,本文参考文献[8,14]的方法,将式（6）中的两个随时间变化的变量 ${[(\bar{{σ^{'}}_{0}} + q (t) - \bar{u}) / \bar{{σ^{'}}_{0}}]}^{- \frac{C_{c}}{C_{k h}} + 1}$ 和 ${[(\bar{{σ^{'}}_{0}} + q (t) - \bar{u}) / \bar{{σ^{'}}_{0}}]}^{- \frac{C_{c}}{C_{k v}} + 1}$ 近似地取平均值替换为 $0.5 {[1 + ((\bar{{σ^{'}}_{0}} + q_{\max} - \bar{u}) / \bar{{σ^{'}}_{0}}])}^{- \frac{C_{c}}{C_{k h}} + 1}$ 和 $0.5 {[1 + ((\bar{{σ^{'}}_{0}} + q_{\max} - \bar{u}) / \bar{{σ^{'}}_{0}}])}^{- \frac{C_{c}}{C_{k v}} + 1}$ ,分别令这两个系数为 $P_{h}$ 和 $P_{v}$ ,其中 $q_{m a x}$ 为土体的最终施加的附加应力值。在式（9）中,矩阵元素的表达式为

$Γ_{i j} = {\begin{cases} 0 当 i \neq j \\ 1 当 i = j \end{cases}$ ,

(10)

$Ψ_{i j} = \sum_{l = 1}^{m} (d T_{h 0}^{l} P_{h}^{l} Λ^{-} + d T_{v 0}^{l} P_{v}^{l} M_{i} M_{j} Λ^{+})$ ,

(11)

$θ_{i} = \sum_{l = 1}^{m} [\frac{\partial q^{l} (t)}{\partial t} C S [M_{i}]]$ ,

(12)

式中,m为计算地基的土层总数,上标l代表在第l层土中对应的物理量,例如 $q^{l} (t)$ 代表在t时刻第l层土对应的附加应力值。符号 $d T_{h 0}^{}$ , $d T_{v 0}^{}$ , $Λ^{\pm}$ 和 $C S (M_{i})$ 是为了简化方程而定义的物理量,其具体表达详见附录A。则非齐次方程（9）的解析解为

$A (t) = vE (t) v^{- 1} A (0) +vE (t) {\int_{0}^{1} E (- τ) (Γv)}^{- 1} θ d τ$ ,

(13)

式中, $v$ 为矩阵 $Γ^{- 1} Ψ$ 的特征向量, $E (t)$ 为由 $Γ^{- 1} Ψ$ 的特征值 $λ_{i}$ （第i个特征值）定义的对角矩阵,其表达为： $E_{i i} = e x p (- λ_{i} t)$ 。 $A (0)$ 由初始条件决定。

当通过式（13）求得 $A (t)$ ,再结合式（7）,即可获得超静孔隙水压力沿着空间和时间分布的表达式。从固结计算过程中可看出,并由式（12）可以看出,该固结计算模型即可以考虑任意的附加应力分布,也可以考虑不同的加载模式（瞬间加载、单级加载、多级加载等）。在任意土层（第l层）深度范围内（在该层顶部深度 $Z^{l t}$ 和底部深度 $Z^{l b}$ 之间）的平均孔压和沉降计算分别为

${\bar{u}}_{a v g}^{l} (Z^{l b}, Z^{l t}, t) = \frac{\int_{Z^{l t}}^{Z^{l b}} Φ d Z}{Z^{l b} - Z^{l t}} A$ ,

(14)

$S (Z^{l b}, Z^{l t}, t) = \frac{C_{c}^{l} (Z^{l b} - Z^{l t})}{1 + {\bar{e}}_{0}^{l}} \lg (1 + \frac{q^{l} (t) - {\bar{u}}_{a v g}^{l}}{{\bar{{σ^{'}}_{0}}}^{l}})$ ,

(15)

式中,上标l同样如上述代表在第l层土中对应的物理量, $Z^{l b}$ 和 $Z^{l t}$ 分别代表在第l层底部和顶部的深度坐标。

3. 退化验证

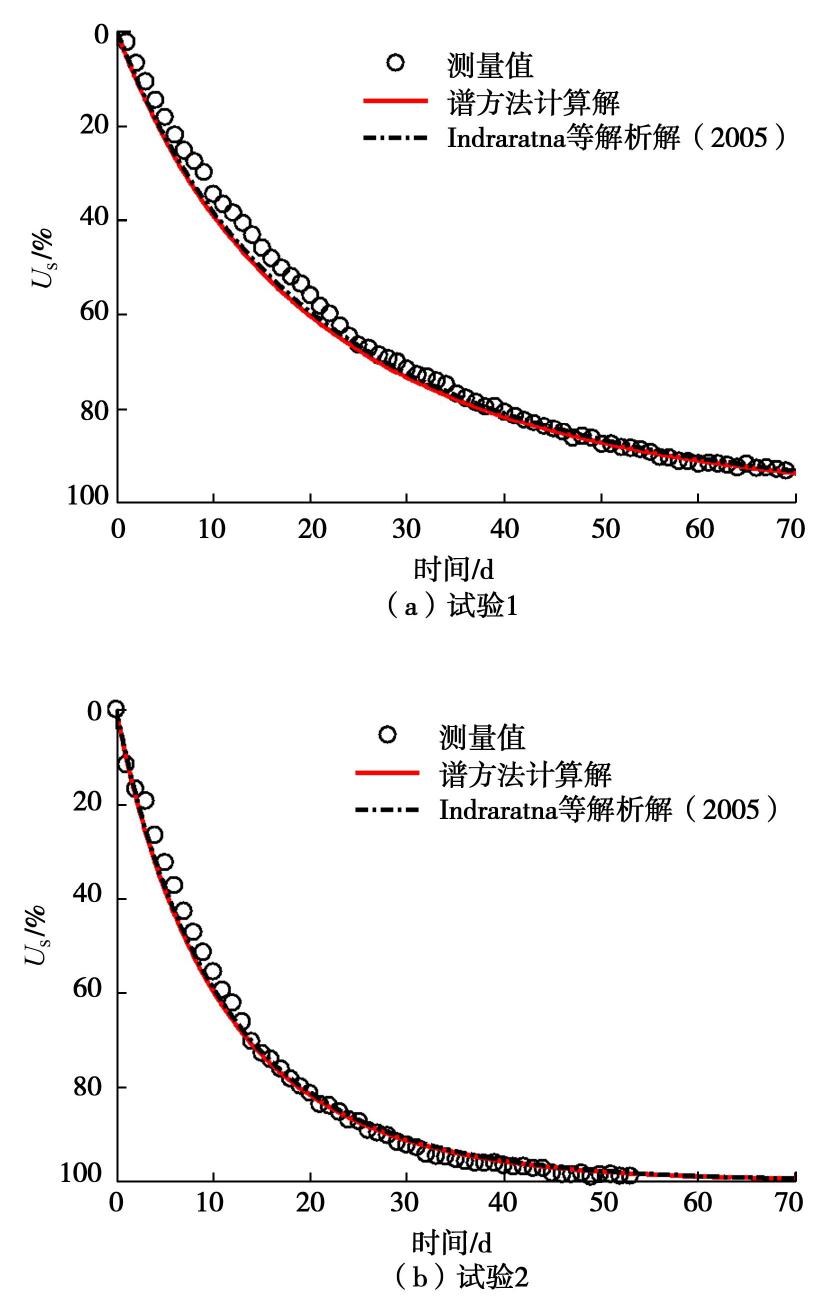
Indraratna等^[8]通过两组塑料排水板加固土体的缩尺室内模型试验,得到了土体的非线性对数关系模型（e-lgσ'和e-lgk）,并结合实测沉降值,计算得到土体的平均固结度。为了验证本计算模型的正确性,本文与Indraratna等^[8]开展的室内试验和非线性径向固结解析解进行对比。当不考虑本文中的固结模型中的竖向排水时,即竖向渗透系数假设为0 m/s,本模型退化为非线性径向固结模型,模型验证参数参考Indraratna等^[8],如表1所示。本验证中的室内试验由于土层单一且厚度不大（小于1 m）,因此假设为单一土层且附加应力延深度不变等于上覆荷载大小。截断级数N的选取取决于对问题计算精度的要求,N值越大精度越高。在使用谱方法时函数的不光滑性和不连续性会导致Gibbs现象（即出现振荡）,可通过增大N值来减少和消除Gibbs现象的影响并提高计算精度。本验证计算中N取50, $μ$ 的计算参考Indraratna等^[8]的处理方法,涂抹区的分布模式采用Hansbo的固定值分段模型,并忽略井阻效应,计算如下式：

$μ = \ln (n) + \frac{k_{h}}{k_{s}} \ln (s) - 0.75$ 。

(16)

表 1 模型验证参数表

Table 1. Parameters used in verification

参数	试验1	试验2
C_c	0.29	0.29
C_kh	0.45	0.45
影响直径D_e/m	0.45	0.45
等效排水直径D_w/m	0.066	0.066
涂抹区直径D_s/m	0.2	0.2
初始水平向渗透系数k_h0/(10^-10m·s^-1)	4.4	4.0
k_h/k_s	1.5	1.5
初始孔隙比e₀	1.000	0.950
初始高度H/m	0.925	0.870
初始应力 ${σ^{'}}_{0}$ /kPa	20	50
外加荷载p/kPa	30	50

下载: 导出CSV

| 显示表格

计算结果如图1所示,由图可知根据本文固结计算模型所得解十分接近试验测量值,两组试验的平均相对误差低于2.0%。同时本文所得解与Indraratna等^[8]的解析解对比几乎一致,与解析解的平均相对误差低于0.7%。结合实测数据与解析解对比验证了本文固结模型的适用性和合理性。由以上退化验证可知,当只考虑径向排水而忽略竖向排水时,本文模型与Indraratna等的径向固结解析解基本吻合。当需要考虑竖向排水时,本文模型无需采用Carrillo定理,且由于耦合竖向和径向渗流的非线性,因此在实际工程中具有更广泛的应用性。

图 1 退化验证结果对比

Figure 1. Comparison for verification results

下载: 全尺寸图片幻灯片

4. 现场案例分析

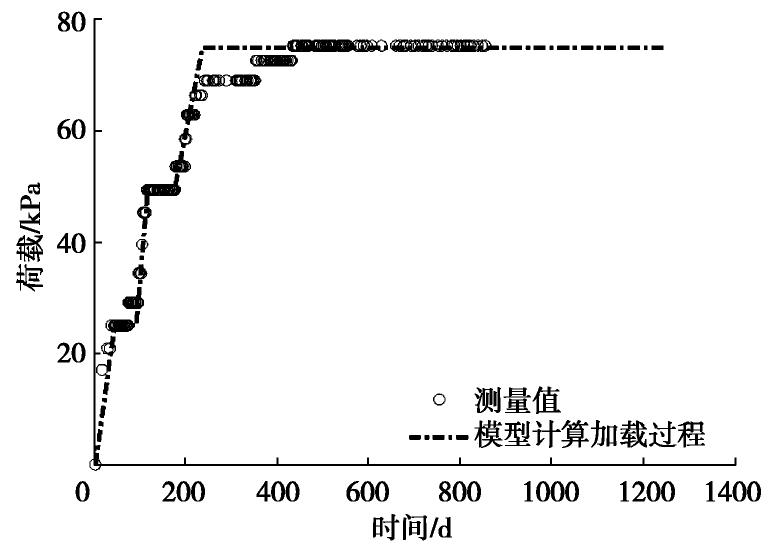
经过上一部分的退化验证确定了模型的适用性,下面将对一具体工程案例进行模型应用分析。现场案例依托杭州湾某高速公路堆载预压试验段项目。试验段场地地表分布有厚度为2.0 m左右的褐黄色及灰黄色亚黏土,为相对硬壳层；其下为厚度约7.5 m的淤泥质亚砂土,该层具有水平层理；往下为厚度为20.1 m左右的淤泥质亚黏土,该层含水率偏高,孔隙比大,强度低,压缩性高,为主要压缩层；再往下为厚度约10.4 m的细砂、粉砂层。根据室内试验测定的各土层固结状态,该项目在地表以下2.0 m范围内土体平均超固结比为7.4,往下10.0 m范围内土体平均超固结比为2.4,再往下20.0 m范围内土体平均超固结比为0.91。因此在本文的计算中,在深度12.0 m以上土体的压缩参数选择再压缩指数,12.0 m以下的土体压缩参数选择压缩指数。试验段排水系统由水平排水层和竖向排水通道组成,水平排水层采用50 cm砂砾垫层,竖向排水通道选用板宽为100 mm的SPB-C型塑料排水板,打设深度为30.0 m,塑料排水板间距为1.2 m,正三角形布置^[1]。根据Lee等^[46]的研究,涂抹区的直径大约为2.6～3.68倍的等效排水直径,因此本案例分析中涂抹区直径假设为等效排水直径的3倍。与排水板相关的参数如表2所示,在现场案例分析中,由于现场所用的排水板的设计通水量较大为65 cm³/s,因此忽略井阻效应,涂抹区的分布模式采用固定值分段模型,计算参考式（16）。各个土层的土性参数如表3所示,工程加载过程如图2,在本文模型计算中简化为三段线性加载。其中现场案例分析中附加应力的分布依据弹性理论中矩形基底受竖直均布荷载和竖直三角形荷载作用求得的附加应力系数叠加所得,各个土层的附加应力系数如表3所示。

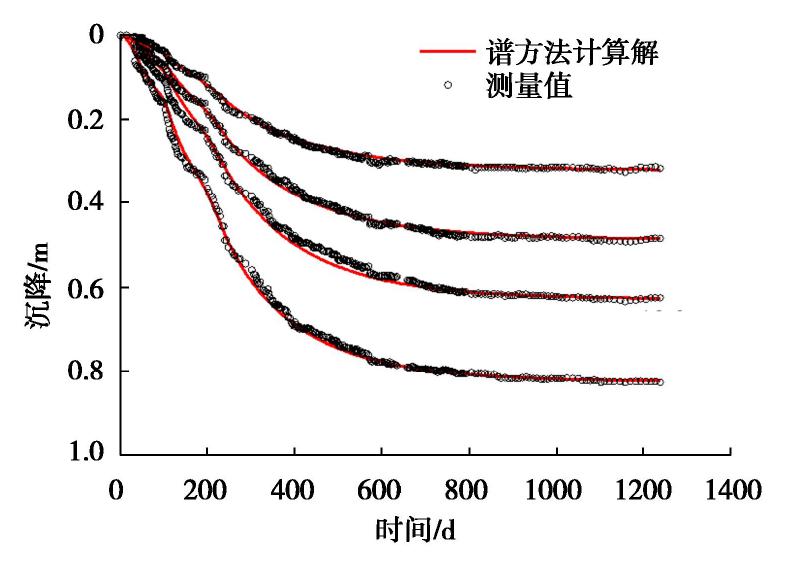
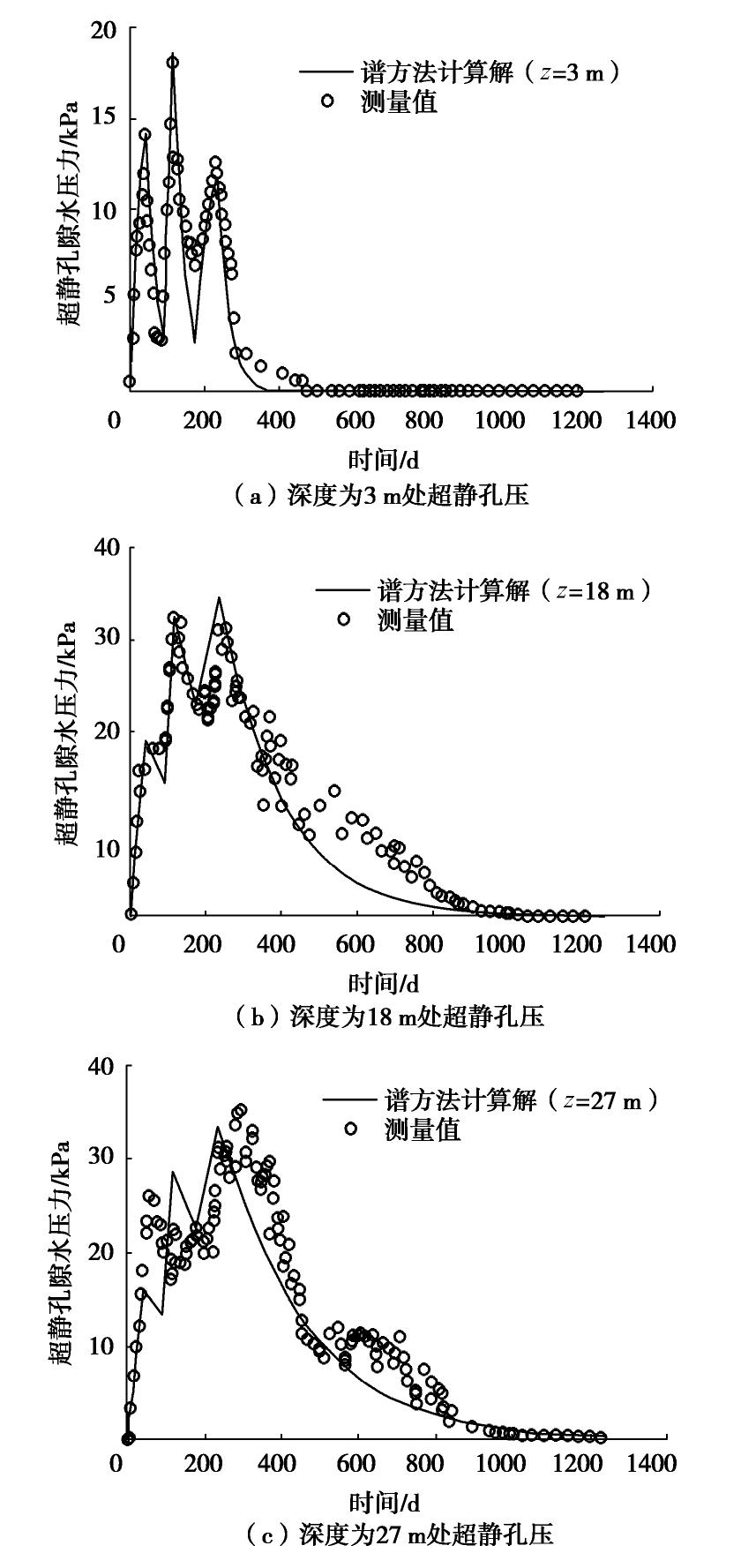
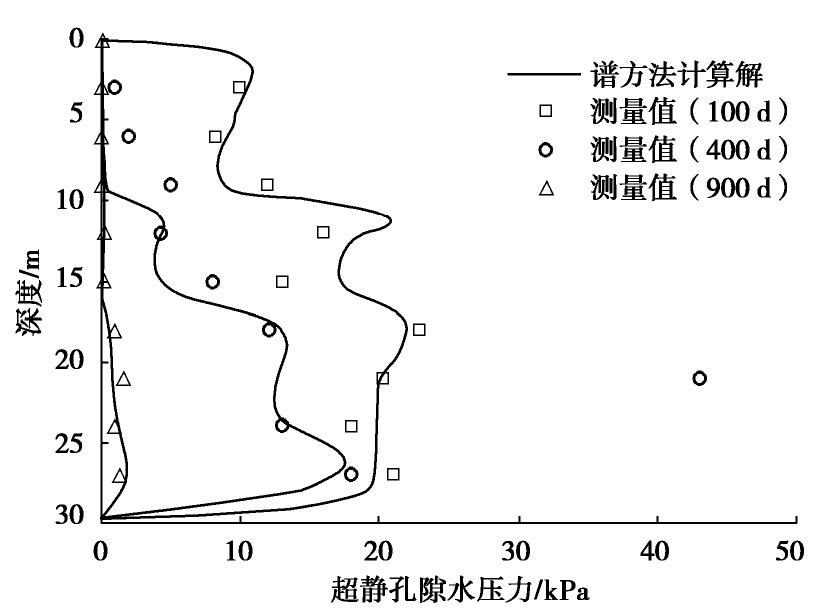
表 2 排水参数表

Table 2. Parameters of drain properties

影响直径 $D_{e}$ /m	等效排水直径 $D_{w}$ /m	涂抹区直径 $D_{s}$ /m	$k_{h} / k_{s}$
1.26	0.067	0.2	5

下载: 导出CSV

| 显示表格

表 3 土性参数表

Table 3. Soil Parameters

深度/m	k_v0/(10^-9m·s^-1)	k_h0/(10^-9m·s^-1)	${σ^{'}}_{0}$ /kPa	$γ_{t}$ /(kN·m^-3)	e₀
0.0~2.0	6.21	6.64	9.40	19.4	0.796
2.0~3.0	3.21	3.60	22.90	18.2	1.098
3.0~6.0	3.21	3.60	39.30	18.2	1.098
6.0~8.5	3.21	3.60	61.85	18.2	1.098
8.5~9.5	3.21	3.60	76.20	18.2	1.098
9.5~12.0	0.69	0.93	90.30	18.0	1.193
12.0~16.0	0.69	0.93	116.30	18.0	1.193
16.0~20.0	0.69	0.93	148.30	18.0	1.193
20.0~24.5	0.69	0.93	182.30	18.0	1.193
24.5~29.6	1.16	1.50	222.74	18.8	1.193
深度/m	C_kv	C_kh	C_c	C_r	K_s
0.0~2.0	0.398	0.398	0.180	0.020	1.00
2.0~3.0	0.549	0.549	0.188	0.020	1.00
3.0~6.0	0.549	0.549	0.188	0.040	1.00
6.0~8.5	0.549	0.549	0.188	0.050	0.98
8.5~9.5	0.549	0.549	0.188	0.050	0.97
9.5~12.0	0.597	0.597	0.413	0.090	0.95
12.0~16.0	0.150	0.150	0.243	0.034	0.91
16.0~20.0	0.100	0.100	0.500	0.034	0.86
20.0~24.5	0.150	0.150	0.660	0.034	0.79
24.5~29.6	0.100	0.100	1.500	0.034	0.70
注：K_s为附加应力系数。

下载: 导出CSV

| 显示表格

图 2 加载过程

Figure 2. Loading process

下载: 全尺寸图片幻灯片

本案例分析中N取150,根据上述地质条件和施工参数,得到了在3个不同深度（z=12,20,24.5 m）的分层沉降和表面沉降、超静孔隙水压力在3个不同深度（z=3,18,27 m）的变化过程以及在3个不同时间段（t=100,500,900 d）延深度的剖面分布,结果分别如图3～5所示。由图3的沉降曲线可以看出,基于谱方法建立的层状竖井地基固结计算模型所得沉降曲线与实测沉降曲线吻合程度较好,4个位置的平均相对误差为0.6%,能够很好的反映在层状竖井地基在不同深度处的沉降发展过程。从图4的超静孔隙水压力变化曲线可知,现场实测数据在300 d以后存在波动以及略滞后于计算值的现象,分析原因现场实测数据可能受到地下水位,孔压传感器随土体发生沉降以及传感滞后等因素影响。但从整体孔压消散趋势上看,计算值与实测值拟合程度较好,能够反映实际超静孔压在加载过程变化过程和加载结束后的消散趋势。由图5超静孔隙水压力剖面图可以看出,在9.5 m以下深度的土体由于渗透系数较小,且与竖直排水面距离较远,孔隙水压力的消散速度明显慢于上部土体。其中在深度21 m处的实测孔压数据在400 d前一直处于较高水平,分析原因可能是孔压传感器传感滞后导致,因此导致在该深度处计算值与实测值偏差较大。从整体剖面分布上分析,本模型所得结果能够较好地反映不同时间超静孔隙水压力沿着深度的分布,说明了本文模型在层状竖井地基固结计算的可行性和适用性。

图 3 沉降曲线

Figure 3. Curves of settlement

下载: 全尺寸图片幻灯片

图 4 超静孔隙水压力曲线

Figure 4. Curves of excess pore water pressure

下载: 全尺寸图片幻灯片

图 5 超静孔隙水压力剖面图

Figure 5. Profile of excess pore water pressure

下载: 全尺寸图片幻灯片

5. 结论

本文结合对数模型的非线性压缩和渗透本构关系,基于谱方法建立了层状竖井地基的非线性固结计算模型,主要得出以下结论：

（1）基于谱方法建立了能够考虑层状地基土竖直和水平渗透系数、压缩模量随固结过程非线性变化的层状竖井地基的非线性固结计算模型。

（2）通过退化研究与Indraratna等^[8]非线性径向固结解析解及室内试验进行对比计算分析,验证了本文固结模型的合理性。

（3）根据本文模型对某一实际工程案例进行了应用固结计算分析,结果显示不同深度处的沉降和孔压计算值与实测数据吻合程度较好,能够反映在固结过程中沉降的发展和孔压的变化过程,进一步说明了本文模型在层状竖井地基固结计算的可行性和工程适用性。

附录A:

部分符号表示为

$\begin{array}{l} d T_{v0} = \frac{k_{v0}}{γ_{w} m_{v 0} H^{2}} & ， & d T_{h0} = \frac{2 k_{h 0}}{r_{e}^{2} γ_{w} m_{v0} μ} \end{array}$ ,

$S N [β] = [\sin (β Z^{1 b}) - \sin (β Z^{l t})] / β$ ,

$C S [β] = [\cos (β Z^{1 b}) - \cos (β Z^{l t})] / β$ ,

$M^{\pm} = M_{j} \pm M_{i}$ ,

$Λ^{\pm} = {\begin{array}{r} S N [M^{-}] \pm S N [M^{+}] i \neq j \\ [Z^{l b} - Z^{l t}] \pm S N [M^{+}] i = j \end{array}$ 。

图 1 退化验证结果对比

Figure 1. Comparison for verification results

下载: 全尺寸图片幻灯片

图 2 加载过程

Figure 2. Loading process

下载: 全尺寸图片幻灯片

图 3 沉降曲线

Figure 3. Curves of settlement

下载: 全尺寸图片幻灯片

图 4 超静孔隙水压力曲线

Figure 4. Curves of excess pore water pressure

下载: 全尺寸图片幻灯片

图 5 超静孔隙水压力剖面图

Figure 5. Profile of excess pore water pressure

下载: 全尺寸图片幻灯片

表 1 模型验证参数表

Table 1 Parameters used in verification

参数	试验1	试验2
C_c	0.29	0.29
C_kh	0.45	0.45
影响直径D_e/m	0.45	0.45
等效排水直径D_w/m	0.066	0.066
涂抹区直径D_s/m	0.2	0.2
初始水平向渗透系数k_h0/(10^-10m·s^-1)	4.4	4.0
k_h/k_s	1.5	1.5
初始孔隙比e₀	1.000	0.950
初始高度H/m	0.925	0.870
初始应力 ${σ^{'}}_{0}$ ${σ^{'}}_{0}$ /kPa	20	50
外加荷载p/kPa	30	50

下载: 导出CSV

表 2 排水参数表

Table 2 Parameters of drain properties

影响直径 $D_{e}$ $D_{e}$ /m	等效排水直径 $D_{w}$ $D_{w}$ /m	涂抹区直径 $D_{s}$ $D_{s}$ /m	$k_{h} / k_{s}$ $k_{h} / k_{s}$
1.26	0.067	0.2	5

下载: 导出CSV

表 3 土性参数表

Table 3 Soil Parameters

深度/m	k_v0/(10^-9m·s^-1)	k_h0/(10^-9m·s^-1)	${σ^{'}}_{0}$ ${σ^{'}}_{0}$ /kPa	$γ_{t}$ $γ_{t}$ /(kN·m^-3)	e₀
0.0~2.0	6.21	6.64	9.40	19.4	0.796
2.0~3.0	3.21	3.60	22.90	18.2	1.098
3.0~6.0	3.21	3.60	39.30	18.2	1.098
6.0~8.5	3.21	3.60	61.85	18.2	1.098
8.5~9.5	3.21	3.60	76.20	18.2	1.098
9.5~12.0	0.69	0.93	90.30	18.0	1.193
12.0~16.0	0.69	0.93	116.30	18.0	1.193
16.0~20.0	0.69	0.93	148.30	18.0	1.193
20.0~24.5	0.69	0.93	182.30	18.0	1.193
24.5~29.6	1.16	1.50	222.74	18.8	1.193
深度/m	C_kv	C_kh	C_c	C_r	K_s
0.0~2.0	0.398	0.398	0.180	0.020	1.00
2.0~3.0	0.549	0.549	0.188	0.020	1.00
3.0~6.0	0.549	0.549	0.188	0.040	1.00
6.0~8.5	0.549	0.549	0.188	0.050	0.98
8.5~9.5	0.549	0.549	0.188	0.050	0.97
9.5~12.0	0.597	0.597	0.413	0.090	0.95
12.0~16.0	0.150	0.150	0.243	0.034	0.91
16.0~20.0	0.100	0.100	0.500	0.034	0.86
20.0~24.5	0.150	0.150	0.660	0.034	0.79
24.5~29.6	0.100	0.100	1.500	0.034	0.70
注：K_s为附加应力系数。

下载: 导出CSV

参考文献(46)

[1]	娄炎, 何宁, 娄斌. 高速公路深厚软基工后沉降控制成套技术[M]. 北京: 人民交通出版社, 2011. LOU Yan, HE Ning, LOU Bin. Complete Set of Technology for Post-Construction Settlement Control of Expressway Deep Soft Foundation[M]. Beijing: China Communications Press, 2011. (in Chinese)
[2]	BARRON R A. Consolidation of fine-grained soils by drain wells[J]. Transactions of the American Society of Civil Engineers, 1948, 113: 718-742. doi: 10.1061/TACEAT.0006098
[3]	YOSHIKUNI H, NAKANODO H. Consolidation of soils by vertical drain wells with finite permeability[J]. Soils and Foundations, 1974, 14(2): 35-46. doi: 10.3208/sandf1972.14.2_35
[4]	HANSBO S. Consolidation of fine-grained soils by prefabricated drains[C]//Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering, 1981, Stockholm.
[5]	INDRARATNA B, REDANA I W. Plane strain modeling of smear effects associated with vertical drains[J]. Journal of Geotechnical Engineering, 1997, 123(5): 474-478. doi: 10.1061/(ASCE)1090-0241(1997)123:5(474)
[6]	TANG X W, ONITSUKA K. Consolidation by vertical drains under time-dependent loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(9): 739-751. doi: 10.1002/1096-9853(20000810)24:9<739::AID-NAG94>3.0.CO;2-B
[7]	ZHU G F, YIN J H. Consolidation analysis of soil with vertical and horizontal drainage under ramp loading considering smear effects[J]. Geotextiles and Geomembranes, 2004, 22(1/2): 63-74. http://www.sciencedirect.com/science/article/pii/S0266114403000529
[8]	INDRARATNA B, RUJIKIATKAMJORN C, SATHANANTHAN L. Radial consolidation of clay using compressibility indices and varying horizontal permeability[J]. Canadian Geotechnical Journal, 2005, 42(5): 1330-1341. doi: 10.1139/t05-052
[9]	INDRARATNA B, RUJIKIATKAMJORN C, SATHANANTHAN I. Analytical and numerical solutions for a single vertical drain including the effects of vacuum preloading[J]. Canadian Geotechnical Journal, 2005, 42: 994-1014. doi: 10.1139/t05-029
[10]	WALKER R, INDRARATNA B. Vertical drain consolidation with parabolic distribution of permeability in smear zone[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(7): 937-941. doi: 10.1061/(ASCE)1090-0241(2006)132:7(937)
[11]	DENG Y B, XIE K H, LU M M. Consolidation by vertical drains when the discharge capacity varies with depth and time[J]. Computers and Geotechnics, 2013, 48: 1-8. doi: 10.1016/j.compgeo.2012.09.012
[12]	LEI G H, ZHENG Q, NG C W W, et al. An analytical solution for consolidation with vertical drains under multi-ramp loading[J]. Géotechnique, 2015, 65(7): 531-541. doi: 10.1680/geot.13.P.196
[13]	XU B H, INDRARATNA B, TRUNG T, et al. A vertical and radial consolidation analysis incorporating drain degradation based on the spectral method[J]. Computers and Geotechnics, Elsevier Ltd, 2021, 129: 103862. doi: 10.1016/j.compgeo.2020.103862
[14]	LEKHA K R, KRISHNASWAMY N R, BASAK P. Consolidation of clays for variable permeability and compressibility[J]. Journal of Geotechnical and Geo- environmental Engineering, 2003, 129(11): 1001-1009. doi: 10.1061/(ASCE)1090-0241(2003)129:11(1001)
[15]	卢萌盟, 谢康和, 王玉林, 等. 碎石桩复合地基非线性固结解析解[J]. 岩石力学, 2010, 31(6): 1833-1840. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ202105007.htm LU Meng-meng, XIE Kang-he, WANG Yu-lin, et al. Analytical solution for nonlinear consolidation of stone column reinforced composite ground[J]. Rock and Soil Mechanics, 2010, 31(6): 1833-1840. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ202105007.htm
[16]	郭霄, 谢康和, 卢萌盟, 等. 直排式真空预压法下竖井地基的非线性固结解析解[J]. 中南大学学报(自然科学版), 2015, 46(2): 384-392. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201802017.htm GUO Xiao, XIE Kang-he, LU Meng-meng, et al. Nonlinear analytical solution for consolidation of vertical drains by straight-line vacuum preloading method[J]. Journal of Central South University (Science and Technology), 2015, 46(2): 384-392. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201802017.htm
[17]	WALKER R, INDRARATNA B, RUJIKIATKAMJORN C. Vertical drain consolidation with non-Darcian flow and void-ratio dependent compressibility and permeability[J]. Géotechnique, 2012, 62(11): 985-997. doi: 10.1680/geot.10.P.084
[18]	LU M, WANG S, SLOAN S W, et al. Nonlinear radial consolidation of vertical drains under a general time-variable loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39: 51-62. doi: 10.1002/nag.2295
[19]	田乙, 吴文兵, 康成, 等. 基于椭圆柱等效的排水板非线性径向固结理论[J]. 岩石力学与工程学报, 2020, 39(增刊1): 3058-3066. doi: 10.13722/j.cnki.jrme.2019.0218 TIAN Yi, WU Wen-bing, KANG Cheng, et al. Nonlinear radial consolidation theory for prefabricated vertical drain based on the equivalent elliptical cylinder model[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(S1): 3058-3066. (in Chinese) doi: 10.13722/j.cnki.jrme.2019.0218
[20]	江文豪, 詹良通. 考虑井阻随时间变化下砂井地基的非线性固结解[J]. 岩石力学与工程学报, 2021, 40(1): 187-195. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101017.htm JIANG Wen-hao, ZHAN Liang-tong. Analytical solution for nonlinear consolidation of sand-drained ground considering time-dependent well resistance[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(1): 187-195. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101017.htm
[21]	LEE D, AN Y, KWAK T, et al. Nonlinear finite-strain self-weight consolidation of dredged material with radial drainage using carrillo’s formula[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2016, 142(6): 06016002. doi: 10.1061/(ASCE)WW.1943-5460.0000351
[22]	高广运, 聂春晓, 张海丘, 等. 塑料排水板结合真空预压法的径向固结解析解[J]. 同济大学学报(自然科学版), 2017, 45(9): 1290-1297. doi: 10.11908/j.issn.0253-374x.2017.09.006 GAO Guang-yun, NIE Chun-xiao, ZHANG Hai-qiu, et al. Radial consolidation solution of plastic wick drain combined vacuum preloading[J]. Journal of Tongji University (Natural Science), 2017, 45(9): 1290-1297. (in Chinese) doi: 10.11908/j.issn.0253-374x.2017.09.006
[23]	黄朝煊. 塑料排水板处理地基非线性固结计算研究[J]. 岩土力学, 2019, 40(12): 4819-4827. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912031.htm HUANG Chao-xuan. Research on nonlinear consolidation calculation of foundation treated with prefabricated vertical drains[J]. Rock and Soil Mechanics, 2019, 40(12): 4819-4827. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912031.htm
[24]	KIM P, KIM H S, KIM Y G, et al. Nonlinear radial consolidation analysis of soft soil with vertical drains under cyclic loadings[J]. Shock and Vibration, 2020: 8810973.
[25]	江文豪, 詹良通. 真空联合堆载预压下基于指数形式渗流的砂井地基非线性固结解[J]. 工程力学, 2021, 38(2): 69-76, 133. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202102010.htm JIANG Wen-hao, ZHAN Liang-tong. Analytical solution for nonlinear consolidation of sand-drained ground with exponential flow under vacuum combined surcharge preloading[J]. Engineering Mechanics, 2021, 38(2): 69-76, 133. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202102010.htm
[26]	ZHANG Y, WU W, MEI G, et al. Three-dimensional consolidation theory of vertical drain based on continuous drainage boundary[J]. Journal of Civil Engineering and Management, 2019, 25(2): 145-155.
[27]	LU M, WANG S, SLOAN S W, et al. Nonlinear consolidation of vertical drains with coupled radial-vertical flow considering well resistance[J]. Geotextiles and Geomembranes, Elsevier Ltd, 2015, 43(2): 182-189.
[28]	LIU S, GENG X, SUN H, et al. Nonlinear consolidation of vertical drains with coupled radial-vertical flow considering time and depth dependent vacuum pressure[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(4): 767-780.
[29]	WANG L, HUANG P, LIU S, et al. Analytical solution for nonlinear consolidation of combined electroosmosis-vacuum -surcharge preloading[J]. Computers and Geotechnics, 2020, 121: 103484.
[30]	黄鹏华, 王柳江, 刘斯宏, 等. 真空堆载预压联合电渗竖向排水地基非线性固结解析解[J]. 岩石力学与工程学报, 2021, 40(1): 206-216. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101019.htm HUANG Peng-hua, WANG Liu-jiang, LIU Si-hong, et al. Nonlinear analytical solutions for vertical drainage consolidation of foundations under vacuum-surcharge preloading combined with electroosmosis[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(1): 206-216. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101019.htm
[31]	TANG X W, ONITSUKA K. Consolidation of double-layered ground with vertical drains[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(14): 1449-1465.
[32]	TANG X W, NIU B, CHENG G C, et al. Closed-form solution for consolidation of three-layer soil with a vertical drain system[J]. Geotextiles and Geomembranes, 2013, 36: 81-91.
[33]	NOGAMI T, LI M. Consolidation of clay with a system of vertical and horizontal drains[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(9): 838-848.
[34]	ZHOU W H, LOK T M H, ZHAO L S, et al. Analytical solutions to the axisymmetric consolidation of a multi-layer soil system under surcharge combined with vacuum preloading[J]. Geotextiles and Geomembranes, Elsevier Ltd, 2017, 45(5): 487-498.
[35]	LIU J C, LEI G H, ZHENG M X. General solutions for consolidation of multilayered soil with a vertical drain system[J]. Geotextiles and Geomembranes, 2014, 42(3): 267-276.
[36]	GENG X, YU H-S. A large-strain radial consolidation theory for soft clays improved by vertical drains[J]. Géotechnique, 2017, 67(11): 1020-1028.
[37]	蒲诃夫, 李展毅, 宋丁豹, 等. 半透水边界下土体大变形非线性固结模型[J]. 华中科技大学报(自然科学版), 2019, 47(9): 107-112. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201909019.htm PU He-fu, LI Zhan-yi, SONG Ding-bao. Large-strain nonlinear consolidation model for soil layer with impeded drainage boundaries[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(9): 107-112. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201909019.htm
[38]	杨鹏, 蒲诃夫, 郑俊杰, 等. 真空-堆载联合预压下竖井地基大变形非线性固结模型[J]. 岩石力学与工程学报, 2019, 38(10): 2103-2111. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910016.htm YANG Peng, PU He-fu, ZHENG Jun-jie. A large-strain nonlinear consolidation model of saturated soft soils stabilized by the vacuum-surcharge combined preloading method[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(10): 2103-2111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910016.htm
[39]	BOYD J P. Chebyshev and Fourier Spectral Methods[M]. New York: Dover, 2000.
[40]	TREFETHEN L N. Spectral Methods in MATLAB[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2000.
[41]	WALKER R, INDRARATNA B, SIVAKUGAN N. Vertical and radial consolidation analysis of multilayered soil using the spectral method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(5): 657-663.
[42]	WALKER R, INDRARATNA B. Consolidation analysis of a stratified soil with vertical and horizontal drainage using the spectral method[J]. Géotechnique, 2009, 59(5): 439-449.
[43]	WALKER R T R, INDRARATNA B. Application of spectral Galerkin method for multilayer consolidation of soft soils stabilised by vertical drains or stone columns[J]. Computers and Geotechnics, Elsevier Ltd, 2015, 69: 529-539.
[44]	DAS M B. Advance Soil Mechanics[M]. 3rd ed. New York: Taylor & Francis, 2008.
[45]	TAVENAS F, JEAN P, LEBLOND P, et al. Permeability of natural soft clays: part ii permeability characteristics: reply[J]. Canadian Geotechnical Journal, 1984, 21(4): 731-732.
[46]	LEE N K, CHUNG S G. Reevaluation of the factors influencing the consolidation of ground by incorporating prefabricated vertical drains[J]. KSCE, Journal of Civil Engineering, 2010, 14(2): 155-164.