基于谱方法的层状竖井地基非线性固结计算模型

许滨华; 何宁; 周彦章; 张中流

doi:10.11779/CJGE202110003

基于谱方法的层状竖井地基非线性固结计算模型 English Version

许滨华^{1, 2,},
何宁^{1, 3, ,},
周彦章¹,
张中流¹

1.
南京水利科学研究院岩土工程研究所,江苏　南京　210024
2.
河海大学土木与交通学院,江苏　南京　210098
3.
水利部水库大坝安全重点实验室,江苏　南京　210029

基金项目:

国家重点研发计划项目 2018YFC1508505

国家自然科学基金面上项目 51379131

详细信息

作者简介:
许滨华(1991— ),男,博士研究生,主要从事软土地基处理和固结计算方面的研究。E-mail：317413076@qq.com

通讯作者:
何宁, E-mail：nhe@nhri.com

中图分类号: TU431
计量
- 文章访问数: 245
- HTML全文浏览量: 43
- PDF下载量: 250
出版历程
- 收稿日期: 2021-02-09
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-09-30

Nonlinear consolidation model for stratified soils with vertical drains based on spectral method

XU Bin-hua^{1, 2,},
HE Ning^{1, 3, ,},
ZHOU Yan-zhang¹,
ZHANG Zhong-liu¹

1.
Department of Geotechnical Engineering, Nanjing Hydraulic Research Institute, Nanjing 210024, China
2.
College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China
3.
Key Laboratory of Reservoir and Dam Safety, Ministry of Water Resources, Nanjing 210029, China

摘要

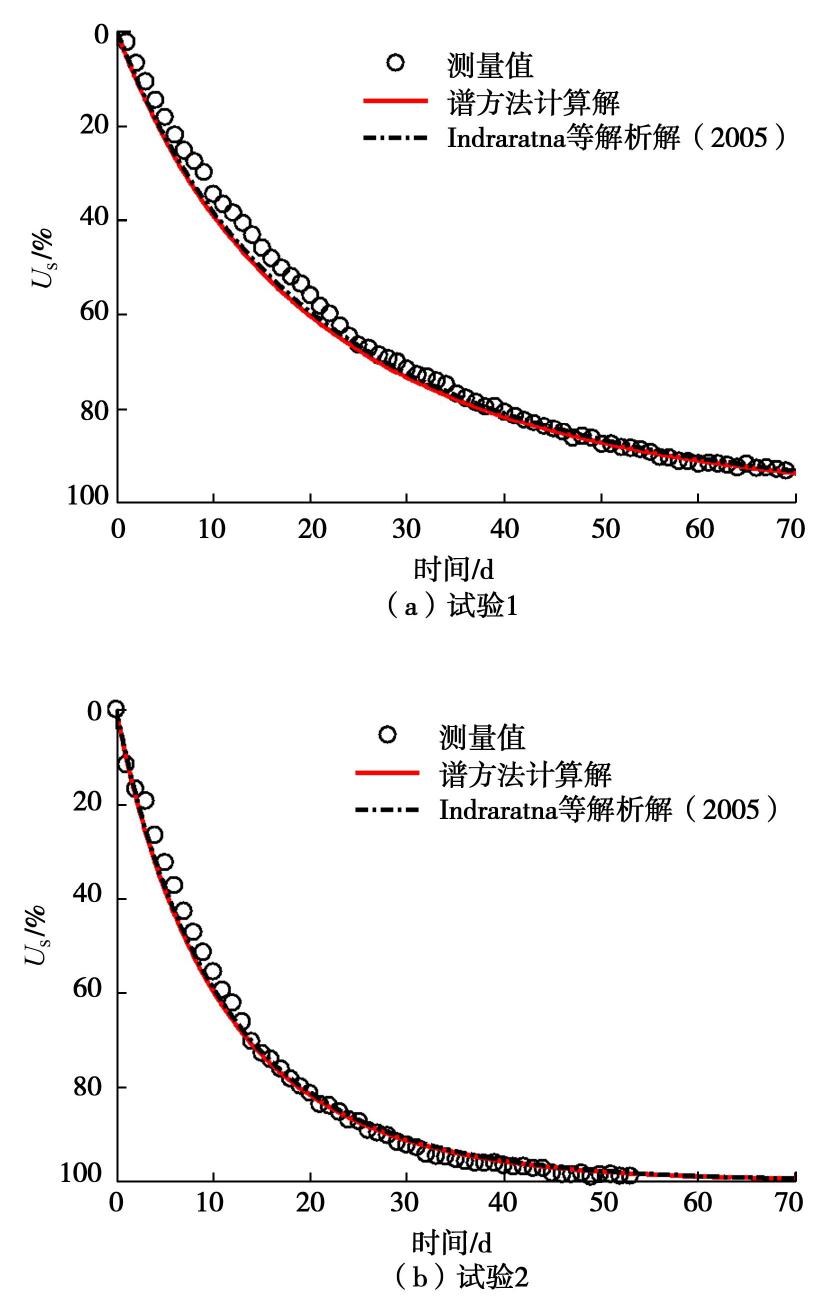
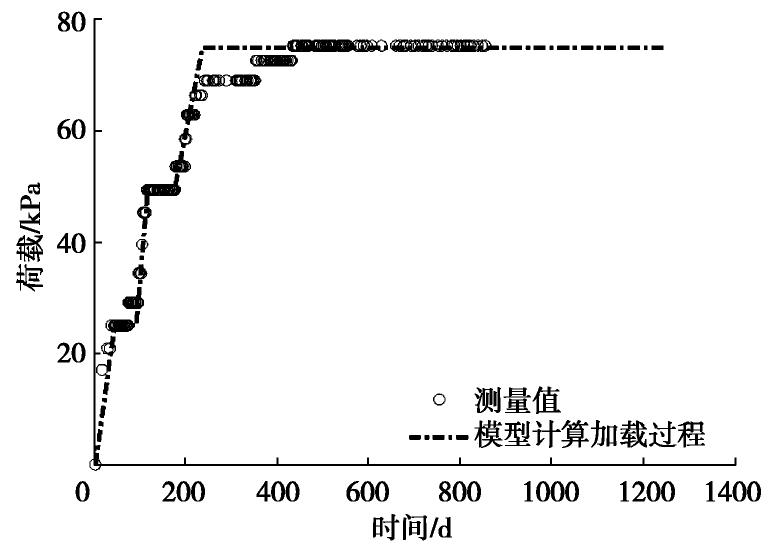
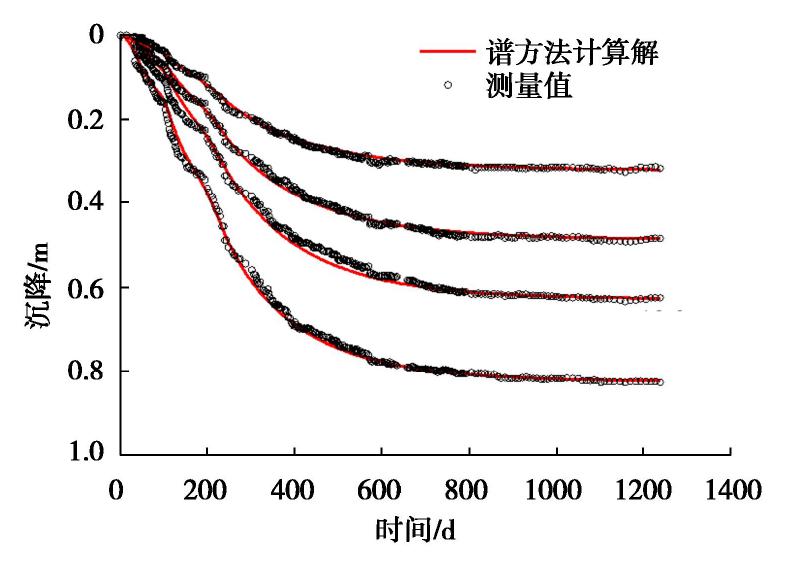
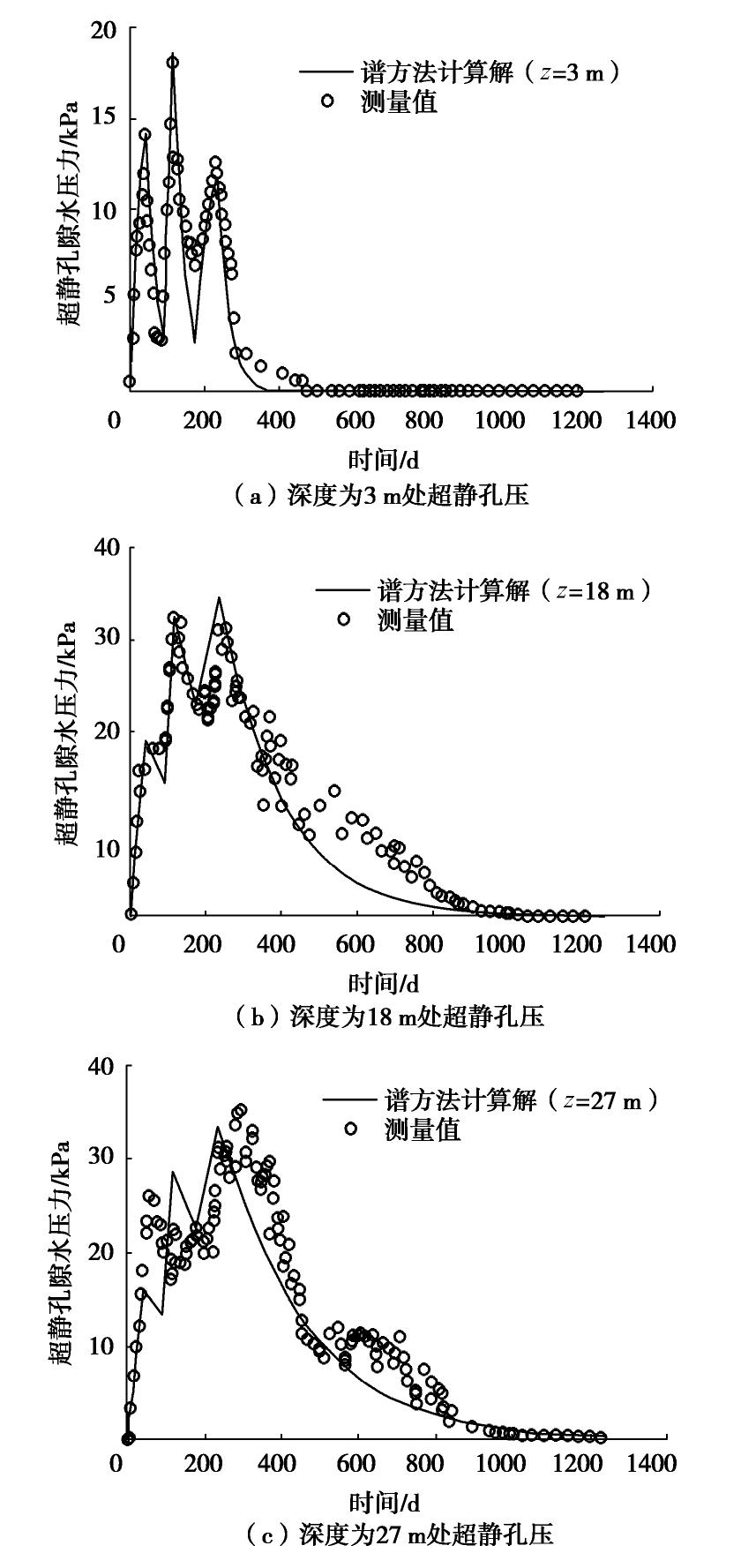
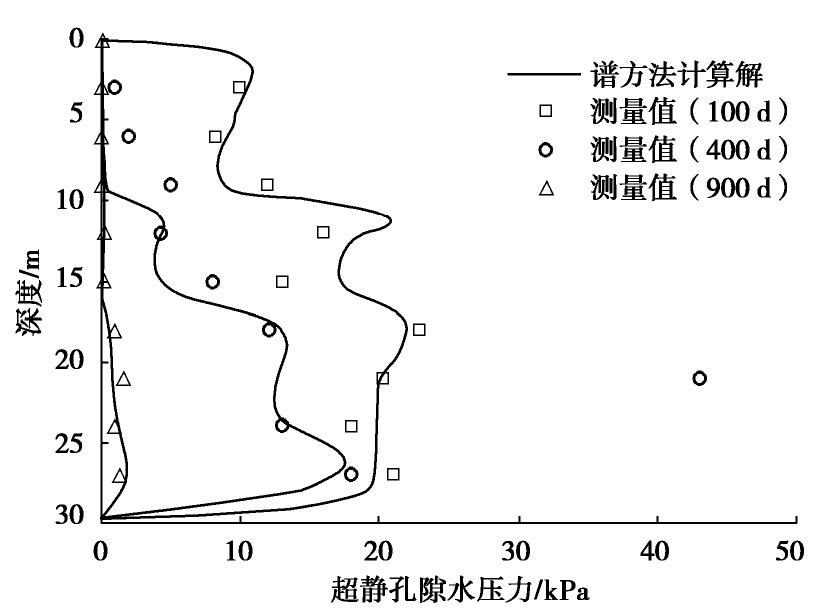
摘要: 针对实际工程中很多竖井地基呈现层状,且在固结过程中渗透系数和压缩模量呈非线性变化等特性,基于对数模型（e-lgσ'和e-lgk）的非线性压缩渗透本构关系,建立了能同时考虑竖向和径向排水的非线性固结模型,并采用谱方法得到了层状竖井地基的非线性固结计算模型。通过退化研究与已有的非线性固结解析解和室内试验进行对比计算分析,结果显示本模型计算值与解析解和实测值的平均相对误差分别低于0.7%和2.0%,验证了本模型的合理性。最后对某一实际工程案例进行了应用计算分析,结果显示不同深度处的沉降和孔压计算值与实测数据吻合程度较好,能够反映在固结过程中不同土层中沉降和孔压的发展变化过程,进一步说明了本模型在层状竖井地基固结计算的可行性和工程适用性。
- 层状地基 /
- 竖井 /
- 非线性固结 /
- 谱方法
Abstract: Many soft soil foundations with vertical drains are stratified, and the permeability and compressibility of soils change nonlinearly during the consolidation process. A nonlinear consolidation model that can consider both vertical and radial drainage is proposed based on the void-ratio dependent compressibility and permeability (e-lgσ' and e-lgk), and a nonlinear consolidation model for the stratified soils with vertical drains is obtained based on the spectral method. The validation of the solution is verified by the degradation study and the comparative analysis with the existing nonlinear consolidation analytical solutions and laboratory tests. The results show that the average relative error between the calculated value and the analytical solution and the measured value is lower than 0.7% and 2.0%, respectively. A field case is also studied and analyzed. The results show that the calculated values of settlement and pore pressure at different depths are in good agreement with the measured data, which can predict the development of settlement and the dissipation of pore pressure in different soil layers during the consolidation process. The case study further illustrates the feasibility and applicability of the proposed model in the consolidation calculation of stratified soils with vertical drains.
- stratified soil /
- vertical drain /
- nonlinear consolidation /
- spectral method

HTML全文

0. 引言

胶结砂砾石料是一种新型改良砂砾石材料,是在天然废弃石料、破碎石料或砂砾石料等材料中加入少量水泥、粉煤灰等胶凝剂形成的^[1-2]。该材料的组成与碾压混凝土基本相同,但与一般碾压混凝土相比,该材料胶凝掺量较小,其集料可就地取材,安全经济,且对环境负面影响较小,已成功在一些胶凝砂砾石坝或围堰建设或边坡、地基加固工程中得到应用^[2]。胶凝砂砾石坝正常运行时,尤其是泄水、蓄水时,其坝身某些部位经历卸载—再加载荷载作用。目前已有的胶结砂砾石料本构模型大多是依据一次加载的三轴试验结果建立的,基于这些模型得出的大坝应力、变形结果与该坝实际运行时的相应值存在一定差异。因此,用于工程筑坝的胶结砂砾石料本构模型有必要考虑其卸载—再加载特性的影响。

当前,国内外学者们已对一些岩土材料的卸载—再加载力学性能进行一番探究：文献[3～7]对黏土、砂土卸载—再加载力学特性进行了研究,发现这些土料均存在卸载体缩现象；文献[8, 9]对多种粗粒土进行了卸载—再加载三轴固结排水剪切试验,重点分析了该类材料在卸载—再加载条件下的强度、变形特性,发现该材料存在卸载体缩现象,其抗剪能力高于一次加载,认为回弹模量E_ur随应力水平的增加先增大后减小,但变化较小,随着围压的增加,该模量显著增大,此外,还给出了回弹模量与初始模量之比K_ur的取值范围。Zhou等^[10]通过开展不同次数卸载再加载条件下花岗岩风化土壤三轴试验研究,揭示了卸载—再加载路径对该材料强度特性、变形模量等力学特性的影响；杨贵等^[11]为了研究高聚物堆石料,采用中型三轴剪切仪对其进行回弹模量试验,分析高聚物堆石料卸载—再加载条件下的变形特性,并结合邓肯-张模型,揭示了回弹模量随围压与应力水平变化的规律；Xu等^[12]通过完成不同水分掺量条件下冻土三轴压缩和加载-卸载循环试验,探究了不同水分掺量对冻结黄土在受荷过程中的力学行为与破坏特征。与上述材料相比,虽然胶结砂砾石料静力三轴剪切试验研究已有一些报道^[13-16],但大多还是采用一次加载的试验条件开展的,对胶结砂砾石料静力卸载—再加载力学特性的研究甚少。仅笔者给出了胶结砂砾石料的卸载回弹模量,但对整个卸载—再加载曲线特征未进行系统分析^[17]。目前用于胶结砂砾石坝有限元计算的回弹模量^[18]一般直接引用砂、黏土或者堆石料的回弹模量与初始模量比值与初始模量的乘积,也可尝试直接采用高聚物堆石料的回弹模量,但这些材料与胶结砂砾石料的集料或胶凝剂存在明显区别,上述材料包括回弹模量在内的卸载—再加载特性是否适用于胶结砂砾石料还尚未可知。

基于此,本文采用大型三轴剪切仪对胶凝掺量100 kg/m³的胶结砂砾石料进行了卸载—再加载试验,并结合相应的一次加载试验结果^[16],重点分析胶结砂砾石料在卸载—再加载条件下的强度特性、卸载模量以及卸载体缩随围压与应力水平变化的规律。

1. 试验仪器、用料及试验方案

参照《胶结颗粒料筑坝技术导则》（SL678— 2014）^[19],此次三轴卸载—再加载试验中胶结砂砾石料采用与之前的胶结砂砾石料一次加载三轴试验^[15-16]试件同样的试验材料与配比,即胶凝剂采用海螺牌普通硅酸盐水泥,水胶比取1.0,胶凝掺量为100 kg/m³；细骨料为南京市场出售的中粗砂；粗骨料为南京郊区的破碎石料,级配如图1所示。

图 1 骨料配合比

Figure 1. Mixture ratios of aggregates

下载: 全尺寸图片幻灯片

三轴试验试件均采用直径300 mm,高700 mm的模具制成,制备过程：①依据骨料级配筛选骨料；②按胶结砂砾石料的材料组成与掺量将胶凝剂、粗细集料及水等材料混合并拌和均匀；③将胶结砂砾石料分5层装入圆筒模具,每层分别采用振动碾振实2 min,使试件成形；④试件养护龄期为28 d。在进行胶结砂砾石料三轴卸载—再加载试验之前,胶结砂砾石料试件需静置2～3 h,再借鉴高聚物堆石料的真空抽气饱和方法^[11]进行本试验试件的饱和,确保其试验过程中测试的饱和度达到95%以上。

胶结砂砾石料卸载—再加载三轴试验同样采用南京水利科学研究院岩土工程所的TYD-1500静动力三轴试验仪进行的,该仪器综合精度指数大于1%,最大围压为4 MPa,最大轴向载荷为1500 kN。

试验试件加载至设定的应力水平后开始卸载,待偏应力卸载至0,再重新加载至原方案设定的下一个应力水平,继续卸载。试验过程中采用的卸载、加载阶段剪切速率均为1 mm/min。试验围压 $σ_{3}$ 分别为300,600,900,1200 kPa,卸载点的应力水平s分别为0.25,0.65,0.80。

2. 试验结果与分析

2.1 应力-应变曲线特征分析

图2为胶凝掺量为100 kg/m³的胶结砂砾石料卸载—再加载三轴剪切试验应力-应变曲线,从图2中可看出：胶结砂砾石料的卸载阶段与其再加载阶段的曲线不能重合,形成了与粗粒土、天然黏土等材料形状^[7-9]略有不同的新月形滞回圈,这在该材料动力特性研究中已得到报道^[20],其主要原因为粗粒土、天然黏土等材料在卸载—再加载过程中仅出现塑性变形,而胶结砂砾石料除会发生塑性变形之外,其胶凝剂使该材料骨料颗粒之间存在一定的黏滞性；随着应力水平的增加,月牙形滞回圈形状基本不变,但尺寸逐渐变大,表明应力水平会在一定程度上影响胶结砂砾石料的黏滞性。

图 2 偏应力与轴向应变的关系

Figure 2. Relationship between deviatoric stress and axial strain

下载: 全尺寸图片幻灯片

为了探究卸载—再加载方式对峰值强度的影响,从图2的试验曲线中提取不同围压下的峰值强度,并结合一次加载试验的峰值强度值^[16],绘制出图3。从图3可看出：胶凝掺量为100 kg/m³的胶结砂砾石料峰值强度略高于单调加载的峰值强度；胶结砂砾石料峰值强度与围压的关系曲线为直线,其斜率与截距均略大于一次加载试验的相应斜率,表明卸载—再加载条件下胶结砂砾石料的内摩擦角与黏聚力均有所增加,但内摩擦角的改变较大,其主要原因可能是已发生胶结破损的骨料颗粒在卸载—再加载过程中会比一次加载试验发生更多地错动,试件的摩擦角度得到明显增加；胶结砂砾石料峰值强度与围压的关系可采用经典摩尔库伦准则表达式表示。

图 3 峰值强度与围压

$σ_{3}$ 的关系

Figure 3. Relationship between peak strength and confining pressure

下载: 全尺寸图片幻灯片

回弹模量是胶结砂砾石料三轴卸载—再加载过程中回弹特性的重要量化指标之一。它一般是指卸载—再加载时的轴向应力 $σ_{1}$ 和轴向应变 $ε_{1}$ 的增量比值,

）

$E_{ur} = Δ σ_{1} / Δ ε_{1} = Δ (σ_{1} - σ_{3} ） / Δ ε_{1}$ 。

(1)

在本次研究中,虽然胶结砂砾石料在卸载—再加载过程中出现与粗粒土不同的新月形滞回圈,但笔者仍以卸载点与再加载点连线的斜率作为胶结砂砾石料的回弹模量。

图4给出了不同应力水平与围压下胶凝掺量100 kg/m³的胶结砂砾石料回弹模量,从图4可看出：各围压下胶结砂砾石料回弹模量随应力水平的增加略有改变,且变幅不超过10%,参考其他岩土材料的回弹特性研究的报道^{[9, 11]},假定不同应力水平条件下胶结砂砾石料的回弹模量直接取平均值进行分析,结果见图5。从图5可看出,胶结砂砾石料的回弹模量随围压的增加而增大,但增幅减小,这也与堆石料、高聚物堆石料的回弹模量与围压的关系类似^{[9, 11]}。为了定量描述胶结砂砾石料回弹模量与围压的关系,笔者首先尝试采用邓肯-张模型常用的相应表达式,

$E_{ur} = K_{ur} p_{a} {(σ_{3} + p_{a})}^{n}$ ,

(2)

图 4 不同围压条件下回弹模量E_ur与应力水平的关系

Figure 4. Relationship between resilient modulus and stress level under different confining pressures

下载: 全尺寸图片幻灯片

图 5 回弹模量E_ur与围压的关系

Figure 5. Relationship between resilient modulus and confining pressure

下载: 全尺寸图片幻灯片

式中 $K_{ur}$ , $n_{ur}$ 为回弹模量参数, $p_{a}$ 为标准大气压。从图5中的拟合结果可看出,该式能很好地拟合其关系。然而在实际工程中,由于当 $σ_{3} = 0$ 时,胶结砂砾石料实际上仍是一个整体,不会松散,直接式（2）计算时,回弹模量为0,这与实际情况不符。为此,笔者认为胶结砂砾石料的回弹模量可借鉴之前提出的初始切线模量公式^[16],即

$E_{ur} = K_{ur} p_{a} {[(σ_{3} + p_{a}) / p_{a}]}^{n}$ 。

(3)

根据上述试验结果,整理出不同围压下应力水平对应的回弹模量平均值E_ur与单调加载初始模量E_i 的比值N,并点绘出 N 与围压 $σ_{3}$ 的关系,如图6所示。在图6中,不同围压下的N值变化很小,可直接取其平均值,在胶凝砂砾石坝实际工程中,胶凝掺量100 kg/m³的胶结砂砾石料回弹模量一般建议取初始弹性模量的1.5倍。

图 6 卸载回弹模量与初始模量之比N与围压的关系

Figure 6. Relationship between ratio of average of resilient modulus to initial modulus N and confining pressure

下载: 全尺寸图片幻灯片

2.2 体积应变

图7为胶凝掺量100 kg/m³的胶结砂砾石料在不同应力水平下的体积应变曲线,从图7可以看出：在卸载—再加载过程中,胶结砂砾石料加载阶段的体积应变—轴向应变曲线与一次加载相同^[16],即先增大后减小,表明胶结砂砾石料在加载条件下发生先剪缩后剪胀现象；当围压为300 kPa时,胶结砂砾石料发生卸载体胀现象,而围压高于600 kPa时,胶结砂砾石料在卸载时主要发生体缩现象,这是由于胶结物填充了颗粒间的孔隙,受围压的作用,破损的颗粒之间更加密实,摩擦力较大,颗粒很难翻越相邻颗粒完成重新排列,从而使试样卸载时更易出现体缩现象。不同围压条件下高聚物堆石料的卸载体胀、体缩机理也是如此。

图 7 体积应变与轴向应变的关系

Figure 7. Relationship between volumetric strain and axial strain

下载: 全尺寸图片幻灯片

为了进一步分析胶结砂砾石卸载体缩量随围压或应力水平的变化特征,假定卸载体缩 $ε_{v}$ 可为

$Δ ε_{v} = ε_{v2} - ε_{v1}$ ,

(4)

式中, $ε_{v2}$ , $ε_{v1}$ 分别对应于某一应力水平下卸载初始点与偏应力卸载至0时的体积应变。

根据上述公式,在不同的围压和应力水平下,卸荷后的体积收缩如图8所示（“-”为卸载体缩,“+”为卸载体胀）。从图8中可以看出,随着围压的增加,胶结砂砾石料卸载体胀逐渐变为卸载体缩,但同一围压下,应力水平的不同仅略微影响卸载时体积改变量。

图 8 体积改变量与应力水平的关系

Figure 8. Relationship between volumetric change and stress level

下载: 全尺寸图片幻灯片

3. 结论

对胶凝掺量100 kg/m³的胶结砂砾石料进行了3种应力水平下的胶结砂砾石料三轴卸载-再加载试验,系统分析了其卸载再加载力学特性,主要结论如下：

（1）在不同应力水平与围压下的胶结砂砾石料卸载再加载方式可在一定程度上提高其颗粒的内摩擦角,增加峰值强度。

（2）回弹模型随围压的增加明显增大,但受应力水平的影响较小,可直接取不同应力水平条件下的平均值；不同围压对回弹模量与初始模量的比值N影响较小,在实际胶凝砂砾石坝工程中,胶凝掺量100 kg/m³的胶结砂砾石料回弹模量约为初始模量的1.5倍。

（3）随着围压的增加,胶结砂砾石料卸载体胀逐渐变为卸载体缩,但应力水平对卸载体缩量或体胀量的影响较小。

以上结论可为胶凝砂砾石坝大坝或其它加固工程的数值计算提供重要的参考。

图 1 退化验证结果对比

Figure 1. Comparison for verification results

下载: 全尺寸图片幻灯片

图 2 加载过程

Figure 2. Loading process

下载: 全尺寸图片幻灯片

图 3 沉降曲线

Figure 3. Curves of settlement

下载: 全尺寸图片幻灯片

图 4 超静孔隙水压力曲线

Figure 4. Curves of excess pore water pressure

下载: 全尺寸图片幻灯片

图 5 超静孔隙水压力剖面图

Figure 5. Profile of excess pore water pressure

下载: 全尺寸图片幻灯片

表 1 模型验证参数表

Table 1 Parameters used in verification

参数	试验1	试验2
C_c	0.29	0.29
C_kh	0.45	0.45
影响直径D_e/m	0.45	0.45
等效排水直径D_w/m	0.066	0.066
涂抹区直径D_s/m	0.2	0.2
初始水平向渗透系数k_h0/(10^-10m·s^-1)	4.4	4.0
k_h/k_s	1.5	1.5
初始孔隙比e₀	1.000	0.950
初始高度H/m	0.925	0.870
初始应力 ${σ^{'}}_{0}$ /kPa	20	50
外加荷载p/kPa	30	50

下载: 导出CSV

表 2 排水参数表

Table 2 Parameters of drain properties

影响直径 $D_{e}$ /m	等效排水直径 $D_{w}$ /m	涂抹区直径 $D_{s}$ /m	$k_{h} / k_{s}$
1.26	0.067	0.2	5

下载: 导出CSV

表 3 土性参数表

Table 3 Soil Parameters

深度/m	k_v0/(10^-9m·s^-1)	k_h0/(10^-9m·s^-1)	${σ^{'}}_{0}$ /kPa	$γ_{t}$ /(kN·m^-3)	e₀
0.0~2.0	6.21	6.64	9.40	19.4	0.796
2.0~3.0	3.21	3.60	22.90	18.2	1.098
3.0~6.0	3.21	3.60	39.30	18.2	1.098
6.0~8.5	3.21	3.60	61.85	18.2	1.098
8.5~9.5	3.21	3.60	76.20	18.2	1.098
9.5~12.0	0.69	0.93	90.30	18.0	1.193
12.0~16.0	0.69	0.93	116.30	18.0	1.193
16.0~20.0	0.69	0.93	148.30	18.0	1.193
20.0~24.5	0.69	0.93	182.30	18.0	1.193
24.5~29.6	1.16	1.50	222.74	18.8	1.193
深度/m	C_kv	C_kh	C_c	C_r	K_s
0.0~2.0	0.398	0.398	0.180	0.020	1.00
2.0~3.0	0.549	0.549	0.188	0.020	1.00
3.0~6.0	0.549	0.549	0.188	0.040	1.00
6.0~8.5	0.549	0.549	0.188	0.050	0.98
8.5~9.5	0.549	0.549	0.188	0.050	0.97
9.5~12.0	0.597	0.597	0.413	0.090	0.95
12.0~16.0	0.150	0.150	0.243	0.034	0.91
16.0~20.0	0.100	0.100	0.500	0.034	0.86
20.0~24.5	0.150	0.150	0.660	0.034	0.79
24.5~29.6	0.100	0.100	1.500	0.034	0.70
注：K_s为附加应力系数。

下载: 导出CSV

参考文献(46)

[1]	娄炎, 何宁, 娄斌. 高速公路深厚软基工后沉降控制成套技术[M]. 北京: 人民交通出版社, 2011. LOU Yan, HE Ning, LOU Bin. Complete Set of Technology for Post-Construction Settlement Control of Expressway Deep Soft Foundation[M]. Beijing: China Communications Press, 2011. (in Chinese)
[2]	BARRON R A. Consolidation of fine-grained soils by drain wells[J]. Transactions of the American Society of Civil Engineers, 1948, 113: 718-742. doi: 10.1061/TACEAT.0006098
[3]	YOSHIKUNI H, NAKANODO H. Consolidation of soils by vertical drain wells with finite permeability[J]. Soils and Foundations, 1974, 14(2): 35-46. doi: 10.3208/sandf1972.14.2_35
[4]	HANSBO S. Consolidation of fine-grained soils by prefabricated drains[C]//Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering, 1981, Stockholm.
[5]	INDRARATNA B, REDANA I W. Plane strain modeling of smear effects associated with vertical drains[J]. Journal of Geotechnical Engineering, 1997, 123(5): 474-478. doi: 10.1061/(ASCE)1090-0241(1997)123:5(474)
[6]	TANG X W, ONITSUKA K. Consolidation by vertical drains under time-dependent loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(9): 739-751. doi: 10.1002/1096-9853(20000810)24:9<739::AID-NAG94>3.0.CO;2-B
[7]	ZHU G F, YIN J H. Consolidation analysis of soil with vertical and horizontal drainage under ramp loading considering smear effects[J]. Geotextiles and Geomembranes, 2004, 22(1/2): 63-74. http://www.sciencedirect.com/science/article/pii/S0266114403000529
[8]	INDRARATNA B, RUJIKIATKAMJORN C, SATHANANTHAN L. Radial consolidation of clay using compressibility indices and varying horizontal permeability[J]. Canadian Geotechnical Journal, 2005, 42(5): 1330-1341. doi: 10.1139/t05-052
[9]	INDRARATNA B, RUJIKIATKAMJORN C, SATHANANTHAN I. Analytical and numerical solutions for a single vertical drain including the effects of vacuum preloading[J]. Canadian Geotechnical Journal, 2005, 42: 994-1014. doi: 10.1139/t05-029
[10]	WALKER R, INDRARATNA B. Vertical drain consolidation with parabolic distribution of permeability in smear zone[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(7): 937-941. doi: 10.1061/(ASCE)1090-0241(2006)132:7(937)
[11]	DENG Y B, XIE K H, LU M M. Consolidation by vertical drains when the discharge capacity varies with depth and time[J]. Computers and Geotechnics, 2013, 48: 1-8. doi: 10.1016/j.compgeo.2012.09.012
[12]	LEI G H, ZHENG Q, NG C W W, et al. An analytical solution for consolidation with vertical drains under multi-ramp loading[J]. Géotechnique, 2015, 65(7): 531-541. doi: 10.1680/geot.13.P.196
[13]	XU B H, INDRARATNA B, TRUNG T, et al. A vertical and radial consolidation analysis incorporating drain degradation based on the spectral method[J]. Computers and Geotechnics, Elsevier Ltd, 2021, 129: 103862. doi: 10.1016/j.compgeo.2020.103862
[14]	LEKHA K R, KRISHNASWAMY N R, BASAK P. Consolidation of clays for variable permeability and compressibility[J]. Journal of Geotechnical and Geo- environmental Engineering, 2003, 129(11): 1001-1009. doi: 10.1061/(ASCE)1090-0241(2003)129:11(1001)
[15]	卢萌盟, 谢康和, 王玉林, 等. 碎石桩复合地基非线性固结解析解[J]. 岩石力学, 2010, 31(6): 1833-1840. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ202105007.htm LU Meng-meng, XIE Kang-he, WANG Yu-lin, et al. Analytical solution for nonlinear consolidation of stone column reinforced composite ground[J]. Rock and Soil Mechanics, 2010, 31(6): 1833-1840. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ202105007.htm
[16]	郭霄, 谢康和, 卢萌盟, 等. 直排式真空预压法下竖井地基的非线性固结解析解[J]. 中南大学学报(自然科学版), 2015, 46(2): 384-392. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201802017.htm GUO Xiao, XIE Kang-he, LU Meng-meng, et al. Nonlinear analytical solution for consolidation of vertical drains by straight-line vacuum preloading method[J]. Journal of Central South University (Science and Technology), 2015, 46(2): 384-392. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201802017.htm
[17]	WALKER R, INDRARATNA B, RUJIKIATKAMJORN C. Vertical drain consolidation with non-Darcian flow and void-ratio dependent compressibility and permeability[J]. Géotechnique, 2012, 62(11): 985-997. doi: 10.1680/geot.10.P.084
[18]	LU M, WANG S, SLOAN S W, et al. Nonlinear radial consolidation of vertical drains under a general time-variable loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39: 51-62. doi: 10.1002/nag.2295
[19]	田乙, 吴文兵, 康成, 等. 基于椭圆柱等效的排水板非线性径向固结理论[J]. 岩石力学与工程学报, 2020, 39(增刊1): 3058-3066. doi: 10.13722/j.cnki.jrme.2019.0218 TIAN Yi, WU Wen-bing, KANG Cheng, et al. Nonlinear radial consolidation theory for prefabricated vertical drain based on the equivalent elliptical cylinder model[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(S1): 3058-3066. (in Chinese) doi: 10.13722/j.cnki.jrme.2019.0218
[20]	江文豪, 詹良通. 考虑井阻随时间变化下砂井地基的非线性固结解[J]. 岩石力学与工程学报, 2021, 40(1): 187-195. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101017.htm JIANG Wen-hao, ZHAN Liang-tong. Analytical solution for nonlinear consolidation of sand-drained ground considering time-dependent well resistance[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(1): 187-195. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101017.htm
[21]	LEE D, AN Y, KWAK T, et al. Nonlinear finite-strain self-weight consolidation of dredged material with radial drainage using carrillo’s formula[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2016, 142(6): 06016002. doi: 10.1061/(ASCE)WW.1943-5460.0000351
[22]	高广运, 聂春晓, 张海丘, 等. 塑料排水板结合真空预压法的径向固结解析解[J]. 同济大学学报(自然科学版), 2017, 45(9): 1290-1297. doi: 10.11908/j.issn.0253-374x.2017.09.006 GAO Guang-yun, NIE Chun-xiao, ZHANG Hai-qiu, et al. Radial consolidation solution of plastic wick drain combined vacuum preloading[J]. Journal of Tongji University (Natural Science), 2017, 45(9): 1290-1297. (in Chinese) doi: 10.11908/j.issn.0253-374x.2017.09.006
[23]	黄朝煊. 塑料排水板处理地基非线性固结计算研究[J]. 岩土力学, 2019, 40(12): 4819-4827. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912031.htm HUANG Chao-xuan. Research on nonlinear consolidation calculation of foundation treated with prefabricated vertical drains[J]. Rock and Soil Mechanics, 2019, 40(12): 4819-4827. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912031.htm
[24]	KIM P, KIM H S, KIM Y G, et al. Nonlinear radial consolidation analysis of soft soil with vertical drains under cyclic loadings[J]. Shock and Vibration, 2020: 8810973.
[25]	江文豪, 詹良通. 真空联合堆载预压下基于指数形式渗流的砂井地基非线性固结解[J]. 工程力学, 2021, 38(2): 69-76, 133. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202102010.htm JIANG Wen-hao, ZHAN Liang-tong. Analytical solution for nonlinear consolidation of sand-drained ground with exponential flow under vacuum combined surcharge preloading[J]. Engineering Mechanics, 2021, 38(2): 69-76, 133. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202102010.htm
[26]	ZHANG Y, WU W, MEI G, et al. Three-dimensional consolidation theory of vertical drain based on continuous drainage boundary[J]. Journal of Civil Engineering and Management, 2019, 25(2): 145-155.
[27]	LU M, WANG S, SLOAN S W, et al. Nonlinear consolidation of vertical drains with coupled radial-vertical flow considering well resistance[J]. Geotextiles and Geomembranes, Elsevier Ltd, 2015, 43(2): 182-189.
[28]	LIU S, GENG X, SUN H, et al. Nonlinear consolidation of vertical drains with coupled radial-vertical flow considering time and depth dependent vacuum pressure[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(4): 767-780.
[29]	WANG L, HUANG P, LIU S, et al. Analytical solution for nonlinear consolidation of combined electroosmosis-vacuum -surcharge preloading[J]. Computers and Geotechnics, 2020, 121: 103484.
[30]	黄鹏华, 王柳江, 刘斯宏, 等. 真空堆载预压联合电渗竖向排水地基非线性固结解析解[J]. 岩石力学与工程学报, 2021, 40(1): 206-216. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101019.htm HUANG Peng-hua, WANG Liu-jiang, LIU Si-hong, et al. Nonlinear analytical solutions for vertical drainage consolidation of foundations under vacuum-surcharge preloading combined with electroosmosis[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(1): 206-216. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202101019.htm
[31]	TANG X W, ONITSUKA K. Consolidation of double-layered ground with vertical drains[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(14): 1449-1465.
[32]	TANG X W, NIU B, CHENG G C, et al. Closed-form solution for consolidation of three-layer soil with a vertical drain system[J]. Geotextiles and Geomembranes, 2013, 36: 81-91.
[33]	NOGAMI T, LI M. Consolidation of clay with a system of vertical and horizontal drains[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(9): 838-848.
[34]	ZHOU W H, LOK T M H, ZHAO L S, et al. Analytical solutions to the axisymmetric consolidation of a multi-layer soil system under surcharge combined with vacuum preloading[J]. Geotextiles and Geomembranes, Elsevier Ltd, 2017, 45(5): 487-498.
[35]	LIU J C, LEI G H, ZHENG M X. General solutions for consolidation of multilayered soil with a vertical drain system[J]. Geotextiles and Geomembranes, 2014, 42(3): 267-276.
[36]	GENG X, YU H-S. A large-strain radial consolidation theory for soft clays improved by vertical drains[J]. Géotechnique, 2017, 67(11): 1020-1028.
[37]	蒲诃夫, 李展毅, 宋丁豹, 等. 半透水边界下土体大变形非线性固结模型[J]. 华中科技大学报(自然科学版), 2019, 47(9): 107-112. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201909019.htm PU He-fu, LI Zhan-yi, SONG Ding-bao. Large-strain nonlinear consolidation model for soil layer with impeded drainage boundaries[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(9): 107-112. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201909019.htm
[38]	杨鹏, 蒲诃夫, 郑俊杰, 等. 真空-堆载联合预压下竖井地基大变形非线性固结模型[J]. 岩石力学与工程学报, 2019, 38(10): 2103-2111. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910016.htm YANG Peng, PU He-fu, ZHENG Jun-jie. A large-strain nonlinear consolidation model of saturated soft soils stabilized by the vacuum-surcharge combined preloading method[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(10): 2103-2111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910016.htm
[39]	BOYD J P. Chebyshev and Fourier Spectral Methods[M]. New York: Dover, 2000.
[40]	TREFETHEN L N. Spectral Methods in MATLAB[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2000.
[41]	WALKER R, INDRARATNA B, SIVAKUGAN N. Vertical and radial consolidation analysis of multilayered soil using the spectral method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(5): 657-663.
[42]	WALKER R, INDRARATNA B. Consolidation analysis of a stratified soil with vertical and horizontal drainage using the spectral method[J]. Géotechnique, 2009, 59(5): 439-449.
[43]	WALKER R T R, INDRARATNA B. Application of spectral Galerkin method for multilayer consolidation of soft soils stabilised by vertical drains or stone columns[J]. Computers and Geotechnics, Elsevier Ltd, 2015, 69: 529-539.
[44]	DAS M B. Advance Soil Mechanics[M]. 3rd ed. New York: Taylor & Francis, 2008.
[45]	TAVENAS F, JEAN P, LEBLOND P, et al. Permeability of natural soft clays: part ii permeability characteristics: reply[J]. Canadian Geotechnical Journal, 1984, 21(4): 731-732.
[46]	LEE N K, CHUNG S G. Reevaluation of the factors influencing the consolidation of ground by incorporating prefabricated vertical drains[J]. KSCE, Journal of Civil Engineering, 2010, 14(2): 155-164.

施引文献(83)

期刊类型引用(49)

1.	马昭，张明礼，段旭晗，赵博. 大断面浅埋隧道地表沉降Peck修正公式及其应用. 长江科学院院报. 2024(03): 118-125 . 百度学术
2.	杨明，杨志浩，王亚. 急曲线电力盾构隧道侧穿桥桩扰动特性研究. 建筑科学与工程学报. 2024(02): 124-133 . 百度学术
3.	刘彦良. 水下大直径盾构下穿施工对防汛大堤影响研究. 建筑机械. 2024(07): 142-146 . 百度学术
4.	王小龙，朱晶晶，叶明鸽，胡卓，伍浩良，覃小纲. 软土地层下穿开挖引发上覆电缆隧道挠曲变形分析. 应用基础与工程科学学报. 2024(04): 944-956 . 百度学术
5.	李济良，罗栋林，胡迪川. 高速铁路隧道下穿尾矿库开挖安全稳定研究. 交通科技. 2024(04): 103-109 . 百度学术
6.	邓超. 基于昆山软土地层隧道工程的Peck公式优化. 低温建筑技术. 2024(07): 148-151+156 . 百度学术
7.	孙常新，胡江凡，裴书锋，张玉洁，臧东升，黄文辉. 地震作用对砂土中土拱效应影响的模型试验研究. 应用基础与工程科学学报. 2024(05): 1394-1406 . 百度学术
8.	李文乾，黄高亮，朱潇昂，刘明洪，陈俞超，胡安峰. 基于HSS模型双线隧道上跨施工对既有地铁影响. 岩土工程技术. 2024(05): 560-565 . 百度学术
9.	李兴虎，何聪，陈忠章. 小直径盾构隧道工程概述. 市政技术. 2024(10): 85-92 . 百度学术
10.	刘德军，乔可可，商奇，左建平，段抗，董海洋，张成瑞. 复合地层大直径盾构隧道侧穿既有桩基扰动影响研究. 中国矿业大学学报. 2024(06): 1144-1156 . 百度学术
11.	冯上泽，丁祖德，郭永发，丁文云，刘正初，王畅羽. 下穿机场隧道悬臂掘进机开挖引起的地表沉降规律研究. 隧道建设(中英文). 2024(S2): 319-328 . 百度学术
12.	王旭伟. Peck修正公式在郑许市域铁路地表沉降预测中的应用. 山西建筑. 2023(01): 163-167 . 百度学术
13.	朱明. 盾构穿越不同地层的地表沉降规律及预测研究. 江苏建筑. 2023(02): 63-66+105 . 百度学术
14.	黄戡，孙逸玮，陈湘生，邓喜，刘汝宁，吴奇江. 基于FDM-DEM耦合的盾构开挖面前方土体三维位移特性研究. 中国公路学报. 2023(06): 190-206 . 百度学术
15.	姜越，高祥志，李彦霖，戎思达. 超大直径盾构隧道下穿交通枢纽地下结构变形特征与机理. 工业建筑. 2023(S1): 575-578 . 百度学术
16.	夏琴，商兆涛，匡星晨，张红彬，王佐才. 芜湖过江隧道掘进对长江大堤沉降影响研究. 工程与建设. 2023(05): 1402-1407 . 百度学术
17.	赵志国. 盾构隧道下穿高速铁路有砟轨道路基不均匀沉降分析. 城市轨道交通研究. 2023(S2): 75-78+99 . 百度学术
18.	刘新峰，曹玉锋，尹泽政. 正常固结土层盾构隧道开挖对既有桥梁桩基的影响. 广东公路交通. 2023(06): 53-59 . 百度学术
19.	应宏伟，姚言，王奎华，张昌桔. 双线平行顶管上跨地铁盾构隧道施工环境影响实测分析. 上海交通大学学报. 2023(12): 1639-1647 . 百度学术
20.	李江. 软土地区钢顶管施工引起的地表变形规律. 西安科技大学学报. 2023(06): 1149-1157 . 百度学术
21.	魏立新，杨春山，刘力英，傅栋梁. 海珠湾过江隧道总体设计方案研究. 隧道建设(中英文). 2023(S2): 359-368 . 百度学术
22.	江帅，朱勇，栗青，周辉，涂洪亮，杨凡杰. 隧道开挖地表沉降动态预测及影响因素分析. 岩土力学. 2022(01): 195-204 . 百度学术
23.	丁智，冯丛烈，仇硕，陆钊，范俊聪. 双线不同盾构机掘进地表变形及施工参数影响分析. 现代隧道技术. 2022(01): 183-194 . 百度学术
24.	孙逸玮，黄戡，李宇健. 既有桥桩对盾构引起地表沉降槽的变形影响. 交通科学与工程. 2022(01): 79-87 . 百度学术
25.	刘磊. 复合地层大直径泥水盾构施工对邻近管道的影响分析. 四川建筑. 2022(02): 164-167 . 百度学术
26.	罗兴财，周小文，张盛红. 盾构施工地层损失控制方法及实例. 土木工程与管理学报. 2022(02): 12-18 . 百度学术
27.	李晗，陈有亮，王良杰，吴东鹏，周飞帆. 盾构开挖冻结法加固隧道的地表沉降对比分析. 工程勘察. 2022(06): 13-19 . 百度学术
28.	赵旭伟. 软土地层盾构下穿铁路枢纽沉降规律及施工控制. 隧道与地下工程灾害防治. 2022(02): 59-65 . 百度学术
29.	刘琤玉，王炳龙，宋福贵，徐俊，韩学芳. 盾构施工对铁路大角度斜交框架桥的影响分析. 地下空间与工程学报. 2022(S1): 318-325 . 百度学术
30.	尹光明，傅鹤林，侯伟治，严石生. Peck公式参数的几种取值方法研究. 铁道科学与工程学报. 2022(07): 2015-2022 . 百度学术
31.	何占坤. 盾构隧道下穿既有车站桩筏基础影响分析及施工控制——以杭州地铁5号线盾构隧道下穿杭州南站站房工程为例. 隧道建设(中英文). 2022(S1): 222-231 . 百度学术
32.	郭根发. 上海某地铁隧道衬砌内力及沉降变形分析. 吉林水利. 2022(08): 29-33+54 . 百度学术
33.	王锦华. 盾构隧道下穿对机场跑道影响的随机有限元数值模拟分析. 施工技术(中英文). 2022(21): 23-29 . 百度学术
34.	赵小虹. 盾构隧道施工引起地层损失率的变化规律. 山西建筑. 2022(24): 168-172 . 百度学术
35.	王立玲. 软土地层盾构法下穿多层浅基民宅施工变形控制. 安徽建筑. 2021(04): 102-103 . 百度学术
36.	朱林. 近距平行双线盾构隧道地表沉降曲线分析. 水利与建筑工程学报. 2021(03): 208-213 . 百度学术
37.	吴锋波，郑卫强，齐剑峰，王晓明. 地铁双线盾构区间地表横向沉降槽参数分析. 地下空间与工程学报. 2021(05): 1653-1663 . 百度学术
38.	谢雄耀，杨昌植，王强，曾里，侯剑锋，周彪. 南京和燕路过江通道盾构穿越长江大堤的沉降分析及控制研究. 岩石力学与工程学报. 2021(S2): 3313-3322 . 百度学术
39.	黄式浩，狄宏规，王友文，姚琦钰. 管片厚度对大直径盾构隧道受力及变形的影响. 华东交通大学学报. 2020(01): 15-22 . 百度学术
40.	李涛，崔远，刘波，刘学成. 岩-土复合地层隧道施工引起建筑物沉降计算. 华中科技大学学报(自然科学版). 2020(03): 86-91 . 百度学术
41.	王先明，鲁茜茜，蹇蕴奇，阮雷，王士民. 盾构隧道下穿既有铁路路基及框架箱涵地表沉降分析. 路基工程. 2020(02): 119-124 . 百度学术
42.	吴锋波，金淮，杨歧焱，郑卫强. 北京地铁隧道地表横向沉降槽参数分析. 隧道建设(中英文). 2020(05): 660-671 . 百度学术
43.	赵雄. 盾构区间地层损失率等参数的研究. 工程勘察. 2020(11): 13-16 . 百度学术
44.	张国权. 地铁隧道盾构施工引发的地层位移影响研究. 山东煤炭科技. 2020(11): 178-179+182+186 . 百度学术
45.	包蓁. 特殊工况超大直径盾构施工地表变形分析研究——以上海市北横通道Ⅱ标盾构隧道施工为例. 现代隧道技术. 2020(S1): 394-403 . 百度学术
46.	甘晓露，俞建霖，龚晓南，朱旻，程康. 新建双线隧道下穿对既有盾构隧道影响研究. 岩石力学与工程学报. 2020(S2): 3586-3594 . 百度学术
47.	易顺，陈健，柯文汇，陈斌，刘府生，黄珏皓. 考虑小应变特性的软土盾构隧道地层变形分析. 岩土工程学报. 2020(S2): 172-178 . 本站查看
48.	胡振联，刘艺，姜梦林，夏辉. 西安地铁某区间盾构施工产生左、右线地面沉降显著差异原因浅析. 地下水. 2019(06): 81-84 . 百度学术
49.	张鹏远. 土压平衡盾构机下穿软弱浅覆土河床施工关键技术. 市政技术. 2019(06): 103-106 . 百度学术